Abstract
Biological networks, such as genetic regulatory networks, often contain positive and negative feedback loops that settle down to dynamically stable patterns. Identifying these patterns, the so-called attractors, can provide important insights for biologists to understand the molecular mechanisms underlying many coordinated cellular processes such as cellular division, differentiation, and homeostasis. Both synchronous and asynchronous Boolean networks have been used to simulate genetic regulatory networks and identify their attractors. The common methods of computing attractors are that start with a randomly selected initial state and finish with exhaustive search of the state space of a network. However, the time complexity of these methods grows exponentially with respect to the number and length of attractors. Here, we build two algorithms to achieve the computation of attractors in synchronous and asynchronous Boolean networks. For the synchronous scenario, combing with iterative methods and reduced order binary decision diagrams (ROBDD), we propose an improved algorithm to compute attractors. For another algorithm, the attractors of synchronous Boolean networks are utilized in asynchronous Boolean translation functions to derive attractors of asynchronous scenario. The proposed algorithms are implemented in a procedure called geneFAtt. Compared to existing tools such as genYsis, geneFAtt is significantly 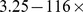 faster in computing attractors for empirical experimental systems.
faster in computing attractors for empirical experimental systems.
Availability
The software package is available at https://sites.google.com/site/desheng619/download.
Introduction
Biological networks contribute a mathematical analysis of connections found in ecological, evolutionary, and physiological studies, such as genetic regulatory networks [1]. Pursuit for the nature of these networks is the central problem for biologists [2]–[4]. In the past decades, a wide variety of research has focused on modeling genetic regulatory networks using Boolean networks and search for their attractors [5]–[10]. Computing the attractors in the Boolean networks is critical in understanding corresponding genetic regulatory networks and coordinated cellular processes such as cell cycle and cell differentiation in living organisms [6], [11]. In classical Boolean networks (CBNs), all nodes update their values at the same time called as synchronous Boolean network (SBNs). However, a criticism of CBNs as models of genetic regulatory networks is that genes do not update their values all simultaneously. To reflect this property of gene regulatory networks, Harvey and Bossomaier defined asynchronous Boolean networks (ABNs) where the random nodes were selected at each time and updated [12]. Since that, depending on the different update schemes, Boolean networks can be generally categorized into synchronous Boolean networks [7]–[9] and asynchronous Boolean networks [7], [10], [13], [14]. For the same update schemes with different priority of activator or inhibitor in genetic regulatory networks, classical equations [15], prior inhibitor equations [10] and a combination of these two [16] are three types of Boolean translation functions. Therefore, given a Boolean network, there will be 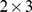 different methods to represent its Boolean translation function.
different methods to represent its Boolean translation function.
In a synchronous Boolean network, all genes update their values simultaneously at consecutive time points. Heidel et al. [17] and Farrow et al. [18] have proposed a scalar equation approach to compute attractors in SBNs. Based on the former, Zhao [19] has proven that the way of computing attractors in SBNs is a NP-complete problem. Dubrova et al. [20] have presented two tools - BooleNet and Bns - to compute attractors of SBNs. By contrast, in an asynchronous Boolean network, all genes update their values at different time points. Because each interaction between two nodes of a biological network follows distinct kinetics, it is generally thought that ABNs more realistically represent biological networks. However, due to the complexity of ABNs, the algorithms for computing network attractors are still mostly based on SBNs.
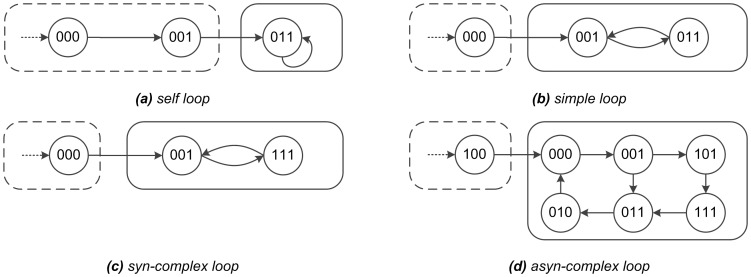
Previously, Garg et al. proposed a solution to compute the attractors in both SBNs and one class of ABNs [10]. First, they demonstrated that there were four types of attractors in a Boolean network: self loop, simple loop, syn-complex loop [or simple loop (type2)], and asyn-complex loop, shown as Fig. 1. The first two types (i.e. self loop and simple loop) were shared by SBNs and ABNs. But the latter two types, the syn-complex loop and the asyn-complex loop, were respectively found in SBNs and ABNs. Subsequently, they developed a series of algorithms which could be applied to compute the four types of attractors in a given Boolean network. Based on Garg’s contribution, Ay F et al. [16] gave a faster method to list the states of self loops and one outgoing edge. Both Garg et al. and Ay et al. used the ROBDD data structure to support their algorithms.
Figure 1. Attractors in Synchronous/Asynchronous Boolean Networks.
Figure 1. Diagrams of four types of attractors in Boolean networks. Attractors are outlined by slide boxes, and transient states by dashed boxes. (a) A self loop is a single state attractor. (b) A simple loop includes two or more states: each state is connected with only another state, and any two adjacent states differ from each other by only one bit. (c) A syn-complex loop is similar to simple loop, but any two adjacent states differ from each other by more than one bit. (d) A asyn-complex loop includes multiple interlinked states: each state is connected with more than one states, and there is only one bit difference between any two adjacent states. In Boolean networks, the self loop and simple loop can be identified in both synchronous Boolean networks and asynchronous Boolean networks. But the syn-complex loop only exists in the synchronous Boolean networks, and the asyn-complex loop only exists in asynchronous Boolean networks.
Here, we developed two algorithms to further improve the computation of complex attractors in both SBNs and ABNs. First, based on the works of Garg et al., and Ay et al., we show that iterative computing can be used to accelerate the identification of the attractors of SBNs. Second, we develop a method to compute the asyn-complex loop (complex loop) using syn-complex loop, which allows us to simplify the computation of attractors of complex loops in ABNs. We have a software package to accomplish our two algorithms which are used to locate attractors of Boolean dynamic networks (for both SBNs and ABNs), with significantly reduced time. The structure of this paper is organized as follows: Section 2 gives the methods to compute attractors and splits them into two subsections. Section 2.1 presents iterative computing attractors’ theory and its algorithms for SBNs. Section 2.2 proves a novel algorithm to locate attractors of ABNs from attractors of SBNs by asynchronous Boolean translation functions (ABTF). Section 3 tests feasibility and efficiency of our algorithm by several classical experimental benchmarks. Section 4 gives a conclusion and description of the future work.
Methods
This section gives two methods to compute attractors in both SBNs and ABNs. The first subsection presents iterative computing attractors’ theory and its algorithms for SBNs. The second subsection provides a novel algorithm to locate attractors of ABNs from attractors of SBNs by asynchronous Boolean translation functions.
Computing Attractors in Synchronous Boolean Networks
In a synchronous Boolean network, all nodes update their values simultaneously at consecutive time points [18]. In another word, at a given time  , each node has only one Boolean value: 1 (Active) or 0 (Inhibit) [19]. Then, the equation of a synchronous Boolean network with
, each node has only one Boolean value: 1 (Active) or 0 (Inhibit) [19]. Then, the equation of a synchronous Boolean network with  nodes is shown as Eq. 1 [19].
nodes is shown as Eq. 1 [19].
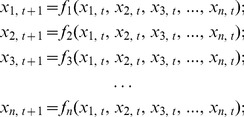 |
(1) |
where 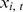 is a node in SBNs,
is a node in SBNs, 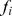 represents the Boolean function of node
represents the Boolean function of node 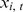 ,
, 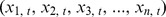 is a state in
is a state in 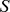 ,
, 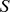 denotes the universal set with
denotes the universal set with 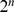 different states,
different states, 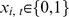 ,
, 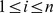 . It can be simplified as follows.
. It can be simplified as follows.
| (2) |
where 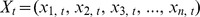 ,
,  ,
, 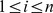 ,
, 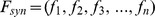 is the synchronous Boolean translation function (SBTF) from
is the synchronous Boolean translation function (SBTF) from 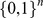 to
to 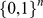 .
. 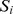 is a subset of
is a subset of 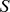 .
. 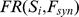 is a set of forward reachable states, which are all the states that can be reached from the states set
is a set of forward reachable states, which are all the states that can be reached from the states set 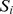 by
by 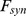 .
. 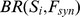 is a set of backward reachable states, which are all the states that can reach the states set
is a set of backward reachable states, which are all the states that can reach the states set 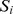 by
by 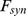 . All the states in
. All the states in 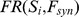 or
or 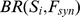 are different.
are different.
Definition 1
An Attractor [10]: It is the set of states 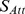 such that for all the states
such that for all the states
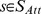 , their
, their
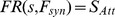 , shown as Fig. 1 (a),(b) and (c) in solid line boxes.
, shown as Fig. 1 (a),(b) and (c) in solid line boxes.
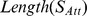 represents state number of attractor
represents state number of attractor
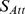 .
. 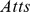 is the union set of all the different attractors
is the union set of all the different attractors
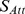 , that is,
, that is,
 .
.
Remark 1
Definition 1 defines an attractor of a synchronous Boolean network. So similarly, we can define an attractor of an asynchronous Boolean network, when using
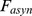 instead of
instead of
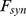 , shown as Fig. 1(a),(b) and (d) in solid line boxes.
, shown as Fig. 1(a),(b) and (d) in solid line boxes.
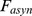 represents an asynchronous Boolean translation function which will be introduced in section. We also use
represents an asynchronous Boolean translation function which will be introduced in section. We also use
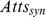 and
and
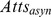 to represent all the attractors of a synchronous Boolean network and its asynchronous Boolean network, respectively. If a state
to represent all the attractors of a synchronous Boolean network and its asynchronous Boolean network, respectively. If a state
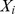 is in an attractor,
is in an attractor,
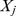 is one of its transient states, where
is one of its transient states, where
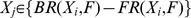 ,
, 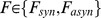 , shown as Fig. 1 in dotted line boxes.
, shown as Fig. 1 in dotted line boxes.
Because an attractor of a Boolean network is not known in advance, a common way to address this problem is setting a randomly chosen state as the initial state and exhaustively searching the entire state space. This approach has been successfully applied in several studies to compute the network attractors using empirically derived biological networks. However, the computational burden of this approach increases exponentially with respect to the number and length of attractors. Thus, it limits the application of this method for large biological networks.
Due to the recurrent nature of attractors, we reason that iterative computing algorithms can be applied on the Boolean translation functions of SBNs, like 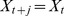 . An important implication is that identifying all attractors (Definition 1) does not require the computation of the entire state space. This suggests that we can use iterative computing to accelerate the identification of attractors in a given Boolean network. In the following, we present three theorems and their proof for iterative computation. Incorporating these theorems, an algorithm is demonstrated to compute attractors of SBNs.
. An important implication is that identifying all attractors (Definition 1) does not require the computation of the entire state space. This suggests that we can use iterative computing to accelerate the identification of attractors in a given Boolean network. In the following, we present three theorems and their proof for iterative computation. Incorporating these theorems, an algorithm is demonstrated to compute attractors of SBNs.
Theorems of computing attractors using iterative computing in synchronous boolean networks
According to Eq. 2, it is easily inferred that 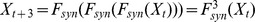 , where
, where 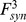 is synchronous Boolean translation function
is synchronous Boolean translation function 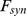 after iteratively computing
after iteratively computing 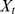 three times. Therefore, a simplified form of iterative computational equations is described as below.
three times. Therefore, a simplified form of iterative computational equations is described as below.
| (3) |
where 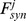 is
is 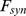 after
after 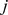 times iterative computing.
times iterative computing. 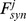 can compute the state
can compute the state 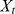 to state
to state 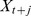 directly instead of
directly instead of  iterative computing steps by
iterative computing steps by 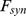 . If state
. If state 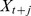 is same with state
is same with state 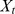 , that means state
, that means state 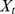 is in an attractor, which can be located as much as
is in an attractor, which can be located as much as 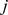 steps iterative computation.
steps iterative computation.
Definition 2
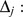 it represents the states that will return to themselves after
it represents the states that will return to themselves after
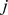 iterations, where
iterations, where
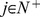 . This can be described by Eq. 4.
. This can be described by Eq. 4.
| (4) |
Definition 2 gives a simplified description of attractors, whose states could return to themselves after finite iterations. A shallow example can be supposed that, in a synchronous Boolean network, there are two attractors with length of 1 and 3 respectively. 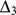 is the sum of the two attractors. Because the attractor whose length is 1 could also return to itself after 3 iterations. This feature can be proved by Theorem 1.
is the sum of the two attractors. Because the attractor whose length is 1 could also return to itself after 3 iterations. This feature can be proved by Theorem 1.
Theorem 1
For all 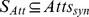 , if
, if 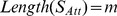 ,
, 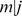 (
( is a factor of
is a factor of 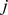 ), then,
), then, 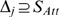 .
.
Proof
Let 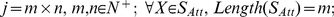
According to Theorem 1, a set of attractors, whose length is 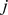 , can be located after
, can be located after 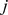 steps of iterative computing, shown as Eq. 5.
steps of iterative computing, shown as Eq. 5.
| (5) |
If a synchronous Boolean translation function  is same with
is same with 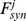 , that means all the states can return to themselves by less than
, that means all the states can return to themselves by less than 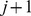 iterations. This is an important character to identify the numerous attractors in the SBNs, which has been proved by Theorem 2 and 3.
iterations. This is an important character to identify the numerous attractors in the SBNs, which has been proved by Theorem 2 and 3.
Theorem 2
Given a synchronous Boolean translation function  with
with  nodes, after
nodes, after  iterations, if
iterations, if 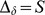 , the period of this synchronous Boolean network is
, the period of this synchronous Boolean network is  , where
, where 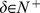 .
.
Proof
We need to prove
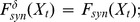
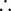 The period of this synchronous Boolean network is
The period of this synchronous Boolean network is
 .
.
Theorem 3
Given a synchronous translation function 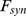 with
with  nodes, after
nodes, after  iterations, if
iterations, if 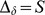 , all the states are in attractors.
, all the states are in attractors.
Proof
An improved algorithm to compute attractors in synchronous boolean networks
Combining iterative computing (Theorem 1, 2, 3 and Eq. 5) and the ROBDD data structure, we have developed Algorithm 1 to compute attractors in SBNs. The input of Algorithm 1 is the synchronous Boolean translation function 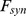 ; its output is states of attractors (
; its output is states of attractors (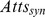 ) and number of all attractors (
) and number of all attractors (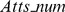 ). Specifically, Algorithm 1 starts with an initializing part, which initializes all the necessary variables. This is followed by a resolving part, which computes and deletes redundant attractors in a network. The resolving part further contains four components. The first component (Lines 12–13) will continue the next iterative computing and delete the visited attractors based on Theorem 1 and Eq. 5. The second component (Lines 15–20) judges whether synchronous Boolean translation functions are periodic or not, which has been proved by Theorem 2 and 3. The third component (Lines 22–27) verifies whether there will be a new attractor generated after one iteration. That is, if existing a new attractor, Algorithm 1 will add it into attractors (
). Specifically, Algorithm 1 starts with an initializing part, which initializes all the necessary variables. This is followed by a resolving part, which computes and deletes redundant attractors in a network. The resolving part further contains four components. The first component (Lines 12–13) will continue the next iterative computing and delete the visited attractors based on Theorem 1 and Eq. 5. The second component (Lines 15–20) judges whether synchronous Boolean translation functions are periodic or not, which has been proved by Theorem 2 and 3. The third component (Lines 22–27) verifies whether there will be a new attractor generated after one iteration. That is, if existing a new attractor, Algorithm 1 will add it into attractors (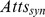 ). Meanwhile, it will also update the attractors’ number (
). Meanwhile, it will also update the attractors’ number (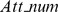 ) and continue the next iteration. If not, Algorithm 1 will go to the next iterative computing. The last component (Lines 11, 29) contains the fix-point condition. When satisfying this condition, it will output attractors and number of attractors. For more detailed information, please read the Algorithms 1.
) and continue the next iteration. If not, Algorithm 1 will go to the next iterative computing. The last component (Lines 11, 29) contains the fix-point condition. When satisfying this condition, it will output attractors and number of attractors. For more detailed information, please read the Algorithms 1.
In the initializing part, 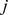 is the times of iterations.
is the times of iterations. 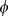 is an empty set.
is an empty set. 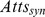 and
and 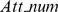 are the attractors and number of attractors, respectively.
are the attractors and number of attractors, respectively. 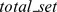 is the fix-point condition to judge whether the algorithm can be terminated or not.
is the fix-point condition to judge whether the algorithm can be terminated or not. 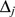 represents the states that will return to themselves after
represents the states that will return to themselves after 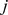 iterations by synchronous Boolean translation function
iterations by synchronous Boolean translation function 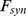 .
. 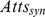 ,
, 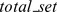 and
and 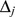 are ROBDD data structures. In the main resolving part,
are ROBDD data structures. In the main resolving part, 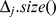 represents state number of
represents state number of 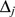 .
. 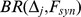 are all the states that can reach to
are all the states that can reach to 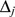 by synchronous Boolean translation function
by synchronous Boolean translation function 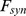 .
.
Algorithm 1 is different with Garg et al., which randomly picks up a state from state space and computes its forward reachable states to get an attractor. If you want to find out the attractors whose length is 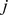 , it needs to exhaustively search the state space. However, our algorithm can easily compute the same attractors in
, it needs to exhaustively search the state space. However, our algorithm can easily compute the same attractors in 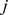 times iterative computing.
times iterative computing.
Algorithm 1: Iterative Computing Attractors on Synchronous Boolean Translation Function
Function:
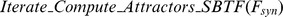 will compute all the attractors of SBTF iteratively;
will compute all the attractors of SBTF iteratively;
Input: The synchronous Boolean translation function 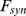 ;
;
Output: All attractors (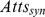 ) and number of attractors (
) and number of attractors (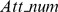 );
);
1 begin
2//Initializing part
3 begin
4
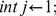
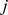 is times of iteration
is times of iteration
5
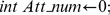 //
//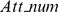 is the number of attractors
is the number of attractors
6
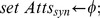
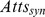 is a set of attractors
is a set of attractors
7
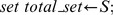
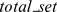 is a set of unvisited states
is a set of unvisited states
8
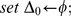 Initialize
Initialize  as empty set
as empty set
9 end
10 //Main resolving part
11
while
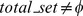 do
do
12
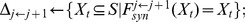 One iterative computing
One iterative computing
13
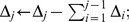 //Delete the visited attractors as Theorem 1 & Eq. 5
//Delete the visited attractors as Theorem 1 & Eq. 5
14 //This part is equivalence with Theorem 2 and 3
15 if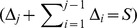 then
then
16 report attractors 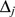 and its number
and its number 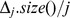
17
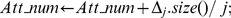 //Update the value of
//Update the value of
18
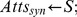 //All states are in attractors by Theorem 2 and 3
//All states are in attractors by Theorem 2 and 3
19
 Exit the while loop
Exit the while loop
20 end
21 //If existing unvisited attractors, record them
22 if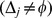 then
then
23 report attractors 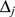 and its number
and its number 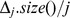
24
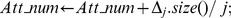 //Update the value of
//Update the value of 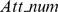
25
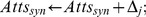 //Add the new attractors into
//Add the new attractors into 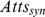
26
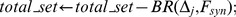 //
//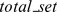 deletes the states can reach
deletes the states can reach 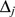
27 end.
28 end.
29 return
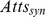 ,
, 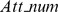 ;
;
30 end.
Computing Attractors in Asynchronous Boolean Networks
As mentioned earlier, SBNs and ABNs differ in nodes updating schemes of Boolean translation functions. Instead of updating values of all the nodes simultaneously, ABNs only allow some of the nodes to update their values at a time point. For this reason, the computing of attractors in ABNs is more time consuming. Especially, it needs more intermediate steps when there are more than one bit different between two states.
Analysis of attractors in asynchronous boolean networks
It is essential to give a simple description of types of attractors. As represented in Fig. 1, there are four types of attractors, self loop, simple loop, syn-complex loop and asyn-complex loop in both SBNs and ABNs. A self loop is a single state attractor, shown in Fig.1 (a). A simple loop includes two or more states, where every state is connected with only another state, and any two adjacent states differ from each other by only one bit, shown in Fig.1 (b). A syn-complex loop is similar to simple loop, but any two adjacent states differ from each other by more than one bit, shown in Fig.1 (c). A asyn-complex loop includes multiple interlinked states: every state is connected with more than one states, and there is only one bit different between any two adjacent states, shown in Fig.1 (d). Fig. 1 (a)(b)(c) and Fig. 1 (a)(b)(d) stand for the different types of attractors in SBNs and ABNs, respectively.
According to the properties of self loops and simple loops, they can easily be identified in SBNs, which also are same in ABNs. Interestingly, a closer examination of the structure of the syn-complex loops and asyn-complex loops suggests that every asyn-complex loop contains one syn-complex loop or some transient states. This suggests that it is possible to use syn-complex loop to easily locate the states in asyn-complex_loop by asynchronous Boolean translation functions.
One example is shown in Fig. 2, here 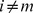 ,
, 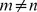 ,
, 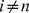 ,
, 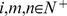 . Fig. 2(a) is an asynchronous attractor, where the current state and its next states are different by one bit. Suppose that the
. Fig. 2(a) is an asynchronous attractor, where the current state and its next states are different by one bit. Suppose that the 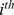 bit of the state
bit of the state 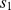 and
and 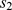 is different. If
is different. If 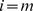 , it means that state
, it means that state 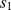 and
and 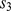 are the same. The situation is also true for
are the same. The situation is also true for  and
and  . If state
. If state  and
and 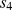 are different at the
are different at the 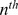 bit, then state
bit, then state 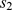 and
and 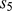 must differ at the
must differ at the 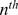 bit. Otherwise, state
bit. Otherwise, state 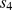 cannot reach state
cannot reach state 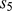 by changing one bit. When state
by changing one bit. When state 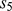 and
and 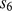 differ at the
differ at the 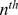 bit, state
bit, state 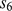 and
and 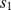 will be different at the
will be different at the 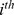 bit, and vice versa. Fig. 2(b) shows the corresponding synchronous attractor to Fig. 2(a). The difference is that state
bit, and vice versa. Fig. 2(b) shows the corresponding synchronous attractor to Fig. 2(a). The difference is that state 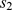 and
and 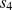 differ in the
differ in the 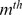 and bits simultaneously. Other relations are the same except for state
and bits simultaneously. Other relations are the same except for state 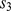 . Therefore, an asyn-complex_loop contains one syn-complex loop or some transient states. That means we can use syn-complex loop to easily locate the states in asyn-complex_loop by asynchronous Boolean translation function
. Therefore, an asyn-complex_loop contains one syn-complex loop or some transient states. That means we can use syn-complex loop to easily locate the states in asyn-complex_loop by asynchronous Boolean translation function 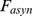 .
.
Figure 2. An Asynchronous Attractor to Synchronous Attractor.
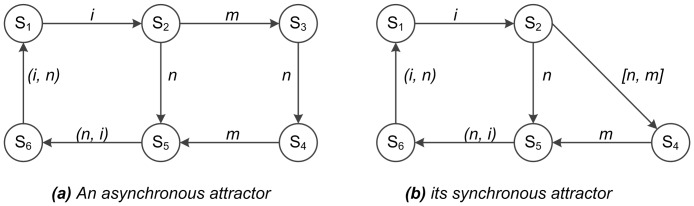
Figure 2. Diagrams of an attractor in asynchronous (a) and synchronous (b) Boolean networks. Each state is represented by a circle, and is designated as 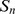 . The variable
. The variable  represents that the
represents that the 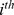 bit of the state
bit of the state 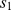 and
and 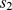 is different, which is also same as
is different, which is also same as  and
and  . The numbers
. The numbers 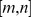 indicate that state
indicate that state 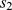 and
and 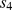 differ by the
differ by the 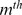 and
and 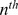 bits respectively. The
bits respectively. The 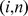 and
and 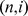 represents when state
represents when state 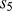 and
and 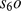 differ at the
differ at the 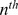 bit, state
bit, state 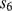 and
and 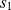 will be different at the
will be different at the 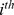 bit, and vice versa. The difference between the two representations (i.e. synchronous versus asynchronous) of the attractor is that
bit, and vice versa. The difference between the two representations (i.e. synchronous versus asynchronous) of the attractor is that 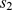 and
and 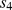 differ in the
differ in the 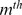 and
and 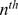 bits,
bits, 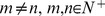 . That means we can use syn-complex loop to easily locate the states in asyn-complex_loop by asynchronous Boolean translation function
. That means we can use syn-complex loop to easily locate the states in asyn-complex_loop by asynchronous Boolean translation function 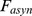 .
.
An algorithm to compute attractors in asynchronous boolean networks
An important implication of the above analysis is that the attractors of the ABNs can be derived from the attractors of the SBNs using synchronous and asynchronous Boolean translation functions. Therefore, we use attractors computed by Algorithm 1 in SBNs as the basis input for the new algorithm (Algorithm 2) to compute attractors of ABNs.
Specifically, Algorithm 2 can be divided into three parts: initializing part (Lines 3–6), main resolving part (Lines 8–41) and checking unvisited states part (Lines 44–52). The initializing part also initializes all necessary variables in Algorithm 2. The main resolving part also can be split into five components. The first component (Lines 11–15) means 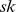 is a self loop. The second component (Lines 18–21) means
is a self loop. The second component (Lines 18–21) means 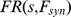 is a simple loop. The third component (Lines 24–29) means
is a simple loop. The third component (Lines 24–29) means 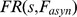 is an unvisited asyn-complex loop and
is an unvisited asyn-complex loop and 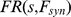 is an unvisited syn-complex loop. The forth component (Lines 32–34) means
is an unvisited syn-complex loop. The forth component (Lines 32–34) means 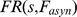 is a visited asyn-complex loop and
is a visited asyn-complex loop and 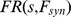 is an unvisited syn-complex loop. The fifth component (Lines 37–40) means
is an unvisited syn-complex loop. The fifth component (Lines 37–40) means 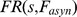 is the set of transient states and
is the set of transient states and 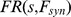 is an unvisited syn-complex loop. After the main resolving part, if there exists unvisited states, Algorithm 2 will go to the checking unvisited states part. This part will check the unvisited states and report the left asyn-complex loops. For more detailed information, please read the Algorithms 2.
is an unvisited syn-complex loop. After the main resolving part, if there exists unvisited states, Algorithm 2 will go to the checking unvisited states part. This part will check the unvisited states and report the left asyn-complex loops. For more detailed information, please read the Algorithms 2.
Furthermore, in the initializing part,  is a state,
is a state,  is an empty set,
is an empty set,  is a set of recording unvisited states by
is a set of recording unvisited states by 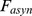 ,
, 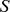 is the universal set. In the main resolving part and checking unvisited part,
is the universal set. In the main resolving part and checking unvisited part, 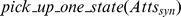 represents picking up anyone state from attractors
represents picking up anyone state from attractors 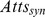 of SBNs.
of SBNs. 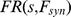 and
and 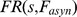 are the reachable states from
are the reachable states from  by synchronous Boolean translation function
by synchronous Boolean translation function 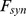 and asynchronous Boolean translation function
and asynchronous Boolean translation function 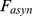 , respectively.
, respectively. 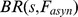 is the reachable states to
is the reachable states to  by asynchronous Boolean translation function
by asynchronous Boolean translation function 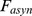 . We note that, our approach of identifying attractors is totaly different with Gary et al. and Ay et al. It is more efficient to compute the asyn-complex loop because it can easily locate the states in
. We note that, our approach of identifying attractors is totaly different with Gary et al. and Ay et al. It is more efficient to compute the asyn-complex loop because it can easily locate the states in 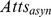 .
.
Algorithm 2: Compute and classify Four Types Attractors
Function.
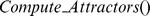 computes and classfies attractors as four types, shown in Fig. 1;
computes and classfies attractors as four types, shown in Fig. 1;
Input. Attractors of SBN(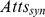 ), SBTF(
), SBTF(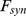 ) and ABTF(
) and ABTF(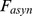 );
);
Output. Four types attractors (a)(b)(c)(d) of SBTF and ABTF shown as Fig. 1;
1 begin
2 // Initializing part
3 begin
4
 //
//  is a state
is a state
5
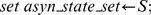 /
/ 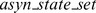 is a set of unvisited states by
is a set of unvisited states by 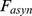
6 end
7 // Main resolving part
8
while
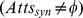 do
do
9
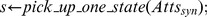 //
//  is any one state in
is any one state in 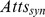
10 //  is a self loop, shown as Fig. 1(a)
is a self loop, shown as Fig. 1(a)
11
if (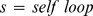 ) then
) then
12 report s is a self loop state
13
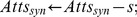 // Delete
// Delete  from
from 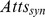
14
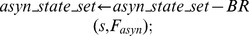 // Delete reachable states to
// Delete reachable states to 
15 end
16 // 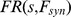 is a simple loop, shown as Fig. 1(b)
is a simple loop, shown as Fig. 1(b)
17 eles if (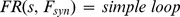 ) then
) then
18
report FR(s, 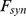 ) is the simple loop
then
) is the simple loop
then
19
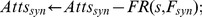 // Delete the simple loop from
// Delete the simple loop from 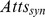
20
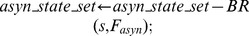 //Delete reachable states to
//Delete reachable states to 
21 end
22 // 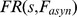 is an unvisited asyn-complex loop, shown as Fig. 1(d)
is an unvisited asyn-complex loop, shown as Fig. 1(d)
23
eles if
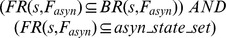 then
then
24
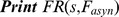 is a asyn-complex loop
is a asyn-complex loop
25 // 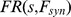 is a syn-complex loop, shown as Fig. 1(c)
is a syn-complex loop, shown as Fig. 1(c)
26
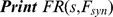 is a syn-complex loop
is a syn-complex loop
27
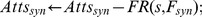 // Delete the syn-complex loop from
// Delete the syn-complex loop from 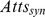
28
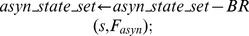 // Delete reachable states to
// Delete reachable states to 
29 end
30 // 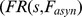 is an visited asyn-complex loop
is an visited asyn-complex loop
31
eles if
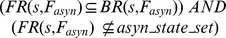 then
then
32
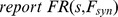 is a syn-complex loop
is a syn-complex loop
33
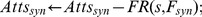 // Delete the syn-complex loop from
// Delete the syn-complex loop from 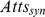
34 end
35 // 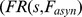 are the transient states
are the transient states
36 else
37
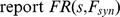 is a syn-complex loop
is a syn-complex loop
38
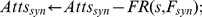 // Delete the syn-complex loop from
// Delete the syn-complex loop from 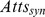
39
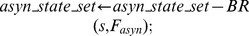 // Delete reachable states to
// Delete reachable states to 
40 end
41 end
42 // Checking unvisited states
43
while
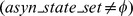 do
do
44
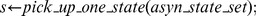 //
//  is a state in
is a state in 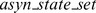
45
if
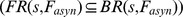 then
then
46
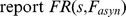 is a asyn-complex loop;
is a asyn-complex loop;
47
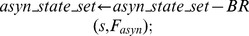 // Delete reachable states to
// Delete reachable states to 
48 end.
49 else.
50
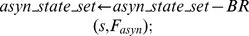 // Delete reachable states to
// Delete reachable states to  .
.
51 end.
52 end.
53 end.
Results and Discussion
We have implemented our methodology in a software package called geneFAtt, which is based on a ROBDD data structure named BuDDy [21]. In this package, there are two parts, source code and benchmark. The source code part implements functions of Algorithm 1 (iterative computing attractors in synchronous Boolean networks) and Algorithm 2 (computing and classifying attractors as four types of synchronous Boolean networks and asynchronous Boolean networks). Algorithm 1 computes the attractors of SBNs, which are then used as the input of Algorithm 2 to classify the attractors of ABNs. Because the self loop (Fig. 1(a)) and simple loop (Fig. 1(b)) of SBNs are same with its corresponding type of attractors of ABNs, respectively. We can easily use syn-complex loops (Fig. 1(c)) to locate the asyn-complex loops (Fig. 1(d)) by the asynchronous Boolean translation functions. The benchmark part includes five biological networks, Mammalian Cell [7], T-helper [22], Dendritic Cell [10], T-cell Receptor [23], and Protein-ex [17]. We ran geneFAtt and genYsis [10] with the five synchronous/asynchronous biological models and have compared their running results.
As shown in Table 1, the first four biological networks, Mammalian Cell [7], T-helper [22], Dendritic Cell [10] and T-cell Receptor [23] have been studied in [10]. Protein-ex is an extended case from Heidel et al. [17]. It also represents a kind of biological networks that all the states are in attractors. Because we adopt to the same methods of modeling the SBNs and ABNs to setup the synchronous and asynchronous Boolean translation functions refereed to Garg et al. Meanwhile, using the same inputs, geneFAtt can obtain the same attractors as those by genYsis [10] shown in Table 1, which suggests that our algorithms are valid for the analysis of biological networks.
Table 1. Characters of Five Different Biological Networks.
| Benchmark | Attractors’ Number | |||
| Self Loop | Simple Loop | Syn-complex Loop | Asyn-complex Loop | |
| Mammalian Cell | 1 | 0 | 1 | 1 |
| T-helper | 3 | 0 | 0 | 0 |
| Dendritic Cell | 0 | 1 | 0 | 0 |
| T-cell Receptor | 1 | 0 | 9 | 7 |
| Protein-ex | 2 | 0 | 4114 | 0 |
With the same validity, geneFAtt shows more efficient and feasible compared to genYsis. Table 2 gives the running time and running time efficiency ratio (RTER, Eq. 6) of the five biological networks which have been produced by the two procedures genYsis and geneFAtt. 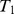 and
and 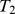 represent the running time on every biological network of the two procedures genYsis and geneFAtt, respectively. All experiments are performed on an Intel® Core
represent the running time on every biological network of the two procedures genYsis and geneFAtt, respectively. All experiments are performed on an Intel® Core CPU 4300 1.80 GHz with 2GB memory and a Ubuntu 9.04 Linux server. Importantly, we note that the running time of geneFAtt is much more shorter than genYsis
[10]. Specifically, compared with genYsis, geneFAtt improves the running time of Mammalian Cell
[7], T-helper
[22], Dendritic Cell
[10], T-cell Receptor
[23], and Protein-ex
[17] by 3.25, 8.19, 116.00, 23.48, and 77.05 times, respectively. Remarkable, geneFAtt improves the running time of the Dendritic Cell ([10]) gene network by a striking 116.00 times.
CPU 4300 1.80 GHz with 2GB memory and a Ubuntu 9.04 Linux server. Importantly, we note that the running time of geneFAtt is much more shorter than genYsis
[10]. Specifically, compared with genYsis, geneFAtt improves the running time of Mammalian Cell
[7], T-helper
[22], Dendritic Cell
[10], T-cell Receptor
[23], and Protein-ex
[17] by 3.25, 8.19, 116.00, 23.48, and 77.05 times, respectively. Remarkable, geneFAtt improves the running time of the Dendritic Cell ([10]) gene network by a striking 116.00 times.
| (6) |
Table 2. Performance Comparison between genYsis [10] and geneFAtt.
| Benchmark | Time (sec) | RTER | |
| genYsis [10] | geneFAtt | ||
| Mammalian Cell | 0.102 | 0.024 | 3.25× |
| T-helper | 0.193 | 0.021 | 8.19× |
| Dendritic Cell | 0.351 | 0.003 | 116.00× |
| T-cell Receptor | 330.643 | 13.506 | 23.48× |
| Protein-ex | 86.162 | 1.104 | 77.05× |
Conclusions
This paper has addressed a method to compute attractors in SBNs and ABNs. We have developed a new iterative computing algorithm to identify the attractors 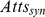 of SBNs. Meanwhile, another computing and classifying algorithm has been proposed to locate the attractors of ABNs rapidly. Our approaches give a significant acceleration of computing and locating attractors in biological networks. It is a big challenge that how to identify attractors in the large biological networks. Based on above research, it is expected that we can find a pathway to resolve this problem from the modeling methods of biological networks.
of SBNs. Meanwhile, another computing and classifying algorithm has been proposed to locate the attractors of ABNs rapidly. Our approaches give a significant acceleration of computing and locating attractors in biological networks. It is a big challenge that how to identify attractors in the large biological networks. Based on above research, it is expected that we can find a pathway to resolve this problem from the modeling methods of biological networks.
Acknowledgments
The authors also would like to express their sincere thanks to Dr. Hsien Hang Shieh and Mr. Rahul Krishnan for their help on the structure of this paper.
Funding Statement
This work was supported by the National Natural Science Foundation of China under Grant (No. 60973016) and 973 Foundation (No. 2010CB328004). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Proulx S, Promislow D, Phillips P (2005) Network thinking in ecology and evolution. Trends in Ecology & Evolution 20: 345–353. [DOI] [PubMed] [Google Scholar]
- 2. Basso K, Margolin A, Stolovitzky G, Klein U, Dalla-Favera R, et al. (2005) Reverse engineering of regulatory networks in human b cells. Nature genetics 37: 382–390. [DOI] [PubMed] [Google Scholar]
- 3. Margolin A, Nemenman I, Basso K, Wiggins C, Stolovitzky G, et al. (2006) Aracne: an algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC bioinformatics 7: S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Hirose O, Yoshida R, Imoto S, Yamaguchi R, Higuchi T, et al. (2008) Statistical inference of transcriptional module-based gene networks from time course gene expression profiles by using state space models. Bioinformatics 24: 932–942. [DOI] [PubMed] [Google Scholar]
- 5.Glass L (1985). Boolean and continuous models for the generation of biological rhythms.
- 6.Kauffman S (1995) At home in the universe. Oxford University Press New York.
- 7. Fauré A, Naldi A, Chaouiya C, Thieffry D (2006) Dynamical analysis of a generic boolean model for the control of the mammalian cell cycle. Bioinformatics 22: e124. [DOI] [PubMed] [Google Scholar]
- 8. Remy E, Ruet P, Mendoza L, Thieffry D, Chaouiya C (2006) From logical regulatory graphs to standard petri nets: dynamical roles and functionality of feedback circuits. Transactions on Computational Systems Biology VII 56–72. [Google Scholar]
- 9.Naldi A, Thieffry D, Chaouiya C (2007) Decision diagrams for the representation and analysis of logical models of genetic networks. In: Proceedings of the 2007 international conference on Computational methods in systems biology. Springer-Verlag, 233–247.
- 10. Garg A, Di Cara A, Xenarios I, Mendoza L, De Micheli G (2008) Synchronous versus asynchronous modeling of gene regulatory networks. Bioinformatics 24: 1917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Davidich M, Bornholdt S (2008) Boolean network model predicts cell cycle sequence of fission yeast. PLoS One 3: e1672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Harvey I, Bossomaier T (1997) Time out of joint: Attractors in asynchronous random boolean networks. In: Proceedings of the Fourth European Conference on Artificial Life. MIT Press, Cambridge, 67–75.
- 13.Devloo Vea (2003) Identification of all steady states in large biological systems by logical anslysis. Bull Math Biol : 1025–1051. [DOI] [PubMed]
- 14. Thomas R (1991) Regulatory networks seen as asynchronous automata: a logical description. Journal of Theoretical Biology 153: 1–23. [Google Scholar]
- 15. Li F, Long T, Lu Y, Ouyang Q, Tang C (2004) The yeast cell-cycle network is robustly designed. Proceedings of the National Academy of Sciences of the United States of America 101: 4781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Ay F, Xu F, Kahveci T (2009) Scalable steady state analysis of boolean biological regulatory networks. PloS one 4: e7992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Heidel J, Maloney J, Farrow C, Rogers J (2003) Finding cycles in synchronous boolean networks with applications to biochemical systems. International Journal of Bifurcation and Chaos in Applied Sciences and Engineering 13: 535–552. [Google Scholar]
- 18. Farrow C, Heidel J, Maloney J, Rogers J (2004) Scalar equations for synchronous boolean networks with biological applications. IEEE Transactions on Neural Networks 15: 348–354. [DOI] [PubMed] [Google Scholar]
- 19. Zhao Q (2005) A remark on “scalar equations for synchronous boolean networks with biological applications by C. Farrow, J. Heidel, J. Maloney, and J. Rogers”. IEEE Transactions on Neural Networks 16: 1715–1716. [DOI] [PubMed] [Google Scholar]
- 20.Dubrova E, Teslenko M, Martinelli A (2005) Kauffman networks: Analysis and applications. In: Proceedings of the 2005 IEEE/ACM International conference on Computer-aided design. IEEE Computer Society, 479–484.
- 21.Lind-Nielsen J (2000). Bdd package buddy, v. 1.9, august 2000, http://www.itu.dk/research/buddy/index.html.
- 22.Luis M, Ioannis X (2006) A method for the generation of standardized qualitative dynamical systems of regulatory networks. Theoretical Biology and Medical Modelling 3. [DOI] [PMC free article] [PubMed]
- 23. Klamt S, Saez-Rodriguez J, Lindquist J, Simeoni L, Gilles E (2006) A methodology for the structural and functional analysis of signaling and regulatory networks. BMC bioinformatics 7: 56. [DOI] [PMC free article] [PubMed] [Google Scholar]