Abstract
We analyze the entire publication database of the American Physical Society generating longitudinal (50 years) citation networks geolocalized at the level of single urban areas. We define the knowledge diffusion proxy, and scientific production ranking algorithms to capture the spatio-temporal dynamics of Physics knowledge worldwide. By using the knowledge diffusion proxy we identify the key cities in the production and consumption of knowledge in Physics as a function of time. The results from the scientific production ranking algorithm allow us to characterize the top cities for scholarly research in Physics. Although we focus on a single dataset concerning a specific field, the methodology presented here opens the path to comparative studies of the dynamics of knowledge across disciplines and research areas.
Over the last decade, the digitalization of publication datasets has propelled bibliographic studies allowing for the first time access to the geospatial distribution of millions of publications, and citations at different granularities1,2,3,4,5,6,7,8 (see Ref. 9 for a review). More precisely, authors' name, affiliations, addresses, and references can be aggregated at different scales, and used to characterize publications and citations patterns of single papers10,11, journals12,13, authors14,15,16, institutions17, cities18, or countries19. The sheer size of the datasets allows also system level analysis on research production and consumption20, migration of authors21,22, and change in production in several regions of the world as a function of time5,6, just to name a few examples. At the same time those analyses have spurred an intense research activity aimed at defining metrics able to capture the importance/ranking of authors, institutions, or even entire countries14,15,17,23,24,25,26,27,28,29. Whereas such large datasets are extremely useful in understanding scholarly networks and in charting the creation of knowledge, they are also pointing out the limits of our conceptual and modeling frameworks30 and call for a deeper understanding of the dynamics ruling the diffusion and fruition of knowledge across the the social and geographical space.
In this paper we study citation patterns of articles published in the American Physical Society (APS) journals in a fifty-year time interval (1960-2009)31. Although in the early years of this period the dataset was obviously biased toward the scholarly activity within the USA, in the last twenty years only about 35% of the papers are produced in the USA. The same amount of production has been observed in databases that include multiple journals, and disciplines7,19. Indeed the journals of the APS are considered worldwide as reference publication venues that well represent the international research activity in Physics. Furthermore this dataset does not bundle different disciplines and publication languages, providing a homogeneous dataset concerning Physics scholarly research. For each paper we geolocalize the institutions contained in the authors' affiliations. In this way we are able to associate each paper in the database with specific urban areas. This defines a time resolved, geolocalized citation network including 2,307 cities around the world engaged in the production of scholarly work in the area of Physics. Following previous works8,17 we assume that the number of given or received citations is a proxy of knowledge consumption or production, respectively. More precisely, we assume that citations are the currency traded between parties in the knowledge exchange. Nodes that receive citations export their knowledge to others. Nodes that cite other works, import knowledge from others. According to this assumption we classify nodes considering the unbalance in their trade. Knowledge producers are nodes that are cited (export) more than they cite (import). On the contrary, we label as consumers nodes that cite (import) more than they are cited (export). Using this classification, we define the knowledge diffusion proxy algorithm to explore how scientific knowledge flows from producers to consumers. This tool explicitly assumes a systemic perspective of knowledge diffusion, highlighting the global structure of scientific production and consumption in Physics.
The temporal analysis reveals interesting patterns and the progressive delocalization of knowledge producers. In particular, we find that in the last twenty years the geographical distribution of knowledge production has drastically changed. A paramount example is the transition in the USA from a knowledge production localized around major urban areas in the east and west coast to a broad geographical distribution where a significant part of the knowledge production is now occurring also in the midwestern and southern states in the USA. Analogously, we observe the early 90s dominance of UK and Northern Europe to subside to an increase of production from France, Italy and several regions of Spain. Interestingly, the last decade shows that several of China's urban areas are emerging as the largest knowledge consumers worldwide. The reasons underlying this phenomenon may be related to the significant growth of the economy and the research/development compartment in China in the early 21th century32. This positive stimulus, pushed up also the scientific consumption with a large number of paper citing work from other world areas. Indeed, the increase of publications is associated to an increase of the citations unbalance, moving China to the top rank as consumers since the recent influx of its new papers has not yet had the time to accumulate citations.
Although the knowledge diffusion proxy provides a measure of knowledge production and consumption, it may be inadequate in providing a rank of the most authoritative cities for Physics research. Indeed, a key issue in appropriately ranking the knowledge production, is that not all citations have the same weight. Citations coming from authoritative nodes are heavier than others coming from less important nodes, thus defining a recursive diffusion of ranking of nodes in the citation network. In order to include this element in the ranking of cities we propose the scientific production ranking algorithm. This tool, inspired by the PageRank33, allows us to define the rank of each node, as function of time, going beyond the knowledge diffusion proxy or simple local measures such as citation counts or h-index14. In this algorithm the importance of each node diffuses through the citation links. The rank of a node is determined by the rank of the nodes that cite it, recursively, thus implicitly weighting differently citations from highly (lowly) ranked nodes. Also in this case we observe noticeable changes in the ranking of cities along the years. For instance the presence of both European and Asian cities in the top 100 list increases by 50% in the last 20 years. This findings suggest that the Internet, digitalization and accessibility of publications are creating a more levelled playing field where the dominance of specific area of the world is being progressively eroded to the advantage of a more widespread and complex knowledge production and consumption dynamic.
Results
We focus our analysis on the APS dataset31. It contains all the papers published by the APS from 1893 to 2009. We consider only the last 50 years due to the incomplete geolocalization information available for the early years. During this period, the large majority of indexed papers, 97.47%, contain complete information such as authors name, journal of publication, day of publication, list of affiliations and list of citations to other articles published in APS journals. We geolocalized 96.97% of papers at urban area level with an accuracy of 98.5%. We refer the reader to the Methods section and to the Supplementary Information (SI) for the detailed description of the dataset and the techniques developed to geolocalize the affiliations.
In total, only 43% of papers has been produced inside the USA. Interestingly, over time this fraction has decreased. For example, in the 60's it was 85.59%, while in the last 10 years decreased to just 36.67%. While one might assume that the APS dataset is biased toward the USA scientific community, the percentage of publications contributed by the USA in APS journals after 1990 is almost the same as in other publication datasets7,19. These alternative datasets contain journals published all over the world and mix different scientific disciplines. This supports the idea that the APS journals are now attracting the worldwide physics scientific community independently of nationality, and fairly represent the world production and consumption of Physics. It is not possible to provide quantitative analysis of possible nationality bias and disentangle it by an actual change of the dynamic of knowledge production. For this reason, and in order to minimize any bias in the analysis we focus our analysis in the last 20 years of data.
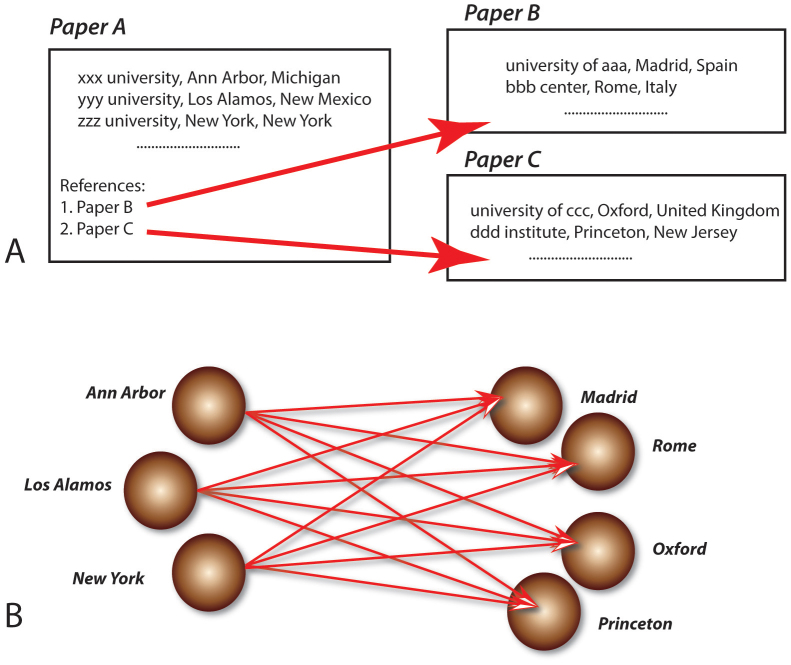
In order to construct the geolocalized citation network we consider nodes (urban areas) and directed links representing the presence of citations from a paper with affiliation in one urban area to a paper with affiliation in another urban area. For example, if a paper written in node i cites one paper written in node j there is an link from i to j, i.e., j receives a citation from i and i sends a citation to j. Each paper may have multiple affiliations and therefore citations have to be proportionally distributed between all the nodes of the papers. For this reason we weight each link in order to take into account the presence of multiple affiliations and multiple citations. In a given time window, the total number of citations for papers written in j received from papers written in i, is the weight of the link i → j, and the total number of citations for those paper written in j sent to the papers written in k is the weight of the link j → k. For instance, if in a time window t, there is one paper written in node j, which cite two papers written in node k and was cited by three papers written in node i, then wjk = 2, wij = 3, and we add all such weights for each paper written in that node j and obtain the weights for links. For papers written in multiple cities, say j1, j2, the weight will be counted equally. The time window we use in this manuscript is one year. We show an example of the network construction in Figure 1.
Figure 1. Projecting a paper citation relationship into a city-to-city citation network.
(A) Paper A written by authors from Ann Arbor, Los Alamos and New York cites one paper B written by authors from Rome and Madrid and another paper C from Oxford and Princeton. (B) In a city-to-city citation network, directed links from Ann Arbor to Madrid, Rome, Oxford and Princeton are generated, and similarly Los Alamos and New York are connected to the above four cited cities.
In order to define main actors in the production and consumption of Physics, we consider citations as a currency of trade. This analogy allows us to immediately grasp the meaning and distinction between producers and consumers of scientific knowledge. Nodes that receive citations export their knowledge to the citing nodes. Instead, nodes that cite, papers produced from other nodes of the network, import knowledge from the cited nodes. Measuring the unbalance trade between citations, we define producers as cities that export more than they import, and consumers as cities that import more than they export. More precisely, we can measure the total knowledge imported by each urban area as 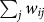 and the total export as
and the total export as 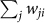 in a given year. Those measures however acquire specific meaning when considered relatively to the total trade of physics knowledge worldwide in the same year; i.e. the total number of citations worldwide
in a given year. Those measures however acquire specific meaning when considered relatively to the total trade of physics knowledge worldwide in the same year; i.e. the total number of citations worldwide 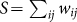 . The relative trade unbalance of each urban area i is then:
. The relative trade unbalance of each urban area i is then:
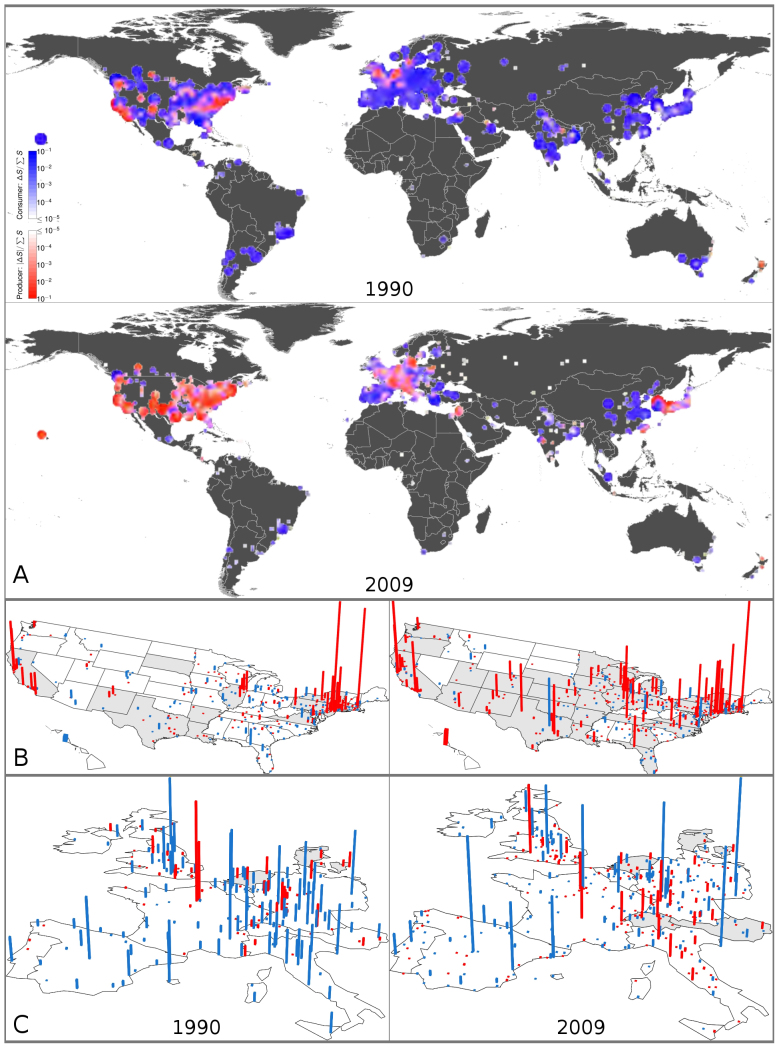
A negative or positive value of this quantity indicates if the urban area i is consumer or producer, respectively. In Figure 2-A we show the worldwide geographical distribution of producer (red) and consumer (blue) urban areas for the 1990 and 2009. Interestingly, during the 90s the production of Physics knowledge was highly localized in a few cities in the eastern and western coasts of the USA and in a few areas of Great Britain and Northern Europe. In 2009 the picture is completely different with many producer cities in central and southern parts of the USA, Europe and Japan. It is interesting to note that despite the fraction of papers produced in the USA is generally decreasing or stable, many more cities in the USA acquire the status of knowledge producers. This implies that the quality of knowledge production from the USA is increasing and thus attracting more citations. This makes it clear that the knowledge produced by an urban area can not be considered to be measured only by the raw number of papers. Citations are a more appropriate proxy that encodes the value of the products. They serve as an approximation of the actual flow of knowledge. The Figure 2-A also makes it clear that cities in China are playing the role of major consumers in both 1990 and 2009. We also observe that cities in other countries like Russia and India consumed less in 2009 than 1990. In other words, in 2009 both the production and consumption of knowledge are less concentrated on specific places and generally spread more evenly geographically. In order to provide visual support to this conclusion we show in Figure 2-B the geographical distribution of producers and consumers inside the USA. From the two maps it is evident the drift of knowledge production from the two coastal areas in the USA to the midwest, central and southern states. Similarly, in Figure 2-C we plot the same information for western Europe. In 1990 only a few urban areas in Germany and France were clearly producers. By 2009 this dominance has been consistently eroded by Italy, Spain and a more widespread geographical distribution of producers in France, Germany and UK.
Figure 2. Spatial distributions of scientific producers and consumers of Physics.
The geospatial distribution of scientific producer and consumer cities. (A) The world map of producers and consumers at the city level in 1990 (top) and 2009 (bottom). A producer city, of which the relative unbalance ΔSi > 0, is coloured in red scale. A consumer with the relative unbalance ΔSi < 0 is coloured in blue scale. The darkness of colour is proportional to the absolute value of unbalance. The larger the absolute value of unbalance, the darker the colour. (B) The map of producer and consumer cities in the continental United States in 1990 (left) and 2009 (right). (C) The map of producer and consumer cities in selected European countries in 1990 (left) and 2009 (right). In (B) and (C), a producer city is marked with a red bar, while a consumer city is marked with a blue bar. The height of each bar is scaled with |ΔSi|. Note that in (C) the height of bars is not scaled with the height in (B) for visibility. Maps in panel (A) are created by using ArcGIS 47, and maps in panel (B) and (C) are created by using R48.
Knowledge diffusion proxy
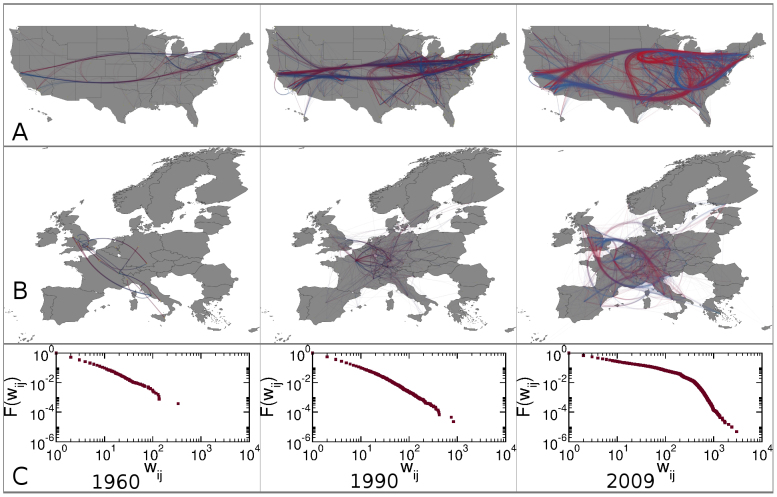
The definition of producers and consumers is based on a local measure, that does not allow to capture all possible correlations and bounds between nodes that are not directly connected. This might result in a partial view and description of the system, especially when connectivity patterns are complex34,35,36,37,38. Interestingly, a close analysis of each citation network, see Figure 3, clearly shows that citation patterns have indeed all the hallmarks of complex systems34,35,36,37,38, especially in the last two decades. The system is self-organized, there is not a central authority that assigns citations and papers to cities, there is not a blueprint of system's interactions, and as clearly shown from Figure 3-C the statistical characteristics of the system are described by heavy-tailed distributions34,35,36,37,38. Not surprisingly, the level of complexity of the system has increased with time. In Figure 3-A we plot the most statistically significant connections of the citation network between cities inside the USA in 1960, 1990 and 2009. We filter links by using the backbone extraction algorithm39 which preserves the relevant connections of weighted networks while removing the least statistically significant ones. We visualize each filtered network by using a bundled representation of links40. The direction of each weighted link goes from blue (citing) to red (cited). Similarly, in Figure 3-B, we visualize the most significant links between cities in Europe (European Union's 27 countries, as well as Switzerland and Norway). It is clear from Figure 3-A that in 1960 the citation patterns inside the USA were limited to a few cities, and in Europe only a few cities were connected. Instead, in 1990 and 2009 we register an increase in the interactions among a larger number of cities. The observed temporal trend is well known and valid not just for Physics41. Among many factors that have been advocated to explain this tendency we find the increase of the research system and the advance in technology that make collaboration and publishing easier20,42,43,44.
Figure 3. Networks structure.
The network structures of city-to-city citation networks. (A) The backbones (α = 0.1) of the citation networks at the city level within the United States in 1960, 1990, 2009 (from the left to right). (B) The backbones (α = 1, 0.1, 0.1 from left to right) of the citation networks at the city level within the European Union 27 countries as well as Switzerland and Norway in 1960, 1990, 2009 (from the left to right). In (A) and (B), the color shows the direction of links: if node i cites node j there is a link starting with blue and ending with red. (C) The cumulative distribution function of the link weights Fw(wij) = P(w ≥ wij) for the city-to-city citation networks in year 1960, 1990 and 2009 (from left to right). The maps of networks in (A) and (B) were created using JFlowMap40.
In order to explicitly consider the complex flow of citations between producers and consumers, we propose the knowledge diffusion proxy algorithm (see Methods section for the formal definition). In this algorithm, producers inject citations in the system that flow along the edges of the network to finally reach consumer cities where the injected citations are finally absorbed. The algorithm allows charting the diffusion of knowledge, going beyond local measures. The entire topology of the networks is explored uncovering nontrivial correlations induced by global citation patterns. For instance, knowledge produced in a city may be consumed by another producer that in turn produces knowledge for other cities who are consumers. This points out that the actual consumer of knowledge is not just signalled by the unbalance of citations but in the overall topology of the production and consumption of knowledge in the whole network. Indeed, the final consumer of each injected citation may not be directly connected with the producer. Citations flow along all possible paths, sometimes through intermediate cities. In Table 1, and Table 2 we report the rankings of Top 10 final consumers evaluated by the knowledge diffusion proxy for the Top 3 producers in 2009 and 1990 respectively. We also list the Top 10 neighbours according to the local citation unbalance. From these two tables, it is clear that the final rank of each consumer, obtained by our algorithm, can be extremely different from the ranking obtained by just considering local unbalances. For instance, in 2009 Bratislava and Mainz rank in top 10 consumers absorbing knowledge produced in Boston. However, according to local measure of unbalance, these two cities are ranked out of top 10 (shown in bold in Table 1). Interestingly, even the Top consumer for New Haven, Berlin, also does not rank among the Top 10 neighbours according to the citation unbalance. These findings confirm that in order to uncover the complex set of relationships among cities, it is crucial to consider the entire structure of the network, going beyond simple local measures.
Table 1. Rankings from Knowledge diffusion proxy algorithm for top 3 producer cities in 2009. In bold, we highlight cities that are present in top 10 consumers ranked according to the knowledge diffusion proxy but do not appear in top 10 cities ranked according to local citation unbalance.
| Boston | Berkeley | New Haven | |||
|---|---|---|---|---|---|
| Diffusion proxy | Citation unbalance | Diffusion proxy | Citation unbalance | Diffusion proxy | Citation unbalance |
| Athens | Madrid | Athens | Athens | Berlin | Vancouver |
| Madrid | Athens | Gwangju | Madrid | Athens | Paris |
| Vancouver | Vancouver | Bratislava | Bratislava | Mainz | Trieste |
| Gwangju | Moscow | Madrid | Paris | Vancouver | Athens |
| Bratislava | Paris | Vancouver | Vancouver | Gwangju | Gwangju |
| Berlin | Tokyo | Trieste | Gwangju | Trieste | Bratislava |
| Trieste | Trieste | Waco | Moscow | Bratislava | Madrid |
| Mainz | Beijing | Paris | Trieste | Coventry | Liverpool |
| Paris | Berlin | Berlin | Seoul | Valencia | Oxford |
| Waco | Gwangju | Mainz | Waco | Madrid | Santa Barbara |
Table 2. Rankings from Knowledge diffusion proxy algorithm for top 3 producer cities in 1990. In bold, we highlight cities that are present in top 10 consumers ranked according to the knowledge diffusion proxy but do not appear in top 10 cities ranked according to local citation unbalance.
| Piscataway | Boston | Palo Alto | |||
|---|---|---|---|---|---|
| Diffusion proxy | Citation unbalance | Diffusion proxy | Citation unbalance | Diffusion proxy | Citation unbalance |
| Tokyo | Stuttgart | Tokyo | Tokyo | Tokyo | Tokyo |
| Beijing | Tokyo | Grenoble | Grenoble | Beijing | Ann Arbor |
| Tsukuba | Los Angeles | Beijing | Los Angeles | Tsukuba | Bloomington |
| Grenoble | Urbana | Tsukuba | College Park | Seoul | Boulder |
| Tallahassee | College Park | Seoul | Los Alamos | Tallahassee | Urbana |
| Hamilton | Grenoble | Vancouver | Urbana | Charlottesville | Berlin |
| Buffalo | Rochester | Tallahassee | Boulder | Vancouver | Orsay |
| Vancouver | Boston | Warsaw | Rochester | Berlin | Denver |
| Charlottesville | Los Alamos | Kolkata | Vancouver | Durham | Seoul |
| Tempe | Hamilton | Charlottesville | Bloomington | Taipei | Los Alamos |
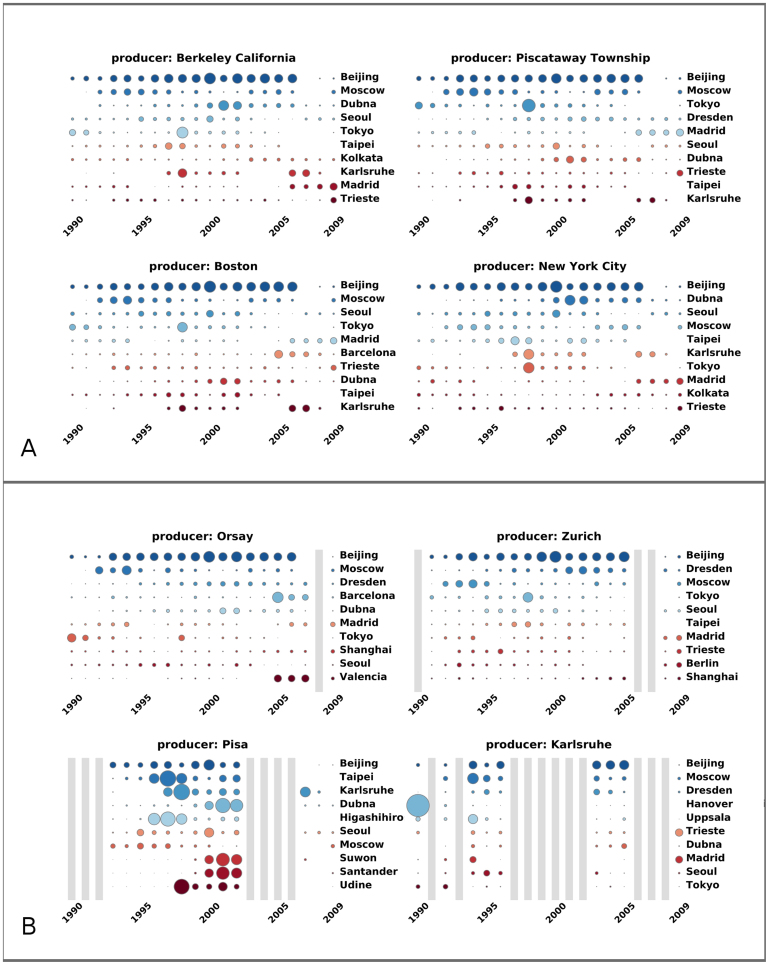
In Figure 4-A and Figure 4-B we visualize the results considering the Top four producer cities in 2009 in the USA and in Europe respectively. We show their Top ten consumers over 20 years as function of time. The size of each circle is proportional to how many times each injected citation is absorbed by that consumer. In the plot, vertical grey strips indicate that the city was not a producer during those years (e.g. Orsay in 2008). The results show that, on average, Beijing is the top consumer for all of these producers in the past 20 years. Since China registered a big economical growth and increment of research population in the early 2000, it is reasonable to assume that, thanks to this positive stimulus, many more papers were written in its capital, a dominant city for scientific research in China. However, the fast publication growth increased the unbalance between sent and received citations. Each paper published in a given city imports knowledge from the cited cities. Reaching a balance might require some time. Each city needs to accumulate citations back to export its knowledge to others cities. We can speculate that in the near future cities in China might be moving among the strongest producers if a fair number of papers start receiving enough citations, which obviously depends on the quality of the research carried out in the last years. This is the case of cities like Tokyo which has gradually approached the citation balance in recent years. For instance, Table 2 shows that in 1990 Tokyo, was among the top consumers. But by 2009, its contribution to citation consumption had become less significant as observed from Figure 4 and Table 1.
Figure 4. Knowledge diffusion proxy results.
(A) The Top 4 producer cities in the USA in 2009 and their Top 10 consumers from knowledge diffusion proxy algorithm in 1990 – 2009. (B) The Top 4 producer cities in the European Union 27 countries as well as Switzerland and Norway in 2009 and their Top 10 consumers from knowledge diffusion proxy algorithm in 1990 – 2009. When a producer city becomes a consumer in some year, a grey strip is marked in that year. For each producer city in (A) and (B), the major consumers of the first producer city m in 20 years are plotted as a function of time from 1990 to 2009. The size of the bubble in position (Y, c) is also proportional to the counter gm,c(Y) in that year. The consumer cities for each producer are ordered according to the total number of counters in 20 years, i.e., 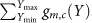 .
.
Ranking cities
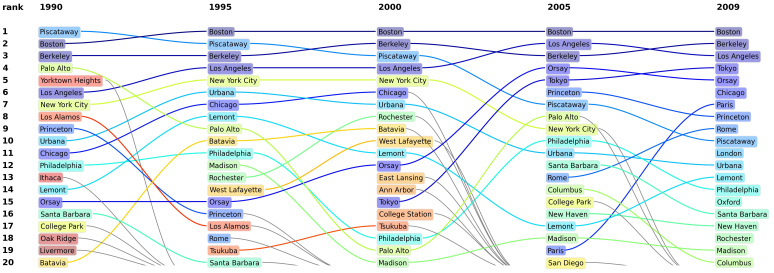
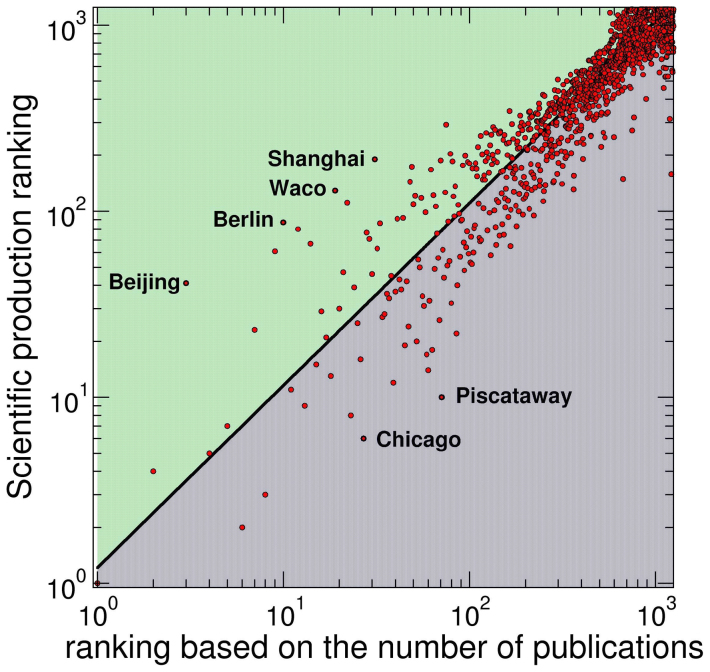
Authors, departments, institutions, government and many funding agencies are extremely interested in defining the most important sources of knowledge. The necessity to find objective measures of the importance of papers, authors, journals, and disciplines leads to the definition of a wide variety of rankings23,24. Measures such as impact factor, number of citations and h-index14 are commonly used to assess the importance of scientific production. However, these common indicators might fail to account for the actual importance and prestige associated to each publication. In order to overcome these limitations, many different measures have been proposed25,26,27,28. Here we introduce the scientific production ranking algorithm (SPR), an iterative algorithm based on the notion of diffusing scientific credits. It is analogous to PageRank33, CiteRank26, HITS25, SARA29, and others ranking metrics. In the algorithm each node receives a credit that is redistributed to its neighbours at the next iteration until the process converges in a stationary distribution of credit to all nodes (see Methods section for the formal definition). The credits diffuse following citations links self-consistently, implying that not all links have the same importance. Any city in the network will be more prominent in rank if it receives citations from high-rank sources. This process ensures that the rank of each city is self-consistently determined not just by the raw number of citations but also if the citations come from highly ranked cities. In Figure 5 we show the Top 20 cities from 1990 to 2009. Interestingly, we clearly see the decline and rise of cities along the years as well as the steady leadership of Boston and Berkeley. This behaviour is clear in Figure 6-B where we show the rank for cities in USA in 1990 and 2009. Meanwhile, the ranking of cities in European and Asian countries like France, Italy and Japan has increased significantly, as shown in both Figure 5 and Figure 6-A. In Figure 6-C we focus on the geographical distribution of ranks for a selected set of European countries in 1990 and 2009. In Table 3 we provide a quantitative measure of the change in the landscape of the most highly ranked cities in the world by showing the percentage of cities in the top 100 ranks for different continents. In Figure 7, we compare the ranking obtained by our recursive algorithm with the ranking obtained by considering the total volume of publications produced in each city. Since we are considering only journals by the APS, the impact factor is consistent across all cities and does not include disproportionate effects that often happen when mixing disciplines or journal with varied readership. It is then natural to consider a ranking based on the raw productivity of each place. As we see in the figure though the two rankings, although obviously correlated, provide different results. A number of cities whose ranking, according to productivity, is in the Top 20 cities in the world, are ranked one order of magnitude lower by the SPR algorithm. Valuing the number of citations and their origin in the ranking of cities produces results often not consistent with the raw number of papers, signaling that in some places a large fraction of papers are not producing knowledge as they are not cited. We believe that the present algorithm may be considered as an appropriate way to rank scientific production taking properly into account the impact of papers as measured by citations.
Figure 5. Top 20 ranked cities as a function of time.
The plot summarizes Top 20 ranked cities in 1990, 1995, 2000, 2005 and 2009 (from left to right), and relations between the rankings in different years. The grey lines are used when the rank of that city drops out of Top 20.
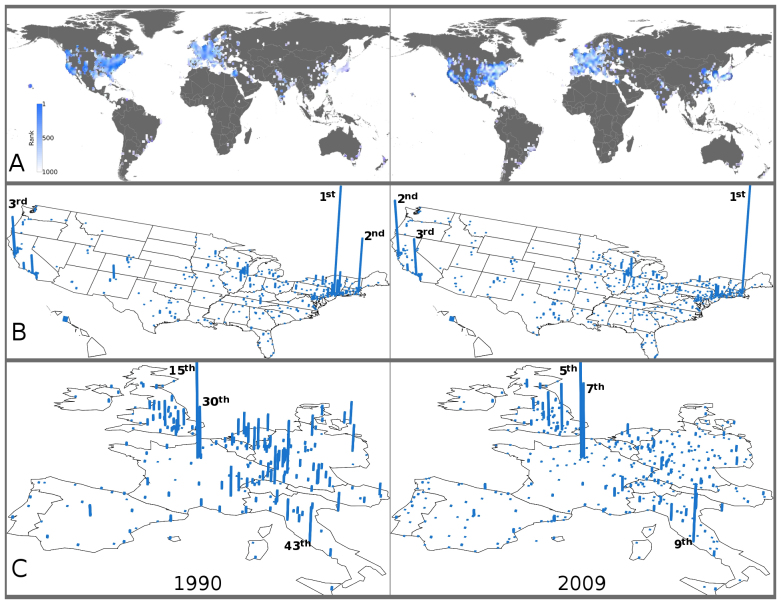
Figure 6. Geospatial distribution of city ranks.
(A) The world map of city ranks in 1990 (left) and 2009 (right). The ranking of each city is represented by color from blue (high ranks) to white (low ranks). (B) The map of ranks for cities in the United States in 1990 (left) and 2009 (right). (C) The map of ranks for cities in the selected European countries in 1990 (left) and 2009 (right). In (B) and (C), each city is marked with a bar, and the height of each bar is inversely proportional to the ranking position. The Top 3 rank positions in each region are labelled for reference. Note that in (C) the height of bars is not scaled with the height in (B) for visibility. Maps in panel (A) are created by using ArcGIS47, and maps in panel (B) and (C) are created by using R48.
Table 3. Percentage of top 100 ranked cities in continents in 1990 and 2009.
| Continent | 1990 | 2009 |
|---|---|---|
| Asia | 4.0% | 11.0% |
| Europe | 24.0% | 33.0% |
| N. America | 72.0% | 56.0% |
Figure 7. Correlation between scientific production ranking and ranking based on the number of publications in 2009.
The x-axis represents rankings based on the number of papers each city published in 2009, and the y-axis represents the scientific production ranking for each city in 2009. The solid line corresponds to the power-law fitting of data with slope –0.98, and separates the space into two regions. In the region below the line (coloured blue), cities gain better rankings from scientific production ranking algorithm even with relatively less publications, such as Chicago and Piscataway. In the region above (coloured green) cities have lower rankings from the algorithm even they have more papers published, such as Beijing, Berlin, Wako and Shanghai.
Discussion
In this paper we study the scientific knowledge flows among cities as measured by papers and citations contained in APS 31 journals. In order to make clear the meaning and difference between producers and consumers in the context of knowledge, we propose an economical analogy referring to citations as a traded currency between urban areas. We then study the flow of citations from producers to consumers with the knowledge production proxy algorithm. Finally, we rank the importance of cities as function of time using the scientific production ranking algorithm. This method, inspired by the PageRank33, allows us to evaluate the importance of cities explicitly considering the complex nature of citation patterns. In our analysis we considered just scientific publications contained in the APS journals31. We do not have information on citations received or assigned to papers outside this dataset. These limitations certainly affect the count of citations of each city, potentially creating biases in our results. However, our findings, while limited to a particular dataset, are aligned with different observations reported by other studies focused on other datasets and fields. For example, we identify major US cities (e.g. Boston and San Francisco areas), as the most important sources of Physics. Similar observations have been done by Börner et al.17 at the institution level considering papers published in the Proceedings of the National Academy of Sciences, by Mazloumian et al.8 at country and city level with Web of Science dataset, and by Batty4 at both institution and country level considering the Institute for Scientific Information (ISI) HighlyCited database. We also find that some European, Russian and Japanese cities have gradually improved their productivities and ranks in recent twenty years. Similarly, such growth in scientific production has been observed by King19 in the ISI database. As discussed in detail in the SI, by aggregating citations of cities to their respective countries, we find the same correlation between the number of citations, as well as the number of papers, and the GDP invested on Research and Development of several countries as reported by Pan et al.7 based on the ISI database. This analogy between our results, and many others in the literature, suggests that the APS dataset, although limited, is representative of the overall scientific production of the largest countries and cities in the recent 20 years. The methodology proposed in this paper could be readily extended to larger datasets for which the geolocalization of multiple affiliation is possible. In view of the different rate of publications and citations in different scientific fields we believe however that the analysis of scientific knowledge production should only consider homogeneous datasets. This would help the understanding of knowledge flows in different areas and identify the hot spot of each discipline worldwide.
Methods
Dataset
The dataset of the American Physical Society journals, considering papers published between 1893 and 2009 of which 450, 655 papers include a list of affiliations31. Each of paper may have multiple affiliations. In total there are 945, 767 affiliation strings.
In order to geolocalize the articles, we parse the city names from the affiliation strings for each article. First, we process each affiliation string and try to match country or US state names from a list of known names and their variations in different languages. We crosscheck the results with Google Map API obtaining validated location information for 97.7% of affiliation strings, corresponding to 445, 223 articles. It is worth noticing that we do not use Google Map API (or other map APIs like Yahoo! or Bing) directly for geocoding because, to our best knowledge, there are no accuracy guarantees to these API results. For each affiliation string with an extracted country or state name, we also match the city name against GeoName database45 corresponding to its country or US state. 92.6% of affiliation strings with extracted city names are subsequently verified with Google Map API. Finally, a total of 425, 233 publication articles successfully pass the filters we describe here.
The dataset also provides 4, 710, 548 records of citations between articles published in APS journals. To build citation networks at the city level, we merge the citation links from the same source node to the same target node, and put the total citations on this link as the weight. For articles with multiple city names, the weight will be equally distributed to the links of these nodes. There are totally 2, 765, 565 links for city-to-city citation networks from 1960 to 2009. (For the full details of parsing country and city names, as well as building networks, see Supplementary Information (SI)).
Knowledge diffusion proxy algorithm
This analysis tool is inspired by the dollar experiment, originally developed to characterized the flow of money in economic networks46. Formally, it is a biased random walk with sources and sinks where a citation diffuses in the network. The diffusion takes place on top of the network of net trade flows. Let us define wij as the number of citation that node i gives to j and wji as the opposite flow. We can define the antisymmetric matrix Tij = wij – wji. The network of the net trade is defined by the matrix F with Fij = |Tij| = |Tji| for all connected pairs (i, j) with Tij < 0 and Fij = 0 for all connected pairs (i, j) with Tij ≥ 0. There are two types of nodes. Producers are nodes with a positive trade unbalance 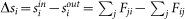 . Their strength-in is larger than their strength-out. On the other hand, consumers are nodes with a negative unbalance Δs. On top of this network a citation is injected in a producer city. The citation follows the outgoing edges with a probability proportional to their intensities, and the probability that the citation is absorbed in a consumer city j equals to
. Their strength-in is larger than their strength-out. On the other hand, consumers are nodes with a negative unbalance Δs. On top of this network a citation is injected in a producer city. The citation follows the outgoing edges with a probability proportional to their intensities, and the probability that the citation is absorbed in a consumer city j equals to 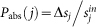 . By repeating many times this process from each starting point (producers) we can build a matrix with elements eij that measure how many times a citation injected in the producer city i is absorbed in a city consumer j.
. By repeating many times this process from each starting point (producers) we can build a matrix with elements eij that measure how many times a citation injected in the producer city i is absorbed in a city consumer j.
Scientific production ranking algorithm
The scientific production rank is defined for each node i according to this self-consistent equation:
Pi is the score of the node i, 0 ≤ q ≤ 1 is the damping factor (defining the probability of random jumps reaching any other node in the network), wji is the weight of the directed connection from j to i, 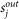 is the strength-out of the node j and finally δ(x), is the Dirac delta function that is 0 for x = 0 and 1 for x = 1. Here we use the damping factor q = 0.15. The first term on the r.h.s. of Eq. (2) defines the redistribution of credits to all nodes in the network due to the random jumps in the diffusion. The second term defines the diffusion of credit through the network. Each node i will get a fraction of credit from each citing node j proportional to the ratio of the weight of link j → i and the strength-out of node j. Finally the last term defines the redistribution of credits to all the nodes in the networks due to the nodes with zero strength-out. In the original PageRank the vector z has all the components equal to 1/N (where N is the total number of nodes). Each component has the same value because the jumps are homogeneous. In this case instead, the vector z considers the normalized scientific credit given to the node i based on his productivity. Mathematically we have:
is the strength-out of the node j and finally δ(x), is the Dirac delta function that is 0 for x = 0 and 1 for x = 1. Here we use the damping factor q = 0.15. The first term on the r.h.s. of Eq. (2) defines the redistribution of credits to all nodes in the network due to the random jumps in the diffusion. The second term defines the diffusion of credit through the network. Each node i will get a fraction of credit from each citing node j proportional to the ratio of the weight of link j → i and the strength-out of node j. Finally the last term defines the redistribution of credits to all the nodes in the networks due to the nodes with zero strength-out. In the original PageRank the vector z has all the components equal to 1/N (where N is the total number of nodes). Each component has the same value because the jumps are homogeneous. In this case instead, the vector z considers the normalized scientific credit given to the node i based on his productivity. Mathematically we have:
where p defines the generic paper and np the number of nodes who have written the paper. It is important to notice that δp,i = 1 only if the i-th node wrote the paper p, otherwise it equals zero.
Author Contributions
A.V., N.P. and Q.Z. designed research, Q.Z., B.G. and F.C. parsed data, Q.Z., N.P. and A.V. analysed data. All authors wrote, reviewed and approved the manuscript.
Supplementary Material
Supplementary Information
Acknowledgments
This work has been partially funded by NSF CCF-1101743 and NSF CMMI-1125095 awards. We acknowledge the American Physical Society for providing the data about Physical Review's journals.
References
- Narin F. & Carpenter M. P. National Publication and Citation Comparisons. Journal of the American Society for Information Science, 26, 80–93 (1975). [Google Scholar]
- Frame J. D. Narin F. & Carpenter M. P. The Distribution of World Science. Social Studies of Science, 7, 501–516 (1977). [Google Scholar]
- May R. M. The Scientific Wealth of Nations. Science, 7, 793–796 (1997). [Google Scholar]
- Batty M. The Geography of Scientific Citation. Environ Plan A 35, 761–765 (2003). [Google Scholar]
- Leydesdorff L. & Zhou P. Are the contributions of China and Korea upsetting the world system of science? Scientometrics, 63, 617–630 (2005). [Google Scholar]
- Horta H. & Veloso F. Opening the box: comparing EU and US scientific output by scientific field. Technological Forecasting & Social Change, 74, 1334–1356 (2007). [Google Scholar]
- Pan R. K. Kaski K. & Fortunato S. World citation and collaboration networks: uncovering the role of geography in science . Sci. Rep. 2, 902 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazloumian A. Helbing D. Lozano S. Light R. P. & Börner K. Global Multi-Level Analysis of the ‘Scientific Food Web’. Sci. Rep. 3, 1167 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frenken K. Hardeman S. & Hoekman J. Spatial scientometrics: Towards a cumulative research program. Journal of Informetrics, 3, 222–232 (2009). [Google Scholar]
- Redner S. How popular is your paper? An empirical study of the citation distribution. Eur. Phys. J. B 4, 131–134 (1998). [Google Scholar]
- Chen P. Xie H. Maslov S. & Redner S. Finding scientific gems with Google's PageRank algorithm. Journal of Informetrics, 1, 8–15 (2007). [Google Scholar]
- Garfield E. Citation Analysis as a Tool in Journal Evaluation. Science, 178, 471–479 (1972). [DOI] [PubMed] [Google Scholar]
- Bergstrom C. Eigenfactor: Measuring the value and prestige of scholarly journals. College & Research Libraries News, 68, 314–316 (2007). [Google Scholar]
- Hirsch J. E. An index to quantify an individual's scientific research output. Proc. Natl. Acad. Sci., 102, 16569–16572 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egghe L. Theory and practise of the g-index. Scientometrics, 69, 131–152 (2006). [Google Scholar]
- Hirsch J. E. Does the h index have predictive power? Proc. Natl. Acad. Sci. 104, 19193–19198 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Börner K. Penumarthy S. Meiss M. & Ke W. Mapping the Diffusion of Information Among Major U.S. Research Institutions. Scientometrics, 68, 415–426 (2006). [Google Scholar]
- Bornmann L. Leydesdorff L., Walch-Solimena C. & Ettl C. Mapping excellence in the geography of science: An approach based on Scopus data. Journal of Informetrics, 5 no. 4, 537–546 (2011). [Google Scholar]
- King D. K. The scientific impact of nations. Nature, 430 311–316 (2004). [DOI] [PubMed] [Google Scholar]
- Adams J. Collaborations: The rise of research networks. Nature, 490 335–336 (2012). [DOI] [PubMed] [Google Scholar]
- Laudel G. Studying the brain drain: Can bibliometric methods help? Scientometrics, 57 215–237 (2003). [Google Scholar]
- Noorden R. V. Global mobility: Science on the move. Nature, 490, 326–329 (2012). [DOI] [PubMed] [Google Scholar]
- Garfield E. Citation Indexing. Its Theory and Application in Science, Technology, and Humanities. John Wiley & Sons Inc., 1979. [Google Scholar]
- Egghe L. & Rousseau R. Introduction to Informetrics : Quantitative Methods in Library, Documentation and Information Science. Elsevier Science Publishers, 1990. [Google Scholar]
- Kleinberg J. M. Authoritative sources in a hyperlinked environment. Journal of the ACM, 46, no. 5, 604–632 (1999). [Google Scholar]
- Walker D. Xie H. Yan K.-K. & Maslov S. Ranking scientific publications using a model of network traffic. Journal of Statistical Mechanics: Theory and Experiment 2007, P06010 (2007). [Google Scholar]
- Castillo C. Donato D. & Gionis A. Estimating Number of Citations Using Author Reputation. in String Processing and Information Retrieval, 4726 of Lecture Notes in Computer Science, Springer Berlin/Heidelberg (2007). [Google Scholar]
- Sidiropoulos A. & Manolopoulos Y. Generalized comparison of graph-based ranking algorithms for publications and authors. Journal of Systems and Software, 79, 1679–1700 (2007). [Google Scholar]
- Radicchi F., Fortunato S., Markines B. & Vespignani A. Diffusion of scientific credits and the ranking of scientists. Phys. Rev. E 80, 056103 (2009). [DOI] [PubMed] [Google Scholar]
- Scharnhorst A., Börner K. & van den Besselaar P. eds., Models of Science Dynamics: Encounters Between Complexity Theory and Information Sciences. Springer-Verlag, (2012). [Google Scholar]
- APS, Data sets for research. (2012). (accessed June 8 2010).
- http://data.worldbank.org/. (2012). (accessed September 12 2012).
- Brin S. & Page L. The anatomy of a large-scale hypertextual web search engine, Comp. Net. ISDN Sys. 30, 107, (1998). [Google Scholar]
- Barabási A.-L. & Albert R. Emergence of scaling in random networks. Science 286, 509 (1999). [DOI] [PubMed] [Google Scholar]
- Barrat A. Barthélemy M. & Vespignani A. Dynamical Processes on Complex Networks. Cambridge Univesity Press (2008). [Google Scholar]
- Newman M. Networks. An Introduction. Oxford Univesity Press (2010). [Google Scholar]
- Vespignani A. Predicting the behavior of techno-social systems. Science 325, 425–428 (2009). [DOI] [PubMed] [Google Scholar]
- Vespignani A. Modeling dynamical processes in complex socio-technical systems. Nature Physics, 8, 32–30 (2012). [Google Scholar]
- Ángeles Serrano M. Boguñá M. & Vespignani A. Extracting the multiscale backbone of complex weighted networks. Proc. Natl. Acad. Sci. 106, 6483–6488, April (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyandin I. Bertini E. & Lalanne D. Using flow maps to explore migrations over time, in Proceedings of Geospatial Visual Analytics Workshop in conjunction with The 13th AGILE International Conference on Geographic Information Science (GeoVA) (2010). [Google Scholar]
- Adams J. & Griliches Z. Measuring science: An exploration. Proc. Natl. Acad. Sci. 93, 12664–12670 (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenblat T. S. & Mobius M. M. Getting Closer or Drifting Apart? Quarterly Journal of Economics, 119, no. 3, 971–1009 (2004). [Google Scholar]
- Havemann F. Heinz M. & Kretschmer H. Collaboration and distances between German immunological institutes a trend analysis. Journal of Biomedical Discovery and Collaboration, 1, 6 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agrawal A. & Goldfar A. Restructuring Research: Communication Costs and the Democratization of University Innovation. American Economic Review, 98, no. 4, 1578–1590 (2008). [Google Scholar]
- GeoNames, GeoNames. http://www.geonames.org/, Retr. (2012). (accessed February 7 2012).
- Ángeles Serrano M. Boguñá M. & Vespignani A. Patterns of dominant flows in the world trade web. J. Econ. Interac. Coord. 2, 111–124 (2007). [Google Scholar]
- ESRI, ArcGIS Desktop: Release 9.3. Environmental Systems Research Institute, Redlands, CA (2010).
- Core Team R. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria, ISBN 3-900051-07-0. (2012). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Information