A Path-Specific SEIR Model for use with General Latent and Infectious Time Distributions

Summary

Most current Bayesian SEIR models either use exponentially distributed latent and infectious periods, allow for a single distribution on the latent and infectious period, or make strong assumptions regarding the quantity of information available regarding time distributions, particulary the time spent in the exposed compartment. Many infectious diseases require a more realistic assumption on the latent and infectious periods. In this paper, we provide an alternative model allowing general distributions to be utilized for both the exposed and infectious compartments, while avoiding the need for full latent time data. The alternative formulation is a path-specific SEIR (PS SEIR) model that follows individual paths through the exposed and infectious compartments, thereby removing the need for an exponential assumption on the latent and infectious time distributions. We show how the PS SEIR model is a stochastic analog to a general class of deterministic SEIR models. We then demonstrate the improvement of this PS SEIR model over more common population averaged models via simulation results and perform a new analysis of the Iowa mumps epidemic from 2006.

1. Introduction

SIR (Susceptible, Infectious, Removed (or Recovered)) and SEIR (Susceptible, Exposed, Infectious, Removed (or Recovered)) models date back to Kermack and McKendrick (1927). However, only recently have stochastic variants of SIR and SEIR models become a mainstay in the statistical literature. One of the salient features of the original models was that the latent and infectious times of the infectious disease under consideration are exponentially distributed, known as the exponential assumption (Anderson and May, 1991). The exponential assumption was one of many assumptions from the early deterministic models that carried into the stochastic methodology.

The exponential assumption tends to be a convenient assumption in modeling, largely due to the simple form of the models and simpler imputation in the stochastic framework. Unfortunately, this assumption is unrealistic for many infectious diseases. The memoryless property of the exponential distribution requires a constant probability of moving to the infectious compartment on day j + 1 after j days of a latent infection, regardless of j.

The idea of relaxing the exponential assumption is not new, with work done as early as 1948 (Kendall, 1948). Recently, a great body of work has been published to relax the exponential assumption. However, one tends to see models which make very strong assumptions in the exposure times (e.g. where it is assumed the initial exposure times are known (Streftaris and Gibson, 2004), or where the latent period is assumed to be fixed (O’Neill and Becker, 2001)). A notable exception is Boys and Giles (2007), who provide a model which can use gamma distributions for the latent and infectious classes and does not require initial exposure times. While their method only handles gamma distributions, this approach may work well for many infectious diseases. Lloyd (2001) and Wearing et al. (2005) suggest that a gamma distribution may fit many infectious diseases well. Additionally, Jewell et al. (2009) propose an SIR model allowing general infectious periods, but do not extend this model to the SEIR structure and propose a very different method than we propose here.

Kenah and Miller (2011) showed that the infectious time distribution has a marked effect on the probability of a major epidemic, and Wearing et al. (2005) demonstrated bias in the basic reproductive number of the microorganism when the time to infection is incorrectly assumed to be exponentially distributed. In fact, the paper by Kenah and Miller provides a method for utilizing general latent and infectious time distributions. In their approach the latent time distribution must be known a priori, and individual infectious contacts are sampled. This has the disadvantage of requiring the latent and infectious distribution to be known before the analysis has begun, but has the advantage of easily being utilized in a contact graph model. Our work does not require the latent and infectious distribution to be known, however we do require some prior information to be used in our model. In the proposed model mixing takes place at the population level, and so population level interventions such as government awareness campaigns are easily assessed and naturally modeled, an issue that we will consider strongly throughout this paper. Our model does not easily adapt to the contact graph scheme, however.

The work by Kenah and Miller has strong implications for the accuracy of predictions of future epidemics in the stochastic framework. If parameters involved in the mixing process are biased, it may result in inaccurate predictions of the final sizes of future epidemics, or in the analysis of the efficacy of public health interventions, if such interventions are utilized in the analysis. To our knowledge, no one has investigated the variance of the parameters when the exponential distributions on the latent and infectious times are misspecified. Because the parameter variances in SEIR models are already large (see, for example Elderd et al. (2006)), we feel this is worth investigating.

At the individual level, work has been done to relax the exponential assumption (e.g., see O’Neill and Becker (2001); Yang et al. (2006)). These models work quite well when individual level information is available for small populations. However, they are limited in the regard that many interventions will be applied at the population level, and the indices of the individuals receiving the interventions may need to be imputed. Additionally, many epidemics occur in large populations, and computation may be slow with individual level models. A hybrid model would allow for the natural approach of population based interventions and large sample sizes, while still allowing the flexibility of the individual level approach in the generation times.

In this paper, we suggest a hybrid model called the path-specific Bayesian SEIR model, abbreviated henceforth as PS SEIR model, that allows for the use of a general distribution for the time spent in the latent and infectious compartments. This will allow greater flexibility in modeling infectious disease with non-exponential latent and/or infectious periods. We then derive the model as a stochastic analog to a broad class of deterministic models. Next, we propose a method for sampling from the posterior distributions. We give simulation results to demonstrate the improvement over analyzing Weibull and gamma distributed infectious diseases according to their true distribution, as opposed to naively analyzing them as exponentially distributed. After the simulation results, we present an analysis of the mumps epidemic that occurred in Iowa in 2006. Finally, we discuss limitations and advantages of the formulation.

2. Methods

In this section, we first propose the PS SEIR model. We next state the assumptions made in deriving it as the analog to a class of deterministic SEIR models.

2.1 Proposed Model

The main goal of this section is to demonstrate how the exponential assumption can be relaxed, and how discretized distributions can be implemented for the latent and infectious periods. We utilize the more realistic assumption that there is a maximum time that an individual may sustain a latent infection before becoming actively infectious. We assume that all individuals in the exposed category will eventually move to the infectious category, as is done in Lekone and Finkenstädt (2006) and Anderson and May (1991), and do not consider cases of exposure without latent infection at this juncture.

The population averaged SEIR model of interest is found in Lekone and Finkenstädt (2006), which is itself the generalization from the SIR model found in Mode and Sleeman (2000):

Define i=1,…,T as a subscript for discrete time and S_i, E_i, I_i, and R_i represent the counts of individuals in the Susceptible, Exposed, Infectious, and Removed compartments at time i, respectively. The notation S_i → E_i+1 denotes a change of category. Let f(ψ̲, i) represent the mixing and possible intervention functions controlling the number of new exposures at time i + 1, and is constrained to be nonnegative, with ψ̲ representing the vector of parameters controlling mixing and interventions. Let h represent the number of days between time points in the data collection partition. The total number of individuals in the population is denoted by N.

$$\begin{array}{c}{S}_i\to E_{i+1}=\mathit{\text{binomial}}(S_i,1-\text{exp}(-f(\mathrm{\psi ̲},i)h\frac{I_i}{N}));\hfill \\ E_i\to I_{i+1}=\mathit{\text{binomial}}(E_i,1-\text{exp}(-\rho h));\hfill \\ I_i\to R_{i+1}=\mathit{\text{binomial}}(I_i,1-\text{exp}(-\gamma h)).\hfill \end{array}$$ (1)

For models utilizing the exponential assumption, the exposure data are typically arranged as a T-dimensional vector of counts, E = (E₁, …, E_T)′. Note that, in these models, the only necessary information for the evaluation of the likelihood is the total count in the exposed category at each time point, E_i. We relax this assumption by not only counting the number of exposed individuals at each time point, but also by utilizing the length of time each individual has been in the exposed compartment. Consider collecting the exposure counts in a T×M₁ matrix E, where M₁ is the maximum amount of time the infectious agent can remain latent. Cell (i,j) then contains a count of the number of individuals who are at time point j of the latent infection process on time point i of the epidemic. In other words, i represents objective time since the start of the epidemic, and j denotes the subjective, individual time in the diseases process. In practice, i and j will typically be measured in days, although this is certainly not required. The T×M₂ infectious matrix I is defined analogously to E, with the rows representing the number of time points elapsed since the start of the epidemic, and the columns representing the number of time points an individual has remained in the infectious compartment.

When an individual is newly exposed and contracts a latent infection at time i, the individual moves from the susceptible class into row i, column 1, of the exposed matrix E. For every time unit in which the individual does not become infectious, the individual moves from row i, column j in a diagonal path, moving one column to the right, j+1, and one row down, i+1. When the individual becomes infectious at time i′, the individual moves to row i′, column 1, of I, and repeats the process until removed. This process allows the length of time each individual is in the exposed category to be imputed, and allows for many latent time and infectious time distributions to be discretized and utilized. Specifying a maximum length of time which a individual can remain in the Exposed or Infectious classes allows the number of columns of the matrix to be defined a priori, and removes the need to adaptively choose the size of the matrix as the analysis is running. While an adaptive scheme may be possible, it is not necessary to do so, since the maximum amount of time an infectious agent may remain in a latent state is often known. Additionally, an adaptive scheme may not be computationally efficient.

Because the exposure data and infectious data are being collected in matrices, the probability of compartmental change can vary with the amount of time an individual has stayed in the compartment. This allows the exponential assumption to be relaxed, and any distribution can be discretized and used to approximate the true, underlying latent and infectious time distributions. As noted in the introduction, this allows more realistic distributions to be used for infectious diseases.

With this structure in place, the investigator is able to use strong prior knowledge of the length of time that individuals spend in the exposed and infectious categories. Typically, this information is available and multiple distributions may be fit and compared. It is unlikely that there will be strong prior information for the mixing and intervention parameters, so relatively weak priors can be used for these parameters.

The proposed PS SEIR model utilizes the following scheme: Let i denote discrete calendar time since the beginning of the epidemic, and j denote discrete time that an individual has spent in the latent or infectious state. Then,

$$\begin{array}{c}{S}_i\to E_{i+1,1}=\mathit{\text{binomial}}(S_i,1-\text{exp}(-f(\mathrm{\psi ̲},i)h\frac{I_{i+}}{N}))\equiv W_i;\hfill \\ E_{\mathit{\text{ij}}}\to I_{i+1,1}=\mathit{\text{binomial}}(E_{\mathit{\text{ij}}},P(Z_1\le j+h|Z_1>j))\equiv X_{\mathit{\text{ij}}};\hfill \\ E_{\mathit{\text{ij}}}\to E_{i+1,j+1}=E_{\mathit{\text{ij}}}-X_{\mathit{\text{ij}}};\hfill \\ I_{\mathit{\text{ij}}}\to R_{i+1}=\mathit{\text{binomial}}(I_{\mathit{\text{ij}}},P(Z_2\le j+h|Z_2>j))\equiv Y_{\mathit{\text{ij}}};\hfill \\ I_{\mathit{\text{ij}}}\to I_{i+1,j+1}=I_{\mathit{\text{ij}}}-Y_{\mathit{\text{ij}}}.\hfill \end{array}$$ (2)

These definitions follow from Equation 1, where X_ij, Y_ij, W_i, and E_ij are all unobserved, while Σ_j X_ij (the total new infections at time i), and Σ_j Y_ij (the total new recoveries at time i) are known. Z₁ is a random variable defined by the exposure distribution and Z₂ is defined by the infectious distribution. As before, f(ψ̲, i) represents the mixing and possible intervention functions controlling the number of new exposures at time i + 1. Here ψ̲ ≥ 0 represents the vector of parameters controlling mixing and interventions. I_i+ represents the total number of infectious individuals at time i, h represents the number of days between data collection times, and N represents the total number of individuals in the population.

The compartments are the Susceptible, Exposed, Infectious, and Removed classes, respectively. Define a bin as the amount of time between data collection times. In our discretization scheme, a bin will be h time units (often measured in days). Bins are used within the exposed and infectious compartments as the basic time unit for the discretizations. Most data sets will use h = 1, but all that is required is 0 < h < ∞. This style of discretization allows for the analysis of large data sets, while still providing the flexibility to use a time-dependent conditional probability of changing compartments. By defining bins within the Exposed and Infectious compartments, it is possible to vary the conditional probability of a compartment change depending on the length of time an individual has spent in the compartment, which, in turn, allows for distributions other than the exponential distribution to be used for the latent and infectious times.

2.2 Derivation of the PS SEIR Model

The PS SEIR model can be derived as a stochastic analog to the following nonlinear deterministic system of equations:

$$\frac{\mathit{\text{dS}}}{\mathit{\text{dt}}}=-f(\mathrm{\psi ̲},t)S\frac{I}{N};$$

$$\frac{\mathit{\text{dE}}}{\mathit{\text{dt}}}=f(\mathrm{\psi ̲},t)S\frac{I}{N}-g(\mathrm{\alpha ̲},E);$$

$$\frac{\mathit{\text{dI}}}{\mathit{\text{dt}}}=g(\mathrm{\alpha ̲},E)-h(\mathrm{\gamma ̲},I);$$

$$\frac{\mathit{\text{dR}}}{\mathit{\text{dt}}}=h(\mathrm{\gamma ̲},I).$$

Several assumptions are made in this process, and we outline the core assumptions here.

1. Assume a homogeneous population with regards to susceptibility. This is commonly assumed in population averaged models.

2. Assume independent Poisson contact distributions for infectious individuals, all of which share a single parameter. This works well for diseases such as mumps or measles, but works poorly in models for sexually transmitted diseases, such as gonorrhea or chlamydia.

3. Define the Exposed compartment as only containing those who will eventually become infectious, and do not consider the possibility of a return to the Susceptible class.

4. Assume constant infectivity throughout the course of the infectious process.

5. Assume independent probabilities of moving from the Exposed Compartment to the Infectious Compartment (as well as from the Infectious Compartment to the Removed Compartment).

6. Individuals are treated as having identical latent and infectious time distributions. There is no individual heterogeneity in these processes.

The full derivation can be found in Web Appendix A.

3. Computing

3.1 MCMC Techniques

Sampling from the full posterior distributions is not feasible for this model. Therefore, we rely on MCMC sampling techniques. Metropolis Hastings sampling is recommended for sampling the parameters in the model. In all of our simulation work, using a normal proposal distribution was adequate. However, it is necessary to find an efficient way to sample from the Exposure matrix. Simply generating the entire matrix at every iteration is not practical, as the MH algorithm will rarely accept a proposal. Our proposed sampling scheme can be found in the Web Appendix B.

3.2 Simulation Results

Many simulations were run, and we report results from a typical set here. Consider the case where the full removal times are available, and the parametric forms of the intervention are known. This will demonstrate the improvement the PS SEIR model offers over population-averaged approaches in an ideal scenario. Additional simulations can be found in the Web Appendix C.

For each simulated data set, there were 20,000 total individuals, with one member in the infectious category and all the other individuals susceptible at the start of the epidemic. The mixing parameter chosen to simulate the data was 0.25, in order to give a large degree of variability to the epidemic sizes. Let ψ₁ be the mixing parameter and ψ₂ be the intervention parameter. The intervention we consider has the form f(ψ̲, i) = ψ₁ exp(−ψ₂1_(i≥i0)), where i₀ is the time that the intervention began. This represents an exponential decay in the probability of moving from the susceptible class to the exposed class. For this form, ψ₂ was selected to be 0.1, and i₀ to be 100 days.

The parameterization selected for the exponential distributions was $f(x)=\frac{1}{\lambda }\text{exp}(-\frac{x}{\lambda })$. For the gamma distributions, the parameterization was $f(x)=\frac{{\beta }^{\alpha }}{\mathrm{\Gamma }(\alpha )}{x}^{\alpha -1}\text{exp}(-\beta x)$. The parameter values were chosen to approximate a disease such as mumps. Mumps has a very well known latent period of 16–18 days, although this period can last as few as 12 or as many as 25 days (CDC, 2009a).

The infectious period is less well known, but shedding typically lasts fewer than nine days after the onset of symptoms, though this is often around five days (Polgreen et al., 2008). A throat swab can isolate the viruses from 40% of individuals infected with mumps 2–3 days prior to the onset of parotitis, and individuals are typically infectious prior to displaying symptoms (CDC, 2009a,b).

For the simulations, the true value for λ in the exponential distribution was chosen to be 18.71 for the exposed mean time, and 8.62 for the infectious mean time. The true α and β related to the gamma distributions, were chosen to be 30 and 1.603 for the exposure time distribution, and 100 and 11.6 were chosen for the infectious time distribution.

The infectious time distributions were chosen to account for the typical amount of time shedding as well as the possibility of an individual being infectious prior to displaying symptoms. The gamma infectious time distribution gives typical infectious periods of seven to ten days, which is in accordance with the typical length of shedding after the onset of symptoms together with the typical infectious period prior to the onset of symptoms. The Exponential distribution was chosen to have the same mean infectious time as the gamma distribution.

We simulated 3,000 possible epidemics, and chose four data sets corresponding to small, medium, large, and very large epidemics from our final size distribution. These four data sets had final epidemic sizes of 34, 62, 122, and 222 individuals infected.

Simulation results are presented in Table 1. In both the exponential and gamma analyses, the priors used for the mixing and intervention parameters were Gamma(.1,.4), and Gamma(.1,1), respectively. These represent the weak but informative information one might possess for a common infectious disease such as Mumps. We note that these priors are weaker than those used in the analysis by Lekone and Finkenstädt (2006). For the exponential analysis of each data set, λ was assigned a Gamma(187.09,10) prior. For the gamma analyses, α was assigned a prior of Gamma(300,10) and β was assigned a Gamma(16.03,10) prior. These values represent the strong prior information that would typically be available for the distribution of latent times. Additionally, we note that weak prior information allows the mean of the latent time to be accurately estimated, but leads to over estimation of the variance for large data sets. We will demonstrate that the most improvement from this method comes from small data sets. Additionally, strong prior information is typically readily available for the latent and infectious time distributions of known pathogens, such as Mumps, and can legitimately be used in the analysis.

Table 1.

Parameter medians and 95% central credible intervals for the analysis of the Gamma data sets featuring an exponential decay intervention. Based on 10,000 realizations after burn-in each.

Analysis	Data Set	Mixing (0.25)	Intervention (0.1)	Alpha (30)	Beta (1.604)	R0 (2.16)	Predicted Epidemic Size
Exp	34 cases	0.23 (0.14, 0.32)	0.62 (0.07, 2.96)	NA	NA	1.83 (1.13,2.74)	7 (1, 574)
Gamma	34 cases	0.20 (0.13, 0.28)	0.12 (0.05, 0.22)	29.78 (26.45, 33.17)	1.54 (1.21, 1.91)	1.69 (1.11,2.38)	17 (1, 173)
Exp	62 cases	0.23 (0.16, 0.31)	0.12 (0.04, 0.35)	NA	NA	1.85 (1.23,2.68)	9 (1, 672)
Gamma	62 cases	0.21 (0.15, 0.28)	0.07 (0.03, 0.11)	29.73 (26.54, 33.23)	1.64 (1.30, 1.97)	1.79 (1.28, 2.39)	26 (1, 242)
Exp	122 cases	0.26 (0.20, 0.34)	0.12 (0.07, 0.22)	NA	NA	2.13 (1.59,2.87)	36 (1, 1212)
Gamma	122 cases	0.26 (0.20, 0.32)	0.10 (0.07,0.14)	29.13 (25.93, 32.50)	2.22 (1.39, 1.97)	2.25 (1.76, 2.75)	78 (1, 475)
Exp	222 cases	0.27 (0.22, 0.32)	0.10 (0.07,0.15)	NA	NA	2.11 (1.68,2.61)	43 (1, 1119)
Gamma	222 cases	0.27 (0.22, 0.31)	0.10 (0.08, 0.13)	28.81 (25.56, 32.16)	1.57 (1.34, 1.82)	2.28 (1.92, 2.70)	84 (1, 424)

P-values greater than 0.05 for the Geweke diagnostic were used to indicate convergence for all model parameters (Geweke, 1992). Note that the PS SEIR model typically offers some improvement in the variances of the parameter estimates, with most improvement coming when the epidemic sizes are small to moderately sized, due to the greater effect each individual path has on the mixing and intervention parameters in these cases. Beyond just the decrease in variance that one would expect from fitting the true model, we hypothesize that the main reason for this phenomenon is that the gamma distribution model supplies more information about the latent process, which allows for much more accurate parameter realizations in situations with small epidemic sizes.

When looking at the final epidemic sizes, one notices much improved prediction with the PS SEIR approach. In these predictions, we have used the true gamma infectious time distribution when generating new epidemics from the gamma analyses, and an exponential infectious time distribution when with the same mean (8.62 days) when generating new epidemics from the infectious time distribution. Small differences in the mixing and intervention parameters can have a marked effect on epidemic size prediction, particularly when exponential infectious times are employed. The PS SEIR approach not only narrows the credible intervals, but protects against this variability in epidemic size prediction by allowing infectious times which are less variable. These predictions argue very strongly for utilizing proper models when analyzing epidemic data and predicting new epidemics. It is important to note that these reports do not distinguish between minor outbreaks and major epidemics. However, one feature that is clear is that the PS SEIR predicted epidemics much more closely approximate the true epidemic size.

4. Data Analysis

The motivating data set consisted of the onset times for the 214 cases of mumps confirmed via swab culture during the 2006 Iowa mumps epidemic, which lasted from January 29, 2006 to June 25, 2006. We note that cases were less likely to be confirmed via swab culture early in the epidemic, which may lead to longer estimates of the infectious time distribution and lower estimates of the mixing parameter. In fact, all of the models we fit tended to underestimate the final size of the epidemic, and the low values of the mixing parameters are likely part of the reason. However, it is quite common in epidemic research that not every infectious individual is diagnosed, and we instead emphasize the improvement of the PS SEIR structure over similar population averaged approaches.

There are two goals for the following analysis. The first is to obtain a more realistic analysis of the Iowa mumps epidemic than can be obtained by utilizing the exponential distribution alone, and to demonstrate the improvement of the PS SEIR formulation over the population averaged formulation. The second is to decide on a reasonable parametric form for the public’s awareness of the epidemic, which acts as an intervention in the data. This will demonstrate the importance of recognizing changes in behavior resulting from public awareness in modern epidemics, as well as the importance of quantifying these changes.

Polgreen et. al. analyzed the Iowa Mumps epidemic using a Generalized Linear Mixed Model (GLMM) approach to map the data, and employed a test of proportions to analyze the effect of spring break. They found there to be a spring break effect in the age composition of Mumps cases after spring break Polgreen et al. (2010). We again note that their analysis considered all probable cases, whereas our analysis considered only confirmed cases. Considering a more granular treatment of time in a SEIR structure may allow us to expand upon the results yielded by their research and identify more temporal structures in the data set.

Simply modeling the data set with no intervention accounting for public awareness was not successful. Epidemics rarely occurred based on the estimated parameter posterior values obtained from models not accounting for public awareness, and epidemics that did occur severely underestimated the final epidemic size, with almost no simulated epidemics reaching half the true epidemic size. Previous literature has used public awareness as an intervention successfully. Note that Lekone and Finkenstädt (2006) use an exponential decay intervention to model public awareness due to a government awareness campaign with promising results.

In modeling public awareness, we will use two parameterizations. The first will be the same style of exponential decay intervention found in Section 3.2, which will begin on March 30, the day that the CDC posted a dispatch to the MMWR website (CDC (2006)). The second will be a logistic intervention, which will have the form $\frac{\text{exp}({\varphi }_0-{\varphi }_1*\mathit{\text{day}})}{1+\text{exp}({\varphi }_0-{\varphi }_1*\mathit{\text{day}})}$, where ϕ₁ > 0, $\frac{\text{exp}({\varphi }_0)}{1+\text{exp}({\varphi }_0)}>0.99$, and day is the number of days since the initial case. This function will be able to reduce the mixing parameter from its initial value over the course the epidemic. In an attempt to accommodate the effect of spring break on mixing, we use a three week constant effect intervention, beginning on March 6, 2006. The parametric form of this intervention can be found in the Web Appendix C.

One of the aspects that must be accounted for in working with mumps is the presence of the MMR vaccine. The CDC states that the 2004–2005 MMR vaccination rate for kindergartners in Iowa was 97% (CDC, 2009b). We therefore use that as our best estimate of the vaccination rate in the state of Iowa. Farley-Kim et al. (1985) suggest that the efficacy of the MMR vaccine in preventing mumps is 85%. One simplifying assumption in the model is that the vaccine is an all or nothing vaccine yielding permanent immunity. According to our vaccination estimates, this yields 523,000 individuals susceptible to mumps in Iowa. 2,570,000 individuals will start in the Removed category, accounting for their immune status. This is an important consideration, as the high rate of immunity plays a role in the magnitude of the mixing and intervention parameters.

Because the prior information available for the infectious time of mumps is not as strong as the prior information available for the latent time (see Section 3.2), we will use two lengths for the infectious period for each distribution. The first set will be short infectious times. These correspond to Exponential(8.6), Gamma(100,11.6), and Weibull(12,9). The second set will be long infectious times. These correspond to Exponential(11), Gamma(25,2.27), and Weibull(6,12).

Models were constructed, and their fit assessed using the posterior predictive p-value approach as outlined in Gelman et al. (1996). At each iteration of the MCMC chain, a single epidemic was generated. The model fit statistic used was an indicator that the final epidemic size was between 107 and 428 (half to twice as large as the epidemic) and the day the simulated epidemic ended was between 117 and 197 (within 40 days of the length of the actual epidemic). These values were chosen based on the variability seen in simulated epidemics.

Table 2 shows the posterior predictive p-values for all the models we ran. The path-specific approach yields the highest posterior p-values for model fit. The best path-specific model (Weibully distributed with an exponential form of the intervention and long infectious times) generated over six times as many accepted epidemics as the best fitting population averaged model (Exponentially distributed with the logisitic form of the intervention and long infectious times). The path specific approach also yields some of the lowest p-values, indicating that it is sensitive to the form of the public-health intervention chosen. Table 3 gives descriptive statistics for the best fitting PS SEIR model, as well as its corresponding exponential model. We note that the credible intervals are quite a bit narrower for the PS SEIR approach than for the population averaged approach. Additionally, it is known that mumps is typically latent 16 to 18 days. The credible interval for the mean latent time in the Weibull model fits this a priori known information better than the exponential model. The better fit in terms of latent time as well as the narrower credible intervals may indicate greater accuracy of model fit for the PS SEIR model as compared to the population averaged model. The basic reproductive number, R₀ has medians in an historically reasonable range for both models (Anderson and May, 1991). However, the PS SEIR model provides a much narrower 95% credible interval for this parameter. This is important, as this number is a basic quantity of interest in these models.

Table 2.

Posterior predictive p-values for the models run for the real data analysis. Each posterior predictive p-value is based on 7,000 realizations.

Distribution	Intervention	Infectious Period	P-value
Exponential	Exponential	Short	0.0203
Exponential	Exponential	Long	0.0284
Exponential	Logistic	Short	0.0245
Exponential	Logistic	Long	0.0305
Gamma	Exponential	Short	0.0881
Gamma	Exponential	Long	0.1061
Gamma	Logistic	Short	0.0028
Gamma	Logistic	Long	0.0033
Weibull	Exponential	Short	0.1668
Weibull	Exponential	Long	0.2184
Weibull	Logistic	Short	0.0004
Weibull	Logistic	Long	0.0335

Table 3.

Descriptive statistics for the posteriors of key parameters or parametric forms for Model 1, which has exponentially distributed exposure times, an exponential decay intervention, and long infectious times, as well as for Model 2, which has Weibully distributed exposure times, an exponential decay intervention, and long infectious times. Based on 7,000 realization each.

Model	Parameter	Median	95% Central Credible Interval
Model 1	Mixing	0.91	(0.43, 1.72)
Model 2	Mixing	1.23	(0.89, 1.66)
Model 1	Spring Break	−0.59	(−2.21, 0.22)
Model 2	Spring Break	−0.21	(−0.82, 0.21)
Model 1	Public Awareness	0.08	(0.03, 0.13)
Model 2	Public Awareness	0.04	(0.03, 0.06)
Model 1	Mean Exposure	18.88	(11.60, 25.23)
Model 2	Mean Exposure	17.25	(16.93, 18.07)
Model 1	R0	10.01	(4.73,18.92)
Model 2	R0	13.69	(9.91, 18.48)
Model 1	Predicted Epidemic Size	15	(5, 126)
Model 2	Predicted Epidemic Size	64	(37, 195)

The autocorrelations for the posterior draws are also of interest. Geweke’s criterion was used to assess burn in, as was done in Section 3. After burn in, we see lower autocorrelation in PS SEIR mixing parameters found in Table 3 as compared to their corresponding population averaged parameters. The mixing parameter ϕ₁ has a lag 10 autocorrelation of 0.10 for the PS approach, but is 0.65 in the population averaged approach. The spring break intervention has a lag 10 autocorrelation of 0.12 for the PS approach versus 0.55 for the population approach. The public health intervention has a lag 10 autocorrelation of 0.07 versus 0.81 for the PS approach versus the population averaged approach. However, the mean of the latent distribution has an autocorrelation of 0.91 in the PS SEIR model versus 0.66 in the population averaged model. The cross correlations between the chains are similar for both models.

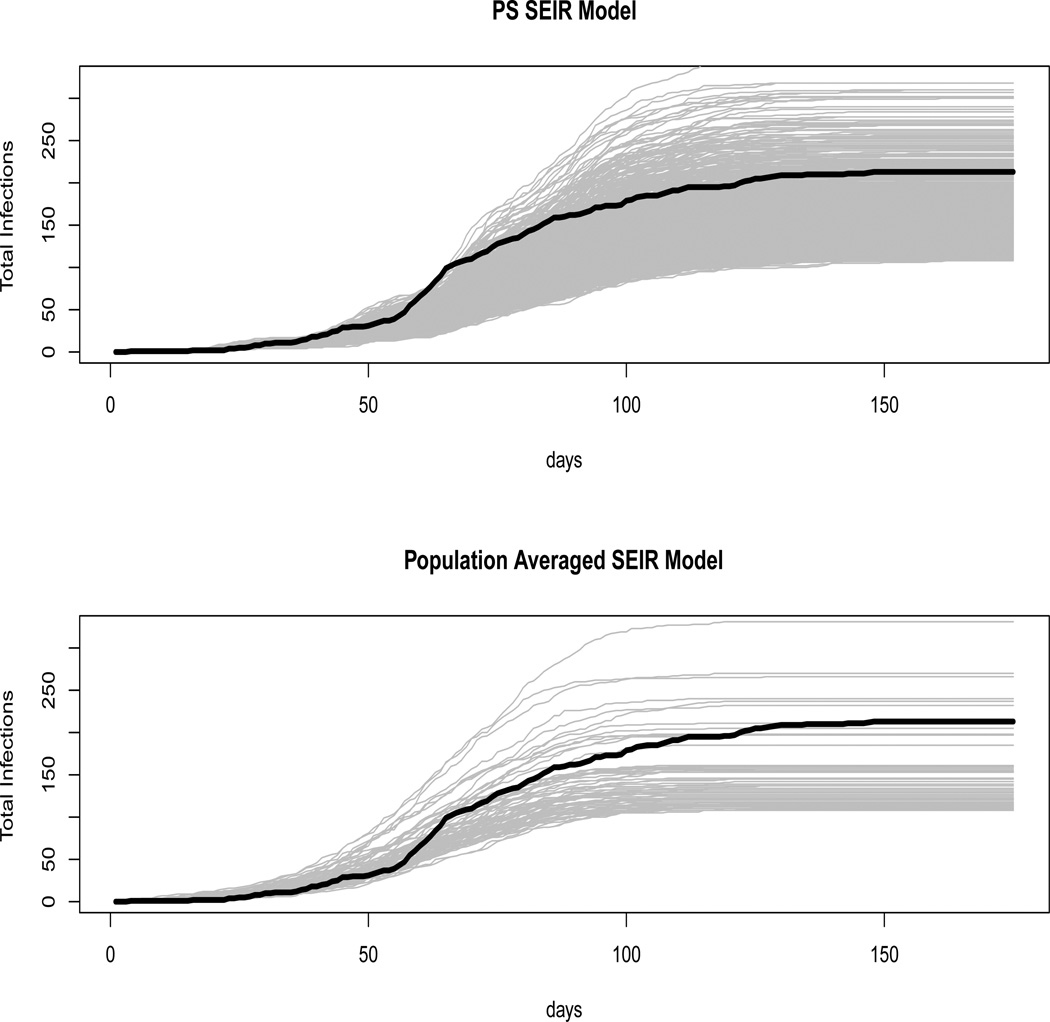
Figure 1 graphs the epidemic curves that fell in the reasonable range for the best fitting PS SEIR model as well as those for the corresponding population averaged model. One can see that the PS SEIR model provides far more predicted epidemics in the reasonable range (21.84% versus 2.84%). Additionally, the shape of the epidemic is fit more accurately with the PS SEIR approach. Those epidemics that fall into the reasonable range in the population approach tend to overestimate the epidemic size early on, whereas the PS SEIR approach provides a more accurate envelope of the epidemic up until day 50. Around day 50, there is a sharp increase in the number of epidemics, a feature neither model captures well. However, the PS SEIR model captures the shape of the remainder of the epidemic as well, with many more curves above the epidemic. Recall that it was expected that the final epidemic size would be underestimated because only the confirmed cases were used. For this data set, the PS SEIR model captured the true form of the epidemic better than the population averaged approach.

Figure 1.

Upper: Accepted epidemic curves for the PS SEIR model with Weibull latent and infectious times, exponential public health intervention and long infectious distributions. Lower: Accepted epidemic curves for the same population averaged model. Gray curves are model predictions while the black curve is the actual epidemic.

5. Discussion

The path-specific formulation typically offers improvement over the population averaged approach to modeling epidemics. In simulation studies, where all the parametric forms of the mixing and intervention processes were known, the path-specific approach typically performed as well as the population averaged approach in terms of the median values for these parameters and almost always gave narrower credible intervals for them. Very small differences in parameter realizations can be important in SEIR modeling, especially in the mixing parameter.

We also note that, in the real data analysis performed on the Iowa mumps epidemic, the PS SEIR model yielded substantially more reasonably sized predicted epidemics than the population-averaged approach. In fact, the best PS SEIR model yielded over seven times as many reasonable epidemic size predictions as the best population averaged model, as based on the statistic defined in Section 4. For this reason, we recommend the path-specific approach be used when analyzing epidemics related to infectious diseases with latent and infectious periods that are not exponentially distributed.

Additionally, there were two unrelated initial cases. The population averaged approach does not handle such a structure well, while the PS SEIR model can handle it quite easily. For the second initial case, which occurred in Dubuque County, we set the individual as having a latent infection for fourteen days previous to the start of the epidemic, which yields a total latent period of seventeen days for that individual. This minimizes the effect on the latent distribution posterior, and is supported by prior knowledge regarding the length of the latent period of mumps. The population averaged model will analyze this as a three day latent period, which may have some effect on the posteriors of the parameters.

There are limitations for our Iowa mumps epidemic analysis. First, the infectiousness of individuals is constant throughout their infectious periods. This is unrealistic, but required by the current form of the PS SEIR model. Secondly, homogeneous mixing is violated in this analysis. Thirdly, vaccinations were handled in a rather naive way, which may affect the accuracy of the mixing and intervention parameters.

Despite these limitations, we have demonstrated that the path-specific approach can yield much more accurate SEIR models for epidemics than the population averaged approach, and avoids many of the weaknesses of the current SEIR and SIR models allowing for general latent and infectious time distributions.