A semi-parametric censoring bias model for estimating the cumulative risk of a false-positive screening test under dependent censoring

Summary

False-positive test results are among the most common harms of screening tests and may lead to more invasive and expensive diagnostic testing procedures. Estimating the cumulative risk of a false-positive screening test result after repeat screening rounds is therefore important for evaluating potential screening regimens. Existing estimators of the cumulative false-positive risk are limited by strong assumptions about censoring mechanisms and parametric assumptions about variation in risk across screening rounds. To address these limitations, we propose a semi-parametric censoring bias model for cumulative false-positive risk that allows for dependent censoring without specifying a fixed functional form for variation in risk across screening rounds. Simulation studies demonstrated that the censoring bias model performs similarly to existing models under independent censoring and can largely eliminate bias under dependent censoring. We used the existing and newly proposed models to estimate the cumulative false-positive risk and variation in risk as a function of baseline age and family history of breast cancer after 10 years of annual screening mammography using data from the Breast Cancer Surveillance Consortium. Ignoring potential dependent censoring in this context leads to underestimation of the cumulative risk of false-positive results. Models that provide accurate estimates under dependent censoring are critical for providing appropriate information for evaluating screening tests.

1. Introduction

Screening a healthy population confers benefits and harms. In the case of screening tests with little inherent risk, such as screening mammography, one of the most common harms is that of false-positive test results, which lead to additional and possibly more invasive diagnostic testing. However, differing approaches to estimating the cumulative false-positive risk produce widely varying estimates. For instance, false-positive mammography results affect an estimated 14% of women at their first screening examination and 8% at subsequent examinations (Yankaskas et al., 2005). Estimates of the cumulative risk after 10 rounds of repeat screening vary from 58% to 77% based on the choice of statistical methodology (Hubbard et al., 2010). A flexible approach that provides unbiased estimates is needed to inform evaluation of guidelines calling for repeat screening.

Guidelines typically recommend repeat screening beginning at a target initiation age and continuing at some specified frequency until a stopping age. For instance, the U.S. Preventive Services Task Force (USPSTF) recommends biennial screening mammography for women age 50–74 years with screening from 40–49 based on personal choice (USPSTF, 2009). Estimating the cumulative false-positive risk for such a regimen requires data from multiple rounds of screening or assumptions about how screening test performance changes across rounds. Typically, observational data are available for a heterogeneous group of patients, some who comply with screening guidelines and others who deviate from them. Statistical methods are needed that allow us to use these data to make inference on the harms associated with repeat screening.

Several approaches have been used to estimate the cumulative false-positive risk associated with repeat screening tests. The cumulative probability of a false-positive test result can be considered the cumulative incidence function in a discrete survival model. The event time is the screening round at which the first false-positive test result occurs and the censoring time is the number of screening rounds observed for a participant. This approach has been used to estimate the cumulative false-positive risk of screening mammography (Elmore et al., 1998; Gelfand and Wang, 2000; Christiansen et al., 2000). It is limited by an assumption of independence of event and censoring times, which may be violated in the case of screening mammography (Xu et al., 2004; Hubbard et al., 2010). Alternative methods that relax this assumption have been proposed (Xu et al., 2004; Hubbard et al., 2010), but these rely on untestable assumptions about false-positive risk following censoring.

The objective of this paper is to develop a flexible, semi-parametric approach to estimating the cumulative false-positive risk of repeat screening that can be employed broadly across different screening modalities and observation schemes. We propose a semi-parametric censoring bias model to account for dependent censoring while relaxing parametric assumptions required by previous models. Our semi-parametric approach consists of a non-parametric discrete survival model augmented by a censoring bias model. This work was motivated by the censoring bias approach of Scharfstein et al. (2001). In Section 2 we describe existing models and propose our new semi-parametric model. We then describe estimation methods and discuss methods for incorporating covariate effects to allow for estimation of personalized risks. In Section 3 we compare the small sample properties of alternative estimators via a simulation study. Finally, we illustrate the use of these models using data on screening mammography from the Breast Cancer Surveillance Consortium (BCSC). We conclude with a summary and discussion of results in Section 4.

2. Methods

2.1 Definitions and Notation

Let Y_i be a binary indicator of the outcome of the ith screening exam, which takes the value 1 if the test result is a false-positive and 0 otherwise. Further, let Y_i = (Y₁, …, Y_i) represent the vector of all screening test outcomes up to time i. Let W represent the screening round at which the first false-positive test result is received and S represent the total number of screening rounds a subject is observed to participate in. We assume subjects are observed for a maximum of M screening rounds. Note that if S < W then W is unknown. However, if W ≤ S we still observe the subject subsequent to the false-positive result and hence both S and W are known. We assume that Y_i is available for a subject up to the end of study follow-up or the time at which he or she discontinues screening or is lost to follow-up.

Our objective is to estimate the cumulative probability of having received a false-positive test result after adhering to a screening program for k rounds, P(W ≤ k). Estimation may focus on the impact of screening at the population-level or may condition on patient or screening program characteristics, in which case the estimand takes the form P(W ≤ k|·). We define $P(W\le k)={\sum }_{i=1}^{k}P(W=i)={\sum }_{i=1}^{k}P(Y_i=1\mid {\mathit{Y}}_{i-1}=\mathbf{0}){\prod }_{j=1}^{i-1}P(Y_j=0\mid {\mathit{Y}}_{j-1}=\mathbf{0})$, where P(Y₀ = 0, Y₁ = 1) and P(Y₁ = 1|Y₀ = 0) are defined to be P(Y₁ = 1) and an empty product is taken to be 1.

Let the probability of a false-positive result at the kth round among subjects attending a total of j screening rounds and with no prior false-positive results be denoted θ_jk ≐ P(Y_k = 1|Y_k−1 = 0, S = j). The cumulative false-positive probability can then be defined as

$$\begin{array}{l}P(W\le k)=\sum _{l=1}^{M}P(S=l)\sum _{i=1}^{k}P(Y_i=1\mid {\mathit{Y}}_{i-1}=\mathbf{0},S=l)\prod _{j=1}^{i-1}P(Y_j=0\mid {\mathit{Y}}_{j-1}=\mathbf{0},S=l)\\ =\sum _{l=1}^{M}P(S=l)\sum _{i=1}^k{\theta }_{li}\prod _{j=1}^{i-1}(1-{\theta }_{lj}).\end{array}$$ (1)

2.2 Review of Existing Models

2.2.1 Discrete Time Survival Model

A discrete time survival model can be used to estimate the cumulative false-positive risk. This model assumes that censoring and event times are independent, that is, false-positive risk does not depend on the number of observed screening rounds. If this holds then the cumulative false-positive risk can be written as

$$P(W\le k)=\sum _{i=1}^k{\theta }_i\prod _{j=1}^{i-1}(1-{\theta }_j),$$ (2)

where θ_i = P(Y_i = 1|Y_i−1 = 0). A formal test of the independence assumption was proposed by Xu et al. (2004). Estimation can be carried out using maximum likelihood (ML) or Bayesian methods (Gelfand and Wang, 2000).

2.2.2 Population Average Model

Recognizing that the independence assumption is often violated in the case of medical screening tests, Xu et al. (2004) proposed an alternative approach, herein referred to as the population average model. This model explicitly takes into account the possibility that false-positive risk may be related to the number of screening rounds a subject is observed to participate in by estimating the cumulative false-positive risk via equation (1). From a medical decision making and policy perspective, this approach estimates the total false-positive burden associated with the screening program if all eligible individuals were to participate in all recommended rounds of screening rather than the false-positive risk only among those who were observed to participate in all rounds of screening. However, additional assumptions are required because Y_i is unobserved for i > S. The specific assumption proposed by Xu et al. (2004) is that P(W = j|S = i) = μ_i(1 − μ_i)^j−1.

This model assumes constant risk across screening rounds, an assumption that is fundamentally unverifiable. This is unrealistic in some screening contexts. For instance, risk is substantially higher at the first screening mammogram compared to subsequent mammograms (Yankaskas et al., 2005; Hubbard et al., 2010). This is likely due to the availability of comparison images at subsequent mammograms, which allow the radiologist to focus on changes in the image (Hubbard et al., 2011). In general, a more flexible approach is required.

2.2.3 Adjusted Population Average Model

Hubbard et al. (2010) proposed an extension to equation (1) using an alternate set of assumptions about false-positive risk following censoring. Specifically, we model θ_jk as

$$log\frac{{\theta }_{jk}}{1-{\theta }_{jk}}={\beta }_{j1}+{\beta }_{2}1(k>1)+\alpha (k-1).$$ (3)

Under this model, the log odds of a false-positive result at the first exam, β_j1, varies as a function of censoring time. However, changes in false-positive risk across screening rounds are assumed independent of censoring time. Assuming β₂ and α are independent of S identifies θ_jk for j < k. Like the population average model, this model relies on parametric assumptions about false-positive risk following censoring. For instance, this model will not be adequate if the rate of change of false-positive risk across screening rounds depends on S. This specific model was motivated by the case of screening mammography because in that context risk is expected to differ across screening rounds. However, it may not be appropriate in other screening contexts.

2.3 A Semi-parametric Censoring Bias Model

2.3.1 Model Specification

To accommodate estimation of the cumulative false-positive risk under dependent censoring without requiring specific parametric assumptions about risk following censoring, we propose a censoring bias model. This approach uses equation (1) to estimate the cumulative false-positive risk but identifies P(W = k|S = j) for j < k by using information from all subjects with more than j screening rounds, assuming that

$$P(W=k\mid S=j)=\frac{P(W=k\mid S>j)q_{jk}(\alpha )}{{\sum }_{i=1}^{M+1}P(W=i\mid S>j)q_{ji}(\alpha )},$$ (4)

where P(W = M + 1|S = j) is defined to be P(W > M|S = j) and q_jk(α) is a censoring bias function governing the relationship between the false-positive risk among subjects with S = j and those with S > j. The censoring bias function can be any positive valued function. In numerical examples below we use q_jk(α) = exp(α(k − (j + 1))).

In typical survival contexts, α is non-identifiable because we never observe both S and W. However, in the special case of screening test results, α is estimable. Specifically, if we assume the functional form of q_jk(α) is known, then letting j = M, we can solve equation (4) for α for any value of k. Depending on the specific functional form chosen for q_jk(α) a closed form solution may not be available for α. However, numerical techniques can easily be applied to obtain the solution.

The advantage of the censoring bias model over existing models is that it allows for both dependent censoring and changes in false-positive risk across screening rounds without requiring parametric assumptions about variation in risk across screening rounds following censoring. In this model false-positive risk is inherently assumed to vary across screening rounds in the same way for subjects with S = j rounds as for subjects with S > j rounds of screening. However, variation in risk is not constrained to follow a specific functional form.

2.3.2 Estimation

The censoring bias parameter, α, can be directly estimated from the available data using equation (4). This approach assumes that a single value of α holds for all j and k and that the relationship between censoring time and false-positive risk is the same when the first false-positive precedes censoring as it would be if censoring precedes the first false-positive. Because these assumptions are strong and untestable, a sensitivity analysis may be preferred to investigate the sensitivity of results to various degrees of dependent censoring, following the approach of Scharfstein et al. (1999). We recommend estimating the cumulative false-positive risk conditional on α estimated using equation (4) as well as a variety of larger and smaller values for α.

ML or Bayesian estimates for θ_jk for all k ≤ j are directly available. For k > j, estimates of θ_jk can be obtained by substituting values for α̂ and θ̂_jk into equation (4). Substitution proceeds in an iterative fashion with estimates first obtained for j = M − 1. Using these estimates it is then possible to estimate θ̂_jk for j = M − 2 and so on until θ̂_jk has been estimated for all j and k.

Under the Bayesian paradigm and assuming estimation is carried out using a Markov Chain Monte Carlo approach, variance estimates for θ̂_jk are readily available based on their simulated posterior distribution. Under ML estimation, variance estimates for θ̂_jk for k ≤ j are directly available because these model parameters are estimated directly from the data. Below we obtain expressions for the approximate variance of ML estimates of θ_jk when k > j.

Let N_j+k represent the number of events at the kth round among subjects with S > j and N_j+ represent the total number of subjects with S > j. The MLE for P(W = k|S > j) is N_j+k/N_j+. By the invariance property of MLEs and assuming α fixed and known,

$${\widehat{\theta }}_{jk}=\frac{q_{jk}(\alpha )N_{j+k}/N_{j+}}{{\sum }_{i=1}^M{q}_{ji}(\alpha )N_{j+i}/N_{j+}}=\frac{q_{jk}(\alpha )N_{j+k}}{{\sum }_{i=1}^M{q}_{ji}(\alpha )N_{j+i}}.$$

The numerator is the expected number of events that would have been observed at round k for subjects with S = j after rescaling by q_jk(α) and the denominator is the total number of events that would have been observed across all screening rounds for subjects with S = j. Considering q_jk(α)N_j+k a count of “pseudo-events” that would have been observed at time k if data were not censored and ${\sum }_{i=1}^{M+1}{q}_{ji}(\alpha )N_{j+i}$ as a pseudo-count of the total population of events that would have been observed if not for censoring suggests that the variance of θ̂_jk can be approximated by using the standard variance estimator for the MLE of the mean of a binomial distribution, $\text{Var}({\widehat{\theta }}_{jk})={\widehat{\theta }}_{jk}(1-{\widehat{\theta }}_{jk})/{\sum }_{i=1}^{M+1}{q}_{ji}(\alpha )N_{j+i}$.

We evaluate the performance of the approximate variance estimator in Section 3.

2.4 Regression Models for Cumulative False-positive Risk

False-positive risk may vary as a function of patient, provider, or screening program characteristics. For an individual evaluating screening regimens, a personalized estimate of the cumulative false-positive risk conditional on patient characteristics and characteristics of the regimens under consideration can aid decision making. Characteristics may be non-time-varying, such as patient sex or race/ethnicity, or may vary over time, such as interval between screening exams. For time-varying characteristics, it may be of interest to estimate a predicted cumulative false-positive risk for a hypothesized sequence of values. For instance, interest may focus on the cumulative false-positive risk associated with a regimen of exams separated by a recommended interval. However, it is important to note that such estimates are associational and not causal in nature. That is, they provide information on the estimated false-positive risk based on patients who were observed to follow a particular screening pattern. These estimates could be confounded by covariates associated with screening interval and screening test results. Comparisons of false-positive risks across screening programs may also be of interest. If patient characteristics are associated with false-positive risk and differ across programs then adjusted estimates can be obtained by estimating false-positive risks conditional on patient characteristics and then using marginal standardization to obtain estimates adjusted to a common distribution of patient characteristics.

In the case of a screening test subject to physician interpretation, variability between providers may also be important to consider. Between-provider variation may be attributable to observed provider characteristics such as years of experience, which can be included in models as fixed effects, or unobserved characteristics, in which case we can estimate provider-specific random effects. We can use these models to provide predicted cumulative false-positive risks for a set of provider characteristics or levels of provider performance. Such estimates aid in understanding provider characteristics associated with better performance and quantify the extent of between-provider variation, which is often of interest as a measure of clinical quality.

We extend our model for cumulative false-positive risk to allow for estimation of predicted cumulative false-positive probabilities individualized for a given set of screening-program, patient, and provider characteristics. To do so we propose a regression model for θ_jk, $log({\theta }_{jk}({\mathit{X}}_k;\gamma )/(1-{\theta }_{jk}({\mathit{X}}_k;\gamma )))={\mathit{X}}_k^{\prime }{\beta }_{jk}+\gamma$, where X_k is a vector of exam-specific covariates and γ is a provider-specific random effect assumed to arise from a known distribution with unknown parameters. Although this model is flexible enough to handle variation in covariate effects across screening rounds and censoring times, in general we will assume that covariate effects are constant, β_jk = β for all j, k.

This regression formulation for θ_jk can be directly incorporated into any of the four models in Sections 2.2 and 2.3. In the case of the discrete survival model θ_i is replaced by θ_i(X_k; γ) in equation (2). In the population average and censoring bias models, a similar substitution is made in equation (1). Terms for fixed and random effects can be added directly to equation (3) for the adjusted population average model.

An alternative method for incorporating covariate effects into the population average model was proposed by Xu et al. (2004). In their formulation a regression model is constructed for the multivariate outcome, W = {I(W = 1), I(W = 2), …, I(W = j), I(W > j)}, given S = j. Covariate effects are estimated using a multinomial logistic regression of the form $log(P(\mathit{W}=k\mid S=j)/P(\mathit{W}>k\mid S=j))={\mathit{X}}_k^{\prime }{\beta }_{jk}$, where (W = k) = (Y₁ = 0, …, Y_k = 1). This formulation models the association between the time of the first false-positive and covariates. By comparison, our approach estimates the association between the odds of a false-positive at each individual screening round and covariates. The advantage of the latter formulation is that the specific effect of covariates on individual screening rounds can be estimated and variations in covariate effects across screening rounds can be identified.

Estimation can be carried out using ML or Bayesian estimation methods for β_jk and γ. Using the invariance property of the MLE, β̂_jk can then be substituted into equation (1) to obtain MLEs for P̂(W ≤ k|X_k). Variance estimates can be obtained either via the delta method or bootstrapping. In our application to the BCSC presented below, bootstrap standard errors were used for the censoring bias model and the delta method was used for other models. These cumulative probabilities can be interpreted as predicted cumulative false-positive risks associated with a specific set of characteristics.

2.5 Disease diagnosis and death as competing risks

Observations may be censored for a number of reasons including loss to follow-up, lack of participation in future screening, and the end of the study. Subjects may also experience events that make future screening tests impossible, such as death. Often diagnosis with the disease of interest also makes future screening impossible because either no future testing is carried out or subsequent examinations are considered diagnostic or surveillance rather than screening. If subjects are censored at the time of death or disease diagnosis, the four methods described above estimate the latent false-positive risk had the censoring event not occurred. For subjects who have been censored due to loss to follow-up, this latent risk is meaningful as it represents the risk they would have experienced had they continued to be observed to screen. However, for subjects who have died or been diagnosed with the disease of interest, this quantity is not meaningful. Death and disease diagnosis should be thought of as competing events in this context.

The above approaches to estimating the false-positive risk can be modified to provide cumulative false-positive estimates in the presence of competing risks. Let D_k = 1 be a binary variable taking the value of 1 if disease diagnosis or death has occurred prior to the kth screening round and 0 otherwise. We further define ${\theta }_{jk}^C=P(Y_k=1\mid {\mathit{Y}}_{k-1}=\mathbf{0},S=j,D_k=0)$. The cumulative false-positive risk accounting for competing risks is

$$P(W\le ,D_k=0)=\sum _{l=1}^M\sum _{i=1}^{k}P(S=l)P(D_i=0){\theta }_{li}^C\prod _{j=1}^{i-1}(1-{\theta }_{lj}^C).$$ (5)

We can use the four methods described above to estimate ${\theta }_{jk}^C$. Because ${\theta }_{jk}^C$ is conditional on D_k = 0, estimates incorporate information from subjects who experience a competing event only prior to the competing event. Estimates treating disease diagnosis and death as competing events may not differ greatly from those ignoring the presence of competing risks if these are rare events in the population of interest. However, for more common diseases the difference may be substantial.

3. Applications

3.1 Simulation Study

We evaluated the small sample properties and performance under model misspecification of the four models discussed in Section 2 using a simulation study. The target of inference in our simulations was the cumulative probability of false-positive results after 10 rounds of screening, P(W ≤ 10). The small sample properties of these models are important to understand because, even in a large sample, the number of subjects observed for many rounds may be small. For the censoring bias model, we estimated α using equation (4) and the approximate variance estimator described in Section 2.3.

3.1.1 Simulation Study Design

We conducted simulations to compare bias and efficiency of the models for cumulative false-positive risk under seven scenarios for variation in risk as a function of censoring time and screening round. In Scenario 1, false-positive risk is independent of censoring time and constant across screening rounds. This scenario satisfies the assumptions of all four models. In Scenario 2, false-positive risk is independent of censoring time but decreases across screening rounds. This violates the assumptions of the population average model. In Scenario 3, false-positive risk is dependent on censoring time and decreases across screening rounds. This violates the assumptions of the discrete survival and population average models. The relationship between false-positive risk and censoring time is also misspecified in the censoring bias model. In Scenario 4, censoring is dependent on time of the first false-positive result but false-positive risk is constant across screening rounds. This violates the independence assumption of the discrete survival model. Additionally, the relationship between false-positive risk and censoring time is misspecified in the adjusted population average model. For scenarios 2, 3, and 4 we investigated two sets of parameter values governing the strength of dependence of false-positive risk and censoring time.

In scenarios 1, 2, and 3, we assumed that the relationship between the probability of a false-positive at the kth screening round for a subject with no prior false-positives and who was observed for j screening rounds was given by

$$P(Y_k=1\mid {\mathit{Y}}_{k-1}=\mathbf{0},S=j)=A-B(k-1)/9-C(j-1)/9+D(j-1)((k-1)/9.$$

Specific values for A, B, C, and D used in each simulation scenario are provided in Table 1 along with the associated cumulative probability of a false-positive after ten screening rounds, P(W ≤ 10). In simulation 4, we assumed that false-positive risk followed the model P(W = k) = 0.09 × (1−0.09)^k. Conditional on simulated values for W, censoring times were then simulated according to equation (4). We set α = −0.005 and −0.01.

Table 1.

Parameter values used to simulate data and associated cumulative probability of a false-positive after 10 rounds (P(W ≤ 10)).

Scenario	Strength of dependence	A	B	C	D	P (W ≤ 10)
1	Independent	0.08	0	0	0	0.565
2	Moderate	0.10	0.02	0	0	0.611
2	Strong	0.10	0.06	0	0	0.517
3	Moderate	0.20	0.05	0.05	0.0056	0.780
3	Strong	0.20	0.10	0.10	0.011	0.750

For all simulation scenarios we generated a cohort of 100,000 subjects. In simulations 1, 2, and 3, we assumed that censoring times were geometrically distributed with rate 0.3. Estimates for our simulation study are based on 10,000 simulated data sets for each scenario.

3.1.2 Simulation Study Results

Under independent censoring with constant risk across screening rounds (Scenario 1), all three models were unbiased (Table 2). Under independent censoring with variable risk across screening rounds (Scenario 2), the discrete survival model and censoring bias model demonstrated low bias. The adjusted population average model was less biased then the population average model. However, under strong variation in risk across screening rounds, both models exhibited substantial bias. Under dependent censoring and variation in risk across screening rounds (Scenario 3), the discrete survival and population average models exhibited more bias than the adjusted population average and censoring bias models. Under moderate dependence and variation in risk, the censoring bias model was approximately unbiased. When dependence and risk variation were stronger, the adjusted population average and censoring bias models performed similarly. Both of these models reduced bias relative to the discrete survival and population average models by more than half. When risk of censoring was dependent on screening round of the first false-positive and risk was constant across screening rounds (Scenario 4), bias was reasonably low for all models. Only the discrete survival model exhibited notable bias under stronger dependence.

Table 2.

Percent bias, model-based standard errors (SE), and empirical standard errors (ESE) for four estimators for cumulative risk after ten rounds of screening for simulated data.

	Moderate dependence			Strong dependence
	% Bias	SE	ESE	% Bias	SE	ESE
Scenario 1: Independent censoring, constant risk
Discrete survival	−0.002	0.005	0.009
Population average	−0.009	0.003	0.005
Adjusted population average	0.007	0.005	0.009
Censoring bias	−0.094	0.010	0.015
Scenario 2: Independent censoring, variable risk
Discrete survival	−0.007	0.005	0.008	−0.010	0.004	0.008
Population average	5.209	0.003	0.005	20.552	0.003	0.005
Adjusted population average	1.574	0.004	0.007	7.043	0.004	0.008
Censoring bias	−0.072	0.011	0.010	−0.074	0.009	0.018
Scenario 3: Dependent censoring, variable risk
Discrete survival	−4.708	0.004	0.005	−11.376	0.004	0.005
Population average	9.630	0.001	0.002	10.148	0.002	0.002
Adjusted population average	3.576	0.003	0.004	3.940	0.003	0.004
Censoring bias	−0.809	0.013	0.010	−4.435	0.011	0.007
Scenario 4: Dependent censoring, constant risk
Discrete survival	−1.993	0.019	0.032	−3.976	0.018	0.031
Population average	0.696	0.003	0.006	0.709	0.003	0.006
Adjusted population average	1.280	0.011	0.018	2.339	0.011	0.018
Censoring bias	−0.699	0.027	0.067	−1.022	0.025	0.070

Across all scenarios, model based standard errors tended to underestimate true standard errors. The censoring bias model was also less efficient than other models, although our proposed approximate standard errors tended to approximate empirical standard errors well.

3.2 Application to the BCSC

We illustrate the performance of the four models for false-positive risk using data collected by seven mammography registries in the National Cancer Institute-funded BCSC (Ballard-Barbash et al., 1997) (http://breastscreening.cancer.gov). These registries link information on women who receive a mammogram at a participating facility to regional cancer registries and pathology databases to determine breast cancer outcomes.

We included women who had their first screening mammogram between the ages of 40 and 59 at a participating BCSC facility. We included this first screening mammogram along with subsequent screening mammograms performed from 1994 to 2007. A screening mammogram was defined as a bilateral mammogram that the interpreting radiologist indicated was for routine screening. To avoid misclassifying diagnostic exams as screening exams, we excluded mammograms performed within 9 months of a prior breast imaging exam.

Mammograms were classified as positive or negative using standard BCSC definitions (see BCSC Glossary of Terms accessed at http://breastscreening.cancer.gov/data/bcsc_data_definitions.pdf) based on the initial Breast Imaging Reporting and Data Systems (BI-RADS) assessment (American College of Radiology, 2003) and recommendations assigned by the radiologist. A positive mammogram was considered to be a false-positive if the woman was not diagnosed with invasive carcinoma or ductal carcinoma in situ within 1 year of the mammogram and prior to the next screening mammogram. We censored women at their last screening mammogram captured by the BCSC or if their self-reported time since last mammogram differed from that in the database by more than six months since women could receive mammograms outside the BCSC. Breast cancer diagnoses, including true-positive screening exam results, and deaths were treated as competing events.

We demonstrate the performance of the four models introduced in Section 2 when applied to estimating the cumulative false-positive risk after 10 rounds of screening mammography. To illustrate how covariates can be incorporated into each model to provide personalized risk estimates, we modeled false-positive risk conditional on age at baseline, family history of breast cancer at baseline, and interval between screening mammograms. We categorized age in two year age groups from age 40 – 59. Interval was categorized as 9–18 months (approximately annual), 19–30 months (approximately biennial), or no prior mammogram within 30 months. We report example cumulative false-positive estimates after 10 years associated with approximately annual screening beginning at age 40–41 or 50–51, with or without a family history of breast cancer at baseline.

In the BCSC cohort, 276,159 mammograms from 143,025 women met inclusion criteria. The majority of women were observed for one or two rounds of screening (69.8%). A summary of the distribution of number of observed rounds of screening, baseline age, and baseline family history is presented in Table 3. The probability of receiving a false-positive mammogram at the first screening round was somewhat lower for women who were observed for 5 or more rounds of screening compared to women who were observed for fewer rounds. False-positive risk at the first screening mammogram also increased with increasing baseline age up until age 52. False-positive risk then began to decrease with increasing age. Risk was higher for women who had a family history of breast cancer at baseline.

Table 3.

The distribution of number of observed rounds of screening, age at first mammogram, and family history of breast cancer at the time of the first mammogram for 143,025 women along with the proportion of women within each category with a false-positive mammography result at their first mammogram.

	N	%	% false-positive at first exam
Number of screening rounds observed
1	71,440	49.9	17.2
2	28,500	19.9	16.3
3	16,584	11.6	16.8
4	10,552	7.4	15.7
5	6,889	4.8	16.1
> 5	9,060	6.3	13.9
Age at first exam
40–41 years	55,145	38.6	15.8
42–43 years	24,005	16.8	16.3
44–45 years	15,358	10.7	17.3
46–47 years	11,406	8.0	17.4
48–49 years	9,080	6.3	18.3
50–51 years	9,184	6.4	18.4
52–53 years	6,355	4.4	17.9
54–55 years	4,893	3.4	17.8
56–57 years	4,041	2.8	15.4
58–59 years	3,558	2.5	15.5
Family history at first exam
No	133,771	93.5	16.5
Yes	9,254	6.5	18.6

For each woman in the study we identified the reason study follow-up had ended. If the mammogram occurred within 2 years of the end of the study we considered the woman censored by the end of follow-up. If the mammogram was followed by a breast cancer diagnosis or death within 2 years we considered this the reason for the end of follow-up. All other women were considered censored by loss to follow-up. Loss to follow-up thus includes women who received no further mammograms and those who continued participating in screening but attended facilities outside the BCSC. Follow-up ended for most women due to either loss to follow-up (61.7%) or the end of the study (36.9%) (Table 4).

Table 4.

Distribution of reasons for end of follow-up in the BCSC database.

	N	%
Loss to follow-up	88,291	61.7
End of study	52,719	36.9
Breast cancer diagnosis	1,251	0.9
Death	764	0.5

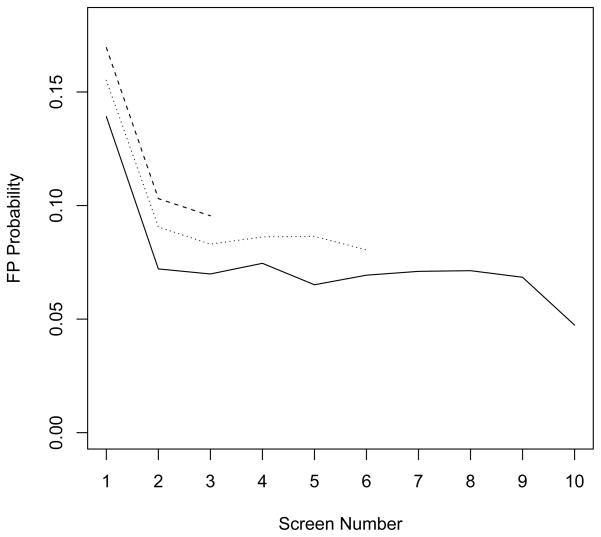
The relationship between false-positive risk, screening round, and censoring time is illustrated in Figure 1. Risk decreases substantially between the first and second screening rounds, regardless of the number of observations available per subject. At any individual screening round, false-positive risk appears lower for women with more observations and higher for women with fewer observations. While observable trends in false-positive risk cannot validate assumptions about false-positive risk following censoring, these trends suggest a decreasing trend in false-positive risk between the first and second rounds that may be independent of censoring time. They are also suggestive of an association between censoring time and false-positive risk.

Figure 1.

False-positive risk at screening rounds 1 to 10 by censoring time. Solid line represents subjects with 7 or more observations, dotted line represents subjects with 4 to 6 observations, and dashed line represents subjects with 1 to 3 observations.

We applied each of the four models for cumulative false-positive risk to this cohort to estimate cumulative risk after 10 rounds of annual screening (Table 5) personalized based on age at first examination and baseline family history of breast cancer. We present example results for women who were 40–41 or 50–51 at baseline with or without a family history of breast cancer. Cumulative false-positive estimates based on the discrete survival model were lowest while those based on the population average model were highest. The adjusted population average and censoring bias models which both allow for dependent censoring and variation in the false-positive risk across screening rounds returned intermediate cumulative false-positive risk estimates. These models were also similar in terms of precision. For the censoring bias model, we estimated α to be -0.04. For the four example covariate combinations presented, all four models estimated that risk is highest for women who begin screening at age 50–51 with a family history of breast cancer and lowest for women who begin screening at age 40–41 without a family history of breast cancer.

Table 5.

Estimated cumulative probability of a false-positive mammography result after 10 rounds of annual screening by baseline age and family history based on four models.

	Discrete survival	Population average	Adjusted population average	Censoring bias
Age 40–41 years at first exam
No family history	57.3 (55.4, 59.1)	65.2 (64.5, 65.9)	63.3 (61.6, 65.0)	61.3 (59.4, 63.1)
Family history	60.4 (58.4, 62.5)	68.6 (68.0, 69.3)	66.6 (64.5, 68.6)	64.2 (62.0, 66.5)
Age 50–51 years at first exam
No family history	59.1 (57.1, 61.2)	67.0 (66.4, 67.7)	65.3 (63.3, 67.3)	63.1 (60.9, 65.3)
Family history	62.3 (60.1, 64.4)	70.4 (69.8, 71.1)	68.6 (66.3, 70.9)	66.0 (63.5, 68.6)

4. Discussion

We have proposed a semi-parametric censoring bias model for cumulative false-positive risk of a screening test. This model performs similarly to other existing approaches when censoring is independent of false-positive risk. When censoring is dependent on risk, especially when risk varies across screening rounds, previously proposed models exhibit substantial bias, which the censoring bias approach is largely able to eliminate. In cases such as screening mammography, where variations in risk across screening rounds are well understood, a parametric model that imposes a plausible functional form for variation in risk across screening rounds can also successfully estimate cumulative risk. However, this model would not be appropriate in settings where variation in risk across screening rounds is not well understood. The semi-parametric censoring bias approach would likely provide the best estimates in this setting.

We developed an approximate variance estimator for the censoring bias model. Simulation studies demonstrated that this approximation led to nearly unbiased estimates for the cumulative false-positive risk and variance estimates close to empirical variances. Like asymptotic variance estimators for the discrete survival, population average, and adjusted population average model, these estimates tended to underestimate empirical variance. This is likely due to the fact that all estimates rely heavily on the false-positive risk among subjects who are observed across all screening rounds. This group will be small if the proportion censored at each screening round is large. Asymptotic variance estimates may not be appropriate in this setting. By adopting a semi-parametric approach, the censoring bias model tends to be less efficient than other models considered here. This loss of efficiency may be preferable to the possible bias which will result from using misspecified parametric models.

We proposed a straightforward method for incorporating covariates into cumulative false-positive estimates using a regression framework. The ability to include covariates in models for false-positive risk is of particular importance for clinical decision making because it allows for personalized risk prediction. We demonstrated this approach in the setting of mammography by comparing estimates of cumulative false-positive risk after 10 years of annual screening for women who begin screening at age 40–41 or 50–51, with or without a family history of breast cancer at baseline. In the case of the specific example investigated, cumulative false-positive probabilities varied only modestly with respect to baseline age and family history. Clinical recommendations would likely not vary for these groups based on these differences. All four models demonstrated the same pattern of association between baseline age and family history and false-positive risk. However, point estimates for cumulative risk varied substantially across models. The population average model likely overestimated cumulative risk by assuming that risk does not vary across screening rounds when, in the case of mammography, it is expected to decrease (Yankaskas et al., 2005). Conversely, the discrete survival model likely underestimated risk by assuming that women who were censored later are representative of those who were censored earlier. Past research has shown that those who are observed for more rounds tend to have lower risk (Hubbard et al., 2010). The adjusted population average and censoring bias models produced similar estimates in this setting. Estimates from these two models also had similar precision.

The proposed models can be modified to incorporate competing events. Individuals diagnosed with the disease of interest during the course of screening are no longer at risk for a false-positive result. If disease diagnosis is treated as a censoring event then the resultant cumulative risk estimates the latent probability of the outcome of interest, had the competing event not occurred (Prentice et al., 1978). In the context of medical screening, diagnosis with the disease of interest, death, or surgical removal of the screened organ makes subsequent occurrence of screening logically impossible. Therefore, censoring at these competing risks leads to estimation of risks that are not meaningful. In many cases the risk of these competing outcomes will be small. In our study of breast cancer screening only 1.4% of women developed breast cancer or died during the study. However, depending upon the risk of disease and mortality in the population under study, these competing risks could be more substantial.

Understanding performance of screening tests after repeat screening is important for individuals, medical providers, and policy makers when considering the harms and benefits of repeat screening. The risk of a false-positive result at an individual screening round may be low, but if repeat screening is recommended over a period of decades, it is important to understand the risk of receiving false-positive results at some point over the course of screening. In future research we plan to investigate methods for estimating the cumulative probability of other repeat screening outcomes including cancer detection (true-positive results) and missed cancers (false-negative results). All of these possible screening outcomes must be considered jointly along with the possibility of dependent censoring when evaluating a proposed course of screening.