Summary
Several statistical approaches for the analysis of longitudinal data require that models be correctly specified for the association betweeen a current outcome and the full history of past outcomes and time-dependent exposures. It is empirically challenging to determine the specific aspects of the outcome and/or exposure history that are predictive of a current outcome because the potential number of variables representing the history can be quite large. The purpose of this manuscript is to outline statistical methods that can characterize lagged effcts and to provide a structured approach for data analysis with the goal of appropriate model development. One of the main contributions of the paper is to emphasize the possibility that in practice transition models may frequently require more than simple additive and linear models for the predictors representing the history of the outcome and covariate processes. We illustrate the concepts using an example from anemia treatment for dialysis patients and show how linear models can be specified with flexible dependence on exposure and/or outcome histories.
Keywords: longitudinal data analysis, time-dependent covariates, dependence
1. Introduction
A key advantage of conducting a longitudinal study is the opportunity to link prospectively measured exposure variables to subsequent individual level health effects. An important biomedical example is the recent research regarding potentially unintended effects of high-dose anemia treatment among dialysis patients (Zhang et al., 2009). Using routine claims data to evaluate the potential impact of high doses of epoetin alpha (Epo) on mortality requires careful statistical evaluation of treatment received in an observational study. Correction for “confounding by indication” where those subjects who are exposed to higher doses are not representative of the target population is necessary to draw proper scientific conclusions. Epoetin treatment is actively managed by increasing or decreasing the dose with the goal of obtaining target levels of hematocrit. Therefore, longitudinal values of hematocrit are both a consequence of past epoetin doses and a cause of future epoetin doses. One approach to correction for longitudinal selection bias is to use marginal structural models (MSM) which require estimation of exposure (treatment) probabilities given the full history of measured intermediate outcomes (Robins, 1998). In related research Brunelli et al. (2008) study the impact of hematocrit variation on mortality, while Cotter et al. (2008) study the effect of epoetin dose on hematocrit. Each of these studies uses marginal structural models and therefore build models for their respective primary exposures (e.g. for hematocrit or epoetin dose) conditional on the full clinical history.
When exposure variables are measured repeatedly over time any statistical analysis needs to explicitly detail key assumptions regarding both the nature of the dynamics of the exposure process itself, and the potential for both short-term (acute) and long-term (chronic) effects of the exposure on the primary outcome variable. First, the factors that drive changes in the exposure process need to be carefully considered since the potential for “feedback” or endogeneity are now well characterized (see chapter 12 of Diggle et al. (2002) for references). Second, key predictors of interest such as environmental exposures or specific treatment dosages are not simple scalar baseline values but rather are characterized by a longitudinal sequence of measurements. In order to correlate a longitudinal exposure process to subsequent individual outcomes either strong assumptions regarding biological effects of exposure need to be adopted, or a general dependence on the full exposure process needs to be considered for any longitudinal regression model. The goal of this manuscript is to overview a sequence of analysis steps that can characterize both simple and complex relationships between longitudinal exposures and outcomes. For data analysts using transition models we emphasize the importance of needing to consider models that are more complex than the commonly adopted conditional models using the exposure and outcome history as simple additive and linear predictors.
The data that motivate this manuscript come from the United States Renal Database System (USRDS) and focus on evaluation of a medication used to treat anemia. The USRDS is a comprehensive database of patients diagnosed with end-stage renal disease (ESRD) undergoing dialysis in the United States who are covered under the Medicare insurance program. We illustrate longitudinal analysis with two different response variables: the exposure of interest, epoetin alpha dose (Epo); and Hematocrit (Hemo), an intermediate variable; The motivation for modelling longitudinal Epo is the potential need to provide a model for exposure when conducting marginal structural model analysis of the effect of epoetin dose on death due to the fact that past hematocrit is used to determine the current epo dose, and the fact that hematocrit is an intermediate outcome. Models for hematocrit may also be used to provide causal inference regarding the effect of epoetin dose when using G-computation (Robins et al., 1999). The overall scientific objective is to determine whether these data suggest that drug exposure may be related to unintended harmful consequences, and in order to study mortality it is first necessary to understand exposure and intermediate outcome dynamics.
In section 2 we overview specific regression models where a multivariate exposure or a multivariate outcome history are used as predictors. In section 3 we detail both univariate and multivariate association models and comment on tools that can explore a potentially high-dimensional predictor space comprised of lagged exposures, outcomes, and possibly non-linear terms or interactions. Finally, we illustrate the main ideas using an example from anemia treatment among dialysis patients where models for a drug dose and an intermediate outcome are of interest.
2. Statistical Models with Lagged Effects
In this section we overview the scientific motivation for considering lagged covariates in the analysis of longitudinal data. First, we comment on analysis with time-dependent exposure histories where interest may be in acute effects of exposure, chronic effects of exposure, or both. Second, we comment on “transition models” where both past exposure and past outcomes are used as predictors for a current outcome variable as described in chapter 10 of Diggle et al. (2002). Finally, we comment on selection models for drop-out (see chapter 17 of Verbeke and Molenberghs (2000)) and exposure models used in marginal structural models (MSMs) where models are used to weight for endogenous selection bias (Robins, 1998). In both drop-out and MSM selection models the full history of exposure and outcomes must be properly modeled to ensure appropriate correction when using inverse probability weights.
We assume that j = 1, 2, …, ni measurements are available for subject i, and that subjects i = 1, 2, …, m are independent. Let Yi(tij) denote the jth outcome for subject i which is measured at time tij. In general we assume a regular set of measurement times, tij = tj as is commonly determined by a study protocol. Let Xi denote a collection of baseline covariates, and let Zi(t) denote time-dependent covariates. In addition, we will denote the full history of a variable using a double overbar. For example, we let , and .
2.1 Time-dependent Exposure
In many biomedical applications the treatments or exposures under study change over time. The statistical challenge is to formulate an appropriate model to capture the impact of a longitudinal exposure on the health outcome of interest. A general statistical approach can be to adopt a longitudinal regression model where the full history of an exposure, Zi(tj), is predictive of the outcome:
| (1) |
In this model we specifically use value of Zi(tj–k) for k ≥ 1 to emphasize that exposure should precede the outcome, but some examples may permit use of k = 0 as well. Note that the general model is difficult to implement since the dimension of the exposure effects parameter, βk(tj), increases with follow-up, tj. In general the key to implemention with time-dependent exposure models is the ability to identify a subset of variables, or summaries of the full exposure history, that are sufficient for valid model specification. Biological considerations can restrict attention to the most relevent aspects of the history such as “acute” exposure for agents that are thought to only exert a short-acting influence. In contrast, for some exposures the cumulative magnitude of exposure may be the key summary and therefore requires summarization of the full history.
2.2 Introduction to Transition Models
In the previous section we focused on models for an outcome, Yi(t), where time-dependent exposure or treatment factors require consideration of a multivariate history, . Alternatively, the analysis of “change” in longitudinal data can direct attention to the use of the full history of the response, , as a predictor of future outcomes. In this section we introduce the basic concept of a transition model while in subsequent sections we will consider the full generalization to include both outcome and exposure histories. The simplest form of a transition model is an Lth-order Markov linear model with baseline covariates where:
| (2) |
Transition models are overviewed in chapter 10 of Diggle et al. (2002) and are particularly useful for categorical data when equation (2) is generalized to include a link function such as the logit link. Transition models can also accomodate time-dependent exposure and the interaction between exposure and past outcomes.
In the case of time-dependent covariates transition models are typically derived via the telescoping factorization of the joint distribution for the longitudinal response vector, Yi = vec[Yi(t)], and the time-dependent covariate, Zi = vec[Zi(t)]:
Using this representation of the joint distribution allows use of the transition models for both Yi(t) and Zi(t) where each can be directly parameterized using univariate response regression models. The fact that the telescoping likelihood is a product over the longitudinal sequence of observations allows simple additive log-likelihood contributions and the use of standard regression methods for maximum likelihood estimation of parameters and standard errors provided the models for Yi(t) and Zi(t) are correctly specified. Correct specification is a challenge since this requires proper modelling of the possibly high-dimensional joint histories and as predictors of the current outcome and/or exposure.
2.3 Selection Models and Marginal Structural Models
The final class of longitudinal models that we consider are those that characterize secondary stochastic processes such as the time until drop-out or the exposure process. While drop-out models and exposure models differ in their focus these are both used in inverse probability weighted (IPW) estimators to correct for specific forms of selection bias. Using the inverse of study retention probabilities is one statistical approach for addressing selectively missing data (Robins et al., 1995), while inverse probability of exposure weights are used to correct for potential intermediate variables that confound the exposure outcome relationship (Robins, 1998). In terms of statistical models with lagged covariates both drop-out and exposure models need to be correctly specified in terms of the full observed history. For example, models for a binary time-dependent exposure, Zi(t), that is partially influenced by unfolding longitudinal outcomes is given as:
and this probability needs to be correctly specified in order to use IPW to correct for endogeneity of the exposure, Zi(t), when estimating causal effects of on Yi(tj).
2.4 Summary of Longitudinal Models
In this section we have overviewed a variety of regression models for which the dependence of a current outcome on a full longitudinal history is of interest. Specification of model details can be challenging since several assumptions are often needed to allow feasible estimation of parameters. In the following section we overview a sequence of regression summaries that can guide longitudinal model development.
3. Estimation with Lagged Variables
With any multivariate regression analysis a key initial step is to summarize the simple bivariate association between predictors of interest and the primary outcome. With longitudinal data this simple summary may involve separate summaries for different times at which the exposure and the outcome are measured. We first overview “cross-association functions” which characterize simple bivariate associations yet consider the time of measurement, t, for the outcome, and a possibly different time of measurement, s, for the exposure. We then return to multivariate model specification for longitudinal exposures and general transition models. Finally we overview one approach to model exploration that can accomodate a potentially large number of functions of the full history and which can reveal important regression structure that is otherwise difficult to identify.
3.1 Single Lagged Variables
In order to explore the association between a longitudinal outcome Yi(t) and past measures of exposure we can adopt a general regression framework that permits adjustment for multiple covariates. The fundamental idea comes from regression where the correlation between two variables can be captured using a simple linear regression:
| (3) |
where coefficient functions β0(t, s) and β1(t, s) are fit jointly using all (t, s) pairs. Standard results establish that β1(t, s) = ρ(t, s)/[σY (t)σZ(s)] for ρ(t, s) defined as the pairwise correlation between Yi(t) and Zi(s), with σY (t) and σZ(s) denoting the standard deviations of outcome and predictor respectively. Diggle et al. (2002) generalize equation (3) to include a link function thereby allowing regression methods to characterize lagged “cross-associations” for any pair of longitudinal processes. The model can be viewed as a special case of the historical linear model of Malfait and Ramsay (2003). In addition, equation (3) can be extended to include additional baseline covariates to adjust the pairwise association β1(t, s). Whitaker et al. (1997) provide an example where different single-lagged measures of childhood obesity obtained from age 1 to age 17 are used to predict adult obesity.
Estimation of β1(t, s) can be accomplished with the use of generalized estimating equations (GEE) using a “working independence” correlation structure (Liang and Zeger, 1986). Care must be exercised in not choosing alternative working correlation structures since bias can result (Schildcrout and Heagerty, 2005).
The pairwise dependence among the outcomes can also be captured through a similar regression:
| (4) |
Heagerty and Zeger (1998) discuss use of such a model to estimate pairwise log odds ratios as a method to characterize the longitudinal dependence structure for repeated binary outcomes.
3.2 Multiple Lagged Variables: Additive Models
Characterization of pairwise association through regression coefficients such as β1(t, s) is a useful prelude to the development of comprehensive multivariate models. As discussed in section 2.1, one important class of models are mean models for a health outcome given the full history of time-varying exposure values. Equation (1) presented a general additive model when the full history Zi(t0), Zi(t1), …, Zi(tj−1) is used as a predictor of Yi(tj). However, in application simpler models are often adopted such as:
| (5) |
| (6) |
The model given by (5) imposes two key restrictions on the general additive model given earlier by equation (1). First, rather than having a time-specific effect of lagged exposure represented by βk(tj) the standard model assumes no effect modification by time and a time-constant value for the association between lagged exposure values and the outcome by restricting βk(tj) ≡ βk. This assumption can be called the “stationarity of effect” assumption since for all times tj the coefficient for the lagged exposures Zi(tj–k) are assumed to depend only on k (the lag) and not j (the measurement time). Second, rather than including an increasing history vector as a predictor with increasing time, tj, it is assumed that only the previous L lagged exposure variables are important. Similarly, equation (6) assumes that only L summaries of the exposure history are needed, but the use of general functions of the full history, fh(z), allows representation of simple scalar summaries such as the cumulative exposure . Many biomedical applications adopt some version of model (6) where the most common functions of the history are in order to capture immediate or acute effects of exposure, and to allow for chronic effects of exposure.
There are two important generalizations of the models given by equations (5) and (6). First, in environmental epidemiology multiple lagged exposures with associated coefficients, βk, are frequently modelled using (5) and distibuted lag models that impose structure on βk as a function of time, tk. See Diggle et al. (2002) section 12.4.2 for discussion and Zanobetti et al. (2000) for illustration. Second, model (6) can also be used to represent regression spline approaches that permit flexible exposure-outcome functional relationships by considering fh(z) as representing basis functions for a given exposure variable.
Estimation for longitudinal mean models with multiple lagged values of exposure can be accomplished using either mixed models or GEE when the the exposure process is exogenous (Diggle et al., 2002). First, if the exposure is exogenous and model (6) is correctly specified then the regression model gives the “full covariate conditional mean”:
where the first equality derives from the assumption of exogeneity, and the second equality derives from assuming that the full history is correctly modeled. In this case the only estimation consideration is the approach to specification of the joint distribution of Yi = vec[Yi(tj)] conditional on Zi and Xi and standard approaches such as generalized linear mixed models can be used for likelihood-based inference. Alternatively, semi-parametric estimation using GEE is also valid and robust to misspecification of the outcome dependence structure. However, when the exposure process is exogenous but the dependence on the full history is not correctly specified by the regression of interest (equation 6) then biased estimation may result from use of mixed models or GEE with a general working correlation structure, while GEE with a working independence model will provide consistent estimates (Schildcrout and Heagerty, 2005). If the exposure process is endogenous such as when current outcomes Yi(tj) are used to guide future treatment Zi(tj), Zi(tj+1), … then causal inference methods such as marginal structural models are recommended for estimation of meaningful parameters given by model (6).
Transition models are a second major class of models where the regression specification contains multiple lagged variables:
| (7) |
In general such models are straight-forward to fit provided the transition model (7) captures the correct dependence on the exposure history and the outcome history. This requires a correct choice for both L1 and L2 which determine the respective number of lagged exposure and outcomes that are needed. Furthermore, the model assumes a simple additive model for inclusion of elements of the history while a more general formulation would allow non-linear terms and interactions. Common implementations of (7) make the additional assumption of stationarity of regression effects: βk(tj) ≡ βk; and γl(tj) ≡ γl. Inclusion of baseline covariates, Xi is straightforward.
3.3 Multiple Lagged Variables: General Models and Regularization
In this subsection we focus on modeling of response and exposure history and suppress dependence on baseline covariates since their inclusion is relatively simple. While transition models are often presented in their basic form with linear and additive lagged exposure and outcome effects a more general model can be considered:
| (8) |
| (9) |
| (10) |
where fk and fl represent general functions of the history. Note that this representation captures the potential for non-linear effects (e.g. and for interactions among exposures and/or among past responses (e.g. . The primary advantage of considering a general model is the potential to accurately capture the detailed dependence on the full history. However, the dimensionality of a general model is potentially problematic since L1 denotes the number of functions of the exposure history that are entertained – and this could be multiple polynomial models for each lagged exposure Zi(tj–k) as well as multiple interaction terms. In addition, the inclusion L1 × L2 potential interactions is specified resulting in a potentially high-dimensional collection of covariates.
In situations where a general model is of interest but the risk of overparameterization exists a common statistical solution is to impose some regularization of the parameter estimate. Let θ denote the full parameter vector: θ = [vec(βk), vec(γl), vec(δk,l)]. A regularized estimator is given as the regression estimate subject to a constraint on θ given by the value of a penalty parameter λ. For example, the LASSO method imposes the constraint ∥θ∥1 < λ (Tibshirani, 1996) while more general contraints are possible. One general representation of the proposed estimation can be given as penalized likelihood using generalized least squares for continuous longitudinal data:
| (11) |
where Vi is the assumed covariance for the response vector Yi and λ is a penalty parameter for the p-norm of the parameter vector θ. Here we assume μi(θ) represents the vector of conditional means given by the regression model of interest. The LASSO method is a special case where p = 1 while ridge regression is another special case when p = 2 (Hoerl and Kennard, 1970). Penalization can also be used with GEE. Heagerty and Zeger (1998) discuss a specific penalized GEE application for longitudinal binary data analysis with interest in pairwise odds ratio dependence models, while Fu (2003) discusses GEE penalization.
The ability to use regularization to fit high-dimensional longitudinal models permits evaluation of key transition model assumptions. By including non-linear terms and interactions the standard transition model assumptions can be systematically evaluated. Furthermore, the ability of software implementations which permit model fitting for a range of penalty values (e.g. full solution paths) allows an ordering of covariates in terms of the stage, or magnitude of penalty, at which they are included in the multivariate model. One of the original motivations for LASSO given by Tibshirani (1996) was to provide one approach to variable selection.
4. Illustration: Epoetin alpha Treatment
To illustrate the alternative methods we analyze a retrospective cohort study of existing data from the United States Renal Database System (USRDS). For our analyses, we restricted attention to incident patients diagnosed with end-stage renal disease (ESRD) in 2003 and followed in the USRDS database. We defined a prospective entry period of six months after the date of diagnosis in order to accurately characterize comorbidities through Medicare utilization. Patients were then followed until the earliest of the date of death or the 18-month follow-up date providing 12 months of observation beyond the entry period. To illustrate the regression methods we selected a 20% subsample of the 2003 incident dialysis cohort yielding m = 7, 280 subjects and 32,540 person-months of follow-up data.
The ESRD treatment of interest for this study is the EPO dosage, summarized by the average number of units administered per day (U/day) in a given month. Clinical indicators of disease progression and outcome measures include: hospitalization (total number of days per month), the last available hematocrit measurement of each month, and date of death. The USRDS data set includes basic baseline demographic information, details on primary and secondary disease diagnosis, and other clinical and laboratory data collected longitudinally through Medicare claims data. Patients with a primary diagnosis of HIV/AIDS were excluded. All models include adjustment for study time, tj, and baseline demographic and clinical characteristics.
4.1 Longitudinal Epoetin (Epo) Dose
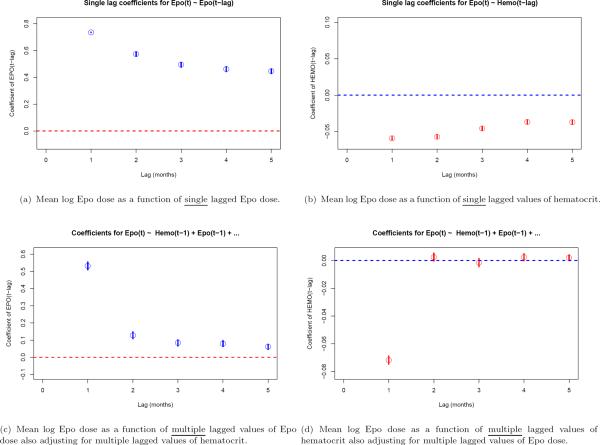
First we consider analysis of log-transformed epoetin alpha dose (Epo). Figure 1(a) shows the univariate association between the current value of epoetin, Epo(tj), and individual lagged Epo values, Epo(tj–k) for k = 1, 2, …, 5. Such a figure shows the longitudinal pairwise dependence among the drug dose variables and displays a commonly found autocorrelation relationship for longitudinal data. One component seen is serial dependence which decays as a function of increasing time-separation, yet a second component shows strong within-subject dependence for dose values 5 months apart.
Figure 1.
Regression models for mean log Epo dose as a function of lagged Epo dose and lagged hematocrit. Univariate associations with single lagged variables are displayed in panels (a) and (b), while coefficients from a multivariate model that includes multiple lagged values for both Epo and hematocrit is shown in panels (c) and (d).
Figure 1(b) shows the coefficient of Hemo(tj–k) for univariate regression models predicting Epo(tj). We find strong association between hematocrit at any lag and epoetin dose although the magnitude of the coefficient decays slightly with increasing time separation. Finally, figures 1(c) and 1(d) consider transition models for Epo(tj) that include multiple lagged values of both epoetin and hematocrit. Note that in contrast to the single-lag models the dependence of Epo(tj) on the full history of epoetin shows that Epo(tj−1) is a strong predictor, but the influence of Epo(tj−2), …, Epo(tj−5) is much smaller once adjustment for Epo(tj−1) is made. Figure 1(d) shows that only the most recent hematocrit, Hemo(tj−1) is predictive of epoetin dose, and although figure 1(b) shows a pairwise association between 2-month through 5-month lagged hematocrit values, these variables are no longer predictive once we control for Hemo(tj−1).
The transition models illustrated in figure 1(c) and 1(d) make the assumptions of additivity and linearity for the lagged epoetin and hematocrit variables. In order to explore more general models we used linear regression with the LASSO penalty for an expanded collection of predictors. We included non-linear terms for both 1-month lagged epoetin and hematocrit, and considered pairwise interactions both among and between the lagged exposure (hematocrit here) and outcome (epoetin here) variables. Figure 2 plots the sequence of model fits subject to a decreasing sequence of penalties. As the penalty is relaxed more variables are included in the regression model. Several aspects of the LASSO fits warrant comment. First, the sequence of fits show that Epo(tj−1)2 is the first variable that is included and this remains the strongest predictor of epoetin. Second, squared hematocrit is the third variable included, and it remains an important predictor even as other variables enter the model. Finally, interactions among lagged epoetin variables appear important and interactions between Epo(tj−1) and Epo(tj−2), as well as between Epo(tj−2) and Epo(tj−3) are terms that are among the top 6 variables in terms of the magnitude of their standardized coefficients. Therefore, the LASSO exploration reveals evidence for both non-linearity and important interactions among the history variables. Interactions are plausible since the clinical guidelines for Epo dosing are based on dynamic adjustment with hesitation for delivering ever increasing doses.
Figure 2.
Linear regression models for mean log Epo dose as a function of lagged Epo dose and lagged hematocrit. The potential predictors are expanded to include quadratic terms for lagged Epo and hematocrit, as well as pairwise interactions between lagged variables. Shown is the trace of estimated standardized coeffiients subjected to the LASSO penalty as a function of the L1 norm of the coefficient vector.
Table (1) shows a GEE regression model for Epo(tj) using variables suggested from the LASSO analysis. These results show that the non-linear effects of both Epo(tj−1) and Hemo(tj−1) appear important, and give evidence for the need to consider the interaction terms. Our results suggest that marginal structural model analysis which requires a model for the current dose of epoetin should consider a fairly complex model in order to accurately capture the dependence on the full history of exposure and intermediate.
Table 1.
Estimates of regression coefficients and standard errors from GEE fits for: Epo (epoetin alpha); and Hemo (hematocrit). The covariates selected are based on those that are the major predictors identified using LASSO. The regression model also includes demographic and comorbidity variables for adjustment (not shown). For this analysis quadratic terms are consider for only the first lag, t − 1.
| Transition Model | LASSO-based Model | |||||
|---|---|---|---|---|---|---|
|
| ||||||
| Outcome: EPO(t) | ||||||
|
| ||||||
| Variable | Coef. | (std. err.) | Z | Coef. | (std. err.) | Z |
| Hemo(t − 1) | −0.0717 | (0.0015) | −48.66 | −0.0591 | (0.0151) | −3.90 |
| Hemo(t − 1)2 | −0.0017 | (0.0002) | −11.06 | |||
|
| ||||||
| Hemo(t − 2) | 0.0025 | (0.0014) | 1.76 | |||
| Hemo(t − 3) | −0.0014 | (0.0015) | −0.96 | |||
| Hemo(t − 4) | 0.0024 | (0.0013) | 1.84 | |||
| Hemo(t − 5) | 0.0020 | (0.0010) | 1.97 | |||
|
| ||||||
| Epo(t − 1) | 0.5320 | (0.0115) | 46.33 | 0.1517 | (0.0764) | 1.98 |
| Epo(t − 1)2 | 0.1280 | (0.0061) | 21.09 | |||
|
| ||||||
| Epo(t − 2) | 0.1282 | (0.0102) | 12.61 | −0.3380 | (0.0854) | −3.95 |
| Epo(t − 3) | 0.0840 | (0.0091) | 9.24 | 0.2520 | (0.0611) | 4.12 |
| Epo(t − 4) | 0.0800 | (0.0088) | 9.14 | |||
| Epo(t − 5) | 0.0610 | (0.0075) | 8.14 | |||
|
| ||||||
| Epo(t − 1):Epo(t − 2) | −0.0946 | (0.0102) | −9.29 | |||
| Epo(t − 1):Epo(t − 3) | −0.0971 | (0.0095) | −10.21 | |||
| Epo(t − 2):Epo(t − 3) | 0.0832 | (0.0077) | 10.75 | |||
| Hemo(t − 1):Epo(t − 2) | 0.0142 | (0.0012) | 12.13 | |||
|
| ||||||
| Outcome: Hemo(t) | ||||||
|
| ||||||
| Epo(t) | −0.5070 | (0.0567) | −8.95 | |||
|
| ||||||
| Hemo(t − 1) | 0.5253 | (0.0108) | 48.50 | 0.2336 | (0.0719) | 3.25 |
| Hemo(t − 1)2 | ||||||
|
| ||||||
| Hemo(t − 2) | 0.0783 | (0.0096) | 8.19 | |||
| Hemo(t − 3) | 0.0150 | (0.0086) | 1.76 | |||
| Hemo(t − 4) | 0.0309 | (0.0084) | 3.67 | |||
| Hemo(t − 5) | 0.0482 | (0.0068) | 7.07 | |||
|
| ||||||
| Epo(t − 1) | 2.0111 | (0.0670) | 30.04 | −3.3692 | (0.4720) | −7.14 |
| Epo(t − 1)2 | 0.2389 | (0.0260) | 9.19 | |||
|
| ||||||
| Epo(t − 2) | −0.1989 | (0.0529) | −3.76 | 3.4010 | (0.4630) | 7.35 |
| Epo(t − 3) | −0.3302 | (0.0478) | −6.92 | |||
| Epo(t − 4) | −0.4149 | (0.0485) | −8.56 | |||
| Epo(t − 5) | −0.2126 | (0.0422) | −5.04 | |||
|
| ||||||
| Epo(t − 1):Epo(t − 2) | −0.3183 | (0.0320) | −9.95 | |||
| Hemo(t − 1):Epo(t − 1) | 0.1022 | (0.0102) | 9.98 | |||
| Hemo(t − 1):Epo(t − 2) | −0.0535 | (0.0106) | −5.05 | |||
4.2 Longitudinal Hematocrit (Hemo)
Models for hematocrit are potentially useful for causal inference regarding the effect of epoetin dose on death since hematocrit is directly influenced by epoetin and then may be an intermediate outcome in the causal pathway to death. G-computation (Robins et al., 1999) is one approach to evaluating dose effects in which data are simulated under controlled dose regimens, and the intermediate effects via hematocrit are accounted for through sequential simulation of hematocrit and death using a transition model for hematocrit and a time-dependent covariate discrete survival model.
The USRDS data are temporally ordered such that Hemo(tj) is the last hematocrit recorded in month tj and Epo(tj) is the daily average dose during the month. Therefore, Epo(tj) is a candidate predictor for the end of month hematocrit. Figure 3(a) shows the pairwise regression of Hemo(tj) on individual lagged values of epoetin, Epo(tj–k) for k = 1, 2, …, 5. Here we find that Epo(tj−1) has a larger coe cient than Epo(tj) which is consistent with the biological mechanisms that suggest the effect of a given dose does not manifest for approximately 60 days. Figure 3(b) shows the coefficient for lagged values of hematocrit as a predictor for the current value and represents a generalization of an autocorrelation function. Here we see strong serial dependence, yet the association is greatly diminished after approximately 3 months.
Figure 3.
Regression models for mean hematocrit as a function of lagged Epo dose and lagged hematocrit. Univariate associations with single lagged variables are displayed in panels (a) and (b), while coefficients from a multivariate model that includes multiple lagged values for both Epo and hematocrit is shown in panels (c) and (d).
Figure 3(c) and 3(d) show the coefficient estimates for a transition model that includes 5 months of epoetin and hematocrit history. For the prediction of Hemo(tj) it appears that the major factors are simply the previous month's values for epoetin and hematocrit. All other lagged variables are only weakly predictive although some are statistically significant in part due to the large sample size.
Finally, in order to explore the transition model assumptions of additivity and linearity we once again use the LASSO with an expanded set of covariates. Similar to our analysis with epoetin we include both non-linear terms and interactions. Figure 4 shows a sequence of model fits with decreasing penalization of the coefficient vector. Again, similar to our analysis with epoetin, we find that both non-linear terms (squared epoetin) and interactions are suggested. Table (1) shows a GEE fit using working independence using select covariates. The results support the need to generalize the standard transition model to accomodate nonlinear association and to represent effect modification by using key interactions.
Figure 4.
Linear regression models for hematocrit as a function of lagged Epo dose and lagged hematocrit. The potential predictors are expanded to include quadratic terms for lagged Epo and hematocrit, as well as pairwise interactions between lagged variables. Shown is the trace of estimated standardized coefficients subjected to the LASSO penalty as a function of the L1 norm of the coefficient vector.
5. Discussion
Analysis of longitudinal data is challenging due to the need to address correlated outcomes, missing data, and time-dependent exposure processes. In this manuscript we have focused on a sequence of analyses that can reveal association between variables and across time. We first discussed the use of cross-association function estimation which allowed a bivariate description of the association between pairs of variables. We then focused on the need to properly consider analysis with a full history of exposures, , and the need to consider multiple functions of the history including non-linear terms and interactions. Finally, we discussed the fitting of transition models where both longitudinal exposure and response history, , are included as predictors in a regression model. The use of the LASSO (Tibshirani, 1996) was one exploratory method for checking the linearity and additivity of lagged variables used for longitudinal prediction. We used a limited collection of polynomial terms to evaluate non-linearity, but regression spline bases can be used to create general dose-response relationships.
Although we have focused on the use of the LASSO as an attractive penalized likelihood method, there are alternative approaches for evaluating multiple candidate regression models. The use of Bayesian model averaging (Raftery et al., 1997) allows posterior inference for whether or not a variable should be included in the regression model. Furthermore, a summary of the posterior distibution for the coefficients of variables that are included is available from Bayesian model averaging. However, with the longitudinal models that we have considered there is considerable correlation among the candidate predictors and this makes proper specification of prior distributions for covariate effects challenging. In addition, the marginal posterior distributions for individual covariate coefficients may not fully capture the important features of the multivariate posterior distribution when predictors are highly correlated. For the USRDS example we did explore Bayesian model averaging but found that the large sample size tends to favor inclusion of a large number of predictors, and therefore does not provide guidance regarding a parsimonious generalized model.
Finally, while the use of the LASSO or alternative model selection strategies is useful for model checking or predictive model development formal inference for model choice and/or specific covariate effects is difficult since the need to account for model selection is warranted. Ultimately we offer a strategy for data analysis that starts with simple analyses and then produces multivariate longitudinal models which can be evaluated using exploratory methods, and which can suggest important directions to consider when performing sensitivity analyses.
Acknowledgements
This work was supported by NIH grants R01 HL072966, UL1 RR024379, and a research contract from RTI International (3-415-0300764,“Confounding by Indication”).
References
- Brunelli SM, Joffe MM, Israni RK, Yang W, Fishbane S, Berns JS, Feldman HI. History-adjusted marginal structural analysis of the association between hemoglobin variability and mortality among chronic hemodialysis patients. Clinical Journal of American Society of Nephrology. 2008;3:777–782. doi: 10.2215/CJN.04281007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cotter S, Zhang Y, Thamer M, Hernan MA. The effect of epoetin dose on hematocrit. Kidney International. 2008;73:347–353. doi: 10.1038/sj.ki.5002688. [DOI] [PubMed] [Google Scholar]
- Diggle P, Heagerty PJ, Liang K-Y, Zeger S. Analysis of Longitudinal Data. Oxford University Press; 2002. [Google Scholar]
- Fu WJ. Penalized estimating equations. Biometrics. 2003;59:126–132. doi: 10.1111/1541-0420.00015. [DOI] [PubMed] [Google Scholar]
- Heagerty PJ, Zeger SL. Lorelogram: a regression approach to exploring association in longitudinal categorical responses. Journal of the American Statistical Association. 1998;93:150–162. [Google Scholar]
- Hoerl AE, Kennard RW. Ridge regression: biased estimation for nonorthogonal problems. Technometrics. 1970;12:55–67. [Google Scholar]
- Liang K-Y, Zeger SL. Longitudinal data analysis using generalized linear models. Biometrika. 1986;73:13–22. [Google Scholar]
- Malfait N, Ramsay JO. The historical functional linear model. Canadian Journal of Statistics. 2003;31:185–201. [Google Scholar]
- Raftery AE, Madigan D, Hoeting JA. Bayesian model averaging for linear regression models. Journal of the American Statistical Association. 1997;92:179–191. [Google Scholar]
- Robins J. Correction for non-compliance in equivalence trials. Statistics in Medicine. 1998;17:269–302. doi: 10.1002/(sici)1097-0258(19980215)17:3<269::aid-sim763>3.0.co;2-j. [DOI] [PubMed] [Google Scholar]
- Robins JM, Greenland S, Hu F-C. Estimation of the causal effect of a time-varying exposure on the marginal mean of a repeated binary outcome. Journal of the American Statistical Association. 1999;94:687–700. [Google Scholar]
- Robins JM, Rotnitzky A, Zhao L-P. Analysis of semiparametric regression models for repeated outcomes in the presence of missing data. Journal of the American Statistical Association. 1995;90:106–121. [Google Scholar]
- Schildcrout JS, Heagerty PJ. Regression analysis of longitudinal binary data with time-dependent environmental covariates: bias and efficiency. Biostatistics. 2005;6(4):633–652. doi: 10.1093/biostatistics/kxi033. [DOI] [PubMed] [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society, Series B. 1996;58:267–288. [Google Scholar]
- Verbeke G, Molenberghs G. Linear Mixed Models for Longitudinal Data. Springer; New York, NY: 2000. [Google Scholar]
- Whitaker RC, Wright JA, Pepe MS, Seidel KD, Dietz WH. Predicting obesity in young adulthood from childhood and parental obesity. New England Journal of Medicine. 1997;337:869–873. doi: 10.1056/NEJM199709253371301. [DOI] [PubMed] [Google Scholar]
- Zanobetti A, Wand MP, Schwartz J, Ryan LM. Generalized additive distributed lag models: quantifying mortality displacement. Biostatistics. 2000;1:279–292. doi: 10.1093/biostatistics/1.3.279. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Thamer M, Cotter D, Kaufman J, Hernan MA. Estimated effect of epoetin dosage on survival among elderly hemodialysis patients in the unites states. Clinical Journal of American Society of Nephrology. 2009;4:638–644. doi: 10.2215/CJN.05071008. [DOI] [PMC free article] [PubMed] [Google Scholar]