A Regularization Corrected Score Method for Nonlinear Regression Models with Covariate Error

Summary

Many regression analyses involve explanatory variables that are measured with error, and failing to account for this error is well known to lead to biased point and interval estimates of the regression coefficients. We present here a new general method for adjusting for covariate error. Our method consists of an approximate version of the Stefanski-Nakamura corrected score approach, using the method of regularization to obtain an approximate solution of the relevant integral equation. We develop the theory in the setting of classical likelihood models; this setting covers, for example, linear regression, nonlinear regression, logistic regression, and Poisson regression. The method is extremely general in terms of the types of measurement error models covered, and is a functional method in the sense of not involving assumptions on the distribution of the true covariate. We discuss the theoretical properties of the method and present simulation results in the logistic regression setting (univariate and multivariate). For illustration, we apply the method to data from the Harvard Nurses’ Health Study concerning the relationship between physical activity and breast cancer mortality in the period following a diagnosis of breast cancer.

1. Introduction

Many regression analyses involve explanatory variables that are measured with error. Failing to account for the covariate error leads to biased estimates of the regression coefficients, and hence a large literature has developed on the problem of correcting for covariate measurement error. Fuller (1987) provides an authoritative account for linear models, while Carroll et al. (2006) summarizes the literature on nonlinear models. The nonlinear case remains an active research area, bearing on such common statistical models as nonlinear regression with a continuous response, logistic regression for binary responses, Poisson regression for count data, and Cox regression for survival data. This paper presents a flexible new method for nonlinear regression problems with covariate error, built on earlier work.

Three basic study designs are of interest: (1) the replicate measures design, where repeat covariate measurements are available (either for all individuals or for a subsample), (2) the internal validation design, where the true covariate values are available on a sample of individuals in the main study, and (3) the external validation design, where the key parameters of the measurement error distribution are estimated (assuming reasonable transportability) from an external study, independent of the main study, with paired measurements of the true and surrogate covariate. Also, two types of methods are of interest: structural methods, which involve model assumptions on the distribution of the true covariates, and functional methods, which do not require such assumptions.

Various approaches have been proposed. We focus on the SIMEX and corrected score approaches, which are functional modeling approaches. These are general approaches that can handle both internal and external validation designs as well as, with slight adaptation, the replicate measures design. Our proposed method is based on the corrected score approach.

The SIMEX method of Cook and Stefanski (1994) involves simulating new covariate values with various levels of artificially added measurement error, carrying out a naive model fit for each of the resulting new data sets, and then back-extrapolating to zero measurement error. While some success has been achieved with this approach, obviously the back-extrapolation process is uncertain. Moreover, SIMEX can be hard to apply in certain non-classical settings. One challenging setting is when the measurement error variance depends on the true covariate value. A version of SIMEX that can handle this setting under the replicate measures design was developed by Devanarayan and Stefanski (2002), but it does not appear that SIMEX can handle this setting under internal or external validation study designs.

The corrected score approach, advanced by Stefanski (1989) and Nakamura (1990, 1992), involves replacing the likelihood score in the conventional likelihood-based analysis with a function of the surrogate covariates that serves as an unbiased substitute. In Section 2, we present the exact definition. For the independent additive error model, Nakamura (1990) showed that this approach yields consistent estimators in the case of normal linear regression, Poisson regression, Gamma regression, and inverse Gaussian regression. Nakamura (1992) presented an approximate corrected score method for the Cox regression model, which Kong and Gu (1999) later showed to yield consistent estimates. Novick and Stefanski (2002) presented a corrected score method that is aimed at the independent additive error model with normal errors, and is valid when the likelihood score function is an entire function in the complex plane (such as, for example, Poisson regression with an exponential link). Stefanski, Novick, and Devanarayan (2005) elaborate on this approach. When the error-prone covariate is discrete, a corrected score can be formulated easily; the relevant theory was developed for generalized linear models by Akazawa, Kinukawa, and Nakamura (1998), and extended to the Cox regression model by Zucker and Spiegelman (2008).

On the other hand, for logistic regression with additive normal error, Stefanski (1989) showed that an exact corrected score method does not exist. Huang and Wang (2001) presented an exact modified corrected score method for logistic regression, with clever reweighting of the terms in the original score function so that an exact corrected score can be found. This reweighting leads to some loss in efficiency. Moreover, the method of Huang and Wang is designed only for the case of independent additive measurement error. Buzas (2009) presents an approximate corrected score method for the logistic regression model with high efficiency when the covariate effect is moderate, but this method is designed only for the case of independent additive normal error.

The basic problem with the corrected score approach in the logistic regression model and other cases with a continuous error-prone covariate X is that obtaining the corrected score requires solving a challenging integral equation. The equation involved is a Fredholm integral equation of the first kind, discussed by Delves and Mohamed (1985, Ch. 12) and Kress (1989, Ch. 16). Such equations do not always have an exact solution; the logistic regression problem is one case of this. Moreover, even when an exact solution exists, the problem can be ill-conditioned. We tried to tackle the case of a continuous covariate by discretizing the covariate to various degrees of fineness and applying the methodology for the discrete case, but with only limited success. The classification matrix tended to be ill-conditioned even with a modest degree of fineness, such as six categories.

In this paper, we develop a new approach. The idea is to handle the integral equation using the method of regularization (Delves and Mohamed, 1985, Sec. 12.3; Kress, 1989, Ch. 16), which involves minimizing a penalized distance function to obtain an approximate solution. In contrast with the original integral equation problem, the regularized problem always has a solution, and is reasonably well conditioned provided that the weight α on the penalty term is not too small. As α tends to infinity, the estimation procedure tends to a naive analysis in which we ignore the covariate error, and simply substitute the surrogate covariate value for the true value. Conversely, under suitable conditions, as α tends to zero the procedure approaches an exact corrected score procedure. The idea is to push α as close as possible to zero to get good estimates of the model parameters. We call our approach the regularized corrected score (RECS) approach.

The advantage of RECS is that it is extremely flexible. Its formulation is very general, and it is a functional method with no modeling of the distribution of the true covariate, but only of the conditional density of the surrogate covariate given the true covariate. The method can handle both internal and external validation designs. It can handle the replicate measures design as well, with the overall surrogate measurement defined as the sample mean (or other summary measure) of the available measurements on the individual. Moreover, the method can handle arbitrary measurement error structures, not just independent additive measurement error. Differential measurement error, where the measurement error depends on the response, is also covered. The goal of this paper is to develop the RECS method in detail for the classical likelihood setting. Section 2 lays out the setting and background. Section 3 presents the proposed procedure and its theoretical properties. Section 4 presents simulation results under the logistic regression model. Section 5 presents a real-data illustration of the method in the logistic regression setting. Section 6 presents a brief discussion.

2. Setting and Background

We assume a typical setup with n independent units whose response values Y_i, i = 1, … n, follow a regression model involving several covariates. We assume for now that only one of the covariates is subject to error; later we will generalize to the case of multiple error-prone covariates. We denote by X_i the true value of the error-prone covariate, and by W_i the measured value. We let Z_i denote the vector of error-free covariates, which may include an arbitrary number of discrete and continuous components. We denote the conditional density or mass function of Y_i given (X_i, Z_i) by f (y|X_i, Z_i, θ), where θ is a p-vector of unknown parameters, including regression coefficients and auxiliary parameters such as error variances. In contrast with the SIMEX method, the Huang and Wang (2001) method, and most other methods in the literature, we provide the option of allowing measurement error to depend on X_i, Z_i, and the outcome Y_i (differential error). We denote by a_i(x, w) the conditional density of W_i given X_i = x, with the subscript i signifying possible dependence on Z_i and Y_i. To ease the presentation of the theoretical results, we assume that (X_i, Z_i) are i.i.d. random vectors. We stress, however, that our method does not involve any modeling (either parametric or nonparametric) of the distribution of (X_i, Z_i). The theory can, in principle, be extended to the case where (X_i, Z_i) are non-random values satisfying suitable ergodicity conditions.

The classical normalized likelihood score function when there is no covariate error is given by U(θ) = n⁻¹Σ_i u_i(X_i, θ), where u_i(x, θ) = u(Y_i, x, Z_i, θ) with u(y, x, z, θ) = [∂/∂θ] log f(y|x, z, θ). The maximum likelihood estimate (MLE) is obtained by solving the equation U(θ) = 0. The idea of the Stefanski-Nakamura corrected score approach is to find a function ū (y, w, z, θ) such that

$$E[\overline{\mathbf{u}}(Y_i,W_i,{\mathbf{Z}}_i,\mathit{\theta })\mid X_i,{\mathbf{Z}}_i,Y_i]=\mathbf{u}(Y_i,X_i,{\mathbf{Z}}_i,\mathit{\theta }).$$ (1)

We define ū_i(w, θ) = ū (Y_i, w, Z_i, θ), and then use the modified likelihood score function Ū (θ) = n⁻¹Σ_i ū_i(W_i, θ) in place of U(θ) as the basis for estimation. The estimation equation thus becomes Ū (θ) = 0.

In the present setting, equation (1) for the corrected score function takes the form

$$\int a_i(x,w){\overline{u}}_{ij}(w)dw=u_{ij}(x),$$ (2)

where u_ij(x) and ū_ij(w), respectively, denote the j-th component of u_i(x, θ) and ū_i(w, θ) (suppressing the argument θ in the definitions), and the integral is over the entire range of W. As indicated in the introduction, we do not seek an exact solution to (2), but instead use the method of regularization to find an approximate solution.

Define the integral operator A_ig(x) = ∫ a_i(x, w)g(w)dw. Write Δ_ij(x) = u_ij(x) − A_iu_ij(x) and Δ̄_ij(x) = ū_ij(x) − u_ij(x). We can then write (2) as A_iΔ̄_ij = Δ_ij. We seek the Δ̄_ij(·, θ, α) that minimizes the penalized loss function

$${\mathcal{L}}_{ij}({\overline{\mathrm{\Delta }}}_{ij})={\left|\right|A_i{\overline{\mathrm{\Delta }}}_{ij}-{\mathrm{\Delta }}_{ij}\left|\right|}^2+\alpha {\left|\right|{\overline{\mathrm{\Delta }}}_{ij}\left|\right|}^2,$$ (3)

where ||g||² denotes the weighted squared L² norm ||g||² = ∫ c(v)g(v)²dv and α > 0 is a penalty factor. The penalty is introduced in order to avoid ill-conditioning and ensure existence of a solution. After obtaining Δ̄_ij(·, θ, α), we use ū_ij(x, θ, α) = u_ij(x)+ Δ̄_ij(x, θ, α) as a corrected score term.

For the weight function c(v), we propose as a generic choice the standard normal density, p i.e., c(v) = ϕ(v) with $\varphi (v)=exp(-v^2/2)/\sqrt{2\pi }$, after standardizing W to mean 0 and variance 1. The weight function is designed to put emphasis on the region of the covariate space where the bulk of the data lie. One could consider tailoring the choice of the weight function to the pattern of the observed distribution of W, but we do not discuss this here.

We formulate the minimization problem in terms of Δ̄_ij(·, θ, α) rather than ū_ij(·, θ, α) in order to anchor the procedure at u_ij(w), which corresponds to the naive analysis where we ignore the covariate error and substitute W_i for X_i. See Hansen (1994, Sec. 2, second paragraph) for the idea of centering the regularization process around an initial estimate of the desired solution to the integral equation. As α → ∞, the loss function (Δ̄_ij) puts increasingly heavy weight on ||Δ̄_ij||², causing the minimizer Δ̄_ij to tend to 0 and thus leading to the naive estimates based on u_ij(w). At the other extreme, as α → 0, the problem of minimizing (Δ̄_ij) approaches the problem of solving AΔ̄_ij = Δ_ij. We first describe the procedure for a fixed α, and then discuss the selection of the value of α.

By using the L² norm, we ensure that the problem of minimizing the loss function always has a unique solution, and the solution has a convenient form. Delves and Mohamed (1985, Sec. 12.3) and Kress (1989, Theorem 16.1) present the relevant theory. Let $A_i^{\ast }h(w)=\int a_i(x,w)h(x)dx$ denote the operator adjoint of A_i. Then, for any L² function δ, the minimizer of 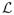(Ū; A_i, δ, α) = ||A_iŪ − δ|| + α ||Ū||² is given by $\overline{\delta }={(A_i^{\ast }{A}_i+\alpha \mathcal{I})}^{-1}{A}_i^{\ast }\delta$ , where is the identity operator. The next section describes a numerical scheme for finding the solution that leads to a simple linear system of equations. We thus obtain an easily implemented procedure.

3. The Procedure

3.1 The Procedure for a Given α

To numerically determine the minimizer of (Δ̄_ij), we use a Galerkin-type basis expansion approach, in the spirit of (though not identical to) Delves and Mohamed (1985, Sec. 12.4). Specifically, we represent the solution Δ̄_ij(·, θ, α) in a basis expansion

$${\overline{\mathrm{\Delta }}}_{ij}(x,\mathit{\theta },\alpha )=\sum _{m=1}^M{d}_{\mathit{ijm}}(\alpha ){\psi }_m(x),$$ (4)

where the ψ_m are specified basis functions. In our numerical work, we use the “probabilists” Hermite polynomials, which are orthonormal with respect to the weight function ϕ. One has to choose the number M of basis functions to include. We found that M = 6 yields good performance; the results with M = 4 are inferior to those with M = 6, while the results with M = 10 are similar to those with M = 6 but with more outliers.

Denote φ_im(x) = A_iψ_m(x) and d_ij = [d_ij1 … d_ijM ]^T (suppressing the argument α in d_ijm for the time being). We then can express the objective function (Δ̄_ij) as

$${\mathcal{L}}_{ij}({\overline{\mathrm{\Delta }}}_{ij})={\left|\right|\sum _{m=1}^M{d}_{\mathit{ijm}}{\phi }_{im}-{\mathrm{\Delta }}_{ij}\left|\right|}^2+\alpha {\mathbf{d}}_{ij}^T{\mathbf{d}}_{ij},$$

where ${\left|\right|{\overline{\mathrm{\Delta }}}_{ij}\left|\right|}^2={\mathbf{d}}_{ij}^T{\mathbf{d}}_{ij}$ because of the orthonormality of the ψ_m functions. We now approximate the L² norm in the first term on the right side via the quadrature approximation

$$\int \phi (v)g(v)dv\doteq \sum _{k=1}^K{q}_{k}g(x_k),$$ (5)

where x_k and q_k are the classical Gauss-Hermite quadrature points and weights (modified p slightly to account for our use of the weight function $exp(-v^2/2)/\sqrt{2\pi }$ as opposed to the standard Hermite weight function exp(−v²)). Given the approximation (5), we can express the objective function as

$$\begin{array}{l}{\mathcal{L}}_{ij}({\overline{\mathrm{\Delta }}}_{ij})=\sum _{k=1}^K{q}_k{\left[\sum _{m=1}^M{d}_{\mathit{ijm}}{\phi }_{im}(x_k)-{\mathrm{\Delta }}_{ij}(x_k)\right]}^2+\alpha {\mathbf{d}}_{ij}^T{\mathbf{d}}_{ij}\\ =\sum _{k=1}^K{\left[\sum _{m=1}^M{d}_{\mathit{ijm}}{\stackrel{\sim }{\phi }}_{im}(x_k)-{\stackrel{\sim }{\mathrm{\Delta }}}_{ij}(x_k)\right]}^2+\alpha {\mathbf{d}}_{ij}^T{\mathbf{d}}_{ij},\end{array}$$

where ${\stackrel{\sim }{\phi }}_{im}(x)=\sqrt{qk}{\phi }_m(x_k)$ and ${\stackrel{\sim }{\mathrm{\Delta }}}_{ij}(x)=\sqrt{qk}{\mathrm{\Delta }}_{ij}(x)$. Next, define the matrix Φ̃_i by Φ̃_ikm = φ̃_im(x_k) and the vector Δ̃_ij = [δ̃_ij(x₁) … Δ̃_ij(x_K)]. We obtain ${\mathcal{L}}_{ij}({\overline{\mathrm{\Delta }}}_{ij})={({\stackrel{\sim }{\mathbf{\Phi }}}_i{\mathbf{d}}_{ij}-{\stackrel{\sim }{\mathbf{\Delta }}}_{ij})}^T({\stackrel{\sim }{\mathbf{\Phi }}}_i{\mathbf{d}}_{ij}-{\stackrel{\sim }{\mathbf{\Delta }}}_{ij})+\alpha {\mathbf{d}}_{ij}^T{\mathbf{d}}_{ij}$. We then find, by standard least squares theory, that the vector d_ij(α) that minimizes the above quantity is given by d_ij(α) = C(α) Δ̃_ij, where C(α) = (Φ̃^TΦ̃ + αI)⁻¹. Note that C(α) does not depend on θ. Finally, we define ū_ij(w, θ, α) = u_ij(w, θ) + Δ̄_ij(w, θ, α), where Δ̄_ij(w, θ, α) is given by (4) with d_ijm(α) as just described. Then, as indicated in the preceding section, we put Ū (θ, α) = n⁻¹Σ_i ū_i(W_i, θ, α) and define the estimator θ̂ ^(α) to be the solution to Ū (θ, α) = 0.

In the course of the foregoing procedure, we have to evaluate integrals of the form

$$E[g(W_i)\mid X_i=x]=A_{i}g(x)=\int a_i(x,w)g(w)dw.$$ (6)

Integrals of this type appear in φ_im(x) = A_iψ_m(x) and in Δ_ij(x) = u_ij(x) − A_iu_ij(x). These integrals can be evaluated by K′-point numerical quadrature for suitable K′. Web Appendix A.1 presents the details. In regard to the choice of K and K′, in our numerical work we generally used K = K′ = 20; we reran selected simulations with K = K′ = 30 and obtained similar results. In a data analysis, the analyst can try a succession of increasing values of K and K′, and stop when there is no further change in the results.

In practice, a_i(x, w) has to be estimated, using data from an internal or external validation study (or a replicate measures study). We assume that a_i(x, w) follows a known parametric model depending on parameters ξ (distinct from θ) which are estimated from the relevant data. We thus write a_i(x, w, ξ). The parametric model is allowed to be of any specified form. Thus, in addition to the classical independent additive error model, we allow models with dependence between the error and the true covariate value, and models with differential error. We have examined the effect of misspecifying the parametric form. In practice, the parametric model would be chosen based on analysis of the validation data. Regression methods can be used to model E[WjX]. Heterogeneity of variance can be assessed and modeled by applying regression methods to the squares of the residuals, as in Davidian and Carroll (1987). These models can be checked using standard tools. The distributional form for the error can be selected by examining the standardized residuals from the regression of W on X.

3.2 Theoretical Properties

In general, θ̂ ^(α) will not converge to the true value θ₀ of θ, but rather to a limit θ̃ ^(α) that is close to θ₀ when α is small. We cannot make α arbitrarily small, but we can try to make it small enough to obtain estimates with small bias, and the numerical studies in the next section indicate that this goal can be achieved. Thus, our method does not produce an exactly consistent estimator, but it does produce an approximately consistent estimator. Moreover, under standard regularity conditions, $\sqrt{n}(\widehat{\mathit{\theta }}-{\stackrel{\sim }{\mathit{\theta }}}^{(\alpha )})$ is asymptotically normal. These properties are formalized in the following theorem, proved in Web Appendix A.2.

Theorem

Define ū_E(θ, α) = E[ū_i(W_i, θ, α)]. Let D̄ ^(α)(θ) be the Jacobian of −Ū (θ, α). Then, under the regularity conditions in Web Appendix A.2, the following results hold.

1. We have E[ū_ij(W_i, θ, α)|X_i, Z_i, Y_i] = u_ij(X_i, θ)+ r_ij(X_i, θ, α) with r_ij(·, θ, α) converging uniformly in θ to zero as α → 0.

2. Similarly, with u_ijs(x, θ) = [∂/∂θ_s]u_ij(x, θ) and ū_ijs(w, θ, α) = [∂/∂θ_s] ū_ijs(w, θ, α), we have E[ū_ijs(W_i, θ, α)|X_i, Z_i, Y_i] = u_ijs(X_i, θ) + r_ijs(X_i, θ, α) with r_ijs(·, θ, α) converging uniformly in θ to zero as α → 0.

3. For all α sufficiently small, the equation ū_E(θ, α) = 0 has a unique solution, which we denote by θ̃ ^(α). For fixed α, we have θ̂ ^(α) → θ̃ ^(α) almost surely as n → ∞.

4. We have θ̃^(α) → θ₀ as α → 0.

5. If a_i(x, w) is known, $\sqrt{n}({\widehat{\mathit{\theta }}}^{(\alpha )}-{\stackrel{\sim }{\mathit{\theta }}}^{(\alpha )})$ is asymptotically mean-zero normal with covariance matrix that can be estimated using the sandwich estimator

   $${\mathbf{V}}^{(\alpha )}({\widehat{\mathit{\theta }}}^{(\alpha )})={\overline{\mathbf{D}}}^{(\alpha )}{({\widehat{\mathit{\theta }}}^{(\alpha )})}^{-1}{\mathbf{F}}^{(\alpha )}({\widehat{\mathit{\theta }}}^{(\alpha )}){\overline{\mathbf{D}}}^{(\alpha )}{({\widehat{\mathit{\theta }}}^{(\alpha )})}^{-1}$$

   with ${\mathbf{F}}^{(\alpha )}(\mathit{\theta })=n^{-1}{\sum }_{i=1}^n{\overline{\mathbf{u}}}_i(\mathit{\theta },\alpha ){\overline{\mathbf{u}}}_i{(\mathit{\theta },\alpha )}^T$. Under a parametric model for a_i(x, w) with estimated parameters ξ, a similar result holds, with a suitable adjustment to the estimated covariance matrix to account for the estimation of ξ, as described in Web Appendix A.3.

Remark

Assumptions A1–A3 are typical assumptions made in asymptotic theory; see, for example, van der Vaart (1998, p. 46, bottom). Assumption A4 is a modest assumption that holds in many cases of interest. For example, suppose (X, W) follows the independent additive error model W = X + σε, where ε is a random variable with density f_ε, independent of X. We then have a(x, w) = σ⁻¹ f_ε ((w − x)/σ) = σ⁻¹ f̃_ε ((x − w)/σ), with f̃_ε (u) = f_ε (−u). The assumption thus will be satisfied provided that the location-scale family of densities f(x, w, σ) = σ⁻¹f̃ θ_ε ((x−w)/σ) is a complete family of densities with respect to the parameters (w, σ). This condition certainly holds if f_ε is a density of exponential family form; see Lehmann (1986, p. 142). Next, consider the extended model W = X + σ(X, γ) ε, which we examine in our numerical studies, where γ is a vector of parameters. Assumption A4 will hold in this setting if the family of densities

$$f(x;w,\mathit{\gamma })=\frac{1}{\sigma (x,\mathit{\gamma })}{\stackrel{\sim }{f}}_{\epsilon }\left(\frac{x-w}{\sigma (x,\mathit{\gamma })}\right)/\int \frac{1}{\sigma (x^{\prime },\mathit{\gamma })}{\stackrel{\sim }{f}}_{\epsilon }\left(\frac{x^{\prime }-w}{\sigma (x^{\prime },\mathit{\gamma })}\right){dx}^{\prime }$$

is a complete family of densities with respect to the parameters (w, γ). Again, this condition will hold if f_ε is a density of exponential family form.

3.3 Choice of the Penalty Parameter Function α

The issue of how to choose the penalty parameter in a regularization problem has been investigated in previous literature. Hansen (1994, 2007) describes three leading criteria: the L-curve criterion, the GCV criterion, and the quasi-optimality criterion. We tried all three, and found the GCV criterion to be the most satisfactory. The GCV criterion is

$$\text{GCV}(\alpha )=\frac{{({\stackrel{\sim }{\mathbf{\Phi }}}_i{\mathbf{d}}_{ij}(\alpha )-{\stackrel{\sim }{\mathbf{\Delta }}}_{ij})}^T({\stackrel{\sim }{\mathbf{\Phi }}}_i{\mathbf{d}}_{ij}(\alpha )-{\stackrel{\sim }{\mathbf{\Delta }}}_{ij})}{{[\text{trace}(\mathbf{I}-\mathbf{C}(\alpha ))]}^2},$$

and α is chosen to minimize this quantity. In our setting, with a separate value GCV_ij(α) for each i and j, we use the summary criterion ${\text{GCV}}^{\ast }(\alpha )={(np)}^{-1}{\sum }_{i=1}^n{\sum }_{j=1}^p{\text{GCV}}_{ij}(\alpha )$. In implementing this rule, we evaluate Δ̃_ij at the naive estimate of θ, and then keep α fixed at the resulting value for the remainder of the estimation process.

3.4 Multiple Error-Prone Covariates

The method can be extended to the case of two error-prone covariates X₁ and X₂. For the basis functions, we use the tensor product of the univariate basis functions. The integrals in quantities of the form A_ig(x) become double integrals, which are evaluated by bivariate quadrature. In the L² norm appearing in the objective function, we take the weight function to be c(w₁, w₂) = ϕ (w₁) ϕ (w₂), and evaluate the integral using the bivariate version of (5).

In the case of three or more error-prone covariates, the situation becomes more complicated. Taking the basis function set to be the tensor product of the univariate basis functions will typically produce too large a basis function set, so some reduction will be necessary. One option is to take the basis function set to include all the univariate basis functions for the individual covariates plus the cross-products of the linear terms. In the evaluation of the integrals A_ig(x) = E[g(W_i)|X_i = x], a Monte-Carlo method will probably be more workable than a classical quadrature method. The L² norms can be computed using a multivariate version of (5), but the computational load may be demanding.

The simulation work presented in the next section includes results for the case of two error-prone covariates. On a practical level, it appears challenging to apply our method with three or more error-prone covariates. However, many applications involve only one or two error-prone covariates, and thus can be handled by our method in a reasonable way. An arbitrary number of error-free covariates can be handled without difficulty.

4. The Logistic Regression Model: Simulation Studies

4.1 Simulation Study Designs

To investigate the finite sample performance of our method, we conducted a series of simulation studies. This subsection describes the simulation study designs; the next subsection describes the results. The studies were conducted in the setting of the logistic regression model. The response variable Y_i equals either 0 or 1. Defining T_i = (X_i, Z_i) and T_i0 ≡ 1, the model is logit $Pr(Y_i=1\mid {\mathbf{X}}_i=\mathbf{x},\mathbf{Z}=\mathbf{z})={\sum }_{j=0}^p{\beta }_j{t}_j$ and the score function u(y, x, z, θ) is

$$u_j(y,x,z,\mathit{\theta })=t_j\left[y-\text{expit}\left(\sum _{j=0}^p{\beta }_j{t}_j\right)\right],\text{expit}(a)=e^a/(1+e^a).$$

We examined the following methods: (1) naive analysis ignoring measurement error, (2) RECS, (3) the Novick and Stefanski (2001) complex variable corrected score method (N&S), (4) SIMEX, (5) the Huang and Wang (2001) nonparametric corrected score method (H&W), (6) a Bayesian MCMC-type method (at the suggestion of a referee), patterned after Richard-son et al. (2002). The SIMEX method was applied with linear (SIMEX-L), quadratic (SIMEX-Q), and nonlinear extrapolation (SIMEX-NL). We show the results for SIMEX-Q in the tables, and the results for the other versions in the web appendix. For the Huang and Wang method, which requires replicate measurements of W, we took two replicates per individual and doubled the error variance for comparability with the other methods. Note that H&W is designed to provide accurate estimates only for the slope, not for the intercept. All simulation results for Methods 1–5 are based on 1,000 simulation replications. The MCMC method is very time-consuming, so for this method we ran only 100 replications.

The SIMEX method is designed for independent additive normal measurement error. The N&S method is designed for the case where the measurement error is independent additive normal and the likelihood score function is an entire function in the complex plane. The latter condition does not hold for logistic regression, and thus the N&S method is not designed to handle any of the simulation scenarios we have studied. The H&W nonparametric method is designed for independent additive measurement error with an arbitrary distribution, which is not modeled in any way. The RECS method is designed for parametric measurement error models of arbitrary form, including non-normal, heteroscedastic, and differential error.

The details of the Bayesian MCMC method are presented in Web Appendix B. The MCMC algorithm was run for 100,000 iterations, with the last 40,000 iterations used for inference. Our adaptation of the Richardson et al. method involves an input parameter η that regulates the variance of the prior distributions on β₀ and β₁. Specifically, the prior on β_j was taken to be normal with mean equal to the naive estimate and variance equal to η times the estimated variance of the naive estimate. We present results for η = 100. Results for η = 10 are provided in the web appendix. It was necessary for the prior on β₀ and β₁ to be moderately informative to ensure convergence of the MCMC sampler. This is an inherent difficulty with the Bayesian approach in the context of the main study/external validation study design that we consider, with no individuals for which the outcome Y and the true covariate X are both observed. The setting η = 100 corresponds to the maximum degree of noninformativeness under which convergence of the MCMC sampler is maintained across all scenarios studied.

For each estimator, we summarize the bias in terms of the mean and median of the difference between the estimated and true parameter values, and the dispersion in terms of the empirical standard deviation and standardized interquartile range (dividing the raw interquartile range by 1.349, which is the ratio between the interquartile range and the standard deviation for a normal distribution). The median and the interquartile distance are more robust to outliers, and thus provide further insight in addition to that provided by the mean and the standard deviation. In addition, we present the coverage rates of the 95% Wald confidence interval based on asymptotic normal theory. For the naive method, variance estimates were computed using the standard asymptotic variance formula. For the RECS and N&S methods, an explicit sandwich-type formula was used. For SIMEX, we used the jackknife estimator in the R package simex, while for H&W we used a bootstrap variance estimator. For the Bayesian MCMC method, interval estimation was based on 95% highest posterior density (HPD) intervals (Box and Tiao, 1973, Section 2.8).

In Simulation Sets A and B, we considered the case of a single continuous error-prone covariate X_i and no other covariates. In these two simulation sets, we worked in the setting of a main study/external validation study design, involving a main study sample with data on W and Y and an external validation sample with data on W and X. The main study sample size was 200 and the external validation sample size was 70. The measurement error parameters were estimated by maximum likelihood. The RECS method was implemented with M = 6 basis functions and K = K′ = 20 quadrature points. The true values of the regression parameters were set at β₀ = β₁ = 1.

Simulation Set A involved measurement error models of the form W_i = X_i + ε_i, where ε_i is normally distributed, but with error variance possibly depending on X_i and Y_i. We examined three simulation scenarios, as follows:

• Scenario A1

  X_i ~ N (0, 1), ε_i|(X_i, Y_i) ~ N (0, γ)

• Scenario A2

  X_i ~ N (0, 1), ε_ij(X_i, Y_i) ~ N (0, γ₁ + γ₂|X_i|)

• Scenario A3

  X_i ~ N (0, 1), ε_i|(X_i, Y_i) ~ N (0, γ₁ + γ₂|X_i| + γ₃|Y_i|)

For each of the above scenarios, we examined two sets of measurement error parameters. In Scenario A1, we took γ = 0.5 or 1. In Scenarios A2 and A3, the two sets of measurement error parameters were chosen to make the unconditional variance of ε_i equal to about 0.5 or 1, respectively. Scenario A1 is the classical additive error model, which is theoretically covered by RECS, SIMEX, and H&W (for N&S, the measurement error model assumption is satisfied but the entire function condition is not). Scenarios A2 and A3 involve heteroscedastic error models that are theoretically covered by RECS but not by N&S, SIMEX, or H&W.

Simulation Set B involved measurement error models of the form W_i = X_i + ε_i, with non-normal ε_i. We considered two distributions for ε_i, the double-exponential distribution (DBLEXP(γ), with γ denoting the variance) and a modified chi-square distribution MOD-CHI which Huang and Wang (2001) used in their simulation work. Specifically, the MODCHI(γ) is defined to be the distribution of a ${\chi }_1^2$ variate truncated at the value 5, recentered to mean zero, and then rescaled to a variance of γ. In Scenario B3, we also take X to have a MODCHI distribution. The DBLEXP distribution is similar to the normal, but with heavier tails. The MODCHI distribution is highly skewed. The specific scenarios examined were as follows:

• Scenario B1

  X_i ~ N (0, 1), ε_i|(X_i, Y_i) ~ DBLEXP(γ)

• Scenario B2

  X_i ~ N (0, 1), ε_i|(X_i, Y_i) ~ MODCHI(γ)

• Scenario B3

  X_i ~ MODCHI(1), ε_i|(X_i, Y_i) ~ MODCHI(γ)

These scenarios are theoretically covered by RECS and H&W, but not by SIMEX or N&S.

For each of these scenarios, we ran simulations for γ = 0.5 and γ = 1. For the MODCHI distribution, integrals of the form A_ig(x) were evaluated as described at the end of Web Appendix A.1. Note that the MODCHI(γ) is a non-regular distributional family: it has support that depends on γ. Hence, classical asymptotic theory for MLE’s does not apply to the MLE of γ. However, due to the restricted range of γ values that are compatible with a given dataset due to the definition of the support, with an external validation sample of 70 the value of γ is estimated with virtually no error.

Simulation Set C considered the case of two error-prone covariates X₁, X₂ and one error-free covariate Z. For this simulation set, the sample size was 500, and the measurement error parameters were taken as known. For the RECS method, the basis function set was taken to be the tensor product of the univariate basis functions sets with M = 6, and in the quadrature calculations we took K′ = 20 and K = 10. The true regression coefficients were β₀ = β₁ = β₂ = β₃ = 1. The scenarios examined were as follows.

• Scenario C1

  X₁, X₂, Z i.i.d. N (0, 1); ε₁, ε₂ i.i.d. N (0, γ), independent of X₁, X₂, Z

• Scenario C2

  X₁, X₂, Z i.i.d. N (0, 1); ε₁, ε₂ conditionally independent given X₁, X₂, Z and distributed as N(0, γ₁ + γ₂(|X₁| + |X₂| + |Z|))

• Scenario C3

  X₁, X₂ ~ MODCHI(1); Z ~ N(0, 1); ε₁, ε₂ ~ MODCHI(γ), all random variables independent of each other

In Scenarios C1 and C3, we took γ = 1, while in Scenario D2 we took γ ₁ = 0.4 and γ₂ = 0.25, so that the unconditional variance of ε₁ and ε₂ was about 1. Scenario C1 is the classical additive error model, which is theoretically covered by RECS, SIMEX, and H&W (for N&S, the measurement error model assumption is satisfied but the entire function condition is not satisfied). Scenario C2 involves a heteroscedastic error model that is theoretically covered by RECS, but not by N&S, SIMEX, or H&W. Scenario C3 involves a non-normal error model that is theoretically covered by RECS and H&W, but not by SIMEX or N&S.

Finally, in Scenario D, we examined the effect of misspecifying the error distribution, in the setting of a single error-prone covariate. The details are described in Web Appendix C.2. The R code for the simulations can be found with the supplemental web materials or on the first author’s website (http://pluto.huji.ac.il/~mszucker).

4.2 Simulation Results

Tables 1 and 2 present, respectively, the results of Simulation Studies A and B, while Table 3 presents the results of Simulation Study C. In Tables 1 and 2 we present the results only for the slope parameter β₁, which is the parameter of main interest. Results for the intercept parameter are given in the web appendix. In Table 3 we present results only for β₁ and β₃, the slope parameters for X₁ and Z, respectively. The web appendix provides the results for β₀ and β₂. The results for β₂ are similar to those for β₁. The results of Simulation Scenario D are in the web appendix. Here we discuss the findings, focusing on estimation of the slope parameter. Overall, the RECS method performs very well in terms of bias and confidence interval coverage. Below we discuss how RECS compares with the competing methods.

Table 1.

Simulation Study A X ~ N(0, 1) and ε ~ N(0, γ₁ + γ₂|X| + γ₃Y) Results for Slope Parameter β₁ – Sample Size n=200, Validation Sample Size m=70

	M	MD	Emp-SD	IQ-SD	95% CI	F	M	MD	Emp-SD	IQ-SD	95% CI	F
	γ1 = 0.5, γ2 = 0, γ3 = 0						γ1 = 1.0, γ2 = 0, γ3 = 0
Naive	0.6469	0.6379	0.1512	0.1520	0.360	0	0.4713	0.4660	0.1262	0.1264	0.027	0
RECS	1.0782	1.0314	0.3373	0.3013	0.958	0	1.1567	1.0231	0.5421	0.4266	0.933	2
N&S	1.0368	1.0257	0.2740	0.2867	0.907	0	0.9487	0.9859	0.2283	0.2365	0.897	8
SIMEX - Q	0.8940	0.8737	0.2245	0.2157	0.877	0	0.7182	0.6989	0.2048	0.2039	0.626	0
H&W	1.0600	0.9514	0.5264	0.3818	0.951	4	0.8840	0.7851	0.5249	0.3751	0.917	4
MCMC η =100	1.2797	1.2364	0.4072	0.4324	0.950	0	1.2304	1.1671	0.4350	0.4848	0.970	0
	γ1 = 0.3, γ2 = 0.25, γ3 = 0						γ1 = 0.7, γ2 = 0.35, γ3 = 0
Naive	0.6573	0.6494	0.1553	0.1573	0.390	0	0.4812	0.4749	0.1284	0.1279	0.036	0
RECS	1.0429	1.0054	0.3102	0.2784	0.949	0	1.0658	0.9797	0.4673	0.3663	0.912	1
N&S	1.0929	1.0881	0.3001	0.3208	0.899	1	0.9926	1.0305	0.2402	0.2348	0.890	7
SIMEX - Q	0.9169	0.8926	0.2368	0.2313	0.891	0	0.7358	0.7167	0.2115	0.2053	0.660	0
H&W	1.0370	0.9679	0.4451	0.2980	0.949	1	1.0310	0.9134	0.5109	0.3566	0.941	4
MCMC η =100	1.2539	1.2292	0.3691	0.3750	0.950	0	1.2866	1.2396	0.4414	0.4678	0.940	0
	γ1 = 0.15, γ2 = 0.25, γ3 = 0.25						γ1 = 0.35, γ2 = 0.25, γ3 = 0.50
Naive	0.6512	0.6437	0.1513	0.1488	0.373	0	0.5091	0.5029	0.1282	0.1285	0.060	0
RECS	1.0782	1.0316	0.3477	0.2921	0.950	0	1.1123	0.9989	0.4765	0.3793	0.929	0
N&S	1.1099	1.1037	0.2987	0.3215	0.896	2	1.0293	1.0674	0.2451	0.2514	0.858	12
SIMEX - Q	0.8718	0.8545	0.2241	0.2194	0.840	0	0.7259	0.7125	0.1986	0.1868	0.605	0
H&W	1.0410	0.9682	0.4373	0.3121	0.957	2	1.0600	0.9600	0.5004	0.3425	0.942	3
MCMC η =100	1.0950	1.0748	0.3028	0.3490	0.990	0	1.1408	1.0934	0.3828	0.3606	0.980	0

N&S - Novick and Stefanski (2002); H&W - Huang and Wang (2001)

SIMEX results are based on B = 100, λ = (0.5, 0.7, 0.9, 1.1, 1.3, 1.5, 1.7, 1.9) and the simex R library

L - linear extrapolation; Q - quadratic extrapolation; NL - non-linear extrapolation of Cook and Stefanski (1994)

M - empirical mean; MD - empirical median; Emp-SD - empirical standard deviation; IQ-SD - inter-quartile dispersion; 95% CI - empirical coverage rate of 95% Wald confidence interval (or HPD interval, for MCMC); F - number of samples with no solution

Table 2.

Simulation Study B Non-Normal Measurement Error with Normal or Non-Normal True Covariate Results for Slope Parameter β₁ – Sample Size n=200, Validation Sample Size m=70

	M	MD	Emp-SD	IQ-SD	95% CI	F	M	MD	Emp-SD	IQ-SD	95% CI	F
X ~ N (0, 1) and ε ~ DBLEXP(γ)
	γ = 0.5						γ = 1.0
Naive	0.6378	0.6287	0.1609	0.1517	0.334	0	0.4659	0.4598	0.1370	0.1349	0.039	0
RECS	1.0684	0.9986	0.3611	0.3264	0.948	0	1.1362	1.0089	0.5714	0.4335	0.933	6
N&S	1.0471	1.0126	0.2970	0.3293	0.888	0	0.9625	1.0099	0.2794	0.2872	0.845	11
SIMEX - Q	0.8905	0.8641	0.2438	0.2276	0.871	0	0.7205	0.6970	0.2289	0.2165	0.629	0
H&W	1.0770	0.9848	0.4523	0.3202	0.951	0	0.9886	0.8985	0.4636	0.3336	0.942	1
MCMC η =100	1.2987	1.2613	0.3796	0.4360	0.970	0	1.1476	1.0940	0.3785	0.4483	0.990	0
X ~ N (0, 1) and ε ~ MODCHI(γ)
	γ = 0.5						γ = 1.0
Naive	0.6822	0.6793	0.1706	0.1672	0.467	0	0.5196	0.5146	0.1547	0.1552	0.126	0
RECS	1.0555	1.0348	0.2981	0.2775	0.959	0	1.0869	1.0345	0.3970	0.3546	0.966	0
N&S	1.1449	1.1451	0.3230	0.3808	0.857	4	1.1232	1.1779	0.2711	0.2319	0.805	18
SIMEX - Q	0.9678	0.9500	0.2624	0.2617	0.890	0	0.8320	0.8234	0.2711	0.2765	0.747	0
H&W	1.0260	0.9809	0.3822	0.2861	0.956	2	0.9640	0.8949	0.4753	0.3069	0.927	3
MCMC η =100	1.2154	1.1673	0.3372	0.2999	0.920	0	1.1502	1.1252	0.2996	0.2924	0.980	0
X ~ MODCHI (1) and ε ~ MODCHI (γ)
	γ = 0.5						γ = 1.0
Naive	0.5461	0.5348	0.1709	0.1662	0.250	0	0.3917	0.3824	0.1448	0.1402	0.063	0
RECS	1.1279	1.0479	0.4989	0.4415	0.938	0	1.1272	1.0319	0.5784	0.5316	0.932	0
N&S	1.2750	1.3552	0.4993	0.6506	0.672	51	1.0147	1.1508	0.4306	0.5522	0.545	212
SIMEX - Q	0.8175	0.7884	0.2870	0.2713	0.791	0	0.6396	0.6176	0.2602	0.2498	0.490	0
H&W	0.9610	0.8409	0.5507	0.3729	0.912	6	0.8084	0.6995	0.5894	0.4255	0.846	13
MCMC η =100	1.0279	1.0105	0.4865	0.4735	0.970	0	0.8416	0.8245	0.4370	0.4278	0.930	0

N&S - Novick and Stefanski (2002); H&W - Huang and Wang (2001)

SIMEX results are based on B = 100, λ = (0.5, 0.7, 0.9, 1.1, 1.3, 1.5, 1.7, 1.9) and the simex R library

L - linear extrapolation; Q - quadratic extrapolation; NL - non-linear extrapolation of Cook and Stefanski (1994)

M - empirical mean; MD - empirical median; Emp-SD - empirical standard deviation; IQ-SD - inter-quartile dispersion; 95% CI - empirical coverage rate of 95% Wald confidence interval (or HPD interval, for MCMC); F - number of samples with no solution

Table 3.

Simulation Study C Two Error-Prone Covariates and One Error-Free Covariate Sample Size n=500

	β1					β3
Scenario C1: X1, X2, Z ~ N(0, 1) and ε1, ε2 ~ N(0, 1)
	M	MD	Emp-SD	IQ-SD	95% CI	M	MD	Emp-SD	IQ-SD	95% CI	F
Naive	0.4296	0.4242	0.0804	0.0781	0.000	0.8626	0.8599	0.1201	0.1223	0.769	0
RECS	1.0817	1.0341	0.3116	0.2595	0.972	1.0525	1.0286	0.2079	0.1907	0.979	0
N&S	0.8286	0.8288	0.1316	0.1319	0.826	0.9483	0.9448	0.1382	0.1412	0.951	52
SIMEX - Q	0.8113	0.8038	0.1377	0.1333	0.571	0.9587	0.9524	0.1452	0.1519	0.920	0
H&W	0.6678	0.6675	0.5038	0.3360	0.800	1.0277	0.9679	0.4669	0.3039	0.918	14
MCMC η =100	1.0608	1.0335	0.2765	0.2508	0.870	1.0445	1.0418	0.1622	0.1834	0.970	0
	Scenario C2: X1, X2, Z ~ N (0, 1) and ε1, ε2 ~ N (0, 0.4 + 0.25(|X1| + |X2| + |Z|))
Naive	0.4386	0.4334	0.0824	0.0792	0.001	0.8712	0.8694	0.1223	0.1223	0.791	0
RECS	1.1884	1.1122	0.3800	0.3126	0.986	1.0828	1.0482	0.2405	0.2007	0.983	1
N&S	0.8606	0.8619	0.1329	0.1312	0.842	0.9668	0.9655	0.1439	0.1465	0.966	46
SIMEX - Q	0.8345	0.8242	0.1431	0.1394	0.819	0.9793	0.9746	0.1516	0.1562	0.933	0
H&W	0.6165	0.6176	0.4809	0.3277	0.733	0.9627	0.9279	0.4248	0.2837	0.905	9
MCMC η =100	1.0338	1.0084	0.2709	0.2637	0.890	1.0358	1.0339	0.1626	0.1701	0.950	0
	Scenario C3: X1, X2 ~ MODCHI(1), Z ~ N (0, 1), and ε1, ε2 ~ MODCHI(1)
Naive	0.3853	0.3814	0.0887	0.0915	0.000	0.8883	0.8893	0.1206	0.1207	0.809	0
RECS	1.0430	0.9841	0.3726	0.3328	0.942	1.0413	1.0232	0.1856	0.1667	0.971	0
N&S	0.8656	0.8664	0.2576	0.2880	0.782	0.9261	0.9201	0.1396	0.1415	0.946	34
SIMEX - Q	0.7463	0.7315	0.1586	0.1598	0.445	0.9626	0.9588	0.1402	0.1399	0.915	0
H&W	0.4723	0.4276	0.2733	0.2108	0.654	0.9155	0.9023	0.1798	0.1638	0.971	1
MCMC η =100	1.1462	1.1199	0.3153	0.3259	0.910	1.0167	0.9887	0.1713	0.1519	0.910	0

N&S - Novick and Stefanski (2002); H&W - Huang and Wang (2001)

SIMEX results are based on B = 100, λ = (0.5, 0.7, 0.9, 1.1, 1.3, 1.5, 1.7, 1.9) and the simex R library

L - linear extrapolation; Q - quadratic extrapolation; NL - non-linear extrapolation of Cook and Stefanski (1994)

M - empirical mean; MD - empirical median; Emp-SD - empirical standard deviation; IQ-SD - inter-quartile dispersion; 95% CI - empirical coverage rate of 95% Wald confidence interval (or HPD interval, for MCMC); F - number of samples with no solution

We begin with the Simulation Study A, the setting of normal measurement error with possible heteroscedasticity. RECS showed low bias throughout, especially when we look at the median of the estimates. N&S also generally showed low bias, although the bias was greater than that of RECS in a number of cases. SIMEX-NL also showed low bias in most cases (the last panel of Table 1 being a notable exception), but the estimation procedure was unsuccessful 6–10% of the time due to failure of the extrapolation process. SIMEX-L, SIMEX-Q, H&W, and MCMC performed markedly less well in terms of bias. The variability of the RECS estimates was comparable to that of the SIMEX-NL estimates and generally higher than that of the other methods.

We turn now to Simulation Study B, with non-normal measurement error. Again, RECS showed low bias throughout. N&S had low bias with double exponential error, and showed the best performance among the various methods in this case. With MODCHI error, RECS had low bias, while all the other methods had substantial bias.

We turn next to Simulation Study C, with two error-prone covariates and one error-free covariate. SIMEX and H&W performed poorly in estimating the slope parameters of the two error-prone covariates. The SIMEX-NL method performed especially poorly, producing estimates way off in the wrong direction. The RECS method performed well. In Scenarios D1 (normal homoscedastic error) and D3 (MODCHI error), RECS performed markedly better than N&S in terms of producing estimates with low bias, while in Scenario D3 (normal heteroscedastic), the performance was similar, with RECS overestimating and N&S underestimating. With MCMC method, the estimates with η = 10 were seriously biased, while the estimates with η = 100 had low to moderate bias.

In all three of the above scenarios, RECS generally yielded substantially better confidence interval coverage rates than the competing methods. Often the difference was substantial. We note that the SIMEX-NL method failed to admit a confidence interval in a considerable number of cases because the estimated variances were negative.

Finally, we turn to Simulation Study D, concerning the performance of RECS when the error model is misspecified (assumed normal but actually skewed normal or MODCHI). Aside from the case with both X and ε distributed MODCHI, the mean bias was in the range of 15–35% and the median bias was in the range 10–20%. Thus, in terms of median bias, RECS performed reasonably – certainly much better than the naive analysis with no measurement error correction. When both X and ε were distributed MODCHI, RECS performed poorly. However, this result is not too disturbing – because of the great difference between the MODCHI and normal distributions, it is unlikely that an analyst would mistakenly fit a normal model to MODCHI measurement errors. In principle, added robustness can be gained by using a flexible distributional form for the error model, such as the “semi-nonparametric normal” model of Gallant and Nychka (1987).

The degree of penalization in the RECS method tended to be very low throughout. The mean α value was less than 0.01 in all simulation scenarios studied.

5. Practical Illustration

We illustrate the method on data from the Nurses’ Health Study (NHS). The NHS began in 1976 when 121,700 female nurses aged 30–55 returned a questionnaire about their lifestyle and their health. Here, we analyze the relationship between physical activity and mortality among women diagnosed with breast cancer during the NHS follow-up. This relationship was previously examined by Holmes et al. (2005). The present analysis involves a subset of the nurses included in the analysis of Holmes et al. Specifically, we consider the group of 1660 nurses who were diagnosed with breast cancer at least 10 years before the administrative end of the study, June 2002. This is the main study. The endpoint is the binary variable defined as breast cancer death within 10 years following diagnosis. The total number of such deaths was 188. In NHS, physical activity was assessed by a questionnaire in which women were asked how much time they spent on average during the past year on each of the most common forms of leisure time physical activity. The questionnaire results were then converted into metabolic equivalent task hours per week (METS). Validation data were available from 149 women from the NHS II study (Wolf et al., 1994), a study begun in 1989 which involved a cohort of U.S. female nurses similar to that of the NHS, and in which the same physical activity questions were asked. In our analysis, these data are regarded as arising from an external validation study. In the validation study, METS was assessed using both the questionnaire and a detailed activity diary, with the diary regarded as the gold standard. We denote the METS value based on diary data by X and the METS value based on questionnaire data by W. The degree of measurement error is considerable, with the correlation between X and W in the validation study being 0.47. Since the distribution of METS was skewed, we developed the measurement error model from the validation data using a transformed version of METS defined by X* = log(1+X). We considered two measurement error models, denoted MEM1 and MEM2. Both models were of the form $W_i^{\ast }={\omega }_0+{\omega }_1{X}_i^{\ast }+{\epsilon }_i$. In MEM1, ε_i was taken to have the N(0, σ²) distribution, independent of $X_i^{\ast }$. MEM2 incorporated dependence between ε_i and $X_i^{\ast }$ , with the conditional distribution of ε_i given $X_i^{\ast }$ taken to be $N(0,{\gamma }_1+{\gamma }_2\mid X_i^{\ast }-\mu \mid )$, with $\mu =E[X_i^{\ast }]$. The parameters ω₀, ω₁ were estimated by simple linear regression in both models (weighted regression based on the MEM2 model for ε_i produced virtually identical estimates of ω₀ and ω₁). For MEM1, σ² was estimated by the regression MSE in the standard manner. For MEM2, γ₁ and γ₂ were estimated via regression analysis of the squares of the residuals obtained from MEM1; in this regression analysis, the t-test on γ₂ was borderline significant (p=0.0614), suggesting some evidence of heteroscedasticity. The estimates obtained were ω̂₀ = 1.2271, ω̂₁ = 0.5653, σ̂² = 0.8181, γ̂₁ = 0.5883, and γ̂₂ = 0.3497. Graphical inspection of the normalized residuals based on the MEM2 model for ε_i showed reasonable conformity to a normal distribution. A preliminary analysis of the main study data indicated that the log odds of breast cancer could be reasonably expressed as a linear function of X*, so we proceeded on this basis.

We ran RECS with 6 basis functions and K = K′ = 20 quadrature points in the quadrature calculations. The relevant R code can be found with the supplemental web materials or on the first author’s website. We also applied the SIMEX and N&S methods to the data. The H&W method is not relevant, since we have an external validation design rather than a replicate measures design. Standard errors for the RECS and N&S methods were computed using a sandwich-type estimator, while standard errors for SIMEX were computed using the jackknife method in the R package simex.

Table 7 presents the results for the various methods. The naive method was applied in two forms: (1) using $W_i^{\ast }$ as is (Naive1) and (2) using ${\stackrel{\sim }{W}}_i^{\ast }=(W_i^{\ast }-{\omega }_0)/{\omega }_1$, thus correcting for location-scale bias but not for measurement error (Naive2). The table includes estimates of β₀ and β₁ and corresponding standard errors. The table also includes an estimate and a 95% confidence interval for the odds ratio associated with a change in X* of 3.4, which corresponds approximately to the difference between the extreme lower and upper METS categories defined in Holmes et al. (2005) (walking less than 1 hour per week vs. walking 8 or more hours per week). SIMEX-L yielded a slope estimate similar to that yielded by Naive2, while SIMEX-Q gave a slightly larger estimate. RECS-MEM1, N&S, and SIMEX-NL yielded slope estimates differing markedly from the Naive2 estimate, and the estimates yielded by these three methods were comparable. RECS-MEM2 yielded a slope estimate differing substantially from RECS-MEM1, showing the impact of a more refined error model.

6. Discussion

We have presented a new “regularized corrected score” (RECS) approach to adjusting for covariate error in nonlinear regression problems. The approach builds on the corrected score method developed by Stefanski, Nakamura, and others. With a continuous error-prone covariate, the corrected score approach involves solving an integral equation. In many problems, an exact solution to this integral equation does not exist or cannot be practically obtained, and so we have proposed using an approximate solution obtained using the method of regularization. For logistic regression, a series of simulation studies showed that the method performs well in general, and offers some advantages over existing methods.

The RECS method yielded estimates with substantially less bias than competing estimators in the case of a single error-prone covariate with MODCHI error and in the case of two error-prone and one error-free covariates under two of the error models studied. The RECS estimator does tend to have higher variance than the other estimators, particularly the N&S estimator. We were unable to pinpoint the exact cause for the higher variance with the RECS method, but it is common for estimators that rely on weaker assumptions to be somewhat more variable than estimators that rely on stronger assumptions. The RECS method had better confidence interval coverage rates than the competing methods in all scenarios studied.

We have developed the theory in the general setting of classical likelihood models, which covers, in particular, generalized linear models such as nonlinear regression, logistic regression, and Poisson regression. It is possible to extend the development to other settings. In particular, it is of interest to extend the method to Cox survival regression, using the work of Zucker and Spiegelman (2008) on corrected score analysis for the Cox model with a discrete error-prone covariate as a starting point. We plan to develop this extension in future work.

The computational complexity and load of the method is modest. For example, the data analysis described in the preceding section finished in about 1 minute of real time, when run in R in batch mode on a VMware virtual machine configured with one AMD 2700 MHz processor and 1GB memory, installed on a physical machine SUN FIRE X4240.

The method presented here is a functional method in the sense of not requiring information on the distribution of the true covariate. This is in contrast to many other measurement error methods, such as regression calibration and likelihood-based methods. We do rely on a parametric model for the conditional distribution of the surrogate variable given the true variable, but our simulations suggest that the performance of the estimates is robust to misspecification of parametric model unless the misspecification is extreme. Also, it is possible in principle to use a flexible parametric model such as Gallant and Nychka’s (1987) “semi-nonparametric” model, which makes the reliance on parametric modeling less restrictive. The method is extremely general in terms of the types of measurement error models covered. It allows the measurement error to depend on the true covariate value and on other covariates. It also allows differential error, where the measurement error depends on the outcome. This flexibility is a distinct advantage relative to other methods.

Table 4.

NHS Results

	β0		β1		Odds Ratio for ΔX* = 3.4
Method	Estimate	SE	Estimate	SE	Estimate	95% CI
Naive1	−1.7213	0.1436	−0.1802	0.0680	0.54	[0.34, 0.85]
Naive2	−1.9425	0.0862	−0.1019	0.0384	0.71	[0.55, 0.91]
RECS-MEM1	−1.7496	0.1328	−0.2733	0.1141	0.39	[0.18, 0.84]
RECS-MEM2	−1.6186	0.1693	−0.3970	0.1758	0.26	[0.08, 0.84]
N&S	−1.7501	0.1348	−0.2726	0.1161	0.40	[0.18, 0.86]
SIMEX-L	−1.9186	0.0887	−0.1223	0.0439	0.66	[0.49, 0.88]
SIMEX-Q	−1.8722	0.0936	−0.1630	0.0539	0.57	[0.40, 0.82]
SIMEX-NL	−1.7256	0.1155	−0.2966	0.0943	0.36	[0.19, 0.68]