Abstract
An extension to the heterogeneous dielectric generalized Born (HDGB) implicit membrane formalism is presented to allow dynamic membrane deformations in response to membrane-inserted biomolecules during molecular dynamic simulations. The flexible membrane is implemented through additional degrees of freedom that represent the membrane deformation at the contact points of a membrane-inserted solute with the membrane. The extra degrees of freedom determine the dielectric and non-polar solvation free energy profiles that are used to obtain the solvation free energy in the presence of the membrane and are used to calculate membrane deformation free energies according to an elastic membrane model. With the dynamic HDGB (DHDGB) model the membrane is able to deform in response to the insertion of charged molecules thereby avoiding the overestimation of insertion free energies with static membrane models. The DHDGB model also allows the membrane to respond to the insertion of membrane-spanning solutes with hydrophobic mismatch. The model is tested with the membrane insertion of amino acid side chain analogs, arginine-containing helices, the WALP23 peptide, and the gramicidin A channel.
Keywords: membrane deformation, elasticity theory, hydrophobic mismatch, insertion penalty
Introduction
Membrane proteins account for about 30% of the proteins in a cell and are responsible for a large number of biological activities.1–3 Therefore, understanding their structure and dynamics is essential for gaining complete knowledge of life processes occurring in a cell. While experimental techniques have provided much of the available structural information, computer simulations of biological systems and of membrane proteins in particular have been able to provide critical information about the dynamics and energetics of these macromolecules.4–6
Molecular dynamics (MD) simulations of membrane-interacting proteins have remained a challenging task due to the complex nature of the membrane bilayer.7–9 Slow relaxation times of the lipid molecules require long simulations at significant computational cost to achieve statistical convergence when lipids and solvent molecules are considered explicitly.10 In order to address this issue, alternative models have been considered that do not involve an all-atom representation of the water and lipid molecules.11–18 In these models, the solvent degrees of freedom are approximated by a mean-field term that only considers the average effect of the environment rather than detailed specific interactions between the solvent and the solute.11–18 In most of these implicit solvent models, the environment is considered as a dielectric continuum where the electrostatic solvation free energy is obtained by numerical solution of the Poisson-Boltzmann (PB) equation.11,13,17,18 The PB model is easily extended to heterogeneous environments and it can describe membranes as systems consisting of layers with different dielectric constants.13,17–19 The PB-based electrostatic solvation free energy can then be combined with an implicit non-polar term to obtain the total solvation free energy. Non-polar terms are commonly calculated using the solvent-accessible surface area (SASA)18,20,21 but may also include an additional implicit solute-solvent van der Waals term.22,23
Because direct solution of the PB equation is computationally expensive and numerically problematic for use in molecular dynamics simulations,24–27 the generalized Born (GB) model is often used as an analytical approximation.28 In the GB formalism, the electrostatic contribution to the total solvation free energy is approximated as a sum of screened pairwise interactions between the charges of a given molecule. Many formulations of GB have been proposed with different levels of accuracy and speed compared to the PB equation.14 The GB formalism has also been extended to heterogeneous environments such as membranes.29–31 In early implementations of implicit membrane GB models, the membrane dielectric was assumed to be equal to the solute dielectric so that a simple two dielectric model could be retained.30,31 A more detailed model involving a variable dielectric constant was proposed by us.29 This so-called heterogeneous dielectric generalized Born (HDGB) model was motivated by dielectric profiles obtained from explicit solvent simulation of lipid bilayers32 and implemented as an extension of the GBMV (GB with molecular volume) model.33 The HDGB model does not require the protein to have the same dielectric as the membrane interior and therefore allows for a polarization response of the lipid bilayer. HDGB was tested for a variety of protein and peptide systems and was found to closely match PB results,29 to reproduce energetics from explicit solvent/lipid simulations,29,34 and to generate conformational sampling in good agreement with experimental data.34–37
All of the implicit membrane models proposed so far, including the HDGB model, assume that the membrane bilayer does not vary over time. In contrast, experiments and explicit solvent simulations suggest that membrane bilayers are dynamic and can deform in response to inserted biomolecules.38 In the presence of a charged particle, for instance, water molecules and lipid head groups may accompany the charge in the membrane interior and keep it partially solvated.39–41 As a result, the penalty for inserting charged groups into the hydrophobic bilayer is greatly reduced compared to what is predicted by implicit membrane models that assume a fixed bilayer width. For instance, the penalty for inserting a positive arginine side chain into an explicit dipalmitoylphosphatidylcholine (DPPC) bilayer was reported to be 17.8 kcal/mol39 while implicit membrane models overestimated the insertion penalty to be as high as 44 kcal/mol.42
Within the context of an implicit membrane formalism, membrane deformations can be included by allowing the dielectric profile to deviate from standard slab geometries and by adding the intrinsic cost of such membrane deformations to the free energy of solvation. The energy required to deform a model membrane can be obtained from elasticity theory.43–48 In this theory, the membrane is considered as an elastic sheet with material properties that describe its resistance towards different deformations such as bending, stretching, and compression.45,49,50 Choe et al. developed such an approach to determine the minimum-energy membrane geometry, deformation energy, and solvation free energy for a membrane-embedded protein.42 This formalism has been tested for a poly-leucine trans-membrane (TM) helix with a positive arginine residue at its center.42 The calculated insertion energies were found to be in good agreement with previously calculated explicit solvent free energies.39 An issue with this approach is that the optimal membrane geometry in the vicinity of the inclusion is not known a priori and has to be obtained by a relatively costly minimization of the overall energy.42 The performance of this approach can be improved by using a search algorithm to choose a reasonable initial geometry.51 However, the membrane geometry minimization followed by the use of PB for calculating the electrostatic contribution to the solvation free energy essentially limits its application to those cases where protein structure and membrane dynamics are decoupled.42,51 In other words, the protein structure is not allowed to vary in response to membrane deformations in this scheme.
In order to obtain a fully dynamic model where both, the membrane shape and solute conformations, can vary in a concerted fashion during MD simulations, we have extended the HDGB model29,34 to include membrane deformations. In the following, a description of the theory and simulation methods is given before first applications to the membrane insertion of amino acid side chain analogs and the dynamics of membrane-embedded peptides are discussed.
Theory
An extended Hamiltonian approach was followed to introduce the membrane deformation through extra degrees of freedom (DOF) that are propagated along with the rest of the system. The modified Hamiltonian (H) is written in terms of the atomic (x3N) and the membrane DOF (SNs) as follows
| 1 |
with Ns being the number of DOF that represent the membrane. Epot and Ekin are the potential and kinetic energies, respectively. The kinetic energy of the extended system is simply written as the sum of the atomic kinetic energies and the new DOFs (Eq. 2) which we are going to refer to from hereon as the membrane deformation parameters (MDP).
| 2 |
vi and vs are the velocities of atom i and the membrane associated DOFs, and mi and ms are the corresponding masses.
The potential energy of the extended system involves a modified implicit solvation term. Following the procedure by Choe et al.,42 the solvation energy of such a system is written in terms of the electrostatic (ΔGGB), the non-polar (ΔGnp), and the membrane deformation energy (ΔGmem) as shown in Eq. 3. The first two terms depend on the MDPs in addition to the atomic coordinates while ΔGmem is only a function of the MDPs.
| 3 |
In the following, the calculation of each of these three terms is described in more details:
Membrane deformation energy (ΔGmem)
Following Choe et al.,42,51 we used elasticity theory to estimate the membrane deformation energy. In this model, ΔGmem for one leaflet is written in terms of three main deformation moduli as follows42–45,47
| 4 |
In Eq. 4, Ka, Kc, and α are the compression, bending and surface tension moduli, respectively. d0 represents the width of the unperturbed membrane while u denotes the deviation of one leaflet from its unperturbed width, which we are going to refer to as leaflet deformation. In our definition, positive and negative deformation values stand for expansion and compression along the membrane normal, respectively. The double integral is taken over the entire plane of the membrane. The values for each modulus is taken from previous work.42
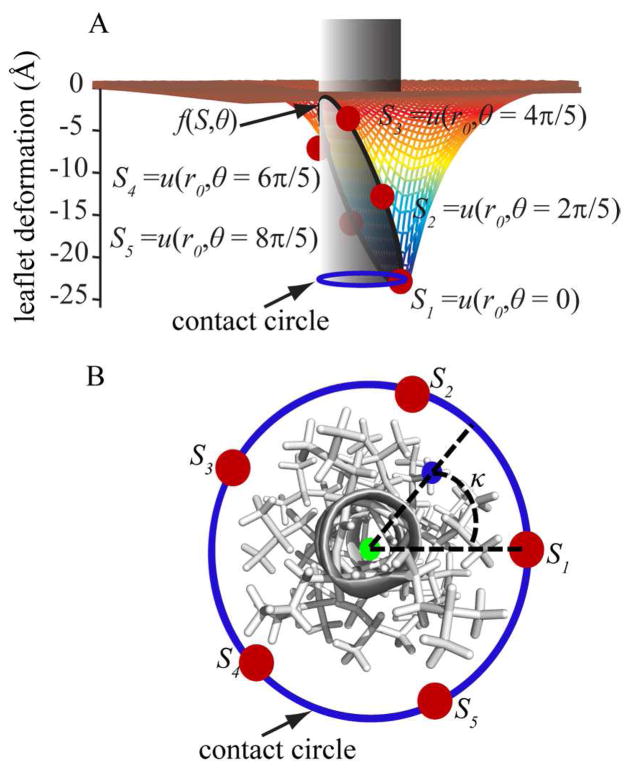
We make the assumption here that the membrane deformation energies in the top and bottom leaflets are independent of each other and that both terms can therefore be simply added to yield the total deformation energy for a bilayer. Furthermore, the overall geometry of the molecules inserted in to the membrane is approximated by a cylindrical inclusion. For the purpose of deformation energy calculation we followed the assumption made by Choe et al.42 and considered the axis of the cylinder to be parallel to the membrane normal. The curve along which the membrane meets the inclusion is going to be referred to as the contact curve. The projection of the contact curve on the xy plane, or any planes parallel to the xy plane, forms a circle called contact circle.(cf. Fig. 1A)
Figure 1.
(A) A schematic representation of an arbitrary deformation around a cylindrical solute inclusion in the top leaflet of the membrane bilayer. Fixed points at chosen angles (θ) around the contact curve where the membrane meets the solute cylinder (shown in gray) are indicated as red points. A cubic spline interpolation (f(S, θ)) of the leaflet deformation vs. θ is defined to calculate the deformation at any arbitrary point around the contact curve. The projection of the contact curve on an arbitrary plane parallel to the xy plane is shown with a blue circle. (B) Top view of the helix modeled with a cylinder in panel A. For an arbitrary atom marked with a blue point on the helix, the center of the contact circle is calculated as described in Eqs. 8 and 9 and shown with a green point. Then κ is calculated as explained in Eq. 10.
In order to obtain an optimal membrane configuration, we minimize the membrane deformation energy in Eq. 4 with respect to u. This leads to the following equation42,43,45,47,51
| 5 |
To solve Eq. 5, four boundary conditions are required. Many membrane-bound peptides such as TM helices for example, are approximated well with a simple cylindrical model. In this case, we can rewrite Eq. 5 in terms of r (the distance from the center of the cylinder) and θ (the angle around the circle where the membrane meets the cylinder). Following Choe et al., 42 we assume that the membrane will be flat with its unperturbed thickness far from the solute. Therefore,
| 6 |
The other two boundary conditions are the leaflet deformation and the contact slope around the contact curve.
To estimate the boundary conditions in the vicinity of the solute, we chose five evenly distributed points around the cylinder model for each leaflet. These points will be referred to as S = {S1, S2, …, S5} for the top leaflet and S′ = {S6, S7, …, S10} for the bottom leaflet. They represent the leaflet deformation at θ ={0, 2π/5, …, 8π/5} (cf. Fig. 1A) i.e. S1=u(r0, θ=0) where r0 is the radius of the cylinder. In our model we chose d0=50 Å as the unperturbed width of a DPPC model membrane as originally parameterized for the static HDGB model.29 This width approximately corresponds to the width of the entire membrane including its head groups.
Membrane deformation occurs when the contact points vary along z away from the equilibrium value for a planar bilayer. All points are allowed to vary independently, thereby allowing angular-dependent complex deformation geometries. The leaflet deformation for any arbitrary point is generated through cubic spline interpolation from the discrete points, f(S, θ).
For any given point on the contact curve, assuming that the radius of the cylinder is fixed, the position of the point on the contact circle on the xy plane can be specified with an angle ϕ. This angle is defined as the angle between the vector that connects the point to the origin and the x axis. Following Choe et al.42 the contact slope at each point on the contact curve with angle ϕ is calculated as
| 7 |
Given the boundary conditions from Eqs. 6 and 7, Eq. 5 was solved numerically using finite difference method with 20 angular and 3000 radial grid points. From the calculated u(r, θ) the corresponding values for ΔGmem were then obtained via Eq. 4. The leaflet deformations at different angles θ were changed from −25 Å to 10 Å with 5 Å increments (total of 8 values) and all possible combinations were sampled exhaustively. The corresponding deformation energy for each combination was calculated, which gave rise to a total of 85 calculations. The resulting energies were tabulated so that ΔGmem and smooth derivatives could be obtained for any given deformation via cubic spline interpolation. Because the test systems considered here only involved TM helices and small amino acid side chain analogs, we tabulated deformation energies only for fixed radii r0 of 7.5 Å (for the helical systems) and 4.0 Å (for the small molecules). In order to simulate other systems, the table would have to be recalculated for the appropriate radius of an approximate cylinder. Alternatively, one could also pre-calculate the deformation energies for discrete values of r0 and interpolate in the r0 dimension as well. However, because the additional dimension greatly increases the memory demands for the deformation energy lookup table beyond what may be available on typical workstations, we did not pursue this option here.
To consider the effect of local membrane deformation on the solvation free energy of each atom, the local deformation at the position of each atom has to be obtained. To calculate the deformation of top and bottom leaflets at the position of any given atom i, uu,i and ul,i, we first found the projection of the contact curve on a plane parallel to the xy plane that passes through this atom (shown with solid blue circle in Fig. 1B). The center of the circle was chosen to be the weighted average of atomic coordinates of all atoms whose z coordinates are within 15 Å from atom i. The weighting function given in Eq. 8 was determined empirically:
| 8 |
The x and y coordinates of the center of the hypothetical circle for atom i (CXi and CYi) were then obtained from Eq. 9
| 9 |
Next, the angle (κi) of atom i on this circle was defined as follows with respect to the x axis (cf. Fig. 1B)
| 10 |
In Eq. 10, and
However, Eq. 10 is not defined for atoms where xi-CXi=0 and yi-CYi=0. In addition, we also observed that for atoms whose distance from their center is smaller than 1.5 Å, the derivatives of κi with respect to the atomic coordinates is not continuous. To address this issue, we considered ri as the distance of each atom from its corresponding circle. Based on the magnitude of ri, two possible states were considered. For ri ≥ 1.5 Å, the calculated angle κi was used in both leaflets spline interpolations f(S, θ) and f(S′, θ) to obtain the corresponding leaflet deformation using the following equations
| 11 |
| 12 |
In the second case, the leaflet deformation was assumed be the average of the top and bottom MDPs for ri < 1.5 Å
| 13 |
| 14 |
This distance cutoff was chosen to ensure the continuity of the derivatives of uu,i and ul,i with respect to xi and yi. Finally, we defined the deformation in top and bottom leaflets as the weighted averages of the two possible states mentioned above. We chose a simple switching function as the weighting function (Eq. 17) and we determined its parameters empirically.
| 15 |
| 16 |
| 17 |
Electrostatic solvation free energy (ΔGGB)
In the HDGB formalism, ΔGGB is written in terms of the atomic charges, qi, qj and the effective local dielectric constant ε′i,j as follows
| 18 |
| 19 |
where αi is the atomic Born radius and the dielectric constants are only a function of the position of each atom along the membrane normal.29,34
Here, we are extending this formalism to include the effect of leaflets deformation at the position of any atom i via the uu,i and ul,i parameters.
| 20 |
This formalism and the following analysis consider only the deformation in one leaflet (i.e. uu,i=ui, ul,i=0), but later in this chapter we will address how to consider deformations in both leaflets.
In order to calculate the effective dielectric constant for an atom i as a function of both, its position along the membrane normal and the local leaflet deformation, we revised the original dielectric profile calculation.29 First, we considered a simple two-dielectric membrane model where the thickness of the hydrophobic core was chosen to be 30 Å with a dielectric constant of 2. The head group region and water dielectric constant was set to 80. The top leaflet was symmetrically deformed from u=+10 Å (expansion) to u=−25 Å (compression towards the center of the bilayer) around a cylinder with the radius of 7.5 Å. For each deformation value, a monovalent probe charge with a radius of 2 Å was displaced along the edge of the cylinder from z=−25 Å to z=+25 Å with 1 Å increments. For each position of the probe charge along the inclusion edge, the solvation free energy of the charge was calculated according to the PB equation using the APBS package.52 161 grid points were used in each direction with grid spacing of 0.5 Å. Fig. 2 illustrates the setup of dielectric profile calculation for u=−15Å.
Figure 2.
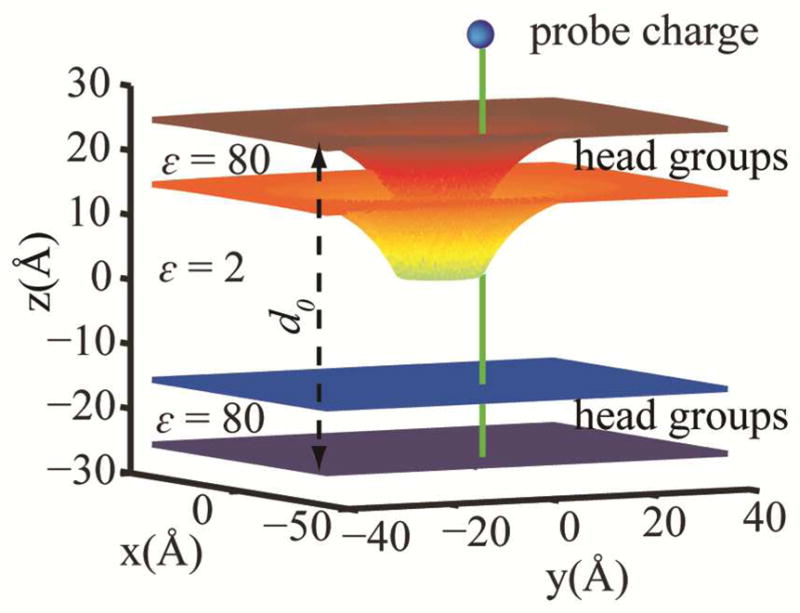
Schematic illustration of the dielectric profile calculation for a symmetric deformation of −15 Å in the top leaflet. The hydrophobic core is assumed to be 30 Å thick with the dielectric constant of 2. The z axis is chosen to be the membrane normal. The probe charge is shown as a blue sphere. It is translated along the green line in 1 Å increments. The unperturbed membrane width (d0) is shown with a black dashed line.
Dielectric profiles ε′(z,u,0) were then obtained from the inverted Born equation using the solvation energies calculated from PB with q2=1 and a=2 Å for the probe charge:
| 21 |
The dielectric profiles calculated from this method were subjected to further optimizations to improve the agreement between the calculated insertion energies of amino acid side chain analogs and the previously reported values by MacCallum et al.40 For each amino acid side chain analog, the center of mass of the analog was first positioned at z=30 Å and the top leaflet was deformed around the hypothetical cylinder from u=0 Å to u=−25 Å with 2 Å increments. The minimum total energy was saved as the reference. The same procedure was repeated for z=0 Å and the insertion energy (from bulk solvent to the center of the membrane) was then calculated as the difference between the two minimum energies. The optimization was continued until a good qualitative agreement between the calculated insertion energies and those obtained from explicit solvent simulation40 was achieved.
As a result of this optimization, a general scheme for calculating dielectric constant for an arbitrary position along the inclusion edge was devised as follows:
| 22 |
| 23 |
| 24 |
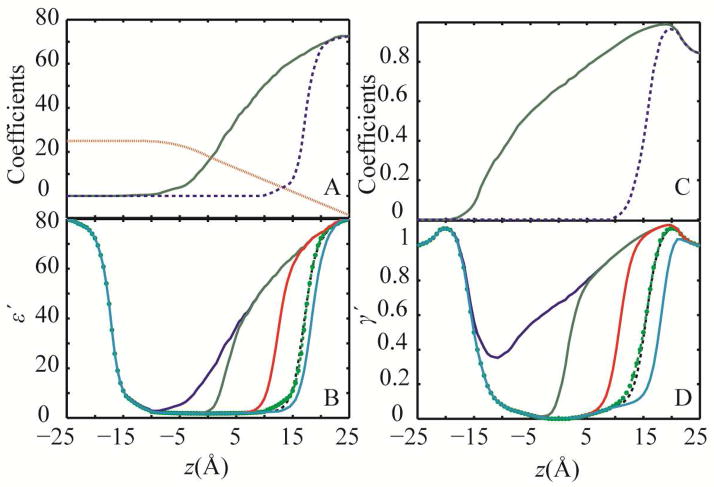
In Eq. 22, ε′(zi,0,0) is the original dielectric profile for a flat membrane29,34, aε, eε and c are adjustable cubic spline functions of z and I=0. The final functions for aε, c and eε are shown in Fig. 3A and the calculated dielectric profiles for some deformation values are shown in Fig. 3B as examples.
Figure 3.
(A) Optimized coefficients in Eq. 24 for the dielectric profile calculations aε: solid green line, c: dotted red line and eε: dashed blue line; (B) dielectric profiles calculated using coefficients in panel A and Eqs. 22–24 for different symmetric deformations in one leaflet: u=−25 Å: blue, u=−15 Å: green, u=−5 Å: red, u=+3 Å: cyan, and u=0 Å dashed black line. The original dielectric profile for a flat membrane is shown with green circles29,34; (C) optimized coefficients for surface tension modulation profile calculations aγ′: solid green line and eγ′: dash blue line (D) calculated non-polar profiles for different deformations in one leaflet with colors as in panel B
The dielectric profiles calculated for the distorted membrane show that, compared to the flat membrane,29,34 the polarization effect extends to longer distances along the membrane normal from the surface of the membrane. In other words, the diffusion of high dielectric solvent to the low dielectric region of the membrane hydrophobic core mimics the water defect that was previously observed in explicit solvent simulations39,40 (see Fig. 3).
Non-polar solvation free energy (ΔGnp)
In the original HDGB model,29 ΔGnp was calculated from the atomic solvent accessible surface areas (SASAi) multiplied by the cost of cavity formation (γ′) at the position of atom i along the membrane normal.
| 25 |
In the new formulation of ΔGnp, γ′ is assumed to be a function of the deformations in both top (uu,i) and bottom (ul,i) leaflets at the position of each atom i and the position of the atom along the membrane normal (zi):
| 26 |
Following the same procedure for obtaining the dielectric constant profiles, here we only consider the deformation in one leaflet (i.e. uu,i=ui, ul,i=0). However, later we will describe how simultaneous deformation in both leaflets are considered
To include the effect of a leaflet deformation in γ′, first aγ′ and then eγ′ were obtained by multiplying aε and eε (Fig. 3A) with 0.015 to match the range of non-polar values from 0 to 1.2. The resulting scaled coefficients were then used to obtain the primary non-polar profiles using the following equation:
| 27 |
where γ′(zi,0,0) is the original non-polar profile of the unperturbed membrane34 and w(ui) is the same as described in Eq. 23. The scaled coefficients were then subjected to optimization to match insertion energies for amino acid analogs from explicit solvent simulations40 as explained above for the dielectric constant profile. The best value for I was found to be 1.5 and c was chosen to be the same for both dielectric and non-polar profile. The optimized functions along with selected non-polar profiles at different deformations are shown in Fig. 3C and D.
In the derivation presented so far, one leaflet was kept flat while the other leaflet was allowed to deform. If both leaflets deform simultaneously, the deformation energy is assumed to be additive but the dielectric and surface tension modulation profiles are obtained as weighted averages of the individual values calculated separately for the top and bottom leaflets according to Eqs. 22–24 and Eq. 27. To determine the weighting function, 21 membrane geometries with different deformations in top and bottom leaflets were generated. The dielectric profiles were calculated from PB following the same procedure as described above. A weighting factor (η) based on a simple switching function was then fitted to match profiles obtained individually according to Eqs. 28 and 29 for the dielectric and surface tension calculations:
| 28 |
| 29 |
for an atom i that resides in a bilayer whose top leaflet is deformed by uu,i and bottom leaflet is deformed by ul,i at the position of atom i. As a result of the optimization, the weighting function was determined to be:
| 30 |
Computational Methodology
The dynamic heterogeneous dielectric generalized Born model (DHDGB) was implemented as an extension of the HDGB model29 in the macromolecular simulation package CHARMM,53 version c36a1. Simulations of the WALP23 peptide were performed using the CHARMM22 force field54 with the CMAP correction55 while the gramicidin A channel was modeled using the CHARMM36 force-field56 with the improved CMAP potential for D-amino acids.56 No cutoffs were used for the non-bonded interactions. The MMTSB Tool Set57 was used for the minimizations, equilibration steps, and for the analysis.
Membrane Insertion of Small Molecules
The performance of the DHDGB model was first tested by comparing amino acid side chain analog insertion free energy profiles with previously calculated data from explicit solvent/lipid simulations.40 For each amino acid analog, the center of mass of the corresponding molecule was translated from 30 Å to 0 Å along the membrane normal (z axis) using 1 Å increments. For each insertion depth, all MDPs corresponding to the top leaflet were varied from u=0 Å (flat leaflet) to u=−25 Å with 2.5 Å increments while the bottom leaflet was kept flat. In calculating deformation energies, we assumed that each side chain analog can be approximated as a cylindrical inclusion with a fixed radius of 4 Å. For each insertion depth of the side chain analogs, the top leaflet was deformed from flat state to −25 Å while the center of mass of the side chain analog was kept fixed. For each resulting membrane deformation, average energies were obtained by exhaustive sampling of different rotation angles of the molecule around its x and y axes at 18° increments and averaging over all possible states. Finally, the insertion energy was obtained as the difference of the minimum average energy at each insertion depth relative to z=30Å where the molecule is outside the membrane and solvated only with water. The deformation energy for each membrane configuration was obtained using tabulated valued for r0=4 Å as described above.
Arg-Containing TM Helix
To compare the insertion free energy of charged arginine (Arg) side chains embedded in long TM helices, a poly-leucine helix with 91 residues was constructed and the middle residue was mutated to Arg, following previous work by Dorairaj et al.39 The helix was oriented in such a way that its long axis is parallel to the z-axis and its center of mass is located at the center of the bilayer. The helix was rotated around the z-axis so that the projection of the Arg center of mass onto the contact curve is located at θ=0. Thus, the MDP closest to the Arg is S1. The insertion depth of Arg was defined as the position of the Cα of Arg side chain along the z-axis. To obtain the insertion profile, the TM helix was translated along z with the Arg location changing from 0 Å to 30 Å. For each Arg insertion depth, the helix and the MDPs were subjected to 50 steps of steepest descent (SD) minimization followed by a long adopted-basis Newton-Raphson (ABNR) minimization run. Minimization was carried out for at least 5000 steps or until the energy changed less than a tolerance of 10−7 kcal/mol. The final energy at each insertion depth was chosen as the minimum energy and the insertion energy was calculated relative to z=30 Å.
WALP23 Peptide
The helical WALP23 peptide (sequence: GWWLALALALALALALALALWWA) was studied to test the effect of hydrophobic mismatch. The peptide was capped with an acetyl group on the C-terminus and an N-methyl amide group on the N-terminus. The initial structure was subjected to 50 steps of SD minimization followed by 1000 steps of ABNR minimization in an implicit membrane represented by the HDGB model29 with the modified dielectric and non-polar profiles.34 Other implicit solvent parameters are described elsewhere.58 The temperature of the minimized structure was gradually increased to 300K during six rounds of equilibration. In each equilibration stage, the temperature of the peptide was increased by 50K and 10,000 MD steps were carried out. The time step was chosen as 1.5 fs to maintain stable simulations with the implicit solvent model.59 The SHAKE algorithm was applied to constrain bonds involving hydrogen atoms.60 The temperature was maintained by using a Nosé-Hoover thermostat61,62 with a temperature coupling constant (qref) of 50 K.cal.s2. The equilibrated structure was used as the initial structure for 32 independent MD simulations using the DHDGB model, each run over 20 ns length for a total simulation time of 640 ns. In each simulation, the temperature of the peptide was set to 303 K and the temperature of the MDPs was set to 0.5 K with a Nosé-Hoover coupling constant of 0.1 K.cal.s2. The mass of the MDPs was set to 50,000 amu. The MDPs parameters were chosen in a way that the fluctuations in membrane deformation in a 20 ns simulation of MDPs mimicked the fluctuations observed in the reference explicit solvent simulation of a DPPC bilayer with the same length. To compare with the DHDGB model, 32 independent simulation using the HDGB29,34 model (with a fixed membrane) were also run for 20 ns each. The last 16 ns of each simulation were used for further analysis.
In order to identify the dominant structures of WALP23 in DPPC using the DHDGB model, 5% of the total sampling was used to generate 2 ensembles: one with the structures with the insertion angle smaller than 15° and a second ensemble with structures where the insertion angle is between 20° to 45°. The dominant structure of each ensemble was obtained using the kclust tool from the MMTSB Tool Set with a radius of 2 Å using heavy atom RMSD values. The RMSD values were obtained after aligning the structures with a modified superposition protocol that preserves the insertion angle and insertion depth36.
Gramicidin A
As another test case for hydrophobic mismatch, the gramicidin A (gA) dimer was simulated with the DHDGB model. The initial structure of the dimer was obtained from the Protein Data Bank (PDB code 1JNO63). The minimization and equilibration steps followed the same protocol as for the WALP23 peptide described above. The equilibrated structure was then used as the starting structure for 16 independent simulations using the DHDGB model, each over 12.3 ns simulation time. The first 3.5 ns of each simulation were discarded and the remaining 8.8 ns were used for analysis.
Results and Discussion
The DHDGB model was implemented in CHARMM and applied to a number of test cases as detailed in the following:
Amino acid side chain analogs
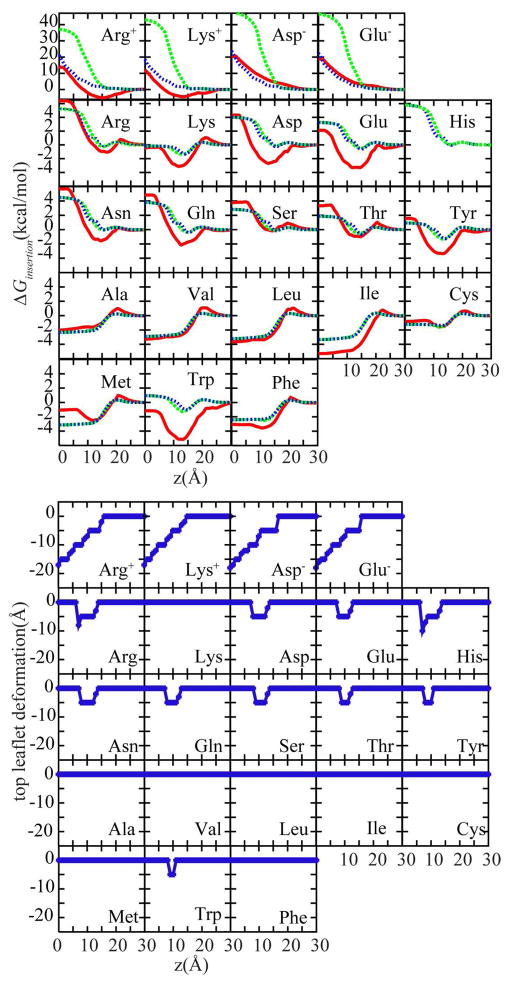
The first test case involves membrane insertion free energy profiles for amino acid side chain analogs. Fig. 4 compares profiles from HDGB and DHDGB with explicit lipid simulation results.40 As discussed previously,29,34 HDGB is in good agreement with the explicit lipid results for most residues except for the charged amino acids (top row). DHDGB closely matches HDGB for non-charged amino acids but greatly improves the profiles for charged amino acids, avoiding the overestimation of the insertion free energies for Arg(+), Lys(+), Asp(−) and Glu(−) residues. This is a consequence of an effective decrease in the membrane thickness as the charged residues enter the membrane (see Fig. 4, bottom panel). In case of the charged analogs, the top leaflet deforms by ~ −19 Å when the charged residues are at z=0. This deformation models the effect of water penetration and leads to a significant reduction of the insertion energy. For Arg(+), for instance, the application of DHDGB reduces the insertion free energy by ~15 kcal/mol. Minor membrane deformations are also found for polar residues at intermediate insertion depths, but the effect on the insertion free energy profiles is small with changes of less than 0.3 kcal/mol.
Figure 4.
Top panel: Amino acid analog insertion free energy profiles with HDGB29,34 (dashed green) and DHDGB (dotted blue) compared to results from explicit solvent/lipid simulations40 (solid red). Bottom panel: Minimized leaflet thickness upon amino acid side chain analog insertion in the DHDGB model.
To calculate deformation energies, the side chain analogs were assumed to be encompassed with a cylinder with a fixed radius of 4 Å. The use of a cylindrical model instead of considering the actual shape of the inserted small molecules is necessitated by practical constraints - our model relies on pre-calculated deformation energies that are possible only for limited sets of geometries – but it can also be justified on physical grounds. Because of the size and shape of the lipids, we expect that the length scale over which the membrane deforms, and over which deformation energies vary, in response to inserted solutes is larger than the scale of shape variations of small molecules. Hence, a simple geometric approximation like a cylinder appears to be a reasonable approximation. The close agreement between insertion energies calculated for different side chain analogs using DHDGB and the explicit solvent model provides partial justification for this assumption, but this point certainly deserves further attention in future efforts to improve our model.
TM Helix with a Central Arg(+)
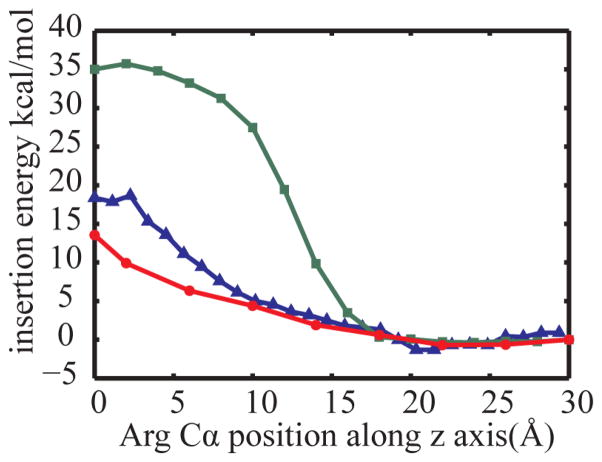
The second test case is a long poly-leucine TM helix with a central Arg(+) that has been previously studied to understand the insertion of charged residues into membranes. The insertion free energy profile was calculated with both, HDGB and DHDGB, and was compared with potentials of mean force from long explicit water/lipid umbrella sampling simulations in a DPPC membrane.39 The results are shown in Fig. 5. As for the charged amino acid side chain analogs, the use of DHDGB matches the explicit lipid insertion profiles much better than the original HDGB model. The explicit lipid and DHDGB curves are in near perfect agreement from 9 Å to 30 Å while for deeper insertions the DHDGB model slightly underestimates the explicit lipid insertion free energies. When Arg(+) is at the center of the membrane, the insertion free energy is reduced from 35 kcal/mol with the HDGB model to 13.5 kcal/mol, compared to the explicit lipid free energy result of 17.8 kcal/mol.39 The discrepancy for deep insertions is likely due to idealizations of the deformation model that may become more problematic for very deep insertions.64 However, differences in how the insertion profiles were obtained (minimization of an MMGB/SA function vs. PMF from umbrella sampling) or sampling inadequacies in the explicit lipid simulations that are notoriously difficult to converge,65 may also play a role.
Figure 5.
Membrane insertion energies for a poly-leucine TM helix with a central Arg(+). Energy calculated with the HDGB29,34 model (green squares) are compared with DHDGB energies (red circles), and explicit solvent results39 (blue triangles).
In the free energy calculations for the same TM helix by Choe et al.42 using the same elasticity model in combination with the PB equation the membrane was compressed systematically around the helix so that the contact curve followed the predetermined sinusoidal equation. As a result, the degree of deformation at a given Arg insertion depth was presumed without considering the coupling between peptide conformation and membrane deformation. In the DHDGB method, the MDPs were allowed to vary freely along with the Arg side chain orientation to find the optimal configuration. Therefore, no constraint was applied to the membrane configuration and no prior knowledge of a contact curve is required.
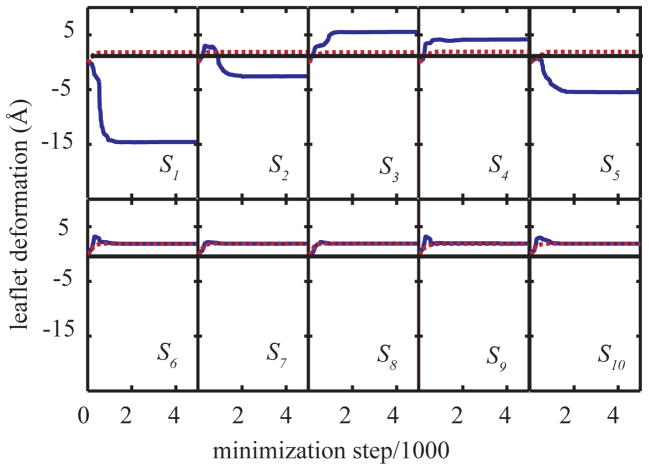
To follow the membrane deformation during the course of minimization, the MDPs were monitored and plotted against the minimization step in Fig. 6 for two different insertion depths of Arg(+). When Arg(+) is outside of the membrane at z=30Å (dashed red line), there is a slight increase in the membrane thickness in both top({S1, …, S5}) and bottom ({S6, …, S10}) leaflets, presumably due to membrane adaptation to the hydrophobic poly-leucine helix that extends out of the membrane. However when the charge is inserted into the hydrophobic core, i.e. z=6Å, the top leaflet in the vicinity of the helix (S1) is significantly perturbed with a deformation of as much as −15 Å.
Figure 6.
Variation of deformations of top {S1,…,S5} and bottom{S6,…,S10} leaflets. The dashed red line represents the variation of MDPs for z(Arg:Cα)=30Å and the solid blue line shows the variation for z(Arg:Cα) =6Å. The thin solid black line represents the flat leaflets.
The insertion energy calculated here is ~5.3 kcal/mol, smaller than the value obtained by Choe et al.42 This difference probably results from using two different approaches for obtaining solvation free energies (GB vs. PB which was employed in Choe et al.42 approach).
MD simulation of WALP23 in a membrane bilayer
The orientation of TM helices in membrane proteins is closely related to their structure and function.66 In mechano-sensitive channels, for example, tilting and reorientation of the TM helices can lead to channel opening and closing.67,68 It is generally believed that the tilt angle of a TM helix is affected by the hydrophobic mismatch between the helix and the membrane bilayer. When the peptide hydrophobic length is greater than the membrane hydrophobic thickness, tilting provides better peptide-membrane interaction and less exposure of hydrophobic residues to the solvent. However, for short peptides whose lengths are comparable to the hydrophobic thickness of the membrane, the tilt angle is reported to be smaller.69
WALP peptides are synthetic short peptides that can model the hydrophobic mismatch in different membrane environments very well and, therefore, they have been the target of both experimental and theoretical studies.70–82
As a further test, the effect of membrane deformations on the tilt angle of WALP23 was examined using MD simulations with both the DHDGB and the HDGB models. The tilt angle of the peptide was defined as the angle of the peptide axis with the membrane normal (z axis) and the membrane deformation was calculated as sum of the average deformations of top and bottom leaflets.
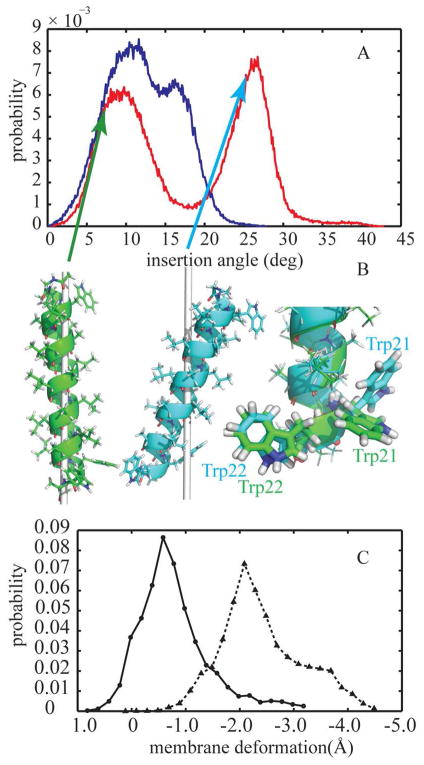
The probability distribution of the tilt angle shows two states in both deformable and non-deformable models (see Fig. 7A). For the static membrane with a fixed thickness modeled by HDGB, the most probable insertion angles are located at 10.8° and 16.3° (Fig. 7A, blue curve) with the smaller angle being slightly more favorable. However, the inclusion of the membrane deformation with the DHDGB model clearly affects the tilt angle distribution (Fig. 7A the red curve). The first peak of the distribution occurs at 9.2°, similar to the first peak with HDGB, but the second peak is shifted to much larger tilt angles of 26.4°. In Fig. 7C the population distribution of membrane variation from DHDGB model is depicted. Closer look at the membrane variation reveals that conformations in the first peak do not coincide with significant variations in membrane thickness (−0.8 Å), while more significantly tilted conformations are concomitant with more significant membrane deformations (−2.4 Å).
Figure 7.
(A) Probability distribution of the membrane insertion angle of WALP23 in implicit membrane environment using HDGB (blue line) and DHDGB (red line) (B) Dominant structures of WALP23 with different insertion angles: green, insertion angle of 8° and cyan, insertion angle of 26°. The gray line shows the z axis (membrane normal). The right side shows aligned structures with different tryptophan side chain orientations highlighted. The structures were rendered with pymol90. (C) Probability distribution of membrane deformations for insertion angles smaller than 15° (solid line with circle marks) and insertion angles between 20° and 45° (dotted line with triangle marks)
Representative structures from clustering at different insertion angles are depicted in Fig. 7B. Aligning the dominant structures for small (8°) and large (26°) insertion angles shows that the orientation of the W21 side chain varies between two distinct conformations that position W21 and W22 to lie at the interface at small and large insertion angles, respectively. Hence, the bimodal distribution in Fig. 7A is likely a consequence of the torsional preferences of the W21 side chain that limit arbitrary orientations of W21 with respect to the membrane.
The overall average insertion angle obtained for WALP23 using the DHDGB model is 17.6° ± 1.2°. This angle is larger than the value of 14.9° observed in explicit solvent simulations of the peptide in a palmitoyloleoyolphosphatidylcholine (POPC) bilayer with a comparable thickness to DPPC, the membrane modeled here with DHDGB.82 The larger value with DHDGB is a result of sampling both smaller and much larger insertion angles. Interestingly, much larger insertion angles have also been observed in MD simulation of WALP23 in DMPC where angles between 28° and 33° were reported.79,82 The sampling of small angles for an undeformed membrane while larger angles are preferred for a deformed membrane with DHDGB is therefore in good qualitative agreement with the explicit solvent simulation results. Interestingly, experimental studies also report values that appear to cluster either around 15° or 30° depending on the membrane and experimental technique that has been used.83–85 The comparison with the experimental data is hindered, though, by apparent difficulties in unambiguously deriving insertion angles from the experimental measurements.79
The suggestion of a two-state equilibrium between undeformed membrane, small peptide insertion angle and deformed membrane, large insertion angle states by our simulation results is not supported by other simulations. However, this may be due to significant kinetic barriers due to the presence of explicit lipids that prevent a transition from an undeformed membrane to a deformed membrane in the limited simulation time scales. Alternatively, it is possible that the elastic membrane model used here slightly underestimates the cost for deforming the membrane, hence allowing such a state to be sampled with a significant population. Finally, it should be noted that the elasticity model used in this work is parameterized for cylindrical inclusions whose main axis is parallel to the membrane normal. Such a model is assumed to work well for small insertion angles but may become problematic as insertion angles become larger.
Further tests should be carried out in the future to examine this system more closely and possibly fine-tune the DHDGB model if necessary.
MD simulation of gramicidin A in a membrane bilayer
Finally, we applied the DHDGB model to gramicidin A (gA), a short dimeric peptide with 15 amino acids per monomer and an alternating L-D sequence. GA forms a small channel that is shorter than most membrane thicknesses and it is, therefore, a good model for studying protein-induced membrane deformations.43,45–50,86 In recent MD simulations of gA in different membrane bilayers with various thicknesses, it has been observed that the tilt angle of the dimer is a function of the thickness, apparently to maximize protein-membrane interactions; in particular, the peptide adopts larger insertion angles in membranes with thinner hydrophobic core. Furthermore, it was also reported that the peptide can induce an overall 4 to 5 Å compression of the membrane in different bilayers.87 A comparison between WALP23 peptides and gA channels suggests that gA responds to hydrophobic mismatch by inducing membrane deformations rather than tilting of the peptide, while the WALP23 peptide predominantly uses tilting to adapt to membrane environments with different thickness.82,87–89
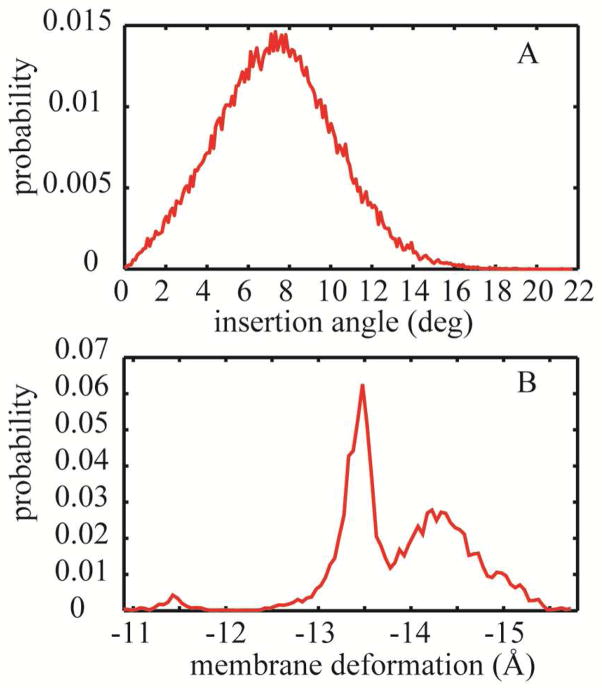
From simulations of the gA channel with the DHDGB model we obtained the tilt angle and membrane deformation shown in Fig. 8. The insertion angle and membrane deformation were calculated using the same definitions as were applied for WALP23.
Figure 8.
(A) Probability distribution of the membrane insertion angle for the gA dimer in the membrane bilayer. (B) Probability distribution of the average membrane deformation.
We found an average insertion angle of 7.4 ± 0.2° which is in good agreement with the insertion angles that were previously obtained for gA in DOPC (~9.1°) and POPC87 (~8.9°). Furthermore, we observe a significant membrane deformation of −13.9 Å ± 0.1 Å. While these values are larger than the 4 to 5 Å that have been reported from explicit solvent simulations87 they support at least qualitatively the hypothesis that gA tilts less than WALP23 but deforms the membrane more significantly.
The discrepancy between the membrane deformation observed in our simulation and the values in explicit solvent87 may be explained in part by different references for measuring deformation. In the analysis of the explicit solvent simulations, the membrane thickness was measured as the average distance between the C2 atoms of acyl chains in both leaflets which amounts to a unperturbed thickness of ~29 Å.87 However our definition of membrane thickness refers to the top of the head-group29 region which is ~10Å away from the hydrophobic core.29 Considering the difference between the thickness definitions and assuming that the membrane deformation would be distributed along the entire membrane the deformation observed in DHDGB may be scaled by 29/50 to estimate a value of ~8.2 Å for the deformation of just the hydrophobic layer. This value compares more favorably with the 5 Å deformation observed in the explicit simulations.87 An additional factor may be that membrane deformation is kinetically inhibited in explicit lipid simulations and may not have been fully realized due to limited simulation lengths. In the DHDGB model, the response of the environment is much more rapid and exhibits no kinetic barriers. Hence, the optimal deformation, within the limits of the model used here, is readily achieved within relatively short simulation times.
Conclusions
We describe the DHDGB implicit membrane model that incorporates change of the local membrane thickness in response to macromolecules embedded into the membrane. DHDGB couples the previously developed HDGB implicit membrane model to elasticity theory in a framework that is suitable for molecular dynamics simulations. DHDGB correctly predicts membrane deformations in response to the insertion of charged residues and as a result of hydrophobic mismatch. DHDGB significantly improves the agreement for the insertion energy of amino acid side chain analogs between the implicit membrane model and results from all-atom explicit solvent simulations.40 The same is found for the insertion of Arg(+) as part of a long TM helix where the inclusion of membrane deformation decreases the insertion free energy by ~21.5 kcal/mol, close to the value obtained by explicit lipid simulations.
We have also tested our model with TM peptides such as WALP23 and gA dimer using MD simulation. In the case of WALP23, we observed significant tilting of the peptide in the response to the hydrophobic mismatch with tilt angles that are in close agreement with the corresponding values from explicit solvent simulations and experiments. For gA, tilting is less pronounced and instead significant membrane deformations are found. Therefore, DHDGB captures the well-known tendency of WALP23 to tilt in favor of significant membrane deformations vs. gA, which favors significant membrane deformations over tilting.
While the DHDGB method represents significant progress over fixed membrane implicit membrane models, there are still a number of limitations in the current implementation. Our method of calculating the dielectric and surface tension modulation is based on a cylindrical approximation of a solute inserted into the membrane. This model fails for peptides that have very large tilt angles, systems that interact only interfacially with the membrane, or peptides that induce pore formation.In principle, such cases can be addressed by improving the calculation of the profiles and possibly along the MDPs to vary in x and y as well as in the z direction. Drastic changes of the membrane, such as pore formation, would also require a better estimate of membrane deformation energies than what is provided by the mattress model used here.
Despite its remaining limitations, the DHDGB is a significant advance over the HDGB model and leads the way to wider applications of implicit membrane models in the study of membrane-bound systems.
Acknowledgments
The authors thank Michael Grabe and Keith Callenberg for providing a numerical solver for the partial differential equation for the elastic membrane model and for insightful comments on elasticity theory. We also greatly appreciate comments by Toby Allen and Wonpil Im with respect to membrane parameterization and gA modeling. Funding from NIH GM084953, NIH GM092949 and NSF CBET 0941055 is acknowledged. Computer resources were used at XSEDE facilities (TG-MCB090003) and at the High-Performance Computing Center at Michigan State University.
Abbreviations
- MD
molecular dynamic
- DOF
degrees of freedom
- MDP
membrane deformation parameter
- PB
Poisson-Boltzmann
- GB
Generalized Born
- GBMV
GB with molecular volume
- HDGB
heterogeneous dielectric generalize Born
- DPPC
dipalmitoylphosphatidylcholine
- gA
gramicidin A
- TM
trans-membrane
- DHDGB
dynamic heterogeneous dielectric generalized Born model
- SD
steepest descent
- ABNR
Adopted Basis Newton-Raphson
- DMPC
dimyristoylphosphastidylcholine
- DOPC
Dioleoylphosphocholine
- NMR
Nuclear magnetic resonance
- DLPC
didodecanoylphosphocholine
- POPC
palmitoyloleoylphosphatidylcholine
References
- 1.von Heijne G. J Intern Med. 2007;261:543–557. doi: 10.1111/j.1365-2796.2007.01792.x. [DOI] [PubMed] [Google Scholar]
- 2.Wallin E, von Heijne G. Protein Sci. 1998;7:1029–1038. doi: 10.1002/pro.5560070420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Boyd D, Schierle C, Beckwith J. Protein Sci. 1998;7:201–205. doi: 10.1002/pro.5560070121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Singam ER, Balamurugan K, Gopalakrishnan R, Subramanian SR, Subramanian V, Ramasami T. Biopolymers. 2012;97:847–863. doi: 10.1002/bip.22085. [DOI] [PubMed] [Google Scholar]
- 5.Darvas M, Hoang PN, Picaud S, Sega M, Jedlovszky P. Phys Chem Chem Phys. 2012;14:12956–12969. doi: 10.1039/c2cp41581j. [DOI] [PubMed] [Google Scholar]
- 6.Nagarajan A, Andersen JP, Woolf TB. J Mol Biol. 2012;422:575–593. doi: 10.1016/j.jmb.2012.06.001. [DOI] [PubMed] [Google Scholar]
- 7.Brooks CL, Karplus M. J Mol Biol. 1989;208:159–181. doi: 10.1016/0022-2836(89)90093-4. [DOI] [PubMed] [Google Scholar]
- 8.Forrest LR, Sansom MSP. Curr Opin Struct Biol. 2000;10:174–181. doi: 10.1016/s0959-440x(00)00066-x. [DOI] [PubMed] [Google Scholar]
- 9.Hansson T, Oostenbrink C, Van Gunsteren WF. Curr Opin Struct Biol. 2002;12:190–196. doi: 10.1016/s0959-440x(02)00308-1. [DOI] [PubMed] [Google Scholar]
- 10.Ulmschneider JP, Ulmschneider MB. Proteins. 2008;75:586–597. doi: 10.1002/prot.22270. [DOI] [PubMed] [Google Scholar]
- 11.Baker NA. Curr Opin Struct Biol. 2005;15:137–143. doi: 10.1016/j.sbi.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 12.Lee MS, Salsbury FR, Jr, Brooks CL. J Chem Phys. 2002;116:10606–10614. [Google Scholar]
- 13.Parsegian A. Nature. 1969;221:844–846. doi: 10.1038/221844a0. [DOI] [PubMed] [Google Scholar]
- 14.Feig M, Brooks CL. Curr Opin Struct Biol. 2004;14:217–224. doi: 10.1016/j.sbi.2004.03.009. [DOI] [PubMed] [Google Scholar]
- 15.Roux B, Simonson T. Biophys Chem. 1999;78:1–20. doi: 10.1016/s0301-4622(98)00226-9. [DOI] [PubMed] [Google Scholar]
- 16.Schaefer M, Karplus M. J Phys Chem. 1996;100:1578–1599. [Google Scholar]
- 17.Sitkoff D, Ben-Tal N, Honig B. J Phys Chem. 1996;100:2744–2752. [Google Scholar]
- 18.Sitkoff D, Sharp KA, Honig B. J Phys Chem. 1994;98:1978–1988. [Google Scholar]
- 19.Callenberg KM, Choudhary OP, de Forest GL, Gohara DW, Baker NA, Grabe M. PLoS One. 2010;5:1–11. doi: 10.1371/journal.pone.0012722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Eisenberg D, McLachlan AD. Nature. 1986;319:199–203. doi: 10.1038/319199a0. [DOI] [PubMed] [Google Scholar]
- 21.Spolar RS, Ha JH, Record MT. Proc Natl Acad Sci U S A. 1989;86:8382–8385. doi: 10.1073/pnas.86.21.8382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gallicchio E, Levy RM. J Comput Chem. 2004;25:479–499. doi: 10.1002/jcc.10400. [DOI] [PubMed] [Google Scholar]
- 23.Zacharias M. J Phys Chem A. 2003;107:3000–3004. [Google Scholar]
- 24.Fogolari F, Brigo A, Molinari H. Biophys J. 2003;85:159–166. doi: 10.1016/S0006-3495(03)74462-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Luecke H, Schobert B, Richter HT, Cartailler JP, Lanyi JK. J Mol Biol. 1999;291:899–911. doi: 10.1006/jmbi.1999.3027. [DOI] [PubMed] [Google Scholar]
- 26.Luo R, David L, Gilson MK. J Comput Chem. 2002;23:1244–1253. doi: 10.1002/jcc.10120. [DOI] [PubMed] [Google Scholar]
- 27.Feig M, Onufriev A, Lee MS, Im W, Case DA, Brooks CL. J Comput Chem. 2004;25:265–284. doi: 10.1002/jcc.10378. [DOI] [PubMed] [Google Scholar]
- 28.Still W, Tempczyk A, Hawley R, Hendrickson T. J Am Chem Soc. 1990;112:6127–6129. [Google Scholar]
- 29.Tanizaki S, Feig M. J Chem Phys. 2005;122:124706–124713. doi: 10.1063/1.1865992. [DOI] [PubMed] [Google Scholar]
- 30.Im W, Feig M, Brooks CL. Biophys J. 2003;85:2900–2918. doi: 10.1016/S0006-3495(03)74712-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Spassov VZ, Yan L, Szalma S. J Phys Chem B. 2002;106:8726–8738. [Google Scholar]
- 32.Stern HA, Feller SE. J Chem Phys. 2003;118:3401–3412. [Google Scholar]
- 33.Lee MS, Feig M, Salsbury FR, Jr, Brooks CL. J Comput Chem. 2003;24:1348–1356. doi: 10.1002/jcc.10272. [DOI] [PubMed] [Google Scholar]
- 34.Sayadi M, Tanizaki S, Feig M. Biophys J. 2010;98:805–814. doi: 10.1016/j.bpj.2009.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Jaskierny AJ, Panahi A, Feig M. Proteins. 2011;79:1109–1117. doi: 10.1002/prot.22947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Panahi A, Feig M. J Phys Chem B. 2010;114:1407–1416. doi: 10.1021/jp907366g. [DOI] [PubMed] [Google Scholar]
- 37.Sayadi M, Feig M. Biochim Biophys Acta, Biomembr. 2013;1828:577–585. doi: 10.1016/j.bbamem.2012.08.017. [DOI] [PubMed] [Google Scholar]
- 38.Lindahl E, Edholm O. Biophys J. 2000;79:426–433. doi: 10.1016/S0006-3495(00)76304-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Dorairaj S, Allen TW. Proc Natl Acad Sci U S A. 2007;104:4943–4948. doi: 10.1073/pnas.0610470104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.MacCallum J, Bennett D, Tieleman P. J Gen Physiol. 2007;129:371–377. doi: 10.1085/jgp.200709745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Freites JA, Tobias DJ, White SH. Proc Natl Acad Sci U S A. 2005;102:15059–15064. doi: 10.1073/pnas.0507618102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Choe S, Hecht K, Grabe M. J Gen Physiol. 2008;131:563–573. doi: 10.1085/jgp.200809959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Nielsen C, Goulian M, Anderson OS. Biophys J. 1998;74:1966–1983. doi: 10.1016/S0006-3495(98)77904-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Helfrich W. Z Naturforsch. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 45.Huang HW. Biophys J. 1986;50:1061–1070. doi: 10.1016/S0006-3495(86)83550-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Aranda-Espinoza H, Berman A, Dan N, Pincus P, Safran S. Biophys J. 1996;71:648–656. doi: 10.1016/S0006-3495(96)79265-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Nielsen C, Anderson OS. Biophys J. 2000;79:2583–2604. doi: 10.1016/S0006-3495(00)76498-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Partenskii MB, Jordan PC. J Chem Phys. 2002;117:10768–10776. [Google Scholar]
- 49.Lundbaek JA, Andersen OS. Biophys J. 1999;76:889–895. doi: 10.1016/S0006-3495(99)77252-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Goulian M, Mesquita ON, Fygenson DK, Nielsen C, Andersen OS, Libchaber A. Biophys J. 1998;74:328–337. doi: 10.1016/S0006-3495(98)77790-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Callenberg KM, Latorraca NR, Grabe M. J Gen Physiol. 2012;140:55–68. doi: 10.1085/jgp.201110766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Baker NA, Sept D, Joseph S, Holst MJ, McCammon JA. Proc Natl Acad Sci U S A. 2001;98:10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Brooks BR, Brooks CL, 3rd, Mackerell AD, Jr, Nilsson L, Petrella RJ, Roux B, Won Y, Archontis G, Bartels C, Boresch S, Caflisch A, Caves L, Cui Q, Dinner AR, Feig M, Fischer S, Gao J, Hodoscek M, Im W, Kuczera K, Lazaridis T, Ma J, Ovchinnikov V, Paci E, Pastor RW, Post CB, Pu JZ, Schaefer M, Tidor B, Venable RM, Woodcock HL, Wu X, Yang W, York DM, Karplus M. J Comput Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Foloppe N, MacKerell AD., Jr J Comp Chem. 2000;21:86–104. [Google Scholar]
- 55.MacKerell AD, Jr, Feig M, Brooks CL. J Am Chem Soc. 2004;126:698–699. doi: 10.1021/ja036959e. [DOI] [PubMed] [Google Scholar]
- 56.Best R, Zhu X, Shim J, Lopes PE, Mittal J, Feig M, Mackerell AD. J Chem Theory Comput. 2012;8:3257–3273. doi: 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Feig M, Karanicolas J, Brooks CL. J Mol Graph Model. 2004;22:377–395. doi: 10.1016/j.jmgm.2003.12.005. [DOI] [PubMed] [Google Scholar]
- 58.Feig M, Im W, Brooks CL. J Chem Phys. 2004;120:903–911. doi: 10.1063/1.1631258. [DOI] [PubMed] [Google Scholar]
- 59.Chocholousova J, Feig M. J Phys Chem B. 2006;110:17240–17251. doi: 10.1021/jp0627675. [DOI] [PubMed] [Google Scholar]
- 60.Ryckaert J, Ciccotti G, Berensdsen H. J Comp Chem. 1977;23:327–340. [Google Scholar]
- 61.Nose S. J Chem Phys. 1984;81:511–519. [Google Scholar]
- 62.Hoover WG. Phys Rev A. 1985;31:1695–1697. doi: 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
- 63.Townsley LE, Tucker WA, Sham S, Hinton JF. Biochemistry. 2001;40:11676–11686. doi: 10.1021/bi010942w. [DOI] [PubMed] [Google Scholar]
- 64.Miloshevsky GV, Hassanein A, Partenskil MB, Jordan PC. J Chem Phys. 2010;132:234707/234701–234711. doi: 10.1063/1.3442414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Neale C, Bennet WFD, Tieleman DP. J Chem Theory Comput. 2011;7:4175–4188. doi: 10.1021/ct200316w. [DOI] [PubMed] [Google Scholar]
- 66.Andersen OS, Koeppe RE. Annu Rev Biophys Biomol Struct. 2007;36:107–130. doi: 10.1146/annurev.biophys.36.040306.132643. [DOI] [PubMed] [Google Scholar]
- 67.Liu Z, Gandhi CS, Rees DC. Nature. 2009;461:120–124. doi: 10.1038/nature08277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Betanzos M, Chiang CS, Guy HR, Sukharev S. Nat Struct Biol. 2002;9:704–710. doi: 10.1038/nsb828. [DOI] [PubMed] [Google Scholar]
- 69.Kandasamy SK, Larson RG. Biophys J. 2006;90:2326–2343. doi: 10.1529/biophysj.105.073395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.de Planque MR, Bonev BB, Demmers JA, Greathouse DV, Koeppe RE, Separovic F, Watts A, Killian JA. Biochemistry. 2003;42:5341–5348. doi: 10.1021/bi027000r. [DOI] [PubMed] [Google Scholar]
- 71.Kol MA, van Laak AN, Rijkers DT, Killian JA, de Kroon AI, de Kruijff B. Biochemistry. 2003;42:231–237. doi: 10.1021/bi0268403. [DOI] [PubMed] [Google Scholar]
- 72.Weiss TM, van der Wel PC, Killian JA, Koeppe RE, Huang HW. Biophys J. 2003;84:379–385. doi: 10.1016/S0006-3495(03)74858-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Strandberg E, Ozdirekcan S, Rijkers DT, van der Wel PC, Koeppe RE, Liskamp RM, Killian JA. Biophys J. 2004;86:3709–3721. doi: 10.1529/biophysj.103.035402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Siegel DP, Cherezov V, Greathouse DV, Koeppe RE, Killian JA, Caffrey M. Biophys J. 2006;90:200–211. doi: 10.1529/biophysj.105.070466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Sparr E, Ash WL, Nazarov PV, Rijkers DT, Hemminga MA, Tieleman DP, Killian JA. J Biol Chem. 2005;280:39324–39331. doi: 10.1074/jbc.M502810200. [DOI] [PubMed] [Google Scholar]
- 76.Im W, Brooks CL. Proc Natl Acad Sci U S A. 2005;102:6771–6776. doi: 10.1073/pnas.0408135102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Holt A, de Almeida RF, Nyholm TK, Loura LM, Daily AE, Staffhorst RW, Rijkers DT, Koeppe RE, Prieto M, Killian JA. Biochemistry. 2008;47:2638–2649. doi: 10.1021/bi702235k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Esteban-Martin S, Gimenez D, Fuertes G, Salgado J. Biochemistry. 2009;48:11441–11448. doi: 10.1021/bi901017y. [DOI] [PubMed] [Google Scholar]
- 79.Ozdirekcan S, Etchebest C, Killian JA, Fuchs PF. J Am Chem Soc. 2007;129:15174–15181. doi: 10.1021/ja073784q. [DOI] [PubMed] [Google Scholar]
- 80.Bond PJ, Holyoake J, Ivetac A, Khalid S, Sansom MS. J Struct Biol. 2007;157:593–605. doi: 10.1016/j.jsb.2006.10.004. [DOI] [PubMed] [Google Scholar]
- 81.Wan CK, Han W, Wu YD. J Chem Theory Comput. 2012;8:300–313. doi: 10.1021/ct2004275. [DOI] [PubMed] [Google Scholar]
- 82.Kim T, Im W. Biophys J. 2010;99:175–183. doi: 10.1016/j.bpj.2010.04.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Strandberg E, Esteban-Martin S, Salgado J, Ulrich AS. Biophys J. 2009;96:3223–3232. doi: 10.1016/j.bpj.2009.02.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.de Planque MR, Goormaghtigh E, Greathouse DV, Koeppe RE, Kruijtzer JA, Liskamp RM, de Kruijff B, Killian JA. Biochemistry. 2001;40:5000–5010. doi: 10.1021/bi000804r. [DOI] [PubMed] [Google Scholar]
- 85.Holt A, Koehorst RB, Rutters-Meijneke T, Gelb MH, Rijkers DT, Hemminga MA, Killian JA. Biophys J. 2009;97:2258–2266. doi: 10.1016/j.bpj.2009.07.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Helfrich P, Jakobsson E. Biophys J. 1990;57:1075–1084. doi: 10.1016/S0006-3495(90)82625-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Kim T, Lee KI, Morris P, Pastor RW, Andersen OS, Im W. Biophys J. 2012;102:1551–1560. doi: 10.1016/j.bpj.2012.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Kim T, Jo S, Im W. Biophys J. 2011;100:2922–2928. doi: 10.1016/j.bpj.2011.02.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Jo S, Im W. Biophys J. 2011;100:2913–2921. doi: 10.1016/j.bpj.2011.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.The PyMOL Molecular Graphics system. 1.5.0.4. Schrodinger, LLC; [Google Scholar]