Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2013 Mar 13;9(4):2126–2136. doi: 10.1021/ct400065j

On the Dielectric “Constant” of Proteins: Smooth Dielectric Function for Macromolecular Modeling and Its Implementation in DelPhi

Lin Li 1, Chuan Li 1, Zhe Zhang 1, Emil Alexov 1,*
PMCID: PMC3622359  PMID: 23585741

Abstract

graphic file with name ct-2013-00065j_0011.jpg

Implicit methods for modeling protein electrostatics require dielectric properties of the system to be known, in particular, the value of the dielectric constant of protein. While numerous values of the internal protein dielectric constant were reported in the literature, still there is no consensus of what the optimal value is. Perhaps this is due to the fact that the protein dielectric constant is not a “constant” but is a complex function reflecting the properties of the protein’s structure and sequence. Here, we report an implementation of a Gaussian-based approach to deliver the dielectric constant distribution throughout the protein and surrounding water phase by utilizing the 3D structure of the corresponding macromolecule. In contrast to previous reports, we construct a smooth dielectric function throughout the space of the system to be modeled rather than just constructing a “Gaussian surface” or smoothing molecule–water boundary. Analysis on a large set of proteins shows that (a) the average dielectric constant inside the protein is relatively low, about 6–7, and reaches a value of about 20–30 at the protein’s surface, and (b) high average local dielectric constant values are associated with charged residues while low dielectric constant values are automatically assigned to the regions occupied by hydrophobic residues. In terms of energetics, a benchmarking test was carried out against the experimental pKa’s of 89 residues in staphylococcal nuclease (SNase) and showed that it results in a much better RMSD (= 1.77 pK) than the corresponding calculations done with a homogeneous high dielectric constant with an optimal value of 10 (RMSD = 2.43 pK).

Introduction

Modeling the electrostatic potential and energies in systems comprised of biological macromolecules is an essential step for each study aimed at understanding the macromolecules’ function, stability, and interactions. However, this is not a trivial task, especially for huge systems made of large biomolecules and their assemblages and for modeling phenomena occurring in microseconds and longer timeframes. Continuum electrostatics offers an advantage over explicit methods in such cases since (a) the atomic details of the water phase are reduced and (b) continuum electrostatics intrinsically provides equilibrium solutions. Typically, the macromolecule is considered to be a low dielectric medium while the water phase is modeled as a homogeneous medium with a dielectric constant of 80. While there is a consensus in the community that a dielectric constant of about 80 is appropriate for describing dielectric properties of bulk water in modeling equilibrated systems, the optimal value of the protein (macromolecular) dielectric constant is still an ongoing debate in the literature.1 This inconsistency is indicated by the use of numerous “optimal” dielectric constant values in various studies. Investigations modeling the macromolecule as a rigid object or using snap-shots obtained from molecular dynamics (MD) simulations to deliver the energies via Molecular Mechanics Poisson–Boltzmann (MMPB) or Generalized Born (MMGB) methods typically use a low dielectric constant of ε = 1 or ε = 2 (to account for electronic polarizability),2,3 although larger values were reported as well.4 In works devoted to modeling protein stability, numerous dielectric constant values were used, from as low as ε = 1 or 25 to as high as ε = 40,6 including multidielectric regions.7 Similarly, in the field of modeling macromolecular interactions, researchers were using various values for the protein internal dielectric constant.8 Perhaps the most widespread of the “optimal” values for the dielectric constant is seen in the continuum methods for pKa calculations.9 The most commonly used dielectric constant value is ε = 4, which is believed to account for electronic polarization and small backbone fluctuations.10 However, larger values, such as ε = 8,11 ε = 10,12 ε = 11,13 and ε = 20,14 were also reported. Other examples can be listed as well, but it is clear that there is no universal value of the dielectric constant that is appropriate for all models and methods.

Perhaps the largest body of work on the dielectric constant of proteins is due to Warshel and co-workers.15,16 It was demonstrated that the dielectric “constants” in semimacroscopic models depend on the definition and the specific treatment.17 Using various models and the discriminative benchmark, Warshel and co-workers demonstrated that the protein dielectric constant is not a universal constant but simply a parameter that also depends on the model being used.15 In terms of structural reorganization occurring during the process being modeled, they pointed out that semimicroscopic models which do not model the structural relaxations are forced to use a large value for the dielectric constant. In addition, including the reorganization of ionized residues and plausible water penetration would require applying an even higher dielectric constant in the modeling algorithm.18 Altogether, the works of Warshel and many other researchers19,20 point out that the specific treatment of the conformational reorganization (both of the solute and the surrounding water phase) in the continuum electrostatics is the major determinant for the “optimal” value of the internal dielectric constant. Modeling reactions involving large conformational changes which are not explicitly treated in the computational protocol requires the usage of large values for the dielectric constant, while other reactions that do not induce conformational changes can be successfully modeled with low dielectric constant even when a rigid structure is used.15,17 The goal is to develop an automatic procedure which can assign an appropriate dielectric constant value by utilizing the 3D structure of the macromolecule alone.

As mentioned above, the continuum electrostatics approach is an alternative to the explicit models, and it is expected to perform the best if it can capture as many details as possible from the explicit model. Explicit models treat the system as a multitude of atoms, some of which are connected via chemical bonds, other interacting via van der Waals (vdW) and electrostatic nonbonded interactions (Figure 1a). Replacing the atomic details of the explicit models with a continuum should address three important questions: (a) how to treat the water molecules within the immediate water shell surrounding the protein, (b) how to model the cavities inside the protein, and (c) how to model the inhomogeneous protein matrix (Figure 1b). Below, we outline the specific considerations associated with each of these regions.

Figure 1.

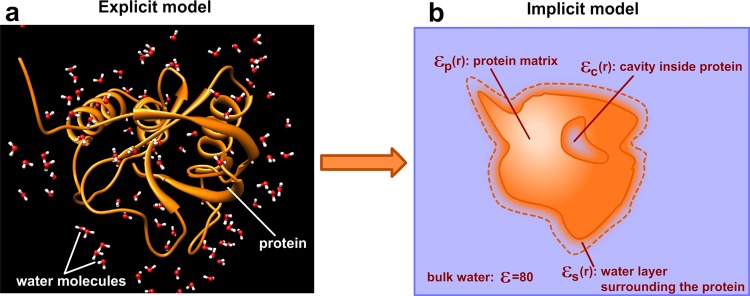
Figure 1

Open in a new tab

Explicit and implicit solvent models.

Many investigations demonstrated the importance of water molecules in the first layer of water shell21 and that their properties differ from those of bulk water.22 The main reason is that a significant fraction of these water molecules may be involved in direct interactions with protein atoms, and thus their ability to move and reorient can be severely restricted in comparison with those of the bulk water.23 In addition, the surface exposed amino acid side chains are quite flexible, and if these alternative conformations are ensemble averaged, the resulting shell surrounding the protein will be a mixture of protein side chains and water molecules. Obviously the dielectric properties of this shell cannot be modeled with the bulk dielectric constant of 80. Instead, a different dielectric constant should be used. In addition, the dielectric constant should depend on the topology of the protein surface, such that the immediate water shell around convex surfaces should be assigned a lower dielectric constant (water and side chain reorganization is more restricted) than that of the concave protein surfaces.24 Because of this, it is also important to be able to determine the artificial boundary between the protein and water, which results in generating the so-called molecular surface.

The treatment of cavities or channels inside the biomolecules is another crucial problem for continuum electrostatics methods.25,26 The water molecules in small cavities are very few, typically their mobility is highly restricted and should be modeled with a dielectric constant lower than that of bulk water.27 In contrast, in large cavities, the waters may form clusters and act collectively.28 In addition, some cavities may be filled with water molecules with short or long residential times;29 thus cavities or channels containing water molecules with low occupancy should be treated as regions with a low dielectric constant and vice versa.

Perhaps the most crucial issue for continuum electrostatics is the treatment of the protein matrix. Atoms in biomolecules have different charges and flexibilities depending on the packing and their mutual interactions. Because of that, macromolecules’ dielectric properties are not homogeneous, resulting in a position-dependent dielectric constant (Figure 1b). Different flexibilities are accounted when comparing the binding site involved in “lock-and-key” versus “induced-fit” binding30−32 as well as those in allosteric regulations.33,34 The proteins involved in electron and proton transfer are shown to be inhomogeneous in their dielectric response to the charge translocation as well.20 In general, the hydrophobic core is much better packed and contains significantly fewer charged atoms than the molecular surface and therefore has a much lower capacity to respond to the local electrostatic field, and thus, from a continuum electrostatics point of view, should be modeled as a low dielectric medium as indicated in ref (35). These observations prompted the development of approaches to assign a specific local dielectric constant to each amino acid type or even to each amino acid. Some of these approaches include the intrinsic polarizabilities of amino acids delivered from the results of MD simulations,36 using residue-specific dielectric constants for pKa calculations37 and optimizing the amino-acid-specific dielectric constant to predict the folding free energy changes due to mutations.38 All of these approaches treat the protein matrix as a kind of mosaic structure made of small blocks with different dielectric properties. Bypassing the question about the applicability of a macroscopic definition of the dielectric constant for such small structural segments, the main problem with such approaches (including our previous work) is the nonrealistic nature of the dielectric boundary between the segments with different dielectric constants.

The smooth dielectric function should reflect the physical nature of the macromolecule, and the most straightforward approach is to be delivered from atomic densities of the corresponding atoms. Space occupied by loosely packed and charged atoms is expected to have the potential to reorganize and to respond to the local electrostatics field and thus should be modeled with a high dielectric constant. Such regions correspond to a protein surface which is loosely packed and rich in charged and polar residues. In contrast, space regions made of tightly packed uncharged atoms, as in the hydrophobic core, have little ability to respond to the local electrostatic field and should be modeled with a low dielectric constant. All of these features can be captured with the so termed Gaussian method of representing atomic densities and then using it to deliver a smooth dielectric function.39,40 It should be clarified that we emphasize using such an approach to deliver a smooth dielectric function for the entire space but not to model the water–molecule boundary40,41 or derive the surface of molecules.39

In this work, we report a Gaussian-based approach to deliver a smooth dielectric function for the entire space domain (the macromolecule(s) and the water phase). To assess the effects of this development on various biophysical quantities which can be computationally modeled, the method was implemented in the DelPhi program,42 and several tests were carried out. The correctness of the approach in reflecting the expected physical properties of macromolecules is demonstrated on a large set of protein structures by showing that the generated smooth dielectric function results in values of about 6–7 in the protein interior and values of 20–30 at the protein–water interface, which is consistent with previous MD-based work.43 In addition, it is shown that the space occupied by charged and polar groups is assigned larger dielectric values as compared to the space occupied by hydrophobic amino acids. Furthermore, in a benchmarking test of a large set of experimentally determined pKa’s in staphylococcal nuclease (SNase), the Gaussian-based smooth dielectric function (with low reference dielectric constant value of 4) delivers much better results (RMSD = 1.77) as compared with the homogeneous dielectric method (RMSD = 2.43), despite the fact that the homogeneous dielectric method optimal results were obtained at a higher dielectric constant value of 10. The results of homogeneous and Gaussian-based smooth dielectric methods for each individual titratable group are shown in Supporting Information (Table S1).

Methods

Smooth Dielectric Function Derivation

Given a molecule in the water phase, we applied the Gaussian equation and implemented three steps as follows to calculate the dielectric distribution of a protein from its density distribution as originally described by Nicholls et al.40 Given a macromolecule with N atoms, the density of an atom i is represented by a Gaussian distribution (Figure 2a,b):

graphic file with name ct-2013-00065j_m001.jpg 1

where ρi(r) is the density at position r, ri is the distance between the center of the atom i and position r, Ri is the vdW radius of atom i, and σ is the relative variance.

Figure 2.

Figure 2

Open in a new tab

Schematic of calculating the dielectric smooth function via atomic density. Upper panels: cartoon presentation in the 2D grid plane, where intensity of the colors reflects the value of either the density or ε. Lower panels: profiles of the density and resulting ε.

After the density of each atom within the macromolecule is generated, the density in the overlapping areas occupied by multiple atoms is calculated by40

graphic file with name ct-2013-00065j_m002.jpg 2

where the ρmol(r) denotes the density at position r coming from multiple atoms, and ρi(r) is the density of a single atom i, which is obtained from eq 1. This function guarantees that the density at the overlapping region is higher than the density generated by any involved single atom, but the density ρmol (r) always stays between 0 and 1 (Figure 2c,d). Finally, the smooth dielectric function is delivered from the density distribution using the linear function:40

graphic file with name ct-2013-00065j_m003.jpg 3

where ε on the left denotes the dielectric distribution function, εin denotes the reference dielectric value when the density is 1, εout denotes the reference dielectric value for the water phase, and ρ is the density obtained from eq 2 (Figure 2e,f).

The above formalism, provided that standard force field atomic vdW radii are used, has only one adjustable parameter, the variance in the Gaussian distribution. The functional forms of eqs 1–3 can also be considered as “adjustable” since atomic density in principle can be modeled with almost any symmetrical smooth function (different from Gaussian), and the corresponding molecular density and dielectric function can be delivered by other means—different from eqs 2 and 3. However, it seems to us that the most important parameter is still the variance in the Gaussian distribution, since its variation will essentially mimic the usage of different functions in eq 1. In the current work, the functional forms of eqs 2 and 3 are kept as originally suggested in ref (40), but alternatives will be explored later. Thus, in order to proceed further with the analysis, the value of the normalized variance in eq 1 must be selected. In this work, we chose to select it based on a benchmarking test of pKa values, because dielectric relaxation is the most profoundly associated with ionization/deionization phenomena (see Discussion for more details).

pKa Calculations

In order to assess the impact of the smooth dielectric function on the accuracy of pKa calculations and to deliver the optimal value of the normalized variance, we utilized the experimental data obtained in Garcia-Moreno’s lab44−47 (http://pkacoop.org/wordpress/?p=28) and used in the pKa Cooperative (http://pkacoop.org/wordpress/). The reason for selecting this data set is not only because it is a representative set for the pKa Cooperative but also because it involves pKa’s both surface-exposed and buried amino acids. This data set is comprised of 89 pKa’s for staphylococcal nuclease (SNase). In 19 of the cases, the pKa calculations were based on the structure of wild type (PDB ID: 1stn)48 SNase and its hyperstable variant (PDB ID: 3bdc),46 which is called Δ+PHS. In 20 of the cases, pKa calculations were based on the X-ray structures of SNase with mutations, and in 50 of the cases, the pKa calculations were based on the in silico generated mutant from the wild type SNase (PDB ID: 3bdc; list of the amino acids, structure used, and experimental pKa’s are available from the pKa Cooperative web page, http://pkacoop.org/wordpress/).

Since the predictions of the pKa’s in our list do not require modeling multiple titration sites, but the prediction of a single pKa per structure, the following surface-free approach (SFA) was developed and applied. Note that because energies are delivered as grid energies of the corresponding finite-difference algorithm, there is no need to define a molecular surface. This provides a significant advantage over previous works, since defining the molecular surface would add additional uncertainty in the protocol. In addition, the SFA reflects best the motivation and the development of the smooth dielectric function: no need to draw a sharp border between the protein and the water phase. For each pKa calculation, four structures were generated (Figure 3): (1) the deprotonated state of the concerned residue in the protein, (2) the protonated state of the concerned residue in the protein, (3) the deprotonated state of the concerned residue in water, and (4) the protonated state of the concerned residue in water. The structures of the protein and the residue for which pKa is calculated were kept identical in the four states in order to cancel the artificial “self-energy” of the grid algorithm. The extra proton of protonated Asp/Glu was not modeled, but its charge was distributed evenly over the carbonyl oxygens (the argument being to avoid artificial grid energy). Similarly, the missing proton of deprotonated Lys/Arg was not removed from the side-chains, but the charge was distributed over all polar hydrogens to result in zero net charge for deprotonated Lys/Arg.

Figure 3.

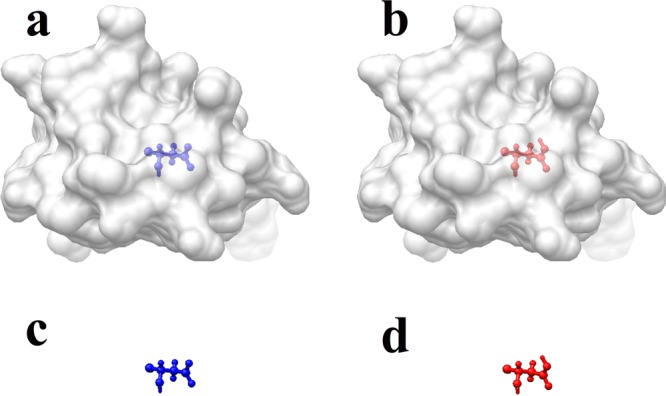
Figure 3

Open in a new tab

pKa of a residue calculated via four step procedures representing four states: (a) the deprotonated state of the residue in the protein, (b) the protonated state of the residue in the protein, (c) the deprotonated state of the residue in water, and (d) the protonated state of the residue in water.

For each state, the grid energy was calculated, keeping the grid and position of the protein and the residue of interest identical among the runs, and the following energies were obtained: (1) G (depro, protein), the protein electrostatic grid energy with the deprotonated residue; (2) G (proto, protein), the protein electrostatic grid energy with the protonated residue; (3) G (depro, water), the electrostatic grid energy of the deprotonated residue in the water phase; and (4) G (proto, water), the electrostatic grid energy of the protonated residue in the water phase. Then, the value of the pKa shift was calculated as

graphic file with name ct-2013-00065j_m004.jpg 4

The parameters used in DelPhi49 were scale = 2 points/Å, perfil = 70, and εout = 80.0. The ionic strength was considered to be zero for simplicity. The convergence criterion was 0.0001 [kT/e], and the linear Poisson–Boltzmann equation was solved. The internal reference dielectric constant and the normalized variance were considered to be adjustable parameters. The charges and radii were taken from the AMBER force field.50

Dielectric Distribution Analysis

In order to ensure the statistical significance of the analysis and to assess the general trend of the smooth dielectric function, the following data set was created. A large set of diverse proteins was taken from the PDB bank (http://www.rcsb.org/pdb/home/home.do), and several filtering steps were performed. First, only structures determined by X-ray experiments with a resolution less than 1.5 Å were selected. Then, the structures with a sequence similarity larger than 30% were removed. Finally, the structures with cofactors which are not made of regular residues were also deleted from the data set. The final data set was made of 91 proteins: 1ARB, 1BGF, 1BKR, 1BYI, 1C8C, 1ES9, 1EW4, 1EZG, 1G8A, 1GPP, 1GQI, 1H1N, 1HZT, 1I1J, 1I2T, 1IDP, 1IJY, 1JL1, 1K0M, 1KMT, 1KNG, 1L3K, 1LKK, 1LLF, 1LU4, 1LZL, 1M1F, 1MF7, 1MN8, 1MY7, 1N62, 1NG6, 1NKD, 1NKO, 1O7I, 1O7J, 1O82, 1O9I, 1OAI, 1OI7, 1R29, 1R7J, 1SG4, 1SJY, 1SMO, 1T3Y, 1TQG, 1TVN, 1UCS, 1UKF, 1ULR, 1USM, 1UTG, 1UXZ, 1UZ3, 1V05, 1VH5, 1W5R, 1W7C, 1X6Z, 1XOD, 1XSZ, 1Z21, 1ZZK, 2A26, 2A6Z, 2B0A, 2CAR, 2E3H, 2END, 2FCJ, 2FHZ, 2FQ3, 2GEC, 2GOM, 2H3L, 2HOX, 2HQX, 2IVY, 2J5Y, 2J6B, 2OHW, 2P5K, 2PMR, 2PTH, 2VE8, 2VN6, 3BBB, 3BZP, 3CJS, 3CT6.

The data set was used to analyze the following plausible relations and distributions: (1) the average dielectric constant (ε) and radius of gyration of the protein and (2) the average ε and residue type distribution.

(1) Average dielectric constant distribution: For each protein in the data set, the center of the mass and gyration radius were calculated. Then, the protein interior was mapped into different shells with a different radius from the center of the protein. For each shell, the average ε value obtained from all grid-midpoints inside this shell was calculated. Thus, an ε-radius map was generated for each of the proteins (Figure 4a).

Figure 4.

Figure 4

Open in a new tab

Average dielectric constant against the radius of gyration (Rg) of a protein. (a) Schematic of calculating the average ε value of a shell with radius r and thickness d; the thickness of the shell is set as 0.1 Rg of a protein. (b) Average ε-radius distribution of 91 proteins in the data set. Left upper corner shows the structure of elongated protein (1uz3.pdb) for which the spherical shape is not a good approximation, and on the right lower corner is shown a protein (1brk.pdb) which is almost spherical in shape.

(2) ε-residue type distribution: The average dielectric constant per residue was calculated using only the side chain atoms (backbone was not included). Then, a sphere of radius 5 Å was drown around each side-chain atom, and the dielectric constants of all midgrid points within the sphere were summed and averaged. Further, these average dielectric constants were summed over all atoms of the side-chain and averaged again to obtain the average dielectric constant per side chain. Finally, the average dielectric constant for each type of residue was obtained from all residues with the 91 protein set.

Solvation Energy Calculations of Small Molecules

The test on small molecule free energies of transfer from a vacuum to water was done on a data set of 504 neutral organic small molecules51 taken from David Mobley’s group. The solvation energies of all of these molecules have been experimentally determined, with the range from −11.95 to 3.16 kcal/mol.

Solvation energy Gsol has two components, polar and nonpolar:

graphic file with name ct-2013-00065j_m005.jpg 5

where Gpolar indicates the polar (electrostatic) term and Gnonpolar denotes the nonpolar term.

The polar component of solvation energy was calculated as the grid energy difference of the system in water and in a vacuum:

graphic file with name ct-2013-00065j_m006.jpg 6

The above grid energies were calculated keeping the corresponding small molecule at the same grid position to cancel the grid artifacts. Specific considerations were made for the calculations in a vacuum since one has to define the molecular surface in this case (the border between molecule and vacuum). Note that in our approach the dielectric function is continuous and runs throughout the entire space and is designed to describe dielectric properties of the molecule in water. Here, we assume that the properties of molecules are unchanged as they are moved from water to a vacuum. Thus, following the strategy implemented in ZAP,40 the molecular surface of molecules is defined by applying a specific cutoff for the dielectric constant, εcutoff. The cutoff was varied in the protocol to obtain the best fit against experimental data.

The nonpolar term of solvation energy Gnonpolar is calculated via the accessible surface area method:52

graphic file with name ct-2013-00065j_m007.jpg 7

where γ and b are constants and SA denotes the solvent accessible surface area, which is calculated using Naccess2.1.1 (http://www.bioinf.manchester.ac.uk/naccess/).

The force field used in the calculations was AM1-BCC,53 which is part of general AMBER force field (GAFF).50 In order to optimize the parameters, reference εin was varied from 0.1 to 4.0, the value of normalized variance σi was varied from 0.80 to 1.40, and the value of epsilon cutoff εbnd was varied from 4.0 to 60.0. For each combination of the σi and εbnd values, the least-squares method was used to obtain the optimized γ and b constants. The best parameters are shown in the Results section (note that because of the different nature of the process, these values are not expected to be the same as those obtained in pKa calculations. See Discussion for details).

Results

In this section, the results of parametrizing and using the smooth Gaussian-based dielectric function are presented. It should be restated that this development is aimed to better capture the effects seen in explicit electrostatic calculations within the framework of continuum electrostatics for proteins. The proteins are the primary target because of their intrinsic conformational flexibility, the presence of small or large cavities inside, and an irregularly shaped protein–water interface. However, introducing a smooth Gaussian-based dielectric function should not deteriorate the performance of continuum electrostatics even in the cases involving modeling molecules rigid by nature with no cavities inside, such as small molecules and drugs. Thus, the features of the smooth Gaussian-based dielectric function are manifested modeling several classes of problems: (a) pKa’s of various titratable groups with the pKa Cooperative initiative, (b) conceptual considerations and linkage to the physical properties of proteins and amino acids, (c) the role of electrostatic potential on the electron transfer in the reaction center protein, (d) free energy of transfer of small molecules, and (e) reducing grid dependency in energy calculations.

a. pKa Calculations

Analysis of the results at the last two pKa Cooperative meetings9 showed that groups using rigid structures for pKa calculations obtain the best results with respect to the experimental data if a large value is assigned for the protein dielectric constant. The works of groups utilizing MD techniques to predict pKa’s indicated that almost in each case the ionization induces small or large conformational change in the proteins.9,54 Because of these observations, the pKa Cooperative data set was chosen for testing the Gaussian-based smooth dielectric function. Thus, the pKa values of 89 residues in staphylococcal nuclease protein (SNase) were calculated using the SFA method described in the Methods section, and predictions were compared between homogeneous dielectric and Gaussian-based methods. In both cases, the value of the internal dielectric constant was independently varied to obtain the smallest RMSD with respect to experimental data. In order to determine the best εprotein value for the pKa calculation in a homogeneous protein dielectric, the εprotein value was varied from 1.0 to 20.0 with an increment of 1.0. For each εprotein value, the pKa values were calculated for all 89 cases and then compared to the experimental results. It was found that the best εprotein value for homogeneous dielectric pKa calculations is 10.0, which resulted in a RMSD between calculated and experimental pKa values of 2.43 pK (Figure 5). Using a Gaussian-based method on the same data set, two parameters need to be determined, the values of the reference dielectric value εin and the normalized variance σ. Here, we varied the reference εin from 1.0 to 10.0 with an increment of 1.0 and σ from 0.80 to 1.20 with an increment of 0.01. For each combination of these two parameters, the calculated pKa values for all 89 cases were compared with the experimental values. From this test, the best parameters for pKa calculations obtained are εin= 4.0 and σ = 0.93, resulting in RMSD = 1.77 (Figure 5).

Figure 5.

Figure 5

Open in a new tab

Results of pKa calculations of 89 residues in staphylococcal nuclease protein (SNase), calculated using the homogeneous method and Gaussian method in DelPhi.

The fact that the Gaussian-based method achieves a much smaller RMSD than the homogeneous protein dielectric method is very encouraging. In addition, the best results using the Gaussian-based method were obtained at a low reference dielectric constant of 4, while the best dielectric constant using the homogeneous method was 10. This indicates that the Gaussian-based method mimics the effects of the conformational changes occurring in the titration better than the homogeneous high dielectric does by distributing dielectric values within the protein structure.

b. Conceptual Considerations and Linkage to the Physical Properties of Proteins and Amino Acids

b.1. Distribution of the Dielectric Constant within a Protein

The first task is to check if the generated smooth Gaussian-based dielectric function addresses the questions mentioned in the Introduction about modeling the protein–water interface, cavities inside the protein, and the protein matrix. For the testing, the optimal values for the reference internal dielectric constant and normalized variance obtained in the pKa section were used. The Reaction Center protein (PDB ID: 1AIJ) was taken as a test case (although the test was done on many other proteins as well). Figure 6 shows the results of (a) a slice of dielectric distribution and the entire protein structure and (b) a slice of dielectric distribution with atoms close to this slice. Several differences from the traditional homogeneous dielectric distribution method can be seen, the smooth Gaussian-based method results in three improvements: (1) The dielectric distribution near the protein–water boundary region no longer contains a discrete dielectric jump. Instead, it now smoothly increases from a low dielectric value inside the protein to εwater = 80 in bulk water. (2) The small cavities inside the protein are assigned proper dielectric values. For small cavities, which may contain only a limited number of water molecules, which are not free to move and reorient, the dielectric value for such cavities is neither εwater nor εprotein. Instead, the Gaussian-based method assigns dielectric values between εwater and εprotein depending on the cavity size and shape. (3) The dielectric distribution inside the entire protein is not simply a constant value (εprotein). It depends on the distribution of atoms and their packing. The regions with tightly packed atoms are assigned lower dielectric values, while the regions with loosely packed atoms get higher dielectric values. This distribution reflects the physical nature of the dielectric response: the regions filled with loosely packed atoms should be treated as polarizable media, since the atoms in those areas can move to respond to the local electrostatic field. In contrast, tightly packed atoms in the hydrophobic core do not carry much charge and cannot respond to the local field and therefore should be considered as regions with low polarizability.

Figure 6.

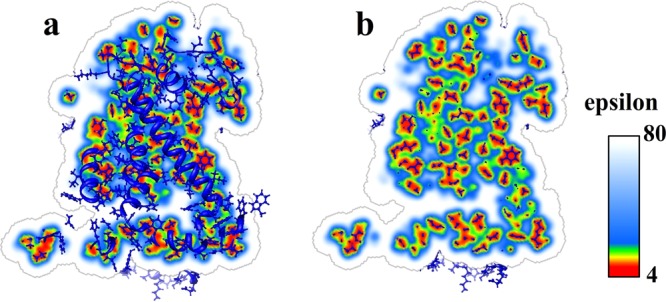
Figure 6

Open in a new tab

Dielectric distribution of reaction center protein (PDB ID: 1AIJ). (a) A slice of dielectric distribution and the entire protein structure. (b) A slice of dielectric distribution with atoms close to the slice surface.

b.2. Distribution of the Average Dielectric Constant As a Function of the Distance from the Center of the Mass

It is expected that the average dielectric constant in the core of the protein is lower than that on the surface, as indicated in a previous MD study.43 Here, the same question is addressed on a set of 91 diverse proteins (see the Methods section). Each black line in Figure 4b denotes the dielectric distribution of a particular protein. It can be seen that the distributions of the dielectric constant of all the proteins in the data set have the same tendency: the dielectric value in the core is close to εprotein. As the shell moves toward the surface of the protein, the dielectric value grows. When the radius of the shell is about two gyration radii, the average dielectric value of the shell region reaches εwater. However, despite the overall similarity, different proteins have different dielectric distributions. When the radius of the shell is equal to the gyration radius, the maximum and minimum average dielectric values of the shell are 64.7 for protein PDB ID 1uz3 and 8.4 for the protein PDB ID 1bkr. The reason for this difference is a different shape of these two proteins (see Figure 4b). The protein 1uz3 is a very elongated, nonspherically shaped protein, and the average dielectric value is large at the shell with a radius equal to the gyration radius because it includes water as well. If the protein has a spherical-like shape, the average dielectric value of the shell with a radius equal to the gyration radius is smaller, as for the protein 1uz3. The red line in Figure 4b indicates the average behavior of the dielectric distribution of all 91 proteins. This general tendency reveals that the inner parts of the proteins have lower average dielectric values and the outer parts have higher values.

b.3. Average Dielectric Properties of Amino Acids

Another analysis was carried out to show the distribution of dielectric values per residue type. For each residue, the average dielectric value of all side chains was calculated as described in the Methods section. The calculations were performed on all 91 proteins in the data set, and then the results were averaged per amino acid type (Figure 7). Figure 7 shows the average dielectric constant value for each type of residue, and it can be seen that the range is from 11.0 to 25.6. Charged amino acids (Lys, Arg, Glu, and Asp) are associated with the highest average dielectric values. They have the propensity to be located on the surface of the protein and to be loosely packed, leaving room for structural rearrangement. The observation that the Gaussian-based dielectric function has the largest value assigned for the space occupied by such residues correctly reflects the physics of dielectric relaxation and supports the usefulness of the developed procedure. Thus assigning high dielectric values for charged residues is physically sound, which has been shown to improve the accuracy of pKa’s38 and the electrostatic potential20,55 calculation. The space occupied by hydrophobic residues is assigned relatively low average dielectric value (Figure 7). Hydrophobic residues are more likely to be found in the core of the protein, typically tightly packed and not able to adopt alternative conformations. In addition, their side chains are made of atoms carrying little charge. Because of that, their ability to alter the local electrostatic field is very limited. The fact that the Gaussian-based method automatically assigns a low dielectric constant for the hydrophobic residues is very encouraging and demonstrates that the method captures the correct physics. In the middle are the polar residues. Their average dielectric values (Figure 7) are higher than that of hydrophobic residues but lower than that of charged residues. Thus, the model reflects the correct physics for these amino acids as well.

Figure 7.

Figure 7

Open in a new tab

Average dielectric constant of different type of residues.

c. Electrostatic Potential Modeling in the Reaction Center Protein

In this section, the analysis is focused on investigating the role of the electrostatic potential on the electron transfer from quinone A (Qa) to quinone B (Qb) in the Reaction Center protein. Previous works20 demonstrated that this process is slow and involves conformational changes in the protein. Since the goal of the Gaussian-based smooth dielectric method is to mimic the effects of conformational changes via properly assigned dielectric constant, this particular reaction is a perfect test for the method. To illustrate the advantages of the Gaussian-based smooth dielectric method over the standard homogeneous dielectric approach, the electrostatic potential distribution in the reaction center protein (PDB ID: 1AIJ) was calculated using both the regular homogeneous method and the Gaussian-based method implemented in DelPhi.42 The electrostatic potential maps are visualized by Chimera56 and shown in Figure 8. Since the electron transfer is from Qa to Qb, the electrostatic potential is expected to be less negative (more positive) at the electron acceptor site (Qb) as compared with the electron donor site (Qa). Previous work20 and Figure 8 demonstrate that the potential delivered with a homogeneous protein dielectric constant opposes the electron transfer; i.e., the potential at Qb is more negative than at Qa site. In our previous investigation,55 this problem was solved by utilizing the results of ref (20), showing that the vicinity of the Qb site is more flexible than that of the Qa site, which made us assign a high dielectric constant of 20 for the residues with a Qb pocket while modeling the rest of the protein with a dielectric constant of 4. Such an approach requires both prior knowledge about the flexibility of different protein regions and manual assignment of an appropriate dielectric constant. In contrast, the Gaussian-based smooth dielectric method automatically assigns adequate dielectric constants based on the 3D structure of the protein and, as seen in Figure 8, greatly reduces the potential barrier for the electron transfer. Compared to the potential in Figure 8a, the potential at the Qa site in Figure 8b is less positive and the Qb site is less negative. Potentials of Qa and Qb in Figure 8b are at a similar level, which agrees with the experimental observation of the electron transfer process.

Figure 8.

Figure 8

Open in a new tab

Electrostatic potential in the Reaction Center protein (PDB ID: 1AIJ), calculated by (a) the homogeneous method in DelPhi and (b) the Gaussian-based method in DelPhi.

d. Small Molecule Transfer Energy Calculations

Previous work on the same data set of 504 small molecules57 utilized MD simulations with the explicit solvent model and reported RMSD of 1.24 kcal/mol.51 Here, we use the same data set of small molecules to test the performance of both the homogeneous and Gaussian-based dielectric. It should be clarified that small molecules are much less flexible than proteins and do not have internal cavities. Because of that, they are not expected to be very polarizable and the Gaussian-based method is not expected to offer any advantage over the homogeneous dielectric. However, if the development is correct, it is anticipated that the results obtained with the Gaussian-based and homogeneous dielectrics should be quite similar. Keeping in mind that small molecules are less polarizable than proteins, it is expected that different (as compared with those in proteins) reference values for the internal dielectric constant and variance will deliver the best RMSD. Here, we optimized the reference internal dielectric constant, the variance of the Gaussian function, the cutoff for the molecule–water interface, and the coefficients of the nonpolar component of the solvation energy (calculated with the solvent assessable surface area, SASA). The best results are achieved when the parameters are set as follows: the reference εin = 1.0, reference variance σi = 1.0, cutoff for the molecular boundary is at εbnd = 16. For the nonpolar term calculation, γ = 0.0028 kcal/(mol Å2) and b = 0.0948 kcal/mol. The corresponding RMSD is 1.59 kcal/mol, which is close to the results obtained with explicit water simulations. The results of the calculations are shown in Figure 9 against the experimentally measured transfer energies. For homogeneous dielectric calculations, the best RMSD = 1.45 kcal/mol (Figure 9), when the parameters are set as follows: εin = 1.0, γ = 0.0094 kcal/(mol Å2), and b = −1.1579 kcal/mol.

Figure 9.

Figure 9

Open in a new tab

Solvation energies of small molecules calculated by Gaussian-based dielectric methods.

e. Reducing Grid Artifacts via Gaussian-Based Smooth Dielectric Function

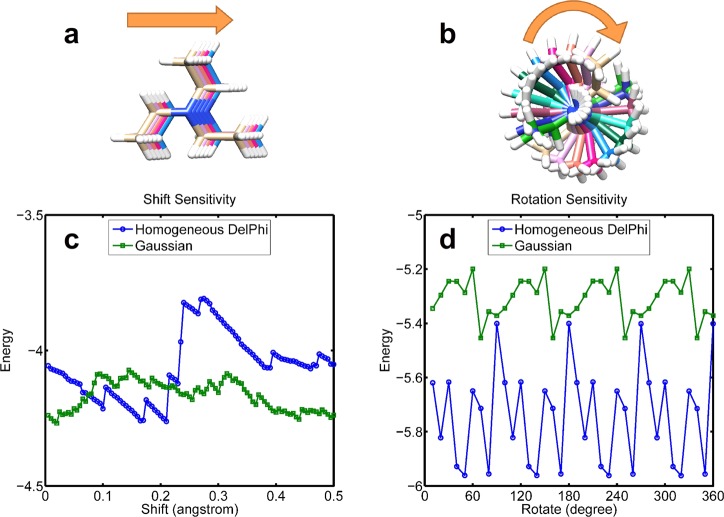
Calculating electrostatic energies by using finite difference methods is grid dependent, because the biomolecules are mapped onto discrete grids. If the concerned biomolecule is shifted to a new position, the newly obtained solvation energy might be different from those obtained at the original position. Since the Gaussian-based method uses smoothed dielectric distribution rather than two-dielectric constants with a sharp jump at the protein–water boundary, it is expected that the energies calculated by the smoothed method should be less grid-sensitive than traditional methods. Figure 10 shows the grid sensitivity of the electrostatic solvation energy of a small molecule calculated with both a Gaussian-based smooth dielectric and with a homogeneous dielectric. The grid length used in this test was 0.5 Å. The first test involved translation such that the small molecule is moved along the X direction in steps of 0.005 Å and the energy calculated for each position (Figure 10a). The second test probed the rotational sensitivity. The molecule was rotated in steps of 10°, and for each rotation the energy was calculated (Figure 10b). Figure 10 shows that energies calculated with the Gaussian-based smooth dielectric function are much less sensitive to the grid details, which is another significant advantage of the proposed approach.

Figure 10.

Figure 10

Open in a new tab

Grid sensitivity of the Gaussian method and homodeneous dielectric DelPhi. (a) A diethylamine molecule is shifted though a grid. (b) A triethylamine molecule is rotated in 360°. (c) Energy sensitivity of shift. (d) Energy sensitivity of rotation.

Discussion

Since the nature and the “optimal” value of the dielectric constant of proteins (and macromolecules in general) was and is the subject of many investigations and scientific publications, it is worth summarizing the outcome of this work with regard to frequently carried research tasks and scenarios. One of the most common tasks in computational research is to calculate the electrostatic component of the solvation energy of a protein or a small molecule. As mentioned in the Introduction, such calculations were reported in the literature utilizing various values for the internal dielectric constant. Which dielectric value is the best? Reiterating once more the lessons outlined by Warshel and co-workers,15,16 we would like to clarify the difference between calculations involving small molecules and those involving proteins. It is useful to envision the case of a molecule for which atomic details are revealed with absolute precision (including hydrogens). Further idealizing the model considering that the thermal motions are not present, the electrostatic interactions among the atoms of the molecule should be calculated with a dielectric constant of 1 (or 2 to account for electronic polarizability). This idealized case represents, to a great extent, the real case scenario of modeling the solvation energy of rigid molecules and, in general, modeling processes which do not induce conformational (and ionization) changes.

The above discussion does not represent the best test case of our approach, since the dielectric response is expected to be manifested the best upon introducing/removal of a charge. The natural process in proteins involving charge creation/removal is ionization/deionization of titratable groups upon pH changes or other factors. Because of that, in our opinion, the most appropriate phenomenon to illustrate the advantages of the smooth dielectric function is the pKa’s modeling. Calculating the pKa shift requires one to find the energy difference (most electrostatic component of the energy) between the corresponding protein with ionized and neutral groups of interest. However, typically only the structure of the protein with the group being ionized or neutral is available. Depending on various structural factors, the ionization/deionization of the group could induce small or large conformational changes, which are not taken into account in the protocols using rigid structures. To account for these structural changes, which in turn will affect the electrostatic interactions, one typically uses a high dielectric constant, as outlined in the Introduction.

We would like to point out that despite the use of a unified reference internal dielectric constant (ε = 4) for our protein modeling, the corresponding smooth dielectric function is unique for each protein. This is because it results from structural characteristics such as packing, the presence of internal cavities, and their shapes. Because of that, it is expected that the proposed approach and delivered parameters can be used without adjustment in future studies involving different sets of proteins.

The analysis of the smooth dielectric function done on a large and diverse set of proteins proved that the approach is physically sound. Indeed, without explicit considerations about physical properties of the amino acid (charged, polar versus hydrophobic), the results on the average dielectric constant value over amino acid types showed that the highest dielectric values were automatically assigned to the space occupied by charged groups, and the lowest dielectric values were attributed to the hydrophobic core. This is obviously related to the packing and the fact that charged and polar residues prefer to be at the protein surface, while hydrophobic groups are typically buried. However, engineered proteins may not follow such a trend and may have a titratable group buried in the packed hydrophobic core, as with many of the cases in the pKa Cooperative data set. A buried titratable group, charged or not, represents a highly polar structural element, for which the contribution to the protein’s polarizability will depend on the ability to change conformation or ionization states and may not be captured by our model. To address the possibility that the local dielectric constant associated with the space taken by titratable groups (especially in case of non-naturally occurring groups) may have to be not only a function of atomic packing but to be further increased, we repeated the pKa calculations with a modified Gaussian-based approach: the radii of titratable atoms of Asp, Glu, Arg, and Lys were artificially lowered by a factor of 2, which resulted in reduced packing and a higher local dielectric constant. The best RMSD (RMSD = 1.75 pK) was found to be almost the same as it was with the original Gaussian-based method (RMSD = 1.77 pK). This observation indicates that the current model captures most of the effects relevant to the dielectric response upon ionization, while it does not rule out further improvement by specific treatment of the ionizable groups.

Acknowledgments

We thank Barry Honig for the continuous support.

Supporting Information Available

The results of pKa calculations using both homogeneous DelPhi and Gaussian methods for each individual titratable group. This information is available free of charge via the Internet at http://pubs.acs.org

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript. L.L. analyzed the data, drafted the manuscript, and maintains the DelPhi package. C.L. and Z.Z. analyzed the data and revised the paper. E.A. supervised the project and finally drafted the manuscript.

Funding Sources

The work was supported by a grant from the Institute of General Medical Sciences, National Institutes of Health, award number R01GM093937.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States

Supplementary Material

ct400065j_si_001.xlsx (19.4KB, xlsx)

References

  1. Kato M.; Pisliakov A. V.; Warshel A. The barrier for proton transport in aquaporins as a challenge for electrostatic models: the role of protein relaxation in mutational calculations. Proteins: Struct., Funct., Bioinf. 2006, 64, 829–844. [DOI] [PubMed] [Google Scholar]
  2. Gouda H.; Kuntz I. D.; Case D. A.; Kollman P. A. Free energy calculations for theophylline binding to an RNA aptamer: Comparison of MM-PBSA and thermodynamic integration methods. Biopolymers 2002, 68, 16–34. [DOI] [PubMed] [Google Scholar]
  3. Kollman P. A.; Massova I.; Reyes C.; Kuhn B.; Huo S.; Chong L.; Lee M.; Lee T.; Duan Y.; Wang W.; Donini O.; Cieplak P.; Srinivasan J.; Case D. A.; Cheatham T. E. 3rd. Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models. Acc. Chem. Res. 2000, 33, 889–897. [DOI] [PubMed] [Google Scholar]
  4. Genheden S.; Ryde U. Comparison of end-point continuum-solvation methods for the calculation of protein–ligand binding free energies. Proteins: Struct., Funct., Bioinf. 2012, 80, 1326–1342. [DOI] [PubMed] [Google Scholar]
  5. Mobley D. L.; Dill K. A.; Chodera J. D. Treating entropy and conformational changes in implicit solvent simulations of small molecules. J. Phys. Chem. B 2008, 112, 938–946. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Vicatos S.; Roca M.; Warshel A. Effective approach for calculations of absolute stability of proteins using focused dielectric constants. Proteins: Struct., Funct., Bioinf. 2009, 77, 670–684. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Dominy B. N.; Minoux H.; Brooks C. L. An electrostatic basis for the stability of thermophilic proteins. Proteins: Struct., Funct., Bioinf. 2004, 57, 128–141. [DOI] [PubMed] [Google Scholar]
  8. Talley K.; Ng C.; Shoppell M.; Kundrotas P.; Alexov E. On the electrostatic component of protein-protein binding free energy. PMC Biophys. 2008, 1, 2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Alexov E.; Mehler E. L.; Baker N.; M. Baptista A.; Huang Y.; Milletti F.; Erik Nielsen J.; Farrell D.; Carstensen T.; Olsson M. H. M.; Shen J. K.; Warwicker J.; Williams S.; Word J. M. Progress in the prediction of pKa values in proteins. Proteins: Struct., Funct., Bioinf. 2011, 79, 3260–3275. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Gilson M. K.; Honig B. Calculation of the total electrostatic energy of a macromolecular system: solvation energies, binding energies, and conformational analysis. Proteins: Struct., Funct., Bioinf. 2004, 4, 7–18. [DOI] [PubMed] [Google Scholar]
  11. Gunner M.; Zhu X.; Klein M. C. MCCE analysis of the pKas of introduced buried acids and bases in staphylococcal nuclease. Proteins: Struct., Funct., Bioinf. 2011, 79, 3306–3319. [DOI] [PubMed] [Google Scholar]
  12. Warwicker J. pKa predictions with a coupled finite difference Poisson–Boltzmann and Debye–Hückel method. Proteins: Struct., Funct., Bioinf. 2011, 79, 3374–3380. [DOI] [PubMed] [Google Scholar]
  13. Spassov V. Z.; Yan L. A fast and accurate computational approach to protein ionization. Protein Sci. 2009, 17, 1955–1970. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Antosiewicz J.; McCammon J. A.; Gilson M. K. Prediction of pH-dependent properties of proteins. J. Mol. Biol. 1994, 238, 415. [DOI] [PubMed] [Google Scholar]
  15. Schutz C. N.; Warshel A. What are the dielectric “constants” of proteins and how to validate electrostatic models?. Proteins: Struct., Funct., Bioinf. 2001, 44, 400–417. [DOI] [PubMed] [Google Scholar]
  16. Warshel A.; Papazyan A. Electrostatic effects in macromolecules: fundamental concepts and practical modeling. Curr. Opin. Struct. Biol. 1998, 8, 211–217. [DOI] [PubMed] [Google Scholar]
  17. Warshel A.; Sharma P. K.; Kato M.; Parson W. W. Modeling electrostatic effects in proteins. Biochim. Biophys. Acta, Proteins Proteomics 2006, 1764, 1647–1676. [DOI] [PubMed] [Google Scholar]
  18. Sham Y. Y.; Muegge I.; Warshel A. The effect of protein relaxation on charge-charge interactions and dielectric constants of proteins. Biophys. J. 1998, 74, 1744. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Simonson T.Protein: ligand recognition: simple models for electrostatic effects. Curr. Pharm. Des. 2012, in press [DOI] [PubMed]
  20. Alexov E.; Gunner M. Calculated protein and proton motions coupled to electron transfer: electron transfer from QA-to QB in bacterial photosynthetic reaction centers. Biochemistry 1999, 38, 8253–8270. [DOI] [PubMed] [Google Scholar]
  21. Corzana F.; Busto J. H.; Jiménez-Osés G.; de Luis M. G.; Asensio J. L.; Jiménez-Barbero J.; Jesús M.; Avenoza A. Serine versus threonine glycosylation: the methyl group causes a drastic alteration on the carbohydrate orientation and on the surrounding water shell. J. Am. Chem. Soc. 2007, 129, 9458–9467. [DOI] [PubMed] [Google Scholar]
  22. Pal S.; Balasubramanian S.; Bagchi B. Anomalous dielectric relaxation of water molecules at the surface of an aqueous micelle. J. Chem. Phys. 2004, 120, 1912–1920. [DOI] [PubMed] [Google Scholar]
  23. Sterpone F.; Stirnemann G.; Laage D. Magnitude and Molecular Origin of Water Slowdown Next to a Protein. J. Am. Chem. Soc. 2012, 134, 4116–4119. [DOI] [PubMed] [Google Scholar]
  24. Oleinikova A.; Brovchenko I. Thermodynamic Properties of Hydration Water Around Solutes: Effect of Solute Size and Water-Solute Interaction. J. Phys. Chem. B 2012, 116, 14650–14659. [DOI] [PubMed] [Google Scholar]
  25. Swanson J. M. J.; Mongan J.; McCammon J. A. Limitations of atom-centered dielectric functions in implicit solvent models. J. Phys. Chem. B 2005, 109, 14769–14772. [DOI] [PubMed] [Google Scholar]
  26. Pang X.; Zhou H. X. Poisson-Boltzmann Calculations: van der Waals or Molecular Surface?. Commun. Comput. Phys. 2013, 13, 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Meyer T.; Kieseritzky G.; Knapp E. W. Electrostatic pKa computations in proteins: Role of internal cavities. Proteins: Struct., Funct., Bioinf. 2011, 79, 3320–3332. [DOI] [PubMed] [Google Scholar]
  28. Vaitheeswaran S.; Yin H.; Rasaiah J. C.; Hummer G. Water clusters in nonpolar cavities. Proc. Natl. Acad. Sci. U. S. A. 2004, 101, 17002–17005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Yin H.; Feng G.; Clore G. M.; Hummer G.; Rasaiah J. C. Water in the polar and nonpolar cavities of the protein interleukin-1β. J. Phys. Chem. B 2010, 114, 16290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Spyrakis F.; BidonChanal A.; Barril X.; Javier Luque F. Protein flexibility and ligand recognition: challenges for molecular modeling. Curr. Top. Med. Chem. 2011, 11, 192–210. [DOI] [PubMed] [Google Scholar]
  31. Boehr D. D.; Nussinov R.; Wright P. E. The role of dynamic conformational ensembles in biomolecular recognition. Nat. Chem. Biol. 2009, 5, 789–796. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Mittag T.; Kay L. E.; Forman-Kay J. D. Protein dynamics and conformational disorder in molecular recognition. J. Mol. Recognit. 2009, 23, 105–116. [DOI] [PubMed] [Google Scholar]
  33. Taylor S. S.; Ilouz R.; Zhang P.; Kornev A. P. Assembly of allosteric macromolecular switches: lessons from PKA. Nat. Rev. Mol. Cell Biol. 2012, 13, 646–658. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Jiao W.; Parker E. J. Using a Combination of Computational and Experimental Techniques to Understand the Molecular Basis for Protein Allostery. Adv. Protein. Chem. Struct. Biol. 2012, 87, 391. [DOI] [PubMed] [Google Scholar]
  35. Simonson T.; Perahia D. Polar fluctuations in proteins: molecular-dynamic studies of cytochrome c in aqueous solution. Faraday Discuss. 1996, 103, 71–90. [DOI] [PubMed] [Google Scholar]
  36. Song X. An inhomogeneous model of protein dielectric properties: Intrinsic polarizabilities of amino acids. J. Chem. Phys. 2002, 116, 9359. [Google Scholar]
  37. Voges D.; Karshikoff A. A model of a local dielectric constant in proteins. J. Chem. Phys. 1998, 108, 2219. [Google Scholar]
  38. Wang L.; Zhang Z.; Rocchia W.; Alexov E. Using DelPhi Capabilities to Mimic Protein’s Conformational Reorganization with Amino Acid Specific Dielectric Constants. Commun. Comput. Phys. 2013, 13, 13–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Im W.; Beglov D.; Roux B. Continuum solvation model: computation of electrostatic forces from numerical solutions to the Poisson-Boltzmann equation. Comput. Phys. Commun. 1998, 111, 59–75. [Google Scholar]
  40. Grant J. A.; Pickup B. T.; Nicholls A. A smooth permittivity function for Poisson–Boltzmann solvation methods. J. Comput. Chem. 2001, 22, 608–640. [Google Scholar]
  41. Word J. M.; Nicholls A. Application of the Gaussian dielectric boundary in Zap to the prediction of protein pKa values. Proteins: Struct., Funct., Bioinf. 2011, 79, 3400–3409. [DOI] [PubMed] [Google Scholar]
  42. Li C.; Li L.; Zhang J.; Alexov E. Highly efficient and exact method for parallelization of grid-based algorithms and its implementation in DelPhi. J. Comput. Chem. 2012, 33, 1960–1966. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Simonson T.; Perahia D. Internal and interfacial dielectric properties of cytochrome c from molecular dynamics in aqueous solution. Proc. Natl. Acad. Sci. U. S. A. 1995, 92, 1082–1086. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Isom D. G.; Castañeda C. A.; Cannon B. R. Large shifts in pKa values of lysine residues buried inside a protein. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 5260–5265. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Pey A. L.; Rodriguez-Larrea D.; Gavira J. A.; Garcia-Moreno B.; Sanchez-Ruiz J. M. Modulation of buried ionizable groups in proteins with engineered surface charge. J. Am. Chem. Soc. 2010, 132, 1218–1219. [DOI] [PubMed] [Google Scholar]
  46. Castaneda C. A.; Fitch C. A.; Majumdar A.; Khangulov V.; Schlessman J. L.; García-Moreno B. E. Molecular determinants of the pKa values of Asp and Glu residues in staphylococcal nuclease. Proteins: Struct., Funct., Bioinf. 2009, 77, 570–588. [DOI] [PubMed] [Google Scholar]
  47. Isom D. G.; Cannon B. R.; Castañeda C. A.; Robinson A. High tolerance for ionizable residues in the hydrophobic interior of proteins. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 17784–17788. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Hynes T. R.; Fox R. O. The crystal structure of staphylococcal nuclease refined at 1.7 Å resolution. Proteins: Struct., Funct., Bioinf. 2004, 10, 92–105. [DOI] [PubMed] [Google Scholar]
  49. Li L.; Li C.; Sarkar S.; Zhang J.; Witham S.; Zhang Z.; Wang L.; Smith N.; Petukh M.; Alexov E. DelPhi: a comprehensive suite for DelPhi software and associated resources. BMC Biophys. 2012, 5, 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [DOI] [PubMed] [Google Scholar]
  51. Mobley D. L.; Bayly C. I.; Cooper M. D.; Shirts M. R.; Dill K. A. Small molecule hydration free energies in explicit solvent: an extensive test of fixed-charge atomistic simulations. J. Chem. Theory Comput. 2009, 5, 350–358. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Wesson L.; Eisenberg D. Atomic solvation parameters applied to molecular dynamics of proteins in solution. Protein Sci. 2008, 1, 227–235. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Wang J.; Wang W.; Kollman P. A.; Case D. A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graphics Modell. 2006, 25, 247–260. [DOI] [PubMed] [Google Scholar]
  54. Nielsen J. E.; Gunner M.; García-Moreno E B. The pKa Cooperative: A collaborative effort to advance structure-based calculations of pKa values and electrostatic effects in proteins. Proteins: Struct., Funct., Bioinf. 2011, 79, 3249–3259. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Rocchia W.; Alexov E.; Honig B. Extending the applicability of the nonlinear Poisson-Boltzmann equation: Multiple dielectric constants and multivalent ions. J. Phys. Chem. B 2001, 105, 6507–6514. [Google Scholar]
  56. Pettersen E. F.; Goddard T. D.; Huang C. C.; Couch G. S.; Greenblatt D. M.; Meng E. C.; Ferrin T. E. UCSF Chimera—a visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [DOI] [PubMed] [Google Scholar]
  57. Rizzo R. C.; Aynechi T.; David A.; Kuntz I. D. Estimation of absolute free energies of hydration using continuum methods: accuracy of partial charge models and optimization of nonpolar contributions. J. Chem. Theory Comput. 2006, 2, 128–139. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ct400065j_si_001.xlsx (19.4KB, xlsx)

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES