Glassy Interfacial Dynamics of Ni Nanoparticles: Part II Discrete Breathers as an Explanation of Two-Level Energy Fluctuations

Abstract

Recent studies of the dynamics of diverse condensed amorphous materials have indicated significant heterogeneity in the local mobility and a progressive increase in collective particle motion upon cooling that takes the form of string-like particle rearrangements. In a previous paper (Part I), we examined the possibility that fluctuations in potential energy E and particle mobility μ associated with this ‘dynamic heterogeneity’ might offer information about the scale of collective motion in glassy materials based on molecular dynamics simulations of the glassy interfacial region of Ni nanoparticles (NPs) at elevated temperatures. We found that the noise exponent associated with fluctuations in the Debye-Waller factor, a mobility related quantity, was directly proportional to the scale of collective motion L under a broad range of conditions, but the noise exponent associated with E(t) fluctuations was seemingly unrelated to L. In the present work, we focus on this unanticipated difference between potential energy and mobility fluctuations by examining these quantities at an atomic scale. We find that the string atoms exhibit a jump-like motion between two well-separated bands of energy states and the rate at which these jumps occur seems to be consistent with the phenomenology of the ‘slow-beta’ relaxation process of glass-forming liquids. Concurrently with these local E(t) jumps, we also find ‘quake-like’ particle displacements having a power-law distribution in magnitude so that particle displacement fluctuations within the strings are strikingly different from local E(t) fluctuations. An analysis of these E(t) fluctuations suggests that we are dealing with ‘discrete breather’ excitations in which large energy fluctuations develop in arrays of non-linear oscillators by virtue of large anharmonicity in the interparticle interactions and discreteness effects associated with particle packing. We quantify string collective motions on a fast caging times scale (picoseconds) and explore the significance of these collective motions for understanding the Boson peak of glass-forming materials.

1. Introduction

There are many aspects of glass-forming liquids, especially their high-frequency dynamics, which remain obscure. For example, abstract ‘two-level systems’ (TLS) are frequently invoked to rationalize universal aspects of the thermodynamics of glasses such as temperature dependence of specific heat and thermal conductivity of glassy materials at low temperatures,^1–4 as well as universally observed high-frequency dynamical features such as the fast excess wing relaxation process observed in these materials by neutron and Raman scattering, ^5–8 and the slow-beta or Johari-Goldstein beta relaxation process⁹ observed in dielectric and mechanical relaxation measurements (Some authors have indicated that the excess wing and slow-beta relaxations are manifestations of the same relaxation process, ^{10, 11} despite the rather different frequency ranges involved in the scattering and dielectric spectroscopy measurements.) The apparent density of these TLS obtained by fitting the TLS model to low temperature specific heat data has been found to correlate strongly¹² with the fragility of glass formation^13–15, a measure of the strength of the temperature dependence of transport properties in glass-forming (GF) materials above their glass transition temperature, T_g. Models of ‘colored’ or ‘flicker’ noise in the electrical transport of disordered metallic materials ¹⁶ have also invoked the abstract TLS model to rationalize noise observations. While the TLS model has a clearly enjoyed remarkable success in rationalizing diverse observations in amorphous solid materials, it is certainly a shortcoming of this model that the actual physical nature of the TLS remains physically obscure. It is particularly unclear why this phenomenon, as in the case of colored noise, should arise in so many different types of condensed materials. Just what is a ‘two-level system’ in a glassy material and how can they be so prevalent in virtually all everyday materials at low temperatures?

The present work approaches this problem starting from our former molecular dynamics (MD) investigation (Part I) ¹⁷ focused on trying to understand the physical origin of colored noise in GF materials based on simulations of the glassy interfacial dynamics of Ni nanoparticles (NPs). In this paper, we invoked a variant of arguments taken from the TLS model to rationalize the observed relation between the ‘color’ of the noise associated with particle displacement fluctuations, i.e., the noise exponent α, to the average length L of the collective atomic motions in the material. The present paper examines potential E(t) and particle displacement fluctuations at the scale of the individual Ni atoms and we fix our attention on the relatively rare fraction of interfacial atoms that are moving collectively in the form of strings. We find that the E(t) fluctuations of the interfacial Ni string atoms exhibit well-defined fluctuations between two well-separated bands of potential energy states (a concrete energetic two-level system) where the rate of jumping between these energy bands exhibits a temperature dependence strikingly similar to the slow-beta relaxation process of GF fluids. Actually, such two state fluctuations are a common feature of the dynamics of NPs and the investigation of such fluctuations in the context of their practical application has recently attracted much interest. Examples of this phenomenon, discussed below, include the fluorescence intensity blinking of quantum dots and proteins, as well as ‘blinking’ transitions in the catalytic activity of individual NPs. Given the superficial similarity of these mysterious NP fluctuations to our two-level E(t) fluctuations, we analyze these fluctuations in the fashion conventional for quantum dot blinking. Our MD simulations suggest that the two-level E(t) fluctuations seen in association with collective atomic motion in the NP interfacial region may be identified with ‘breathers’ in which large energy fluctuations develop in arrays of non-linear oscillators by virtue of large anharmonicity in the interparticle interactions and discreteness effects associated with particle packing.^{18, 19} This is potentially an important observation since there is rather limited understanding of the universal observation of two-level systems in disordered materials (There has been some progress in understanding two-level systems in vitreous silica ^{20, 21} and some other materials ²², but the extension of this type of molecular modeling to virtually all amorphous condensed materials at low temperatures seems rather unclear.) An examination of the displacement fluctuations associated with our two-level E(t) energy jumps indicates that they have a strongly fluctuating magnitude and, in particular, an analysis of these ‘quake-like’ events indicates that have much in common with earthquake phenomenology. We next considered what role collective motion might play in these quake events in the NPs. In particular, we consider collective motion on the picosecond ‘caging’ timescale on which the Debye-Waller factor <u²> is defined and measured. Since the slow-beta relaxation process seems to be implicated in our two-level E(t) jump rates, then following arguments of Debeneddi and Stillinger²³ for the origin of the slow-beta relaxation process, we expect to see collective motions associated with thermally activated hopping events connecting sub-basins of within some megabasin of the potential energy landscape; larger, more extended collective motions should correspond to transitions between the megabasins and thus involve many sub-basin transition events along the way. Schrøder et al. ²⁴ have illustrated these collective particle exchange events in a model GF liquid through an explicit inherent structure quench analysis taken after a series sequential caging times, clearly revealing the suggested transitions between inherent structure local minima (sub-basins) on the potential energy surface.²⁵ A further inherent structure analysis of these string-like collective motions was made later by Riggleman et al. ^{24, 25} where it was shown that the length of these string-like motions in the inherent structure dynamics correlates strongly with the energy barrier heights on the potential energy surface. In the present paper, we examine the real picosecond (‘fast’) dynamics of the our NPs and observe string-like collective atomic displacements that accord qualitatively with previous inherent dynamics studies and we conclude that the atomic jump displacements associated with the two-level energy fluctuations involve highly collective particle displacements. Vogel et al. ²⁶ have also investigated fast collective atomic motions in a model metallic GF material, but they offered no quantification of the geometry of these structures. In particular, we find the length distribution of the string-like motions in the fast dynamics (‘stringlets’) is exponential, as found for the long-time and larger scale string motions associated with diffusion and alpha relaxation. As one might expect, and indicated previously in inherent structure dynamics calculations, ²⁴ the average length of the stringlets is significantly shorter than the strings associated with α structural relaxation and their length has a relatively weak temperature dependence. An unexpected feature of stringlets, however, is their average length actually increases with heating, a trend opposite to the observed trend for strings.

With applications of NPs to catalysis in mind, we step back from our examination of the strings and their relation to noise and our consideration of the physical origin of TLS’s, and show how all these features come together to give a complete picture of interfacial dynamics of NPs. Within this global view, we see that the NP interface at elevated catalysis relevant temperatures on the order of O(1000 K) is comprised of locally well-packed atomic regions where the atoms have relatively low mobility and complementary regions of frustrated atomic packing where the string-like motion associated with two-level E(t) fluctuations is heavily concentrated. The physical situation is similar to the dynamics of Ni grain boundaries between the well-packed crystal grains where string-like collective motion is likewise prevalent.

Having the free boundary makes the NPs have some unique features not shared by GF materials broadly. We find an amusing parallel between Ni NP interfacial dynamics and the dynamics of the Earth’s crust where the theory of plate tectonics recognizes that large continental regions of low mobility drift about in the earth’s interfacial region and where displacement events, i.e. earthquakes, occur highly intermittently in time and with large fluctuations in magnitude near the boundaries of the solid plate regions. In figurative terms, we then observe a kind on nanoscale analog of the earth’s plate tectonics rather than a uniform surface-melted interfacial layer on the surfaces of our NPs.

Finally, we examine the Boson peak phenomenon, which is another universal, but physically obscure, feature of GF liquids that has often been suggested to be related to fast collective particle motions. While we find evidence consistent with the connection of this ubiquitous scattering feature with collective atomic motion, we do not achieve a definitive explanation of the Boson peak in terms of the geometrical properties governing the collective motion as we had hoped. On the other hand, we do find a striking relationship between the Boson peak frequency ω_p and the Debye-Waller factor <u²> in our simulations of Ni NP interfacial dynamics. As in the case of our other findings for NP interfacial dynamics relating to the relation between noise and collective motion, this relationship requires validation for other types of glassy systems. However, a general relationship of this kind would be extremely useful in materials characterization because of the relative ease of Boson peak measurements by neutron and Raman scattering.

One of the most intriguing observations of the present study is the propagation of the breather excitations along the strings, providing a possible mechanism for driving the correlated string-like atomic displacements movements that ultimately give raise to structural relaxation. Recently, we found interstitial defects to play a similar role in driving collective string-like collective motion associated with homogeneous melting of bulk crystalline Ni.²⁷ These simulation observations and those of the present paper provide glimpses into the fundamental non-linear dynamic processes that underlie the collective motion in condensed materials and occurrence of colored noise in glass-forming liquids and other strongly interacting disordered particle systems.

2. Simulation Methods

Molecular dynamics simulations utilizing LAMMPS²⁸ were performed to analyze the fluctuation of atomic motions and characterize the string-like collective atom motions on the interfacial region of Ni NPs in our accompanying paper. In short, the atomic interactions were described using the Voter-Chen form²⁹ of an Embedded Atom Method (EAM) potential³⁰ for Ni. Free boundary conditions (free surfaces with vacuum) were applied for all simulations, which were performed within the canonical ensemble (NVT) where a constant temperature was maintained using the Nose-Hoover method.^{31, 32} The NPs in the present paper have N=369 and N = 2899 Ni atoms corresponding to a NP having a radius r of about 1nm and 2 nm, respectively. The NPs were initiated from an approximately spherical shape having a face-centered cubic structure and the NPs were subsequently relaxed at room temperature for 1.5 ns with zero angular and linear momentum values.

3. Energy Fluctuations, ‘Breathers’ and ‘Blinking’?

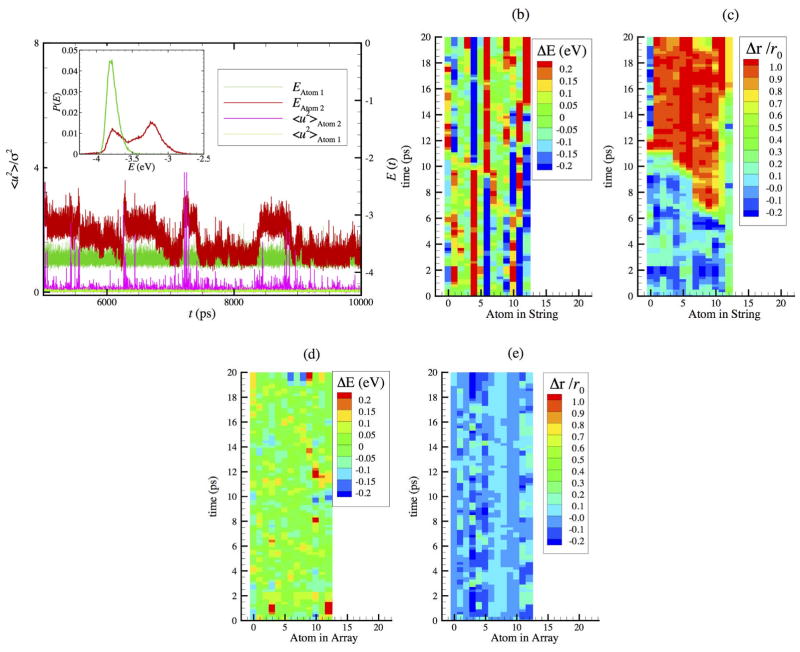
So why are the E(t) fluctuations so different from <u²> fluctuations in our simulations of NP interfacial dynamics and what is the nature of the difference between the local ‘free volume’³³ <u²>^3/2 fluctuations and local potential energy E(t) of the atoms in the interfacial region of the NP? To better understand the origin of the difference between the T dependence of the noise involved in the potential energy E(t) and <u²> fluctuations, we focus in Fig. 1a on the E(t) fluctuations of a ‘mobile’ interfacial atom involved in string-like collective motion³⁴ and compare these fluctuations to a representative ‘normal’ particle in the NP interfacial layer. We immediately see something striking in the E(t) fluctuations of these mobile particles that has no counterpart in the <u²> fluctuations. While E(t) of the representative caged particle (atom 1) in the interfacial layer fluctuates in a relatively regular way around its average value, the mobile particle (atom 2) exhibits telegraph signal or ‘blinking’ fluctuations. The timescale for E(t) to jump is on the order of ps, but the timescale over which the energy switch back to its former state tends to be a much longer time, as we now illustrate.

Figure 1.

Comparison of potential energy fluctuations of atoms that are caged (atom 1) and atoms that are involved in collective string-like motion (atom 2) over the timescale longer than the lifetime of the strings t^* = 130 ps where N = 2899 at T = 1000 K. a) Potential fluctuations of individual atoms 1 and 2 within the interfacial region of NP. Note the correlation between potential energy changes and the spikes in the local Debye-Waller factor, <u²> for atom 2. b), c) Potential energy and particle displacements Δr of type 2 atoms at T = 1400 K where the y-axis denotes time in units of the caging time at which <u²> is defined. The time on the y-axis extends to the string lifetime, t*. d), e) E(t) and displacement plots for an array of normal (type 1) atoms along a crystal face having the same length of the string in b), c).

In Figure 1b, we show how E(t) fluctuates for type 2 atoms along a representative string at T = 1400 K and in Fig. 1c we show changes in particle displacement Δr/r₀ for these same atoms. The energy is taken the difference between the average potential energy over a ps and the average energy over the string lifetime t* for each atom in string. The particle displacement is taken with respect to the initial position of the atom itself rescaled by the distance to its neighbor along the string and can be positive or negative depending on its relative position to the neighbor. The y-axis denotes time in units of the caging time at which <u²> is defined and time range on this axis extends to the string lifetime, t*. (Plots of this kind are conventional in studies of energy localization in one-dimensional chains of non-linear oscillators where they are termed ‘hyposometric plots’).^35–39 The color map legends of these figures define the magnitude of the potential energy and particle displacement jumps. We see that the overall positive displacement of the particles along the string seen in Fig. 1c is signaled by a propagating wave of energy jump events in Fig. 1b, reminiscent of traveling cluster waves in chains of anharmonic oscillators.⁴⁰ After having displaced, the particle positions then become relatively stable. Note the long persistence of the atoms in high and low potential energy states and the fluctuations in the persistence times of the atoms in these energy levels. We contrast this behavior with potential energy and displacement plots in Figs. 1d and 1e for an array of normal, or type 1 atoms, along a face of the NP that has the same length as the string chosen Figs. 7b and 7c. Large-scale energy fluctuations and the net particle displacement are simply absent in the normal particles that are not involved in collective particle motion. Energy fluctuations and coordinated particle movement are concentrated in the strings. Hypsometric plots of E(t) and displacement for mobile particles at T = 1000 K are given in Supplementary Material where the correlation between the energy jump progression and particle displacement along the string is again evident.

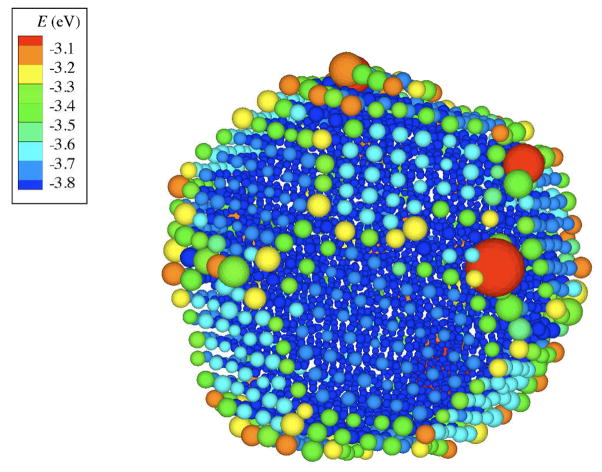
Figure 7.

Atomic configuration of N = 2899 NP at T = 1000K. The atoms are colored by the potential energy and size is proportional to the <u²>. Both potential energy and <u²> are time average over t^* = 130 ps, which is corresponding to the time interval that strings show maximum length.

The foregoing analysis has revealed some essential aspects of the energy fluctuations of atoms within the strings. This type of energy fluctuation is characteristic of chains of anharmonic oscillators where it is know that energy can spontaneously concentrate along the chain. ⁴¹ These ‘breather modes’ have recently been observed in a variety of crystalline materials ¹⁸ and in a disordered material context they found in the large amplitude ‘bubbles’ defining the local unbinding of DNA helices near the DNA denaturation transition. ^{36, 37, 42–44} Simulations have indicated that these ‘breathers’ lead to inhibited energy relaxation and to many of the phenomenological characteristics of GF liquids such as stretched exponential relaxation and intermittency in relaxation dynamics, colored noise, etc.^{38, 45, 46} In this context, it is known that strong energy localization occurs preferentially in elastically soft regions,^{46, 47} and this physical situation seems to match the occurrence of the strings rather well. These energetically ‘hot spots’ have been under intense interest because of the potential relevance for understanding catalysis^48–54 and model calculations have indicated that anharmonicity in intermolecular interactions can give large changes in rate constants and can reproduce phenomenological aspects of catalysis phenomenology such as the widely observed entropy-enthalpy compensation effect in the reaction rate free energy parameters.⁵⁵ Ngai has previously suggested the relevance of breather modes to the fast dynamics of GF fluids ⁵⁶, based on parallels in experimental trends in the fast dynamics of GF fluids and simulations of the dynamics of non-linear oscillator networks so that the inference was rather indirect.

An examination of the distribution of the energy jumps of the string atoms, illustrated in the inset to Fig. 1a, indicates a bimodal distribution. Evidently, these mobile particles are jumping between two apparently well-defined bands of energy states. This phenomenon brings to mind the telegraph signal like intensity polarization fluctuations found in glassy polyvinyl acetatefilms by non-contact atomic force microscopy.⁵⁷ We suggest that polarization fluctuations might likewise involve predominantly energy fluctuations rather than density or ‘free volume’ (<u²>) fluctuations. A similar ‘dynamic coexistence’ phenomena in energy fluctuations has often been observed in molecular dynamics simulations of small atomic clusters^58–62 and corresponding observations of dynamic fluctuations in nanoparticle ordering have been made.^{63, 64} We now take a look at the T dependence of these E(t) jumps.

4. Temperature Dependence of E(t) Fluctuations and ‘Slow-Beta’ Relaxation?

The intermittent fluctuations in the fluorescence intensity of optically excited quantum dots, such as CdSe NPs have been the focus of a tremendous research effort recently and, as in the case of glass formation and colored noise, there is no generally agreed upon explanation of this intermittent optical ‘blinking’ phenomenon. In these measurements, you likewise see switching between two bands of energy states as in Fig. 1a, corresponding to the on and off fluorescence states. ^65–67 This striking phenomenon has been associated with some sort of ‘structural fluctuation’ near the interface of the quantum dots⁶⁸ or non-radiative relaxation processes associated with the amorphous nature of the quantum dot surface or the surrounding medium.^{67, 69–72} Since the quantum dot blinking phenomenon appears so similar to the E(t) fluctuations found in our simulations, we analyze these fluctuations in a similar way, despite the fact that any relation between these phenomena is currently unclear.

Measurements of the interconversion between the ‘on’ and ‘off’ state in quantum dots have indicated that the total number of these off-on events after a fixed time and the reciprocal of the time over which the particles are bright both follow Arrhenius temperature dependence⁷³ ; we then check the kinetics of our ‘blinking’ to see if a similar phenomenology emerges. We shall see that this is indeed the case. A few words about the generality of blinking seem in order before we begin our analysis, since previous experimental studies of this phenomenon motivate our analysis of E(t) fluctuations and the diverse physical contexts of this ‘blinking’ phenomenon also motivate applications of our observations.

Direct observations of catalytic activity in individual Au NP has also indicated on and off ‘blinking’ between catalytically active and inactive reactivity states, ^{74, 75} an effect attributed to some kind of nebulous dynamic restructuring of the NP surface. Regardless of the cause, ‘blinking’ in the physical properties and reactivity of NPs is a generic phenomenon affecting the optical, magnetic and reactivity properties of these particles (See Conclusions). This intermittency is often a limiting factor in the application of these particles as sensors, optical labels, etc. On the other hand, colored noise blinking can have practical benefits, however, e.g., under some conditions colored noise can lead signal amplification through stochastic resonance.⁷⁶ This amplification effect has potential benefits in enhancing the sensitivity of nanoelectromechanical devices⁷⁶ and amplification of signal discrimination in sensory systems in biological systems by stochastic resonance has been demonstrated.⁷⁷ The underlying conductance noise found in biological systems is characteristically colored⁷⁸ and such fluctuations have been hypothesized to be essential for correct biological function.^{79, 80} Colored energy fluctuations have also been found in simulations in such basic systems as proteins and duplex DNA near their ‘melting’ transition.^{81, 82} Noise phenomenon is certainly ubiquitous in biological systems and it is probably functional in its significance. How can we explain and characterize this ubiquitous phenomenon?

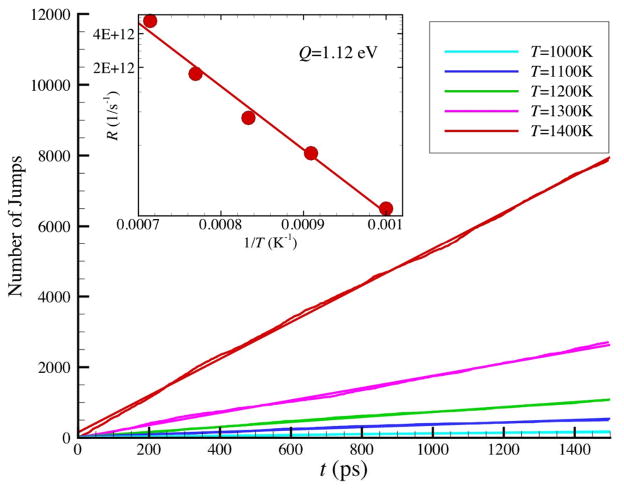
Following previous research on ‘optical’ blinking’ phenomenon, we characterize E(t) fluctuations by examining the rate at which transitions occur between these distinct bands of energy states. We then define an energy jump counter that increments by 1 every time a transition from the lower and upper energy state band (jump greater than ΔE > 0.3 eV) occurs. Figure 2 reveals that the number of state transitions (‘jumps’) increases with time t in a strikingly linear way. We then see a well-defined rate of potential energy state transitions, despite the overall colored nature of the E(t) noise in the ensemble average for the interfacial Ni atoms. This linearity of slope in Fig. 2 persists over the entire T range of our simulations and the inset of Fig. 2 indicates that the slope of these curves, the energy ‘jump rate’ R, is well approximated by an Arrhenius relation. The activation energy Q in Fig. 2 is almost a factor of about 3.7 times that for the surface diffusion³⁴ of Ni atoms at bulk planar interfaces and specifically we find Q = 1.12 eV. An activation energy Q of roughly 3 or 4 times that for local conformational changes in polymers ¹⁰ or for the diffusion coefficient of small molecule liquids is characteristic of the ‘slow beta’ relaxation of GF liquids (Q_β≈ 24 k T_g)^{10, 83–86} and we suggest that this energy jump process might be identified with the mysterious slow beta relaxation process of GF fluids. Due to its relatively large activation energy, Mattsson et al. have attributed slow beta relaxation, a universal, but poorly understood, feature of GF liquids generally,^87–89 to some kind of relatively local, but collective, relaxation process that is somehow linked to the slower alpha relaxation process governing structural relaxation in the intermediate scattering function^{83, 84, 90} and shear stress relaxation. It is also notable that the ‘slow beta’ or ‘Johari-Goldstein’ relaxation process in GF materials is normally apparent in dielectric, mechanical and thermal relaxation measurements⁹¹, unless obscured by overlap with α structural relaxation. High frequency or ‘fast’ relaxation observed in neutron and Raman scattering occurs for a different frequency range than the slow beta relaxation of dielectric measurements, but we suggest that these relaxation processes may well have similar physical origin. Based on our observations above, we suggest that this timescale difference might reflect the fact that the intermediate scattering function I(q,t) of Raman and neutron scattering measures density fluctuations while the dielectric measurements predominantly measure the relaxation of energy fluctuations associated with local fluctuations in the material polarization (a cross coupling between stress and polarization fluctuations naturally explains the observation that a similar high frequency beta relaxation occurs in both mechanical and dielectric relaxation measurements). Consistent with the suggestion mentioned above of a common physical origin of the excess wing and slow-beta relaxation processes, recent successful modeling⁸⁹ of the slow-beta relaxation has been based on the same type of TLS model introduced previously to describe fast relaxation in glasses. ³ The two-state energy fluctuations that we observe are clearly an interesting candidate for understanding fundamental nature and the universal occurrence of the fast ‘excess wing’ and slow-beta relaxation processes of GF liquids. The physical nature of the hypothetical two level systems of glasses has been a long-standing problem in the physics of these materials.

Figure 2.

The number of successful jumps from low energy level to high energy level as a function of simulation time at different temperatures where N = 2899 NP. A successful jump is defined as the increase of the potential energy of one atom larger than 0.3 eV. The slope defines the total jump rate. In inset, the Arrhenius plot of jump rate yields activation energy of 1.12 eV.

5. Quantification of Fast Collective String-like Motion or ‘Stringlets’

The most prevalent view of the origin of this ‘slow-beta’ relaxation in glasses and polycrystalline materials is that it involves some relatively local, but nonetheless correlated, molecular motions within regions of relatively poor packing in the amorphous material where the mobility of the material is higher.^{85, 86, 92, 93} Figuratively speaking, the slow beta relaxation process has been conjectured to be associated with a ‘connective tissue’⁹⁴ existing outside the relatively well-packed regions of the fluid where there is relatively good short-range packing. This physical picture is entirely consistent with our identification of the slow-beta relaxation process with atoms undergoing two-state potential fluctuations as part of the string sub-dynamics. If anti-plasticizer additives are added to a GF liquid to reduce the fragility of glass formation in model polymer GF liquids by suppressing the extent the local string-like collective atomic motion ^{13, 95–98}, the slow-beta relaxation process is found to be largely suppressed.⁹⁹ Finally, we note that there is direct neutron scattering evidence for the ‘fast’ correlated motion of groups of atoms on a fast (picoseconds) timescale by neutron scattering.¹⁰⁰ Motivated by these observations and considerations, we next examine whether there is an evidence for appreciable string-like collective motion on the fast (ps) timescale on which the energy jumps are occurring, motions actually driving the E(t) fluctuations.

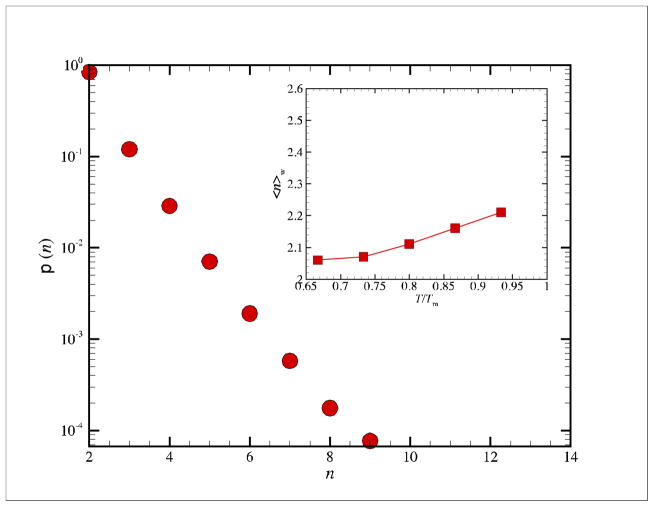
In Figure 3, we show the length distribution (n) for fast string-like particle displacement events occurring on a short (ps) timescales, i.e., the caging timescale at which the Debye-Waller factor <u²> is defined. This seems to be essentially these same string-like motions in the fast dynamics investigated some time ago by Hiwatari and coworkers^{101, 102} and Schober and coworkers^{103, 104}, but the size distribution and size of these dynamic clusters was not quantified before. Vogel et al. ²⁶ also investigated these dynamic structures from a qualitative standpoint. Here the size distribution (n) of the ‘fast strings’ was calculated for an N = 2899 atom Ni NP at T = 1400 K where the calculations utilize a displacement cut-off equal to the interparticle distance and involve an averaging over many ps intervals to obtain a good statistical averaging. This same time interval is employed to define ¹⁰⁵ the mean particle distance or ‘caging scale’ <u²>^1/2. As opposed to the string size distribution P(n) at t = t^*, the length of the fast string-like collective motions (‘stringlets’) is rather insensitive to T. The inset in Fig. 3 illustrates the T dependence of weight average string length ℓ_w and this quantity actually grows somewhat upon heating, an effect found qualitatively before by Schober and coworkers. ^{103, 104} (The weight average length ℓ_w = <n>_w of these ‘stringlets’ is approximately 2.21 while the number average length ℓ is close to 1 because of the large contribution of isolated mobile particles (n = 1) not involved in collective atom motion to this type of average.) It should be appreciated the ‘stringlets’ are short in comparison to the collective string motions described above associated with large-scale diffusive motions. The stringlets define the sub-dynamics of the strings ^{25, 26} and they presumably remain an active mode of motion in the glass regime where large-scale string particle exchange events are rare events.

Figure 3.

Length distribution of collective string-like displacements occurring on a picosecond timescale.

Now that we can visualize the fast local collective motion in our simulations and can quantify changes in this motion with thermodynamic conditions, it should now be possible to modulate this phenomenon for the control of material properties and to use noise measurements to monitor alterations in the collective motion induced by perturbing the material. For example, in metals at low temperatures,¹⁶ conductance fluctuations are again dominated by two-state E(t) fluctuations, as in Fig. 1a, where the activation energy for these fluctuations can be tuned by varying the strength of an applied magnetic field. We expect the application of strains (extension, compression, pressure) and other fields on NPs, GBs and GF materials to generally have a similar perturbing effect on the activation energy governing this fast particle displacement process, an effect of great interest in relation to the plasticity of amorphous materials. We next contrast the E(t) fluctuations of the mobile particle with the <u²> fluctuations of the same particle. Why are these E(t) and <u²> fluctuations so different in character?

6. Displacement <u²> Versus Potential Energy E(t) Fluctuations

A direct comparison of the E(t) and <u²> fluctuations during the evolution of the string particle over the lifetime of the string, t*, is indicated in Fig. 1a. We observe that <u²> exhibits sharp jumps in magnitude at the times where the E(t) jumps from high to low potential energy states occur. The singular nature of these jumps is even more apparent at lower T. Evidently, the larger average value of <u²>, which is substantially larger for the string particle (atom 2) than for the normal caged particle (atom 1), reflects the contribution of rather singular ‘escape’ events of the string particle dynamics. Otherwise, the mobile string atoms are rattling about much like the caged particles (See Fig. 1a).

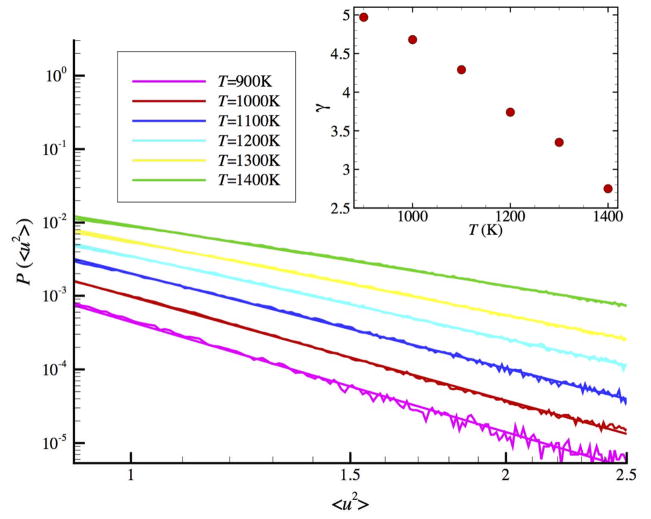
The singular particle displacement events of the string-like particles at intermittent times are reminiscent of an avalanche behavior that has been seen in diverse amorphous materials, especially under conditions of plastic deformation.¹⁰⁶ We next take a closer look at this ‘erratic’ jump behavior for a simulation at lower T where this phenomenon becomes even more developed. Figure 4(a) shows the ‘spectrum’ of avalanche-like events for <u²> for N = 2899 NP for T = 1000 K and Fig. 4(b) shows the probability distribution function of the avalanche like events, which exhibits a power-law. As shown in Fig. 5, the size distribution in all cases (ensemble average) is a power-law in form and the avalanche magnitude exponent increases almost linearly with T upon cooling, reflecting the growing scale of collective motion and mobility fluctuations described by L and α_DWF. ¹⁷

Figure 4.

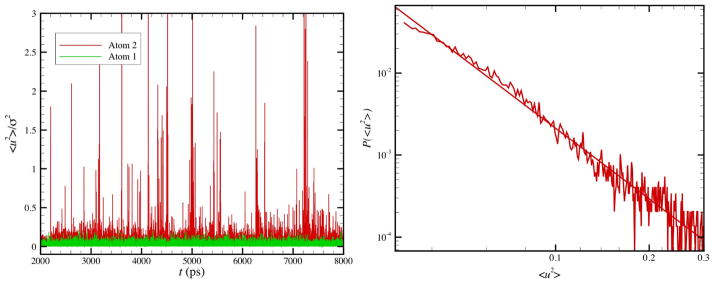
The time evolution of <u²> for an interfacial string atom undergoing cooperative motion showing avalanche events and the distribution of singular avalanche events P(<u²>). Left: <u²> for a string particle over a timescale over which the strings persist for a Ni NP having N = 2899 and T = 1000 K. Right: Probability distribution function of <u²> of atom 2, where P(<u²>) ~ (<u²>)^−γ and γ ≈ 3.0 for this atom.

Figure 5.

Probability distribution function P(<u²>) for the singular avalanche events for the <u²>. The inset shows how varying T affects this avalanche phenomenon. We find that scaling exponent γ varies approximately in a linear way with T.

7. Global View of Nanoparticle Interfacial Dynamics at Elevated Temperature

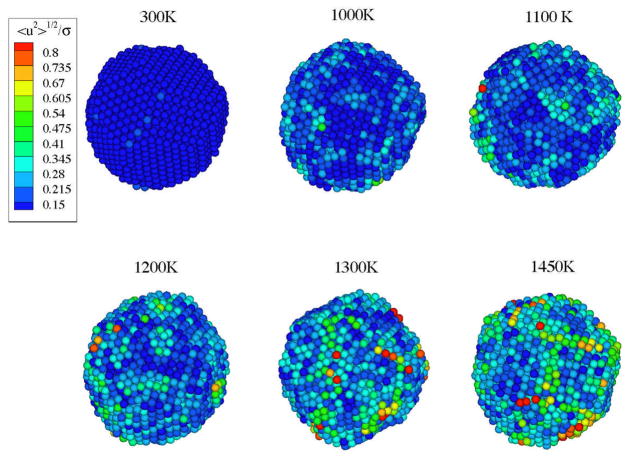
As evident from Fig. 1(a) of paper I ¹⁷, illustrating the collective string-like motions of the atoms on the surface of the NP, the strings are heterogeneously dispersed on the surface of the NPs, a feature very likely relevant to the catalytic behavior of these particles (See Discussion). To better understand the origin and nature of the string-like collective motion, it is helpful to step back from our atomic scale perspective to viewing the NPs at the scale of the particle radius. Figure 6 shows a map of the local Debye-Waller factor <u²> describing the mean particle displacement after a caging time of a ps ^{33, 110} for a range of T. At low T, the NP surface geometry reflects the well-ordered structure of the crystal lattice structure within the particle, but upon heating the atomic motion grows and the faceted patterns of the NP surface at low T give rise to island structures of local order that have a loose correlation with the crystal structure of the core of the NP. We see that the highly mobile particles and the strings arise on the ‘coastlines’ of these islands, a situation quite similar to the strings arising in the GB separating grains having different crystallographic orientations in polycrystalline materials. ^{105, 111, 112}

Figure 6.

Map of the local Debye-Waller factor <u²> for a range of T showing the heterogeneity of the mobility as T is varied. Particles of high mobility string-like motion are concentrated in filamentary grain boundary like domains that separate regions having relatively strong short range order. The interfacial ordering also bears some similarity to the two-dimensional ordering of a hexatic fluid ¹⁰⁷, as suggested before for the surfaces of metal nanoparticles¹⁰⁸ and for fluids confined to nanopores.¹⁰⁹

Figuratively speaking, the highly correlated atomic motions arise in the ‘turbulent sea’ of relatively disordered atoms surrounding the locally well-packed ‘continental’ regions of immobile atoms that continuously disintegrate into the sea as new ‘land’ rises up dynamically from the sea of chaotic motion. The whole phenomenon is somewhat reminiscent of continental drift in the earth crust where there are also singular and intermittent quake events at the edges of the continental plates (See Fig. 1 of ref. ¹¹³). The ‘ledges’, defined by the ‘continental’ interfacial regions of the NP, are thought to be important in understanding the catalytic properties of metal interfaces. ^{34, 114–120} A power-law scaling relation between the number of quake events and displacement event size is also characteristic of geological quakes.¹²¹ The interfacial dynamics of the NP is evidently governed by something akin to ‘nanotectonics’ rather than a uniformly surface melted fluid.

8. Fluctuations on the NP interfacial Versus Those Within the NP Core

Corresponding to these large fluctuations in the local interfacial mobility, there are also large fluctuations in the local potential that have great interest in relation to understanding the unique catalytic behavior of nanoparticles and crystal interfaces generally.^{115, 118, 119} In Figure 7, we show the magnitude of the local potential energy over the surface of the NP N = 2899 at T = 1000 K averaged over a timescale t^*, the diffusive decorrelation time. The local displacement fluctuations are notably less prevalent after this long-time averaging.

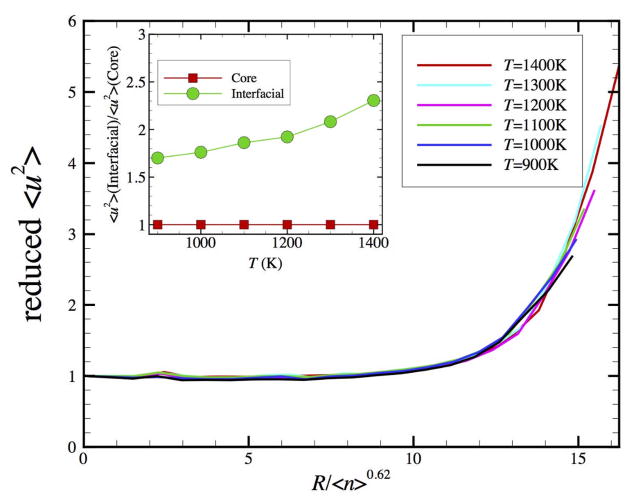
The distribution of highly mobile particles is also non-uniformly distributed within the NP, the highly collective motion and high relative mobility being highly concentrated to the outer surface of the NP at T well below the NP melting temperature, which itself is highly dependent on NP size and surface functionalization.³⁴ There is some regularity to this distribution of particle mobility as measured by <u²> which we illustrate in Fig. 8. Here we show the radially averaged value of <u²>, normalized by its value at the center of the particle, as a function of the distance from the center of the particles. Note that the magnitude of <u²> in the interfacial layer tends to be about a factor of two greater than the value of in the core of the NP. This behavior is quite in line with measurements of interfacial values compared to bulk in metal films,¹²² and similar ratios have been reported in simulations of GF liquids such as silica..¹²³ The ratio of the surface value of <u²> to its bulk value is central to recent modeling of shifts in the melting temperature of NPs^{124, 125} and this ratio seems to have a similar basic significance for understanding the finite size shifts of T_g in amorphous NPs and thin films.^{126, 127}

Figure 8.

The reduced DWF as a function of distance to the mass center of N = 2899 NP at six temperatures. The reduced DWF is scaled by the DWF values at the center of NP and the distance to the center is scaled by the average string length to the power of 0.62, a scaling characteristic of the scaling of the radius of gyration of self-avoiding walks. The inset shows the ratio of <u²>_Interfacial to <u²>_Core as a function of temperature, where the interfacial layer is defined as the region for which the reduced radial distance (R / <n>^0.62) is greater than 12.

We obtain a reduced variable description of this radial variation of <u²> by reducing the radial coordinate R by a length ξ related to the average string length determined in our accompanying paper. In particular, we find the empirical scaling ξ ~ L^0.6. The scale of the collective motion R_g in the interfacial region of the NP evidently sets the size of the crystalline NP. This finding is by no means obvious. Measurement of the thickness of these characteristic scales seems to offer another possibility for estimating the extent of collective motions in condensed materials and for understanding and controlling thermal noise arising at interfaces. It is interesting that this interfacial scale has such a direct relationship to the scale L of particle collective motion and we plan to examine if this type of relation is also found in GBs of polycrystalline materials, the interfacial dynamics of crystals and glass-forming liquids.

9. Boson Peak of Ni Nanoparticles

The so-called Boson peak is a universal¹²⁸ feature of GF materials, but a molecular understanding of this scattering feature remains an enigma. We next consider what light our perspective of emphasizing collective motion can cast on this problem. So what are a Boson peak and its physical significance?

An examination of power spectrum of the velocity autocorrelation function <v(t)v(0)> of the interfacial atoms also encodes basic information about correlations in the molecular mobility that arise in strongly interacting fluids. In particular, the cosine transform (power spectrum) of the velocity autocorrelation function VAF(t) ≡ <v(t)v(0)>/<v(0)²> determines the vibrational density of states g(ω).¹²⁹ Glass-forming liquids have as one of their distinctive hallmarks an excess density of states relative to crystals at low frequencies and the vibrational density of states g(ω), normalized by the Debye g_D(ω) for a crystal, exhibits a peak in glass-forming liquids. This universal feature of glass-forming liquids is termed the “Boson peak’ ^{22, 113, 130, 131} because its intensity scales according to Bose-Einstein statistics¹³², an appellation that certainly suggests some type of collective excitation phenomena is involved.

Despite a rather intense investigation of the Boson peak for diverse amorphous solid materials, there is still no general consensus on its molecular nature; indeed, the resolution of this problem remains one of the great problems of condensed matter physics. To determine the Boson peak, we first determine VAF(t) for our NP interfacial atoms [See Supplementary Material]. We recall that the VAF(t) is generally related to the mean particle displacement <r²> by differentiation, d² <r²> / dt²∝ VAF(t), and this quantity is well-known to exhibit a long-time power-law tail in simple fluids due to correlated molecular motions associated with momentum diffusion within the fluid, ^133–136 We see from VAF in SM (Fig. S3) that this long time tail is not apparent in our VAF(t) for the interfacial atomic dynamics of our NP. Instead, the long-time dynamics is conspicuously rather oscillatory and noisy - more suggestive of a disordered solid, or hexatically ordered fluid, than a simple liquid. Next, we calculate the cosine transform of VAF(t) of the interfacial atoms to obtain the vibrational density of states g(ω),

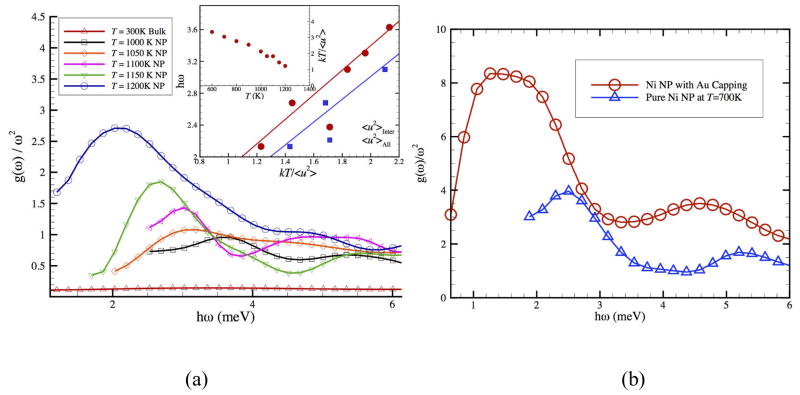
$$g(\omega )~\sum \mathit{VAF}(t)cos(2\pi \omega t)\mathrm{\Delta }t$$ (1)

and then divide by ω² to obtain the reduced density of states, g(ω) / ω². Figure 9(a) shows that the NP interfacial dynamics indeed exhibits the ubiquitous Boson peak of glassy materials.^{22, 113, 130, 131, 137} The peak in this curve defines the ‘Boson peak frequency’ ω_B and we observe that ω_B decreases upon heating. The collective motions responsible for this scattering feature, seen both in neutron and Raman scattering measurements, ‘soften’ upon approaching T_m where the stiffness of the NP (e.g., shear modulus G) of the NP becomes small. A similar trend in the magnitude of ω_B with T has been observed in simulations and measurements of bulk ‘glassy’ materials,^{138, 139} including the dynamics of organic nanoparticles such as proteins in solution.¹⁴⁰ This trend is readily understood. Measurements on bulk fluids have often indicated a tendency of ω_B to correlate with G of the material^{141, 142} so that the drop in ω_B is naturally associated with the ‘softening’ of the NP upon heating. We quantify this relation between ω_B and stiffness by showing the variation of ω_B versus the local ‘stiffness parameter’ kT /<u²>. ^{95, 143} These properties are nearly proportional and the inset also shows the T dependence of kT /<u²>, which extrapolates to zero near T_m and varies slowly at low T (In each of these cases <u²> corresponds to the interfacial atoms, but similar trends are found if we use all the atoms.).While there have been numerous Boson peak measurements on NPs,^{144, 145} there are few studies of the T dependence of the Boson peak for these materials.

Figure 9.

(a) The reduced vibrational density of states g(ω) / ω² for Ni NP having N = 369 as a function of ω at different temperatures. Inset shows the Boson peak frequency versus kT / <u²>. (b) Alloying effect (capping with an 18 % Au by relative mass) on the Boson peak frequency for Ni NP having N = 2899 and r = 2 nm using Sutton-Chen EAM potential.

The measurement of the Boson peak of NP seems to have much potential as an effective method for monitoring how impurities or functionalization alter the rigidity of the NP, the stability of the particles upon heating, their aging due to property drift arising from environmental exposure, etc. Such measurements and simulations are also interesting for what they might reveal about this universal¹²⁸ and still mysterious feature of glassy materials. For example, it would be interesting to explore what specific role string-like collective excitations in the interfacial layer of the NP contribute to the Boson peak scattering feature. We know how to tune the scale of collective in NP and GF liquids so we can readily probe this effect.

Reducing the fragility of glass formation in bulk materials normally increase the rigidity (shear or bulk modulus) of the material in the glass state ⁹⁶ and thus increase the intensity of the Boson peak feature ⁹⁵, but these same additives have also been found to reduce the strength of the T dependence of L in bulk glass forming liquids. ^{95, 97} We explore the effect of additives that tune the collective interfacial dynamics (See Fig. 2 of Paper I and associated discussion). Figure 9(b) shows the calculated Boson peak obtained from molecular dynamics simulation data for a representative Ni NP (N = 2899) at T = 700 K with a Au capping (18 % relative mass) layer (the addition of Au reduce the extent of collective atomic motion in the interfacial region of the NP). As expected, the Boson peak intensity becomes much stronger compared to the pure Ni NP without the capping layer. Understanding the magnitude of the Boson peak requires an understanding of the shift in the NP melting point with interfacial alloying.

If collective permutational atomic motion is responsible for the Boson peak in glassy systems, as has been suggested,^{100, 144} then it must be associated with the fast (ps timescale) collective string-like collective hopping events ²⁵ rather than the string motion on the diffusive timescale, t^*. Judging by the scale of the activation energy associated with these fast correlated motions (about a factor 3 times the activation energy for uncooperative surface diffusion), these events should involve just a few particles moving coherently. (Figure 3 indicates an average stringlet length of about 2) The length scale of these primitive collective excitations should be comparable to the few interparticle distances, just like the collective motions in Feynman’s roton.^146–148 Consistent with this physical interpretation of the Boson peak, Shintani and Tanaka¹⁴⁹ have found independent evidence that the Boson peak involves transverse collective vibrational motions associated with ‘soft regions’ in the disordered material and Chen et al. ¹⁵⁰, Manning and Liu¹⁵¹ and Tan et al. ¹⁵² have all identified both experimental and simulation evidence that the Boson peak largely correlates with ‘soft spots’ in the glass where correlated particle rearrangements are heavily concentrated. These interpretations of the Boson peak are broadly consistent with our suggestion that this phenomenon can be primarily associated with string-like collective atomic motions of delocalized particles on short (picoseconds) timescales, the characteristic timescale of the Boson peak in molecular fluids.

We also attribute the fast energy fluctuations to the slow beta relaxation process and we suggest that these transitions are driven impulsively by monomeric string-like particle displacements or ‘stringlets’ (Fig. 3) that are a crucial part of the sub-dynamics of the large-scale collective string motions. In turn, the large scale collective motion of the strings resulting from a superposition of many primitive stringlet displacements are responsible for diffusive relaxation events that, in turn, mediate the longer timescale alpha structural relaxation process. A whole hierarchy of relaxation processes is then involved in the relaxation of glassy materials and multiple distinct relaxation times then emerge from this process. Habasaki et al. ¹⁵³ have previously attributed the Boson peak feature to fast collective atomic motions underlying the slow-beta relaxation process.

Does increasing strength of the Boson peak by factors (particle size, shape, interfacial additives, etc.) reducing the scale of collective motion, and thus the fragility of glass formation ⁹⁵, suggests that the density of the fast ‘stringlet’ excitations is higher in stronger GF systems? We might then expect that an increase in the density of these excitations scales inversely with the string length, as in the well-known phenomenon where the average length of polymerizing chains at equilibrium (‘living polymers’) can be reduced by adding more chemical initiator to the solution of self-assembling polymers.^{154, 155} In future work, we will pursue these possibilities more thoroughly.

10. Conclusions

Structural relaxation in glass-forming liquids, and diverse other amorphous forms of condensed matter exhibit many regularities that seem to be independent of the chemical and geometrical nature of the particles involved. An understanding of these regularities has been slow to develop, although it is broadly appreciated that these materials are dynamically heterogeneous, a feature somehow related to the observed regularities in both thermodynamic and relaxation properties of amorphous materials.

In a previous paper (Part I), we explored the implications of this dynamic heterogeneity phenomena in relation to colored noise based on the simple premise that if the mobility is strongly fluctuating, the very definition of dynamic heterogeneity, then there must be noise in basic transport properties measurements such as the electrical conductivity, etc. A striking connection between the average extent of string-like collective motion and the noise exponent governing particle displacement fluctuations was observed in our previous paper on Ni nanoparticle interfacial dynamics, linking the physics of glass-forming liquids to the problem of colored noise in condensed materials at or near equilibrium. The interfacial dynamics of nanoparticles has particular interest for study since it involves a manageable compensation computational scale and the material itself has practical interest for sensor and catalysis applications. We find that the atoms undergoing string-like collective motion in the interfacial dynamics of the nanoparticles also exhibit highly nontrivial energy fluctuations between two well-separated bands of energy states. We thus have concrete route realization for two-level system intermolecular dynamics simulation this new feature in the dynamics of these glassy materials is tentatively attributed to nonlinear breather modes and we analyze energy fluctuations using standard methods used previously for the study of breathers and other physical context such as the bubble excitations in hybridized DNA. We go on to show that these excitations can have a propagating within the strings, suggesting that they are playing an active role in actually driving the atomic displacements in glassy materials such as interfacial region of NPs. Although the generality of these observations for other glassy materials has not yet been investigated, we think these observations point to a new perspective for understanding the general origin of two-level systems in glassy materials.

Apart from the fundamental interest in linking colored noise and the physics of glass-formation, the observation of well-defined two-level systems having a concrete nature should have independent technological interest. The slow-beta relaxation is also thought to be a crucial significance in relation to the plasticity of amorphous materials and the loosely defined ‘shear transformation zones’ of recent theories of plasticity in amorphous materials have been tentatively identified with this high frequency relation process. ^{85, 156–159} The two-level energy potential energy fluctuations that we observe then also provide a candidate molecular phenomenon for interpreting the abstract ‘shear transformation zones’ proposed for understanding essential aspects of the plasticity of amorphous materials. ^{85, 156–159}

So what is the potential practical significance of these collective excitations on the nanoparticle surface? We think these dynamic structures might be crucial significance in relation to catalysis. Exploration of the truly nanometric Au NPs utilized in catalysis applications by aberration-corrected transmission scanning electron microscopy¹⁶⁰ has revealed that the surface atoms of metal NPs used in catalysis can be in a highly dynamic fluctuating state, qualitatively consistent with our simulations indicating that the NP surface atoms have a much higher mobility than the NP core atoms. ³⁴ Based on observations indicating such high interfacial mobilities under thermodynamics conditions relevant to catalysis, Li et al. ¹⁶⁰ suggested that this interfacial dynamics might be extremely relevant to understanding the catalytic properties of Au NP, and by implication many other NPs, but he does not prescribe how geometry gives rise to these changes in reaction kinetics. MD simulation provides an opportunity for exploring this interfacial dynamics without the perturbations of the electron beam, the supporting substrate for the nanoparticles, and other complications that often exist in scanning microscopy measurements. There are many applications that more specifically relate to the increasing use of nanoparticles in catalysis for energy storage and production as well as materials fabrication applications and we make some specific comments on some scientific problems raised by these use of these particles and the use of catalysts more broadly that relate to our work and which will guide our future research.

The economic and social value of creating improved catalysts is extremely large, even hard to imagine. Roughly ¼ of the world’s GDP can be traced to material production by catalysis.¹¹⁴ In recent times, the need for a greater control of pollution associated with manufacturing, emission gases in the energy and automobile industries, and for developing more efficient fuel cells and economical processes for cleaning the air and ground water are pressing societal problems that require the creation of new catalytic materials.^{114, 161} Despite the practical importance of catalysts, there is a relatively limited understanding of how they actually work at a molecular scale. It has long been speculated, and recently confirmed, that the ‘ledges’ on the catalyst surface are the predominantly active areas for the catalytic activity of metal interfaces. ^{34, 114–120} These string-like ledge regions seem to correspond to the figurative shore regions that surround the immobile particle continental regions of the NPs in our discussion of the global nature of the NP interfacial dynamics. It is just in these ledge regions that we found apparent breather modes and the string-like collective motion. Energy concentration in breathers due to anharmonic interparticle interactions is increasingly being appreciated to have a large potential influence on chemical reactivity in condensed materials. ^48–54 While breathers have been generating much excitement for their potential for understanding reaction processes in condensed materials, evidence and specific models indicating specifically how these structures influence chemical reactivity are limited, although such quantitative studies are beginning to appear. ^{52, 54} Nonetheless, our observation of breather-like structures on the surface of Ni, a commonly utilized nanoparticle in catalysis applications, provides impetus for systematic studies of their effect on chemical reactivity more broadly. We find it encouraging that direct observations of catalytic activity of individual Au nanoparticles has indicated on and off ‘blinking’ between catalytically active and inactive reactivity states, ^{74, 75} an effect that has been attributed to an ill-defined dynamic restructuring of the nanoparticle surface. This is just the type of phenomena that one might expect to be associated with breathers in the interfacial region of nanoparticles.

Changing the nanoparticle shape has also been shown to significantly influence nanoparticle reactivity in fuel cell type reactions¹⁶² and nanoparticle size can affect molecular binding affinities.¹⁶³ We have previously shown that the fragility of the interfacial glassy dynamics of our Ni nanoparticles increases as they are made smaller, reflecting the increasing interfacial curvature of the nanoparticle surface. This is a natural trend as greater curvature should enhance packing frustration, thus increasing the scale of collective motion³⁴ and, presumably, the density of breather excitations and resulting chemical reactivity. These existing observations of NP shape effects on the reactivity of nanoparticle catalysts suggest that we should systematically study the influence of particle size, shape and surface composition on interfacial collective motion of our Ni nanoparticles and shape effects on the breather modes wit catalytic effects directly in mind.

Another basic scientific, as well as technical, catalysis problem relates to controlling the stability of NP catalysts at elevated temperatures. Promising new nanoparticle catalysts, such as Au nanoparticles dispersed on ceramic substrate supports,¹⁶⁴ have a propensity to ‘degrade’ by coalescence where the particles lose their activity when they become sufficiently large. The same large interfacial molecular motions that underlies their attractive catalytic behavior can unfortunately also lead to their instability.¹⁶⁵ Direct observation of the coalescence process of metal nanoparticles by high resolution electron microscopy has revealed that the ‘liquid-like’ properties of the surface layers of the nanoparticles play an essential role in this process”. ¹⁶⁶ The high interfacial mobility in nanoparticles and grain boundaries of semi-crystalline ice also has profound geophysical consequences so that this is a problem of widespread scientific and technical significance.¹⁶⁷ To address this nanoparticle stability problem, we plan to build on recent simulations of nanoparticle sintering^{168, 169} where we will simply examine to the role of collective motion and colored noise in displacement fluctuations on the sintering process. We expect that tuning the breather density on the NP surface through judiciously chosen additives or altering the substrate on which the nanoparticles are placed ¹⁷⁰ will provide a useful strategy for stabilizing nanoparticles in numerous applications. Boson peak measurements, and other experimental tools probing the high frequency fluid dynamics, should provide an experimental means of monitoring nanoparticle catalyst stability and activity.