Optical signature of symmetry variations and spin-valley coupling in atomically thin tungsten dichalcogenides

Abstract

We report systematic optical studies of WS₂ and WSe₂ monolayers and multilayers. The efficiency of second harmonic generation shows a dramatic even-odd oscillation with the number of layers, consistent with the presence (absence) of inversion symmetry in even-layer (odd-layer). Photoluminescence (PL) measurements show the crossover from an indirect band gap semiconductor at multilayers to a direct-gap one at monolayers. A hot luminescence peak (B) is observed at ~0.4 eV above the prominent band edge peak (A) in all samples. The magnitude of A-B splitting is independent of the number of layers and coincides with the spin-valley coupling strength in monolayers. Ab initio calculations show that this thickness independent splitting pattern is a direct consequence of the giant spin-valley coupling which fully suppresses interlayer hopping at valence band edge near K points because of the sign change of the spin-valley coupling from layer to layer in the 2H stacking order.

Motivated by the triumph and limitation of graphene for electronic applications¹, atomically thin layers of group VI transition metal dichalcogenides are attracting extensive interest as a class of graphene-like semiconductors with a desirable band-gap in the visible frequency range²,³,⁴,⁵,⁶,⁷,⁸. This family of dichalcogenides MX₂ (M = Mo,W; X = S,Se) has a structure of X-M-X covalently bonded hexagonal quasi-2D network stacked by weak Van der Waals forces. MX₂ thin films exhibit 2H stacking order: the neighboring layers are 180 degree in plane rotation of each other with the metal atom of a given layer sitting exactly on top of the chalcogenide atom of the adjacent layer. There is an even-odd variation in the structural symmetry of ultrathin films: inversion symmetry is absent (present) in films with odd (even) number of layers with space group of D¹_3h (D⁴_6h). Ab initio calculations predict that MX₂ exhibits a transition from an indirect-gapped semiconductor in multilayer form to a direct band-gap one at visible range in monolayer, which has been experimentally verified in MoS₂⁷,⁸.

MX₂ monolayer, the elementary unit to form ultrathin films by weak stacking, features a novel spin-valley coupled band structure⁹. At the corners of the 1st Brillouin zone, the valence (conduction) band has two inequivalent valleys described by massive Dirac fermions. Owing to the broken inversion symmetry in monolayers, the strong spin-orbit coupling from the d-orbitals of metal atom results in a valence band spin splitting at K points, with a magnitude as large as ~0.4 eV in tungsten dichalcogenides⁹,¹⁰. The spin-splitting has opposite signs at the K and K′ valleys as they are time reversal of each other. This spin-valley coupling forms the basis for manipulation of spin and valley degrees of freedom in these novel 2D semiconductors when combined with valley contrasted electric, magnetic and optical properties arising from inversion symmetry breaking⁹,¹¹,¹²,¹³,¹⁴,¹⁵,¹⁶.

Here we report our experimental study on optical properties of ultrathin WS₂ and WSe₂ mono-, bi-, tri- and quad-layer samples by means of Raman scattering, second harmonic generation (SHG) and photoluminescence (PL). The efficiency of SHG at normal incidence on WS₂ and WSe₂ ultrathin films shows a dramatic even-odd oscillation with the number of layers: negligible at even-layer and nonzero at odd-layer, with maximum strength at monolayers. PL measurements demonstrate that WS₂ and WSe₂ exhibit a transition from an indirect-gap semiconductor at multi-layers to a direct-gap one at monolayers with an enhancement of the PL quantum efficiency (QE) at a factor of more than 10³ compared to bulk samples. Remarkably, a weak emission peak (B) is observed at an energy ~0.4 eV higher than the prominent direct bandgap transition peak (A) in all monolayer and multilayer samples. Unlike the case in MoS₂ (B exicton absent in MoS₂ monolayer PL though)⁷, the magnitude of A-B splitting in both WS₂ and WSe₂ is independent of the number of layers and coincides with the spin-valley coupling strength in monolayers. Ab initio calculations show that this thickness independent splitting pattern is a direct consequence of the giant spin-valley coupling which fully suppresses interlayer hopping at valence band edge at K points because of the sign change of the spin-valley coupling from layer to layer in the 2H stacking order.

Results

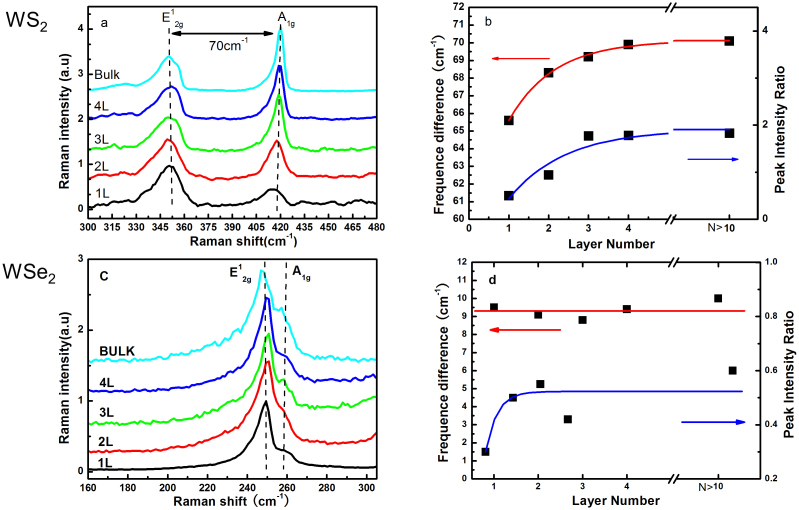
For MX₂ layered compounds, there are generally four Raman-active modes, namely A_1g, E_1g, E¹_2g and E²_2g modes¹⁷,¹⁸. E_1g mode and low energy E²_2g mode are absent in our measurements due to the forbidden selection rule in the back-scattering geometry and the limited rejection against Rayleigh scattering respectively. The presented study focuses on the in-plane vibrational E¹_2g mode and the out-of-plane vibrational A_1g mode. As these two modes are both polarization sensitive, the exciting laser line was tuned to an unpolarized state. Figure 2.a–d present the representative Raman spectra of WS₂ and WSe₂ slabs with layer number N = 1 to 4 and bulk. In the case of WS₂, we observe the E¹_2g mode at ~350 cm⁻¹ and the A_1g mode at ~420 cm⁻¹ (Fig. 2.a)¹⁹. The E¹_2g mode shows little dependence on the film thickness, while the A_1g mode undergoes a blue shift with increasing layer number, showing a lattice stiffening effect as expected when additional layers are added. By examining the frequency differences (Δω) between the E¹_2g mode and A_1g mode, the sample thickness could be identified accordingly. As indicated in Fig. 2.b showing the frequency difference as a function of layer number N, we label Δω = 65.5 cm⁻¹, 68.3 cm⁻¹ and 69.2 cm⁻¹ to monolayer, bilayer and trilayer respectively. For slabs composed of four and more layers, Δω converges to the bulk value at around 70 cm⁻¹. Notably, from monolayer to trilayer the A_1g peak is roughly 0.5, 1 and 1.8 times the height of the E¹_2g peak (Fig. 2.b), demonstrating that the ratio of the intensity of A_1g mode to that of E¹_2g mode could also be used as an indicator of sample thickness. For WSe₂, two dominant peaks are observed around 250 cm⁻¹ in various samples from monolayer to bulk (Fig. 2.c). However, little systematic trend could be observed on both the two modes as shown in Fig. 2.d.

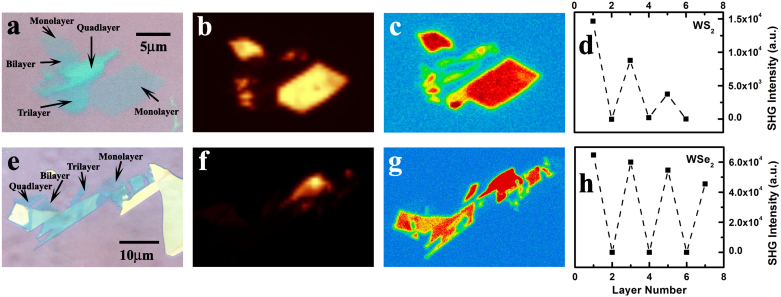
Figure 1.

(a) and (e): optical images of WS₂ (a) and WSe₂ (e) slabs on Si substrates with 300 nm SiO₂ cap-layer; (b) and (f): photoluminescence images at direct gap transition energy of the corresponding WS₂ (b) and WSe₂ (f) slabs excited at 2.41 eV. Only monolayers are visible at the present contrast; (c) and (g): the corresponding SHG under a 800 nm excitation at normal incidence (150 fs, 80 MHZ) on WS₂ (c) and WSe₂ (g) respectively. The highest intensity labeled in red arises from monolayers. The SHG signal from the silicon/silicon oxide surface is negligible compared with those from multilayers; (d) and (h): The relative intensity of SHG as a function of the film thickness in WS₂ (d) and WSe₂ (h). The SHG shows an even-odd oscillation dependence on the layer number.

Figure 2.

(a) and (c): Raman spectra of WS₂ (a) and WSe₂ (c) ultrathin layers; (b) and (d): The frequency difference (red) and the peak intensity ratio (blue) between E¹_2g and A_1g modes as a function of film thickness in WS₂ (b) and WSe₂ (d) respectively.

An experimental method to examine the inversion symmetry in ultrathin film is to study the nonlinear optical effect such as SHG determined by the second order susceptibility χ^{(2) 20}. In the presence of inversion symmetry, χ⁽²⁾ is zero. A dramatic even-odd oscillation pattern is indeed observed on the SHG intensity consistent with the presence (absence) of inversion symmetry in even-layer (odd-layer) as shown in Fig. 1.c and 1.g. WS₂ and WSe₂ ultrathin slabs are scanned by a 150 fs pulsed laser beam with a wavelength of 800 nm at normal incidence and the signal at the double frequency (400 nm) is collected. As expected, in both WS₂ and WSe₂ slabs with even layer number or bulk samples, negligible SHG are observed as same in the case of the bare substrate (SiO₂ on Si), and strong second harmonic emission arises from multilayer slabs with odd layer number. Notably, the brightest second harmonic emission is observed in monolayers of both WS₂ and WSe₂. The intensity of the second harmonic emission decays gradually with the increasing layer number, as indicated in Fig. 1.d and 1.h.

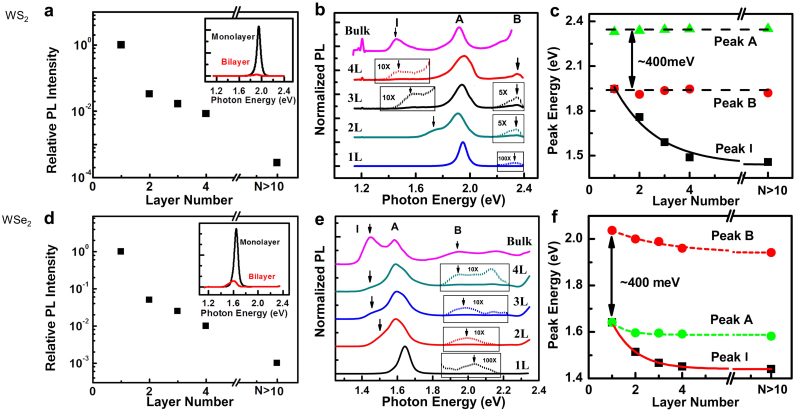
The Photoluminescence study shows that WS₂ and WSe₂ exhibit a transition from indirect band-gap semiconductor in the form of bulk and multilayers to direct band-gap one in monolayers, similar to MoS₂⁷,⁸,²¹,²². Figure 3 illustrates the PL spectra of WS₂ and WSe₂ samples with various thicknesses measured under the same condition with an excitation at 2.41 eV. Fig. 3.a and 3.d show the PL peak intensity as a function of thickness. The PL intensity is found to be extremely weak on bulk samples, consistent with an indirect band-gap semiconductor in bulk form. As WS₂ and WSe₂ thin to a few atomic layers, the intensity of PL from direct interband transition dramatically increases and reaches maximum at monolayers, more than 3 orders of magnitude stronger than that from bulk. Both WS₂ and WSe₂ monolayers show much brighter PL with intensity at one order of magnitude higher than bilayers. The peak originating from the indirect band-gap transition (labeled as “I” in Fig. 3.b and 3.e) gradually shifts toward higher energy and fades to null at monolayers. These behaviors are fully consistent with the calculated band structures (see Fig. 4 and supplementary information).

Figure 3.

(a) and (d): The relative PL intensity of WS₂ (a) and WSe₂ (d) multilayers respectively as a function of film thickness under the same conditions (normalized by the PL intensity of monolayer at 1). Insets present PL spectra from WS₂ (a) and WSe₂ (d) monolayers and bilayers respectively. The spectra were taken at the same conditions (excitation power, exposure time, etc.); (b) and (e): The normalized PL spectra (with respect to the peak A) of WS₂ (b) and WSe₂ (e) ultrathin films. I labels the luminescence from indirect gap interband transition, A and B label the direct-gap transitions from the split valence band edge to the conduction band edge at K points (see text). Spectra (dash line) in the zoom windows have been multiplied by a factor as indicated for clarity; (c) and (f): The peak positions of I, A and B transitions as a function of the film thickness in WS₂ (c) and WSe₂ (f). Both cases show a nearly constant energy difference of ~0.4 eV which corresponds to the splitting of the valence band edge. The universal A-B splitting implies a suppression of interlayer hopping in tungsten dichalcogenides ultrathin thin films.

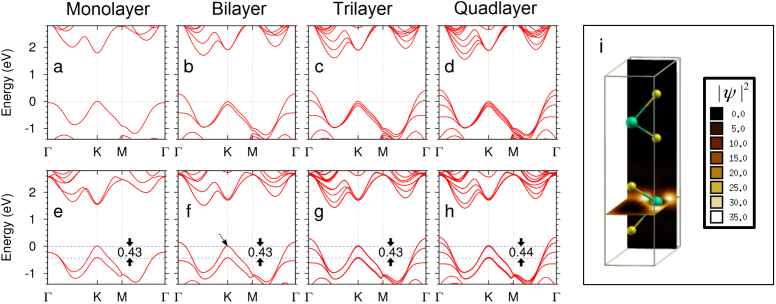
Figure 4. Ab initio calculated band structures for WS₂ ultrathin films.

(a–d): without spin-orbit coupling; (e–h): with spin-orbit coupling. The valence band splittings at K point are nearly constants, around 0.43 eV for mono-,bi-, tri, and quad-layers; (i) Electron density map for one valence band Bloch state at K point in WS₂ bilayer (indicated by the dashed arrow in (f)). The wavefunction is fully spin polarized in the down state and almost fully localized in the bottom layer. The other degenerate state at the same K point can be obtained by a spatial inversion plus a time reversal operation.

Besides the peaks from indirect transition and the prominent direct transition peak (A), weak PL peak (B) is observed at higher energy in WS₂ and WSe₂ at all thickness. Note that the similar peak B appearing in MoS₂ multilayers is absent in monolayers⁷. The linewidth of peak A and B implies their excitonic origin as the case in MoS₂⁷,²³. Strikingly, the splitting between A and B peaks are almost identical, around 0.4 eV for mono-, bi-, tri- and quad-layer samples (see Fig 3.c and 3.f). In monolayers, it is now well understood that the valence band edges at K points have a spin splitting purely arising from the strong spin-orbit coupling in the d-orbitals of the W atom, and we can attribute A and B to the direct-gap transitions between the spin split valence bands and the conduction band at the K points⁷. However, in multilayers, both the spin-orbit coupling and the interlayer hopping contribute to the valence band splitting at K points. Besides, even layer samples are inversion symmetric while odd layer samples are asymmetric. These in general would result in complex and layer-number dependent splitting patterns in multilayers, which is obviously different from the universal A-B splitting in the PL spectra observed. It implies a novel cause in tungsten dichalcogenides ultrathin thin films.

Discussion

To understand the A-B splitting pattern in WS₂ and WSe₂ ultrathin films, we perform ab initio calculations of the band structures using the projector augmented wave method²⁴ and generalized gradient approximation²⁵ implemented in the ABINIT code²⁶,²⁷. The structure parameters are taken from Ref. 10. Figure 4.a–d show the band structures of mono-, bi-, tri-, and quad-layer WS₂ in the absence of SOC. As expected, the valence band edge at K point splits into two, three, and four bands respectively for bi-, tri-, and quad-layer WS₂ due to the interlayer hopping. A hopping matrix element t ~0.1 eV can be extracted from the splitting pattern. However, when spin-orbit coupling (SOC) is included, the splitting pattern is completely changed as shown in Fig. 4.e–h. The valence band edges split into two degenerate manifolds with a splitting magnitude independent of the film thickness for both WS₂ and WSe₂. The band structures of WSe₂ ultrathin films could be found in supplementary information. This is in perfect agreement with the A-B splitting patterns observed in the photoluminescence of mono-, bi-, tri-, and quad-layer WS₂ and WSe₂. The calculated valence band edge splittings of 0.43 eV in WS₂ and 0.47 eV in WSe₂ also agree with the measured A-B splitting of 0.4 eV as shown in Fig. 3 and the supplementary information.

In fact, the unexpected splitting patterns in multilayer WS₂ and WSe₂ are manifestations of the giant spin-valley coupling in valence band⁹. In monolayers, the Kramer's doublet and 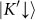are separated from the other doublet 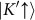and 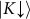by the spin-valley coupling energy of λ_svc ~ 0.4 eV⁹. In the 2H stacked multilayers, any two neighboring layers are 180 degree in plane rotation of each other. This rotation switches K and K′ valleys but leaves the spin unchanged, which results in a sign change for the spin-valley coupling from layer to layer. Thus, the spin-conserving interlayer hopping can only couple states in neighboring layers with a detuning λ_svc. Interlayer hopping is therefore strongly suppressed by the giant spin-valley coupling. A direct consequence is that the splitting patterns remain the same as that of monolayers, and the valence band Bloch states near K points are largely localized in individual layers, as if the interlayer hopping is absent. This is indeed confirmed by ab initio calculations of electron density distributions of these Bloch states (see Fig. 4.i and table S2 in supplementary information). The full suppression of interlayer hopping at K points by the spin-valley coupling is unique to tungsten dichalcogenides where λ_svc ≫ t. For molybdenum dichalcogenides where λ_svc ~ t, interlayer hopping will manifest in both the splitting pattern and Bloch function²⁸.

The above picture also explains why the hot luminescence peak B can be observable from monolayers to multilayers at an energy much higher than the prominent direct bandgap transition peak A. In monolayers, near K points, the spin-valley coupling gives rise to two non-degenerate valence bands with opposite spin separated by an energy of λ_svc ~ 0.4 eV. The relaxation of hot carriers between the spin-split valence bands requires a spin flip and is much slower than intra-band relaxation. Hot carriers can thus have a finite lifetime at the higher energy band edge, giving rise to hot luminescence, i.e. the direct bandgap transition peak B⁸. In multilayers, we have the same picture for hot carrier relaxation and hot luminescence at the valence band edges near K points where interlayer hopping is fully suppressed by the spin-valley coupling. The giant spin-valley coupling offers a new strategy to manipulate electron spin and makes tungsten dichalcogenides ultrathin films promising materials for semiconductor based spintronics and conceptual valley-based electronics.

Methods

WS₂ and WSe₂ flakes were mechanically exfoliated from synthesized single crystal bulk samples onto silicon wafers capped with a 300 nm thick SiO₂ by a method analogous to the way of producing graphene¹. WS₂ and WSe₂ slabs were first visually screened with interference color through optical microscope. Typical optical images of WS₂ and WSe₂ ultrathin slabs are presented in Fig. 1.a and 1.e. The film thickness is confirmed by atomic force microscope. PL spectra are also used as an indicator of monolayer samples (Fig. 1.b and 1.f). Raman scattering was carried out with a confocal setup.

Author Contributions

X.C. and H.Z. designed the experiments. X.Chen. and Y.Y. fabricated the single crystal WS₂ and WSe₂, H.Z., J.D., B.Z., R.H. and L.X. performed the experiments. W.Y. and G.L. contributed to the theoretical interpretations and ab initio calculations. All authors discussed the results and co-wrote the paper.

Supplementary Material

Supplementary Information

Supplementary Information