Joint Modeling Quality of Life and Survival Using a Terminal Decline Model in Palliative Care Studies

Abstract

Palliative medicine is a relatively new specialty that focuses on preventing and relieving the suffering of patients facing life-threatening illness. For cancer patients, clinical trials have been carried out to compare concurrent palliative care with usual cancer care in terms of longitudinal measurements of quality of life (QOL) until death, and overall survival is usually treated as a secondary endpoint. It is known that QOL of patients with advanced cancer decreases as death approaches; however in previous clinical trials this association has generally not been taken into account when inferences about the effect of an intervention on QOL or survival have been made. We developed a new joint modeling approach, a terminal decline model, to study the trajectory of repeated measurements and survival in a recently completed palliative care study. This approach takes the association of survival and QOL into account by modeling QOL retrospectively from death. For those patients whose death times are censored, marginal likelihood is used to incorporate them into the analysis. Our approach has two submodels: a piecewise linear random intercept model with serial correlation and measurement error for the retrospective trajectory of QOL; and a piecewise exponential model for the survival distribution. Maximum likelihood estimators of the parameters are obtained by maximizing the closed-form expression of log-likelihood function. An explicit expression of quality-adjusted life years can also be derived from our approach. A detailed data analysis of our previously reported palliative care randomized clinical trial is presented.

1. Introduction

Palliative medicine is a relatively new specialty that focuses on preventing and relieving the suffering of patients facing life-threatening illness [1]. Palliative care involves a coordinated team approach that includes physicians, nurses, social workers, pastoral care providers, and volunteers[2]. As a new specialty, a critical mass of researchers and a growing evidence-base is evolving. However, there is general agreement about the need for improved research methods, study designs and data analysis techniques that can be applied to this population [3].

Because of the advanced disease states of patients receiving palliative care, research on improved outcomes has focused on quality of life rather than extension of life as is common in traditional treatment studies. However two recent randomized clinical trials (RCTs) [4, 5] comparing palliative care with usual oncology care showed both improved quality of life (QOL)and prolonged survival (a secondary endpoint) in patients receiving concurrent palliative care compared with patients receiving usual cancer care in the months preceding death. Patients in the palliative care arm had longer median survivals of 14 months vs. 8.5 months [4] and 11.6 months vs. 8.9 months [5]. Therefore, measures such as quality adjusted life years are also of interest. In these and other palliative studies, QOL and survival time are typically analyzed separately, with the expectation being that survival times will not differ. While it is known that QOL of patients with advanced cancer decreases as death approaches, this association is generally not taken into account when inferences of the effect of an intervention on QOL or survival times are made. For the purpose of this paper we will examine the unique issues raised by palliative care studies in which quality of life is the primary outcome rather than survival and we will propose a novel joint modeling approach that considers both quality of life and survival outcomes.

A number of models have been proposed for jointly modeling the longitudinal outcome processes and event times where there are trajectories of longitudinal (repeated measurements) data truncated by death. Reviews of these approaches can be found in [6–8]. One approach has been to form mixture models[9–12], where the joint distribution of repeated measurements Y and event time D, f(Y,D) , is factored into f(Y|D)f(D) and f(Y|D) and f(D) are modeled with two submodels. Usually f(Y|D) is modeled by a multivariate normal distribution conditional on the death time and hence the marginal distribution of Y is a mixture of normal distributions over the survival distribution. In these approaches, the trajectories of longitudinal outcomes are assumed to have different patterns given different death or dropout times. Another model is called selection model [13, 14], where the joint distribution is factored into f(D|Y)f(Y) , and f(D|Y) and f(Y) are modeled with two submodels (e.g., Cox model and linear mixed model respectively). The primary response of interest in a selection model is survival. A third type of model uses two submodels for f(Y) and f(D) and models the dependence between Y and D with shared or correlated random effects [15–18]. A fourth approach called "partly conditional" approach [19] models the longitudinal outcomes conditional on the subjects being alive using weighted GEE. This approach does not have to explicitly model the survival data.

In an approach related to the mixture model, Kurland et al. [8] described a terminal decline model where the time scale counts backward from death for patients whose death times are observed. In this paper, we extend the terminal decline model to include a submodel for the survival times including those subjects whose death times are censored in the study.

Each of the approaches to joint modeling implies a different emphasis on the targets of inference. With low life expectancies for palliative care patients, the primary goal may be maintaining a high QOL for as long as possible, suggesting that the mean QOL in a period shortly before death could be the key estimand. We believe this makes terminal decline models of particular interest for this application, where comparisons between quality of life in the two intervention groups close to death are of primary interest.

In our terminal decline approach for cancer palliative care studies, two submodels (piecewise linear random intercept model with serial correlation and measurement error and piecewise exponential model respectively) are used for the repeated measurements and the survival times. The time scale in the submodel for the repeatedly measured QOL data counts backward from the death time. A primary target of inference of our model is to address questions such as "What is the expected QOL3 months before death?". However manipulation of the estimated joint distribution for f(Y,D) can also permit quality adjusted life expectancy and partly conditional interpretations of the data.

The paper is structured as follows. Notation and model are introduced in Section 2. Connections to other joint models are given in Section 3. Inference procedures are provided in Section 4. Application of the model to ENABLE II study is described in Section 5. Estimation of quality-adjusted survival is addressed in Section 6. A simulation study is provided in Section 7, with a discussion in Section 8.

2. Notation and model

Suppose there are N cancer patients in the study. Let Y_i(t) denote the outcome measured at time t counting backward from the time of death for the i th patient, i = 1, …, N . Under a piecewise linear random intercept model with serial correlation and measurement error for the longitudinal measurements ([20]), we assume

$$Y_i(t)=X_i^T(t)\beta +b_i+{\epsilon }_i(t)+W_i(t),$$ (1)

where t is the time counting backward from the death time; $X_i^T(t)$ is the covariate vector at time t including terms that are piecewise linear functions of t (the superscript T denotes transpose of a vector or matrix); β is the p-vector of fixed effect including parameters for different pieces and intercept; b_i is the subject-specific random effect following N(0,σ²); and µ_i(t) are independent stationary Gaussian processes with E{ε_i(t)} = 0 and cov{ε_i (t),ε_i(s)} = τ²1(t = s), where 1(t = s) is an indicator function.

The terms W_i(t), i = 1, …, N, are independent stationary Gaussian processes with E {W_i (t)}=0 and cov{W_i (t), W_i (s)} = ν² ρ(|t − s|), where ρ(.) is a decreasing function with ρ(0)= 1. A choice of the function can be taken as ρ(u) = exp (− αu^c) with a pre-specified c (e.g., exponential correlation with c = 1 or Gaussian correlation with c = 2). This process results in a correlation between serial measurements as a decreasing function of the time separation between these measurements. The random intercept b_i, ε_i (t) and W_i(t) are independent.

Let D_i denote the death time of the ith subject calculated as the duration from the date of enrollment (time origin in calendar time) to the date of death. It may be right censored by another event time denoted by C_i (e.g., withdrawal or study end). We assume that the censoring is noninformative or administrative, which is reasonable in a palliative care study where censoring primarily occurs when those patients who are still alive are censored by the termination of the study. The death time D_i is also assumed to be independent of b_i and the two Gaussian processes in model (1). We model the death time with a piecewise exponential distribution, using p(θ, D_i) to denote the density of the distribution of the death time D_i, where θ is a vector of parameters and the density could depend on variables of interest (e.g., treatment) which have been suppressed in the notation for simplicity.

3. Connection to previous joint models

To see the relationship between our terminal decline model and a mixture model, consider a mixture model with D_i modeled by a piecewise exponential survival and y_i (t*)|D_i modeled by

$$Y_i(t^{*})|D_i=X_i^T(D_i-t^{*})\beta +b_i+{\epsilon }_i(D_i-t^{*})+W_i(D_i-t^{*}),$$ (2)

where t* is the time of measurement counting forward from the enrollment time, and ε_i (D_i − t*) and W_i(D_i − t*) as functions of t* having the same properties as ε_i and W_i in model (1). Notice that Y_i (t*) is the measurement at time t = D_i − t* counting backward from the death. Thus model (2) becomes the terminal decline model (1) after substituting t for D_i − t*. The connection to a selection model is through a mixture model ashas been discussed in [6].

Interpretation as a partly conditional model is also straightforward by analytically or numerically calculating

$$f\{Y_i(t^{*})|D_i>t^{*}\}=\frac{{\displaystyle {\int }_{t^{*}}^{\infty }f\{Y_i(t^{*})|D_i\}f(D_i)d{D}_i}}{P(D_i>t^{*})}$$

In our development, f{Y_i(t*)|D_i} is as modeled in (2) and f(D_i) is modeled by a piecewise exponential density.

In summary, our terminal decline model can be also used to indirectly estimate all the estimands of interest in joint models. Analytical conversions between them are possible through derivations based on the estimate of f(Y,D).

4. Estimation of model parameters

The breakpoints in the two piecewise linear submodels are assumed to be specified before estimating the parameters β, σ², τ², ν², α and θ. For the submodel (1) in our example, a breakpoint is chosen at 6 months before death (t = 6). Motivation for this breakpoint is based on hospice enrollment criteria [21] and a systematic review of cancer presentations [22] that indicate faster decrease of QOL once a patient enters the last 6 months of his life. Breakpoints for the piecewise survival were determined by plotting the nonparametric estimate of cumulative hazard function. An obvious change in slope of the cumulative hazard function suggests the placement of the breakpoint.

With the determined breakpoints, the complete log-likelihood function can be expressed as a closed form expression involving the standard normal distribution function and can be maximized to obtain the maximum likelihood estimators (MLE) of the parameters β, σ², τ², ν², α and θ. Let Y_ij denote the outcome measured at t_ij for the ith subject, i = 1, …, N;j = 1, …, n_i. Keep in mind that the time scale counts backward, which implies that y_i1 is the first measurement counting backward from the death time. The number and times of repeated measurements are not necessarily the same for all the subjects. The outcome vector Y_i = (Y_i1, …, Y_ini)^T has a multivariate normal distribution N(μ_i, V_i) with μ_i =X_iβ and V_i = τ²I + σ²J + ν² R(t_i), where X_i is the design matrix with the jth row X_i(t_ij), I is the n_i by n_i identity matrix, J is the n_i by n_i matrix of one’s and R(t_i) is the n_i by n_i symmetric matrix with (j,l)th element ρ(|t_ij − t_il|), j,l = 1, …, n_i. Define ϕ = (τ², σ², ν²)^T. To calculate the complete likelihood function, we divide the patients into four groups.

The first group consists of the patients who died in the study and had at least one measurement of QOL (suppose they are the first r₁ patients), their log-likelihood contribution is given by $l_1=-0.5{\displaystyle {\sum }_{i=1}^{r_1}\{n_i\text{ln}(2\pi )+\text{ln}|V_i(\varphi )|+{(Y_i-X_i\beta )}^T{V}_i{(\varphi )}^{-1}(Y_i-X_i\beta )\}+{\displaystyle {\sum }_{i=1}^{r_1}\text{ln}(p(\theta ,D_i))}}$.

The second group consists of those patients who died in the study but had no measurements of QOL. Supposing they are the first r₂ patients after the first group, their log-likelihood contribution is given by the marginal likelihood of the survival $l_2={\displaystyle {\sum }_{i=r_1+1}^{r_1+r_2}\text{ln}\left(p(\theta ,D_i)\right)}$.

The third group consists of those patients whose death times are censored and have at least one measurement of QOL (suppose they are the first r₃ patients after the second group), writing the outcome vector of QOL as $Y_i^{*}={(Y_i(D_i-t_{i1}^{*}),\dots ,Y_i(D_i-t_{i{n}_i}^{*}))}^T$, where $t_{ij}^{*}$ is the time of the jth measurement for the ith patient counting from enrollment, their log-likelihood contribution is $l_3={\sum }_{i=r_1+r_2+1}^{r_1+r_2+r_3}\text{ln}({\int }_{C_i}^{\infty }f(Y_i^{*}|D_i)f(D_i)d{D}_i)$, where $f(Y_i^{*}|D_i)$ is the conditional multivariate normal density function given death time.

The fourth group consists of those patients whose death times are censored and have no measurements of QOL (suppose they are the last r₄ patients), their log-likelihood contribution is given by the marginal likelihood of the survival $l_4={\displaystyle {\sum }_{i=N-r_4+1}^N\text{ln}\left(1-F(C_i)\right)}$, where F(.)is the marginal CDF of the piecewise survival distribution.

If there are no censored death times, MLE's of β, σ², τ², ν², α and θ can be obtained by simply maximizing l₁ + l₂. Furthermore,the log-likelihood functions for submodel (1) and the submodel of survival are independent of each other. They can be maximized separately to generate MLE’s of the parameters. For studies with censored data, the complete log-likelihood l = l₁ + l₂ + l₃ + l₄ needs to be maximized. It is straightforward to calculate l₁, l₂ and l₄. Closed form expression of l₃ involving the standard normal distribution function can be derived under the piecewise mean structure model and piecewise hazard survival model (see Appendix). Variances for the parameter estimates are obtained from the Fisher information matrix.

5. Application

The ENABLE II [4] RCT conducted by our group compared advanced cancer patient QOL, symptom intensity, and depression outcomes in a nurse-led, phone-based palliative care intervention to patients who received usual cancer care. Usual cancer care included all cancer and supportive care treatments that are typically available at a comprehensive cancer center. Greater detail regarding these treatment conditions has been previously described[4, 23].Between November 2003 and May 2007,322 patients were enrolled in with 161 randomly assigned to treatment (palliative care) group and the other 161 to control (usual care) group. Patient-reported outcomes were measured by paper and pencil questionnaires completed upon enrollment (baseline), 1 month and then every three months until the participant died or the study was completed (May 2008). All follow up data was also collected by mailed questionnaires. QOL was measured by the Functional Assessment of Chronic Illness Therapy for Palliative Care (FACIT-PAL). Scores on this scale range from 0 to 184, and higher scores indicating better QOL. Two hundred and thirty one participants died prior the end of the study.

We fit the piecewise linear mixed model (1) for the trajectories of QOL and a piecewise exponential distribution for the survival times. As mentioned earlier, the breakpoint for the linear mixed model is set at t = 6 since the rate of decrease of QOL is expected to be faster once a patient enters the last 6 months of life [21, 22]. We did not include any baseline characteristics in the model since patients had been randomized and the distributions were not significantly different between the two treatment groups. The submodel for the repeated measurements can be written as

$$Y_i(t)={\beta }_0+{\beta }_1{A}_i+6({\beta }_2+{\beta }_4{A}_i-{\beta }_3-{\beta }_5{A}_i)1\{t>6\}+({\beta }_2+{\beta }_4{A}_i)t1\{t\le 6\}+({\beta }_3+{\beta }_5{A}_i)t1(t>6)+b_i+{\epsilon }_i(t)+W_i(t)$$ (3)

where A_i is the treatment indicator taking values of 0 and 1 indicating control and treatment respectively. The parameter β₁ is the treatment effect at (t = 0) (death). This parameter can be interpreted as the treatment effect right before the patient dies. The parameters β₂ and ;₃ are, respectively, the slopes of the trajectory before and after 6 months in control group. Parameters β₄ and β₅ denote the effects of the treatment on the two slopes.

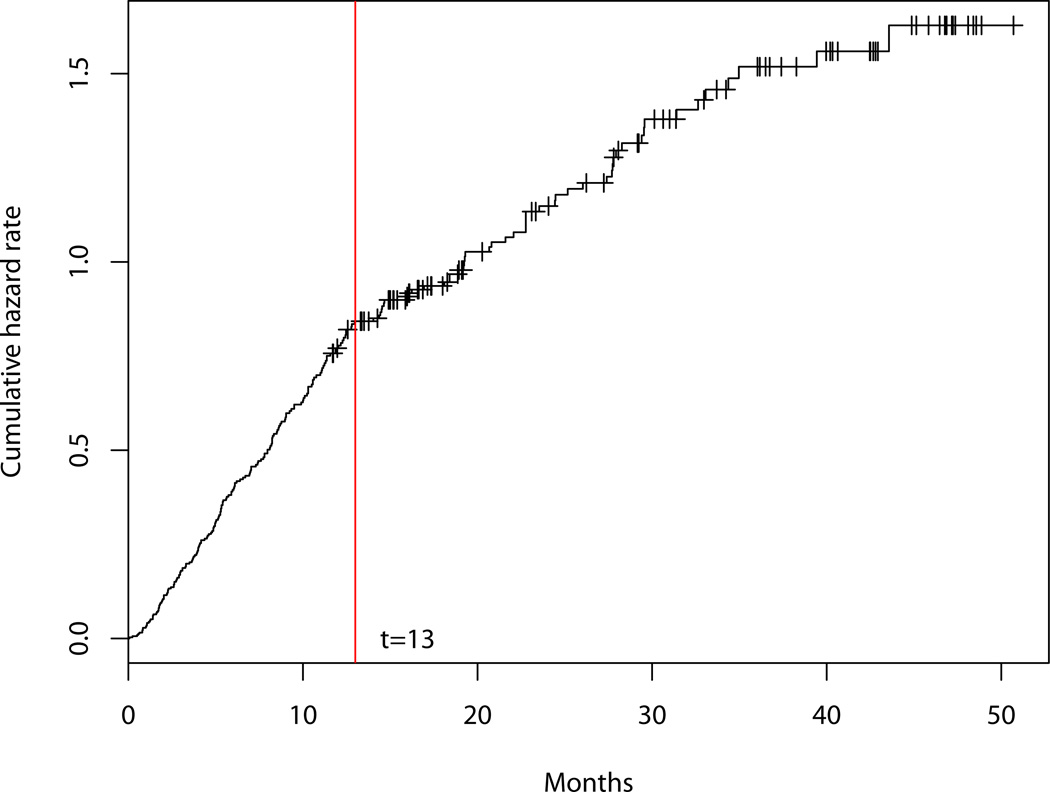
A piecewise exponential distribution is used to model the death times. As mentioned earlier in Section 2, death time is defined as the duration from the date of enrollment (time origin in calendar time) to the date of death. We assume a two-piece exponential distribution with the change point at 13 month since enrollment after examination of the plot of the cumulative hazard rate versus time as shown in Figure 1.

Figure 1.

Cumulative hazard rate

The probability density function of the death times can be written as

$$p(\theta ,D)=\left\{\begin{array}{c}{\theta }_1\text{exp}(-{\theta }_{1}D),D\le 13,A_i=1\\ {\theta }_2\text{exp}\{-{\theta }_{2}D-13({\theta }_1-{\theta }_2)\},D>13,A_i=1\\ {\theta }_3\text{exp}(-{\theta }_{3}D),D\le 13,A_i=0\\ {\theta }_4\text{exp}\{-{\theta }_{4}D-13({\theta }_3-{\theta }_4)\},D>13,A_i=0\end{array}\right\},$$ (4)

where θ = (θ₁, θ₂, θ₃, θ₄)_T, θ₁ and θ₂ are the hazard rates before and after 13 months respectively in the treatment group, and θ₃ and θ₄ denote the hazard rates before and after 13 months respectively in the control group.

The parameter estimates are given in Table 1. The slopes of terminal decline are 3.99 (95% CI: 2.85, 5.14) and 3.99−1.37 = 2.62 in the control and treatment groups respectively indicating that terminal decline in the treatment group is slower although the difference 1.37 (95% CI: −0.38, 3.11) is not statistically significant at 0.05 significance level. The treatment effect at time t is equal to 12.03 − 1.37t for t < 6 and 3.81−0.06t for t > 6. When patients enter approximately the last 4.4 months of life, the treatment effect (6.02, 95% CI: 0.03, 12.01) becomes significant. The survival parameter estimates shows that the hazard rates before 13 months are 0.052 (95% CI: 0.041, 0.064) and 0.077 (95% CI: 0.062, 0.092) in the treatment and control group respectively. After 13 months the hazard rates are 0.033 (95% CI: 0.022, 0.045) and 0.018 (95% CI: 0.010, 0.027). Comparing the two groups, the hazard rates are both significantly different (ps<0.05) for the two segments. However, the control group has a lower hazard after 13 months.

Table I.

Estimates of model parameters (including baseline as outcome)

	Terminal Decline Model		Survival Model
Sample used	Parameter	Estimate (SE)	Parameter	Estimate (SE)
Full sample	β0	108.44 (3.18)	θ1	0.052 (0.006)
	β1	12.03 (4.87)	θ2	0.033 (0.006)
	β2	3.99 (0.58)	θ3	0.077 (0.008)
	β3	0.088 (0.059)	θ4	0.019 (0.005)
	β4	−1.37 (0.89)
	β5	−0.060 (0.096)
	σ	18.22 (1.18)
	τ	11.36 (0.44)
	ν	9.95 (1.03)
	α	0.019 (0.009)

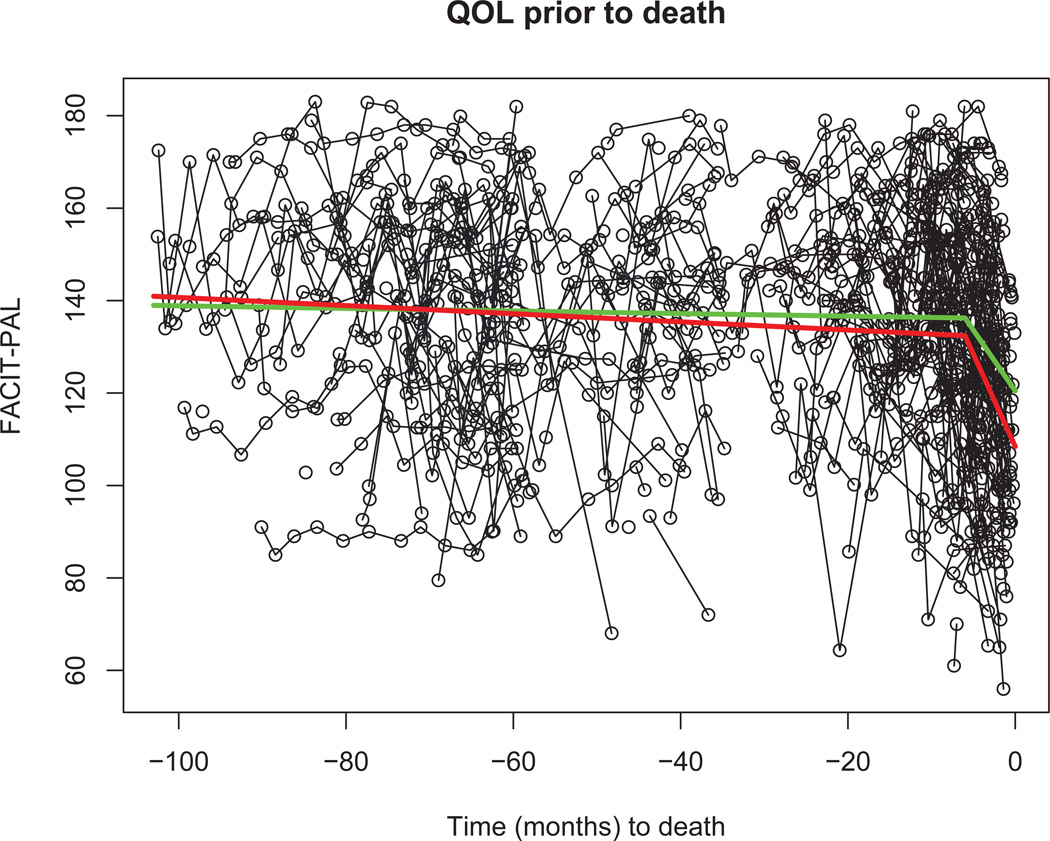
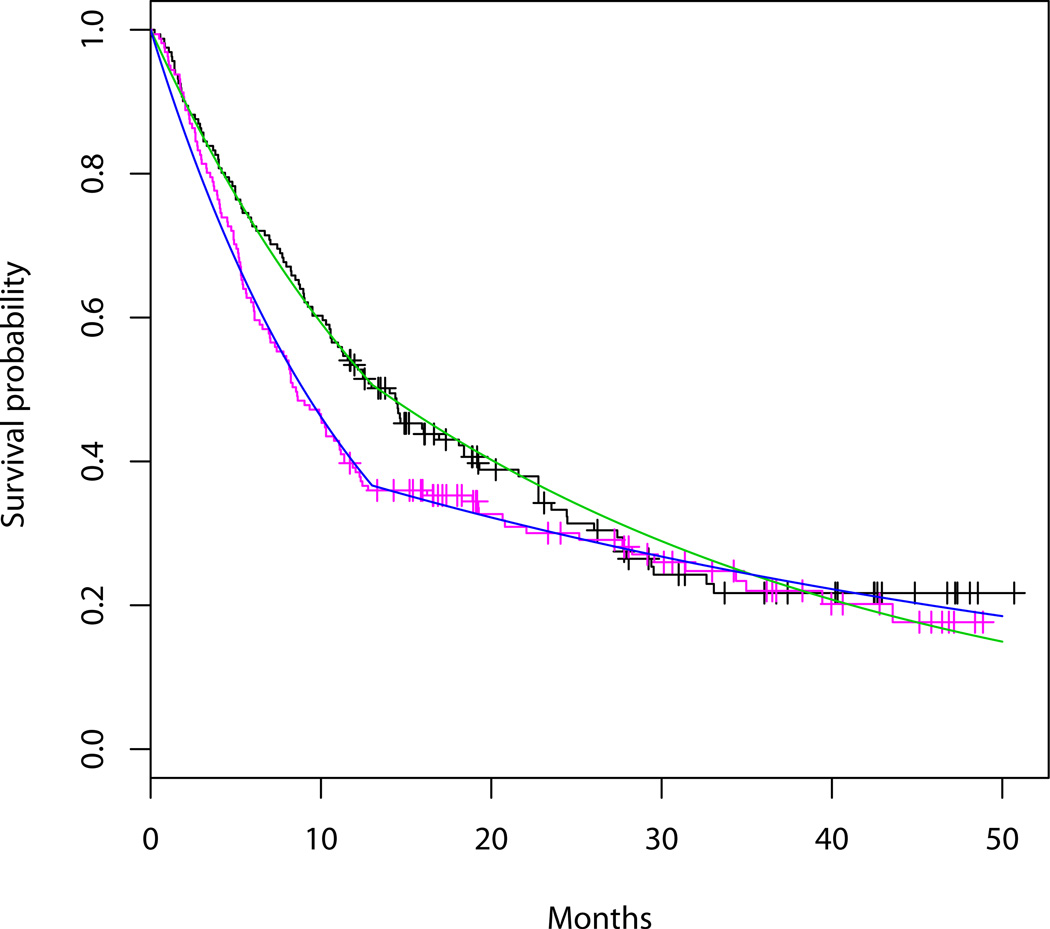
To assess the model fit, we draw the estimated terminal declines in the plot of observed repeated QOL as shown in Figure 2. We plot the estimated survival curves and the observed Kaplan-Meier curves as shown in Figure 3 to compare them. The goodness of fit appears to be reasonable. Notice that in Figure 2, plots of the observed QOL for patients with censored death times are based on expected death times conditional on censoring from the survival model (4). We also used the Bayesian information criterion (BIC) approach for longitudinal and clustered data proposed by Jones [24] to compare different models in the sensitivity analysis at the end of this section.

Figure 2.

QOL before death. Green and red lines are the fitted piecewise linear regressions in treatment and control groups respectively. The negative sign on the time axis indicates retrospective scaling (e.g., −20 means 20 months before death). Blue points are for those patients with censored death times.

Figure 3.

Black and pink curves are the K-M curves in treatment and control groups respectively. Green and blue curves are the corresponding fitted survival curves.

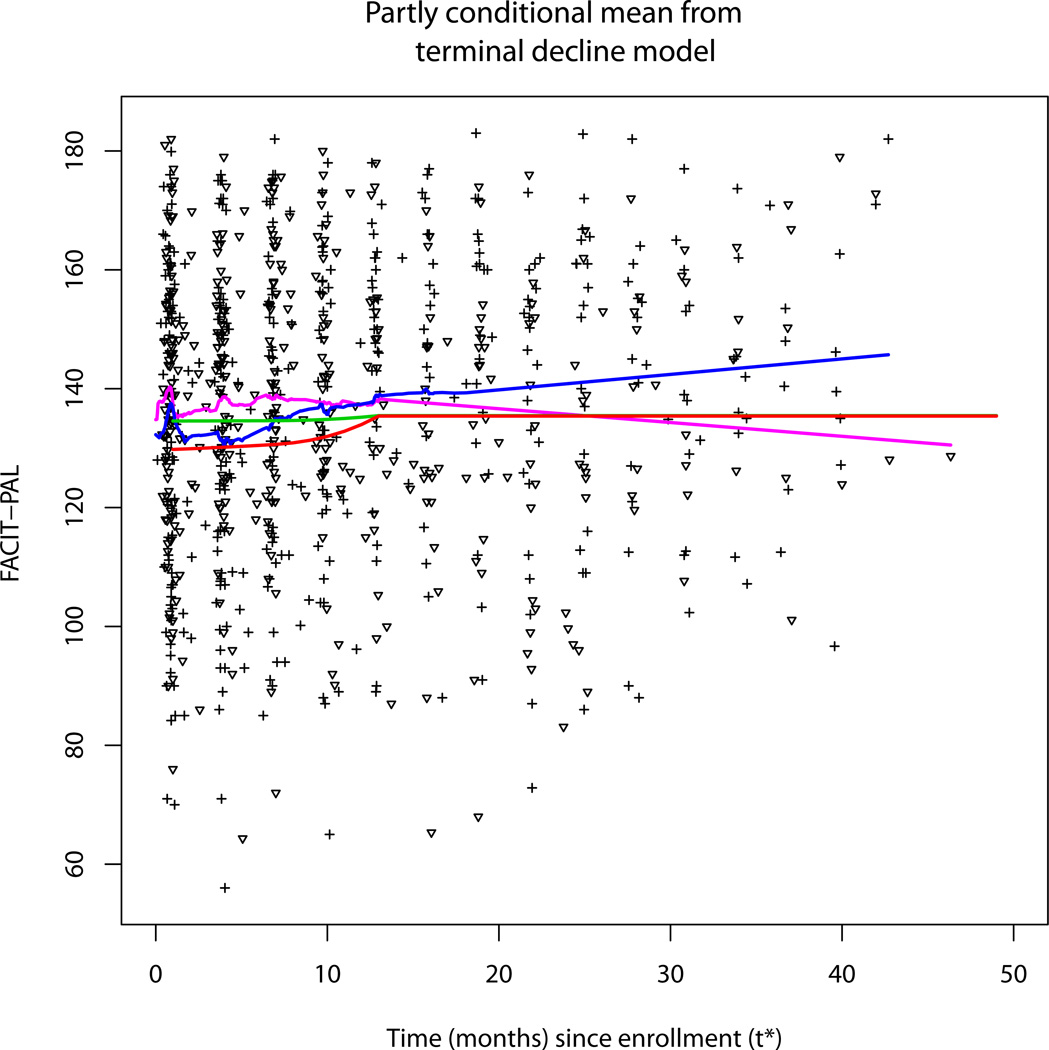
We derived the estimate of the QOL under a partly conditional model through the expression given in Section 3, where the time scale counts forward and the estimate is conditional on being alive. Figure 4 displays the estimated mean function starting from 1 month since enrollment from partly conditional model, and compares this to the observed quality of life data and a scatterplot smoother [25] of the longitudinal data over time from enrollment. The early differences seen tend to converge over time.

Figure 4.

Estimate of QOL at time from baseline conditional on being alive from the terminal decline model. Red and Green curves are the partly conditional means for the treatment and control groups respectively. Pink and blue curves are the scatterplot smoothers for the treatment and control groups respectively. The triangular symbols are for intervention data and the plus signs are for the control data.

There are two reasons for the pattern seen in Figure 4: 1) both treatment and control groups have higher hazard rates in the first 13 months based on the parameter estimates for the piecewise survival distributions and 2) the treatment has a greater effect as patients approach death as shown in Figure 2. As a result, patients near enrollment have the lowest remaining life expectancy, where the treatment is most effective. As time progresses, the surviving patients in the study face a lower relative risk of dying, and tend to be further from death and in a flatter more equal part of the terminal decline model where the treatment effect is smaller. Therefore, the difference in QOL between the two groups (or treatment effect) is the largest near the starting point of Figure 4. The scatter plot smoother also shows a similar pattern, albeit noisier. In simulations involving very large data sets, we have confirmed that the fitted and smoothed curves in Figure 4 converge.

To investigate the robustness of the conclusions to model assumptions, we performed a sensitivity analysis where different choices of correlation structures for W_i(t) and survival models were explored. Specifically, we used three different correlation structures: Gaussian correlation, exponential correlation and compound symmetry correlation structure with an arbitrary ρ=0.3. Three different choices of survival function were also used: a piecewise exponential distribution with two pieces for each group, an exponential distribution for each group and one exponential distribution for both groups. Results(Table II) showed that parameter estimates of the regression coefficients and variancesin model (1) are fairly robust to these different specifications. Generally speaking from this limited experience, fitting alternatives of survival distributions has a relatively larger impact on the slopes (β₃ and β₅) before entering last 6 months of life. The BIC scores show that the model with a Gaussian correlation structure and piecewise exponential distributions for survival outperformed other models.

Table II.

Sensitivity analysis and model comparisons

Correlation structure	Gaussian correlation			Exponential correlation			Compound Symmetry (ρ=0.3)
survival distribution	piecewise exponential	exponential	one exponential for both groups	piecewise exponential	exponential	one exponential for both groups	piecewise exponential	exponential	one exponential for both groups
β0	108.43	108.69	108.67	108.32	108.57	108.54	107.77	108.09	108.07
β1	12.02	11.77	11.80	12.12	11.88	11.91	11.39	11.10	11.13
β2	3.99	4.01	4.00	4.01	4.02	4.02	4.18	4.22	4.21
β3	0.09	0.13	0.13	0.09	0.14	0.14	0.08	0.10	0.10
β4	−1.36	−1.40	−1.40	−1.38	−1.42	−1.42	−1.23	−1.29	−1.29
β5	−0.06	−0.10	−0.09	−0.06	−0.09	−0.09	−0.05	−0.06	−0.06
σ	18.22	18.28	18.28	17.96	18.02	18.01	18.84	18.90	18.90
τ	11.35	11.36	11.36	9.97	9.98	9.97	10.73	10.72	10.73
ν	9.95	9.96	9.96	11.70	11.72	11.71	9.61	9.62	9.59
α	0.02	0.02	0.02	0.15	0.15	0.15	--	--	--
BIC	11595.70	11628.53	11624.42	11596.48	11628.82	11624.49	11648.46	11680.84	11676.40

6. Quality-adjusted life years

Quality-adjusted life years (QALY) has been extensively discussed in the literature [e.g., 26, 27]. It is defined as the life years weighted by utility with a formula given by $U={\displaystyle {\sum }_{j=1}^k{q}_j{S}_j}$ for discrete utility scores, where q₁, …, q_k are the utility scores in each of the 'k' health states, and S1, …, S_k are the times spent in each state in a study. When the utility is a continuous score along time denoted by q(t*), the QALY becomes the area under the longitudinal curve of the utility score, i.e., ${\int }_0^{\mathrm{\Delta }\wedge \mathrm{D}}q(t^{*})d{t}^{*}$, where Δ∧D = min (Δ,D), D is the death time and Δ is the study duration or other time horizon for quality-adjusted life years. Mean QALY is $\mathrm{E}[{\int }_0^{\mathrm{\Delta }\wedge \mathrm{D}}q(t^{*})d{t}^{*}]=\mathrm{E}[{\int }_0^{\mathrm{\Delta }}q(t^{*})1(t^{*}\le D)d{t}^{*}]={\int }_0^{\mathrm{\Delta }}E[q(t^{*})1(t^{*}\le D)]d{t}^{*}={\int }_0^{\mathrm{\Delta }}{\int }_{t^{*}}^{\infty }E[q(t^{*})|D]p(\theta ,D)dDd{t}^{*}$. Under the proposed model, an explicit formula can be derived for the mean QALY. For our ENABLE II, we consider the continuous standardized QOL (original score divided by the maximum of the scale 184) as the utility. Additional analyses will be conducted with a measured utility scale based on the same instrument as these data become available. The study duration/time horizon is taken as 54 months, the maximum observation time in the original data, and 12 months, to compare earlier time horizons. The mean QALY and standard errors are given in Table 3, where delta method was used to obtain the 95% CIs.

Table III.

Comparison of mean life years, mean quality-adjusted life years and QOL before death.

	Palliative care group	Usual care group
Mean life years (months)	54 months: 20.81 (17.69, 23.94)	54 months: 18.73 (15.55, 21.92)
Mean quality- adjusted life years (quality months)	54 months: 15.27 (12.90, 17.64) 12 months: 6.52 (6.07, 6.97)	54 months: 13.59 (11.12, 16.06) 12 months: 5.56 (5.07, 6.05)
Average QOL in last 6 months of life	128.35 (123.73, 132.97)	120.42 (116.04, 124.80)

7. Simulation

A simulation study was carried out to study the small sample statistical properties of the parameter estimators from our method. The data were simulated under a structure similar to the ENABLE II study, where the proportion of censored patients is 28.3%. Censoring was assumed to be non-informative and was generated from a Weibull distribution with shape and scale parameters equal to 10 and 30 respectively. Model (3) was used to generate survival data and model (4) to generate QOL. Repeated measurements of QOL were assumed to be taken at every 3 months since enrollment until death. Values of parameters were specified as in Table 1. We generated 1000 replicated samples. Each sample had 322 patients. The proportion of censored patients in the samples ranges from 21.1% to 36.3%. The results are summarized in Table 4. The parameter estimators are virtually unbiased. The mean of standard error estimators reflect well the empirical variability of the parameter estimators, and the associated Wald-type 95% confidence intervals have proper coverage probabilities.

Table IV.

Simulation results for the estimation of the parameters. Bias is the mean of estimates minus the true values; Percent of Biasis the bias as a percentage of the true value. SE is the empirical standard error of the estimates; Mean SE is the mean of estimated standard errors; CP is the empirical coverage probability of the 95 per cent confidence interval for the parameters.

Terminal Decline Model
Parameter	True	Bias	Percent of Bias (%)	SE	Mean.SE	CP (%)
β0	108.44	−0.048	−0.04	2.45	2.45	95.27
β1	12.03	0.073	0.61	3.51	3.46	95.16
β2	3.99	0.028	0.70	0.43	0.44	94.84
β3	0.088	−0.0054	−6.14	0.055	0.06	95.69
β4	−1.37	−0.051	3.72	0.58	0.60	95.43
β5	−0.060	0.007	−11.67	0.089	0.096	95.11
σ	18.22	−0.21	−1.15	1.02	1.04	95.00
τ	11.36	−0.023	−0.20	0.34	0.34	95.69
ν	9.95	0.02	0.20	0.70	0.73	95.11
α	0.019	0.0007	3.68	0.006	0.005	93.40
Survival Model
θ1	0.052	0.0003	0.58	0.006	0.006	96.12
θ2	0.033	0.0003	0.91	0.006	0.006	95.00
θ3	0.077	0.0001	0.13	0.007	0.008	95.85
θ4	0.019	0.0003	1.58	0.005	0.005	94.95

8. Discussion

This paper has proposed a novel approach for modeling the terminal decline of QOL that is typical in palliative care studies. Compared to other joint models mentioned in the introduction, our terminal decline model is particularly advantageous given the emphasis on QOL before death. The joint modeling of survival and QOL appropriately accounts for censoring (unknown time origins on a retrospective time scale) and the dependence between QOL and the time of death. The model also acknowledges that the treatment effect is associated with survival. In other words, palliative care intervention shows a greater effect as patients approach death. The use of a parametric piecewise linear random intercept model specifying serial correlation and measurement errors for the QOL data and a piecewise exponential distribution model for the survival times allows for highly flexible and useful joint model. A unique feature of this approach is the combination of retrospective time scale of terminal decline and joint modeling of the QOL trajectory and death. In the analysis of palliative care trials, the trajectories of terminal decline can be compared between treatment groups, perhaps focusing on a direct estimate of the difference in the QOL between treatment and control groups at a fixed time point before death.

Compared to a terminal decline analysis of the QOL using the subsample with observed death times (known time origins on a retrospective time scale), our joint model gains efficiency estimating the parameters in submodel (1) because all the censored subjects are included in our analysis. This can be seen by comparing the standard errors of full sample analysis to those of the subsample analysis. However, compared to a separate survival analysis using all of the subjects, we did not find a benefit in efficiency for estimating the parameters of the submodel for survival. If the death times were observed for all patients, the submodel for survival would not be necessary to estimate the parameters in the submodel (1). This is also reflected in the parameter estimation approach provided in Section 4, where the log-likelihood functions of the submodel (1) and survival model are independent and can be maximized separately when there are no censored subjects.

In our application, we chose the breakpoint t = 6 in the model (3) for cancer patients based on the hospice enrollment criteria [21] and a systematic review of cancer presentations [22]. Depending on the circumstances, this model can be adapted by choosing appropriate breakpoints for both the piecewise exponential survival and QOL models. Extensions currently being explored will incorporate nonlinear splines. Breakpoint estimation methods [e.g., 28, 29]might also be explored, although these are likely to be challenging in the setting of joint models.

As far as we know, development of model diagnostic techniques for joint modeling has not been given much attention in the literature. Under shared parameter models, Dobson and Henderson [30]presented informal graphical procedures for model diagnostics and Rizopoulos et al. [31]proposed a multiple-imputation-based approach to generate residuals and diagnostic plots. For our terminal decline model, we included the imputed survival times for those censored subjects to examine the model fit for submodel (1). This method may be extended to a more sophisticated approach in the future. To check the fit of the survival model, we compared the fitted model with K-M curve. Other techniques (Cox-Snell residuals) for a single survival model can also be used.

Time-order is an intrinsic part of the definition of a causal relationship, and our model is specified by defining the terminal decline according to time measured backwards from death. However, the causal inference of interest here regards the effect of the randomized intervention on the joint distribution of time to death and quality of life and the outcome data used to estimate the parameters were collected after the time-stationary randomized treatments started. Thus the causal interpretation of treatment on both quality of life and survival is preserved.

In the ENABLE II study, inference was based on a model without adjusting for covariates because of the randomized design. Our methods can easily be modified to include covariates with a little more complex expression for the log-likelihood function.

A number of limitations should be noted. A practical limitation of our model is that there is no existing statistical package to run this model. We have SAS macro program available upon request. An R package for implementing our terminal decline model has been planned. Two other limitations are the required assumptions of non-informative censoring and QOL data missing at random. In the ENABLE II study, we were able to identify the survival status for all patients at the end of the study, and hence non-informative censoring (administrative censoring) applied. For studies with censoring subjects other than administrative censoring, reasons for censoring needs to be investigated to ensure that it is non-informative. QOL data missing at random is another issue, because some QOL may be missing due to increasing morbidity and presumably low QOL. In the ENABLE II study, we know that there were several reasons for missing: traveling, sickness and dying, unknown, etc. The missing pattern was intermittent. Under the assumption of missing at random, our piecewise linear mixed model works well. However, if missingness is not at random (or non-ignorable), the parameter estimates will be biased. It is possible that additional assumptions for the missing mechanism will lead to improved estimators [32].

Appendix

We derive closed form of l₃ under models (3) and (4), where a two-piece linear random intercept model specifying serial correlation and measurement errors for QOL and a two-piece exponential hazard survival model are used. The derivation can be easily extended to more general cases with more than two pieces in the model. Let C denote the break point of the two-piece exponential survival model. We derive the closed form of likelihood contribution from each subject i =r₁ + r₂ + 1, …, r₁ + r₂ + r₃.

First consider C_i < C. For subject i, the expression of the likelihood contribution is ${\mathrm{\Delta }}_1^1+\cdots +{\mathrm{\Delta }}_1^{k-j+2}+{\mathrm{\Delta }}_2^1+\cdots +{\mathrm{\Delta }}_2^{n_i-m+2}$, where $t_{ij}^{*}$ is the smallest measurement time such that $t_{ij}^{*}+6>C_i,t_{ik}^{*}$ is the largest measurement time such that $t_{ik}^{*}+6<C\text{ and }{t}_{im}^{*}$ is the smallest measurement time such that $t_{im}^{*}+6>C$. Expressions of Δ’s are given in the following derivation.

Let Φ (.) denote the standard normal distribution function. Notice that ${\int }_{C_i}^{\infty }f(Y_i^{*}|D_i)f(D_i)d{D}_i={\int }_{C_i}^{C}f(Y_i^{*}|D_i)f(D_i)d{D}_i+{\int }_C^{\infty }f(Y_i^{*}|D_i)f(D_i)d{D}_i\triangleq {\mathrm{\Delta }}_1+{\mathrm{\Delta }}_2$, where ≜ means “defined as”. Let $t_{ij}^{*}$ be the smallest measurement time such that $t_{ij}^{*}+6>C_i\text{ and }{t}_{ik}^{*}$ be the largest measurement time such that $t_{ik}^{*}+6<C$. Dividing Δ₁ into k – j + 2 integrals ${\mathrm{\Delta }}_1={\int }_{C_i}^{t_{ij}^{*}+6}f(Y_i^{*}|D_i)f(D_i)d{D}_i+{\int }_{t_{ij}^{*}+6}^{t_{i,j+1}^{*}+6}f(Y_i^{*}|D_i)f(D_i)d{D}_i+\cdots +{\int }_{t_{ik}^{*}+6}^{C}f(Y_i^{*}|D_i)f(D_i)d{D}_i\triangleq {\mathrm{\Delta }}_1^1+\cdots +{\mathrm{\Delta }}_1^{k-j+2}$. For any let b_l and a_l denote the upper and lower integration limits respectively. After some fundamental calculations, we have ${\mathrm{\Delta }}_1^l={(\sqrt{2\pi })}^{-n_i+1}|V_i{|}^{-\frac{1}{2}}\text{ exp }(-\frac{1}{2}{(Y_i^{*}-f_l)}^T{V}_i^{-1}(Y_i^{*}-f_l))\text{ exp }(\frac{1}{2}\frac{{({f_l}^T{V}_i^{-1}{g}_l-{\theta }_1)}^2}{{g_l}^T{V}_i^{-1}{g}_l})(\Sigma \mathrm{\Phi }\left(\frac{b_l-{\mu }_l}{\Sigma }\right)-\Sigma \mathrm{\Phi }(\frac{a_l-{\mu }_l}{\Sigma }))$, where f_l is a n_i dimensional vector with the first j + l − 2 elements calculated as ${\beta }_0+{\beta }_1{A}_i+6({\beta }_2+{\beta }_4{A}_i-{\beta }_3-{\beta }_5{A}_i)-({\beta }_3+{\beta }_5{A}_i)t_{ih}^{*},h=1,\dots ,j+l-2$ and the rest of the elements calculated as ${\beta }_0+{\beta }_1{A}_i-({\beta }_2+{\beta }_4{A}_i)t_{ih}^{*},h=j+l-1,\dots ,n_{i.}$ g_l is a n_i dimensional vector with the first j + l − 2 elements calculated as β₃ + β₅A_i and the rest of the elements calculates as β₂ + β₄A_i.. μ_l is equal to $\frac{{f_l}^T{V}_i^{-1}{g}_l-{\theta }_1}{{g_l}^T{v}_i^{-1}{g}_l}$ and Σ is equal to ${({g_l}^T{V}_i^{-1}{g}_l)}^{-\frac{1}{2}}$. Therefore, we have a closed form for Δ₁. Notice that $t_{ij}^{*}\text{ and }{t}_{ik}^{*}$ might not exist at the same time, ie., none of the $t_{ih}^{*},h=1,\dots ,n_i$ satisfy $C_i<t_{ih}^{*}+6<C$. In that case, Δ₁ has only one partition integrating from C_i to C.

Similarly, Δ₂ can be partitioned as follows ${\mathrm{\Delta }}_2={\int }_C^{t_{im}^{*}+6}f(Y_i^{*}|D_i)f(D_i)d{D}_i+{\int }_{t_{im}^{*}+6}^{t_{i,m+1}^{*}+6}f(Y_i^{*}|D_i)f(D_i)d{D}_i+\cdots +{\int }_{t_{{\mathit{\text{in}}}_i}^{*}+6}^{\infty }f(Y_i^{*}|D_i)f(D_i)d{D}_i\triangleq {\mathrm{\Delta }}_2^1+\cdots +{\mathrm{\Delta }}_2^{n_i-m+2}$, where $t_{im}^{*}$ is the smallest measurement time such that $t_{im}^{*}+6>C$. For any ${\mathrm{\Delta }}_2^l,l=1,\dots ,n_i-m+2$, also let b_l and a_l denote the upper and lower integration limits respectively. After some fundamental calculations, we have ${\mathrm{\Delta }}_1^l={(\sqrt{2\pi })}^{-n_i+1}|V_i{|}^{-\frac{1}{2}}\text{ exp }(-\frac{1}{2}{(Y_i^{*}-f_l)}^T{V}_i^{-1}(Y_i^{*}-f_l))\text{ exp }(\frac{1}{2}\frac{{({f_l}^T{V}_i^{-1}{g}_l-{\theta }_1)}^2}{{g_l}^T{V}_i^{-1}{g}_l})(\Sigma \mathrm{\Phi }\left(\frac{b_l-{\mu }_l}{\Sigma }\right)-\Sigma \mathrm{\Phi }(\frac{a_l-{\mu }_l}{\Sigma }))$, where f_l is a n_i dimensional vector with the first m + l − 2 elements calculated as ${\beta }_0+{\beta }_1{A}_i+6({\beta }_2+{\beta }_4{A}_i-{\beta }_3-{\beta }_5{A}_i)-({\beta }_3+{\beta }_5{A}_i)t_{ih}^{*},h=1,\dots ,m+l-2$ and the rest of the elements calculated as ${\beta }_0+{\beta }_1{A}_i-({\beta }_2+{\beta }_4{A}_i)t_{ih}^{*},h=m+l-1,\dots ,n_{i.}$. g_l is a n_i dimensional vector with the first m + l − 2 elements calculated as β₃ + β₅A_i and the rest of the elements calculates as β₂ + β₄ A_i. μ_l is equal to $\frac{{f_l}^T{v}_i^{-1}{g}_l-{\theta }_1}{{g_l}^T{v}_i^{-1}{g}_l}$ and Σ is equal to ${({g_l}^T{V}_i^{-1}{g}_l)}^{-\frac{1}{2}}$. Therefore, we have a closed form for Δ₂. When $t_{im}^{*}$ does not exist, ie, all $t_{ih}^{*}+6,h=1,\dots ,n_i$ are less than C, Δ₂ consists of only one partition integrating from C to infinity.

In summary, the closed form of ${\int }_{C_i}^{\infty }f(Y_i^{*}|D_i)f(D_i)d{D}_i$ is derived when C_i < C. For C_i > C, the closed form is equal to Δ₂ with C_i replaced by C. Thus, closed expression of l₃ is obtained for the two-piece models. For models with more than two pieces, there would be more partitioned integrations. However, calculation of each partition is straightforward. If the model adjusts for baseline characteristics, expressions for f_l and g_l become more complex. Calculations still follow the same way.