Software for Dosage Individualization of Voriconazole for Immunocompromised Patients

Abstract

The efficacy of voriconazole is potentially compromised by considerable pharmacokinetic variability. There are increasing insights into voriconazole concentrations that are safe and effective for treatment of invasive fungal infections. Therapeutic drug monitoring is increasingly advocated. Software to aid in the individualization of dosing would be an extremely useful clinical tool. We developed software to enable the individualization of voriconazole dosing to attain predefined serum concentration targets. The process of individualized voriconazole therapy was based on concepts of Bayesian stochastic adaptive control. Multiple-model dosage design with feedback control was used to calculate dosages that achieved desired concentration targets with maximum precision. The performance of the software program was assessed using the data from 10 recipients of an allogeneic hematopoietic stem cell transplant (HSCT) receiving intravenous (i.v.) voriconazole. The program was able to model the plasma concentrations with a high level of precision, despite the wide range of concentration trajectories and interindividual pharmacokinetic variability. The voriconazole concentrations predicted after the last dosages were largely concordant with those actually measured. Simulations provided an illustration of the way in which the software can be used to adjust dosages of patients falling outside desired concentration targets. This software appears to be an extremely useful tool to further optimize voriconazole therapy and aid in therapeutic drug monitoring. Further prospective studies are now required to define the utility of the controller in daily clinical practice.

INTRODUCTION

Voriconazole is a second-generation triazole that is a first-line agent for the treatment of invasive aspergillosis, invasive candidiasis, and a number of other opportunistic fungal pathogens (1–3). Exposure-response and exposure-toxicity relationships are increasingly well described in experimental and clinical contexts (4–6). A trough concentration of ≥1 mg/liter is associated with improved clinical outcomes and survival in adults and children (7–10). Furthermore, a trough concentration of >4.5 to 6 mg/liter is associated with an increased risk of both hepatotoxicity and central nervous system toxicity (8, 9, 11). Therapeutic drug monitoring to enable dosage adjustment to achieve these drug exposure targets is increasingly advocated.

The pharmacokinetics (PK) of voriconazole are complicated. Drug exposure is highly variable, and concentrations typically vary approximately 100-fold even in healthy volunteers (12). Little of this variability is explained by directly measurable and clinically relevant covariates, such as weight or the CYP2C19 genotype. Furthermore, the pharmacokinetic behavior of voriconazole is nonlinear (i.e., Michaelis-Menten) as a consequence of saturable clearance mechanisms. At increasing concentrations, therefore, elimination of drug is limited to a constant amount per unit of time, rather than a constant fraction of the concentration in serum. For some patients, this results in a disproportionate increase in drug exposure following dosage escalation. These properties pose a significant challenge to the real-time adjustment of voriconazole dosages for critically ill patients to achieve prespecified drug exposure targets.

“Stochastic control” refers to the control of dynamic systems whose underlying properties can only be estimated. Concepts of stochastic control are ubiquitous and established in many engineering processes and problems, such as flight control and rocket telemetry. These ideas can also be applied to clinical pharmacology. In this regard, the pharmacokinetic behavior of voriconazole in an individual patient is a “dynamic system” whose properties, such as clearance, are inferred from measured drug concentrations. Here we describe the conceptual foundation that is required for the stochastic control of plasma voriconazole concentrations in critically ill immunocompromised patients. We describe the development of software that is required for this process and illustrate how this software can be used.

(This work was presented in part at the 22nd European Congress of Clinical Microbiology and Infectious Diseases [ECCMID], London, United Kingdom, 2012.)

MATERIALS AND METHODS

Conceptual underpinning and construction of the controller.

The controller was based on concepts and software originally developed by the University of Southern California Laboratory for Applied Pharmacokinetics (LAPK) (http://www.lapk.org). The multiple-model design and stochastic control of dosage regimens were initially described nearly 20 years ago (13) and have been applied to compounds such as vancomycin (14) and to antiretroviral therapy for HIV infection (15). This software, now called RightDose, can be used to individualize drug therapy. RightDose is menu driven, runs under Windows operating systems, and employs a relatively simple graphical user interface. Models for many commonly monitored drugs exist in RightDose, but they are limited to straightforward pharmacokinetic systems with solutions that can be estimated algebraically. However, progressive developments in the algorithms for adaptive control have recently enabled this same control process to be applied to much more complex models for compounds, such as voriconazole, which require a differential equation solver to estimate an individual patient's pharmacokinetic parameter values.

RightDose currently exists only as an “engine” of Fortran files that must be compiled in a terminal (DOS) window. Five of the engine files are fixed, but the sixth file is a Fortran file that contains the mathematical equations defining the structural model of the drug to be controlled (voriconazole in this case). Estimating the values of the parameters in these equations for an individual patient enables calculation of the plasma voriconazole concentration at any time after a given voriconazole dose, which in turn permits calculation of the optimal dose that achieves specified target plasma concentrations with maximum precision and accuracy. We used a free-access G95 Fortran compiler (http://ftp.g95.org/) to compile the six files into an executable software program, which was then run within a DOS window. To distinguish this program from RightDose, we will refer to it as “rightdose.exe” throughout this article.

Once executed, to calculate the optimal voriconazole dose for a given patient, rightdose.exe required the following three input files: (i) a “population prior” distribution of voriconazole pharmacokinetic model parameter values obtained from a previous study of patients receiving voriconazole, which is described in more detail in the next section, (ii) the patient's history of voriconazole dosages and measured plasma concentrations, and (iii) the future concentration targets, the time(s) at which the concentration target(s) should be achieved, and an initial estimate of the dosage regimen to achieve the target(s) most precisely.

Building the population prior for voriconazole.

In order to control plasma voriconazole concentrations in an individual patient, it was necessary to have an idea about the general distribution of values for each parameter in the equations that define voriconazole pharmacokinetic behavior in adult patients. This is known as a “population prior” distribution of parameter values, and it is ideally described using data from richly sampled participants in carefully conducted phase I-III clinical studies. We constructed our voriconazole population prior using data from the samples of 64 adults (21 healthy volunteers and 43 patients) who had been enrolled in phase I and III clinical trials of voriconazole (12). The 21 healthy volunteers consisted of 14 patients who had received voriconazole at 6 mg/kg of body weight intravenously (i.v.) for two dosages, 3 mg/kg i.v. every 12 h (Q12h) for 1 week, and then 200 mg Q12h orally thereafter. Following a washout period, these same patients had received 6 mg/kg i.v. for two dosages, 5 mg/kg Q12h i.v. for 1 week, and then 400 mg Q12h orally thereafter. A second cohort of healthy volunteers had received 6 mg/kg i.v. for two dosages, 4 mg/kg i.v. Q12h, and then 300 mg orally Q12h thereafter. Intensive sampling of these patients yielded a rich data set. Trough concentrations had been obtained at the end of days 1 to 7, with 13 samples throughout the dosing interval at the end of the first and second weeks. The pharmacokinetic data were combined with the sparse data from another 43 patients who had been enrolled in a phase III clinical trial. Voriconazole was measured using a well-validated high-performance liquid chromatography (HPLC) assay with a limit of detection of 0.01 mg/liter as described in a recent publication (12).

The mathematical structural model for voriconazole consisted of a series of equations that defined absorption into a central compartment after a delay, a peripheral compartment with distribution of drug to and from the central compartment, and Michaelis-Menten saturable elimination from the central compartment, which made it necessary to use differential equation solvers to estimate the population prior distribution of parameter values from the study data. This was achieved using the nonparametric population pharmacokinetic software program Big NPAG (now embedded in the Pmetrics package, available from http://www.lapk.org). We have recently published this population model and the prior parameter value distributions (5). We chose the nonlinear Michaelis-Menten model over a simpler linear pharmacokinetic model as recently described (9) to more adequately fit a wider range of dosage regimens and patients. Nonlinear pharmacokinetics for voriconazole are invariably seen with higher voriconazole doses, which then require the use of a structural pharmacokinetic model with saturable clearance to adequately describe the data (as was the case in the model used to construct the controller). Importantly, however, such a model can still describe patients whose voriconazole concentration falls at a constant fraction per hour (i.e., patients with seemingly linear PK). In this case, the patient's estimate for K_m will be significantly higher than for that those patients who exhibit typical nonlinear PK. Similar to any drug with Michaelis-Menten behavior, the linearity or nonlinearity of voriconazole PK in the literature and in individual patients is a function of the dose and resulting plasma concentrations, relative to the patient's K_m parameter value.

The nonparametric population prior for voriconazole is a collection of discrete support points. Each support point is a vector, comprising a value for each parameter in the structural model equations plus the probability of those values to describe voriconazole pharmacokinetic behavior in the study population. The parameters in the structural model were the following: K_a, rate constant of voriconazole absorption from the gut to the central compartment (h⁻¹); F, fraction of oral voriconazole absorbed with respect to intravenous administration, i.e., bioavailability (no units); lag, delay in absorption (h); V_c, volume of the central compartment (liters); V_max, the maximum rate of elimination by metabolism (mg/h); K_m, the serum concentration of voriconazole at which metabolism is half-maximal (mg/liter); K_cp, rate constant of voriconazole distribution from the central compartment to the peripheral compartment (h⁻¹); and K_pc, rate constant of voriconazole distribution from the peripheral compartment to the central compartment (h⁻¹).

The probabilities of all the support points add up to unity. The better a given support point describes the behavior of voriconazole in a population, the higher its associated probability. At most, there can be the same number of support points in the joint density as study patients (64 in this case). However, fewer support points are typical and reflect patients who are similar enough relative to noise and model misspecification as to be described by the same set of pharmacokinetic parameter values. In this case, 42 support points were calculated from the original study population of 64 patients receiving voriconazole (12).

General process of calculating the optimal voriconazole dose for an individual patient.

The nonparametric population prior serves as the basis for multiple-model stochastic control for each new patient for whom voriconazole therapy needs to be individualized. For a patient who has already been receiving voriconazole and has measured plasma concentrations, the procedure is as follows. (i) Update the prior probabilities of each point to new “Bayesian posterior” probabilities based on the ability of each support point to describe the patient's measured voriconazole concentrations given the dosing history. (ii) Define a plasma voriconazole target, such as a concentration of 1 mg/liter 12 h after the most recent dose. (iii) Calculate the voriconazole dose that minimizes the weighted squared error between the calculated concentration from the parameter values of each point in the Bayesian posterior and the target.

Steps i and iii are accomplished by the rightdose.exe program with appropriate patient data and model equation files, and step ii requires consideration from the user. For patients who are initiating voriconazole therapy (i.e., have no previous dosing or concentration data), step i is skipped, and step iii is carried out using the full population prior distribution.

The number of support points in the Bayesian posterior distribution for an individual patient (step i above) is typically smaller than that in the prior distribution obtained from a larger population of patients and may be as few as one. This is because many of the support points in the population prior, which capture much of the pharmacokinetic variability of voriconazole in adult patients, are unlikely to describe the new patient's observed voriconazole concentrations. Rather, an individual patient tends to be described by a discrete subset of support points. Each of the support points in the Bayesian posterior distribution for the new patient is, in effect, one of the multiple pharmacokinetic models for that patient, each weighted by its Bayesian posterior probability. Those support points that describe the patient well have a higher probability, whereas those support points that do less well have a lower associated probability. In this way, the pharmacokinetic behavior of voriconazole in the individual patient can be estimated using information that has been obtained from a broader population of patients, even with sparse or erratic samples. This Bayesian posterior distribution for the individual patient forms the basis for stochastic control of the voriconazole plasma concentrations using the dosage as the means of control.

The next step (step ii above) in the process of dosage individualization is that the user must define the desired concentration target, the time in the future that target must be achieved, and the schedule of drug administration. The user must also provide a best guess for the likely dosage, which provides a reference point from which the estimation process begins. The multiple-model algorithm then calculates the dosage that minimizes the weighted sum of squared differences between the desired target concentration(s) and those that are calculated from each point in the Bayesian posterior (step iii above). Less-probable support points contribute proportionally less than highly probable points to the calculated dosage that matches the desired concentration target with maximum precision and accuracy.

Testing the voriconazole controller.

The performance of our voriconazole controller was assessed using the pharmacokinetic data derived from 10 hematopoietic stem cell transplant (HSCT) recipients who had received a standard regimen of voriconazole of 6 mg/kg Q12h i.v. for two dosages followed by 4 mg/kg Q12h i.v. for 2 weeks; the results have been previously published (16). Briefly, these patients were 18 to 65 years old and weighed 66 to 100 kg. There was no clinical evidence of invasive fungal infection. Voriconazole was commenced 1 week prior to transplantation and continued for 14 days.

These patients were not included in the original 64 patients used to construct the population prior (those patients are described in reference 12). Concentrations of voriconazole in plasma were measured using HPLC with a dynamic range for the assay of 0.1 to 10 mg/liter, as described in the original publication (16). The use of additional pharmacokinetic data contained in previous publications for validation of the controller (see, for example, data contained within references 7 and 10) was not possible because the vast majority of these patients did not have enough data points to simultaneously estimate pharmacokinetics and assess the performance of the controller.

All voriconazole dosages and concentrations available from the HSCT cohort were used, with the exception of the last dose and the single plasma concentration measured 12 h after that dose, which had been obtained 336 h after the first voriconazole dose. This data set constituted the past experience of each individual patient with voriconazole and allowed the pharmacokinetics of each of the HSCT recipients to be estimated, using the population prior obtained from the original voriconazole population pharmacokinetic model (see step i in the section above) (12). The last measured observation (i.e., voriconazole concentration), which was obtained 12 h postdose, was used as the concentration target to plan the future regimen (step ii). The dosage that was calculated by the controller (step iii) was compared with the dosage that was actually given to the patient. A plot of the observed-versus-predicted dosages was then constructed.

Simulations to demonstrate potential utility of the controller under realistic conditions.

We used rightdose.exe to illustrate its potential use for a patient with trough concentrations of <1 mg/liter and at increased risk of concentration-dependent therapeutic failure. For this exercise, we could have chosen any target concentration deemed important by a treating clinician (e.g., a trough concentration of 2 mg/liter). The simulated patient received the standard (currently licensed) regimen on day 1 (6 mg/kg i.v. Q12 h, with drug infused over a 1-h period). We set the concentrations obtained 12 h after the first dose to be <1 mg/liter. We used rightdose.exe to calculate concentration-time out to 120 h after initiation of voriconazole when a dose adjustment was made at 24 h based on the “measured” drug concentrations or when the original (licensed) dose was continued. The dose adjustment was not implemented until 24 h (i.e., the third dose) to more realistically simulate the time required to transport the specimen to the laboratory, measure concentrations of voriconazole in plasma using an established analytical method (e.g., HPLC or mass spectroscopy), and communicate the results back to the clinician for calculation of a future regimen.

RESULTS

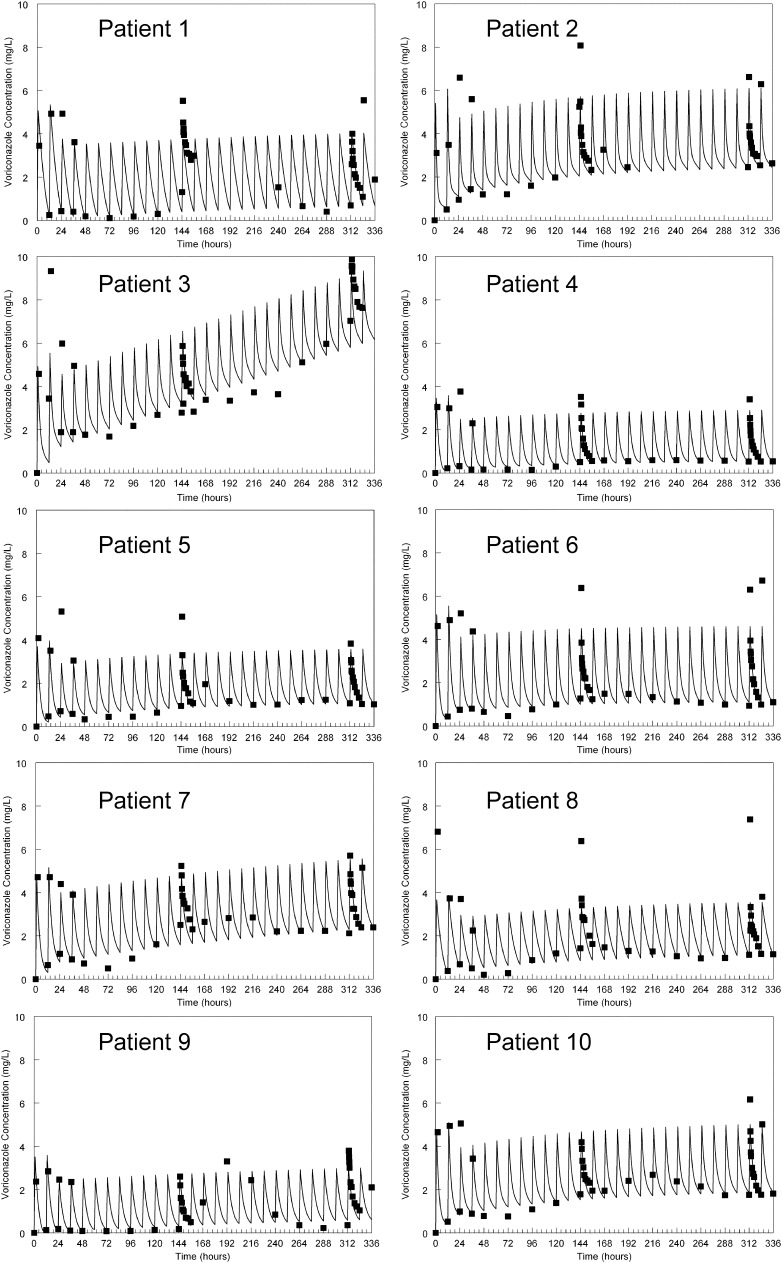
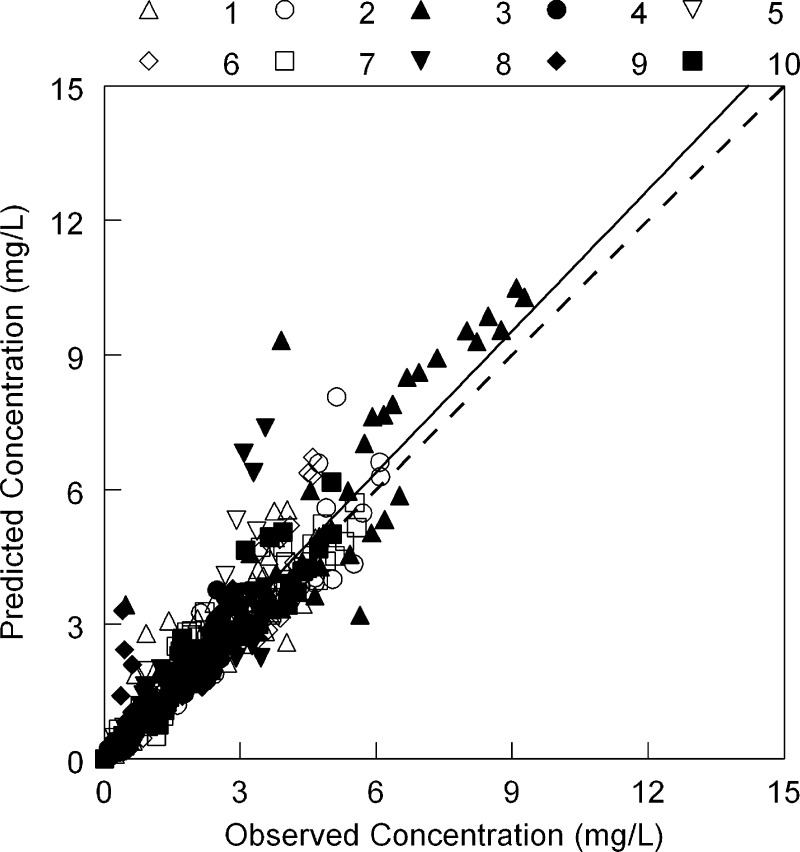
The observed data for each of the 10 HSCT recipients were readily described using each patient's Bayesian posterior pharmacokinetic parameter values (Fig. 1). A linear regression of the observed-versus-predicted data that were pooled for each individual patient is shown in Fig. 2. The regression line was given by the following: predicted concentration = 0.086 + (1.05 × observed concentration), with a coefficient of determination (r²) of 0.86.

Fig 1.

The fit of the voriconazole population pharmacokinetic model to serum concentrations obtained from 10 hematopoietic stem cell transplant recipients. The solid squares are the raw serum data, and the solid line is the mean weighted prediction of the model fitted to the data. All patients received a standard i.v. regimen of 6 mg/kg i.v. for two dosages, followed by 4 mg/kg i.v. every 12 h.

Fig 2.

The observed-versus-predicted values for the 10 individual patients shown in Fig. 1. The dotted line is the line of identity (observed = predicted). The solid line is the regression line fitted to pooled data and is given by the following: predicted concentration = 0.086 + (1.05 × observed concentration) (r² = 0.86). Patient numbers and symbols are shown at the top of the figure.

Validation of performance of the controller.

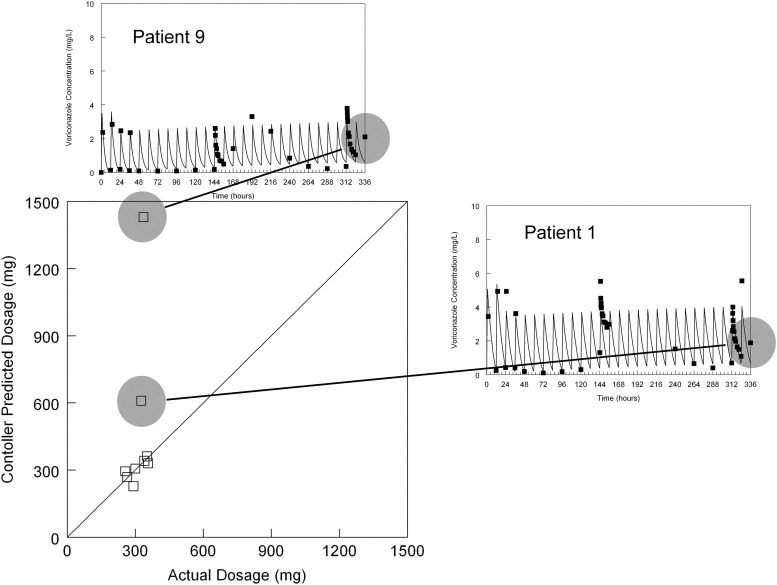
In the majority of cases, there was close agreement between the voriconazole dose calculated by the controller to optimally achieve the last observed serum concentration and the actual dose that had been administered (Fig. 3). Notably, there were two HSCT recipients for whom the controller predicted significantly more drug than was actually administered. Inspection of the raw data from HSCT recipients 1 and 9 (Fig. 1) shows that the last data points that served as the therapeutic targets for these two patients were notably different from the predicted profiles in comparison to the other patients (i.e., this was a problem with the data, not the performance of the controller). The predicted dosage was not affected by the initial guess for the dosage provided by the user (i.e., the same estimate for the dosage was provided by the software regardless of whether a realistic initial guess (e.g., 300 mg) or a completely unrealistic initial guess (e.g., 1 mg) was made.

Fig 3.

Predictive performance of the controller. All but the last concentration from the 10 patients shown in Fig. 1 were used to estimate each individual's pharmacokinetics. The controller was used to calculate the dosage to achieve the last observed concentration. This dosage was then compared with the dosage that was actually administered. The solid line is the line of identity (i.e., predicted dose = actual dose). Two dosages recommended by the controller were significantly different from those that were ultimately administered. In both cases, this is a result of outlying measurements at 336 h for patient 1 and patient 9.

Simulations to demonstrate potential utility of the controller under realistic conditions.

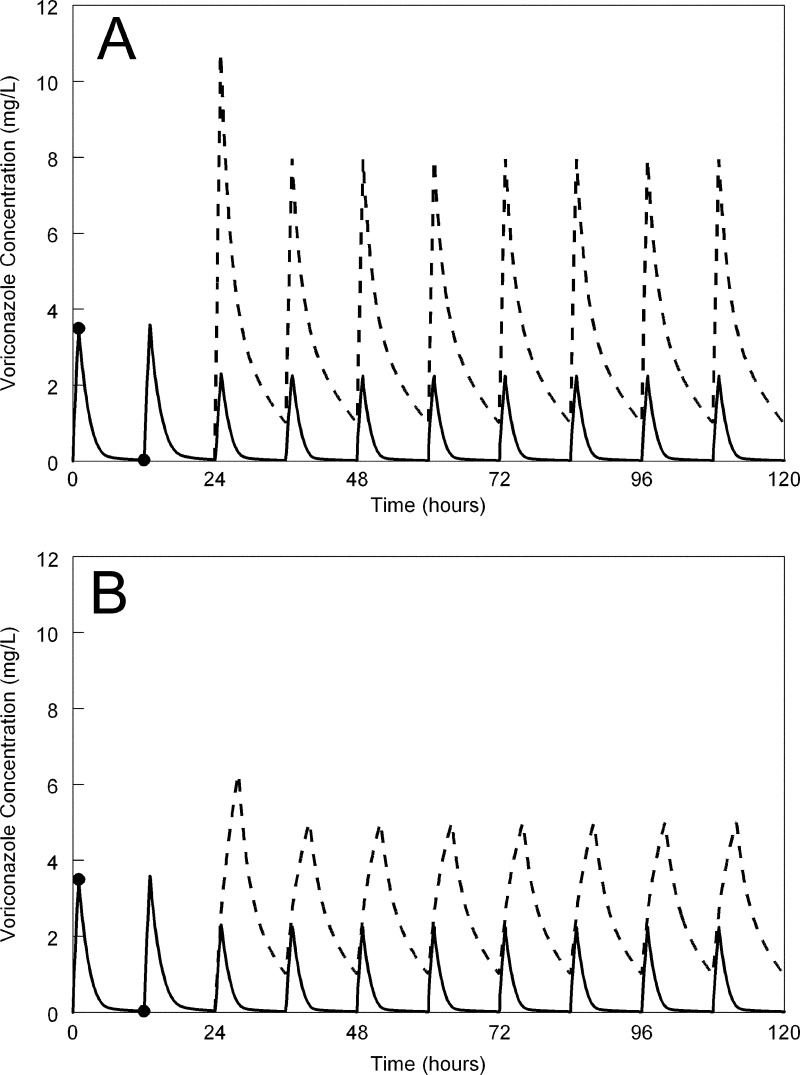
The potential utility of the controller is illustrated in Fig. 4, which depicts a typical patient for whom the standard voriconazole regimen immediately results in a trough concentration significantly lower than the target of 1 mg/liter. Adjusting the dose to 10 mg/kg Q12h i.v. at 24 h rapidly corrects the plasma profile and achieves therapeutic trough concentrations of 1 mg/liter. Prolongation of the infusion from 1 to 4 h resulted in the same trough concentration, but a significantly lower peak concentration.

Fig 4.

The potential advantage of a controller for the individualization of voriconazole therapy. (A) A patient receiving a standard voriconazole regimen (6 mg/kg i.v. for two dosages, followed by 4 mg/kg i.v. Q12h infused over 1 h) is sampled at 1 and 12 h post-initiation of therapy. The solid line represents the concentration-time profile without any intervention. The trough concentrations are low and significantly less than 1 mg/liter. The controller-predicted alteration in dosages results in a trough concentration of 1 mg/liter. (B) The same process is used except the drug is now infused i.v. over 4 h and results in the same trough concentrations but lower peak concentrations.

DISCUSSION

Although control theory has a long and robust history in engineering, it has not been widely applied or practiced in clinical medicine or pharmacology. However, it can and should be embraced, since the necessary computational and analytical expertise to control highly variable and inherently unpredictable systems is available. The control of variable systems (patients) whose outcomes are dependent on achieving rapid and optimally precise control is an urgent health care need and is central to current notions of personalized pharmacotherapy.

Voriconazole is a fascinating agent. The structural modifications from fluconazole that extend the spectrum of activity from Candida spp. to medically important molds have been engineered at a cost of less-predictable pharmacokinetics (17). Voriconazole is an ideal candidate for therapeutic drug monitoring for the following reasons: (i) there are well-established drug exposure-effect and drug exposure-toxicity relationships (7, 8, 10); (ii) there is evidence that therapeutic drug monitoring may lead to improved therapeutic outcomes (8, 18); and (iii) voriconazole exhibits significant interpatient variability with classical nonlinear pharmacokinetics (12). While therapeutic drug monitoring may be a desirable adjunct to the routine use of voriconazole, at this time there are no algorithms that can be used to adjust the regimen to attain predefined serum concentration targets in an optimally precise manner. The multiple-model design with stochastic control described in this study is a way in which this can now be achieved.

The process of real-time dosage adjustment (adaptive control) begins with a population prior pharmacokinetic model. A population prior model summarizes and stores past experiences with a drug when administered to a population of interest. One of the issues with voriconazole has been difficulty in constructing population pharmacokinetic models. In order to describe the extent of nonlinear pharmacokinetics that is characteristic of voriconazole, a range of dosages must be studied to enable a rigorous estimate of the K_m-V_max pair that jointly describes nonlinear, Michaelis-Menten clearance. While a range of i.v. and oral regimens were studied in phase I studies, a single fixed regimen was used in phase II and III trials (1, 19). This limitation has been an obstacle for the development of population pharmacokinetic models of infected adult patients. Recently, this limitation was circumvented by comodeling data from healthy volunteers with those from patients (12). While such an approach is not perfect, it at least provides a foundation for further pharmacokinetic studies and has enabled the construction of this stochastic controller.

We used a nonparametric approach throughout. For the purposes of feedback control, a fully parametric approach has the limitation of allowing only one possible value for each parameter and therefore does not allow for the possibility that the model does not fully describe the patient in question. Because parametric models are a single-model approach, they have no means to evaluate and optimize the expected precision with which a dosage regimen will achieve a desired target. This fact is well described by the separation principle (20), which states that whenever a system is controlled by first obtaining single point parameter estimates (as in a parametric model) and then controlled using these single point values, the result is suboptimal because there is no performance index to optimize the outcome.

This multiple-model stochastic controller represents a first critical step in the process of further optimizing voriconazole therapy for the treatment of critically ill immunocompromised patients. Clearly there are a number of challenges that must still be overcome before this software can be used in the routine care of patients. The first challenge relates to the nonlinear pharmacokinetics of voriconazole. Safe adjustment of voriconazole dosages requires a reasonable estimate of how and when nonlinear pharmacokinetic behavior occurs in an individual patient, which is governed by the K_m-V_max pair for that patient. Just as for clinical trial data, it is not possible to estimate the extent of nonlinearity until it is triggered or observed. One way this can be achieved is to alter the rate of the initial infusion of voriconazole to try to capture nonlinear behavior. This process is similar to stressing any dynamic system to observe and better understand the behavior of that system. The second challenge is that the current software needs a graphical user interface (GUI) to make it practical for extensive use in clinical settings. We are currently working on this. The third challenge is that the adaptive control problem using differential equation solvers is computationally intensive, and handheld devices, which are increasingly popular, are unlikely to be adequate. A solution could be that a handheld device can be used to access a larger computer and run the software remotely (21). The fourth challenge is that the performance of the controller in terms of its accuracy needs to be assessed in prospective clinical trials. The fifth challenge is that the controller needs to be tested for oral voriconazole therapy, which may be complicated by high degrees of interoccasion and within-patient variability that make Bayesian posterior estimation more difficult. Finally, the sixth challenge relates to changing pharmacokinetics as a result of physiological derangement or some other factor. The current RightDose software for simple models contains an interacting multiple-model method to account for changing parameter values over time within a single patient (see, for example, reference 22), but this has not yet been implemented within the rightdose.exe program described in this article.

In summary, the utility of this stochastic controller for voriconazole can now be further investigated, refined, and generalized to other compounds. The development of software that can be used individualize voriconazole therapy represents a natural progression from intensive pharmacokinetic studies and studies in which concentration-effect relationships have been elucidated. This controller offers promising potential for further improvement in clinical outcomes for immunocompromised patients and can be embedded within therapeutic drug monitoring strategies for patients receiving voriconazole.