A Physiologically Based Pharmacokinetic Model of Rifampin in Mice

Abstract

One problem associated with regimen-based development of antituberculosis (anti-TB) drugs is the difficulty of a systematic and thorough in vivo evaluation of the large number of possible regimens that arise from consideration of multiple drugs tested together. A mathematical model capable of simulating the pharmacokinetics and pharmacodynamics of experimental combination chemotherapy of TB offers a way to mitigate this problem by extending the use of available data to investigate regimens that are not initially tested. In order to increase the available mathematical tools needed to support such a model for preclinical anti-TB drug development, we constructed a preliminary whole-body physiologically based pharmacokinetic (PBPK) model of rifampin in mice, using data from the literature. Interindividual variability was approximated using Monte Carlo (MC) simulation with assigned probability distributions for the model parameters. An MC sensitivity analysis was also performed to determine correlations between model parameters and plasma concentration to inform future model development. Model predictions for rifampin concentrations in plasma, liver, kidneys, and lungs, following oral administration, were generally in agreement with published experimental data from multiple studies. Sensitive model parameters included those descriptive of oral absorption, total clearance, and partitioning of rifampin between blood and muscle. This PBPK model can serve as a starting point for the integration of rifampin pharmacokinetics in mice into a larger mathematical framework, including the immune response to Mycobacterium tuberculosis infection, and pharmacokinetic models for other anti-TB drugs.

INTRODUCTION

Tuberculosis (TB), caused by Mycobacterium tuberculosis, is an infectious disease which continues to be a major cause of death in large parts of the world (1). While the current first-line therapy for drug-susceptible TB (composed of rifampin, isoniazid, pyrazinamide, and ethambutol) has been in clinical use for nearly 30 years, the emergence and spread of drug-resistant M. tuberculosis strains have motivated the search for new, more-effective combination regimens (2). Our interest here is the development of mathematical tools to supplement the animal studies necessary for the identification and testing of such new anti-TB drug regimens.

The mouse is the primary animal species used for preclinical anti-TB drug development (3). Despite the differences between mice and humans, the activities of many anti-TB drugs against disease caused by M. tuberculosis are similar in both species (4, 5). Mice also provide for a range of TB susceptibility and pathology through a variety of outbred and inbred strains; a notable example is C3HeB/FeJ mice (6), which form necrotic pulmonary lesions similar to those observed in TB patients (7). The recent Critical Path to TB Drug Regimens (CPTR) Initiative (8) includes an added emphasis on the mouse for identification of new optimized three-drug regimens as a key step in advancing novel drug combinations into clinical trials (instead of sequential, single-drug replacement in the current four-drug regimen) (2).

In vivo evaluation of novel drugs against TB is usually performed through the study of correlations between drug exposure and efficacy data, mainly experimental measurements of plasma drug concentrations and bacterial killing kinetics, respectively (9, 10). While it may be desirable to obtain these data for multidrug regimens through a full factorial design, the large number of possible combinations of drugs, dose levels, and schedules of administration precludes such an approach due to practical limitations on the needed resources. Rather, investigations of new combination therapies in animal TB infection models are currently guided by empirical considerations (11, 12), with only a small fraction of potential regimens being subject to experimental evaluation.

We consider a systems pharmacology (13) approach, focused on physiologically based pharmacokinetic/pharmacodynamic (PBPK/PD) modeling, to more efficiently determine the in vivo multidrug dose-response relationships needed for the preclinical identification of new optimal anti-TB combination regimens. By including essential details of the drug-drug and host-drug-bacteria interactions, such a systems-level mathematical model for combination drug therapy against TB in mice can, in principle, simulate a variety of experimental studies and generate hypotheses regarding the efficacy of drug regimens that are not initially tested. While systems biology approaches have been used previously to describe the immune response to M. tuberculosis infection (14), both in humans (15) and in mice (16), efforts to include pharmacokinetics have been limited to human disease (17, 18). Additionally, these pharmacokinetic submodels incorporated minimal experimental data compared to data which is otherwise obtainable in animal models.

With the aim of increasing the available mathematical tools needed to support a systems pharmacology framework for preclinical anti-TB drug development, we constructed a preliminary whole-body PBPK model of rifampin in mice by using experimental data from the literature. Rifampin is an essential component of current short-course regimens for drug-susceptible TB (19) and remains a drug of interest in the search for improved combination regimens (20). As the treatment of TB requires multiple drugs (19), and as M. tuberculosis can potentially infect tissues and organs throughout the body (21), the extensive pharmacokinetics of a whole-body framework may be of use in quantifying drug-bacteria interactions in organs such as the lungs and spleen as well as providing drug concentrations in locations relevant to drug-drug interactions and toxicity, such as the liver and kidneys.

MATERIALS AND METHODS

Computational software.

MCSim v5.4.0 (22) was used for numerical solution of the PBPK model equations, including Monte Carlo (MC) and Markov chain Monte Carlo (MCMC) simulations. MCSim uses LSODES (23) as the differential equation solver and Metropolis-within-Gibbs (24) sampling for MCMC simulation. R v2.15.1 (25) was used for statistical calculations.

Experimental data.

Pharmacokinetic data consisting of rifampin concentrations in mouse tissues and fluids, with various doses and routes of administration, were obtained from the literature and separated into those used for model development (26–29) and those used for additional comparison with model output (9, 10, 30–35). Rifampin was the only rifamycin considered in this study; data for other rifamycins, such as rifapentine or rifabutin, were not used, as drugs in this class differ widely in their pharmacokinetic properties (36). Data for rifampin in other animals and humans (37–39) were used for model development when the corresponding data for mice were not available. No distinction was made between rifampin concentrations measured in serum and plasma or between measurements of concentrations obtained from different methods, such as high-performance liquid chromatography (HPLC) or bioassay. A rifampin blood/plasma ratio equal to 0.9 (40) was used to convert between blood and plasma (or serum)-based quantities. The original data from reference 33 were kindly provided by Joseph Raybon (personal communication). Other data that were published only in graphical form were digitally extracted using g3data (41).

PBPK model.

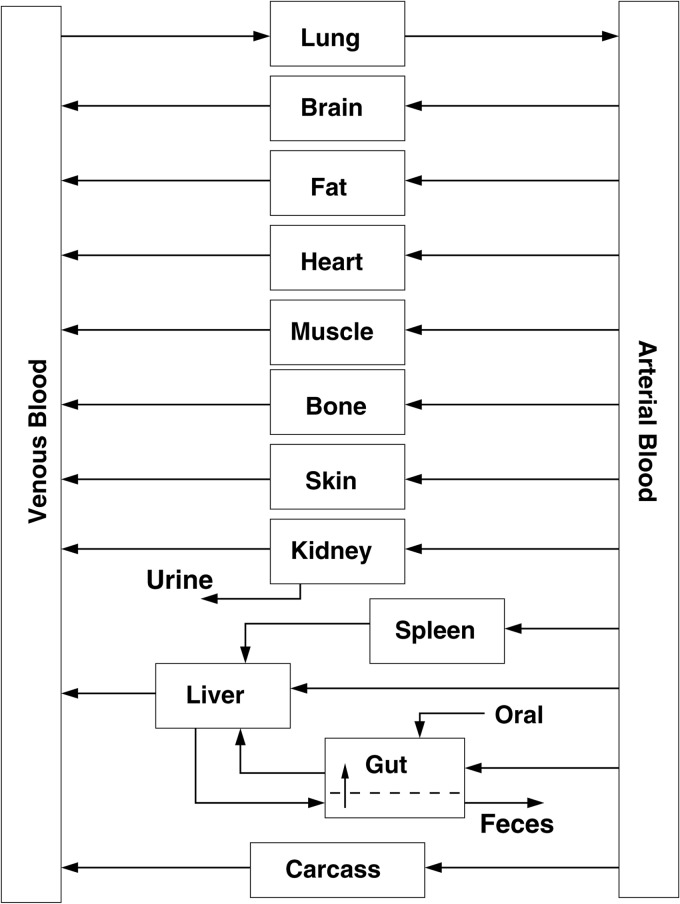
The PBPK model (Fig. 1) was based on a generic whole-body structure (42, 43) consisting of perfusion-limited compartments parameterized by tissue volumes, blood flow rates, and drug-dependent tissue/blood partition coefficients. Oral administration of rifampin was included as a pulsed input with first-order absorption into the gut. Clearance through the liver and kidneys was described in terms of total body clearance and fraction apportioned to the kidneys, with the remaining fraction being that for the liver. Enterohepatic circulation was included using a one-compartment model for the gut lumen, with first-order reabsorption into the gut and first-order elimination in the feces. Blood flows and total clearance were scaled to the three-fourths power of body weight, and tissue volumes were scaled linearly to body weight (44, 45). Model input consisted of (i) a specified dosing regimen, (ii) a set of parameter values, and (iii) initial conditions for drug amounts in each compartment. Model output consisted of time-dependent drug amounts and concentrations in blood and other tissues obtained by numerical solution of mass-balance differential equations for each compartment. The full set of PBPK model equations is provided in the appendix. Interindividual variability was accounted for by treating the model parameters as random variables with assigned probability distributions and using MC simulation to generate distributions for the model outputs.

Fig 1.

PBPK structural model.

Specification of parameter values.

The model parameters and probability distributions are given in Tables 1 and 2. The distribution types and coefficients of variation chosen were consistent with those typically used for PBPK models (46–49). Distributions were truncated at the mean ± 3 standard deviations (SD) to exclude biologically implausible values.

Table 1.

Mouse anatomical/physiological parameters

Parameter (units)	Abbreviation	Distributiona	Mean	CVb	Sourcec
Body wt (kg)	BW	L	0.025	0.16	52
Cardiac output (liters/h/kg0.75)	QCC	N	16.5	0.3	52
Gut lumen transit rate (1/h)	kF	L	0.6	0.3	51
Fractional tissue volumesd
Lung	VLUC	N	0.007	0.2	52
Brain	VBRC	N	0.017	0.2	52
Fat	VFC	N	0.07	0.2	52
Heart	VHC	N	0.005	0.2	52
Muscle	VMC	N	0.384	0.2	52
Bone	VBC	N	0.107	0.2	52
Skin	VSKC	N	0.165	0.2	52
Kidney	VKC	N	0.017	0.2	52
Spleen	VSC	N	0.0035	0.2	52
Gut	VGC	N	0.042	0.2	52
Liver	VLC	N	0.055	0.2	52
Venous blood	VVC	N	0.0327	0.2	52
Arterial blood	VAC	N	0.0163	0.2	52
Carcass	VCRC	N	0.0785	0.2	Present study
Fractional blood flowse
Brain	QBRC	N	0.033	0.3	52
Fat	QFC	N	0.09	0.3	50
Heart	QHC	N	0.066	0.3	52
Muscle	QMC	N	0.159	0.3	52
Bone	QBC	N	0.11	0.3	52
Skin	QSKC	N	0.058	0.3	52
Kidney	QKC	N	0.091	0.3	52
Spleen	QSC	N	0.01	0.3	52
Gut	QGC	N	0.13	0.3	52
Hepatic artery	QLAC	N	0.02	0.3	52
Carcass	QCBC	N	0.233	0.3	Present study

^aL, lognormal; N, normal.

^bCoefficient of variation. CV = SD/mean.

^cSources of the mean values.

^dFraction of body weight.

^eFraction of cardiac output.

Table 2.

Rifampin-dependent mouse parameters

Parameter (units)	Abbreviation	Distributiona	Mean	CVb	Sourcec
Fractional absorption	Fa	C	1.0	–d	27
Oral absorption rate (1/h)	ka	L	1.61	0.3	27
Total blood clearance (liters/h/kg0.75)	CLC	L	0.04	0.3	27
Fractional renal clearance	fR	L	0.19	0.3	26
Gut reabsorption rate (1/h)	kr	L	0.17	0.3	Fit (present study)
Partition coefficients
Lung/blood	PLU	L	0.49	0.2	27
Brain/blood	PBR	L	0.11	0.2	29
Fat/blood	PF	L	0.34	0.2	38
Heart/blood	PH	L	0.74	0.2	37, 38
Muscle/blood	PM	L	0.76	0.2	38
Bone/blood	PB	L	0.22	0.2	39
Skin/blood	PSK	L	0.76	0.2	38
Kidney/blood	PK	L	0.59	0.2	27
Spleen/blood	PS	L	0.25	0.2	28
Gut/blood	PG	L	0.74	0.2	29
Liver/blood	PL	L	3.1	0.2	27
Carcass/blood	PCR	L	0.59	0.2	Median (present study)

^aL, lognormal; C, constant.

^bCoefficient of variation. CV = SD/mean.

^cSources of the mean values.

^dNo variation.

The mean values for body weight, cardiac output, gut lumen transit rate, and fractional tissue volumes and blood flow rates were set to standard reference values for the mouse (50–52). Fractional tissue volumes and blood flow rates for the carcass (rest of body) were calculated as the remaining fractions.

The fraction of dose absorbed, oral absorption rate, and total clearance were obtained from the noncompartmental analysis of mouse serum concentration measurements following 10 mg/kg of body weight of oral and intravenous rifampin administration reported in Bruzzese et al. (27), where the oral absorption rate was calculated as the reciprocal of the difference between the mean residence times for oral and intravenous administration (53). The fractional renal clearance was set to the fraction of rifampin recovered in 24-hour urine in mice as reported by Binda et al. (26). The gut reabsorption rate was determined by a fit to the 0-to-24-h data for mean rifampin concentrations in serum, liver, lungs, and kidneys from Bruzzese et al. (27), with all other parameters held constant at their mean values. The fit was obtained using the Bayesian functionality of MCSim (22, 54), with a uniform prior distribution over [0,1], a normal likelihood with log-transformed experimental data, and noninformative log-uniform error. Three separate chains of 50,000 iterations each were obtained from a one-level MCMC simulation. Convergence was assessed with the potential scale reduction factor (54), obtained as an R value of 1.00. The fitted value was calculated as the mean of the posterior distribution consisting of the aggregate of the three individual chains.

Mean values for the tissue/blood partition coefficients (P) were set from measured rifampin concentrations (C) in plasma (or serum) and tissues, as P = C_tissue/C_plasma/BP, where BP is the rifampin blood/plasma ratio. Partition coefficients for lung, liver, kidney, spleen, brain, and gut were set using mouse data (27–29). There were multiple time points available for rifampin concentrations in lung, liver, kidney, and spleen; the data at 6 h postdosing were chosen as an estimated end of a distribution phase, with an approximate equilibrium between rifampin concentrations in blood and tissues. The remaining partition coefficients were set using human and other animal data (37–39), with the heart/blood coefficient determined as the average of those for human heart valve (37) and muscle (38). The carcass/blood partition coefficient was set equal to the median value of all the other partition coefficients.

Simulations.

A simulation of the rifampin plasma concentration following a single 10-mg/kg oral dose, using the mean parameter values from Tables 1 and 2, was run for calculation of the standard pharmacokinetic parameters (i) total area under the plasma concentration-time curve (AUC), (ii) terminal half-life (t_1/2), (iii) peak plasma concentration (C_max), and (iv) time to peak plasma concentration (t_max). MC simulations of rifampin plasma and tissue concentrations were run for single and repeated oral doses ranging from 10 mg/kg to 40 mg/kg. These simulations consisted of 10,000 iterations, where each iteration corresponded to evaluation of the model equations with a parameter set defined by a random sample from the probability distributions in Tables 1 and 2. The resulting output distributions were characterized by the 5th, 50th (median), and 95th percentiles. The initial conditions for drug amounts in the tissue compartments were set to zero for all simulations.

Sensitivity analysis.

An MC sensitivity analysis was performed using uniform distributions for each model parameter, bounded by ±10% of their mean values (55). One MC simulation using an oral dose of 10 mg/kg was run for 10,000 iterations. The Pearson correlation coefficient between each parameter and the rifampin concentration in plasma was calculated at 0.5, 1, 2, 4, 6, 8, 12, 16, and 24 h postdosing, with those having an absolute value greater than 0.2 considered sensitive and plotted as a function of time. The effect on the plasma concentration-time line shape due to variation in the mean values of some of the most sensitive parameters was examined.

RESULTS

Simulations.

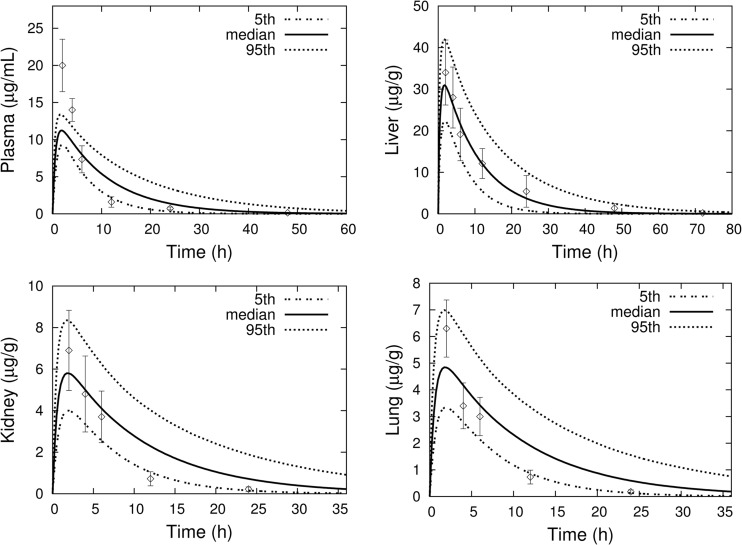
All simulations were performed using the parameter values given in Tables 1 and 2. With the exception of the experimental data from Bruzzese et al. (27), shown in Fig. 4, none of the other data shown for comparison with model simulations/predictions were used for model development.

Fig 4.

MC simulations (percentiles as solid and dashed lines) of rifampin concentrations in mouse plasma, lung, liver, and kidney following a single 10-mg/kg oral dose. Experimental data (mean ± SD) are from Bruzzese et al. (27).

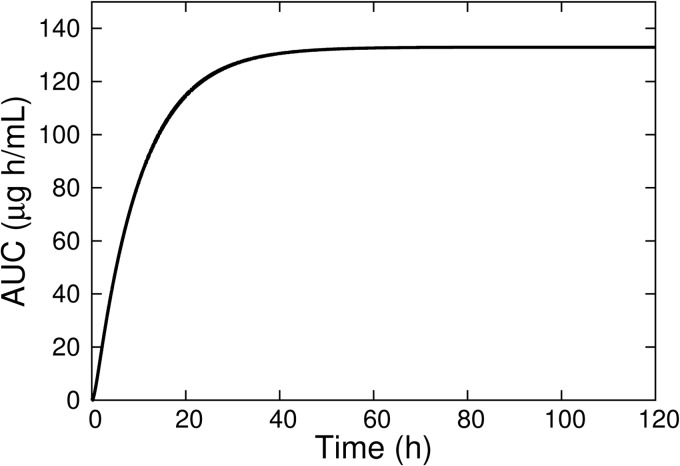
Model predictions of rifampin plasma pharmacokinetic parameters for a 10-mg/kg oral dose are shown in Table 3 together with experimental results from Ji et al. (32). The predicted values were calculated from a concentration-time curve generated using the mean parameter values from Tables 1 and 2. AUC was calculated by numerical integration (using MCSim [22]) of the concentration-time curve from 0 h to 120 h as an approximation of total AUC, and t_1/2 was calculated from the line passing through the log of the plasma concentration at 10 h and 12 h. Figure 2 shows the time dependence of the AUC, indicating a nearly constant value after approximately 50 h postdose.

Table 3.

Plasma pharmacokinetic parameters of rifampin for a single 10-mg/kg oral dose

Parameter (units)	Predicted	Observeda
Cmax (μg/ml)	11.41	10.58 ± 0.28
tmax (h)	1.78	1.33 ± 0.58
t1/2 (h)	6.77	7.61 ± 1.32
AUC (μg · h/ml)	132.9	139.7 ± 10.7

^aObserved values are the means and SD reported by Ji et al. (32).

Fig 2.

Model simulation of rifampin plasma AUC for a single 10-mg/kg oral dose.

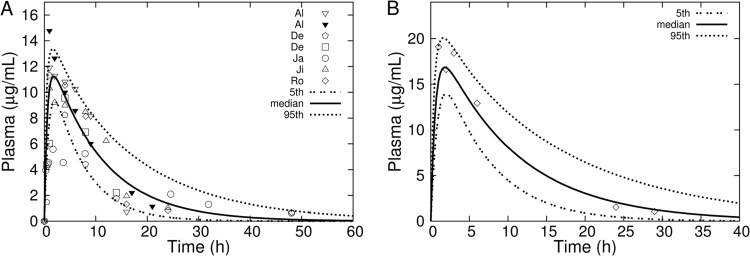
Figure 3 shows results of MC simulations for rifampin plasma concentrations following single 10-mg/kg and 15-mg/kg oral doses, together with corresponding experimental data from a variety of separate studies. The range of experimental data shown in the plot for the 10-mg/kg dose represents interstudy variability and falls generally within the 5th and 95th percentiles generated by the interindividual variability of the model. The experimental data shown with the 15-mg/kg simulation indicate a secondary absorption peak at the 3-h time point, indicative of enterohepatic circulation. The use of a single gut reabsorption rate constant does not capture the detail of the secondary absorption peak but does decrease the elimination rate, providing for good agreement with observation at the later time points.

Fig 3.

MC simulations (percentiles as solid and dashed lines) of rifampin concentrations in plasma following a single oral dose of 10 mg/kg (A) or 15 mg/kg (B). Data points are mean rifampin concentrations in plasma or serum obtained by digital extraction from plots in the sources: (A) Al, reference 30; De, reference 9; Ja, reference 10; Ji, reference 32; Ro, reference 34; (B) reference 31.

Figure 4 shows the results of an MC simulation of rifampin concentration-time profiles in plasma, lung, liver, and kidneys following a single 10-mg/kg oral dose, together with the experimental data reported in Bruzzese et al. (27). The tissue/plasma ratios for liver, lung, and kidney at 6 h postdosing that were reported in Bruzzese et al. (27) were used to set the values for the corresponding partition coefficients, and good agreement between model output and data at that time point is seen in the plots. The model underpredicts the plasma C_max but otherwise shows good agreement with the observed liver data.

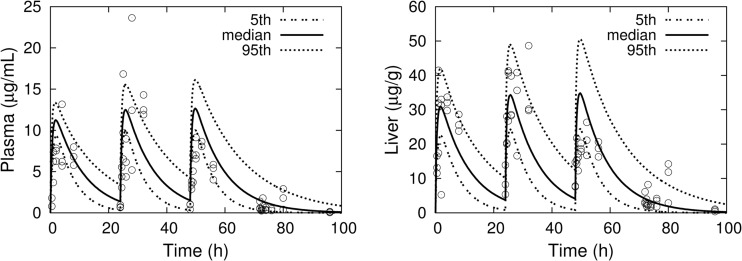
Figure 5 shows MC simulations of concentration-time profiles for plasma and liver following once-daily 10-mg/kg oral dosing for three consecutive days. The corresponding experimental data points are individual measurements from xenobiotic X receptor (SXR)-humanized mice that were reported by Raybon et al. (33). The model tends to overpredict the C_max for plasma concentrations but is in good agreement with the liver concentrations, including interindividual variability.

Fig 5.

MC simulations (percentiles as solid and dashed lines) of rifampin concentrations in plasma and liver for three consecutive daily 10-mg/kg oral doses. Experimental data (three mice per time point) are from Raybon et al. (33).

Figure 6 shows MC simulations of rifampin plasma concentrations in a 24-hour period following the fifth consecutive daily oral dose of either 10, 20, or 40 mg/kg. This dosing schedule represents a simulation of steady-state concentrations. The experimental data points from Rosenthal et al. (35) were also obtained under steady-state conditions, described as being measured after the 10th (for the 10-mg/kg dose) or 13th (for the 20- and 40-mg/kg doses) dose of a 5-days-per-week dosing. While the 20-mg/kg dose simulation underpredicted the observed plasma concentration, the 10- and 40-mg/kg dose simulations agree well with the experimental data.

Fig 6.

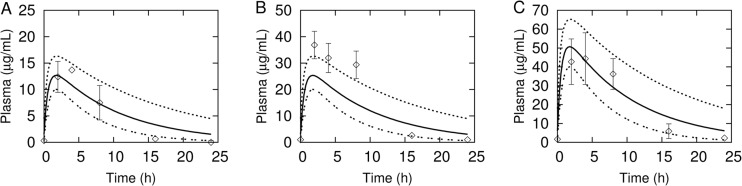
MC simulations (percentiles as solid and dashed lines) of rifampin plasma concentrations following steady-state oral dosing of 10 mg/kg (A), 20 mg/kg (B), and 40 mg/kg (C). Data points (mean ± SD) are rifampin serum concentrations digitally extracted from plots in Rosenthal et al. (35) (the error bars in the original published plot for panel B were lower-half bars only, and in panel C they were upper-half bars only).

Sensitivity analysis.

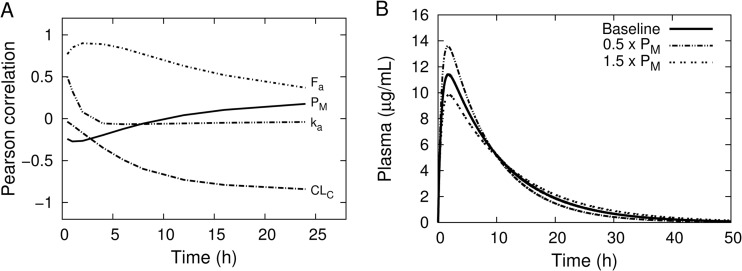
Figure 7A shows the Pearson correlation coefficient between the concentration of rifampin in plasma and the most-sensitive parameters as a function of time. The plot indicates that the rifampin plasma concentration is sensitive to fractional absorption (F_a) and oral absorption rate (k_a) early after dosing but becomes less so with increasing time, while total blood clearance (CL_C) shows the opposite behavior. This is consistent with the interpretation of these parameters as descriptive of absorption and elimination, respectively. The muscle/blood partition coefficient shows an early negative correlation with rifampin plasma concentration that changes later to a positive correlation, indicating that a decrease in this parameter would result in an early time increase in plasma concentration but a more-rapid decrease at later times. This has the effect of providing for a change in the shape of the concentration-time profile to increase the maximum concentration and decrease the terminal half-life. This is illustrated in Fig. 7B for the plasma concentration using a 10-mg/kg oral dose with the baseline, 0.5 times, and 1.5 times the muscle/blood partition coefficient. The correlation coefficient between body weight and rifampin plasma concentration monotonically increased from approximately 0.001 at 0.5 h to 0.2 at 24 h. In contrast, preliminary simulations (data not shown) with clearance scaled linearly to body weight resulted in this same correlation coefficient remaining at less than 0.01 throughout the 0-to-24-h time interval. This indicates a small, but not negligible, sensitivity of the rifampin plasma concentration to the allometric exponent for body weight in the clearance term.

Fig 7.

(A) Pearson correlation coefficients between sensitive parameters and rifampin plasma concentration as a function of time, following a single 10-mg/kg oral dose. The parameter names in the plot correspond to those listed in Table 1. (B) Simulation of plasma rifampin concentrations following a 10-mg/kg oral dose using the baseline mean values from Tables 1 and 2, compared with a 50% increase or 50% decrease in the baseline mean value of the muscle/blood partition coefficient.

DISCUSSION

The objective of this work was to develop a pharmacokinetic model of rifampin in mice which may serve as a component of a larger host-drug-bacteria/drug-drug interaction model, applicable to preclinical anti-TB drug development. The pharmacokinetic component of such a systems-level model should provide drug concentrations at target sites that include those for disease, toxicity, and drug-drug interactions. In the mouse TB infection model, both the lung and spleen are often sampled for bacterial load (9), and as rifampin is a cytochrome P450 and P-glycoprotein inducer (56), the liver, kidneys, gut, and brain may be of interest for drug-drug interactions. We considered PBPK modeling appropriate to our objective, as it provides drug concentrations throughout the body with minimal use of free parameters and, with many examples of modeling complex chemical mixtures (55, 57), provides an established framework for addressing multidrug combinations. Although PBPK modeling has had limited application to anti-TB drugs thus far (58, 59), it is well established in other areas of drug development and toxicological risk assessment (60); examples include anticancer (51) and immunosuppresive (61) drugs, monoclonal antibodies (62), nanoparticles (63), and a wide range of environmental toxicants (64). Empirical and semiphysiologically based pharmacokinetic models for rifampin, which include plasma and a tissue compartment such as liver (33) or lung (65, 66), are available. While these models were developed with a focus on a single target organ, they could be incorporated into our rifampin PBPK model as a lung lesion subcompartment (66), pulmonary epithelial lining fluid and alveolar cells (65), and enzyme induction in the liver (33).

The basic qualitative pharmacokinetic characteristics of rifampin (26, 38, 67), described by the PBPK model presented in this study, are (i) rapid and complete oral absorption (on an empty stomach), (ii) good penetration into tissues, (iii) enterohepatic reabsorption, and (iv) elimination in urine and feces. Metabolism was not included, as there is a lack of evidence that mice generate 25-desacetyl rifampin (C. Peloquin, personal communication), in contrast to this being the main metabolite of rifampin in humans (68). The parameter distributions for the PBPK model were descriptive of variability of rifampin pharmacokinetics in standard laboratory mice. Greater variability in the line shape of rifampin absorption than was exhibited in the available mouse data, including delay in absorption onset and increasing absorption rate, has been described in TB patients (69). While PBPK modeling is often motivated by animal-to-human scaling (60), the differences in variability, absorption, and metabolism of rifampin between mice and humans should be considered before such scaling of this PBPK model.

The PBPK model simulations were generally in good agreement with experimental data reported for rifampin concentrations in plasma, lungs, liver, and kidneys. However, rifampin concentration-time data for the remaining model compartments, shown in Fig. 1, would aid in further evaluation of the model. Such data may also be used to determine tissue/blood partition coefficients that were not available for mice in this initial study. The use of partition coefficients for species other than the mouse is one potential source of inaccuracy in our PBPK model predictions. This is evident, for example, in the sensitivity of the rifampin plasma concentration-time line shape for the muscle/blood partition coefficient. Experimental measurements of the time course of biliary excretion and elimination of rifampin in urine would be useful in better determining the clearance terms. The inclusion of a more-detailed model for enterohepatic circulation, containing, for example, a gallbladder compartment with delayed emptying, may better describe the peak concentration behavior seen in some of the plasma concentration-time data. Of additional importance is the determination of pharmacokinetic measurements in TB-infected mice; in particular, a complete set of tissue concentration-time measurements for both diseased and healthy mice would aid greatly in further model development.

APPENDIX

The PBPK model consisted of ordinary differential equations for drug amounts, A_i = A_i(t), where t is time and i is an index over tissue compartments or other quantities. The subscript abbreviations for tissue volumes and blood flow rates used in the equations below correspond to the quantities in Table 1 as follows: T, any of the following; LU, lung; BR, brain; F, fat; H, heart; M, muscle; B, bone; SK, skin; K, kidney; S, spleen; G, gut; L, liver; LA, hepatic artery; V, venous blood; A, arterial blood. Tissue drug concentrations were expressed as C_T = A_T/V_T, where V_T is the tissue volume. The concentration of drug in venous blood draining a tissue was expressed as C_VT = C_T/P_T, where P_T is the tissue/blood partition coefficient.

Scaling relations.

Cardiac output, Q_C, was scaled to body weight, BW, as Q_C = Q_CC × BW^0.75, where Q_CC is given in Table 1. The blood flow rates, Q_T, were scaled to cardiac output as Q_T = (Q_TC/Q_totC) × Q_C, where Q_TC is the corresponding fractional flow rate from Table 1 and Q_totC is the sum of all the fractional flow rates. Similarly, the tissue volumes were scaled to body weight as V_T = (V_TC/V_totC) × BW, where V_TC is the fractional tissue volume and V_totC is the sum of all the fractional volumes. Division of the tissue volumes and flow rates by V_totC and Q_totC, respectively, was used to maintain the constraint of constant total volume and blood flow during MC simulations (70). Total clearance was scaled as CL = CL_C × BW^0.75, where CL_C is the fractional value given in Table 2.

Venous and arterial blood.

$$\frac{d{\text{A}}_{\text{V}}}{dt}={\displaystyle \sum _{\text{T}}{Q}_{\text{T}}{C}_{\text{VT}}-Q_{\text{C}}{C}_{\text{V}}}$$ (1)

$$\frac{d{A}_{\text{A}}}{dt}=Q_{\text{C}}\left(C_{\text{VLU}}-C_{\text{A}}\right)$$ (2)

The summation in the equation for venous blood is over all tissues draining into the venous blood compartment in Fig. 1, with the term corresponding to the liver being Q_L × C_VL = (Q_LA + Q_S + Q_G)C_VL. The plasma drug concentration was determined by C_plasma = C_V/BP, with BP indicating the rifampin blood-to-plasma ratio.

Lungs.

$$\frac{d{A}_{\text{LU}}}{dt}=Q_{\text{C}}\left(C_{\text{V}}-C_{\text{VLU}}\right)$$ (3)

Brain, fat, heart, muscle, bone, skin, spleen, and carcass.

$$\frac{d{A}_{\text{T}}}{dt}=Q_{\text{T}}\left(C_{\text{A}}-C_{\text{VT}}\right)$$ (4)

Kidneys.

$$\frac{d{A}_{\text{K}}}{dt}=Q_{\text{K}}\left(C_{\text{A}}-C_{\text{VK}}\right)-f_{\text{R}}·\text{CL}·C_{\text{A}}$$ (5)

where CL is the total blood clearance of rifampin and f_R is the fraction of this total clearance apportioned to the kidneys.

Liver.

$$\frac{d{A}_{\text{L}}}{dt}=Q_{\text{LA}}{C}_{\text{A}}+Q_{\text{S}}{C}_{\text{VS}}+Q_{\text{G}}{C}_{\text{VG}}-Q_{\text{L}}{C}_{\text{VL}}-\left(1-f_R\right)·\text{CL}·\left(Q_{\text{LA}}{C}_{\text{A}}+Q_{\text{S}}{C}_{\text{VS}}+Q_{\text{G}}{C}_{\text{VG}}\right)/Q_{\text{L}}$$ (6)

Gut.

$$\frac{d{A}_{\text{G}}}{dt}=Q_{\text{G}}\left(C_{\text{A}}-C_{\text{VG}}\right)+k_{\text{a}}·A_{\text{OD}}+k_{\text{r}}·A_{\text{GL}}$$ (7)

where k_r is the rifampin gut reabsorption rate, A_GL is the amount of drug in the gut lumen, and A_OD is the amount of drug input to the gut as an oral dose.

Gut lumen.

$$\frac{d{A}_{\text{GL}}}{dt}=\left(1-f_R\right)·\text{CL}·\left(Q_{\text{LA}}{C}_{\text{A}}+Q_{\text{S}}{C}_{\text{VS}}+Q_{\text{G}}{C}_{\text{VG}}\right)/Q_{\text{L}}-k_{\text{r}}·A_{\text{GL}}-k_{\text{F}}·A_{\text{GL}}$$ (8)

where k_F is the gut lumen transit rate.

Oral dose.

$$\frac{d{A}_{\text{OD}}}{dt}=-k_{\text{a}}·A_{\text{OD}}+\frac{F_{\text{a}}·D}{\Delta }{\displaystyle \sum _{n=0}\left[\theta \left(t-t_{\text{n}}\right)-\theta \left(t-\left(t_{\text{n}}+\Delta \right)\right)\right]}$$ (9)

where k_a is the rifampin oral absorption rate, D is the dose, and F_a is the fraction of dose absorbed. The terms in the summation represent pulsed dosing at times t₀, t₁, etc., where Δ is the pulse width (e.g., 0.001 h) and θ(x) = 1(0) for x ≥ 0(x < 0) is a step function.