Time Series Analysis as a Tool To Predict the Impact of Antimicrobial Restriction in Antibiotic Stewardship Programs Using the Example of Multidrug-Resistant Pseudomonas aeruginosa

Abstract

The association between antimicrobial consumption and resistance in nonfermentative Gram-negative bacteria is well-known. Antimicrobial restriction, implemented in clinical routines by antibiotic stewardship programs (ASPs), is considered a means to reduce resistance rates. Whether and how antimicrobial restriction can accomplish this goal is still unknown though. This leads to an element of uncertainty when designing strategies for ASPs. From January 2002 until December 2011, an observational study was performed at the University Hospital Tübingen, Tübingen, Germany, to investigate the association between antimicrobial use and resistance rates in Pseudomonas aeruginosa. Transfer function models were used to determine such associations and to simulate antimicrobial restriction strategies. Various positive associations between antimicrobial consumption and resistance were observed in our setting. Surprisingly, impact estimations of different antimicrobial restriction strategies revealed relatively low intervention expenses to effectively attenuate the observed increase in resistance. For example, a simulated intervention of an annual 4% reduction in the use of meropenem over 3 years from 2009 until 2011 yielded a 62.5% attenuation (95% confidence interval, 15% to 110%) in the rising trend of multidrug-resistant Pseudomonas aeruginosa (three- and four-class-resistant P. aeruginosa [34MRGN-PA]). Time series analysis models derived from past data may be a tool to predict the outcome of antimicrobial restriction strategies, and could be used to design ASPs.

INTRODUCTION

Pseudomonas aeruginosa is an important opportunist associated with a broad spectrum of nosocomial infections in humans (1). Antimicrobial resistance among isolates is regarded as a major problem worldwide with increasing trends reported in several countries (2–6). Previous studies suggested a link between antimicrobial consumption and resistance in nonfermentative Gram-negative bacteria but yielded a range of diverse results (4, 5, 7, 8).

The different methodologies used are one likely reason for this diversity. A number of studies investigated whether a patient colonized or infected with a resistant isolate had previously been exposed to particular antimicrobial agents (mostly case control or case case control design) (9–12). Others cross-correlated the prescription rate of antimicrobials with the incidence of a certain resistance type, usually in a hospital-wide setting (3, 5, 8). Unlike such conservative approaches, time series analysis provides methods that can account for autocorrelation. Without these methods, any cross-correlation between two time series can be severely biased (13). One practical technique is the construction of autoregressive integrated moving average (ARIMA) models as described by Box and Jenkins (14). These models aim to describe the nature of a time series variable with the aid of past values (autoregression) and the weighted average of past random shocks (moving average). Such functions are used in several fields including medical specialties (15, 16). To explore the relationship between two or more time series, an extension of the method called a transfer function can be applied (14). Univariate transfer function models have previously been used to determine the relationship between antimicrobial use and resistance rate (17, 18).

The association between antimicrobial use and resistance rate in P. aeruginosa at the University Hospital of Tübingen, Tübingen, Germany, was investigated here by using multivariate transfer function models. Calculated parameter estimates provided a measure of the extent and direction of the observed association and were subsequently applied to quantify the impact of individual restriction strategies for each antibiotic significantly and positively associated with resistance rate. Additionally, the scale of such an effect was estimated and is thought to provide the foundation for future strategies employed in antibiotic stewardship programs (ASPs).

MATERIALS AND METHODS

Setting.

University Hospital of Tübingen is a 1,513-bed tertiary care teaching hospital affiliated with the Eberhard Karls University, Tübingen, Germany. The hospital provides various medical and surgical specialties, a pediatric unit, maternity ward, and dialysis unit. Organ transplantations, including bone marrow, are performed at the hospital.

Study design and data.

An observational study was conducted from 1 January 2002 until 31 December 2011. Data were obtained from all clinical departments except for psychiatric wards. Hospital inpatient days for each participating department were obtained from the hospital's administrative records and used as the denominator for every quarter. Antibiotic prescription data were gathered from the electronic pharmacy information system and converted into defined daily doses per 1,000 inpatient days according to the 2012 World Health Organization (WHO) anatomical therapeutic chemical (ATC) classification system (19). The antimicrobial agents tracked and investigated included carbapenems (meropenem and imipenem), cephalosporins (cefuroxime, cefotaxime, ceftriaxone, ceftazidime, and cefepime), aminoglycosides (gentamicin, tobramycin, and amikacin), fluoroquinolones (ciprofloxacin and levofloxacin) and beta-lactam/inhibitor combinations (ampicillin-sulbactam, amoxicillin-clavulanate, and piperacillin-tazobactam).

All in vitro bacterial susceptibility testing of P. aeruginosa isolates was predominantly performed on a Vitek 2 system (bioMérieux, Marcy l'Etoile, France), supplemented by disk susceptibility testing. MICs and zone diameters were interpreted following CLSI breakpoints (20). Carbapenem-resistant isolates were confirmed by the Etest method (bioMérieux, Marcy l'Etoile, France). Microbiological data were extracted from the laboratory information system using Hybase software (Tieto GmbH, Eschborn, Germany). Multidrug resistance (MDR) and extensive drug resistance (XDR) for isolates were defined referring to the European Centre for Disease Prevention and Control (ECDC)/CDC classification system (21). MDR isolates of P. aeruginosa were not susceptible to ≥1 agent in ≥3 of the following antimicrobial agent categories: aminoglycosides, antipseudomonal carbapenems, antipseudomonal cephalosporins, antipseudomonal quinolones, antipseudomonal penicillins and beta-lactamase inhibitors, monobactams, phosphonic acids, and polymyxins. XDR isolates of P. aeruginosa were not susceptible to ≥1 agent in all but ≤2 of the same antimicrobial categories mentioned above. These definitions are primarily used for epidemiological purposes. For this reason, we decided to employ a more clinically relevant classification of multidrug resistance (three- and four-class resistance [34MRGN]), defined as resistance to at least three of the following antimicrobial agents: piperacillin-tazobactam, ceftazidime, meropenem, and ciprofloxacin (22). Isolates from the same patient were counted only once for multidrug-resistant phenotypes. Intermediately susceptible isolates were considered resistant. Since the total number of isolates per 10,000 inpatient days fluctuated strongly in consecutive quarters, we abandoned the use of rates, and resistance was defined as the percentage of total isolates that were not susceptible to a single antimicrobial agent or a combination of antimicrobial agents. A total minimum of at least 50 isolates per time unit was required, because otherwise resistance could not be considered a representative value. All time units of the study episode were included in the analysis.

Statistical analysis.

Initially, the trend over time was analyzed by linear regression for each series of antimicrobial use and resistance. To explore and quantify the effect of antimicrobial use on resistance, transfer function models were constructed. Antimicrobial resistance was defined as the output series AR(t) whereas antimicrobial consumption was the input variable AC(t) which was assumed to be a potential cause of the output series. An additive noise term NT that follows a stationary autoregressive-moving average process and is independent of the input series was integrated when existent. Quarterly time lags of antimicrobial consumption of up to 1 year were applied to the antimicrobial resistance series.

To avoid multiple testing, an initial screening was used to find promising candidates of AC(t). Therefore, cross-correlation of AR(t) and AC(t) was performed at lags of up to 1 year. A candidate was deemed suitable for further testing if the correlation coefficient was significantly different from zero (based on 2.5 standard error limits). Additionally, to take autocorrelation into account, a prewhitening process was performed. ARIMA models were constructed for any time series of antimicrobial use and resistance. Stationarity was tested by using the Dickey-Fuller and Phillips-Perron test. Autocorrelation and partial autocorrelation function plots (ACF and PACF, respectively) were employed to identify the order of an ARIMA model. Subsequently, the parameters of the identified model were estimated by an unconditional maximum likelihood approach. An ARIMA model was accepted if residuals corresponded to a white noise process which was examined with Bartlett's periodogram-based test. After applying the ARIMA filter of the input series on the output series, the residual of both series were cross-correlated (23). Candidate identification was attained as with simple cross-correlation.

Selected candidates of AC(t) were integrated into transfer function (TF) models. To adjust for multiple hypothesis testing due to more than one suitable candidate, we used Bonferroni's correction (24). The Bayesian information criterion (BIC) and the mean squared error (MSE) were computed as diagnostic checks. All observed associations having a significant parameter estimate ω were further tested for a potential causal relationship. Causality was considered possible when past or present values of the input series AC(t) would help to predict the output series AR(t) better than past values of the output series alone, following the concept of Wiener-Granger causality. This required the BIC and MSE of the TF model to be improved to any degree and by at least 10%, respectively, compared with the BIC and MSE of the output series ARIMA model. Only associations that fulfilled these criteria were considered for further exploration in multivariate TM models.

Suitable input variables were included in one multivariate TM model. A multivariate model was accepted if it complied with the criteria mentioned for univariate models. Potential interventions like restriction of antimicrobial use were subsequently tested. To estimate the minimum intervention expense that would be needed to have an effect on AR(t), all AC(t) input series significant in multivariate models were altered to simulate an intervention. The minimum intervention tested was a cessation of further increase in antimicrobial usage for a certain antibiotic. Therefore, drug consumption between the beginning of 2009 and end of 2011 was kept identical to the level of 2008 (0% reduction). An increasing degree of restriction was further tested by reducing antimicrobial usage annually over this 3-year period. For instance, an intervention of 1% reduction means that in 2009 the level of consumption equaled the level of 2008 minus 1%. In 2010 and 2011, a further reduction of 1% each was simulated. Ascending restriction levels were modeled. An altered input time series was exchanged with the original series within the identified TF model, and predicted values of the manipulated and nonmanipulated TF model were calculated. Trends over the course of intervention were computed for both predicted output time series using linear regression. Changes in trends after simulated intervention were visualized by generating the alpha factor. This was done as follows: α = (δo − δi)/δo. The alpha factor is used to interpret the impact of a simulated intervention where δo is the trend of the predicted series with unaltered input variables and δi is the trend of the predicted series with altered input variables. For all trend directions, alpha was interpreted as follows: α < 0 constitutes an enhanced trend, α = 0 constitutes a steady trend, 0 < α < 1 constitutes trend attenuation, α = 1 constitutes trend neutralization, and α > 1 constitutes trend inversion. Calculation was not performed in the absence of a significant trend in the AR(t) output series. An intervention was rated as effective when alpha showed a desired trend alteration and when its 95% confidence interval did not include zero. Importantly, computing alpha was performed only when δo lay within the 95% confidence interval of the observed time series trend to ensure an appropriate prediction by the model. All analyses were made by using Stata version 12.0 (Stat Corp., College Station, TX). A P of <0.05 (two sided) was regarded as statistically significant.

RESULTS

Antimicrobial drug use.

Trend analysis of overall antibiotic prescription over 10 years is presented in Table 1. Most antimicrobial agents tracked revealed a significant gradual increase in consumption. Imipenem and the aminoglycoside group did not significantly increase over 10 years (P = 0.48 and P = 0.72, respectively), while gentamicin alone and ampicillin-sulbactam exhibited a negative trend. The overall antimicrobial consumption showed an increase (P < 0.001) with a median use of 392.8 defined daily doses (DDD)/1,000 inpatient days per quarter.

Table 1.

Characteristics and trends in antibiotic prescription at University Hospital Tübingen (January 2002 to December 2011)

Antimicrobial agent(s)	Avg usea	Gradient (95% CI)b	Trend	P value
All	392.8 (322.1–446.1)	6.618 (6.043 to 7.194)	Increasing	<0.001
Meropenem	37.5 (33.2–41.3)	0.502 (0.367 to 0.636)	Increasing	<0.001
Imipenem	1.8 (1.5–2.4)	−0.009 (−0.037 to 0.017)	Stable	0.46
Carbapenems	39 (35.6–43.1)	0.492 (0.356 to 0.627)	Increasing	<0.001
Cefuroxime	61 (16.6–76.9)	2.882 (2.663 to 3.102)	Increasing	<0.001
Cefotaxime	3.7 (3–4.8)	0.109 (0.032 to 0.186)	Increasing	0.007
Ceftriaxone	16.6 (13.3–17.9)	0.209 (0.155 to 0.263)	Increasing	<0.001
Ceftazidime	11.7 (9.6–12.9)	0.161 (0.107 to 0.215)	Increasing	<0.001
ESCc	30.9 (26.3–36.1)	0.479 (0.397 to 0.562)	Increasing	<0.001
Cefepime	4.1 (1.7–6.3)	0.246 (0.189 to 0.304)	Increasing	<0.001
Cephalosporins	97.7 (45.4–119.5)	3.608 (3.368 to 3.847)	Increasing	<0.001
Gentamicin	4.1 (1.7–6.3)	−0.128 (−0.167 to −0.085)	Decreasing	<0.001
Amikacin	1.8 (1.3–2.7)	0.053 (0.038 to 0.068)	Increasing	<0.001
Tobramycin	5.1 (4.1–6.1)	0.089 (0.017 to 0.161)	Increasing	0.017
Aminoglycosides	16.8 (15.1–18.3)	0.013 (−0.061 to 0.087)	Stable	0.721
Ampicillin-sulbactam	7.7 (6.7–8.8)	−0.103 (−0.157 to −0.05)	Decreasing	<0.001
Amoxicillin-clavulanate	83.1 (73.1–92.1)	0.469 (0.158 to 0.781)	Increasing	0.004
Piperacillin-tazobactam	30.5 (19.2–40)	0.847 (0.695 to 0.999)	Increasing	<0.001
Ciprofloxacin	50.8 (45.7–54.9)	0.448 (0.228 to 0.669)	Increasing	<0.001
Levofloxacin	71.1 (61.6–78.4)	0.598 (0.309 to 0.886)	Increasing	<0.001
Fluoroquinolones	128.1 (112.6–136.3)	1.293 (0.792 to 1.793)	Increasing	<0.001

^aAverage use is shown in defined daily doses (DDD)/1,000 inpatient days per quarter. The median value is shown. The values for interquartile range are shown in parentheses.

^bThe gradient is shown in DDD/1,000 inpatient days per quarter. The 95% confidence interval (95% CI) is shown in parentheses.

^cESC, expanded-spectrum cephalosporins.

Antimicrobial resistance.

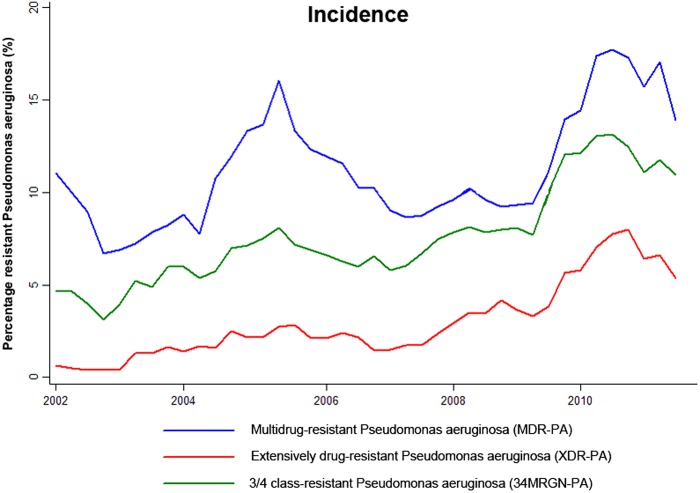
A total number of 5,157 isolates of P. aeruginosa were recovered from patients and tested. The incidences of multidrug-resistant P. aeruginosa (MDR-PA), extensively drug-resistant P. aeruginosa (XDR-PA), and three- and four-class-resistant P. aeruginosa (34MRGN-PA) increased dramatically over time (Table 2 and Fig. 1), with a remarkable rise in XDR-PA as indicated by a positive gradient in the XDR-PA/MDR-PA ratio (0.92; P < 0.001).

Table 2.

Characteristics and trends of multidrug-resistant Pseudomonas aeruginosa at University Hospital Tübingen (January 2002 to December 2011)

Phenotypea	Resistance (%)b	Gradient (95% CI)c	Trend	P value	ARIMAd	BICe	MSEf
MDR-PA	10.34 (7.88–13.17)	0.14 (0.02–0.27)	Increasing	0.029	2,0,0	244.89	20.25
XDR-PA	1.98 (0.98–4.49)	0.15 (0.09–0.21)	Increasing	<0.001	1+4,0,0	194.63	5.27
34MRGN-PA	7.35 (4.72–9.84)	0.19 (0.12–0.28)	Increasing	<0.001	1,0,0	217.13	10.12
XDR-PA/MDR-PA	NAg	0.92 (0.43–1.41)	Increasing	<0.001	NA	NA	NA

^aMDR-PA, multidrug-resistant Pseudomonas aeruginosa; XDR-PA, extensively drug-resistant Pseudomonas aeruginosa; 34MRGN-PA, three- and four class-resistant Pseudomonas aeruginosa.

^bResistance is shown as a percentage of resistant isolates per quarter. The median value is shown. The interquartile range is shown in parentheses.

^cThe gradient is shown as a percent change in resistance per quarter. The 95% confidence interval (95% CI) is shown in parentheses.

^dARIMA, autoregressive integrated moving average.

^eBIC, Bayesian information criterion.

^fMSE, mean squared error.

^gNA, not assessed.

Fig 1.

Incidence of resistant Pseudomonas aeruginosa at University Hospital Tübingen from 2002 until 2011 (using two-point moving averages).

Table 3 presents the trend and average resistance rate when resistance to a single agent was observed over the study period. High average resistance rates in P. aeruginosa isolates were seen for ciprofloxacin and levofloxacin (21.9% and 25.35%, respectively), attended by a significant positive trend (P < 0.001). However, resistance to piperacillin or piperacillin-tazobactam remains low (9.4% and 7.2%, respectively) with no evidence of any particular trend.

Table 3.

Characteristics and trends in antimicrobial resistance of Pseudomonas aeruginosa at University Hospital Tübingen (January 2002 to December 2011)

Antimicrobial resistance phenotype	Resistance (%)a	Gradient (95% CI)b	Trend	P value	ARIMAc	BICd	MSEe
Gentamicin	13.95 (11.25–20.2)	0.18 (−0.45 to 0.08)	Stable	0.17	1,0,0	287.79	59.35
Tobramycin	5.05 (3.45–6.65)	0.15 (0.08 to 0.23)	Increasing	<0.001	1+4,0,0	191.93	4.95
Piperacillin	9.4 (6.85–17.85)	0.09 (−0.16 to 0.34)	Stable	0.49	1,0,0	283.17	52.96
Piperacillin-tazobactam	7.2 (4.35–14.2)	0.09 (−0.13 to 0.32)	Stable	0.41	1,0,0	274.11	42.25
Levofloxacin	25.35 (19.6–31.25)	0.44 (0.29 to 0.58)	Increasing	<0.001	0,1,1	249.69	27.1
Ciprofloxacin	21.9 (17.6–24)	0.28 (0.15 to 0.42)	Increasing	<0.001	1,0,0	257.73	27.91
Meropenem	10.75 (8.15–14.4)	0.16 (0.06 to 0.25)	Increasing	0.001	1,0,0	223.32	11.81
Ceftazidime	11.7 (9.3–15.05)	0.18 (0.09 to 0.26)	Increasing	<0.001	1,0,0	217.66	10.25
Cefepime	9.9 (6.15–13.45)	0.25 (0.15 to 0.35)	Increasing	<0.001	1,0,0	232.43	14.86

^aResistance is shown as a percentage of resistant isolates per quarter. The median value is shown. The interquartile range is shown in parentheses.

^bThe gradient is shown as a percent change in resistance per quarter. The 95% confidence interval (95% CI) is shown in parentheses.

^cARIMA, autoregressive integrated moving average.

^dBIC, Bayesian information criterion.

^eMSE, mean squared error.

Univariate association of antimicrobial consumption with resistance.

In univariate analysis, the consumption of any antimicrobial agent tracked was investigated for an association with incidence of defined resistant types. While incidence of MDR-PA was not associated with antimicrobial use of any antibiotic tracked (data not shown), XDR-PA incidence was positively associated with the rising consumption of expanded-spectrum cephalosporins (ESC), cefepime, cephalosporins, and amoxicillin-clavulanate at zero time lag (Table 4). Association of 34MRGN-PA incidence and rising consumption of meropenem, piperacillin-tazobactam, ceftriaxone, ESC, cefepime, and cephalosporins was observed at different time lags.

Table 4.

Univariate transfer function models^a

Consumption of antimicrobial agent(s)	XDR-PA						34MRGN-PA
	Lag	ω	P value	NT	BIC	MSE	Lag	ω	P value	NT	BIC	MSE
Meropenem	−	−	−	−	−	−	1	0.28	<0.001	−	207.3	9
Piperacillin-tazobactam	−	−	−	−	−	−	0	0.15	0.011	AR 1	215.6	8.9
Ceftriaxone	−	−	−	−	−	−	1	0.6	0.001	AR 1	207.6	8.3
ESC	0	0.27	<0.001	−	186.8	4.7	1	0.35	<0.001	−	206.2	8.7
Cefepime	0	0.51	<0.001	−	185.8	4.6	0	0.6	<0.001	−	211.2	8.7
Cephalosporins	0	0.04	<0.001	−	186.4	4.7	0	0.05	<0.001	−	210.5	8.6
Amoxicillin-clavulanate	0	0.07	0.052	AR 1+4	193.3	4.6	−	−	−	−	−	−

^aXDR-PA, extensively drug-resistant Pseudomonas aeruginosa; 34MRGN-PA, three- and four-class-resistant Pseudomonas aeruginosa; ESC, expanded-spectrum cephalosporins; Lag, time lag in quarters; ω, parameter estimate; NT, noise term; BIC, Bayesian information criterion; MSE, mean squared error; −, no significant parameter estimate; AR, autoregressive component.

Multivariate association of antimicrobial consumption with resistance.

Two multivariate models were generated for the association between 34MRGN-PA and antimicrobial consumption (Table 5). After correction for the effect of all antibiotics within model 1, 34MRGN-PA incidence was significantly associated with the use of meropenem (P = 0.03). After the inclusion of cefepime as an additional input series, no significant association was observed (model 2). However, since the parameter estimate of meropenem use is still close to significance (P = 0.086), we considered meropenem use as independently and positively associated with 34MRGN-PA incidence. Subsequently, the alpha values were calculated for both models, simulating the intervention of an annual 0% reduction in meropenem consumption from 2009 onwards but keeping the 2008 level over the following 3 years constant (α₀), and the intervention of an annual 4% reduction. Intervention of an annual 4% reduction in meropenem use, trend lines, predicted series, and the observed incidence of 34MRGN-PA for model 2 are shown in Fig. 2. The graphical analysis shows an almost complete trend match of both the observed and the noninterventional predicted time series of 34MRGN-PA incidence, indicating a fine prediction by our model.

Table 5.

Multivariate transfer function models^a

Phenotype, model, and consumption of antimicrobial agent(s)b	Lag	ω (95% CI)	P value	α0 (95% CI)	%R	α (95% CI)	BIC	MSE
34MRGN-PA
Model 1				0.62 (0.22 to 1)	4	0.78 (0.38–1.19)	210.2	8
Meropenem	1	0.15 (0.015 to 0.29)	0.03
Piperacillin-tazobactam	0	0.03 (−0.09 to 0.15)	0.61
ESC	1	0.18 (−0.09 to 0.45)	0.2
Model 2				0.5 (0.03 to 0.98)	4	0.625 (0.15–1.1)	213.1	7.9
Meropenem	1	0.13 (−0.02 to 0.28)	0.086
Piperacillin-tazobactam	0	0.02 (−0.1 to 0.14)	0.76
ESC	1	0.11 (−0.16 to 0.38)	0.42
Cefepime	0	0.22 (−0.2 to 0.65)	0.3
XDR-PA
Model 1				0.23 (−0.16 to 0.66)	10	0.56 (0.16–0.96)	187.8	4
ESC	0	0.15 (0.02 to 0.28)	0.025
Cefepime	0	0.25 (−0.02 to 0.52)	0.067
Amoxicillin-clavulanate	0	0.04 (−0.01 to 0.09)	0.17
Model 2				0.54 (0.15 to 0.88)	4	0.65 (0.27–1.02)	187.8	4.4
Cephalosporins	0	0.03 (0.02 to 0.05)	<0.001
Amoxicillin-clavulanate	0	0.05 (−0.003 to 0.05)	0.072

^aLag, time lag in quarters; ω, parameter estimate; α₀, alpha value if the consumption level of 2008 held over 3 years without further reduction; %R, percentage of annual reduction over 3 years; α, alpha value regarding %R; BIC, Bayesian information criterion; MSE, mean squared error; XDR-PA, extensively drug-resistant Pseudomonas aeruginosa; 34MRGN-PA, three- and four-class-resistant Pseudomonas aeruginosa; ESC, expanded-spectrum cephalosporins.

^bThe antimicrobial agent(s) shown in boldface type indicate that the agent(s) was significant and it was altered for intervention simulation and consecutive alpha calculation. The noise term was included as additional parameter if significant.

Fig 2.

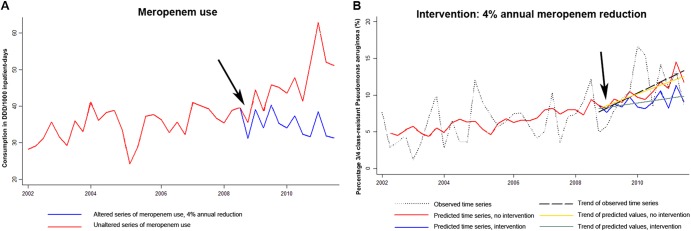
Illustration of simulated intervention. (A) Observed and altered meropenem consumption. DDD, defined daily doses. (B) Estimated resistance trends with and without antimicrobial restriction in comparison with the observed trend in three- or four-class-resistant Pseudomonas aeruginosa (34MRGN-PA). The black arrows indicate the start point of intervention.

Table 5 shows two multivariate models that investigate the association between XDR-PA and antimicrobial consumption. Both models exhibit a significant association with cephalosporins but not amoxicillin-clavulanate use. An intervention simulation of an annual 10% reduction of ESC or 4% reduction of all cephalosporins resulted in alpha values of 0.56 and 0.65, respectively.

For all tracked antimicrobial agents and groups, all potential associations between the incidence of isolates resistant to a specific antibiotic and antimicrobial use were investigated. Significant results are presented in the supplemental material (see Table S1 in the supplemental material).

DISCUSSION

The present study demonstrated significant associations between antimicrobial consumption and incidence of resistance among P. aeruginosa in a tertiary care hospital. A sharp rise in resistance was noted, which was particularly alarming for XDR-PA, which grew by about 1% per quarter within the MDR-PA group. In multivariate transfer function models, the incidence of 34MRGN-PA was strongly and independently associated with meropenem but no other antimicrobial use. Although different analytical tools and definitions of resistant phenotypes were used, our results are in line with previous studies, indicating that group 2 carbapenems cause relevant selection pressure on resistant P. aeruginosa (17, 25).

For the first time, simulating the intervention of antimicrobial decrease with the help of transfer function models was attempted. Our results indicate that preventing a further increase in meropenem consumption from 2009 onwards (0% reduction) could have attenuated the current incidence trend of 34MRGN-PA by 62% or 50% (model 1 or model 2, respectively) per the best α₀ estimates (Table 5). Because zero is not included in the 95% confidence interval, the intervention was considered likely effective. However, the second model reveals a 95% confidence interval range close to zero. We would therefore propose a strategy with an additional reduction of meropenem consumption to improve this safety gap. An annual 4% reduction over 3 years revealed alpha values of 78% and 62.5% (model 1 and model 2, respectively) with a safety gap of at least 15%, and would thus be a desirable goal in ASPs. Surprisingly, this amount of meropenem reduction needed for an effective impact on 34MRGN-PA incidence is relatively small. In two reports, implementation of ASPs resulted in a 54% to 97% decrease of the targeted antimicrobial agents over a study period of 3 to 5 years (26, 27). According to our results, such intensive restriction may not be necessary in all cases, especially as countereffects could be a consequence. The 80.1% hospital-wide reduction in cephalosporin use in one study went along with a 44% reduction in the incidence of cephalosporin-resistant Klebsiella spp. but also with a concomitant increase in the use of imipenem and a subsequent 68.7% increase in the incidence of imipenem-resistant P. aeruginosa infections (28). To prevent such countereffects, minor restrictions over longer time periods could be an alternative procedure.

The incidence of XDR-PA was associated with the use of ESC and all cephalosporins in multivariate models. In alpha modeling, maintaining the 2008 consumption level of ESC for the following 3 years could attenuate the incidence trend of XDR-PA by 23% (Table 5). However, due to a 95% confidence interval which includes an alpha value of zero, stopping the increase in ESC consumption without further reduction did not turn out to be a safe strategy. As an alternative, decreasing the annual consumption by 10% achieves more promising results and attenuated the trend by 56% with a safety gap of 16%. Interestingly, variations in carbapenem use had no measurable impact on the XDR-PA incidence, though all of these isolates were meropenem resistant. A possible reason might be the circulation of only a limited number of XDR-PA clones in our hospital (data not shown), suggesting a degree of nosocomial transmissions that could not be taken into account in this analysis. No influence of any antimicrobial use on the incidence of MDR-PA was observed, most likely due to the wide definition of multidrug resistance and different phenotypes within this group.

Our study is marked by limitations that result mainly from the imperfect nature of any model that tries to be an appropriate mirror of reality. The lack of reliable surrogate markers for other factors that contribute to the incidence of multidrug-resistant pathogens can result in incomplete models. An appropriate safety gap that excludes an alpha value of zero within the 95% confidence intervals is thus advisable. Additionally, direct comparison of alpha values when using the same intervention is an issue. Even if an antimicrobial agent had a superior alpha value over another does not necessarily mean that such an agent would be the better choice for targeting in ASPs. For example, an annual 4% reduction of different antimicrobial agents could demand different efforts, depending on the setting, and needs to be discussed to find the optimal strategy. Finally, this approach cannot clarify how a restriction should be established and implemented into clinical routines. This will largely depend on the local situation and resources.

Despite such constraints, transfer function modeling provides a measure of the extent of intervention effects, and thus we propose the following course of actions when planning strategies for ASPs. (i) Antimicrobial consumption data and resistance patterns should be analyzed, and the most alarming pathogens that need to be targeted should be identified. (ii) The association between antimicrobial resistance and consumption should be determined by employing time series analysis within the local setting. (iii) The minimal level of restriction needed for an intervention to be potentially effective can be estimated from modeling ascending restriction levels and the calculation of alpha values.

Taken together, multivariate transfer function models can be helpful when planning restriction strategies for ASPs to fight current trends in resistance development. Such models could suggest which antimicrobial agent a restriction strategy should primarily focus on. Interventions that were considered effective in our models were surprisingly low demanding and induced promising trend attenuations which could lower patient morbidity and hospital costs.