Abstract
Understanding virtually any process in cellular and molecular biology depends on knowledge of the rates of the biochemical reactions, so it is regrettable that few cellular and molecular biologists take advantage of kinetics experiments in their work. Fortunately, the kinetics experiments that are most useful for understanding cellular systems are within reach for everyone whose research would benefit from this information. This essay describes simple methods to measure the valuable kinetic parameters that characterize the dynamics of life processes. These “transient-state” methods not only differ in concept from traditional approaches used to analyze enzyme reactions at steady state, but they are also applicable to learning about the dynamics of any biological process.
INTRODUCTION
Life depends on dynamic biochemical processes, and understanding these reactions requires knowledge of physical constants called rate constants. Unfortunately, few cellular and molecular biologists know how to measure these key biochemical parameters, and many do not appreciate the value of rate constants because their only exposure to kinetics was in a biochemistry class that considered only steady-state enzyme kinetics. On the other hand, many cellular reactions do not involve catalysis or chemical cleavage of a substrate. Examples include proteins binding to other proteins, nucleic acids, membranes, or small molecules. Approaches other than those used for steady-state enzyme cycling are required to understand the dynamics of these reactions. Fortunately, relatively simple methods called transient-state kinetics or pre–steady state kinetics are available to characterize the dynamics of any biological system of interest. See Johnson (1992) for a detailed account of the method.
The approach involves changing conditions (e.g., reactant concentrations or solution conditions) and observing how a system of molecules changes over time as it reaches a new equilibrium. For example, two interacting molecules are mixed together, and the time course of their association is recorded. Alternatively, a mixture of two interacting molecules at equilibrium is diluted, or the solution conditions are changed, and the time course of the approach to the new equilibrium is recorded. Variations of these experiments yield the kinetic constants that characterize the interactions.
Fortunately, the results of transient kinetics experiments are intuitively obvious, and the approach is universally applicable to any molecules, including enzyme-catalyzed reactions. An important bonus of kinetic analysis is that the parameters not only provide insights about dynamics but can also be used to calculate equilibrium constants (and thus thermodynamics), even when equilibrium experiments are difficult or impossible. Although highly informative, transient kinetics experiments are much less common in cellular and molecular biology labs than equilibrium binding experiments or steady-state enzyme reactions, because few investigators have classroom or practical experience with pre–steady state kinetic assays.
This essay explains the concepts behind transient kinetics analysis and the design of experiments to measure kinetic parameters, with the hope that cellular and molecular biologists will overcome their fear of kinetics and embrace an approach that provides a new dimension, time, to their work. Taking advantage of time is powerful and rewarding. Some reactions are fast, requiring special assays or equipment, but many reactions are slow enough to allow the use of routine biochemical assays with the same materials prepared for equilibrium binding experiments.
Fortunately, just two types of chemical reactions account for essentially all biochemical processes. First-order reactions have one reactant; second-order reactions have two reactants. Getting started requires appreciation of a few basic concepts originally presented in a previous MBoC essay on equilibrium binding reactions (Pollard, 2010). We will start with binding reactions, which involve both first- and second-order reactions.
BINDING REACTIONS
In a reversible, bimolecular binding reaction, molecule A binds molecule B, forming complex AB:
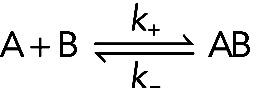 (Reaction 1) (Reaction 1)
|
Conceptually both the forward and reverse reactions are straightforward.
Association reaction
In the forward reaction (A + B → AB) one molecule of A and one molecule of B collide and bind together with a 1:1 stoichiometry. Association involves two reactants, so it is a second-order reaction. Structures consisting of more than two molecules usually assemble by a series of bimolecular reactions. The rate of this second-order association reaction is
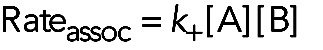 (1) (1)
|
The rate of the reaction, the change in concentration per unit time, has units of M s−1, where M is moles per liter. This rate depends on three parameters. The term k+ is a second-order association rate constant (lower case k) with units of M−1s−1 (pronounced per molar per second) that is characteristic of the reaction under a particular set of conditions. [A] and [B] are the concentrations of free molecules (in units of M, so the product on the right-hand side of Eq. 1 gives the association rate in units of M s−1) available for reacting at a given moment in time. In other words, the rate of binding scales linearly with the value of the rate constant and with the concentrations of both reactants. The objective of a kinetic analysis is to measure the value of the association rate constant. Then one can calculate the rate of the reaction with any concentrations of A and B.
Dissociation reaction
AB is the only reactant when the complex dissociates (AB → A + B), so this is a first-order reaction. The rate of the dissociation reaction, the change in concentration per unit time, has units of M s−1:
|
|
The parameter k− is a first-order rate constant called a dissociation rate constant, with units of s−1 (pronounced per second), and [AB] is the molar concentration of AB at a given moment in time. The dissociation rate constant reflects the probability that the complex will spontaneously fall apart in a unit of time. This probability is independent of the concentration, although [AB] appears in the rate equation, because it determines the bulk rate of the reaction in solution. A familiar example of a first-order reaction is radioactive decay, wherein the rate constant is the probability that an atom will decay, and the overall rate of decay depends on the size of the sample.
Relation of rate constants to equilibrium constants for binding reactions
A number called the equilibrium constant characterizes the affinity of molecules for each other. At equilibrium, the forward and reverse rates of a binding reaction are equal:
|
|
The equilibrium constant (uppercase K) is equal to the ratio of the forward and reverse rate constants or the ratio of the concentrations of products to free reactants at equilibrium:
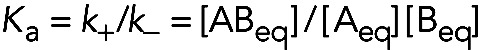 (4) (4)
|
Defined in this way, the equilibrium constant K for the binding reaction is an association equilibrium constant (Ka), with the units of M−1 (although, as noted below, equilibrium constants are really unitless). This definition has the advantage that the value of Ka is proportional to the affinity. Thus, the larger the value of Ka, the stronger the interaction and the more completely the reactants A and B are converted into the product AB.
The reciprocal of this expression for a binding reaction describes the dissociation equilibrium constant, or Kd:
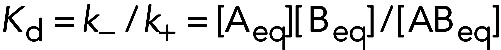 (5) (5)
|
This form of the equilibrium constant has the units of M. Biologists favor this definition, owing to the familiar units. Defined thus, the smaller the value of Kd, the higher the affinity and the more completely reactants A and B are converted into the product AB.
REVERSIBLE FIRST-ORDER REACTIONS
Changes in conformation (i.e., isomerization) are another common type of first-order reaction. For example, if molecule A exists in two conformations, A and A*. The reaction is
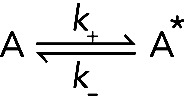 (Reaction 2) (Reaction 2)
|
The rates of the forward and reverse first-order reactions are
 (6) (6)
|
The parameters k+ and k− are the first-order rate constants for the forward and reverse reactions, with units of s−1, and [A] and [A*] are the concentrations of A and A* at a given moment in time. As with dissociation (Eq. 2), these first-order rate constants are the probabilities of the events per unit time and do not depend on the concentration of A or A*. However, the overall rates of such reactions in bulk samples depend on the rate constant and concentration as defined in Eq. 6.
Relation of rate constants to equilibrium constants for reversible first-order reactions
An equilibrium constant characterizes the balance between the two conformations. At equilibrium, the forward and reverse rates of this pair of first-order reactions are equal, so
|
|
and the association equilibrium constant is
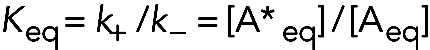 (8) (8)
|
Note that, in contrast to the binding reaction, the equilibrium constant for a pair of reversible first-order reactions is unitless. This difference might be troubling, but actually all equilibrium constants are unitless—even those for bimolecular reactions! This is because the equations for equilibrium constants actually call for “chemical activities” rather than the concentrations that everyone uses in their experiments. Recall from your general chemistry class that the chemical activity of a molecule is given by a comparison with a standard-state condition. This comparison is made by dividing the actual concentration by the standard-state concentration. In biochemistry, the standard condition is 1 M, so activities are defined as ratios of concentrations in M relative to 1 M. As a result, chemical activities are unitless but have the same numerical values as the molar concentrations.
This is a good place to note that chemical activities also depend on the environment because of the effects that solution conditions can have on the activity coefficient of molecules. The activity coefficient is a scaling factor that accounts for interactions among molecules (i.e., nonideality) that influence their ability to react. In dilute solution, the activity coefficient is unity, so the chemical activities of molecules are the same as the molar concentrations. However, in crowded environments, such as cytoplasm, activities may be much higher than the molar concentrations (Zhou et al., 2008). Hence many bimolecular reactions and some first-order reactions are faster in cytoplasm than in dilute buffers.
ADVANTAGES OF KINETICS EXPERIMENTS OVER EQUILIBRIUM EXPERIMENTS
One has two options to characterize a chemical reaction. Equilibrium experiments over a range of concentrations of reactants provide data to calculate equilibrium constants (Pollard, 2010). In a kinetics experiment, one determines the rate constants for the forward and reverse reactions. Because the ratio of these rate constants is the equilibrium constant, one learns about both dynamics and thermodynamics in one experiment. Note that this is a one-way street because equilibrium experiments reveal nothing about the rate constants of the forward or reverse reactions. Therefore one gets more for one's effort out of a kinetics experiment.
KINETIC ANALYSIS OF BINDING REACTIONS
The reaction is  , and the goal is to measure the rate constants, k+ and k−, for the forward and reverse reactions. In pre–steady state kinetics, one simply changes conditions, for example mixing A and B. Then one observes the time course of the reequilibration of the system to the new equilibrium distribution of species, as dictated by the concentrations and binding affinity.
, and the goal is to measure the rate constants, k+ and k−, for the forward and reverse reactions. In pre–steady state kinetics, one simply changes conditions, for example mixing A and B. Then one observes the time course of the reequilibration of the system to the new equilibrium distribution of species, as dictated by the concentrations and binding affinity.
The time course of an approach or “relaxation” to a new equilibrium generally follows a single exponential or sum of exponentials. Such reactions (Figure 1, A and C) start at the maximum rate, because none of the reactants has been consumed, and then slow down in a predictable way, as reactants are consumed until the rate is zero. If the reaction is a single exponential (rise or decay), the extent of the reaction (Signal) over time can be expressed as
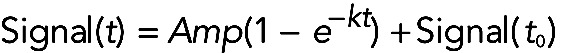 (9) (9)
|
FIGURE 1:
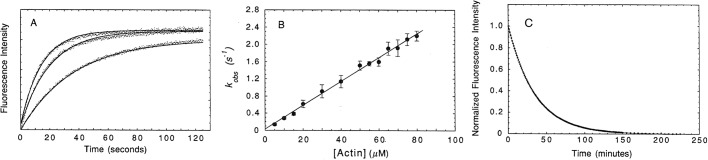
Kinetic analysis of a bimolecular binding reaction, phalloidin binding to actin filaments. Ligand B in this experiment is the cyclical peptide phalloidin labeled with the fluorescent dye rhodamine. Receptor A is polymerized actin. A low concentration of rhodamine–phalloidin is mixed with a range of high concentrations of actin filaments. The fluorescence of rhodamine–phalloidin bound to actin is 20-fold higher than free rhodamine–phalloidin, a convenient assay for bound ligand. (A) Time course of the fluorescence change after mixing 10 nM rhodamine phalloidin with 4 μM (left curve), 3 μM (middle curve), or 2 μM (right curve) muscle actin filaments in polymerizing buffer. The tiny points are the data and the solid lines are best fits to single exponentials. (B) Dependence of the observed rate constant (kobs) for rhodamine–phalloidin binding to actin filaments as a function of actin concentration. The association rate constant (k+) for the reaction given by the slope is 2.8 × 104 M−1 s−1. Vertical bars are ±l SD from the mean (n = 4–16). Binding is slow due to few binding sites being available at any moment in time. (C) Time course of the dissociation of rhodamine–phalloidin from actin filaments. An equilibrium mixture of 300 nM polymerized actin and 100 nM rhodamine–phalloidin in polymerizing buffer was mixed with 20 μM phalloidin at time zero, and changes in fluorescence intensity were monitored. The tiny points are the data and the solid line is the best fit to a single exponential yielding a dissociation rate constant (k−) of 4.6 × 10−4 s−1. Dissociation is slow due to the high stability (i.e., affinity) of the complex of phalloidin with actin filaments. (From De La Cruz and Pollard, 1994.)
where Signal (t) on the y-axis is any signal corresponding to the concentration of a reactant or product at time t (x-axis of time course); Amp is the amplitude (positive for an exponential rise or negative for a decay) or extent of the reaction at equilibrium; k is the characteristic rate constant of the exponential decay or rise toward the equilibrium value; and Signal (t0) is the starting signal, including any offset or background signal at time zero.
In a transient kinetic analysis, one measures how the time course of the approach to equilibrium depends on reactant concentration, so one refers to the rate constant for each exponential time course as an “observed rate constant” (kobs) for that concentration, to distinguish it from the fundamental reaction rate constants described above. This essay is limited to time courses that display single exponential behavior. Many papers consider multiexponential time courses (Henn and De La Cruz, 2005; Henn et al. 2008; De La Cruz and Ostap, 2009; Bradley and De La Cruz, 2012).
Association reaction
This second-order reaction is A + B → AB, with rate = k+[A][B]. For this section of our argument, we assume that binding is irreversible. One measures the rate constant by observing the time course of the formation of AB or the disappearance of A or B after mixing A and B (Figure 1A). To simplify the experiment, one usually uses “pseudo–first order conditions,” with a low concentration of one reactant (for example B) and greater than 10-fold higher concentrations of the other reactant (A). As in equilibrium binding experiments (Pollard, 2010), this strategy assures that most A is free, and its concentration does not change appreciably during the reaction, as the low concentration of B is converted over time into AB. Under these conditions, the total concentration of A is about the same as free A. With A in excess, the time course to form AB is an exponential with observed rate constant kobs that depends on [A] (Figure 1A) according to kobs = k+[A]. Therefore, by varying [A], one can evaluate k+ from the slope of a plot of kobs versus [A] (Figure 1B). Performing a binding experiment like this is simple compared with the effort to make the reagents, and with a good assay, the whole experiment may take only a few minutes. Six steps yield k+:
Step 1: Consider which reactant, A or B, to fix and which to vary. Make the decision based on the availability and solubility of the reactants and the ease of the measurements. Use a low concentration of the reactant that allows you to follow the time course of the reaction, and vary the reactant that is easier to purify or is more soluble. The following examples use a low fixed concentration of B. This key decision greatly simplifies the experiment and its analysis.
Step 2: Develop a sensitive assay to measure the concentration of B or AB. Note that [B] is the concentration of free B. Measuring one of these concentrations usually suffices for a simple reaction, because one can calculate the unknown concentrations by difference from the total concentrations and measurements of [B] or [AB]. Any assay will do, but spectroscopic assays are simple, and the signal can be followed on a millisecond timescale. Pollard (2010) reviews common optical assays.
Step 3: Design an experiment with the lowest concentration of B or AB that can be measured accurately.
Step 4: One at a time, mix a range of concentrations of A with the low, fixed concentration of B, and follow the time courses of each reaction until the system equilibrates at a plateau at which the concentrations of B and AB are stable (Figure 1A).
Step 5: Time courses of the change in the concentrations of B and AB should follow an exponential, each yielding an observed rate constant, kobs, that depends on the concentration of A. One can fit the data with a graphing program or estimate kobs from the half-time of the reaction (time for reaction to reach half of maximum change) and the equation kobs = ln 2/half-time. Alternatively a semi–log plot of an exponential function is a straight line, so you can plot log [B] or log [AB] versus time and measure kobs from the slope.
Step 6: Plot kobs versus [A] (Figure 1B). Because kobs = k+[A], the plot should be a straight line with a slope of k+ and an intercept of zero, as we assumed that the reaction is irreversible (see Reversible Reactions). A kobs that displays no or a nonlinear dependence on [A] indicates a binding reaction more complex than that illustrated in Reaction 1, such as multistep binding (one example discussed below under Linked Reactions) or a first-order isomerization preceding and limiting binding.
Dissociation reaction
The rate of a first-order dissociation reaction AB → A + B is equal to k−[AB]. The simplest way to observe a dissociation reaction is to “chase” bound ligand B off its receptor A with a large excess of a competitor, thereby eliminating contributions of rebinding to kobs. This requires a tag on the B bound to A to distinguish it from the free B added to the solution. If B can be labeled with a fluorescent dye, an optical assay (Pollard, 2010) can be used to follow tagged B bound to A after adding an excess of unlabeled B to compete with the fluorescent ligand for the receptor (Figure 1C). The fluorescent ligand dissociates spontaneously at a rate determined by k− and does not rebind, because the unlabeled ligand takes its place. Five steps will yield the dissociation rate constant.
Step 1: Chose a reactant that you can label and follow during the reaction. It helps if this reactant is also easy to purify and highly soluble. This example uses B as the ligand and A as the receptor.
Step 2: Use a sensitive assay to measure the concentration of B or AB. Spectroscopic assays have many advantages (Pollard, 2010).
Step 3: Equilibrate a mixture of A and B at concentrations that favor formation of the complex AB. Knowledge about the affinity from prior experiments or learned during the experiment allows for a reasonable choice of concentrations (Pollard, 2010). It is useful for the sample to contain a high proportion of AB, but the extent of the reaction is not crucial, as long as one can measure the concentration of B or AB or something proportional to their relative concentrations (e.g., absorbance or fluorescence change).
Step 4: At time zero, add a high concentration of unlabeled B and follow the time course until the system equilibrates at a plateau at which the concentrations of free and bound labeled B are stable.
Step 5: The kobs obtained from a single exponential fit of the time course of the change in the concentration of free or bound labeled A is equal to k−. In this case of irreversible dissociation, one does not have to vary the concentrations, because the rate constant of such a first-order reaction is independent of reactant concentration. However, confirm that dissociation is irreversible by checking that the value of kobs does not change significantly at a higher competitor concentration.
As alternatives to spectroscopic assays, one can use any chemical or physical tag on the bound ligand, such as an epitope or a radioactive tag (Chin et al., 2009). A convenient way to separate bound from free tagged B is to attach receptor A to a bead. Start the experiment by equilibrating tagged B with the beads carrying bound A. At time zero, add a large excess of untagged B. At intervals, pellet the beads and measure the concentration of tagged B in the supernatant with a chemical assay (SDS–PAGE and staining) or immunoassay (enzyme-linked immunosorbent assay or immunoblotting) or by counting radioactivity. Note that pelleting the beads does not disturb the equilibrium, because the equilibrium concentration of ligand B fills the spaces between the beads. As above, kobs equals k−.
REVERSIBLE REACTIONS
All of the examples up to this point ignored the fact that binding reactions are reversible. Ignoring reverse reactions is legitimate in a competition dissociation experiment, because the experiment is designed to ensure this condition is fulfilled. On the other hand, many kinetics experiments must take into account both reactions. An important but unintuitive feature of a reversible binding reaction is that kobs for the formation of AB from A and B is equal to the sum of the rate constants for the forward and reverse reactions, so for a binding reaction under pseudo–first order conditions with a low concentration of B, kobs = k+[A] + k−. One way to reconcile this in your mind is to know that the reverse reaction limits the extent of the reaction and therefore reduces the time to reach equilibrium.
Reversible association reaction
Accounting for contributions of reversibility of association reactions is not complicated. A plot of kobs versus concentration of A will be a straight line, but the y-intercept will not be zero. Because kobs = k+[A] + k−, the y-intercept will give a value for k−. However, this extrapolated value is often not as accurate as a direct measurement of k− in a chase or dilution experiment, particularly if it is near the origin of the graph.
Reversible dissociation reaction
The simplest dissociation experiment is to dilute an equilibrium mixture of A, B, and AB and observe the dissociation of AB over time as new equilibrium concentrations of A and B are established. Under these conditions, both association and dissociation reactions take place continuously, so association reaction must be avoided or taken into account during the reequilibration of the system. One way to avoid the association reaction is to make a very large dilution to slow the association reaction, which depends on the concentrations of free A and B. This is practical if one can dilute the reaction well below the Kd and still measure the concentrations of B or AB over time. If this is not practical, the time course of the reaction will not be an exponential. Nevertheless, one can estimate the rate constants by fitting simulations of a mathematical model of the reaction to the data (see below under The Value of Kinetic Simulations).
PRACTICAL CONSIDERATIONS
Slow reactions can be measured manually. Using low concentrations of reactants is a simple way to slow bimolecular reactions but will have no effect on the time course of a first-order reaction. Mechanical mixing in stopped-flow or quenched-flow devices is required for fast reactions that take place on a subsecond timescale. Most institutions will have a dedicated stopped-flow machine or a device to mix reactants in special cuvette that fits into a regular fluorimeter.
VALUE IN INCOMPLETE DATA
Ideally, one evaluates all of the parameters for a reaction, but partial data can be useful. Knowing a Kd from an equilibrium experiment and either k− or k+, one can calculate the missing rate constant, because Kd = k−/k+.
THE MAGNITUDES OF RATE CONSTANTS HAVE SIGNIFICANCE
Bimolecular reactions depend on random collisions between the reactants, and the collision rate constants depend on the sum of the diffusion coefficients of the two reactants, as well as the sizes of the interacting surfaces (see chapter 4 of Pollard and Earnshaw, 2007). Large reactants diffuse slowly but have large surfaces, while small, rapidly diffusing reactants have small interaction surfaces. The fastest bimolecular reactions are those in which two molecules react upon collisional encounter. These reactions have second-order association rate constants ∼109 M−1s−1 and are referred to as diffusion-limited reactions, because they are limited by translational diffusion of the reacting molecules.
Most macromolecular binding reactions are slower, because many collisions are needed to yield productive binding, as molecules are not uniformly reactive on their surfaces (i.e., they have binding sites), so the reactants are rarely oriented correctly for binding. Remarkably, many association rate constants are very high, in the range 106 to 107 M−1s−1. These reactions are also diffusion-limited, but the reactants are oriented correctly in only ∼0.1–1% of the collisions. If an association rate constant is larger than 107 M−1s−1, additional factors, such as a favorable electrostatic field around the binding site, make the reaction faster than the random collision rate. If an association rate constant is much smaller than 106 M−1s−1, it is likely that the binding sites of one or both reactants are rarely in a conformation suitable for binding a partner (see Figure 1 for an example).
Given that the values of many association rate constants are in the same range of 106 to 107 M−1s−1, dissociation rate constants are major determinants of affinities. For example, taking into account that Kd = k−/k+, dissociation rate constants will be on the order of 1 s−1 for low-affinity interactions with a Kd of 1 μM and 0.001 s−1 for high-affinity reactions with a Kd of 1 nM. With k− = 1 s−1, the half-time for dissociation is 0.7 s, so the complex is unstable, whereas, if k− = 0.001 s−1, the half-time for dissociation is 700 s. Thus, preserving interactions in a pulldown or immunoprecipitation experiment requires relatively high affinities in the nanomolar range (Pollard, 2010).
KINETIC ANALYSIS OF REVERSIBLE FIRST-ORDER REACTIONS
The reaction is 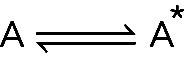 , and the goal is to measure the rate constants, k+ and k−, for the forward and reverse reactions. In this case, the observed rate constant is still the sum of forward and reverse reactions, taking the form of kobs = k+ + k−. As emphasized earlier in this essay, the kobs of a first-order reaction is independent of reactant concentration.
, and the goal is to measure the rate constants, k+ and k−, for the forward and reverse reactions. In this case, the observed rate constant is still the sum of forward and reverse reactions, taking the form of kobs = k+ + k−. As emphasized earlier in this essay, the kobs of a first-order reaction is independent of reactant concentration.
The only way to probe such a reaction by pre–steady state kinetics is to change a condition that influences the equilibrium between the two states and observe the time course of the reequilibration of the system. Buffer conditions (ionic strength, pH) are the most common variable, but temperature and pressure can be used for some systems. More commonly, kinetic parameters for reversible first-order reactions emerge from the analysis of linked reactions.
LINKED REACTIONS
Many binding reactions actually occur in two steps:
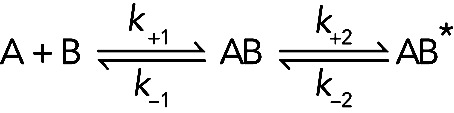 (Reaction 3) (Reaction 3)
|
where the conformation of AB* differs from AB and the second reaction is a pair of reversible first-order reactions. Often, such a conformational change is favorable and pulls the overall reaction to the right. This pair of linked reactions is very common in biochemistry, because interactions between two molecules, such as A and B, often result in a change of conformation.
Kinetic analysis offers two ways to probe such a conformational change. In fortunate cases, an optical signal, such as fluorescence intensity, may differ between AB and AB*. The conformational change can then be followed directly. Kinetic analysis of a binding reaction often will reveal the linked first-order reaction. In some cases, nonexponential time courses under pseudo–first order conditions provide evidence for multiple steps. More commonly, the time courses of the pseudo–first order reaction follow single exponentials (Figure 2A), but kobs depends hyperbolically on [A] (Figure 2B). At high concentrations of A, the observed rate constant plateaus because the rate of  exceeds the rate of
exceeds the rate of  , so the second reaction is rate-limiting. The observed rate constant of the overall reaction on the plateau is k+2 + k−2, the sum of forward and reverse rate constants of the second reaction. Note that a wide range of concentrations of B may be required to observe the nonlinear part of a plot of kobs versus [A].
, so the second reaction is rate-limiting. The observed rate constant of the overall reaction on the plateau is k+2 + k−2, the sum of forward and reverse rate constants of the second reaction. Note that a wide range of concentrations of B may be required to observe the nonlinear part of a plot of kobs versus [A].
FIGURE 2:
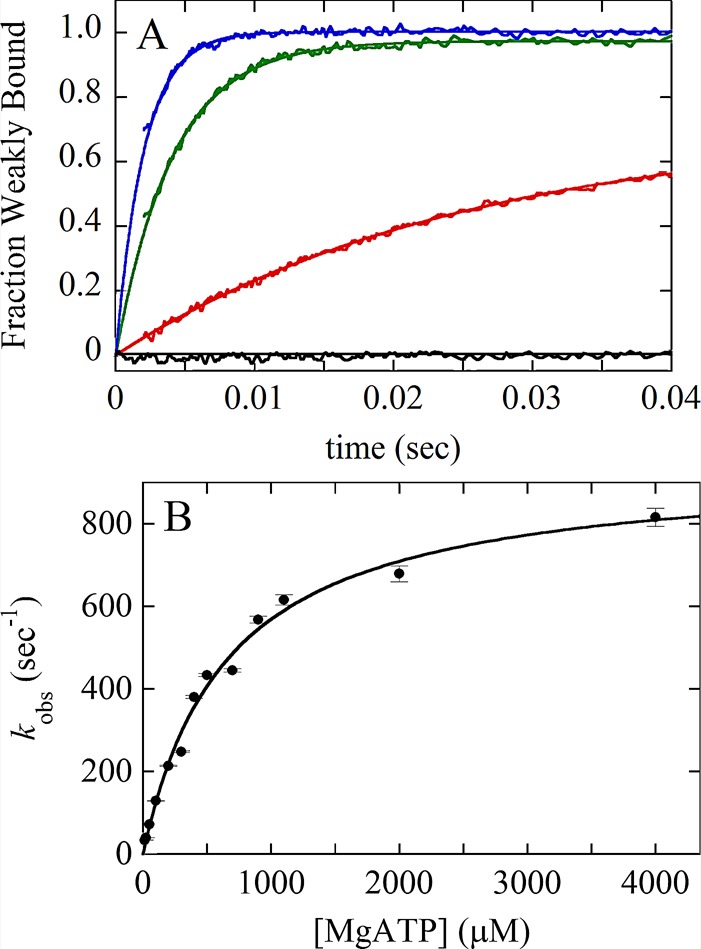
Kinetic analysis of a two-step association reaction: Mg-ATP binding to actomyosin VIIb. (A) Time courses of pyrene fluorescence after mixing 0.1 μM myosin VIIb bound to 0.1 μM pyrene-labeled actin filaments with a range of final concentrations of Mg-ATP: black, 0 μM; red, 25 μM; green, 250 μM; blue, 700 μM. The fluorescence of pyrene-labeled actin filaments is low when associated strongly with myosin without bound nucleotide (AM, black curve). The fluorescence is higher when associated with myosin in a weakly bound conformation induced by bound ATP (AM–ATP*) as observed over time for the other transients. (B) [ATP] dependence of the observed rate constant of fluorescence enhancement. The solid line through the data points is the best fit to a rectangular hyperbola, indicating a multistep mechanism, such as 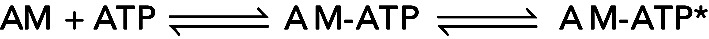 , where * indicates high fluorescence. The first step is rate-limiting at low concentrations of ATP. The second step is rate-limiting at high concentrations of ATP, so the observed rate constant at the plateau gives the sum of the rate constants for the second step, the reversible strong-to-weak actomyosin isomerization reaction. Figure adapted from Henn and De La Cruz (2005).
, where * indicates high fluorescence. The first step is rate-limiting at low concentrations of ATP. The second step is rate-limiting at high concentrations of ATP, so the observed rate constant at the plateau gives the sum of the rate constants for the second step, the reversible strong-to-weak actomyosin isomerization reaction. Figure adapted from Henn and De La Cruz (2005).
Enzyme reactions
Enzymes work through a series of linked reactions. The simplest possible enzyme mechanism is
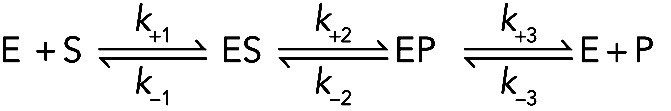 (Reaction 4) (Reaction 4)
|
where E is enzyme, S is substrate, ES is enzyme with bound substrate, and EP is enzyme with bound product P. The first and last reactions on this pathway are reversible second-order binding reactions. The middle reaction is a reversible first-order reaction.
One works out the mechanism by measuring the six rate constants (for examples, see De La Cruz and Ostap, 2009; Bradley and De La Cruz, 2012), using the strategies described up to this point in this essay. For example, one measures the rate constants for S and P binding E. Either chemical or spectroscopic assays can be devised to measure the rate constants for the chemical reaction that converts S to P. Note that this kinetic analysis defines not only the dynamics but also the thermodynamics of the pathway.
In the past, enzyme reactions were studied exclusively by measuring the generation of products at steady state with a low concentration of enzyme and an excess of substrate. This is still the best way to start characterizing a new enzyme. About 100 years ago, Michaelis and Menten made a brilliant breakthrough in the analysis of enzyme reactions (Michaelis et al., 2011) when they proposed the simplifying assumption that the reaction at steady state consists of just two steps:
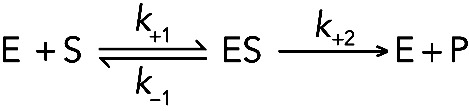 (Reaction 5) (Reaction 5)
|
This approach allows for the analysis of the dependence of the steady-state rate on substrate concentration in terms of an apparent affinity of the enzyme for substrate (KS) and catalytic rate. However, in reality, enzyme pathways always include an intermediate with product(s) bound to the enzyme, products usually bind reversibly to the enzyme, and product dissociation rather than product formation is often the rate-limiting step. Only transient kinetic analysis will reveal these important mechanistic features.
THE VALUE OF KINETIC SIMULATIONS
Often individual steps of a complex reaction mechanism, such as an enzyme, cannot be isolated experimentally and therefore cannot be measured directly (e.g., isomerization reactions that occur within the ES or EP complex). Furthermore, satisfying experimental requirements, such as pseudo–first order conditions, may be difficult. In these cases, kinetic simulations of reaction time courses may be able to extract otherwise unattainable rate and equilibrium constants. For example, simulations can be used to determine rate constants by fitting nonexponential time courses for a binding reaction done with similar concentrations of reactants.
Kinetic simulation programs compute time courses of reactions according to mechanisms and concentrations provided by the user (see Appendix). Accordingly, one can provide a minimal mechanism, such as Reaction 4, simulate a reaction time course for a range of combinations of rate and equilibrium constants, and observe how well the simulations coincide with experimentally observed reaction time courses over a broad range of reactant concentrations. Programs exist for fitting such data (see De La Cruz and Ostap, 2009), but in many cases, manual manipulation of parameters using trial and error and human intuition can rapidly achieve remarkable results, allowing one to identify a combination of reaction parameters that fit a complete data set well. Such procedures can identify otherwise hidden or silent reactions and even assign plausible rate and equilibrium constants to them (Frieden, 1983; Paul and Pollard, 2008, 2009; Henn et al., 2010). However, caution is required, as many combinations of rate and equilibrium constants can often fit a complex, multistep mechanism. For example, some reactions (e.g., fast, non–rate limiting ones) may have little effect on the overall reaction time courses, leaving their parameters poorly constrained by the data. It is therefore necessary to measure experimentally as many reaction constants as possible and to compare the simulated and experimental time courses over a wide range of concentrations.
In addition, kinetic simulations can and should be used regularly to confirm that experimentally determined rate and equilibrium constants reliably account for experimental data. This is particularly useful when one wishes to carefully analyze the amplitudes of the reactions. Kinetic simulations are also useful in designing experiments (e.g., one can select concentrations and timescales to collect data).
PRACTICE IS REQUIRED FOR TRANSIENT KINETICS TO MAKE SENSE TO A NEWCOMER
Our personal experience has made it clear that anyone new to transient kinetics needs to work through some examples to appreciate the concepts presented in this essay. We have found that the best way to offer this experience is to run some simple computer simulations of transient kinetics experiments. The Appendix offers a short tutorial. Knowing how to run simulation software is also valuable in analyzing experimental data, so please give the tutorial a try.
MAIN POINTS TO CONSIDER WHEN PLANNING A KINETICS EXPERIMENT
Create a good assay to measure reactants or products; consider the advantages of optical assays.
To analyze a bimolecular binding reaction, measure the time course of product formation using a low concentration of one reactant and a range of concentrations of the other reactant.
Calculate rate constants from the dependence of observed rate constants on the concentration of the varied reactant.
For dissociation reactions, measure the time course of dissociation of a tagged species after dilution or swamping the system with a high concentration of untagged species.
Use the rate constants to calculate equilibrium constants for the reactions.
APPENDIX: KINETICS TUTORIAL
This tutorial requires a computer and software to simulate the time course of reactions. Commercial software such as MATLAB is widely available. Fortunately, useful software is also available at no cost. A simple kinetics simulator called Tenua is available at http://bililite.com/tenua. Very powerful Virtual Cell simulation tools are available from the National Resource of Cell Analysis & Modeling (www.nrcam.uchc.edu).
We will assume the use of Tenua in this tutorial. Note that the units in these examples and the Tenua software are seconds and micromolar. A very helpful relationship is that the half-time of a first-order reaction or pseudo–first order reaction, t1/2 (the time required for half of the existing reactant to be converted to product), depends only on the rate constant and therefore is the same regardless of the starting concentration of the reactant. The relationship is
where 0.693 is the natural log of 2. Chapter 4 in Pollard and Earnshaw (2007) has the derivation of the equation. Starting anywhere along an exponential time course, the time to get halfway to the plateau is the same half-time. Use this relationship in solving the problems in this tutorial.
Problem 1. An irreversible first-order reaction, where A changes conformation to a.
-
Open Tenua, then indicate the reaction mechanism and the desired output by typing into the Editor window:
A <-> a;
*output
A; a;
Note that <-> stands for the two arrows representing a reversible reaction. A; a; indicates which output values to display.
In the Initial Variable Values window, enter the following parameters: startTime = 0; endTime = 10; timeSTEP = 0.05; A = 10; a = 0; k+ = 0.7; k− = 0.
These inputs will generate a time course of A and a from zero to 10 s in steps of 0.05 s, starting with (A) = 10 μM, (a) = 0, k+ = 0.7 s−1, and k− = 0.
Open the Graph window and click on the symbol for “start simulation” in the bar above. The computer calculates the time course and displays the data as a graph. The slope of the curve at every point is the rate of the reaction at that point. What is the maximum concentration of a? What is the maximum rate? What is the minimum rate? Which rate constant value results in complete conversion of A into a? Take a look at the Table window with the numerical data to get the exact time when half of A is converted into a, and use this half-time to calculate the observed rate constant for the reaction. Select “optimize axes” if the graph does not display your results appropriately. Note also that you can control the display by changing the time of the simulation.
What happens as you vary the value of k+ from 0.07 to 70 s−1? You will have to change the duration of the time course to find out.
Problem 2. A reversible first-order reaction where A changes conformation reversibly to a.
Use the same mechanism as Problem 1.
In the Initial Variable Values window, enter the following parameters: startTime = 0; endTime = 10; timeSTEP = 0.05; A = 10; a = 0; k+ = 0.7; k− = 0.7
Can you predict the final concentrations of A and a and the half-time of the reaction?
Open the Graph window and click on “start simulation” in the bar above. What is the maximum concentration of a? What is the half-time for the reaction? Calculate the observed rate constant, kobs, from the half-time. How does kobs relate to the (relative and absolute) forward and reverse rate constants? Vary the values of k+ and k− to confirm the relationship between kobs and these two rate constants.
Problem 3. An irreversible second-order reaction where A binds B to form AB with a low concentration of B and an excess of A (pseudo–first order conditions).
-
Open Tenua and type the mechanism into the Editor window.
A + B <-> AB;
*output
B; AB;
In the Initial Variable Values window, enter the following parameters: startTime = 0; endTime = 10; timeSTEP = 0.05; A = 1; B = 0.01; k+ = 0.7; k− = 0
Open the Graph window and click on “start simulation” in the bar above. What is the maximum concentration of AB? Which parameter limits the maximum value of AB? What is the maximum rate? What is the minimum rate? Which rate constant value results in complete conversion of B into AB? Take a look at the Table window to get the exact time when half of B is converted into AB, and use this half-time to calculate the rate constant (kobs) for the reaction. What is the relation of kobs to k+, [A], and [B]? Do all three parameters contribute to kobs?
Test your hypothesis by varying the values of k+, [A], and [B] to learn how they influence kobs.
Problem 4. A reversible second-order reaction with an excess of one reactant (pseudo–first order conditions), where A binds B reversibly to form AB. Use the same mechanism as Problem 3.
In the Initial Variable Values window, enter the following parameters: startTime = 0; endTime = 10; timeSTEP = 0.05; A = 1; B = 0.01; k+ = 0.7; k− = 0.7
Before you open the Graph window and click on “start simulation,” predict how changing the dissociation rate constant (k−) from zero to 0.7 s−1 will influence the amplitude of the change and the half-time of the reaction. What is the maximum concentration of AB? How do the rate constants influence the conversion of B into AB? What is the maximum rate? What is the minimum rate? What is the half-time for the reaction? Take a look at the Table window to get the exact time when half of B is converted into AB. Calculate the kobs from the half-time. What is the relation of kobs to k+, k−, [A], and [B]? Vary the values of k+, k−, [A], and [B] to determine which of these four parameters contribute to kobs. What is the relationship?
Problem 5. Impact of an irreversible first-order reaction linked to a second-order reaction. This problem uses an excess of one reactant to give pseudo–first order conditions. A binds B to form AB, and AB undergoes a conformational change to ab. This type of reaction is very common in biology. One example is a conformational change after a ligand binds a receptor. Open Tenua and type the mechanism into the Editor window.
A + B <-> AB <-> ab;
*output
B; AB; ab;
Start with just an irreversible second-order reaction. In the Initial Variable Values window, enter the following parameters: startTime = 0; endTime = 10; timeSTEP = 0.05; A = 1; B = 0.01; AB = 0; ab = 0; k+1 = 0.7; k–1 = 0; k+2 = 0; k–2 = 0.
This is the same as Problem 3. Run the simulation to refresh your memory. Then make k + 2 = 10, and predict the final concentrations of AB and ab. How will adding the irreversible first-order reaction influence the half-time of the overall reaction? Run the simulation. What are the maximum concentrations of AB and ab? Why does the concentration of AB peak, rise, and then fall after 0.3 s? What is the half-time for the formation of ab? Calculate the kobs from the half-time. Is this close to one of the rate constants? Which rate constant limits the overall time course of the reaction?
Problem 6. Impact of a reversible first-order reaction linked to a second-order reaction. Use the same mechanism as Problem 5. Start with the same initial parameter values: startTime = 0; endTime = 10; timeSTEP = 0.05; A = 1; B = 0.01; AB = 0; ab = 0; k+1 = 0.7; k–1 = 0; k+2 = 10; k–2 = 0.
Vary the value of A from 1 to 500. Reduce the length of the time course appropriately as you go. What happens to the maximum concentrations of AB and ab as you raise the concentration of A? Which step is rate-limiting at low concentrations of A? Which step is rate-limiting at high concentrations of A? Take a close look at the shapes of the curves. Are they all single exponentials (i.e., half-time constant at every point along each curve)? If not, why not? Which of these curves closely approximates single exponentials? Plot kobs versus A. What is the shape of the curve? What is the slope of the initial part of this curve? What is the plateau value of kobs?
Problem 7. Impact of a reversible first-order reaction linked to a reversible second-order reaction. Use the mechanism in problem 5, but start with a reversible but unfavorable first step. Enter these parameters: startTime = 0; endTime = 10; timeSTEP = 0.05; A = 1; B = 0.01; AB = 0; ab = 0; k+1 = 0.7; k–1 = 7; k+2 = 0; k+2 = 0.
Predict the half-time and amplitude of the change in AB. Run the simulation to see how your kinetics intuition is developing. What were the real values?
Predict what happens to the amplitude and the half-time if k+2 = 1. Give it a try to see what actually happens. How would you describe the time course of AB and ab? Which reactions determine the rate of accumulation of ab?
Predict what happens to the amplitude and the half-time if k+2 = 10. What were the real values? Are you getting better at predicting the outcomes of these experiments?
Predict what happens to the amplitude and the half-time if k+2 = 10 and k–2 = 2. Run the simulation to see what happens. What were the real values? Are you surprised? Can you figure out what determines the amplitude of the reactions?
Acknowledgments
Work in T.D.P.’s laboratory is supported by National Institutes of Health (NIH) research grants GM-026132, GM-026338, and GM-066311. Work in E.M.D.L.C.’s laboratory is supported by NIH research grant GM097348. E.M.D.L.C. is an American Heart Association Established Investigator (0655849T). The authors thank their laboratory colleagues Wenxiang Cao, Lynn Liu, Shalini Nag, Irene Reynolds Tebbs, and Emily Wong for their suggestions on the text.
Footnotes
REFERENCES
- Bradley MJ, De La Cruz EM. Analyzing ATP utilization by DEAD-box RNA helicases using kinetic and equilibrium methods. Methods Enzymol. 2012;511:29–63. doi: 10.1016/B978-0-12-396546-2.00002-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chin HF, Cai Y, Menon S, Ferro-Novick S, Reinisch KM, De La Cruz EM. Kinetic analysis of the guanine nucleotide exchange activity of TRAPP, a multimeric Ypt1p exchange factor. J Mol Biol. 2009;389:275–288. doi: 10.1016/j.jmb.2009.03.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De La Cruz EM, Ostap EM. Kinetic and equilibrium analysis of the myosin ATPase. Methods Enzymol. 2009;455:157–192. doi: 10.1016/S0076-6879(08)04206-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De La Cruz EM, Pollard TD. Transient kinetic analysis of rhodamine phalloidin binding to actin filaments. Biochemistry. 1994;33:14387–14392. doi: 10.1021/bi00252a003. [DOI] [PubMed] [Google Scholar]
- Frieden C. Polymerization of actin—mechanism of the Mg2+-induced process at pH 8 and 20 degrees C. Proc Natl Acad Sci USA. 1983;80:6513–6517. doi: 10.1073/pnas.80.21.6513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henn A, Cao W, Hackney DD, De La Cruz EM. The ATPase cycle mechanism of the DEAD-box rRNA helicase, DbpA. J Mol Biol. 2008;377:193–205. doi: 10.1016/j.jmb.2007.12.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henn A, Cao W, Licciardello N, Heitkamp SE, Hackney DD, De La Cruz EM. Pathway of ATP utilization and duplex rRNA unwinding by the DEAD-box helicase, DbpA. Proc Natl Acad Sci USA. 2010;107:4046–4050. doi: 10.1073/pnas.0913081107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henn A, De La Cruz EM. Vertebrate myosin VIIb is a high duty ratio motor adapted for generating and maintaining tension. J Biol Chem. 2005;280:39665–39676. doi: 10.1074/jbc.M507667200. [DOI] [PubMed] [Google Scholar]
- Johnson KA. Transient state kinetic analysis of enzyme reaction pathways. Enzymes. 1992;20:1–61. [Google Scholar]
- Michaelis L, Menten ML, Johnson KA, Goody RS. The original Michaelis constant: translation of the 1913 Michaelis-Menten paper. Biochemistry. 2011;50:8264–8269. doi: 10.1021/bi201284u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paul AS, Pollard TD. The role of the FH1 domain and profilin in formin-mediated actin-filament elongation and nucleation. Curr Biol. 2008;18:9–19. doi: 10.1016/j.cub.2007.11.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paul AS, Pollard TD. Energetic requirements for processive elongation of actin filaments by FH1FH2-formins. J Biol Chem. 2009;284:12533–12540. doi: 10.1074/jbc.M808587200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollard TD. A guide to simple and informative binding assays. Mol Biol Cell. 2010;21:4061–4067. doi: 10.1091/mbc.E10-08-0683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollard TD, Earnshaw WC. Cell Biology. 2nd ed. New York: Saunders; 2007. p. 902. [Google Scholar]
- Zhou HX, Rivas G, Minton AP. Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences. Annu Rev Biophys. 2008;237:375–397. doi: 10.1146/annurev.biophys.37.032807.125817. [DOI] [PMC free article] [PubMed] [Google Scholar]


