Functional Magnetic Resonance Imaging Phase Synchronization as a Measure of Dynamic Functional Connectivity

Abstract

Functional brain activity and connectivity have been studied by calculating intersubject and seed-based correlations of hemodynamic data acquired with functional magnetic resonance imaging (fMRI). To inspect temporal dynamics, these correlation measures have been calculated over sliding time windows with necessary restrictions on the length of the temporal window that compromises the temporal resolution. Here, we show that it is possible to increase temporal resolution by using instantaneous phase synchronization (PS) as a measure of dynamic (time-varying) functional connectivity. We applied PS on an fMRI dataset obtained while 12 healthy volunteers watched a feature film. Narrow frequency band (0.04–0.07 Hz) was used in the PS analysis to avoid artifactual results. We defined three metrics for computing time-varying functional connectivity and time-varying intersubject reliability based on estimation of instantaneous PS across the subjects: (1) seed-based PS, (2) intersubject PS, and (3) intersubject seed-based PS. Our findings show that these PS-based metrics yield results consistent with both seed-based correlation and intersubject correlation methods when inspected over the whole time series, but provide an important advantage of maximal single-TR temporal resolution. These metrics can be applied both in studies with complex naturalistic stimuli (e.g., watching a movie or listening to music in the MRI scanner) and more controlled (e.g., event-related or blocked design) paradigms. A MATLAB toolbox FUNPSY (http://becs.aalto.fi/bml/software.html) is openly available for using these metrics in fMRI data analysis.

Introduction

In cognitive neuroscience, there is growing interest toward the use of highly complex naturalistic stimuli, for example, movies, narrated stories, and music, to increase ecological validity of neuroimaging studies and to enable new type of research on emotions and higher-order cognitive functions (Alluri et al., 2012; Brennan et al., 2010; Hasson et al., 2004; Jääskeläinen et al., 2008). In their seminal article, Hasson et al. (2004) showed that when subjects are watching a feature movie, blood oxygen level-dependent (BOLD) signal time series in various brain structures of different subjects exhibit strong similarity and quantified it with intersubject correlation (ISC). To assess the dynamics of ISC, time-varying ISC can be computed over sliding temporal windows—at the expense of reduced temporal resolution—to identify the triggering event in a rich dynamic stimulus.

Indeed, it can be argued that synchronization, which the ISC measure reflects, is one of the most common ways of sharing information between entities of a system (Mesulam, 1990; Strogatz, 2004). Synchronization has been studied with both linear (temporal correlation, spectral coherence) and nonlinear (mutual information, phase synchronization [PS]) methods (Quian Quiroga et al., 2002).

PS is a specific synchronization measure that was initially introduced in physics when studying the behavior of two weakly coupled oscillators (Rosenblum et al., 1996). The original idea was to compare two signals by first separating their instantaneous amplitude from instantaneous phase information and then compare only phase time series. This is achieved by converting the real signal into its complex analytic version (Boashash, 1992) with signal processing techniques, like the Hilbert transform, Gabor expansion, or Wavelet filtering (for comparisons see Le Van Quyen et al., 2001; Schack and Weiss, 2005; Sun and Small, 2009).

While PS is a relatively well-established tool in magnetoencephalography (MEG)/electroencephalography (EEG) research, its usefulness in functional magnetic resonance imaging (fMRI) analysis has been explored only in a handful of studies. Laird et al. (2002) used PS based on Hilbert transform to identify synchronization of BOLD responses during a finger tapping experiment, demonstrating the potential of the method compared with the general linear model. Deshmukh et al. (2004) also used PS analysis in a finger tapping fMRI experiment to determine clusters of functionally connected brain areas. However, neither of these studies applied narrowband filtering of data, which is a necessary requirement when working with instantaneous phases—this follows from the Bedrosian's theorem (see the Methods section of the present article and Sun and Small, 2009).

More recently, Kitzbichler et al. (2009) investigated the power-law scaling of synchronization metrics in the human brain for simulated and recorded MEG and fMRI “resting state” data. They explored the inter-regional temporal dynamics of PS derived from wavelet coefficients of BOLD signal. However, the authors failed to consider possible artifacts arising from pulse and breathing that contaminate the relatively high frequency bands of BOLD activity that were explored. Further, the choice of an arbitrary phase difference threshold (π/4) was not statistically justified. In addition there are three other studies that have explored the dynamics of the complex phase of the BOLD signal during rest using wavelet coherence phase (Chang and Glover, 2010; Müller et al., 2004) and empirical mode decomposition (Niazy et al., 2011).

Despite these attempts, instantaneous PS has not gained popularity in fMRI data analysis. One possible reason for this is that when conventional controlled paradigms (e.g., event related or blocked design) are used, it is customary to look at signal properties that remain stable over the entire block or several repetitions, rather than instantaneous activations. However, the instantaneous characteristic of PS becomes handy when high temporal resolution is critical, such as when inspecting which aspects of a highly complex and dynamic stimulus relate to hemodynamic brain responses.

Dynamic functional connectivity measured with fMRI

Characterizing connectivity in the brain is important not only to gain a better understanding of brain functions (Jirsa and McIntosh, 2007), but also to classify clinical populations (Lynall et al., 2010) and monitor their recovery (Nakamura et al., 2009). Compared with anatomical or with effective connectivity (Friston, 1994), functional connectivity is just a measure of the similarity between activity in two brain areas, allowing a data-driven approach in the analysis of the connections. Various model-free measures of functional connectivity based on fMRI data exist (Margulies et al., 2010; Smith et al., 2011) with seed-based correlation (SBC) being one of the most used and straightforward methods for studying connectivity with low amount of assumptions and parameters. Measures of fMRI functional connectivity are usually time independent, examining connectivity between regions of interest over the whole scanning session, by computing pairwise temporal correlation coefficient between BOLD signal time series from the regions. It is only recently that the temporal dynamics of resting state fMRI connectivity have been explored with computational models (Cabral et al., 2011; Honey et al., 2007) and with real data using sliding time window correlation (Majeed et al., 2011), sliding time window ICA (Kiviniemi et al., 2011), wavelet coherence (Chang and Glover, 2010), partial least squares (Grigg and Grady, 2010), and Kalman filtering (Kang et al., 2011).

It is also of interest to study how connectivity changes due to stimuli or task demands in a model-free manner. Sakoğlu et al. (2010) addressed the issue of dynamic functional connectivity during task modulation. The authors defined Dynamic Functional Network Connectivity as the functional connectivity over a sliding time window. Various time window widths were compared but it was not possible to reduce the temporal window under a critical sample size (64 samples in this case) without compromising the reliability of the resulting correlation value (Fisher, 1921); shorter temporal windows (i.e., too few samples) will produce biased estimates. Longer time windows increase reliability at the expense of temporal resolution.

PS as a measure of dynamic functional connectivity

Here, we hypothesized that it is possible to solve the time resolution/reliability trade-off by adopting PS as an instantaneous measure of dynamic functional connectivity during stimulation. We specifically hypothesized that instantaneous PS is a reliable measure comparable to correlation-based methods (SBC and ISC) but with maximal temporal resolution, enabling assessment of time-varying functional connectivity in a model-free fashion. The aim of this study is to introduce a set of metrics to evaluate functional connectivity of fMRI time series with PS, test the statistical significance of connections, and compare the PS metrics with established correlation-based methods. We expected that there are several advantages in using instantaneous phase as a measure of functional connectivity: (1) PS is not affected by intersubject amplitude variability (i.e., the phase captures the temporal dynamics); (2) PS instantly identifies full temporal dynamics without any need for time-windowed averaging; (3) PS is a nonlinear measure, which can be more suitable for identifying complex dynamic processes in the brain (Pereda et al., 2005); (4) PS is computationally faster than temporal correlation: with one transform we obtain the phase value for each time point for the whole brain, and PS is then a sum of complex numbers over the unit circle.

Methods

The analytic signal, instantaneous phase, and instantaneous frequency

The analytic representation of a real valued signal x(t) is a complex signal x_a(t) with the same Fourier transform of x(t) but defined only for positive frequencies. The analytic signal can be built from the real signal by using the Hilbert transform:

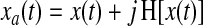(1)

Where H[•] is the Hilbert transform and j is the imaginary unit. The main advantages of using the analytic signal are that, given some real data represented by one function of time, we can determine two functions of time to better access meaningful properties of the signal. We consider now a narrowband signal that can be written as an amplitude-modulated low-pass signal a(t) with carrier frequency expressed by φ(t):

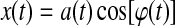(2)

If the Bedrosian's theorem (Bedrosian, 1962) is respected by a(t) and cos[ϕ(t)] (i.e., if the Fourier transforms of the two signals have separate supports) then the analytic signal of a narrowband signal can be rewritten as the product of two meaningful components:

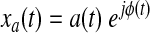(3)

Where a(t) is the instantaneous envelope and ϕ(t) the instantaneous phase. The Bedrosian's theorem has a clear implication: the narrower the bandwidth of the signal of interest, the better does the Hilbert transform produce an analytic signal with meaningful envelope and phase. Adopting a band-pass filtered version of the BOLD time series improves the separation between the phase and envelope spectra. The information from the original signal is hence redistributed in the phase component for frequencies in the pass-band and in the amplitude component at low frequencies out of pass-band. For an exhaustive review of the mathematical and practical aspects of the analytic signal and its applications please refer to Boashash (1992), and Sun and Small (2009).

BOLD signal as a narrowband signal

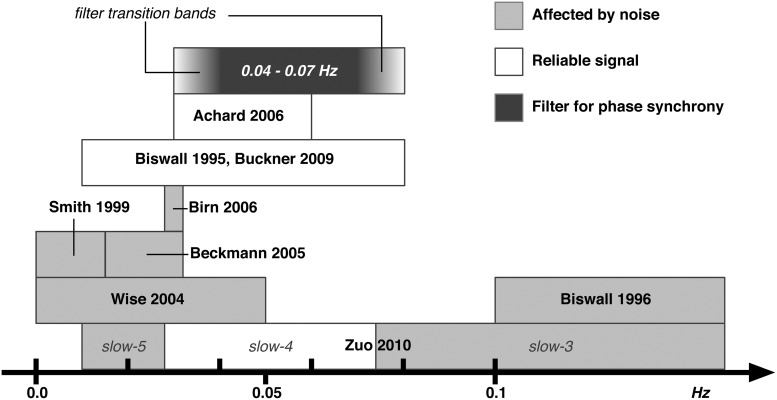
The frequency spectrum of fMRI BOLD signal has been extensively studied since the early days of fMRI (Weisskoff et al., 1993). In 1996 Biswal et al. studied the effects of cardiac and respiratory rates on the BOLD signal with typical frequencies around 1–2 Hz and 0.3 Hz, respectively. Since fMRI data are often collected with time to repetition (TR) in the order of 2 sec (0.25 Hz Nyquist frequency), respiratory and cardiac frequencies are out of band, causing aliasing in the higher frequency range of the BOLD signal (>0.1 Hz). The lower end of the BOLD spectrum (0.0–0.015 Hz) is also not immune to noise such as “low frequency drift” (Smith et al. 1999). It is nowadays common practice to band-pass filter the BOLD signal between 0.01–0.08 Hz (Biswal et al., 1995; Buckner et al., 2009; Zou et al., 2008), but even within this frequency range there is noise contamination. Wise et al. (2004) investigated the spontaneous fluctuations in arterial carbon dioxide level mainly affecting the BOLD signal in the frequency range 0.0–0.05 Hz. Beckmann et al. (2005) and Birn et al. (2006) reported a noise component around 0.03 Hz attributed to respiratory-related fluctuations when a slow TR is used. Recently Zuo et al. (2010) explored the BOLD signal at sub-bands relevant in electrophysiological DC and intracranial recordings (Penttonen and Buzsáki, 2003): slow-5 (0.01–0.027 Hz), slow-4 (0.027–0.073 Hz), slow-3 (0.073–0.198 Hz), and slow-2 (0.198–0.25 Hz). The slow-3 and slow-2 bands were mainly mapped to the white matter and attributed to aliased respiratory and cardiac signals. Slow-4 and slow-5 bands were mainly identified in the gray matter, with slow-4 more prominent in the thalamus, basal ganglia, and sensorimotor regions while slow-5 was more prominent in ventromedial cortical areas. Slow-4 was the most reliable sub-band with more widespread spatial distribution of reliable voxels. A similar band (0.03–0.06 Hz) was also reported to give greater small-world topology when considering resting state data with complex network tools (Achard et al., 2006).

Based on these studies, we chose the frequency range of ∼0.04–0.07 Hz, equivalent to the slow-4 band minus the 0.03 Hz critical frequency. Figure 1 shows a graphical summary of the frequency bands addressed in the mentioned literature and our chosen sub-band.

FIG. 1.

Frequency bands of blood oxygen level-dependent (BOLD) signal. A summary of functional relevance of various frequency bands of the BOLD signal based on previous studies. Light gray bars indicate frequency bands that have been observed to contain noise, white bars indicate frequency bands noted as functionally relevant, and the dark gray bar indicates the narrow frequency band that was used in the current study to calculate the phase synchronization (PS) measures.

Metrics of PS

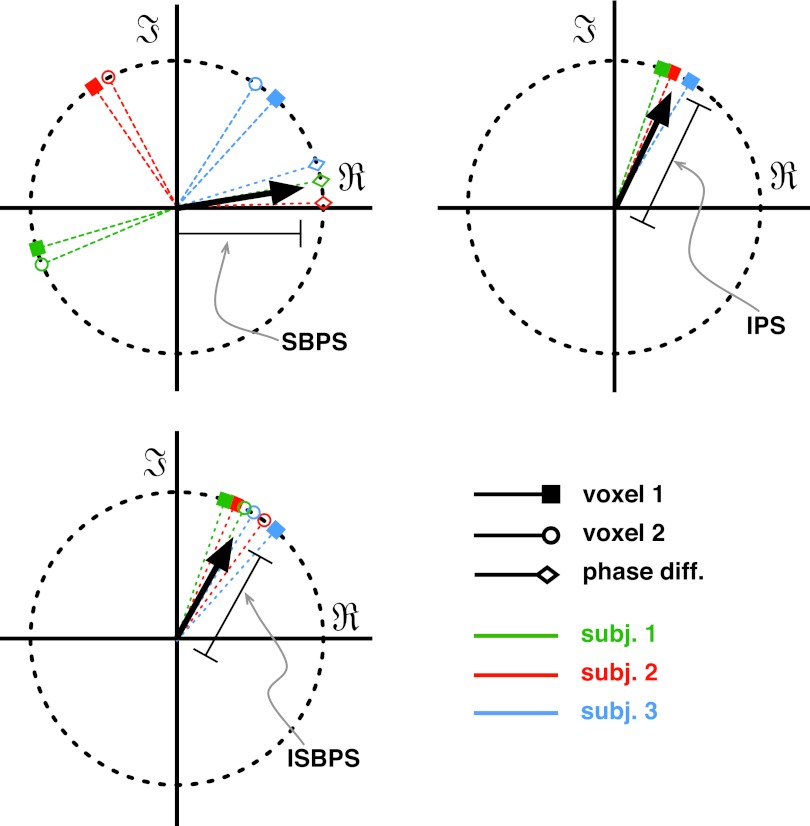
We define three different metrics to analyze the PS of fMRI data (see Fig. 2).

1. Seed-based phase synchronization (SBPS): within-subject functional synchrony;

2. Intersubject phase synchronization (IPS): between-subject synchrony;

3. Intersubject seed-based phase synchronization (ISBPS): within- and between-subject functional synchrony.

FIG. 2.

Functional magnetic resonance imaging PS metrics. Each picture is a temporal snapshot for one time point. (1) Seed-based phase synchronization (SBPS): for each subject the instantaneous phase difference between two ROI time series is considered (diamonds), if all differences are close to zero, the length of the resulting vector (in black) shows a high level of synchrony over the group. (2) Intersubject phase synchronization (IPS): only one ROI is considered, if all subjects have the same phase at the same time, the resulting vector length will be closer to unity. (3) Intersubject seed-based phase synchronization (ISBPS): a combination of the two metrics where two regions have to be in exact synchrony within a subject's brain and between the group. ROI, regions of interest.

Seed-based PS

SBPS is a group measure of functional connectivity, taking into account possible individual differences within each subject.

Let ϕ_s,1(t) and ϕ_s,2(t) be the phase signals for subject s on two different brain regions (voxels or regions of interest [ROI]). We compute the differential phase for subject s as follows:

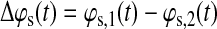(4)

We define the seed-based phase coefficient as follows:

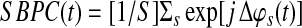(5)

Where 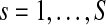. Its absolute value—the resultant vector length (Jammalamadaka and Sengupta, 2001)—is a measure of circular dispersion of phases over the unit circle, which also corresponds to the phase locking value (Lachaux et al., 1999) commonly used in neuroscience. By looking at the magnitude of the complex signal SBPC(t) multiplied by the cosine of the mean angle we obtain the SBPS as follows:

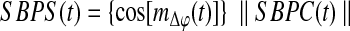(6)

where

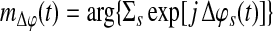(7)

Equation 7 is the group mean angle of all the individual phase differences. The range of SBPS is continuous between −1 and 1, that is, accounting also for possible anti-correlations. Equation 6 can be also re-written as the Real part of Equation 5.

Intersubject PS

IPS is a measure of reliability of the data. Being a measure of synchrony between subjects for each voxel, IPS gives similar results as ISC with the advantage that instantaneous information is intrinsically present.

First, the intersubject phase coefficient for a given voxel is computed.

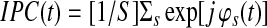(8)

Where 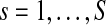is the number of subjects. The absolute value of IPC gives the IPS in time.

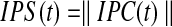(9)

The range of IPS is continuous between 0 and 1. An alternative coefficient called pairwise phase consistency (PPC) (Vinck et al., 2010) can also be adopted to compute intersubject phase synchrony. PPC is comparable to the pairwise ISC coefficient described by Kauppi et al. (2010). It has the advantage that it is less affected by potential bias due to a small number of subjects. PPC is defined as follows:

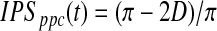(10)

where

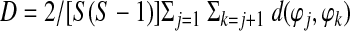(11)

with d(ϕ_j, ϕ_k) being the absolute angular distance between two angles. As noted in the original article (Vinck et al., 2010), one possible disadvantage of using PPC is that small negative values are possible; this is a consequence of the unbiasedness of the PPC.

Intersubject seed-based PS

ISBPS is a measure of functional synchrony, where we require all subjects to have the same phase value for the selected brain regions (voxels or ROIs).

Given

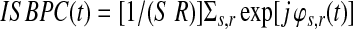(12)

Where 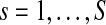is the number of subjects and 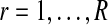is the number of brain regions (two regions only in our pairwise comparisons). The absolute value of ISBPC gives the ISBPS in time.

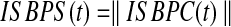(13)

The range of ISBPS is continuous between 0 and 1.

Statistical significance of fMRI phase synchrony

Statistical significance can be estimated with parametric and nonparametric tests. With parametric tests the null hypothesis is that the phases (or the phase differences for SBPS) have a uniform distribution around the unit circle, while the alternative hypothesis is that the values have a von Mises distribution, the circular equivalent of a normal distribution. Statistical significance for IPS and ISBPS is then computed with the Rayleigh test for each time point (Fisher, 1995; Mardia and Jupp, 2000). For SBPS, since the alternative hypothesis has a known mean phase equal to zero, the most suitable parametric test is the V test (Zar, 1999). However, the most reliable results are obtained with nonparametric permutation tests (Good, 2005; Nichols and Holmes, 2002), where no assumptions are made on the distributions of the null and alternative hypotheses, solving at the same time the multiple comparison problem.

In permutation testing, it is a common approach to create surrogate data by simulating or re-sampling the original time series, for example, by preserving the magnitude of the frequency spectrum of the time series while randomizing the Fourier phases (Dolan and Spano, 2001), or by re-sampling via wavelet as in Laird et al. (2002) or with twin surrogates (Thiel et al., 2006) specifically designed for phase synchrony tests. However, generating surrogate time series with similar spectra or similar statistics might destroy the actual complex nonlinear temporal dependencies between time samples. To circumvent this potential problem, it is possible to use bootstrap re-sampling, with surrogate data obtained by applying random circular shifting to the original time series for each permutation (Politis and Romano, 1992).

Temporal averages of phase synchrony metrics

While all the proposed metrics are time varying, it is also useful to infer average functional values from the dynamic data. The simplest scenario is by calculating a percentage of time points that are significantly phase synchronized over the whole duration of the scanning. This approach was adopted by Ville (1948) in the early days of studying analytic signal properties. He demonstrated that the average instantaneous frequency corresponds to the temporal average frequency of the signal. In the present case this implies that by adopting PS as a functional measure, we can also study global PS by considering the average PS over the whole time series.

Data and comparison of methods

To test the new metrics proposed in this study, we used a naturalistic fMRI dataset obtained from 12 healthy subjects who watched a feature movie in a 3T fMRI scanner with TR=2 sec. Standard preprocessing steps were performed with FSL (for more details, see Lahnakoski et al., 2012) and all subjects were co-registered to the MNI 152 two-millimeter template. We performed two types of analyses using ROIs and whole-brain data. For ROI analysis, we used a template with 264 functional areas (Power et al., 2011), with a sphere of radius of 4 mm for each ROI. Visualizations are done for two areas in the right visual cortex: V1/V2 (template area 140, MNI coordinates [8, −91, −7]) and MT/V5+(template area 161, MNI coordinates [42, −66, −8]).

IPS was compared with ISC measured with temporal sliding windows with lengths varying from 4 to 32 samples (i.e., 8 to 64 sec). The ISC curves were obtained by computing pairwise ISCs between subjects and then averaging the upper triangle entries of the correlation matrix. Whole-brain temporal average IPS was compared with ISC over the whole time series. We also computed the Euclidean distance between IPS and ISC time series for each voxel to localize the differences between the two approaches.

SBPS was compared with sliding window group temporal correlation between all pairs of regions of interest for a total of 34716 pairs. Group temporal correlation time series is obtained by first computing individual sliding window temporal correlation time series between the two regions, and then averaging the Fisher-transformed correlation values to obtain group data (for a similar approach, see Buckner et al., 2009). The center time point of each time window is the value of temporal reference for comparisons.

To quantify the effect of the size of the sliding windows versus the phase-based measures, we computed the average percentage of significant time points across all 264 regions in the ISC/IPS case and across all 34716 links for SBC/SBPS. Since ISBPS does not have a correlation-based equivalent, it was only compared with SBPS and IPS for the two selected regions. Further, to verify that the amplitude part of the analytic signal did not contain relevant information, we also computed ISC and SBC using the instantaneous envelope time series. All comparisons are carried out on band-pass filtered BOLD time series with frequencies 0.04–0.07 Hz, identical to the one used to compute the analytic signal. We adopted the Parks-McClellan algorithm (McClellan et al., 1973) for optimum design of linear phase FIR filter (0.01 weight in pass-band, attenuation of ∼30 dB in stop-band, and transition band of ∼0.015 Hz). Due to the group delay of the FIR filter and its transient, the filtered signal delay is compensated and the first N-1 filtered samples are discarded (Oppenheim and Schafer, 2009). All statistical analyses were carried out with nonparametric testing using bootstrap resampling of original time series to generate surrogate probability distributions for the null hypothesis estimated over at least 0.5 million points (equivalent to 1000 independent permutations for each time series of ∼500 time points). Correction for multiple comparisons was performed using maximal statistic combined with multistep tests (for details see Nichols and Holmes, 2002).

Results

Comparing intersubject PS with ISC

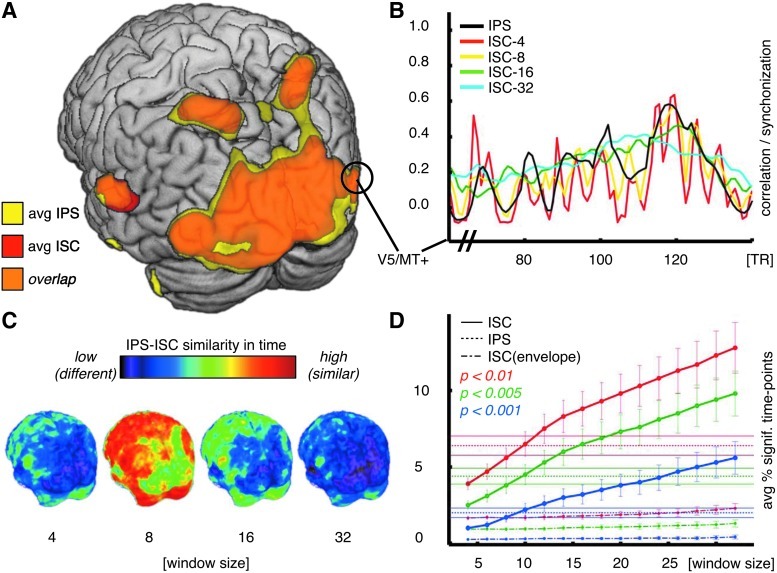
Figure 3A shows the comparison between average IPS and global ISC for the whole brain, thresholded at p<0.01. When calculated over the whole time series, IPS and ISC yield similar estimates of brain areas exhibiting intersubject synchronization. Figure 3B shows IPS and sliding window ISC time series for multiple window sizes in one region of interest (V5/MT+). ISC calculated over a very short four-sample time window shows dynamic changes similar to IPS, but is strongly affected by computational bias, with low mean percentage of significant time points (Fig. 3D). On the other hand, ISC calculated over longer time windows (16 and 32 samples) resembles a moving average of IPS, compromising temporal resolution for the sake of a reliable measure of correlation. ISC over eight samples is closest to IPS both in space (Fig. 3C) and in average number of significant time points (Fig. 3D). In contrast to phase, the instantaneous amplitude of the analytic signal did not seem to contain relevant intersubject information, giving very low percentages of significant time points (Fig. 3D, dot-dashed curves).

FIG. 3.

Intersubject correlation (ISC) and intersubject PS. (A) Shown are maps, computed over the whole time series (p<0.01), of brain areas showing significant averaged IPS (yellow) and areas showing significant ISC (red); orange color denotes the brain areas that exhibited both significant IPS and ISC. (B) Shown are time courses of IPS (black) and ISC calculated over sliding windows of different sizes from area V5/MT+. ISC over short sliding window (red curve, window size: four samples) shows computational bias as evidenced by rapid and strong fluctuation in the time course. ISC time series over longer sliding windows (8, 16, and 32 samples), although being more stable, are missing the temporal changes identified by IPS. (C) Distance maps between the IPS and sliding window ISC time courses at different time window lengths. ISC calculated with a sliding window of 8 time to repetition (TRs) is closest to IPS, with differences located in areas that process faster BOLD changes that IPS can track unlike time-windowed ISC. (D) Plotted are average percentages of significant time points with error bars for IPS (horizontal dotted lines) at three levels of significance (p<0.01, p<0.005, and p<0.001) and, respectively, ISC with multiple time windows (continuous curves). ISC with multiple time windows calculated using the instantaneous amplitude envelope information is plotted with the dash-dotted curves.

Comparing seed-based PS with sliding window SBC

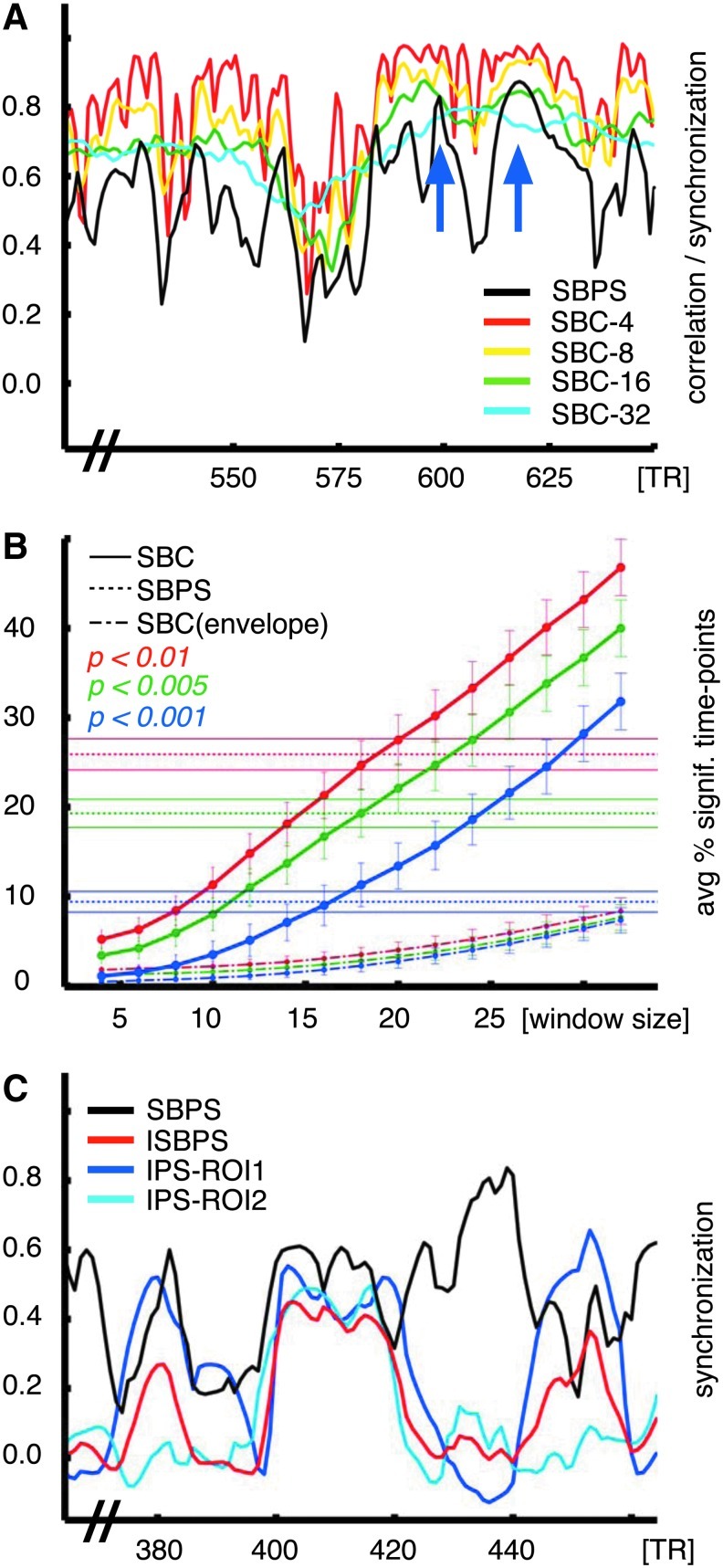
Figure 4A shows the comparison of SBPS calculated over multiple window sizes and sliding window group temporal correlation (SBC) between V1/V2 and V5/MT+ regions of interest. SBC over short time windows approximately follows the SBPS curve despite the high amount of uncertainty due to the shortness of the time window. With longer time windows, correlation values are more reliable, but miss the temporal dynamics of functional connectivity and become more prone to statistical errors. For an example of the latter, the time interval of 600–625 is falsely statistically significant with SBC, because of the two peaks at 600 and 625. These two peaks (marked in Fig. 4A) corresponded to close-up scenes with movement (high SBPS) versus large-angle panoramic scenes (low SBPS) in the movie stimulus. As can be seen, SBPS clearly identifies intervals of synchronization, without suffering the bias of using very short temporal windows. In contrast, the correlation-based methods, when using longer time windows, fail to identify such rapid changes in synchronization, yielding high level of correlation for all temporal intervals.

FIG. 4.

Functional connectivity between two regions of interest with PS and seed-based correlation (SBC). (A) Shown are SBPS (in black) and SBC calculated over sliding windows of different lengths (4, 8, 16, and 32 samples) between two regions of interest. The two blue arrows indicate peaks at 600 and 625 that corresponded to close-up scenes with movement (vs. large-angle panoramic scenes in the middle) that the SBPS method can effectively differentiate in contrast to SBC when using longer time windows. (B) Average number of significant time points with error bars for SBPS (horizontal dotted lines), SBC with multiple time windows (continuous curves), and SBC with multiple time windows performed over the instantaneous envelope (dash-dotted curves). Comparable amount of significant time points is reached for SBC over windows of at least 16 samples, sacrificing the fast temporal dynamics identified with PS. (C) Comparison between ISBPS (red) and SBPS (black) along with the IPS curves for the two regions (blue and light blue). ISBPS is more strict than SBPS since both ROIs must manifest intersubject synchronization; SBPS relaxes this condition allowing significant functional synchrony across the subjects even when there is no local intersubject synchronization.

In Figure 4B the effect of window sizes is quantified as the average percentage of significant time points across all links, compared with SBPS and SBC computed using the instantaneous amplitude of the analytic signal. To achieve a similar amount of significant time points with SBC, one needs to sacrifice temporal resolution using windows of at least 16 samples. Also in this case the amplitude of the analytic signal did not seem to carry relevant information.

Finally, Figure 4C shows a graphical comparison between ISBPS (red) and SBPS (black) for the two sample regions selected and the two IPS curves for each region. As previously noted, this metric is stricter than SBPS since we impose intersubject synchronization for both regions of interest. ISBPS is significantly high only during intervals of intersubject synchronization over the two ROIs (time points 400–420), while SBPS can increase even without ROI intersubject synchronization (time points 420–440).

Discussion

In the present study, we showed that instantaneous PS is a reliable measure comparable to correlation-based methods (SBC and ISC) but with maximal single-TR temporal resolution, thus enabling assessment of time-varying functional connectivity based on fMRI data in a model-free fashion. When comparing IPS with sliding time window ISC, we obtained similar results for windows of 8–10 TRs in length (Fig. 3D), with differences being located in those areas where intersubject synchrony can change rapidly (Fig. 3C). These happen to be the sensory cortical areas with short visual (Hasson et al., 2008) and auditory (Lerner et al., 2011) temporal receptive windows. When comparing SBPS with SBC, sliding windows of at least 16 samples/TRs are needed to reach similar performance (Fig. 4B). Evidently, PS-based methods significantly increase temporal resolution at which dynamic functional connectivity can be estimated. Further, comparison of ISBPS and SBPS demonstrates that SBPS allows detecting functional connectivity even when there is no significant intersubject synchronization within each area.

Improving time-varying analysis

The method proposed here is based on the general concept represented by recently introduced methods, such as ISC or multivoxel pattern analysis (MVPA), that focus on spatiotemporal properties of the signal and not on activations over a specific baseline. ISC (Hasson et al., 2010), intuitive and elegant in its simplicity, was an important innovation in fMRI analysis methodology. ISC is a measure of reliability (i.e., how similar the BOLD signals of different subjects are in different parts of the brain when an identical stimulus is used as external source of synchrony). Moreover, ISC does not require a linear relationship between the external stimuli and the BOLD responses. Finally, due to its simplicity, when ISC is compared with more complex techniques (e.g., MVPA), we can still clearly understand its neuronal correlates by going back to the BOLD signal itself rather than looking at intricate multivoxel patterns. With ISC one may study, for instance, how complex stimulus can affect processing at multiple cognitive stages (Lerner et al., 2011) and how brain activity of one person affects brain activity of another person during social interaction (Stephens et al., 2010) without simplifications assumed in linear models. IPS extends the use of ISC by providing more accurate timing of brain events in a reliable way, with the additional requirement of band-pass filtering the BOLD signal. We argue, however, that the part of the BOLD signal not affected by artifacts is intrinsically narrowband, and thus well suited for PS analysis.

Enabling time-varying connectivity analysis

Another important and novel feature of our method is the ability to look at the intersubject reliability of the connectivity between two brain areas with the highest possible temporal resolution; this is necessary especially with complex continuous stimulation, where each volume is comparable to a different experimental condition. SBC groups together many volumes into a time window to compute the average connectivity, missing the complex event that triggered the connection. SBPS on the other hand is intrinsically instantaneous, providing connectivity information for each time point.

Importantly, this allows shifting of intersubjectivity estimates from individual voxels or brain areas (ISC) to connections between voxels and brain areas (SBPS), in other words, from the nodes to the links of the brain network, opening new opportunities to examine the relationship between brain areas with graph-theoretical tools (Sporns, 2010). Further, by adding the temporal accuracy of the PS measures, it is possible to progress from inspection of static to time-varying networks (Holme and Saramäki, 2012). PS is a dynamic measure of functional connectivity; we can evaluate which pairs of brain areas are significantly synchronizing across the subjects and we can also determine when they are synchronizing.

Limitations of phase synchrony approach

Frequency bands of BOLD signal

The necessity of dealing with narrowband signals to compute meaningful PS raises the important question of which BOLD frequency band best captures functionally relevant information. Sub-bands of BOLD have been explored in ISC (Kauppi et al., 2010) and functional connectivity studies (Chang and Glover, 2010). While ISC is more immune to physiological noises, functional connectivity can be greatly affected since within-subject time series are compared where there is a high possibility for synchronous artifacts. Removal of artifactual signals from BOLD time series (e.g., Särkkä et al., 2012) can allow multiple explorations across all the frequency bands of BOLD signals. PS could then be investigated over the whole spectrum with multiple narrowband filters, allowing exploration of within-band and between-band PS, in a similar vein as with EEG and MEG data (Tass et al., 1998). Studies with combined techniques (such as simultaneous fMRI and intracranial recordings) might provide additional information on the existence of meaningful slow sub-bands, corresponding to various processes or connectivity stages, as suggested by early animal studies (Leopold et al., 2003) and more recent resting-state research (Chang and Glover, 2010).

Phase synchrony as a group measure

The proposed PS metrics, like ISC, are measures of reliability over the subjects (i.e., they can only be computed at group level). Although in principle it is possible to compute individual PS connectivity, assessing its statistical significance is challenging due to the lower statistical power; in our measures, statistical power is increased by increasing the number of subjects. Further—like in ISC—when using intersubject group measures, all subjects must be exposed to the same external source of synchronization (i.e., stimulus).

On the instantaneous envelope of the analytic signal

In PS literature, the amplitude part is almost always discarded, as it is assumed to be irrelevant or uncorrelated with the actual phase dynamics. Indeed, we were able to confirm this assumption with our data. Temporal dynamics are contained in the phase part of the analytic signal. However, the issue is far from being resolved in physics and neuroscience. The effect of the amplitude part of the analytic signal has been studied analytically for two oscillators (Xiao-Wen and Zhi-Gang, 2007), concluding that when the envelopes are matched, there is no influence over PS from the amplitude part. A similar conclusion, relevant for neuroscience, was recently reached by Daffertshofer and van Wijk (2011). Using computational modeling, they studied how the amplitude part biases the PS functional connectivity compared with the effective structural connectivity. They also concluded that the amplitudes of the analytic signals do not affect the PS results if the two ROIs have comparable magnitudes. As a general rule, the instantaneous amplitude of the signals should be tested to ensure that it is not relevant to the temporal dynamics, especially when lower frequency bands are explored (e.g., for the slow-5 frequency band, where the spectrum of the phase starts to overlap with the spectrum of the envelope, possibly violating the Bedrosian's theorem).

Conclusions

Our proposed PS method addresses some of the current limitations of time-varying ISC and SBC, and creates the basis for bridging ISC with complex network analysis by shifting the interest toward intersubject synchronization of functional connectivity patterns, rather than properties of single voxels. Despite the necessary mathematical compromise of having to use a narrowband signal, the method proved to be reliable, yielding (1) similar results as ISC when inspected over the whole time course and (2) yielding significantly improved temporal resolution as compared with time-varying ISC and SBC functional connectivity measures. All the methods described in this article have been released publicly as a MATLAB toolbox (FUNPSY, http://becs.aalto.fi/bml/software.html) and an alternative version is available in the ISC toolbox (http://code.google.com/p/isc-toolbox/).

Acknowledgments

This study was supported by the aivoAALTO project of the Aalto University and by the Academy of Finland (grant numbers: 129670, 130412, and 138145).

Author Disclosure Statement

No competing financial interests exist.