Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2013 Feb 19;29(8):1044–1051. doi: 10.1093/bioinformatics/btt083

Systematic parameter estimation in data-rich environments for cell signalling dynamics

Tri Hieu Nim 1, Le Luo 2, Marie-Véronique Clément 2, Jacob K White 1,3, Lisa Tucker-Kellogg 1,4,5,*
PMCID: PMC3624804  PMID: 23426255

Abstract

Motivation: Computational models of biological signalling networks, based on ordinary differential equations (ODEs), have generated many insights into cellular dynamics, but the model-building process typically requires estimating rate parameters based on experimentally observed concentrations. New proteomic methods can measure concentrations for all molecular species in a pathway; this creates a new opportunity to decompose the optimization of rate parameters.

Results: In contrast with conventional parameter estimation methods that minimize the disagreement between simulated and observed concentrations, the SPEDRE method fits spline curves through observed concentration points, estimates derivatives and then matches the derivatives to the production and consumption of each species. This reformulation of the problem permits an extreme decomposition of the high-dimensional optimization into a product of low-dimensional factors, each factor enforcing the equality of one ODE at one time slice. Coarsely discretized solutions to the factors can be computed systematically. Then the discrete solutions are combined using loopy belief propagation, and refined using local optimization. SPEDRE has unique asymptotic behaviour with runtime polynomial in the number of molecules and timepoints, but exponential in the degree of the biochemical network. SPEDRE performance is comparatively evaluated on a novel model of Akt activation dynamics including redox-mediated inactivation of PTEN (phosphatase and tensin homologue).

Availability and implementation: Web service, software and supplementary information are available at www.LtkLab.org/SPEDRE

Supplementary information: Supplementary data are available at Bioinformatics online.

Contact: LisaTK@nus.edu.sg

1 INTRODUCTION

Dynamic behaviours of biochemical networks can be captured by ordinary differential equation (ODE) models that compute the change of molecular concentrations with respect to time (Fall et al., 2002; Palsson, 2006). For most biochemical pathways with known topology, most reaction rate constants (i.e. the coefficients of the differential equations) are not available from direct experiments. Rate parameters are typically estimated by regression, in other words by fitting the global behaviour of the simulated model to the experimentally observed concentrations. This is a difficult high-dimensional non-linear problem, and search strategies often experience poor convergence and local optima (Kleinstein et al., 2006). The rate parameter estimation problem can naturally be formulated as minimizing a sum of squared errors (SSE), where each error is a difference between simulated concentration and observed concentration, and the summation is over time points and/or experimental treatments. Optimizing this type of SSE objective function can be attacked using a variety of ‘traditional’ global and local search methods: LM (Levenberg–Marquardt, local), SD (steepest descent, local), SRES (stochastic ranking evolution strategy, global), PSO (particle swarm optimization, global) and GA (genetic algorithm, global) (Fogel et al., 1991; Kennedy and Eberhart, 1942; Levenberg, 1944; Marquardt, 1963; Michalewicz, 1994; Runarsson and Yao, 2000). Local and global search methods both have drawbacks, and global–local hybrid searches have also become popular (Ashyraliyev et al., 2008; Fomekong-Nanfack et al., 2007; Rodriguez-Fernandez et al., 2006).

Traditional search methods generate a full vector of rate parameters, simulate the model with this full set of parameters and then accept, reject or adjust the parameters based on how well the simulation agrees with experimental measurements. For networks with few unknown parameters, these ‘simulate-and-match’ methods have been successful at finding good values, or multiple good candidates. The search space for parameter vectors is exponential, and the inevitable trend with any type of exponential growth is that there will eventually be a large enough number of unknown parameters, such that reasonable sampling will not explore very many of the ‘basins of convergence’, and the results will deteriorate. Indeed many high-impact models of biological pathways continue to be built without automating the parameter estimation process (Albeck et al., 2008; Basak et al., 2007; Purvis et al., 2008).

In contrast to standard ‘simulate-and-match’ methods of parameter estimation, spline-based collocation methods have recently been developed that use experimental observations of a protein over time to interpolate the time derivative of the concentration, rather than computing the derivatives based on simulating the ODEs. Traditional methods minimize the violation of experimental observations, subject to obeying the ODE trajectories, while the spline-based collocation methods can be seen as optimizing a dual-like objective function because they minimize the violation of the ODE trajectories, subject to obeying the experimental observations. Note that the spline-based collocation methods require an extensive input dataset with observations for many or all of the proteins. In the past, few large networks had such comprehensive measurements available, but recent trends in proteomic technology (Zhang and Neubert, 2009) suggest that data-rich cases may be increasingly common in the future.

Several spline-based collocation methods have been published recently for the context of biological networks. A spline-based collocation scheme for parameter fitting problems using a modified data-smoothing method and a generalization of profiled estimation was proposed by Ramsay et al. (2007). A similar method for problems with high noise and short time-course was introduced by Brewer et al. (2008). Zhan and Yeung (2011) used non-linear programming (NLP) to optimize the dual objective. Several ‘decoupling’ strategies (Jia et al., 2011; Vilela et al., 2009; Voit and Almeida, 2004) also use some forms of ‘slope approximation’ from time-series data to avoid doing multiple simulations. Estimating ODE parameters has been studied in the mathematical literature for decades, and an important class of data-rich methods called ‘multiple shooting’ (Bock, 1983; Bock and Schlöder, 1986a, b) has recently been applied to biological networks (Peifer and Timmer, 2007).

To the best of our knowledge, no data-rich parameter estimation methods have implementations publicly available for practical problems with biological networks. The asymptotic runtime of data-rich methods has also been neglected. Many data-rich methods have been published with claims of good accuracy, but to the best of our knowledge, efficiency and runtime have not yet been compared with state-of-the-art, ‘simulate-and-match’ parameter estimation methods.

Scalability with network size is a major remaining challenge in the parameter estimation field, regardless of the objective function or optimization approach. A common strategy for large systems is to decompose the problem. However, the objective functions of parameter estimation are not generally decomposable. Some decomposition approaches exploit specific situations, such as having derivatives available at all timepoints (Chou et al., 2006), or having small sub-networks connected by species with observed concentrations (Koh et al., 2006). The dual-like objective functions of spline-based collocation methods are not readily decomposable, but they do exhibit the important property of sparse interdependence (‘locality’) between the variables. This locality can be a basis for conditional decomposition.

Belief propagation [see (Meltzer et al., 2009) review and (Pearl, 1988) textbook] is an inference method for probabilistic graphical networks with sparse interdependence or locality. It can compute the maximum a posteriori (MAP) values for variable parameters in a factor graph, given joint probability distributions that describe the dependencies between adjacent variables. For acyclic graphs, belief propagation guarantees exact optima, and for general graphs, a variant called ‘loopy belief propagation’ (LBP) has had empirical success at approximating the MAP (McEliece et al., 1998; Murphy et al., 1999).

Our method of Systematic Parameter Estimation in Data-Rich Environments (SPEDRE) optimizes the dual objective approximately, via LBP. The innovation is conditional decomposition of the problem into local terms, with pre-computed look-up tables for the discretized solutions to the local terms of the dual objective function. SPEDRE provides dramatic improvement in empirical efficiency, and in effect brings the spline-based collocation (dual objective) methods to the same level of efficiency as the state-of-the-art (primal objective) methods. Asymptotic runtime is polynomial with respect to the number of species, parameters and timepoints in the biological networks, while it is exponential only in the degree of the network.

Finally, we compare the scalability and robustness of SPEDRE against state-of-the-art standalone and hybrid parameter estimation methods, using both a spectrum of artificial cases, and also a novel model of Akt activation based on our previous experimental studies of Akt (Lim and Clement, 2007). Aberrant hyper-activation of the Akt pathway has been detected in up to 50% of all human tumours, and the Akt pathway is an attractive target for anti-cancer drug discovery (Mitsiades et al., 2004). Our model of Akt includes oxidative inactivation of the lipid phosphatase and tensin homologue on chromosome 10 (PTEN), as well as the phosphatidylinositol 3-kinases (PI3K) activation, as competing regulators of Akt in serum-stimulated fibroblasts (Kwon et al., 2004; Testa and Bellacosa, 2001). A more detailed understanding of PTEN dynamics is important because many cancers activate Akt through disruptions of PTEN.

2 PRELIMINARIES

2.1 Ordinary differential equations

The production and consumption of each species in a biochemical system can thus be described using ODEs. For example, consider a two-species artificial pathway A⇄B. Using k1 (and k2) to denote the forward (and reverse) reaction rates, we can model the system as follows:

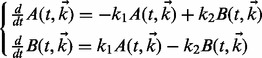graphic file with name btt083m1.jpg (1)

For the simplicity of later figures, our example uses mass action, but more general equations are also permitted. Solving these equations (1) provides the time evolution of the species, dependent on rate parameter vector 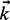Inline graphic. The inverse problem, estimating the rate parameters from observed levels of the species, is a deceptively difficult non-linear optimization problem (Kleinstein et al., 2006). We define the degree of each ODE to be the number of terms in its right hand side, analogous to the node degree in a biochemical network diagram.

2.2 Rate constant estimation objective

To estimate the rate constants, the most standard (‘primal’) approach is to use a non-linear least squares technique to minimize the weighted SSE objective function

graphic file with name btt083m2.jpg (2)

where Nt is the number of observed timepoints per experiment, 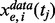Inline graphic is the observed concentration of species i in experiment e and 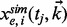Inline graphic is the simulated level of species i in experiment e as a function of time and rate constants 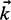Inline graphic. SSE is the most widely used objective for evaluating the success of parameter estimation, but SSE grows with the size of the network. Therefore, we also use the species maximum relative error (MRE), and parameter percentage error (PPE), discussed in Supplementary Text S1 and defined as follows:

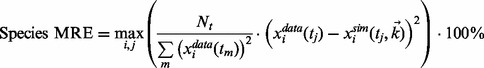graphic file with name btt083m3.jpg (3)
graphic file with name btt083m4.jpg (4)
graphic file with name btt083m5.jpg (5)

Note that the PPE metric requires the knowledge of the nominal parameter values, which is only feasible in simulated tests.

3 ALTERNATIVE OBJECTIVE FUNCTION

3.1 Error terms of dual objective function

The error terms of our dual objective function, εe,i,j, minimize the disagreement between the right hand sides of the ODEs [which we denote 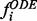Inline graphic, see Equation (1)] and the species derivatives (computed using the species derivatives interpolated from the observed data):

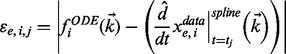graphic file with name btt083m6.jpg (6)

indexed over experiments e, species i and timepoints tj. 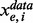Inline graphic are the time-series observations of species i in experiment e. The interpolated derivative 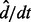Inline graphic with splines is explained in Supplementary Text S2. The εe,i,j terms are similar to the terms of other spline-based collocation methods, but we remark that each εe,i,j is defined in terms of a small subset of the parameters 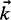Inline graphic, while each term of a ‘primal’ SSE objective uses all parameters via simulation.

3.2 Product of functions

Among different schemes for combining error functions into an objective (e.g. sum of squares), we chose multiplication.

graphic file with name btt083m7.jpg (7)

The product of functions (POF) objective will need to be evaluated in practical tests because it has numerical vulnerabilities, such as going to zero if any single term goes to zero. The benefit of using the POF objective is that it is a decomposable expression to facilitate belief propagation for probabilistic inference on a factor graph (Section 4.1). By inspection, the POF is minimized when individual error terms εe,i,j are minimized. Assuming the network is low-degree, each εe,i,j is a low-dimensional term involving a small subset of the rate parameters 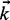Inline graphic. The εe,i,j error terms cannot be optimized as independent problems because the subsets of 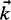Inline graphic are not mutually exclusive. However, the low dimensionality of εe,i,j means we can pre-compute solutions for each εe,i,j sub-problem systematically. We pre-compute a complete look-up table Te,i,j that gives the value of εe,i,j for each possible (discretized) combination of the relevant 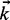Inline graphic parameters. To combine many low-dimensional systematic εe,i,j solutions into an optimal high-dimensional parameter vector is a problem that resembles belief propagation, except with a sparsely connected, cyclic graph instead of an acyclic graph. We next describe in Section 4 how to compute a global estimate of 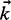Inline graphic as a graphical inference problem using LBP.

4 LOOPY BELIEF PROPAGATION

We now express the POF optimization as an inference problem on a factor graph, in preparation for using LBP to compute the MAP values of the variable parameters, corresponding to the values that minimize the POF objective (Pearl, 1988; Yedidia et al., 2003).

4.1 Factor graph

A factor graph is a bipartite graph with factor nodes εe,i,j (for each experiment e, ODE i and timepoint tj) and variable parameter nodes ki (for the members of 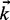Inline graphic). We connect a factor node εe,i,j to a parameter node ki if and only if ki appears in the equation for εe,i,j.

For each factor node, a factor graph has a joint table (or joint probability distribution) to describe the probability of each combination of values for the adjacent variable nodes. We compute a constant look-up table Te,i,j, based on the error term εe,i,j, for the joint probability of each combination of the adjacent variable parameters. (Section 4.2 describes how errors are converted into probabilities.) Note that εe,i,j represents the discrepancy between the right-hand side of the i-th ODE (computed using the variable parameters) and the left-hand side of the ODE (computed from spline-based interpolation of the data for experiment e, species i and timepoint tj). Each factor node thus serves to enforce the equality of one ODE at one timeslice and one experiment. An example factor graph corresponding to the two-species A⇄B system is shown in Figure 1, with variable nodes (rate parameters) represented by circles, and factor nodes (εe,i,j) by rectangles.

Fig. 1.

Fig. 1.

Open in a new tab

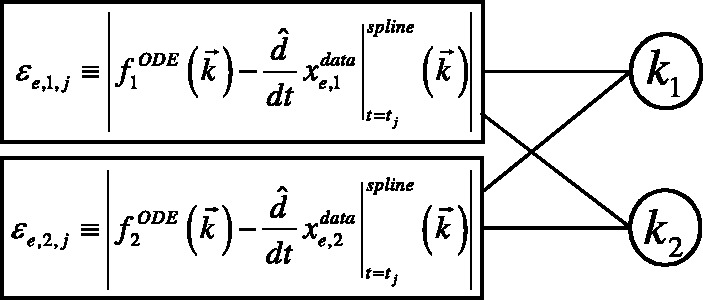
A partial factor graph of the example two-species system, shown for one timepoint tj and one experiment e. The complete factor graph would include factor nodes for every timepoint and every experimental treatment, each connected to the k1 and k2 variable nodes

4.2 Discretization and joint probability tables

Each variable node ki is associated with a one-dimensional discrete probability distribution, which represents the current belief about the likeliness of that value being in the optimal parameter vector. In theory, variable parameters are real numbers, but to permit us to evaluate combinations ‘systematically’, we discretize the domain of each parameter into a finite number of sub-intervals, or bins, and we represent each bin by its midpoint. Coarser intervals (larger bins) will yield faster runtime at the expense of accuracy. At the start of the algorithm, the one-dimensional discrete probability distribution for each variable parameter is uniform, representing lack of prior knowledge about the value of that parameter. During the process of belief propagation (Section 4.3), the discrete probability distributions will be updated by a message passing algorithm, until convergence or until an iteration limit.

If factor node εe,i,j has degree d, then the joint table Te,i,j is a d-dimensional table, and each dimension is discretized with the same binning as the variable parameters of the d adjacent variable nodes (Fig. 2). To convert the error terms εe,i,j into probabilities, we use a Boltzmann-like exponential weighting: 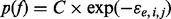Inline graphic. This empirical choice makes large violations exponentially unlikely, and C is a normalization constant to make p(f) a valid probability distribution, i.e. all entries in the discrete joint table sum up to 1. (Alternative methods of representing a systematic solution of εe,i,j would also have been possible.)

Fig. 2.

Fig. 2.

Open in a new tab

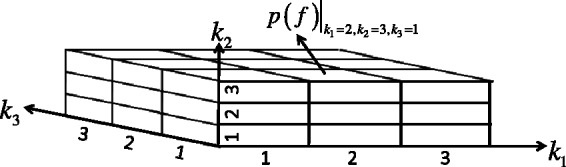
Illustration of a joint probability table of three dimensions, corresponding to rate constants k1, k2 and k3. Each dimension of the look-up table corresponds to one associated variable parameter (variable node in the factor graph), binned into three possible values. The joint probability computed for each cell of the table (e.g. 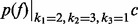Inline graphic for the cell with k1 = 2nd bin, k2 = 3rd bin, k3 = 1st bin) is obtained by converting the εe,i,j error term into a probability, via exponential weighting and normalization

Note that minimizing the error means maximizing the probability. These probability distributions do not change during the course of belief propagation and can be pre-computed. The error term εe,i,j must be computed for every possible discrete combination of the relevant parameters, using the midpoint of each parameter bin, and the errors can then be converted to probabilities to fill in the joint probability table Te,i,j. The optimal combination of parameters for each εe,i,j sub-problem can be found trivially by scanning the Te,i,j table.

Owing to the discretization required by this method, the estimated value of each parameter is a range rather than a single value. Although discretization sacrifices some accuracy (analogous to round-off error), we choose the variable parameters to be discretized, sometimes quite coarsely, because the output of such a method might be ideal input for a local search method, such as Levenberg–Marquardt or Steepest Descent, to refine afterwards, using a more precise simulation-based objective function.

4.3 Loopy belief propagation

Belief propagation can be described informally as two types of message passing: variable nodes K pass messages (one-dimensional probability distributions, 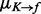Inline graphic) to adjacent factor nodes f to communicate what the variable node believes to be the value of its variable. Factor nodes f in turn pass a message (one-dimensional probability distribution, 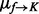Inline graphic) to adjacent variable nodes K communicating what they believe the variable values to be. Each message from a factor causes the variable nodes to update their probability distributions, and that update also alters the later messages sent out by the variable nodes. In acyclic graphs, the message passing algorithm yields a provably exact, optimal MAP solution for the variables, efficiently. Murphy et al. (1999) describe the LBP algorithm, extending the message passing framework to achieve good heuristic approximations for cyclic graphs. We use a variant of the LBP message-passing algorithm detailed in Koh et al. (2007), summarized in Box1 as ‘SPEDRE-base’.

Box. 1. SPEDRE-base algorithm for computing the MAP estimates on a factor graph. N(node) is the set of neighbours adjacent to node. Steps B.1.1.2 and B.2.1 include a logarithm operation as a heuristic to avoid rounding off small numbers to zero. Because normalizing the messages or probability distributions does not affect the final MAP results (Yedidia et al., 2003), we also perform normalization after the computation of step B.1.1.2 and B.2.1 so that the messages and beliefs are always valid probability distributions at every iteration. The messages history serves as a buffer for incoming messages, and the algorithm makes implicit use of the message history during steps B.1.1.2 and B.2.1.

A. Initialization:

 A.1. Compute look-up joint tables, 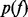Inline graphic, for each factor node

 A.2. Set all variable nodes to uniform distribution

B. Propagation: repeat until convergence

 B.1. For each factor node 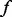Inline graphic

  B.1.1. For each variable node 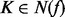Inline graphic

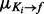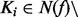
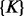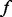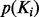   B.1.1.1. Collect Inline graphic: the message from variable node Inline graphic Inline graphic to Inline graphic, which is Inline graphic, the current probability distribution of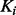 Inline graphic

   B.1.1.2. Compute 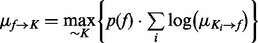Inline graphic

   B.1.1.3. Send 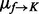Inline graphic to the message history of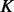 Inline graphic

 B.2. For each variable node 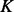Inline graphic

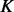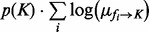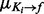  B.2.1. Update the distribution of Inline graphic to Inline graphic, where Inline graphic are stored in the message history of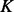 Inline graphic

C. Output: compute the MAP probability of each variable node

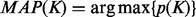
   Inline graphic

In a discrete joint distribution g with dimensions K1,K2,..,Km, we define the maximization over a dimension Ki as follows:

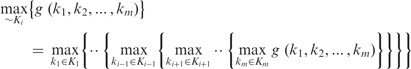graphic file with name btt083m8.jpg (8)

where ∼Ki denotes the set of all dimensions in g except Ki.

Convergence in step B occurs when no normalized message in the current iteration differs by more than a tolerance value from the corresponding message in the previous iteration. As the LBP algorithm is not guaranteed to converge, and in some cases might oscillate (Murphy et al., 1999), we impose an additional criterion to limit the total number of iterations.

From Box 1, the asymptotic runtime of the modified LBP algorithm, including pre-computation of all the look-up joint tables, can be expressed as:

graphic file with name btt083um1.jpg

See Supplementary Text S3 for a derivation of the asymptotic runtime. The time complexity scales exponentially with the factor graph degree, which is defined as the maximum number of variable nodes adjacent to any factor node, or the maximum number of unknown rate parameters appearing in any ODE. For a factor graph with bounded degree, the method scales polynomially with respect to the number of species, timepoints and discrete bins. This means the method scales well on biological pathways with a small bounded number of reactions per species. Our asymptotic runtime compares favourably with conventional (‘primal’) methods, because primal methods search for full-length parameter vectors in a space that grows exponentially with the number of parameters. Although primal methods with heuristic sampling do not have to cover the entire parameter space, they must maintain some coverage of the major ‘valleys’ of the objective function. If the number of valleys and inflection points grows with the size of the parameter space, then primal methods will perform poorly (accuracy versus runtime) on large networks.

5 Results

Before testing the overall performance of the method on full problems, we first performed simplistic tests with partial problems, to isolate specific variables of interest such as #species and #timepoints. We monitored performance as a function of network size and timepoint spacing, to probe two sources of potential error in the SPEDRE-base method: spline accuracy and the POF objective function. The simplistic tests used ring-shaped networks (Fig. 3A), with nominal parameters randomly chosen to be at exact mid-points of the parameter discretization bins. Simulated data were generated with random initial concentrations, using the nominal rate parameters. For each run of SPEDRE-base, we monitored the objective

graphic file with name btt083m9.jpg (9)

normalized with respect to the number of factors in the product of Equation (9). The objective declined when the number of timepoints increased (Fig. 3B), indicating as expected that SPEDRE gives better estimates of the parameters when timepoints are densely sampled.

Fig. 3.

Fig. 3.

Open in a new tab

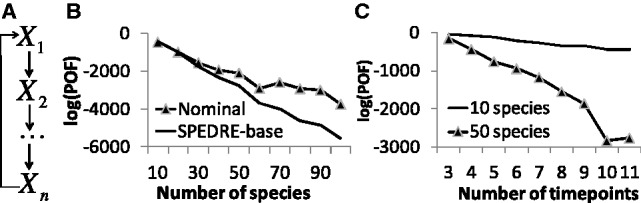
(A) Ring network diagram; (B) normalized log(POF) with respect to the number of timepoints on different network sizes; (C) normalized log(POF) of LBP-predicted rate constants, versus the normalized log(POF) of nominal (‘correct’) rate constants on circular networks of 10 to 100 species with 11 timepoints. (Total simulation duration was 4 s, with 0.4 s for each time step). Each rate constant was discretized into 10 equidistant bins from 0.05 to 1.05, with the nominal rate constants selected from among the bin midpoints. Dataset appears in Supplementary Source Files

Next we compared the normalized log(POF) value between the results of SPEDRE-base, and the nominal (‘correct’) rate constants, using 10 time steps (i.e. 11 timepoints) for each test. Figure 3C shows that the POF scores of the exact nominal parameters were higher than the POF scores of the parameters found by SPEDRE-base, for all networks of significant size. Because SPEDRE-base found parameters with better scores than the ‘correct’ parameters, we infer that the POF objective is an imperfect score of parameter accuracy.

5.1 Scalability with artificial networks

The complete SPEDRE method consists of SPEDRE-base (Sections 3–4) followed by LM to refine the discretized results from SPEDRE-base. The major task of SPEDRE-base is to find good starting values for local optimization, and post-fitting is a necessary part of the procedure. We compared the performance of the complete SPEDRE method against a selection of popular local, global and hybrid methods, on parameter estimation problems from low-degree networks. All tests were full problems with parameters set randomly, without regard to bins or bin midpoints. Random networks of increasing size (from 30 to 150 species) were constructed with low degree (two-thirds of the reactions involving three species, and one-third involving two species), to generate parameter estimation problems with increasing scale. We tested 14 parameter estimation methods including SPEDRE-base, LM (local), SD (local), SRES (global), PSO (global) and GA (global), plus hybrid global–local combinations of these methods (e.g. SRES_LM denotes the global method SRES plus the local method LM). Runtime and multiple error scores were measured as a large-scale screen (see Supplementary Text S5, Supplementary Figs S6 and S8 and Supplementary Tables S7 and S9). The best-performing methods (asterisks in Supplementary Fig. S6) are consistently SPEDRE and a subset of hybrid stochastic-local methods. Highly similar scores can occur when multiple methods converge to the same local optimum. Accuracy tests showed the following trends: (i) for small networks, local methods performed well; (ii) hybrid methods (including SPEDRE) showed superior accuracy to standalone local or global methods; (iii) SPEDRE accuracy was comparable with the accuracy of other hybrid methods; (iv) the quality scores of SPEDRE-base were significantly worse than SPEDRE, confirming that the LM post-processor is indeed important for refining discretized results. Supplementary Text S5 also clarifies the trade-off between accuracy and speed. We conclude that SPEDRE was ‘tied’ with other state-of-the-art methods, for the spectrum of low-degree data-rich problems we constructed.

5.2 Performance on a novel model of Akt pathway activation

To test SPEDRE on a realistic biological pathway, we built a novel model of Akt activation (‘Akt model’), using our experimental data from recent studies (Lim and Clément, 2007). Akt is a kinase, frequently over-activated in cancers, that signals for survival and proliferation. The signalling events in our model of Akt activation are illustrated in Figure 4 and described below. Akt is activated after stimulation by serum (growth factors), not only via the canonical activation of PI3Kinase (PI3K) by serum, but also via reactive oxygen species (ROS) and ROS-induced inactivation of the phosphatase PTEN. ROS are produced by NADPH oxidase (NOX), and degraded by anti-oxidants. The phosphorylation and activation of Akt is a multi-step process, involving the translocation of Akt from the cytosol to the cell membrane and its phosphorylation by the kinase PDK1 at Thr308. The translocation of Akt and PDK1 to the membrane is controlled by the level of phosphatidylinositol 3,4,5-trisphosphate (PIP3), which is determined by the balance between PIP3 production (by serum-activated PI3Kinase) and PIP3 degradation (by the phosphatase PTEN). Phosphorylated Akt returns to the cytosol and is subject to dephosphorylation by PP2A.

Fig. 4.

Fig. 4.

Open in a new tab

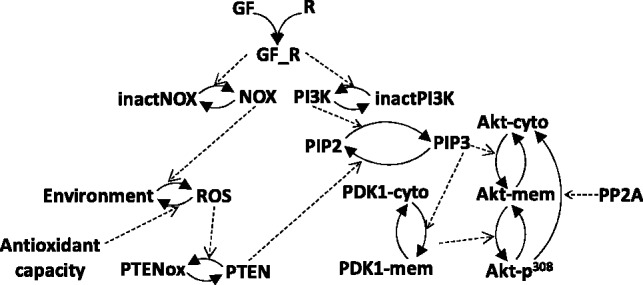
Network diagram of the Akt model, including redox regulation of PTEN. The prefix ‘inact’ denotes inactive species; the suffix ‘cyto’ (or ‘mem’) indicates cytosolic (or plasma membrane) localization. The suffix ‘p308’ indicates phosphorylation at residue Thr308

The model was built manually based on dynamic measurements of the Akt pathway, observed in serum-starved mouse embryonic fibroblasts stimulated by the addition of 10% serum to the culture medium (Lim and Clément, 2007). Supplementary Table S11 defines the full model.

Using simulation, we generated complete datasets with artificial noise at levels of 0, 1 and 20%. Parameter estimation performance was compared between SPEDRE and some popular methods (Fig. 5, with complete results in Supplementary Table S12).

Fig. 5.

Fig. 5.

Open in a new tab

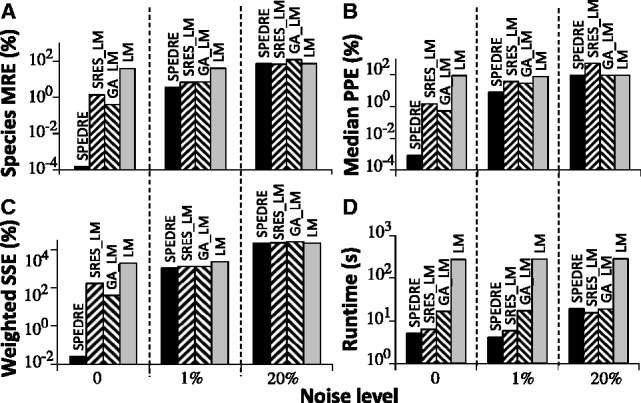
Comparison of parameter estimation algorithms applied to the Akt network, with noise levels 0, 1 and 20%, evaluated by (A) species MRE, (B) median PPE, (C) weighted SSE and (D) runtime

According to Figure 5A–C, the prediction quality of SPEDRE (leftmost bar, shaded black) is better than the other methods for noise-free and 1%-noise datasets. With noise levels of 20%, all methods perform unacceptably, providing worse than 100% species MRE, as shown in Figure 5A. Similarly, on the 20%-noise data set, all methods have unacceptably high median PPE and weighted SSE, as shown in Figure 5B–C. In this parameter optimization test with Akt dynamics, SPEDRE out-performed other methods, indicating that the parameter neighbourhoods it gave to LM were better than the neighbourhoods from other global methods, even though SPEDRE-base had equivalent performance in non-biological tests.

Figure 5D also displays a counterintuitive phenomenon, in which the local search method LM takes longer to run than any hybrid method including LM as a post-processor. LM performs many iterations if it starts with a random guess, but it converges quickly if it starts with the output of a global search method. Adding more phases of search would be expected to increase rather than decrease the total runtime, but in this case, a phase of global search led to faster LM convergence, which more than compensated for the time of running the global search.

6 DISCUSSION

The key innovations of SPEDRE are the use of a probabilistic graphical model to decompose the dual objective function, and pre-computation of discrete solutions to each sub-problem. The method has a well-defined asymptotic runtime and good scalability, in exchange for approximate heuristic optimization.

The SPEDRE approach aims for asymptotic scalability at the expense of accuracy. This philosophy appears in (i) the use of splines to approximate the species derivative, (ii) the use of binning to discretize the parameter space and (iii) the use of LBP for probabilistic inference. Each of these elements can introduce error. We believed the dangers of compounded errors would make the SPEDRE method less robust to noisy data than simulation-based methods. The expected sensitivity of SPEDRE to input noise has not yet been confirmed in the tests shown (and in other tests, such as Supplementary Table S12); rather we found that all methods gave unacceptably poor answers with noisy data. Future work must continue to characterize the numerical stability, approximation error and noise tolerance of SPEDRE and other parameter estimation methods. SPEDRE is in fact a general algorithm for ODE parameter fitting, applicable to any case in which the right-hand sides of the ODEs have few terms (low degree), and where the data-fitting problem provides dense observations of all variables.

The accuracy and speed of SPEDRE were compared against several methods of parameter estimation, in low-degree, data-rich test cases. SPEDRE performance was competitive in all tests, and SPEDRE was the best-performing method for the Akt network test. We conclude that SPEDRE performs well when tested in the specific niche of problems for which it was designed. Naturally the SPEDRE performance would degrade (perhaps exponentially) outside of its intended niche. SPEDRE exhibits an abrupt trade-off between problem type and performance, but performance trade-offs are not new to parameter estimation research. Major pathway simulation software packages already maintain collections of multiple parameter estimation methods, rather than expecting a single best method to cover all problems.

A current hurdle for broader applicability of SPEDRE is the inability to handle high-degree nodes. Many small networks are low-degree, but large networks often have at least one hub. In order for new spline-based collocation methods to be truly superior to conventional (‘primal’ objective) parameter estimation methods, they would have to handle high-degree networks and extensive gaps in experimental observations, robustly. Future innovations may be able to develop a new composition of parameter estimation methods, so that low-degree sub-problems can be solved by SPEDRE and high-degree hubs can be treated separately.

A side-effect of our work is to provide performance comparisons for several hybrid and standalone parameter estimation methods. Our tests reproduced the earlier observation that hybrid methods generally perform better than standalone global methods (Ashyraliyev et al., 2009; Rodriguez-Fernandez et al., 2006). One surprising phenomenon we observed was that performing a global search prior to a local search sometimes caused the total runtime to be faster than using the local search alone (Fig. 5D). Future work may be able to exploit this non-additive runtime effect, perhaps through deeper integration of global and local search methods, rather than applying independent methods sequentially.

A distinguishing feature of SPEDRE is that it requires large amounts of concentration measurement data, which would have been prohibitive a decade ago. Traditional experimental methods required an investment of labour and resources that was roughly linear in the number of proteins studied. New proteomic methods can measure additional proteins at virtually no additional cost, and proteomic datasets are starting to provide data-rich environments with measurements of all proteins in a system. SILAC technology has recently been used for time-series measurements of 147 proteins (Tasaki et al., 2010) in NIH3T3-derived cells, and again for time-series of 534 proteins in the cytosol and 626 proteins in the nucleus in glucocorticoid-exposed myogenic cells (Reeves et al., 2009). Most proteomic studies have not been performed with time-series repeats for studying dynamics, but large-scale dynamic data will become increasingly available with the explosive growth in the number of proteomic experiments (Zhang et al., 2011). New studies of large networks will give rise to huge parameter estimation problems, with rich datasets, but with too many unknown parameters for conventional methods to solve.

We believe that proteomic technology both enables and requires novel approaches to parameter estimation such as SPEDRE. As models grow in size owing to technological advances, decomposition-based methods will probably dominate non–decomposition-based search methods, which suffer from the curse of dimensionality. The trade-offs exhibited by our method may be increasingly desirable for future trends in parameter estimation.

Funding: Lee Kuan Yew Postdoctoral Fellowship and grant R-252-000-342-112 (to L.T.-K.); Singapore-MIT Alliance grant C-382-641-004-091 (to L.T.-K. and J.K.W); grant BMRC 09/1/21/19/603 (to M.-V.C.)

Conflict of Interest: none declared.

Supplementary Material

Supplementary Data
supp_29_8_1044__index.html (1,006B, html)

References

  1. Albeck JG, et al. Quantitative analysis of pathways controlling extrinsic apoptosis in single cells. Mol. Cell. 2008;30:11–25. doi: 10.1016/j.molcel.2008.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Ashyraliyev M, et al. Parameter estimation and determinability analysis applied to Drosophila gap gene circuits. BMC Syst. Biol. 2008;2:83. doi: 10.1186/1752-0509-2-83. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Ashyraliyev M, et al. Systems biology: parameter estimation for biochemical models. FEBS J. 2009;276:886–902. doi: 10.1111/j.1742-4658.2008.06844.x. [DOI] [PubMed] [Google Scholar]
  4. Basak S, et al. A fourth IkappaB protein within the NF-kappaB signaling module. Cell. 2007;128:369–381. doi: 10.1016/j.cell.2006.12.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bock HG. Recent advances in parameter identification techniques for O.D.E. Prog. Sci. Comput. 1983;2:95–121. [Google Scholar]
  6. Bock HG, Schlöder JP. Fit, fitter, the fittest: methods for modelling and validation of dynamical systems. In: Möller D, editor. Systems Analysis. Wiesbaden, Germany: Vieweg; 1986a. [Google Scholar]
  7. Bock HG, Schlöder JP. IFAC Conference Automatic Control in Petrol, Petrochemical and Desalination Industries. Kuwait; 1986b. Recent progress in the development of algorithms and software for large scale parameter estimation problems in chemical reaction systems. [Google Scholar]
  8. Brewer D, et al. Fitting ordinary differential equations to short time course data. Philos. Transact. A Math. Phys. Eng. Sci. 2008;366:519–544. doi: 10.1098/rsta.2007.2108. [DOI] [PubMed] [Google Scholar]
  9. Chou IC, et al. Parameter estimation in biochemical systems models with alternating regression. Theor. Biol. Med. Model. 2006;3:25. doi: 10.1186/1742-4682-3-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Fall C, et al. Computational Cell Biology. New York, USA: Springer; 2002. [Google Scholar]
  11. Fogel DB, et al. Meta-evolutionary programming. In: Chen RR, editor. Conference Record of the Twenty-Fifth Asilomar Conference on Signals, Systems and Computers. 1 and 2. Los Alamitos, CA, USA: IEEE Computer Society; 1991. pp. 540–545. 1274. [Google Scholar]
  12. Fomekong-Nanfack Y, et al. Efficient parameter estimation for spatio-temporal models of pattern formation: case study of Drosophila melanogaster. Bioinformatics. 2007;23:3356–3363. doi: 10.1093/bioinformatics/btm433. [DOI] [PubMed] [Google Scholar]
  13. Jia G, et al. Parameter estimation of kinetic models from metabolic profiles: two-phase dynamic decoupling method. Bioinformatics. 2011;27:1964–1970. doi: 10.1093/bioinformatics/btr293. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Kennedy J, Eberhart R. Proceedings of the Fourth IEEE International Conference on Neural Networks, Perth, Australia, 1942. New York City, New York, USA: Institute of Electrical and Electronics Engineers; 1942. Particle swarm optimization; pp. 1942–1948. [Google Scholar]
  15. Kleinstein SH, et al. Proceedings of the 2006 Winter Simulation Conference. 1–5. New York City, New York, USA: Institute of Electrical and Electronics Engineers; 2006. Nonuniform sampling for global optimization of kinetic rate constants in biological pathways; pp. 1611–1616. 2307. [Google Scholar]
  16. Koh G, et al. A decompositional approach to parameter estimation in pathway modeling: a case study of the Akt and MAPK pathways and their crosstalk. Bioinformatics. 2006;22:e271–e280. doi: 10.1093/bioinformatics/btl264. [DOI] [PubMed] [Google Scholar]
  17. Koh G, et al. Algorithms in Bioinformatics, 7th International Workshop. 2007. Composing globally consistent pathway parameter estimates through belief propagation. WABI 2007, Philadelphia, PA, USA. [Google Scholar]
  18. Kwon J, et al. Reversible oxidation and inactivation of the tumor suppressor PTEN in cells stimulated with peptide growth factors. Proc. Natl Acad. Sci. USA. 2004;101:16419–16424. doi: 10.1073/pnas.0407396101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Levenberg K. A method for the solution of certain nonlinear problems in least squares. Quart. Appl. Math. 1944;2:164–168. [Google Scholar]
  20. Lim S, Clément MV. Phosphorylation of the survival kinase Akt by superoxide is dependent on an ascorbate-reversible oxidation of PTEN. Free Radic. Biol. Med. 2007;42:1178–1192. doi: 10.1016/j.freeradbiomed.2007.01.013. [DOI] [PubMed] [Google Scholar]
  21. Marquardt D. An algorithm for least-squares estimation of nonlinear parameters. SIAM J. Appl. Math. 1963;11:431. [Google Scholar]
  22. McEliece RJ, et al. Turbo decoding as an instance of Pearl’s ‘beliefpropagation’ algorithm. IEEE J. Sel. Area Comm. 1998;16:140–152. [Google Scholar]
  23. Meltzer T, et al. Conference on Uncertainty in Artificial Intelligence (UAI ’09) Arlington, Virginia, USA: AUAI Press; 2009. Convergent message passing algorithms-a unifying view. [Google Scholar]
  24. Michalewicz Z. Genetic Algorithms + Data Structures = Evolution Programs. Berlin: Springer-Verlag; 1994. [Google Scholar]
  25. Mitsiades CS, et al. The Akt pathway: molecular targets for anti-cancer drug development. Curr. Cancer Drug Targets. 2004;4:235–256. doi: 10.2174/1568009043333032. [DOI] [PubMed] [Google Scholar]
  26. Murphy K, et al. Proceedings of Uncertainty in AI. 1999. Loopy belief propagation for approximate inference: an empirical study; p. 467. [Google Scholar]
  27. Palsson BO. Systems Biology: Properties of Reconstructed Networks. Cambridge, UK: Cambridge University Press; 2006. [Google Scholar]
  28. Pearl J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. 2nd. San Francisco, CA: Morgan Kaufmann; 1988. [Google Scholar]
  29. Peifer M, Timmer J. Parameter estimation in ordinary differential equations for biochemical processes using the method of multiple shooting. IET Syst. Biol. 2007;1:78–88. doi: 10.1049/iet-syb:20060067. [DOI] [PubMed] [Google Scholar]
  30. Purvis JE, et al. A molecular signaling model of platelet phosphoinositide and calcium regulation during homeostasis and P2Y1 activation. Blood. 2008;112:4069–4079. doi: 10.1182/blood-2008-05-157883. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Ramsay JO, et al. Parameter estimation for differential equations a generalized smoothing approach. J. R. Stat. Soc. B Stat. Methodol. 2007;69:741–796. [Google Scholar]
  32. Reeves EK, et al. Proteomic profiling of glucocorticoid-exposed myogenic cells: time series assessment of protein translocation and transcription of inactive mRNAs. Proteome Sci. 2009;7:26. doi: 10.1186/1477-5956-7-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Rodriguez-Fernandez M, et al. A hybrid approach for efficient and robust parameter estimation in biochemical pathways. Biosystems. 2006;83:248–265. doi: 10.1016/j.biosystems.2005.06.016. [DOI] [PubMed] [Google Scholar]
  34. Runarsson T, Yao X. Stochastic ranking for constrained evolutionary optimization. IEEE Trans. Evol. Comput. 2000;4:284–294. [Google Scholar]
  35. Tasaki S, et al. Phosphoproteomics-based modeling defines the regulatory mechanism underlying aberrant EGFR signaling. PLoS One. 2010;5:e13926. doi: 10.1371/journal.pone.0013926. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Testa JR, Bellacosa A. AKT plays a central role in tumorigenesis. Proc. Natl Acad. Sci. USA. 2001;98:10983–10985. doi: 10.1073/pnas.211430998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Vilela M, et al. Identification of neutral biochemical network models from time series data. BMC Syst. Biol. 2009;3:47. doi: 10.1186/1752-0509-3-47. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Voit EO, Almeida J. Decoupling dynamical systems for pathway identification from metabolic profiles. Bioinformatics. 2004;20:1670–1681. doi: 10.1093/bioinformatics/bth140. [DOI] [PubMed] [Google Scholar]
  39. Yedidia J, et al. Understanding belief propagation and its generalizations. In: Lakemeyer G, Nebel B, editors. Exploring Artificial Intelligence in the New Millennium. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc.; 2003. pp. 239–269. [Google Scholar]
  40. Zhan C, Yeung LF. Parameter estimation in systems biology models using spline approximation. BMC Syst. Biol. 2011;5:14. doi: 10.1186/1752-0509-5-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Zhang G, Neubert TA. Use of stable isotope labeling by amino acids in cell culture (SILAC) for phosphotyrosine protein identification and quantitation. Methods Mol. Biol. 2009;527:79–92. doi: 10.1007/978-1-60327-834-8_7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Zhang GL, et al. Database resources for proteomics-based analysis of cancer. Methods Mol. Biol. 2011;723:349–364. doi: 10.1007/978-1-61779-043-0_22. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_29_8_1044__index.html (1,006B, html)
supp_btt083_SPEDRE_Supplement.pdf (547.8KB, pdf)
supp_btt083_SPEDRE_SourceFiles.zip (8.3MB, zip)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES