Abstract
The A-type potassium current has been implicated in the regulation of several physiological processes. Here, we explore a role for the A-type potassium current in regulating the release of calcium through inositol trisphosphate receptors (InsP3R) that reside on the endoplasmic reticulum (ER) of hippocampal pyramidal neurons. To do this, we constructed morphologically realistic, conductance-based models equipped with kinetic schemes that govern several calcium signalling modules and pathways, and constrained the distributions and properties of constitutive components by experimental measurements from these neurons. Employing these models, we establish a bell-shaped dependence of calcium release through InsP3Rs on the density of A-type potassium channels, during the propagation of an intraneuronal calcium wave initiated through established protocols. Exploring the sensitivities of calcium wave initiation and propagation to several underlying parameters, we found that ER calcium release critically depends on dendritic diameter and that wave initiation occurred at branch points as a consequence of a high surface area to volume ratio of oblique dendrites. Furthermore, analogous to the role of A-type potassium channels in regulating spike latency, we found that an increase in the density of A-type potassium channels led to increases in the latency and the temporal spread of a propagating calcium wave. Next, we incorporated kinetic models for the metabotropic glutamate receptor (mGluR) signalling components and a calcium-controlled plasticity rule into our model and demonstrate that the presence of mGluRs induced a leftward shift in a Bienenstock–Cooper–Munro-like synaptic plasticity profile. Finally, we show that the A-type potassium current could regulate the relative contribution of ER calcium to synaptic plasticity induced either through 900 pulses of various stimulus frequencies or through theta burst stimulation. Our results establish a novel form of interaction between active dendrites and the ER membrane, uncovering a powerful mechanism that could regulate biophysical/biochemical signal integration and steer the spatiotemporal spread of signalling microdomains through changes in dendritic excitability.
Key points
Active calcium signal propagation occurs when an initial calcium trigger elicits calcium release through endoplasmic reticulum (ER) receptors. A high concentration of the calcium trigger in thin-calibre dendrites would suppress release of calcium through hippocampal inositol trisphosphate receptors (InsP3Rs).
Could the high-density expression of A-type K+ channels in thin-calibre dendrites be a mechanism for inhibiting this suppression, thereby restoring the utility of the ER as a substrate for active calcium propagation?
Quantitative analyses involving experimentally constrained models reveal a bell-shaped dependence of calcium released through InsP3Rs on the A-type K+ channel density, during the propagation of a calcium wave.
A-type K+ channels regulated the relative contribution of ER calcium to the induction of synaptic plasticity in the presence of model metabotropic glutamate receptors.
These results identify a novel form of interaction between active dendrites and the ER membrane and suggest that A-type K+ channels are ideally placed for inhibiting the suppression of InsP3Rs in thin-calibre dendrites.
Introduction
In the reaction–diffusion system that governs Ca2+ signal propagation, passive propagation attenuates the Ca2+ signal heavily, leading to Ca2+ signalling domains that are central to the specificity of several forms of neuronal plasticity. However, under certain physiological conditions that require lossless propagation of Ca2+ signals, regenerative release of Ca2+ from the endoplasmic reticulum (ER) is recruited to initiate a Ca2+ wave that traverses significantly larger distances compared to passive propagation of Ca2+ signals. This positive feedback signal from the ER stores, which is triggered by an initial Ca2+ influx and is mediated by calcium-induced calcium release (CICR) mechanisms involving the inositol trisphosphate receptors (InsP3R) and the ryanodine receptors, constitutes the central premise of lossless Ca2+ signal propagation (Berridge et al. 2000; Berridge, 2002, 2006; Augustine et al. 2003; Verkhratsky, 2005; Clapham, 2007; Neves & Iyengar, 2009; Ross, 2012).
For such active Ca2+ signal propagation to occur, it is essential that the initial Ca2+ trigger, which is mostly relayed through plasma membrane channels, elicits CICR from receptors that reside on the ER membrane. Given the properties of receptors that reside on the ER of hippocampal pyramidal neurons (Bezprozvanny et al. 1991; Choe & Ehrlich, 2006; Hertle & Yeckel, 2007), Ca2+ release from the ER will occur only when cytosolic Ca2+ concentration ([Ca2+]c) is moderate; high levels of [Ca2+]c suppress release, thus rendering the ER and its release mechanisms redundant. Against this background, in thin-calibre dendrites with high surface area to volume ratio (SVR), the initial [Ca2+]c is very high because of the inherently heavy dependence of any reaction–diffusion system on the SVR (Sabatini et al. 2002; Frick et al. 2003; Neves & Iyengar, 2009; Kotaleski & Blackwell, 2010). As high levels of [Ca2+]c suppress release of ER Ca2+, this would render ER and its release mechanisms redundant in all thin-calibre dendrites. However, evidence in the literature is contrary in this regard, and ER Ca2+ has been demonstrated to play a very critical physiological role across dendritic locations (Berridge et al. 2000; Berridge, 2002; Verkhratsky, 2005; Rizzuto & Pozzan, 2006; Clapham, 2007; Stutzmann & Mattson, 2011; Ross, 2012). How can we reconcile this contradiction?
In this study, we present a possible answer to this question through the observation that thin-calibre dendrites in hippocampal pyramidal cells express A-type K+ channels in abundance (Hoffman et al. 1997; Kerti et al. 2011). We hypothesized that the high density of A-type K+ channels in thin-calibre dendrites constitutes a strategy to suppress the initial influx of local [Ca2+]c, so that the ER and its release mechanisms are not rendered redundant in these dendritic compartments. We quantitatively test this hypothesis through morphologically realistic conductance-based models, and uncover a novel role for A-type K+ channels in regulating Ca2+ release through InsP3Rs, thereby altering propagation of Ca2+ waves and induction of synaptic plasticity. Our results suggest that such interactions between restorative conductances on the dendritic membrane and Ca2+ channels on the ER membrane could critically regulate biophysical/biochemical signal integration and steer the spatiotemporal spread of signalling microdomains within neurons.
Methods
Models and their passive properties
The models used in this study consisted of a large number of individual components with the model output designed to be an emergent property of non-linear interactions among these constitutive components. To understand the mechanistic details of how each component interacts with the others in the model and thereby influences the output characteristics of the model, it was first necessary to understand the constitutive components in a simpler system before incorporating them into morphologically precise models. Concordantly, two different types of models were employed.
Three-cylinder model
To understand the parametric dependencies of various factors affecting the release of Ca2+ from the intracellular stores, a simpler biophysically realistic model consisting of three cylindrical compartments (three-cylinder model) was used. This model (Fig. 1A) constitutes an extension to the classical ball-and-stick model and consisted of a somatic compartment of 20 μm diameter and 40 μm length, a main apical dendritic trunk of 3 μm diameter and 500 μm length and an oblique dendrite of 0.80 μm diameter and 80 μm length. The oblique dendrite branches from the main apical dendrite at a distance of 50 μm from the soma. For the sake of simplicity, in this model the passive electrical parameters across all the compartments were uniform: specific membrane resistivity, Rm = 20 kΩ cm2; specific cytoplasmic resistivity, Ra = 200 Ω cm; and specific membrane capacitance, Cm = 1 μF cm−2. The apical dendrite and the oblique dendrites were compartmentalized into 100 segments each.
Figure 1. Dependence of calcium transients evoked by a backpropagating action potential on the A-type K+ channel density.
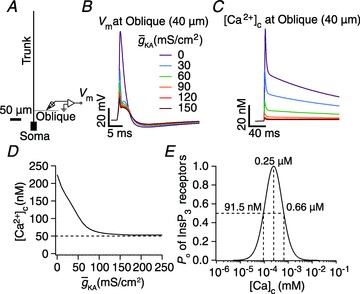
A, morphology of the simplified three-cylinder model neuron used in the study. B, voltage traces recorded at the midpoint of the oblique dendrite in response to a bAP at different A-conductance densities. C, [Ca2+]c traces in response to the bAPs shown in B. D, peak [Ca2+]c, in response to a bAP, plotted as a function of A-conductance density obtained from the experiments depicted in B–C. E, open probability of InsP3R (Po) plotted as a function of [Ca2+]c.
Morphologically realistic model
A morphologically realistic multicompartmental three-dimensional model (see Fig. 4G) was constructed from a restructured CA1 pyramidal neuron (n123) taken from the Neuromorpho database (Pyapali et al. 1998; Ascoli et al. 2007). Passive parameters were set as follows: Cm = 1 μF cm−2; Rm and Ra for various compartments along the somato-apical trunk were functions of radial distance of the compartment from the soma, x (Narayanan & Johnston, 2007):
Figure 4. Calcium waves in a morphologically realistic neuronal model.
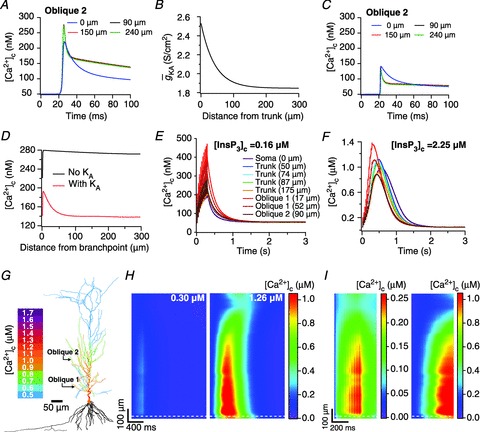
A, [Ca2+]c transients in response to a single backpropagating action potential at various locations in a proximal oblique (Oblique 2 in G), in the absence of A-type K+ channels. B, gradient in A-conductance required for normalizing [Ca2+]c transients across various locations in the oblique dendrite under consideration. C, as A, but in the presence of A-type K+ channels with a gradient shown in B. D, peak [Ca2+]c at different locations in the oblique 2 in the absence and in the presence of A-type K+ channels, quantified from experiments depicted in A and C, respectively. E, [Ca2+]c trace with baseline [InsP3]c (= 0.16 μm) at various locations in response to a train of 10 bAPs, separated regularly by 30 ms intervals. F, as E, but with elevated [InsP3]c (= 2.25 μm) to model bath application of group I mGluR agonists. Note differences in the peak [Ca2+]c with respect to E. For E and F, distances for trunk locations are radial distances from the soma. For locations on oblique dendrites, distances are path distances from their respective branch points on the trunk. G, shape plot of the model neuron showing peak [Ca2+]c along the neuronal topograph during the Ca2+ wave shown in F. Note that [Ca2+]c in basal dendrites is not shown, owing to lack of experimental data on basal dendrites in CA1 pyramidal neurons. H, kymographs showing time-dependent changes in the [Ca2+]c in response to a train of 10 bAPs, separated regularly by 30 ms intervals, under baseline (left) and elevated (right) InsP3 levels, derived from experiments depicted in E and F, respectively. The ordinate represents the path distance along the somato-dendritic axis (apical dendrites only) and the abscissa represents time. Numbers on the kymograph represent the highest peak value of [Ca2+]c measured across different locations on the somato-dendritic axis. I, as H, but the kymograph shows [Ca2+]c only for the first 500 ms. Note that the scales (presented to the right of each subpanel) are different for the left and the right subpanels. White dashed lines in H and I represent the border between the soma (below the line) and the apical trunk.
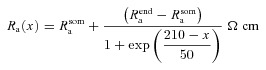 |
(1) |
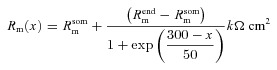 |
(2) |
where 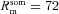 kΩ cm2 and
kΩ cm2 and 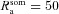 Ω cm were values at the soma, and
Ω cm were values at the soma, and 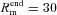 kΩ cm2 and
kΩ cm2 and 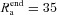 Ω cm were values assigned to the terminal end of the apical trunk (which was ∼425 μm from the soma for the reconstruction under consideration). This was done to keep the local input resistance (Rin) almost constant (∼120 MΩ) throughout the trunk (Narayanan & Johnston, 2007). The basal dendrites and the axonal compartments had somatic Rm and Ra, and apical obliques had the same Rm and Ra as the trunk compartment from which they originated. Unless otherwise stated this neuronal model was compartmentalized using dλ rule (Carnevale & Hines 2006) to ensure that each compartment was smaller than 0.1λ100, where λ100 is the space constant, computed at 100 Hz for the section under consideration. Eliminating numerical errors in the estimation of Ca2+ signals required smaller compartment sizes than such electrical compartmentalization. To obtain error-free estimates, we performed specific recompartmentalization through trial and error, involving progressive reductions in compartment size until a point where further reductions led to negligible changes in Ca2+ transients.
Ω cm were values assigned to the terminal end of the apical trunk (which was ∼425 μm from the soma for the reconstruction under consideration). This was done to keep the local input resistance (Rin) almost constant (∼120 MΩ) throughout the trunk (Narayanan & Johnston, 2007). The basal dendrites and the axonal compartments had somatic Rm and Ra, and apical obliques had the same Rm and Ra as the trunk compartment from which they originated. Unless otherwise stated this neuronal model was compartmentalized using dλ rule (Carnevale & Hines 2006) to ensure that each compartment was smaller than 0.1λ100, where λ100 is the space constant, computed at 100 Hz for the section under consideration. Eliminating numerical errors in the estimation of Ca2+ signals required smaller compartment sizes than such electrical compartmentalization. To obtain error-free estimates, we performed specific recompartmentalization through trial and error, involving progressive reductions in compartment size until a point where further reductions led to negligible changes in Ca2+ transients.
Active properties
Five different types of voltage-gated ion channels (VGICs) were incorporated into these models: a fast Na+, a delayed rectifier K+ (KDR), an A-type K+ (KA), and L- and T-type Ca2+. Biophysically realistic, Hodgkin–Huxley type conductance-based models derived from hippocampal pyramidal neurons were employed for modelling all these channels. The implementation for Na+, KDR and KA was adopted from Migliore et al. (1999), and L- and T-type Ca2+ channels were from Poirazi et al. (2003).
Three-cylinder model
In the three-cylinder model, Na+ and KDR channels were distributed uniformly throughout the soma and the dendrites (Magee & Johnston, 1995; Hoffman et al. 1997), with maximal conductance values set at 10 mS cm−2 (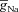 ) and 15 mS cm−2
) and 15 mS cm−2
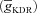 . The density of Ca2+ channels was constant throughout all three cylinders with maximal conductance values of 100 μS cm−2 for T-type Ca2+ channels (
. The density of Ca2+ channels was constant throughout all three cylinders with maximal conductance values of 100 μS cm−2 for T-type Ca2+ channels (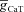 ), and 316 μS cm−2 for L-type Ca2+ channels (
), and 316 μS cm−2 for L-type Ca2+ channels (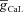 ). As the main objective behind the construction of this three-cylinder model was to perform a sensitivity analysis across various constitutive parameters, we maintained uniform densities of these channels rather than implementing a physiological gradient of these different channels along the main dendritic trunk, only for the three-cylinder model.
). As the main objective behind the construction of this three-cylinder model was to perform a sensitivity analysis across various constitutive parameters, we maintained uniform densities of these channels rather than implementing a physiological gradient of these different channels along the main dendritic trunk, only for the three-cylinder model.
Morphologically realistic model
In the morphologically realistic multi-compartmental model, the same five types of ion channels were inserted but with the following differences in their densities and properties. To account for the lower membrane potential threshold for spike generation at the axon initiation segment, the Na+ channel density at this location was increased five-fold compared to the somato-dendritic values (Fleidervish et al. 2010). The rest of the axon was considered as passive. To account for slower recovery from inactivation of dendritic Na+ channels, an extra inactivation gate was added while modelling the channel kinetics for dendritic Na+ channels (Colbert et al. 1997; Migliore et al. 1999). The Na+ channel density in basal dendrites was the same as the soma. Values of 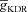 and
and 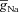 were fixed at 3 and 90 mS cm−2, respectively. These parameters were adjusted so as to obtain an action potential (AP) firing frequency of around 10 Hz when the cell rested at –70 mV and a 150 pA current was injected into the soma (Narayanan & Johnston, 2007).
were fixed at 3 and 90 mS cm−2, respectively. These parameters were adjusted so as to obtain an action potential (AP) firing frequency of around 10 Hz when the cell rested at –70 mV and a 150 pA current was injected into the soma (Narayanan & Johnston, 2007).
In incorporating A-type K+ channels, kinetics and voltage dependencies of the channels were different for the proximal (≤100 μm from the soma) and distal (>100 μm) compartments (Hoffman et al. 1997; Migliore et al. 1999). The density of A-type K+ channels was linearly increased with respect to distance of the compartment from the soma (Hoffman et al. 1997; Migliore et al. 1999). The density distribution of A-type K+ channels in the apical dendritic locations was:
| (3) |
where 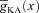 represented the maximal A-type K+ conductance at radial distance x μm from the soma, and
represented the maximal A-type K+ conductance at radial distance x μm from the soma, and 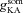 represented the maximal conductance value for A-type K+ channels at the soma, with a default value of 22 mS cm−2. This gradient was set such that the backpropagating AP amplitude at a trunk location ∼300 μm from the soma was around 10 mV (Hoffman et al. 1997; Migliore et al. 1999).
represented the maximal conductance value for A-type K+ channels at the soma, with a default value of 22 mS cm−2. This gradient was set such that the backpropagating AP amplitude at a trunk location ∼300 μm from the soma was around 10 mV (Hoffman et al. 1997; Migliore et al. 1999).
Unless noted otherwise, the  in the proximal oblique dendrites (corresponding to obliques branching at trunk locations having radial distance ≤100 μm from soma) was set to 21 times its value at the branch point. This, along with reduced density of Ca2+ channels in the proximal obliques (see below), was done to approximate the experimental observation that the Ca2+ transients at the branch point on the main apical dendritic trunk and in the daughter oblique dendrite are the same when a single spike invades these regions (Frick et al. 2003; Fig. 2A–D). The value of
in the proximal oblique dendrites (corresponding to obliques branching at trunk locations having radial distance ≤100 μm from soma) was set to 21 times its value at the branch point. This, along with reduced density of Ca2+ channels in the proximal obliques (see below), was done to approximate the experimental observation that the Ca2+ transients at the branch point on the main apical dendritic trunk and in the daughter oblique dendrite are the same when a single spike invades these regions (Frick et al. 2003; Fig. 2A–D). The value of 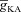 in the distal oblique dendrites (corresponding to obliques branching at trunk locations beyond a radial distance of 100 μm from soma) was three times its value at the branch point. Note that evidence for a higher density of A-type K+ channels in proximal oblique dendrites was derived from both physiological evidence (Frick et al. 2003) as well as evidence from an immunogold labelling study of Kv4.2, a subunit that encodes A-type K+ currents (Kerti et al. 2011). In the absence of experimental data in the basal dendrites, A-type K+ channel density was kept the same as that of the soma.
in the distal oblique dendrites (corresponding to obliques branching at trunk locations beyond a radial distance of 100 μm from soma) was three times its value at the branch point. Note that evidence for a higher density of A-type K+ channels in proximal oblique dendrites was derived from both physiological evidence (Frick et al. 2003) as well as evidence from an immunogold labelling study of Kv4.2, a subunit that encodes A-type K+ currents (Kerti et al. 2011). In the absence of experimental data in the basal dendrites, A-type K+ channel density was kept the same as that of the soma.
Figure 2. Sensitivity analyses of critical parameters that regulated calcium waves in a three-cylinder model neuron.
A, [Ca2+]c traces as a function of time for selected locations on the three-cylinder model when calcium waves were initiated by pairing 10 bAPs separated by 30 ms ISI with elevated [InsP3]c. B–C, shape plots of the model neuron depicting peak [Ca2+]c (B) and the time at which this peak occurred (C) along the neuronal topograph for the experiment depicted in A. D, area under the curve (AUC) for the flux of Ca2+ through InsP3R (JInsP3R), measured at different oblique dendritic locations, plotted as a function of the diameter of the oblique dendrite. E–G, as A–C, but simulations were performed with oblique diameter set at 3 μm. H, as A, but simulations were performed with uniform InsP3R density throughout the neuron. Location codes for E and H are the same as in A.
The density of L-type Ca2+ channels decreased along the dendritic trunk, whereas that of the T-type channels increased as a function of distance from the soma (Johnston et al. 1996). Specifically, the distribution of these channels were set as:
| (4) |
| (5) |
where  and
and 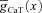 represent the maximal conductance value at a somato-dendritic location x μm away from the soma, for L- and T-type channels, respectively. Parameters
represent the maximal conductance value at a somato-dendritic location x μm away from the soma, for L- and T-type channels, respectively. Parameters 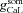 and
and 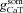 represent the densities of the L- and T-type conductances at the soma. To incorporate the experimental observation that the total Ca2+ current, in the proximal obliques, is slightly less than that of the corresponding branch points on the parent trunk (Frick et al. 2003), the L- and T- type Ca2+ channel density in the proximal obliques was set to 0.75 times its value on the parent trunk near the branch point. In the distal obliques, the L- and T- type Ca2+ channel density was the same as that of the parent trunk near the branch point. In the basal dendrites, L-type channel density was twice that of the soma and T-type channel density was same as that of the soma.
represent the densities of the L- and T-type conductances at the soma. To incorporate the experimental observation that the total Ca2+ current, in the proximal obliques, is slightly less than that of the corresponding branch points on the parent trunk (Frick et al. 2003), the L- and T- type Ca2+ channel density in the proximal obliques was set to 0.75 times its value on the parent trunk near the branch point. In the distal obliques, the L- and T- type Ca2+ channel density was the same as that of the parent trunk near the branch point. In the basal dendrites, L-type channel density was twice that of the soma and T-type channel density was same as that of the soma.
Calcium dynamics
The overall Ca2+ dynamics was modelled as a function of various mechanisms that lead to changes in [Ca2+]c within a neuron. The partial differential equation governing the cytosolic Ca2+ dynamics was (Sneyd et al. 1995; Fink et al. 2000):
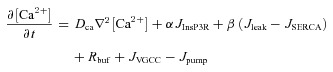 |
(6) |
where DCa is the experimentally determined diffusion coefficient for Ca2+ (Allbritton et al. 1992; Klingauf & Neher, 1997), α is the density gradient of InsP3Rs on the ER and β is the density of SERCA pumps and leak channels on the ER along the somato-dendritic axis. 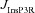 ,
, 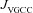 ,
, 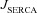 ,
, 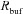 ,
, 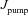 and
and 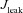 represent the Ca2+ flux due to InsP3Rs, VGCCs, SERCA pumps, buffering, plasma membrane Ca2+ extrusion pumps and the ER leak channels, respectively (Tables 1 and 2). Radial diffusion of Ca2+ was incorporated by radial compartmentalization of the neuronal compartments into four concentric annuli, and diffusion along the longitudinal axis of the neuron was also implemented (Carnevale & Hines, 2006). Detailed descriptions for each of the fluxes are presented below.
represent the Ca2+ flux due to InsP3Rs, VGCCs, SERCA pumps, buffering, plasma membrane Ca2+ extrusion pumps and the ER leak channels, respectively (Tables 1 and 2). Radial diffusion of Ca2+ was incorporated by radial compartmentalization of the neuronal compartments into four concentric annuli, and diffusion along the longitudinal axis of the neuron was also implemented (Carnevale & Hines, 2006). Detailed descriptions for each of the fluxes are presented below.
Table 1.
Parameters used in InsP3 dynamics
| Parameter | Symbol | Value | Unit | Reference(s) |
|---|---|---|---|---|
| Degradation rate | kdegr | 0.14 | s−1 | (Fink et al. 2000) |
| Initial InsP3 concentration | [InsP3]0 | 0.16 | μm | (Fink et al. 2000) |
| InsP3 diffusion coefficient | DInsP3 | 283 | μm2 s−1 | (Allbritton et al. 1992) |
| InsP3 receptor density |
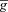 InsP3R InsP3R
|
1.85 | — | Set based on calcium wave amplitude (Nakamura et al. 1999, 2000) |
| Average amplitude of InsP3 release | 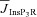 |
3500 | μm s−1 | (Fink et al. 2000) |
Table 2.
Parameters used in calcium dynamics
| Parameter | Symbol | Value | Unit | Reference |
|---|---|---|---|---|
| Average amplitude of SERCA pump uptake | Vmax | 1 × 10−4 | mm ms−1 | |
| Leak constant | L | Determined by steady-state balance | mm ms−1 | (Fink et al. 2000) |
| Dissociation constant for Ca2+ binding to an activation site | Kact | 0.3 | μm | (Fink et al. 2000) |
| Dissociation constant for Ca2+ binding to an inhibition site | Kinh | 0.2 | μm | (Fink et al. 2000) |
| On-rate for Ca2+ binding to an inhibition site | kon | 2.7 | μm−1 s−1 | (Fink et al. 2000) |
| Dissociation constant for InsP3 binding to a channel | KInsP3 | 0.8 | μm | (Fink et al. 2000) |
| Dissociation constant for Ca2+ binding to a pump | Kp | 0.27 | μm | (Lytton et al. 1992) |
| Initial cytosolic Ca2+ concentration | [Ca2+]0 | 0.05 | μm | (Fink et al. 2000) |
| Ca2+ concentration in ER | [Ca2+]ER | 400 | μm | (Meldolesi & Pozzan, 1998) |
| Average rate of Ca2+ flux density at the plasma membrane | γ0 | 8.0 | μm s−1 | (Herrington et al. 1996) |
| Threshold condition for Ca2+ extrusion at plasma membrane | [Ca2+]crt | 0.2 | μm | (Herrington et al. 1996) |
| Ca2+ diffusion coefficient | DCa | 220 | μm2 s−1 | (Allbritton et al. 1992) |
InsP3R-dependent release
We incorporated an experimentally determined density gradient for the InsP3R subunits in CA1 pyramidal neurons of young rats (Hertle & Yeckel, 2007), where α (in eqn (6)) takes the form:
| (7) |
where 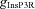 represents the density of InsP3Rs at the soma (Table 1). The numerical value of
represents the density of InsP3Rs at the soma (Table 1). The numerical value of 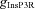 was chosen such that the Ca2+ wave amplitude and kinetics is in agreement with the experimentally observed Ca2+ waves (Nakamura et al. 1999, 2000), when similar protocols were used to initiate the waves (Fig. 2F). The presence of ER leak channels and SERCA pumps on the neuronal ER membrane is well established (Verkhratsky, 2005). However, there is no quantitative data available for the subcellular distribution and density gradient of these molecules along the hippocampal pyramidal neuronal topograph. Therefore, the distribution of ER leak channels and SERCA pump were considered to be homogeneous across the somato-dendritic axis.
was chosen such that the Ca2+ wave amplitude and kinetics is in agreement with the experimentally observed Ca2+ waves (Nakamura et al. 1999, 2000), when similar protocols were used to initiate the waves (Fig. 2F). The presence of ER leak channels and SERCA pumps on the neuronal ER membrane is well established (Verkhratsky, 2005). However, there is no quantitative data available for the subcellular distribution and density gradient of these molecules along the hippocampal pyramidal neuronal topograph. Therefore, the distribution of ER leak channels and SERCA pump were considered to be homogeneous across the somato-dendritic axis.
Ca2+ release from the ER through InsP3R was defined using a simplified model for the InsP3R (Li & Rinzel, 1994). Specifically, Ca2+ release through InsP3Rs as a function of cytosolic InsP3 concentration ([InsP3]c) and [Ca2+]c was modelled as (Li & Rinzel, 1994; Fink et al. 2000):
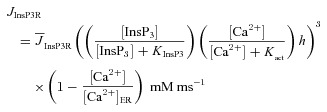 |
(8) |
where 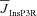 represents the maximal rate of release;
represents the maximal rate of release; 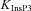 stands for the dissociation constant for InsP3 binding to InsP3R;
stands for the dissociation constant for InsP3 binding to InsP3R; 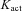 constitutes the dissociation constant for Ca2+ binding to an activation site on the receptor;
constitutes the dissociation constant for Ca2+ binding to an activation site on the receptor; 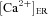 represents the Ca2+ concentration within the ER (Tables 1 and 2); h depicts the probability of the inhibition site (on InsP3Rs) not being occupied, and evolved as function of time as (Li & Rinzel, 1994):
represents the Ca2+ concentration within the ER (Tables 1 and 2); h depicts the probability of the inhibition site (on InsP3Rs) not being occupied, and evolved as function of time as (Li & Rinzel, 1994):
| (9) |
where kon represents the on rate of Ca2+ binding to the inhibition site and Kinh denotes the corresponding dissociation constant (Li & Rinzel, 1994; Fink et al. 2000). Note that the inhibition site was employed to model the inhibition of Ca2+ release from InsP3Rs at higher concentrations of cytosolic Ca2+ (Bezprozvanny et al. 1991; De Young & Keizer, 1992; Li & Rinzel, 1994).
ER leak channels
The rate of Ca2+ influx into the cytoplasm through ER leak channels was modelled as (Fink et al. 2000):
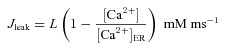 |
(10) |
where L was chosen such that there was no net flux of Ca2+ between the ER and the cytosol at resting state.
Voltage-gated calcium channels (VGCCs)
Ca2+ current through VGCCs (L- and T-type) was converted to Ca2+ concentration as (Poirazi et al. 2003):
| (11) |
where ICa depicts the net inward Ca2+ current, diam stands for the diameter of the compartment and F is Faraday's constant.
SERCA pump
The Ca2+ uptake by sarcoplasmic endoplasmic reticulum Ca2+ ATPase (SERCA) pump was modelled as (Fink et al. 2000):
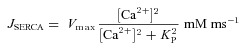 |
(12) |
where 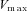 depicts the maximal rate of pump and
depicts the maximal rate of pump and 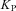 is the dissociation constant of Ca2+ binding to the pump (Table 2).
is the dissociation constant of Ca2+ binding to the pump (Table 2).
Plasma membrane calcium extrusion pump
Ca2+ extrusion through plasma membrane pumps was regulated by a threshold on the [Ca2+]c. The pumps were inactive below a critical Ca2+ concentration, [Ca2+]crt, above which the extrusion rate depended linearly on [Ca2+]c (Fink et al. 2000):
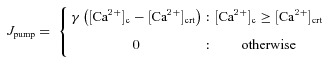 |
(13) |
where [Ca2+]crt was set at 0.2 μm based on previous experimental observations (Herrington et al. 1996), and γ (Table 2) defines the sensitivity of pump extrusion (Fink et al. 2000).
Calcium buffering
We incorporated buffers uniformly through the somatodendritic axis. Rbuf defined the rate of change in [Ca2+]c due to buffers:
| (14) |
Rs is the rate due to stationary buffers and Rmob the rate due to mobile buffers:
| (15) |
| (16) |
[Bs] (= 450 μm) and [Bmob] (= 100 μm) are concentrations of stationary and mobile buffers, respectively. [Ca2+Bs] and [Ca2+Bmob] are the concentrations of Ca2+ bound to stationary and mobile buffers, respectively. Bound buffer was considered to be in rapid equilibrium with the surrounding Ca2+ and pseudo-steady-state approximation was applied to simulate buffering (Fink et al. 2000):
| (17) |
| (18) |
| (19) |
The equilibrium constants for stationary and mobile buffering were:
| (20) |
| (21) |
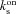 = on rate constant for Ca2+ binding to stationary buffer
= on rate constant for Ca2+ binding to stationary buffer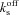 = off rate constant for Ca2+ binding to stationary buffer
= off rate constant for Ca2+ binding to stationary buffer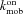 = on rate constant for Ca2+ binding to mobile buffer
= on rate constant for Ca2+ binding to mobile buffer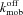 = off rate constant for Ca2+ binding to stationary buffer
= off rate constant for Ca2+ binding to stationary buffer
Dbuf was the diffusion coefficient of the mobile buffer, which was set to 50 μm2 s−1, the experimentally determined value for the Ca2+ indicator dye Fura-2 (Klingauf & Neher, 1997). Ks was 10 μm (Klingauf & Neher, 1997; Fink et al. 2000) and Kmob was varied between 0.4 and 400 μm. Note that the mobile buffer was introduced only to assess the effects of Ca2+ indicator dyes on the Ca2+ dynamics within a neuron (Fig. 3F–H).
Figure 3. A-type K+ channels regulated calcium release from ER stores during calcium waves in a three-cylinder neuronal model.
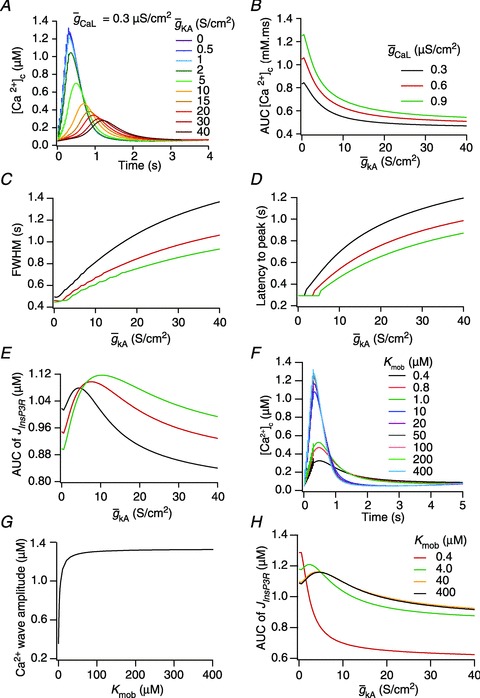
A, effect of the A-type conductance in the oblique dendrite on [Ca2+]c during a Ca2+ wave. [Ca2+]c traces were recorded at a distance of 8 μm from the branch point with different densities of the A conductance in the oblique dendrite. B–E, area under the curve (AUC) for the [Ca2+]c transients depicted in A (B), full width at half maximum, FWHM (C) and latency-to-peak for these [Ca2+]c transients (D) and AUC for the flux of Ca2+ through InsP3 receptors, 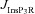 (E), in achieving these transients, plotted as functions of A-conductance density,
(E), in achieving these transients, plotted as functions of A-conductance density, 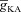 . Plots are shown for different densities of the L-type Ca2+ channel,
. Plots are shown for different densities of the L-type Ca2+ channel, 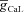 . F and G, time-dependent [Ca2+]c changes (F) and the amplitude (G) of Ca2+ wave, computed in the presence of mobile buffers at different affinities (Kmob) to Ca2+ binding. Ca2+ wave was initiated with 100 μm mobile buffer with the same protocol as in A. H, AUC for
. F and G, time-dependent [Ca2+]c changes (F) and the amplitude (G) of Ca2+ wave, computed in the presence of mobile buffers at different affinities (Kmob) to Ca2+ binding. Ca2+ wave was initiated with 100 μm mobile buffer with the same protocol as in A. H, AUC for 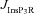 plotted as functions of A-conductance density,
plotted as functions of A-conductance density, 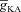 , when the Ca2+ wave was initiated in the presence of 100 μm mobile buffer and with different values of Kmob.
, when the Ca2+ wave was initiated in the presence of 100 μm mobile buffer and with different values of Kmob.
InsP3 dynamics
The overall InsP3 dynamics were governed by:
| (22) |
where 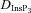 represents the diffusion coefficient for InsP3, kdegr is the degradation rate of InsP3 and [InsP3]0 stands for the baseline [InsP3] (Table 1).
represents the diffusion coefficient for InsP3, kdegr is the degradation rate of InsP3 and [InsP3]0 stands for the baseline [InsP3] (Table 1).
Synaptic receptors and plasticity
For most simulations involving synaptic inputs, a synapse was placed at the mid point of a proximal oblique (Oblique2 in Fig. 4; at a path distance of 148.5 μm from the trunk). This oblique was recompartmentalized into 297 compartments such that each compartment was approximately 1 μm long.
Ionotropic glutamate receptors
A canonical synapse consisting of co-localized N-methyl-d-aspartate receptor (NMDAR) and 2-amino-3-(5-methyl-3-oxo-1,2- oxazol-4-yl) propanoic acid receptor (AMPAR) was modelled as in Narayanan & Johnston (2010). Specifically, the NMDAR currents were modelled as combination of three different types of ionic currents, namely Ca2+, Na+ and K+:
| (23) |
where
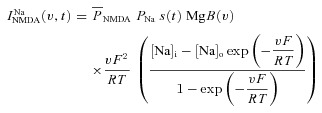 |
(24) |
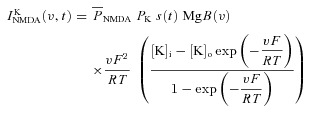 |
(25) |
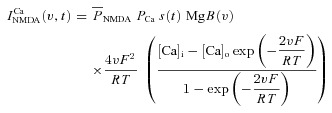 |
(26) |
where 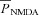 is the maximum permeability of the NMDAR; and PCa = 10.6, PNa = 1, PK = 1, owing to the permeability of the NMDAR to different ions, where PCa/PNa/PK = 10.6:1:1 (Mayer & Westbrook, 1987; Canavier, 1999). Default concentration values were (in mm): [Na]i = 18, [Na]o = 140, [K]i = 140, [K]o = 5, [Ca]i = 100 × 10−6, [Ca]o = 2. The concentrations for sodium set its equilibrium potential at +55 mV and that for potassium at –90 mV. MgB(v) governs the magnesium dependence of the NMDAR current, given as (Jahr & Stevens, 1990):
is the maximum permeability of the NMDAR; and PCa = 10.6, PNa = 1, PK = 1, owing to the permeability of the NMDAR to different ions, where PCa/PNa/PK = 10.6:1:1 (Mayer & Westbrook, 1987; Canavier, 1999). Default concentration values were (in mm): [Na]i = 18, [Na]o = 140, [K]i = 140, [K]o = 5, [Ca]i = 100 × 10−6, [Ca]o = 2. The concentrations for sodium set its equilibrium potential at +55 mV and that for potassium at –90 mV. MgB(v) governs the magnesium dependence of the NMDAR current, given as (Jahr & Stevens, 1990):
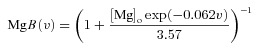 |
(27) |
with the default value of [Mg]o set at 2 mm. The parameter s(t) governed the kinetics of the NMDAR current, and was set as:
| (28) |
where a is a normalization constant, ensuring that 0 ≤s(t) ≤ 1, td is the decay time constant and tr is rise time, with tr = 5 ms, and td = 50 ms.
Current through the AMPAR was modelled as the sum of currents carried by sodium and potassium ions:
| (29) |
where
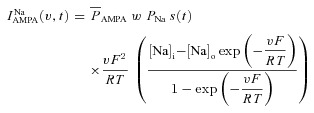 |
(30) |
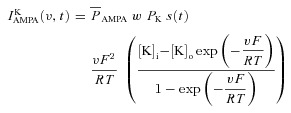 |
(31) |
where 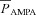 is the maximum permeability of the AMPAR, whose default value was set at 10 nm s−1. PNa was taken to be equal to PK (Dingledine et al. 1999). w denoted the weight parameter that undergoes activity-dependent plasticity (see below). s(t) was the same as that for the NMDA receptor, but with τr = 2 ms and τd = 10 ms (Narayanan & Johnston, 2010).
is the maximum permeability of the AMPAR, whose default value was set at 10 nm s−1. PNa was taken to be equal to PK (Dingledine et al. 1999). w denoted the weight parameter that undergoes activity-dependent plasticity (see below). s(t) was the same as that for the NMDA receptor, but with τr = 2 ms and τd = 10 ms (Narayanan & Johnston, 2010). 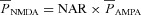 , with a default value for the NMDAR/AMPAR ratio (NAR) set at 1.5.
, with a default value for the NMDAR/AMPAR ratio (NAR) set at 1.5.
Metabotropic glutamate receptors
The role of group-1 metabotropic glutamate (mGluR) receptor in mobilizing intracellular InsP3 and the biochemical signalling pathways for the same are well established and have been explored both biochemically as well as computationally (Pin & Duvoisin, 1995; Bhalla & Iyengar, 1999; Blackwell, 2005; Mikoshiba, 2006). The activation of group 1 mGluR, near an active synapse, and the subsequent mobilization of InsP3 were modelled as a series of kinetic schemes that represent abstractions of the corresponding biochemical processes (Blackwell, 2005). In our representation below, the kinetic scheme is followed by the forward and backward reaction rates within parentheses; if the reaction is unidirectional, only a single number representing the rate for that reaction is provided. First, we modelled the binding of glutamate (Glu) to mGluR to form the glutamate-bound receptor (Glu_mGluR) as:
| (32) |
where k1 = 0.28 ms−1 and k2 = 0.016 ms−1. Then, the binding of Glu_mGluR to a G protein (G) to form a GlumGluR bound G protein (GluGmGluR) complex was modelled as:
| (33) |
where k3 = 15 ms−1 and k4 = 7.2 ms−1. In the next step, GluGmGluR dissociated to form the active α subunit of the G protein (Gα) as:
| (34) |
where k5 = 1.8 ms−1. Activated Gα reverted to its inactive form as:
| (35) |
where k6 = 9 ms−1. Activated Gα reversibly bound to phospholipase C (PLC) to form Gα-bound activated PLC (PLCα_Gα):
| (36) |
where k7 = 100 ms−1 and k8 = 100 ms−1. PLCα_Gα then reversibly bound to phosphatidylinositol 4,5-bisphosphate (PIP2) to form PLCα-bound PIP2 as:
| (37) |
with k9 = 0.83 ms−1 and k10 = 0.68 ms−1. PIP2 bound PLC (PLCα_PIP2) cleaved PIP2 to form InsP3:
| (38) |
where k11 = 0.58 ms−1. The InsP3 that was formed through this series of kinetic reaction degraded with a degradation constant kdegr as:
| (39) |
where kdegr (Table 1) was assigned to an experimentally estimated degradation rate of InsP3 (Fink et al. 2000).
Synaptic plasticity
A weight parameter w was used to model the strength of a given synapse (Narayanan & Johnston, 2010) and it was updated as a function of [Ca2+]c according to the Ca2+ control hypothesis (Shouval et al. 2002). Specifically,
| (40) |
where, 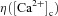 is the calcium-dependent learning rate, inversely related to the learning time constant
is the calcium-dependent learning rate, inversely related to the learning time constant 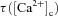 :
:
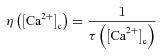 |
(41) |
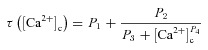 |
(42) |
where P1 = 1 s, P2 = 0.1 s, P3 = P2 × 10−4 and P4 = 3 (Shouval et al. 2002; Narayanan & Johnston, 2010). 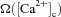 was defined as (Fig. 6B):
was defined as (Fig. 6B):
Figure 6. Increase in mGluR density induced a saturating leftward shift to a BCM-like synaptic plasticity profile.
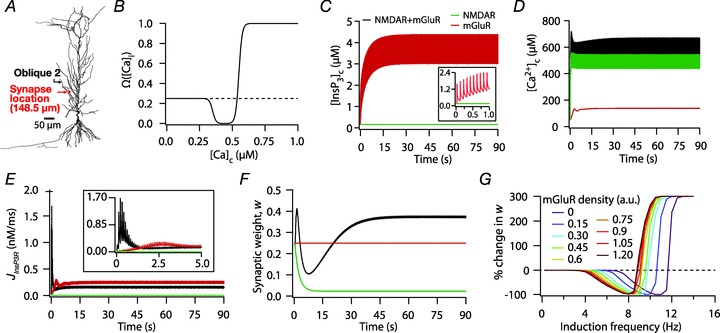
A, projection of the three-dimensional neuronal reconstruction depicting the location of the synapse where all plasticity experiments were performed. The circle in the middle of Oblique 2 (arrow), located at 148.5 μm away from the trunk branch point represents the synaptic location. B, functional form of the plasticity-regulating function,  (eqn (43)), plotted for various concentrations of [Ca2+]c. C–F, evolution of local [InsP3]c (C), local [Ca2+]c (D), local Ca2+ flux through InsP3 receptors,
(eqn (43)), plotted for various concentrations of [Ca2+]c. C–F, evolution of local [InsP3]c (C), local [Ca2+]c (D), local Ca2+ flux through InsP3 receptors,  (E), and normalized synaptic weight, w (F), when a synapse was stimulated by 900 presynaptic action potentials at 10 Hz, shown for cases where the synapse contained only mGluRs or only NMDARs or both mGluRs and NMDARs. Note that the trace obtained in the presence of only mGluRs and the trace obtained in the presence of both mGluRs and NMDARs are overlapping in C. Insets in C and E show the same plots in C and E, expanded over the first 1 and 5 s of the induction protocol, respectively. G, synaptic plasticity profile across various induction frequencies (900 pulses), shown for various densities of mGluRs in the synaptic compartment.
(E), and normalized synaptic weight, w (F), when a synapse was stimulated by 900 presynaptic action potentials at 10 Hz, shown for cases where the synapse contained only mGluRs or only NMDARs or both mGluRs and NMDARs. Note that the trace obtained in the presence of only mGluRs and the trace obtained in the presence of both mGluRs and NMDARs are overlapping in C. Insets in C and E show the same plots in C and E, expanded over the first 1 and 5 s of the induction protocol, respectively. G, synaptic plasticity profile across various induction frequencies (900 pulses), shown for various densities of mGluRs in the synaptic compartment.
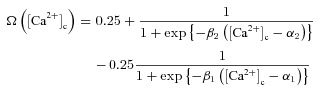 |
(43) |
where α1 = 0.35, α2 = 0.55, β1 = 80 and β2 = 80 (Narayanan & Johnston, 2010). The default initial value of w, winit, was set at 0.25.
In CA1 pyramidal neurons the distribution of group 1 mGluR is perisynaptic and its distance from the postsynaptic density is in the sub-micrometre range (Lujan et al. 1996). Therefore, when mGluRs were modelled, they were inserted in the same compartment where the NMDAR and AMPAR were inserted.
Plasticity induction protocols
We employed two established protocols for induction of plasticity in the model synapse: 900 pulse stimulation at different induction frequencies (Dudek & Bear, 1992; Shouval et al. 2002; Narayanan & Johnston, 2010) and theta burst stimulation (TBS; Larson et al. 1986). For 900 pulse stimulation, 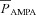 was set at 1.29207135 nm s−1 so that the modification threshold was ∼10 Hz (Fig. 6F–G), and the default mGluR density was 0.30 × 10−3 a.u. (eqn (32)). For TBS, the synapse was stimulated with a burst of five APs at 100 Hz, and this burst was repeated either 150 or 250 times at 200 ms interval (theta frequency) each. This was done to achieve steady state values for [Ca2+]c and w.
was set at 1.29207135 nm s−1 so that the modification threshold was ∼10 Hz (Fig. 6F–G), and the default mGluR density was 0.30 × 10−3 a.u. (eqn (32)). For TBS, the synapse was stimulated with a burst of five APs at 100 Hz, and this burst was repeated either 150 or 250 times at 200 ms interval (theta frequency) each. This was done to achieve steady state values for [Ca2+]c and w. 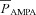 for TBS was fixed at 0.5 nm s−1 and default mGluR density was set at 0.1 × 10−3 a.u., so that the synapse underwent potentiation when stimulated with this protocol.
for TBS was fixed at 0.5 nm s−1 and default mGluR density was set at 0.1 × 10−3 a.u., so that the synapse underwent potentiation when stimulated with this protocol.
Initiation of Ca2+ waves
Calcium waves were initiated using the experimental protocol employed by Nakamura et al. (1999, 2000). Specifically, the baseline [InsP3]c was increased (2 and 2.25 μm in the three-cylinder model and morphologically realistic multi-compartmental model, respectively) to simulate the effect of bath application of mGluR agonist. This was then paired with 10 APs, at 30 ms interval each, by injecting brief current pulses into the somatic compartment of the model (2 nA for 2 ms in the multi-compartmental model and 2 nA for 1 ms in the three-cylinder model).
Computer simulations and analysis
All simulations were performed in the NEURON simulation environment (Carnevale & Hines, 2006). Resting membrane potential of the model neurons was fixed at –65 mV. For all experiments, the simulation temperature was kept at 34°C and ion channel kinetics were adjusted appropriately according to their experimentally determined Q10 coefficients. Given the considerable computational complexity of the morphologically realistic model, a variable time step method was used for solving the differential equations associated with this model (except for Figs 6 and 7) to reduce the run-time of the simulations. For Figs 1–3, the integration time step was 25 μs, and for Figs 6–7, the integration time step was 50 μs. Data analysis was performed using custom-built software under the Igor Pro (Wavemetrics Inc., Lake Oswego, OR, USA) programming environment.
Figure 7. Interplay between the InsP3Rs and the A-type K+ channels in regulating the modification threshold in a BCM-like synaptic plasticity model.
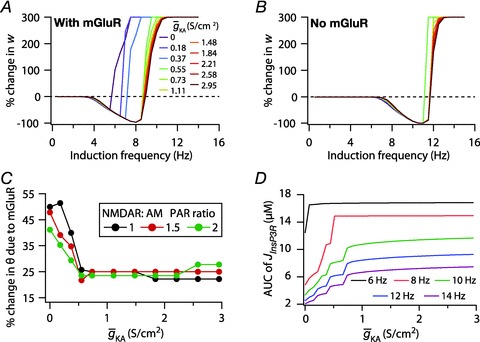
A and B, synaptic plasticity profile across various induction frequencies (900 pulses), shown for various densities of the A-type K+ channel (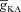 ) in the synaptic compartment, in the presence (A, density = 1.2 a.u.) and the absence (B) of mGluR. C, percentage change in θ due to mGluR, calculated as 100 × (θmGluR – θnomGluR)/θnomGluR (obtained from experiments shown in A and B), plotted as a function of
) in the synaptic compartment, in the presence (A, density = 1.2 a.u.) and the absence (B) of mGluR. C, percentage change in θ due to mGluR, calculated as 100 × (θmGluR – θnomGluR)/θnomGluR (obtained from experiments shown in A and B), plotted as a function of 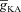 . The different plots correspond to simulations performed with different values for the NAR, to assess the relative contribution of NMDAR and mGluR to plasticity. D, area under the curve (AUC) of
. The different plots correspond to simulations performed with different values for the NAR, to assess the relative contribution of NMDAR and mGluR to plasticity. D, area under the curve (AUC) of 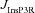 through the 900 pulses protocol plotted as a function of
through the 900 pulses protocol plotted as a function of 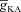 at various induction frequencies employed, for saturating mGluR density (= 1.2 × 10−3 a.u.) at 1.5 NAR. AMPAR densities remained the same across these simulations.
at various induction frequencies employed, for saturating mGluR density (= 1.2 × 10−3 a.u.) at 1.5 NAR. AMPAR densities remained the same across these simulations.
Results
The prime objective of this study was to understand the mechanisms through which the VGICs on the plasma membrane can regulate Ca2+ release through channels on the ER. To accomplish this objective, we chose the specific case of the interactions between the A-type K+ channels on the plasma membrane and InsP3Rs on the ER. The reasons behind this choice are manifold. First, in hippocampal pyramidal dendrites, the A-type K+ current has been demonstrated to reduce the amplitude of back propagating APs (bAPs; Fig. 1B) and synaptic potentials, and hence the consequent influx of Ca2+ (Fig. 1C) through VGCCs and/or NMDARs (Hoffman et al. 1997; Migliore et al. 1999; Frick et al. 2003, 2004; Johnston et al. 2003; Kim et al. 2005; Chen et al. 2006). This, in conjunction with the established bell-shaped dependence (Fig. 1E) of the open probability of InsP3Rs on cytosolic Ca2+ concentration (Bezprozvanny et al. 1991; De Young & Keizer, 1992), translates to our hypothesis that the A-type K+ channel should play a critical role in regulating Ca2+ release through the InsP3Rs. Second, similar to the ER and the InsP3Rs, the A-type K+ channel is also known to be expressed ubiquitously in the CA1 dendrites, thus allowing us a structural basis for exploring the interactions between these channels (Hoffman et al. 1997; Losonczy & Magee, 2006; Hertle & Yeckel, 2007; Losonczy et al. 2008; Kerti et al. 2011). Third, the dendritic densities of subunits of A-type K+ channels and InsP3Rs in hippocampal pyramids have been quantified in detail through multiple experimental methods (Hoffman et al. 1997; Nakamura et al. 1999; Frick et al. 2003; Losonczy & Magee, 2006; Hertle & Yeckel, 2007; Losonczy et al. 2008; Kerti et al. 2011; Ross, 2012), thus enabling us to constrain our model in as many experimentally realistic ways as possible (see Methods). Finally, several physiological processes involving Ca2+ waves and synaptic/intrinsic plasticity have been shown to recruit the A-type K+ channels and InsP3Rs (Nakamura et al. 1999, 2000; Nishiyama et al. 2000; Chen et al. 2006; Dudman et al. 2007; Kim et al. 2007; Jung et al. 2008; Narayanan et al. 2010; Ross, 2012), thus providing the motivation to understand the interaction between these channels in regulating several physiological processes. In what follows, we quantitatively evaluate our hypothesis on the interactions between the A-type K+ channels and InsP3Rs through morphologically and biophysically realistic models, especially in the context of Ca2+ waves and various forms of synaptic plasticity.
Pairing a train of bAPs with elevated [InsP3]c led to intraneuronal Ca2+ waves
The models employed in this study consisted of a large number of experimentally constrained individual components, which interact with the other model components to result in the observed phenomena. Given the complexity of these kinetic interactions in terms of neuronal space as well as time, and to understand the sensitivities of model outputs to several underlying parameters, we first employed a minimal morphology as the substrate for our simulations. The minimal morphology contained a soma, an apical trunk dendrite and an oblique dendrite that branches out of the apical trunk (Fig. 1A). As our sensitivity analyses involved understanding the effects of dendritic branch points, SVR and VGIC densities in dendritic branches, we added the oblique branch, which formed the test ground for all our sensitivity analyses. We incorporated passive and active components into this bare model, and added Ca2+ handling mechanisms (see Methods) to quantitatively evaluate our hypothesis on the interactions between plasma membrane channels and the ER receptors.
To do this, we simulated Ca2+ waves in this three-cylinder model using an experimental protocol that involves the pairing of bAPs with bath application of mGluR agonists (Nakamura et al. 1999, 2000). As Ca2+ waves generated by this protocol are a synergistic consequence of the interaction between the InsP3 generated by mGluR activation and the bAP-induced Ca2+ influx through VGCCs, we reasoned that the bath application of mGluR agonists could be modelled as an elevation of baseline InsP3 concentration in the cytosol ([InsP3]c). Consequently, we increased the baseline [InsP3]c from 0.16 to 2 μm, and paired this elevation with a train of 10 APs, with a constant 30 ms interspike interval (ISI), initiated at the soma to mimic the established experimental protocol (Nakamura et al. 1999, 2000). In response to the backpropagation of these spikes, there was a characteristic rapid increase in [Ca2+]c, which was primarily due to the opening of VGCCs, followed by a slower increase in [Ca2+]c, which is attributed to the release of Ca2+ from the ER stores, the propagation of which through the dendritic morphology constitutes the Ca2+ wave (Fig. 2A–C). We noted that [Ca2+]c amplitudes in our simulations were quantitatively similar to [Ca2+]c amplitudes elicited during experimentally observed Ca2+ waves, and that the relative wave amplitude and kinetics across compartments also matched qualitatively (Nakamura et al. 1999, 2000). For instance, the somatic trace had the lowest amplitude and the longest latency to peak, which is similar to experimental observations.
ER calcium release critically depended on dendritic diameter and wave initiation occurred at the branch point as a consequence of high SVR of oblique dendrites
Examining the [Ca2+]c traces at different locations and the shape plot (Fig. 2A–C), we observed that the initial increase in [Ca2+]c through VGCCs was rapid and large in the oblique dendrite, given the established dependence of [Ca2+]c on SVR (Sabatini et al. 2002; Frick et al. 2003). Given the bell-shaped dependence of the open probability of the InsP3R on [Ca2+]c, this rapid and large increase in local [Ca2+]c should be sufficient to inhibit the waves present locally (Fig. 1E). This would imply that the amount of Ca2+ released from stores should be minimal in dendrites with high SVR. To test this directly, we altered the diameter of the oblique dendrite, and assessed Ca2+ flux through InsP3Rs for each value of the diameter. We found that the flux of Ca2+ through InsP3Rs increased with increase in the oblique diameter (Fig. 2D). Thus, the high SVR of the oblique dendrite and the consequent large initial increase in local [Ca2+]c through VGCCs led to a reduction in the release of Ca2+ from the ER.
Where within the neuronal morphology did wave initiation occur? The earliest increase in the [Ca2+]c was found to be in the oblique followed by its branch point with the apical trunk (Fig. 2A and C). It should also be noted that initiation of the Ca2+ wave at the branch point of the primary oblique dendrite and at the proximal apical dendritic region, along the main trunk, has also been observed in in vitro brain slice experiments when a similar protocol was used to initiate a Ca2+ wave in the CA1 pyramidal neurons (Nakamura et al. 2002). What was the reason behind the initiation of the Ca2+ wave at the oblique and its branch point with the apical trunk? What were the contributions of the various Ca2+ handling mechanisms in determining the location of wave initiation? To answer these questions, we noted that the fast initial rise of [Ca2+]c in the oblique dendrite could be attributed to the effect of high SVR on rise time of [Ca2+]c (Sabatini et al. 2002; Cornelisse et al. 2007), and hypothesized that high SVR of the oblique accompanied by the high InsP3R density in proximal dendritic regions (Hertle & Yeckel, 2007) would be critical parameters in determining the location of wave initiation. To directly investigate the effect of SVR on the location of wave initiation, we set the diameter of the oblique to be the same as the main trunk and initiated the Ca2+ wave using the same protocol. We observed that the location of the earliest [Ca2+]c increase now shifted to the branch point between the soma and the main trunk (Fig. 2E and G), because the dendritic compartments closest to the soma had the highest InsP3R density (eqn (7)).
Which of these two parameters, SVR and InsP3R density, was more critical in determining the location of wave initiation? To answer this question, we set the InsP3R density to be uniform across all the compartments of the model neuron, but with oblique diameter set at the default 0.8 μm, and initiated the Ca2+ wave using the same protocol. We found that even with uniform density of InsP3Rs, the earliest and highest increase in [Ca2+]c was in the oblique dendrite followed by the branch point on the trunk and then the soma (Fig. 2H), which was in agreement with the decreasing order of SVR of these compartments. Furthermore, the amplitude of the wave was more uniform across the entire stretch of compartments of equal SVR, suggesting that InsP3R density plays a critical role in regulating the amplitude of the wave, but a secondary role in regulating its initiation point. Thus, in the presence as well as the absence of an InsP3R density gradient, SVR played the most critical role in determining the location of Ca2+ wave initiation along the neuronal topograph. Further evidence towards these conclusions might be obtained from the case shown in Fig. 2E–G, where in spite of the InsP3R density set to be the highest at the soma (Hertle & Yeckel, 2007; eqn (7)), the somatic [Ca2+]c transients were still slow and had lower amplitude, owing to the low SVR of the somatic compartment (Fig. 2E–G).
We finally asked if changing DCa altered the initiation point of the calcium wave. We found that, in the oblique and the apical dendrite, varying DCa (over the range 220 μm2 s−1 to 2 mm2 s−1) did not have a significant effect on the release of Ca2+ through InsP3Rs (quantified through JInsP3R). However, as the soma is a large compartment with low SVR, it acts as a sink for the Ca2+ that diffuses out of the dendrites. When DCa was increased, we noted higher diffusion of Ca2+ into the soma from the dendrites, resulting in a larger [Ca2+]c in the soma. Consequent to the dependence of the open probability of InsP3Rs on [Ca2+]c, this led to a decrease in JInsP3R with increase in DCa at the soma. However, this relationship held only at the soma owing to its lower SVR, and initiation of Ca2+ waves occurred at the oblique and its branch point with the trunk where DCa did not alter JInsP3R. Changing DCa did not alter the initiation point of the calcium wave. This was consistent with earlier observations that diffusion cannot explain faster calcium dynamics in high SVR compartments (Cornelisse et al. 2007). In summary, the high SVR of the oblique dendrite enabled rapid buildup of high initial [Ca2+]c there, which was followed by its diffusion to the branch point where it further synergized the release of Ca2+ from the stores, and enabled wave initiation at these locations.
We concluded that the calibre of the neuronal compartment played a very critical role in Ca2+ wave initiation and propagation, regulating the amount of local ER Ca2+ release and the location of initiation of the wave.
Calcium release through InsP3R displayed a bell-shaped dependence on A-type K+ conductance
From the analyses presented above, it was obvious that the store component in Ca2+ signals during a wave was very minimal in dendrites with smaller calibre. This was primarily due to the high SVR of small-calibre dendrites that led to higher apparent concentrations of Ca2+ influx through VGCCs (Sabatini et al. 2002), which inhibit InsP3Rs given their bell-shaped dependence on cytosolic Ca2+ (Fig. 1E). Could the high density of restorative conductances in general, and of A-type K+ channels in particular, in small-calibre dendrites of pyramidal neurons be a mechanism to enable higher release of Ca2+ through InsP3Rs in these dendritic compartments? To answer this question, we inserted A-type K+ channels into the oblique branch at various densities and recorded [Ca2+]c and the flux of Ca2+ through InsP3R (JInsP3R in eqn (8)) during a Ca2+ wave. With an increase in the A-type K+ conductance, the overall amplitude of the Ca2+ wave invading the oblique dendrite decreased, and there was a progressive delay in the secondary release of [Ca2+]c (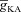 , in the oblique dendrite (Fig. 3B). This is to be expected because an increase in
, in the oblique dendrite (Fig. 3B). This is to be expected because an increase in 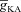 reduces Ca2+ influx through VGCCs (Fig. 1D).
reduces Ca2+ influx through VGCCs (Fig. 1D).
Next, assessing the temporal aspects of wave propagation into the oblique, we found that increasing 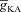 increases both the latency to peak, and the full width at half-maximum (FWHM) of the wave (Fig. 3C–D). Note that the increase in latency to peak with increased
increases both the latency to peak, and the full width at half-maximum (FWHM) of the wave (Fig. 3C–D). Note that the increase in latency to peak with increased 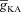 is analogous to the established role of transient K+ current in delaying the onset of spikes in multiple cell types (Kanold & Manis, 1999; Shibata et al. 2000; Kim et al. 2005). This latency resulted from the concurrence of two phenomena: (i) the inability of low-amplitude bAP, owing to high
is analogous to the established role of transient K+ current in delaying the onset of spikes in multiple cell types (Kanold & Manis, 1999; Shibata et al. 2000; Kim et al. 2005). This latency resulted from the concurrence of two phenomena: (i) the inability of low-amplitude bAP, owing to high 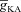 , to elicit the initial Ca2+ influx through VGCCs (Figs 1D and 3B); and (ii) the diffusion of Ca2+ from adjacent compartments leading to local secondary release through InsP3Rs given their dependence on [Ca2+]c (Fig. 1E). Whereas the former suppresses initial Ca2+ influx, the latter constitutes the delayed rise in [Ca2+]c. Finally, and importantly, the flux of Ca2+ through InsP3Rs displayed a bell-shaped dependence on
, to elicit the initial Ca2+ influx through VGCCs (Figs 1D and 3B); and (ii) the diffusion of Ca2+ from adjacent compartments leading to local secondary release through InsP3Rs given their dependence on [Ca2+]c (Fig. 1E). Whereas the former suppresses initial Ca2+ influx, the latter constitutes the delayed rise in [Ca2+]c. Finally, and importantly, the flux of Ca2+ through InsP3Rs displayed a bell-shaped dependence on 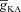 (Fig. 3E). To elaborate, when
(Fig. 3E). To elaborate, when 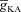 was very low (or absent), the increase in [Ca2+]c in response to bAPs was high enough to act as an inhibitor for InsP3Rs (Fig. 1E). As
was very low (or absent), the increase in [Ca2+]c in response to bAPs was high enough to act as an inhibitor for InsP3Rs (Fig. 1E). As 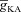 increased, [Ca2+]c through VGCCs decreased to a range that acted as a co-activator of InsP3Rs (Fig. 1E), thus increasing the contribution of store Ca2+ to the Ca2+ wave. Further increase in
increased, [Ca2+]c through VGCCs decreased to a range that acted as a co-activator of InsP3Rs (Fig. 1E), thus increasing the contribution of store Ca2+ to the Ca2+ wave. Further increase in 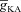 led to a decrease (Figs 1D and 3B) in this ‘activating’ Ca2+ for InsP3Rs and hence the flux of Ca2+ through InsP3Rs decreased, leading to the bell-shaped dependence (Fig. 3E). We performed these analyses for various densities of L-type Ca2+ channels and found that the relationships held for all tested densities of L-type Ca2+ channels (Fig. 3B–E).
led to a decrease (Figs 1D and 3B) in this ‘activating’ Ca2+ for InsP3Rs and hence the flux of Ca2+ through InsP3Rs decreased, leading to the bell-shaped dependence (Fig. 3E). We performed these analyses for various densities of L-type Ca2+ channels and found that the relationships held for all tested densities of L-type Ca2+ channels (Fig. 3B–E).
How does the inclusion of Ca2+ indicator dyes, which are used to measure the changes in [Ca2+]c during in vitro experiments, alter Ca2+ wave amplitude and the dependence of Ca2+ released through InsP3Rs on 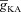 ? To answer this, we incorporated additional mobile buffers to simulate the effect of Ca2+ indicator dyes on Ca2+ waves and recorded [Ca2+]c dynamics for Ca2+ dyes with different affinities (see Methods). An increase in the affinity of the mobile buffer to Ca2+ (as denoted by a decrease in the equilibrium constant for mobile buffering, Kmob, eqn (21)) resulted in a decrease in the amplitude and an increase in the duration of the Ca2+ waves (Fig. 3F–G). These results were consistent with in vitro experimental observations (Nakamura et al. 2000). We also found that Ca2+ waves failed to initiate for very high-affinity mobile buffers (Kmob = 0.4) (Fig. 3F) suggesting that only large-amplitude Ca2+ waves (obtained with, say, a high endogenous InsP3R density) may be reliably detected in the presence of high-affinity Ca2+ indicator dyes (such as Fura-2) during in vitro experiments. Finally, we computed the dependence of JInsp3R on
? To answer this, we incorporated additional mobile buffers to simulate the effect of Ca2+ indicator dyes on Ca2+ waves and recorded [Ca2+]c dynamics for Ca2+ dyes with different affinities (see Methods). An increase in the affinity of the mobile buffer to Ca2+ (as denoted by a decrease in the equilibrium constant for mobile buffering, Kmob, eqn (21)) resulted in a decrease in the amplitude and an increase in the duration of the Ca2+ waves (Fig. 3F–G). These results were consistent with in vitro experimental observations (Nakamura et al. 2000). We also found that Ca2+ waves failed to initiate for very high-affinity mobile buffers (Kmob = 0.4) (Fig. 3F) suggesting that only large-amplitude Ca2+ waves (obtained with, say, a high endogenous InsP3R density) may be reliably detected in the presence of high-affinity Ca2+ indicator dyes (such as Fura-2) during in vitro experiments. Finally, we computed the dependence of JInsp3R on 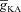 and found that the bell-shaped relationship also held true even in the presence of mobile buffers at various affinities of Ca2+ binding (Fig. 3H), some of which correspond to the specific affinities of the different Ca2+ indicator dyes used to study Ca2+ waves (Nakamura et al. 2000). At very high affinities of Ca2+ binding to the mobile buffer, we found that the release of Ca2+ through InsP3R monotonically decreased with increase in
and found that the bell-shaped relationship also held true even in the presence of mobile buffers at various affinities of Ca2+ binding (Fig. 3H), some of which correspond to the specific affinities of the different Ca2+ indicator dyes used to study Ca2+ waves (Nakamura et al. 2000). At very high affinities of Ca2+ binding to the mobile buffer, we found that the release of Ca2+ through InsP3R monotonically decreased with increase in 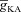 (Fig. 3H). We noted this to be a direct consequence of the reduction of Ca2+ influx through the plasma membrane when
(Fig. 3H). We noted this to be a direct consequence of the reduction of Ca2+ influx through the plasma membrane when 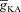 was increased (Fig. 3B), and the consequent reduction in Ca2+ release through InsP3Rs (Fig. 1E). The bell-shaped dependence was absent because of lower amplitudes of Ca2+ transients in the presence of high-affinity Ca2+ indicator dyes (Fig. 3F). This highlights the need to employ lower affinity dyes during in vitro experiments, so that the measurement of Ca2+ waves and their dependencies on underlying parameters are not marred by heavy buffering of Ca2+ by indicator dyes (Nakamura et al. 2000).
was increased (Fig. 3B), and the consequent reduction in Ca2+ release through InsP3Rs (Fig. 1E). The bell-shaped dependence was absent because of lower amplitudes of Ca2+ transients in the presence of high-affinity Ca2+ indicator dyes (Fig. 3F). This highlights the need to employ lower affinity dyes during in vitro experiments, so that the measurement of Ca2+ waves and their dependencies on underlying parameters are not marred by heavy buffering of Ca2+ by indicator dyes (Nakamura et al. 2000).
Calcium waves in a morphologically realistic model reaffirmed bell-shaped dependence of Ca2+ release through InsP3Rs on A-type K+ conductance
Thus far, we had employed a simple morphological model to establish the interactions between the A-type K+ channels and InsP3Rs and understand their sensitivities to several critical parameters during the course of Ca2+ wave propagation. Next, we investigated if these results held in a morphologically realistic model with gradients of underlying channel and receptor densities following experimental observations quantitatively. To this end, we incorporated different VGICs and InsP3Rs into this model according to their experimentally determined density gradients (see Methods). Although there are no direct experimental data for the density and properties of A-type K+ channels in oblique dendrites of CA1 pyramidal neurons, we employed experimentally available physiological data to set 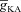 in oblique dendrites. Specifically, it has been experimentally demonstrated that the [Ca2+]c increase at a branch point on the apical trunk and in the branching oblique is of similar magnitude when a single bAP invades these dendritic locations (Frick et al. 2003). Furthermore, recent electron microscopy data also reported a higher density for an A-type K+ channel subunit Kv4.2 in the oblique dendrites as compared to the main apical dendritic trunk (Kerti et al. 2011). To account for these, we fine tuned
in oblique dendrites. Specifically, it has been experimentally demonstrated that the [Ca2+]c increase at a branch point on the apical trunk and in the branching oblique is of similar magnitude when a single bAP invades these dendritic locations (Frick et al. 2003). Furthermore, recent electron microscopy data also reported a higher density for an A-type K+ channel subunit Kv4.2 in the oblique dendrites as compared to the main apical dendritic trunk (Kerti et al. 2011). To account for these, we fine tuned 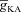 along a proximal oblique (Fig. 4B) such that the [Ca2+]c increase in response to a single bAP invasion was similar for most locations along the oblique and had the same magnitude as [Ca2+]c at the branch point on the main trunk (Fig. 4A–D). Note that this requirement on normalized [Ca2+]c along the oblique also made
along a proximal oblique (Fig. 4B) such that the [Ca2+]c increase in response to a single bAP invasion was similar for most locations along the oblique and had the same magnitude as [Ca2+]c at the branch point on the main trunk (Fig. 4A–D). Note that this requirement on normalized [Ca2+]c along the oblique also made 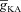 in the oblique to be greater than the trunk
in the oblique to be greater than the trunk 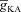 (= 12.05 mS cm−2) in order to nullify the effects of increased SVR in the oblique dendrite in comparison to the trunk (Frick et al. 2003; Kerti et al. 2011). We also observed that the amplitude of calcium influx in response to a single bAP at the branch point and at the mid point of the proximal oblique under consideration was in close agreement with the experimentally determined value of ∼150 nm for the proximal apical dendrites in CA1 pyramidal neurons (Helmchen et al. 1996). Finally, when a double exponential function was used to fit the decay time course of [Ca2+]c in response to a single bAP, the fast and slow decay time constants (τf and τs) were 84 and 303 ms (soma), 14 and 314 ms (branch point on trunk), and 2 and 297 ms (oblique dendrite), respectively.
(= 12.05 mS cm−2) in order to nullify the effects of increased SVR in the oblique dendrite in comparison to the trunk (Frick et al. 2003; Kerti et al. 2011). We also observed that the amplitude of calcium influx in response to a single bAP at the branch point and at the mid point of the proximal oblique under consideration was in close agreement with the experimentally determined value of ∼150 nm for the proximal apical dendrites in CA1 pyramidal neurons (Helmchen et al. 1996). Finally, when a double exponential function was used to fit the decay time course of [Ca2+]c in response to a single bAP, the fast and slow decay time constants (τf and τs) were 84 and 303 ms (soma), 14 and 314 ms (branch point on trunk), and 2 and 297 ms (oblique dendrite), respectively.
After accounting for experimental distributions of underlying channels and receptors in the morphologically realistic model and setting [InsP3]c to baseline values, we first noted that a train of bAPs (10 APs with 30 ms ISI) and the consequent influx of Ca2+ through VGCCs was insufficient to initiate a Ca2+ wave (Fig. 4E and H–I). This is consistent with in vitro experimental observations using the same protocol (Nakamura et al. 1999, 2000; Ross, 2012). Next, similar to our experiments with the simple morphological model, we elevated [InsP3]c to 2.25 μm to mimic bath application of mGluR agonists and paired this with the same train of bAPs (10 APs with 30 ms ISI). Such pairing led to a successful initiation of a Ca2+ wave (Fig. 4F–I), with the peak [Ca2+]c values in the proximal apical trunk was in the micromolar range, and was comparable to corresponding in vitro experiments. Furthermore, similar to our observations with the simple model (Fig. 2) and with in vitro experiments (Nakamura et al. 1999, 2000), we found that the region corresponding to earliest and highest increase in [Ca2+]c was a proximal oblique followed by proximal apical dendritic region on the main trunk (Fig. 4F and I). Finally, upon moving away from the soma and towards the distal apical end of the neuron, the waves gradually ceased to propagate (Fig. 4G–I), which was attributable to high 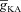 in distal dendrites that reduces the bAP-induced Ca2+ influx into the neuron, coupled with the reduced density of InsP3Rs in the distal dendrites that led to a further reduction in the amount of Ca2+ released from the stores.
in distal dendrites that reduces the bAP-induced Ca2+ influx into the neuron, coupled with the reduced density of InsP3Rs in the distal dendrites that led to a further reduction in the amount of Ca2+ released from the stores.
Can the A-type K+ current act as a mechanism that enables higher release of Ca2+ through InsP3Rs in small-calibre dendritic compartments of this morphologically and biophysically realistic model? To answer this, we varied 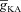 and observed wave propagation across different compartments of the multi-compartmental model for each of these values of
and observed wave propagation across different compartments of the multi-compartmental model for each of these values of 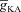 (Fig. 5A–B). Qualitatively, we found that the results obtained across all compartments were very similar to what we had observed with the simple morphological model (Fig. 3). Quantitatively, the total Ca2+ influx was a monotonically reducing function of
(Fig. 5A–B). Qualitatively, we found that the results obtained across all compartments were very similar to what we had observed with the simple morphological model (Fig. 3). Quantitatively, the total Ca2+ influx was a monotonically reducing function of 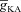 (Fig. 5C–D), and Ca2+ flux through InsP3Rs displayed a bell-shaped dependence on
(Fig. 5C–D), and Ca2+ flux through InsP3Rs displayed a bell-shaped dependence on 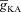 (Fig. 5E–F). Although the qualitative descriptions of monotonic reduction in total Ca2+ and a bell-shaped dependence for flux through InsP3Rs were true across different compartments, it must be noted that the specific shape of such dependence was dependent on the specific compartment under consideration (Fig. 5C–F). Finally, evaluating the temporal aspects of wave propagation, we again found that both the FWHM and the latency to peak of the wave at different locations increased as a function of
(Fig. 5E–F). Although the qualitative descriptions of monotonic reduction in total Ca2+ and a bell-shaped dependence for flux through InsP3Rs were true across different compartments, it must be noted that the specific shape of such dependence was dependent on the specific compartment under consideration (Fig. 5C–F). Finally, evaluating the temporal aspects of wave propagation, we again found that both the FWHM and the latency to peak of the wave at different locations increased as a function of 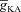 .
.
Figure 5. In a morphologically realistic model, A-type K+ channels altered the amplitude, width and latency of Ca2+ waves through regulation of both intrinsic excitability and release of Ca2+ from the stores.
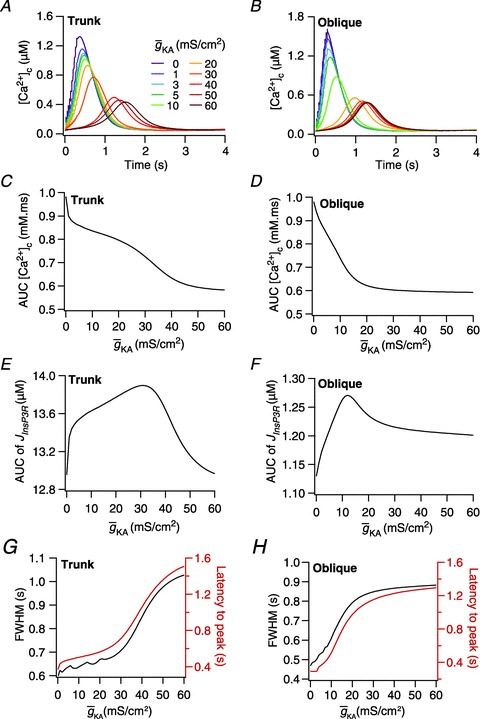
A and B, [Ca2+]c traces plotted for various A-type K+ channel densities (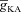 ), at representative trunk (A) and proximal oblique (B) locations. C and D, area under the curve (AUC) for total [Ca2+]c plotted as a function of
), at representative trunk (A) and proximal oblique (B) locations. C and D, area under the curve (AUC) for total [Ca2+]c plotted as a function of 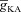 , at representative trunk (C) and proximal oblique (D) locations. E and F, AUC for the Ca2+ flux through InsP3 receptors (
, at representative trunk (C) and proximal oblique (D) locations. E and F, AUC for the Ca2+ flux through InsP3 receptors (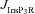 ) plotted as a function of
) plotted as a function of 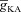 , at representative trunk (E) and proximal oblique (F) locations. G and H, temporal aspects of the Ca2+ wave quantified as the wave's full-width at half-maximum (FWHM) and latency to peak, and plotted as functions of
, at representative trunk (E) and proximal oblique (F) locations. G and H, temporal aspects of the Ca2+ wave quantified as the wave's full-width at half-maximum (FWHM) and latency to peak, and plotted as functions of 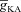 , at representative trunk (A) and proximal oblique (B) locations. Trunk: location on the apical trunk 77 μm (radial distance) from the soma; Oblique: location on Oblique 1 (Fig. 4G) 17 μm (path distance) away from the branch point on the trunk. For A–H
, at representative trunk (A) and proximal oblique (B) locations. Trunk: location on the apical trunk 77 μm (radial distance) from the soma; Oblique: location on Oblique 1 (Fig. 4G) 17 μm (path distance) away from the branch point on the trunk. For A–H
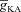 represents the value of A-type K+ channel densities at the soma while the individual compartments had local
represents the value of A-type K+ channel densities at the soma while the individual compartments had local 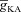 according to eqn (3) along the neuronal topograph.
according to eqn (3) along the neuronal topograph.
Taking the data together, across models, moderate values of 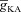 contributed to an increase in the ER component of [Ca2+]c during calcium wave propagation across different compartments, whereas higher values of
contributed to an increase in the ER component of [Ca2+]c during calcium wave propagation across different compartments, whereas higher values of 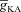 decreased the ER component (Figs 3D and 5E–F). Furthermore, during wave propagation, the presence of A-type K+ channels introduced a delay in the onset of the wave, and increased the time window over which the Ca2+ levels were elevated (Figs 3C–D and 5G–H).
decreased the ER component (Figs 3D and 5E–F). Furthermore, during wave propagation, the presence of A-type K+ channels introduced a delay in the onset of the wave, and increased the time window over which the Ca2+ levels were elevated (Figs 3C–D and 5G–H).
Presence of co-localized NMDAR and mGluR led to a larger increase in [Ca2+]c in the postsynaptic compartment
The role of Ca2+ released from the stores in various forms of neuronal plasticity is well established (Berridge et al. 2000; Huber et al. 2000; Nishiyama et al. 2000; Emptage et al. 2001; Rose & Konnerth, 2001; Doi et al. 2005; Verkhratsky, 2005; Dudman et al. 2007; Narayanan et al. 2010; Ross, 2012). In many forms of synaptic plasticity, release of Ca2+ from the stores requires activation of perisynaptic mGluR, the subsequent mobilization of InsP3 inside the cell followed by its binding to InsP3Rs on the ER membrane. From our results above, it was clear that the A-type K+ current regulates the contribution of store Ca2+ to wave propagation. We noted that several induction protocols employed for synaptic plasticity also elicit Ca2+ wave-like patterns in hippocampal pyramidal neurons (Nakamura et al. 1999, 2002; Ross, 2012), with the direction and amplitude of synaptic plasticity theorized to be a function of specific levels of the local Ca2+ influx (Lisman, 1989, 2001; Shouval et al. 2002).
Against this background and motivated by our results above, we asked if A-type K+ current could regulate the contribution of mGluRs to various forms of synaptic plasticity. To answer this and to understand the contribution of store Ca2+ in homosynaptic plasticity we simulated a synapse with co-localized AMPAR, NMDAR and mGluR, induced plasticity with 900 presynaptic APs at various frequencies. Consistent with the kinetic model we employed for mGluRs (Methods), the activation of mGluRs resulted in a gradual increase in [InsP3]c in the postsynaptic compartment, and reached a steady-state equilibrium (Fig. 6C). As synaptic stimulus-induced Ca2+ influx into the neuron was due to NMDARs, VGCCs as well as store release, the kinetics of Ca2+ evolution was faster than the evolution of InsP3 at the synaptic location, which was dependent on the slower mGluR signalling pathway (compare Fig. 6C and D). Further, when both mGluR and NMDAR were present at the synapse, an increase in the steady state postsynaptic [Ca2+]c was higher than when only NMDAR or only mGluR was present (Fig. 6D). The inflections in the [Ca2+]c traces when both NMDAR and mGluR were present (Fig. 6D) were attributable to the interactions between the initial fast influx of Ca2+ through NMDARs, the mobilization of InsP3 after mGluR activation, and the relatively slower release of Ca2+ through InsP3Rs. This was analogous to the interactions between fast Ca2+ influx through VGCCs and slow Ca2+ release through InsP3Rs during the course of a Ca2+ wave (Figs 2 and 4). Moreover, the flux of Ca2+ through InsP3Rs was also governed by the bell-shaped dependence of InsP3R open probability of [Ca2+]c (Fig. 1E). Specifically, we noted that this flux increased initially as an effect of the initial Ca2+ influx through NMDARs accompanied by InsP3 mobilization following mGluR activation. However, as [Ca2+]c increased (Fig. 6D), despite high levels of [InsP3]c (Fig. 6E), the flux of Ca2+ through InsP3Rs reduced owing to the bell-shaped dependence discussed above (Fig. 1E). Furthermore, as the [Ca2+]c reached higher concentrations faster in the presence of both mGluRs and NMDARs rather than the sole presence of mGluRs, the inhibition of Ca2+ flux through InsP3Rs had a delayed onset in the latter case compared to the former (Fig. 6E, inset). Finally, when only NMDARs were present, there was no mobilization of InsP3, and thus Ca2+ flux through InsP3Rs was low (Fig. 6E).
Increase in mGluR density led to a leftward shift in a Bienenstock–Cooper–Munro (BCM)-like synaptic plasticity profile
How does this mGluR-induced enhancement in the influx of postsynaptic Ca2+ alter synaptic plasticity profile across several induction frequencies? To answer this, we observed the evolution of synaptic weight under cases where mGluRs and NMDARs were present together or separately. As expected from the calcium control hypothesis (Fig. 6B), we found that, with 10 Hz/900 pulses stimulation, the presence of mGluRs with NMDARs led to synaptic potentiation, whereas the lone presence of NMDARs or mGluRs led to synaptic depression or no change in synaptic weight, respectively (Fig. 6F). Furthermore, as a direct consequence of the initial inflections in [Ca2+]c kinetics owing to interactions between mGluRs and NMDARs (Fig. 6D), the weight evolution also displayed inflections before settling to its steady-state value for the case where both receptors were present (Fig. 6F). Next, to assess the specific role of mGluRs in regulating the plasticity profile, we induced plasticity through 900 pulses of multiple induction frequencies, and plotted the percentage change in synaptic weight (at steady state) as a function of induction frequency (Dudek & Bear, 1992; Shouval et al. 2002; Narayanan & Johnston, 2010) for various densities of mGluRs in the synaptic compartment (Fig. 6G). Consistent with a greater increase in [Ca2+]c in the presence of mGluRs, we found that the presence of mGluR decreased the modification threshold, resulting in a saturating leftward shift in the BCM curve in a density-dependent manner (Fig. 6G). We noted that the saturation in the shift reflected the saturation of InsP3Rs by higher concentrations of [InsP3]c (De Young & Keizer, 1992).
mGluR regulation of BCM-like plasticity profile depended on A-type K+ current
From our results above, it was clear that the relative contribution of mGluRs to synaptic plasticity was reduced (Fig. 6E) if the initial influx of Ca2+ through NMDARs was large enough to inhibit the InsP3Rs (Fig. 1E). This was similar to the inhibitory role played by the influx of Ca2+ through VGCCs during wave propagation (Figs 3 and 5). Moreover, the A-type K+ current has been demonstrated to modulate Ca2+ entry through NMDARs consequent to their ability to modulate synaptic potentials and the voltage dependence of NMDARs, apart from regulating various forms of synaptic plasticity (Hoffman et al. 1997; Watanabe et al. 2002; Johnston et al. 2003; Chen et al. 2006; Jung et al. 2008; Narayanan & Johnston, 2010; Zhao et al. 2011). Combining these two observations, we asked if A-type K+ current could regulate Ca2+ release through InsP3Rs, thereby modulating the relative contributions of mGluRs, and thus of the stores, to this form of synaptic plasticity.
To answer this question, we constructed the BCM-like curve with saturating levels of mGluR density at various A-type K+ conductances and investigated how changes in 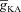 affected the plasticity profile. Under this experimental setup, an increase in
affected the plasticity profile. Under this experimental setup, an increase in 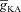 increased the modification threshold, shifting the curve to the right (Fig. 7A). However, when we repeated this experiment in the absence of mGluRs, the changes in modification threshold were much smaller (Fig. 7B). When we quantified the percentage difference in modification threshold between the cases where mGluRs were present (Fig. 7A) and were absent (Fig. 7B), we found that the presence of mGluRs increased the dynamic range of changes in modification threshold obtained with changes in
increased the modification threshold, shifting the curve to the right (Fig. 7A). However, when we repeated this experiment in the absence of mGluRs, the changes in modification threshold were much smaller (Fig. 7B). When we quantified the percentage difference in modification threshold between the cases where mGluRs were present (Fig. 7A) and were absent (Fig. 7B), we found that the presence of mGluRs increased the dynamic range of changes in modification threshold obtained with changes in 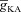 , across various values of NAR (Fig. 7A–C). Finally, to further quantify this regulation of mGluR contribution to [Ca2+]c by
, across various values of NAR (Fig. 7A–C). Finally, to further quantify this regulation of mGluR contribution to [Ca2+]c by 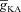 , we plotted the AUC of JInsP3R as a function of
, we plotted the AUC of JInsP3R as a function of 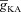 at various induction frequencies with the saturating density of mGluR (= 1.2 × 10−3 a.u.) at the stimulated synapse (Fig. 7D). The release of Ca2+ through InsP3R increased with the increase in A-type K+ conductance. We also noted that the release of store Ca2+ decreased with the increase in the induction frequency, which was consistent with NMDAR-dependent inhibition of InsP3R. To elaborate, a higher frequency of stimulation allowed for higher temporal summation of the [Ca2+]c that entered through the NMDAR. This high level of [Ca2+]c reduced the open probability of InsP3R, consistent with the bell-shaped dependence of these receptors on the [Ca2+]c as discussed earlier (Fig. 1E). Taken together, our results suggest that the A-type K+ current can regulate the contribution of mGluRs and the ER stores to synaptic plasticity by controlling Ca2+ influx through NMDARs.
at various induction frequencies with the saturating density of mGluR (= 1.2 × 10−3 a.u.) at the stimulated synapse (Fig. 7D). The release of Ca2+ through InsP3R increased with the increase in A-type K+ conductance. We also noted that the release of store Ca2+ decreased with the increase in the induction frequency, which was consistent with NMDAR-dependent inhibition of InsP3R. To elaborate, a higher frequency of stimulation allowed for higher temporal summation of the [Ca2+]c that entered through the NMDAR. This high level of [Ca2+]c reduced the open probability of InsP3R, consistent with the bell-shaped dependence of these receptors on the [Ca2+]c as discussed earlier (Fig. 1E). Taken together, our results suggest that the A-type K+ current can regulate the contribution of mGluRs and the ER stores to synaptic plasticity by controlling Ca2+ influx through NMDARs.
Increase in A-type K+ channel density increased the contribution of store Ca2+ during synaptic plasticity induced through TBS
We next examined if such dependence of store Ca2+ release on A-type K+ current was specific to only the induction protocol that we have employed. To do this, we employed TBS (Fig. 8A), another established plasticity-inducing protocol, and tested whether high densities of A-type K+ channels found in small-calibre dendrites could play a role in regulating store Ca2+ release during plasticity protocols. When subjected to TBS, the temporal evolution of [InsP3]c, [Ca2+]c and 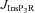 (Fig. 8B–D) followed patterns that were analogous to the previous protocol (Fig. 6C–E). Specifically, the flux of Ca2+ through InsP3Rs was inhibited by high initial Ca2+ influx through NMDARs, thus reducing the contribution of mGluRs to the total [Ca2+]c, when NMDARs were coexpressed in the synapse (Fig. 8D). Consistent with the Ca2+ control hypothesis that was employed in inducing plasticity (Fig. 6B), the steady-state synaptic weight was higher when both mGluRs and NMDARs were present as the source of cytosolic Ca2+ at the synapse (Fig. 8E). Specifically, the presence of mGluRs with NMDARs led to synaptic potentiation, whereas the lone presence of NMDARs or mGluRs led to synaptic depression or no change in synaptic weight, respectively (Fig. 8E). Furthermore, an increase in mGluR density, as a direct consequence of enhancing [Ca2+]c and the calcium control hypothesis (Fig. 6B), led to synaptic depression with TBS, which later transformed into increasing potentiation with increased mGluR density (Fig. 8F).
(Fig. 8B–D) followed patterns that were analogous to the previous protocol (Fig. 6C–E). Specifically, the flux of Ca2+ through InsP3Rs was inhibited by high initial Ca2+ influx through NMDARs, thus reducing the contribution of mGluRs to the total [Ca2+]c, when NMDARs were coexpressed in the synapse (Fig. 8D). Consistent with the Ca2+ control hypothesis that was employed in inducing plasticity (Fig. 6B), the steady-state synaptic weight was higher when both mGluRs and NMDARs were present as the source of cytosolic Ca2+ at the synapse (Fig. 8E). Specifically, the presence of mGluRs with NMDARs led to synaptic potentiation, whereas the lone presence of NMDARs or mGluRs led to synaptic depression or no change in synaptic weight, respectively (Fig. 8E). Furthermore, an increase in mGluR density, as a direct consequence of enhancing [Ca2+]c and the calcium control hypothesis (Fig. 6B), led to synaptic depression with TBS, which later transformed into increasing potentiation with increased mGluR density (Fig. 8F).
Figure 8. Interplay between the InsP3Rs and the A-type K+ channels in regulating synaptic plasticity induced through TBS.
A, protocol employed for induction of synaptic plasticity through TBS. Ten bursts are shown, with each burst made of five stimuli separated by 10 ms, and interburst interval set at 200 ms. Synaptic location was the same as depicted in Fig. 6A. B–E, evolution of local [InsP3]c (B), local [Ca2+]c (C), local Ca2+ flux through InsP3 receptors, 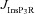 (D), and normalized synaptic weight, w (E), when a synapse was stimulated by TBS, shown for cases where the synapse contained only mGluRs or only NMDARs or both mGluRs and NMDARs. Note that the trace obtained in the presence of only mGluRs and the trace obtained in the presence of both mGluRs and NMDARs are overlapping in B. Insets in B and D show the same plots in B and D, expanded over the first 1 and 5 s of the induction protocol, respectively. F, steady state change in synaptic weight after TBS, shown for various densities of mGluRs in the synaptic compartment. G, Steady-state change in synaptic weight after TBS, plotted as a function of the A-type K+ conductance density (
(D), and normalized synaptic weight, w (E), when a synapse was stimulated by TBS, shown for cases where the synapse contained only mGluRs or only NMDARs or both mGluRs and NMDARs. Note that the trace obtained in the presence of only mGluRs and the trace obtained in the presence of both mGluRs and NMDARs are overlapping in B. Insets in B and D show the same plots in B and D, expanded over the first 1 and 5 s of the induction protocol, respectively. F, steady state change in synaptic weight after TBS, shown for various densities of mGluRs in the synaptic compartment. G, Steady-state change in synaptic weight after TBS, plotted as a function of the A-type K+ conductance density (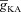 ) for different values of NMDAR:AMPAR ratio (NAR), in the presence and absence of mGluRs. H, percentage change in synaptic weight due to mGluR, calculated as 100 × (Δ%wmGluR
– Δ%wnomGluR)/Δ%wnomGluR (obtained from experiments shown in G), plotted as a function of
) for different values of NMDAR:AMPAR ratio (NAR), in the presence and absence of mGluRs. H, percentage change in synaptic weight due to mGluR, calculated as 100 × (Δ%wmGluR
– Δ%wnomGluR)/Δ%wnomGluR (obtained from experiments shown in G), plotted as a function of 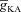 . The different plots correspond to simulations performed with different values for the NAR, to assess the relative contribution of NMDAR and mGluR to plasticity. I, area under the curve (AUC) of
. The different plots correspond to simulations performed with different values for the NAR, to assess the relative contribution of NMDAR and mGluR to plasticity. I, area under the curve (AUC) of 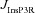 through the TBS protocol plotted as a function of
through the TBS protocol plotted as a function of 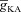 , for various values of NAR at saturating concentration of mGluR (= 1.1 × 10−3 a.u.). AMPAR densities remained the same across these simulations.
, for various values of NAR at saturating concentration of mGluR (= 1.1 × 10−3 a.u.). AMPAR densities remained the same across these simulations.
Next, to understand how changes in A-type K+ density affected release of store Ca2+ through InsP3R, we induced TBS at various values of 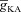 and plotted steady-state change in synaptic weight, Δw. To quantify the specific roles of store Ca2+, which is specifically governed by mGluRs, we performed these experiments under conditions where mGluRs were present or absent (Fig. 8G). Under either condition, we found that an increase in
and plotted steady-state change in synaptic weight, Δw. To quantify the specific roles of store Ca2+, which is specifically governed by mGluRs, we performed these experiments under conditions where mGluRs were present or absent (Fig. 8G). Under either condition, we found that an increase in 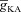 led to a decrease in the synaptic weight, as would be expected from the consequent reduction in the influx of Ca2+ through NMDAR. However, when mGluRs were present at the synapse, the higher levels of [Ca2+]c induced by the presence of mGluRs played a critical role in determining the direction and strength of plasticity (Fig. 8G). We quantified this mGluR-induced percentage change in plasticity across different values of NAR, to assess the relative contributions of NMDAR vs. mGluR to TBS-induced plasticity (Fig. 8H). Whereas at lower values of NAR (0.5), the [Ca2+]c increase in response to TBS was too low to cause any change in the synaptic weight, at very high values (2.5), synaptic weight always potentiated to saturating levels, thus leaving the mGluR-induced percentage changes insignificant. However, at moderate values of NAR (1.5), the regulation of Ca2+ through InsP3Rs by
led to a decrease in the synaptic weight, as would be expected from the consequent reduction in the influx of Ca2+ through NMDAR. However, when mGluRs were present at the synapse, the higher levels of [Ca2+]c induced by the presence of mGluRs played a critical role in determining the direction and strength of plasticity (Fig. 8G). We quantified this mGluR-induced percentage change in plasticity across different values of NAR, to assess the relative contributions of NMDAR vs. mGluR to TBS-induced plasticity (Fig. 8H). Whereas at lower values of NAR (0.5), the [Ca2+]c increase in response to TBS was too low to cause any change in the synaptic weight, at very high values (2.5), synaptic weight always potentiated to saturating levels, thus leaving the mGluR-induced percentage changes insignificant. However, at moderate values of NAR (1.5), the regulation of Ca2+ through InsP3Rs by 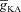 implied a critical role for mGluRs in regulating the direction and strength of synaptic plasticity (Fig. 8H). This may also be observed from the quantification of the amount of flux of Ca2+ through InsP3Rs, shown for the three values of NAR considered here (Fig. 8I), where an increase in A-type K+ conductance increased the release of Ca2+ through InsP3Rs. This was consistent with the NMDAR-dependent inhibition of release of Ca2+ through InsP3Rs at the mGluR-containing synapse (Fig. 8D). Increase in A-type K+ conductance decreased the inhibitory Ca2+ through NMDAR and hence increased the flux of Ca2+ through InsP3Rs (JInsP3R). Together, these results suggest that A-type K+ current plays a critical role in regulating release of Ca2+ through InsP3Rs, and thus the contribution of mGluRs to various plasticity-inducing protocols.
implied a critical role for mGluRs in regulating the direction and strength of synaptic plasticity (Fig. 8H). This may also be observed from the quantification of the amount of flux of Ca2+ through InsP3Rs, shown for the three values of NAR considered here (Fig. 8I), where an increase in A-type K+ conductance increased the release of Ca2+ through InsP3Rs. This was consistent with the NMDAR-dependent inhibition of release of Ca2+ through InsP3Rs at the mGluR-containing synapse (Fig. 8D). Increase in A-type K+ conductance decreased the inhibitory Ca2+ through NMDAR and hence increased the flux of Ca2+ through InsP3Rs (JInsP3R). Together, these results suggest that A-type K+ current plays a critical role in regulating release of Ca2+ through InsP3Rs, and thus the contribution of mGluRs to various plasticity-inducing protocols.
Discussion
In this study, we quantitatively demonstrated that ER Ca2+ release through InsP3Rs exhibited a bell-shaped dependence on A-type K+ channels expressed on the plasma membrane. Assessing the physiological consequences of this dependence, we presented novel roles for A-type K+ current in regulating the spatiotemporal spread of Ca2+ wave propagation and in modulating the relative contribution of mGluRs in induction of synaptic plasticity. This interaction between a restorative conductance expressed on the plasma membrane and a Ca2+ channel resident on the ER membrane is effected by the ability of A-type K+ current to modulate local Ca2+ influx through voltage-dependent channels on the plasma membrane (Fig. 1C–D), and the modulation of InsP3R function by cytosolic Ca2+ (Fig. 1E). In what follows, we present some implications of our study to biophysical and biochemical signal integration and spread within active dendrites, also providing some experimentally testable predictions that follow from our findings.
Active propagation of calcium signals and signalling microdomains
In the reaction–diffusion system that governs Ca2+ signal propagation, regenerative Ca2+-dependent channels on the ER membrane mediate lossless Ca2+ signal propagation. The ER membrane and the plasma membrane run in parallel through the entire neuronal morphology, and are known to interact with each other in several ways. Such interactions include depletion-induced signalling involving the STIM and Orai proteins and VGCCs (Prakriya et al. 2006; Vig et al. 2006; Park et al. 2010; Wang et al. 2010; Lewis, 2011), the interactions between VGCCs, NMDARs, mGluRs and InsP3Rs during calcium waves and calcium-dependent inhibition of VGCCs (Nakamura et al. 1999; Budde et al. 2002; El-Hassar et al. 2011; Manita et al. 2011; Kato et al. 2012; Ross, 2012), the actions of mGluRs and the ER on Ca2+-dependent K+ channels including structural links (Abdul-Ghani et al. 1996; Augustine et al. 2003; Weaver et al. 2007; Adelman et al. 2012), and the plasticity of plasma membrane VGICs and receptors induced by ER Ca2+ (Anwyl, 1999; Huber et al. 2000; Nishiyama et al. 2000; Hansel et al. 2001; Ito, 2002; Sourdet et al. 2003; Brager & Johnston, 2007). Such tight interactions between these two membranes have highlighted several roles of the ER in the integration of intraneuronal information, in regulating signalling microdomains and in regulating the downstream signalling pathways that are regulated by these Ca2+ signals (Berridge, 2002, 2006; Augustine et al. 2003; Kennedy et al. 2005; Verkhratsky, 2005; Park et al. 2008; Kotaleski & Blackwell, 2010).
Our results establish a novel form of interaction between the two membranes, and demonstrate a bell-shaped dependence of calcium release through InsP3R on the density of A-type potassium channels, during the propagation of an intraneuronal calcium wave initiated through established protocols. We propose this dependence as a mechanism for enhancing calcium release from the ER residing in thin-calibre dendrites. Specifically, given the high SVR of thin-calibre dendrites, the initial influx of calcium through plasma membrane channels is too high, thus inhibiting the ER receptors and rendering the ER calcium store irrelevant. If these thin-calibre dendrites were to express a high density of A-type potassium channels, the initial influx of calcium would be reduced, thus allowing for the release of calcium through the ER receptors. Thus, if active propagation of calcium signals were to be sustained through regenerative ER calcium release, it is necessary to suppress the initial calcium influx through plasma membrane channels. We note that A-type potassium channels do express heavily in thin-calibre dendrites of hippocampal pyramidal neurons (Hoffman et al. 1997; Frick et al. 2003; Kerti et al. 2011), and propose the regulation of ER calcium release as a novel physiological role for these dendritic channels.
Furthermore, our results also uncover a powerful and localized mechanism through which a neuron could steer the spread of signalling microdomains by altering local dendritic excitability. Specifically, we demonstrated that the A-type K+ current could regulate the release of ER Ca2+ by altering local dendritic excitability. This, coupled with spatially restricted plasticity that A-type K+ channels have been demonstrated to undergo (Frick et al. 2004; Losonczy et al. 2008), equips the cell with a powerful regulatory mechanism to steer signalling spread towards specific subregions within a neuron. For instance, branch-specific plasticity in A-type K+ channels, apart from altering dendritic spike initiation at the branches that undergo plasticity (Losonczy et al. 2008), could also regulate the invasion of Ca2+ waves into these branches and alter the spread of microdomains consequent to the activation of synaptic receptors on the dendritic membrane. Finally, various neuromodulatory and pathophysiological processes have also been experimentally demonstrated to induce changes in the density and/or biophysical properties of A-type K+ channels, thus suggesting a role for this regulatory mechanism in different behavioural paradigms and neurological disorders (Hasselmo, 1995; Hoffman & Johnston, 1999; Sabatini et al. 2002; Bernard et al. 2004; Verkhratsky, 2005; Choe & Ehrlich, 2006; Shah et al. 2010). Given the universality of Ca2+ signals and their microdomains, our results have implications for various aspects of neuronal physiology and pathophysiology (Berridge et al. 2000; Augustine et al. 2003; Verkhratsky, 2005; Berridge, 2006; Rizzuto & Pozzan, 2006).
mGluRs, synaptic plasticity and active dendrites
The contribution of mGluRs to various forms of neuronal plasticity is well established (Anwyl, 1999; Huber et al. 2000; Nishiyama et al. 2000; Hansel et al. 2001; Ito, 2002; Sourdet et al. 2003; Brager & Johnston, 2007). However, theoretical biophysical models designed to understand hippocampal synaptic plasticity have largely ignored their contribution to various forms of plasticity. In this study, we incorporated a detailed kinetic model for mGluRs, and performed detailed analyses of their metaplastic effects on different forms of synaptic plasticity. From our results, we predict that the higher accumulation and delayed saturation of Ca2+ in the postsynaptic compartment consequent to the activation of perisynaptic mGluR shifts both the long-term potentiation (LTP) and long-term depression (LTD) induction threshold in the BCM-like plasticity profile (Fig. 6). This is in contrast to the metaplastic effects of the A-type K+ current, which shifted the LTP threshold but not the LTD threshold (Fig. 7). This is consistent with the voltage-dependent activation profile of the A-type K+ channels, and with previous findings that mGluR activation by low-frequency synaptic stimulation predominantly contributed to LTD of the synapse (Hoffman et al. 1997; Huber et al. 2000). From these results, we propose that plasticity in mGluR could be a major determinant for the bidirectional shift in the LTD threshold.
Furthermore, we performed simulations to understand the mechanistic details of how A-type K+ channels alter Ca2+ entry through InsP3Rs and NMDARs, thereby affecting the relative contribution of mGluRs to two different forms of synaptic plasticity (Figs 6–8). Our results conform to experimental findings (Nishiyama et al. 2000) that Ca2+ influx through NMDARs at the stimulated synapse acts as inhibitor for the release of Ca2+ from the stores through InsP3R (Figs 6E and 8D). Our results suggest that such suppression is substantially pronounced in thin-calibre dendrites, where high SVR amplifies the initial Ca2+ influx through NMDARs. In this context, based on our results with synaptic plasticity protocols (Figs 6–8), we present an experimentally testable prediction that the A-type K+ channels are ideally suited for suppressing this inhibition, given their ability to modulate synaptic potentials and their abundant expression in thin-calibre dendrites of hippocampal pyramidal cells (Hoffman et al. 1997; Frick et al. 2003; Kerti et al. 2011).
An implication for our postulate is that the A-type K+ channels would regulate the spatiotemporal spread of Ca2+ by altering the relative contributions of mGluRs to different forms of synaptic plasticity (Figs 7–8), thus regulating time windows in heterosynaptic plasticity protocols. Specifically, InsP3R-dependent regenerative release of Ca2+ from the stores has been shown to be a critical determinant of various forms of timing-dependent heterosynaptic plasticity (Ito, 2002; Doi et al. 2005; Dudman et al. 2007). For instance, during the input timing-dependent plasticity (ITDP) protocol in CA1 pyramidal neurons, InsP3R-dependent potentiation is induced in Schaffer collateral (SC) synapses if their stimulation is paired with the stimulation of temporoammonic (TA) synapses occurring 20 ms earlier (Dudman et al. 2007). This temporal window has been suggested to be critical for the influx of Ca2+ at the TA synapses to supralinearly sum with the subsequent influx of Ca2+ at the SC synapses by recruiting CICR through InsP3Rs, thereby inducing potentiation at SC synapses. Based on our results that the A-type K+ current could alter the latency to regenerative release of Ca2+, and the temporal window over which these events occur (Figs 3 and 5), we predict that dendritic A-type K+ channels would play a critical role in regulating the temporal window for several forms of heterosynaptic plasticity, including ITDP, by altering Ca2+ release through InsP3Rs. This prediction could be experimentally tested by inducing ITDP in the presence of pharmacological blockers targeting the InsP3Rs, with various concentrations of agonists/antagonists of A-type K+ channels.
In summary, we have quantitatively established interactions between dendritic A-type K+ channels and ER InsP3Rs, demonstrating specific roles for such interactions in Ca2+ wave propagation and in the induction of synaptic plasticity. Generalizing these results to other dendritic VGICs that can regulate excitability, we suggest that our results establish novel roles for active dendrites and their plasticity, and endow neurons with a powerful and localized mechanism to steer the spatiotemporal spread of signalling microdomains. As our models and simulation protocols were heavily constrained by experimental data, several of our specific predictions on the interactions between dendritic ion channels and ER receptors could be tested experimentally, apart from assessing the role of different dendritic channels in regulating spatiotemporal aspects of the Ca2+ microdomains. Finally, although our focus was restricted to hippocampal neurons, A-type K+ channels, mGluRs and ER InsP3Rs driven by the abundance of associated experimental data, future studies could focus on theoretically and experimentally extending our analyses to interactions between other dendritic ion channels, alternative receptors that can mobilize InsP3 (e.g. muscarinic acetylcholine receptors) and ER receptors in neurons from different brain regions.
Acknowledgments
The authors thank Dr Daniel Johnston and members of the cellular neurophysiology laboratory for helpful discussions and for critical comments on a draft of this manuscript. This work was supported by a career development award to R.N. by the International Human Frontier Science Program Organization, the Department of Biotechnology through the US–India brain research collaborative programme and by the Indian Institute of Science.
Glossary
- AMPAR
α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid receptor
- AP
action potential
- AUC
area under the curve
- bAP
backpropagating action potential
- BCM
Bienenstock–Cooper–Munro
- CICR
calcium-induced calcium release
- ER
endoplasmic reticulum
- FWHM
full-width at half-maximum
- InsP3
inositol trisphosphate
- InsP3R
inositol trisphosphate receptor
- ISI
interspike interval
- ITDP
input timing-dependent plasticity
- LTD
long-term depression
- LTP
long-term potentiation
- mGluR
metabotropic glutamate receptor
- NMDAR
N-methyl-d-aspartate receptor
- NAR
NMDAR:AMPAR ratio
- SC
Schaffer collateral
- SERCA
sarcoplasmic endoplasmic reticulum calcium ATPase
- SVR
surface area to volume ratio
- TA
temporoammonic
- TBS
theta burst stimulation
- VGCC
voltage-gated calcium channel
- VGIC
voltage-gated ion channel
Author contributions
S.A. and R.N. conceived and designed the experiments; S.A. performed the experiments; S.A. and R.N. performed data analyses, including interpretation of results; S.A. drafted the article; S.A. and R.N. revised it critically for important intellectual content.
References
- Abdul-Ghani MA, Valiante TA, Carlen PL, Pennefather PS. Metabotropic glutamate receptors coupled to IP3 production mediate inhibition of IAHP in rat dentate granule neurons. J Neurophysiol. 1996;76:2691–2700. doi: 10.1152/jn.1996.76.4.2691. [DOI] [PubMed] [Google Scholar]
- Adelman JP, Maylie J, Sah P. Small-conductance Ca2+-activated K+ channels: form and function. Annu Rev Physiol. 2012;74:245–269. doi: 10.1146/annurev-physiol-020911-153336. [DOI] [PubMed] [Google Scholar]
- Allbritton NL, Meyer T, Stryer L. Range of messenger action of calcium ion and inositol 1,4,5-trisphosphate. Science. 1992;258:1812–1815. doi: 10.1126/science.1465619. [DOI] [PubMed] [Google Scholar]
- Anwyl R. Metabotropic glutamate receptors: electrophysiological properties and role in plasticity. Brain Res Brain Res Rev. 1999;29:83–120. doi: 10.1016/s0165-0173(98)00050-2. [DOI] [PubMed] [Google Scholar]
- Ascoli GA, Donohue DE, Halavi M. NeuroMorpho.Org: a central resource for neuronal morphologies. J Neurosci. 2007;27:9247–9251. doi: 10.1523/JNEUROSCI.2055-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Augustine GJ, Santamaria F, Tanaka K. Local calcium signaling in neurons. Neuron. 2003;40:331–346. doi: 10.1016/s0896-6273(03)00639-1. [DOI] [PubMed] [Google Scholar]
- Bernard C, Anderson A, Becker A, Poolos NP, Beck H, Johnston D. Acquired dendritic channelopathy in temporal lobe epilepsy. Science. 2004;305:532–535. doi: 10.1126/science.1097065. [DOI] [PubMed] [Google Scholar]
- Berridge MJ. The endoplasmic reticulum: a multifunctional signaling organelle. Cell Calcium. 2002;32:235–249. doi: 10.1016/s0143416002001823. [DOI] [PubMed] [Google Scholar]
- Berridge MJ. Calcium microdomains: organization and function. Cell Calcium. 2006;40:405–412. doi: 10.1016/j.ceca.2006.09.002. [DOI] [PubMed] [Google Scholar]
- Berridge MJ, Lipp P, Bootman MD. The versatility and universality of calcium signalling. Nat Rev Mol Cell Biol. 2000;1:11–21. doi: 10.1038/35036035. [DOI] [PubMed] [Google Scholar]
- Bezprozvanny I, Watras J, Ehrlich BE. Bell-shaped calcium-response curves of Ins(1,4,5)P3- and calcium-gated channels from endoplasmic reticulum of cerebellum. Nature. 1991;351:751–754. doi: 10.1038/351751a0. [DOI] [PubMed] [Google Scholar]
- Bhalla US, Iyengar R. Emergent properties of networks of biological signaling pathways. Science. 1999;283:381–387. doi: 10.1126/science.283.5400.381. [DOI] [PubMed] [Google Scholar]
- Blackwell KT. Modeling calcium concentration and biochemical reactions. Brains Minds Media. 2005;1:27. [Google Scholar]
- Brager DH, Johnston D. Plasticity of intrinsic excitability during long-term depression is mediated through mGluR-dependent changes in Ih in hippocampal CA1 pyramidal neurons. J Neurosci. 2007;27:13926–13937. doi: 10.1523/JNEUROSCI.3520-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Budde T, Meuth S, Pape HC. Calcium-dependent inactivation of neuronal calcium channels. Nat Rev Neurosci. 2002;3:873–883. doi: 10.1038/nrn959. [DOI] [PubMed] [Google Scholar]
- Canavier CC. Sodium dynamics underlying burst firing and putative mechanisms for the regulation of the firing pattern in midbrain dopamine neurons: a computational approach. J Comput Neurosci. 1999;6:49–69. doi: 10.1023/a:1008809000182. [DOI] [PubMed] [Google Scholar]
- Carnevale NT, Hines ML. The NEURON Book. Cambridge: Cambridge University Press; 2006. [Google Scholar]
- Chen X, Yuan LL, Zhao C, Birnbaum SG, Frick A, Jung WE, Schwarz TL, Sweatt JD, Johnston D. Deletion of Kv4.2 gene eliminates dendritic A-type K+ current and enhances induction of long-term potentiation in hippocampal CA1 pyramidal neurons. J Neurosci. 2006;26:12143–12151. doi: 10.1523/JNEUROSCI.2667-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choe CU, Ehrlich BE. The inositol 1,4,5-trisphosphate receptor (IP3R) and its regulators: sometimes good and sometimes bad teamwork. Sci STKE. 2006;2006:re15. doi: 10.1126/stke.3632006re15. [DOI] [PubMed] [Google Scholar]
- Clapham DE. Calcium signaling. Cell. 2007;131:1047–1058. doi: 10.1016/j.cell.2007.11.028. [DOI] [PubMed] [Google Scholar]
- Colbert CM, Magee JC, Hoffman DA, Johnston D. Slow recovery from inactivation of Na+ channels underlies the activity-dependent attenuation of dendritic action potentials in hippocampal CA1 pyramidal neurons. J Neurosci. 1997;17:6512–6521. doi: 10.1523/JNEUROSCI.17-17-06512.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornelisse LN, van Elburg RA, Meredith RM, Yuste R, Mansvelder HD. High speed two-photon imaging of calcium dynamics in dendritic spines: consequences for spine calcium kinetics and buffer capacity. PLoS One. 2007;2:e1073. doi: 10.1371/journal.pone.0001073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Young GW, Keizer J. A single-pool inositol 1,4,5-trisphosphate-receptor-based model for agonist-stimulated oscillations in Ca2+ concentration. Proc Natl Acad Sci U S A. 1992;89:9895–9899. doi: 10.1073/pnas.89.20.9895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dingledine R, Borges K, Bowie D, Traynelis SF. The glutamate receptor ion channels. Pharmacol Rev. 1999;51:7–61. [PubMed] [Google Scholar]
- Doi T, Kuroda S, Michikawa T, Kawato M. Inositol 1,4,5-trisphosphate-dependent Ca2+ threshold dynamics detect spike timing in cerebellar Purkinje cells. J Neurosci. 2005;25:950–961. doi: 10.1523/JNEUROSCI.2727-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dudek SM, Bear MF. Homosynaptic long-term depression in area CA1 of hippocampus and effects of N-methyl-D-aspartate receptor blockade. Proc Natl Acad Sci U S A. 1992;89:4363–4367. doi: 10.1073/pnas.89.10.4363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dudman JT, Tsay D, Siegelbaum SA. A role for synaptic inputs at distal dendrites: instructive signals for hippocampal long-term plasticity. Neuron. 2007;56:866–879. doi: 10.1016/j.neuron.2007.10.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- El-Hassar L, Hagenston AM, D’Angelo LB, Yeckel MF. Metabotropic glutamate receptors regulate hippocampal CA1 pyramidal neuron excitability via Ca2+ wave-dependent activation of SK and TRPC channels. J Physiol. 2011;589:3211–3229. doi: 10.1113/jphysiol.2011.209783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emptage NJ, Reid CA, Fine A. Calcium stores in hippocampal synaptic boutons mediate short-term plasticity, store-operated Ca2+ entry, and spontaneous transmitter release. Neuron. 2001;29:197–208. doi: 10.1016/s0896-6273(01)00190-8. [DOI] [PubMed] [Google Scholar]
- Fink CC, Slepchenko B, Moraru II, Watras J, Schaff JC, Loew LM. An image-based model of calcium waves in differentiated neuroblastoma cells. Biophys J. 2000;79:163–183. doi: 10.1016/S0006-3495(00)76281-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleidervish IA, Lasser-Ross N, Gutnick MJ, Ross WN. Na+ imaging reveals little difference in action potential-evoked Na+ influx between axon and soma. Nat Neurosci. 2010;13:852–860. doi: 10.1038/nn.2574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frick A, Magee J, Johnston D. LTP is accompanied by an enhanced local excitability of pyramidal neuron dendrites. Nat Neurosci. 2004;7:126–135. doi: 10.1038/nn1178. [DOI] [PubMed] [Google Scholar]
- Frick A, Magee J, Koester HJ, Migliore M, Johnston D. Normalization of Ca2+ signals by small oblique dendrites of CA1 pyramidal neurons. J Neurosci. 2003;23:3243–3250. doi: 10.1523/JNEUROSCI.23-08-03243.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansel C, Linden DJ, D’Angelo E. Beyond parallel fiber LTD: the diversity of synaptic and non-synaptic plasticity in the cerebellum. Nat Neurosci. 2001;4:467–475. doi: 10.1038/87419. [DOI] [PubMed] [Google Scholar]
- Hasselmo ME. Neuromodulation and cortical function: modeling the physiological basis of behaviour. Behav Brain Res. 1995;67:1–27. doi: 10.1016/0166-4328(94)00113-t. [DOI] [PubMed] [Google Scholar]
- Helmchen F, Imoto K, Sakmann B. Ca2+ buffering and action potential-evoked Ca2+ signaling in dendrites of pyramidal neurons. Biophys J. 1996;70:1069–1081. doi: 10.1016/S0006-3495(96)79653-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrington J, Park YB, Babcock DF, Hille B. Dominant role of mitochondria in clearance of large Ca2+ loads from rat adrenal chromaffin cells. Neuron. 1996;16:219–228. doi: 10.1016/s0896-6273(00)80038-0. [DOI] [PubMed] [Google Scholar]
- Hertle DN, Yeckel MF. Distribution of inositol-1,4,5-trisphosphate receptor isotypes and ryanodine receptor isotypes during maturation of the rat hippocampus. Neuroscience. 2007;150:625–638. doi: 10.1016/j.neuroscience.2007.09.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman DA, Johnston D. Neuromodulation of dendritic action potentials. J Neurophysiol. 1999;81:408–411. doi: 10.1152/jn.1999.81.1.408. [DOI] [PubMed] [Google Scholar]
- Hoffman DA, Magee JC, Colbert CM, Johnston D. K+ channel regulation of signal propagation in dendrites of hippocampal pyramidal neurons. Nature. 1997;387:869–875. doi: 10.1038/43119. [DOI] [PubMed] [Google Scholar]
- Huber KM, Kayser MS, Bear MF. Role for rapid dendritic protein synthesis in hippocampal mGluR-dependent long-term depression. Science. 2000;288:1254–1257. doi: 10.1126/science.288.5469.1254. [DOI] [PubMed] [Google Scholar]
- Ito M. The molecular organization of cerebellar long-term depression. Nat Rev Neurosci. 2002;3:896–902. doi: 10.1038/nrn962. [DOI] [PubMed] [Google Scholar]
- Jahr CE, Stevens CF. Voltage dependence of NMDA-activated macroscopic conductances predicted by single-channel kinetics. J Neurosci. 1990;10:3178–3182. doi: 10.1523/JNEUROSCI.10-09-03178.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston D, Christie BR, Frick A, Gray R, Hoffman DA, Schexnayder LK, Watanabe S, Yuan LL. Active dendrites, potassium channels and synaptic plasticity. Philos Trans R Soc Lond B Biol Sci. 2003;358:667–674. doi: 10.1098/rstb.2002.1248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston D, Magee JC, Colbert CM, Cristie BR. Active properties of neuronal dendrites. Annu Rev Neurosci. 1996;19:165–186. doi: 10.1146/annurev.ne.19.030196.001121. [DOI] [PubMed] [Google Scholar]
- Jung SC, Kim J, Hoffman DA. Rapid, bidirectional remodeling of synaptic NMDA receptor subunit composition by A-type K+ channel activity in hippocampal CA1 pyramidal neurons. Neuron. 2008;60:657–671. doi: 10.1016/j.neuron.2008.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanold PO, Manis PB. Transient potassium currents regulate the discharge patterns of dorsal cochlear nucleus pyramidal cells. J Neurosci. 1999;19:2195–2208. doi: 10.1523/JNEUROSCI.19-06-02195.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kato HK, Kassai H, Watabe AM, Aiba A, Manabe T. Functional coupling of the metabotropic glutamate receptor, InsP3 receptor and L-type Ca2+ channel in mouse CA1 pyramidal cells. J Physiol. 2012;590:3019–3034. doi: 10.1113/jphysiol.2012.232942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy MB, Beale HC, Carlisle HJ, Washburn LR. Integration of biochemical signalling in spines. Nat Rev Neurosci. 2005;6:423–434. doi: 10.1038/nrn1685. [DOI] [PubMed] [Google Scholar]
- Kerti K, Lorincz A, Nusser Z. Unique somato-dendritic distribution pattern of Kv4.2 channels on hippocampal CA1 pyramidal cells. Eur J Neurosci. 2011;35:66–75. doi: 10.1111/j.1460-9568.2011.07907.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J, Jung SC, Clemens AM, Petralia RS, Hoffman DA. Regulation of dendritic excitability by activity-dependent trafficking of the A-type K+ channel subunit Kv4.2 in hippocampal neurons. Neuron. 2007;54:933–947. doi: 10.1016/j.neuron.2007.05.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J, Wei DS, Hoffman DA. Kv4 potassium channel subunits control action potential repolarization and frequency-dependent broadening in rat hippocampal CA1 pyramidal neurones. J Physiol. 2005;569:41–57. doi: 10.1113/jphysiol.2005.095042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klingauf J, Neher E. Modeling buffered Ca2+ diffusion near the membrane: implications for secretion in neuroendocrine cells. Biophys J. 1997;72:674–690. doi: 10.1016/s0006-3495(97)78704-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kotaleski JH, Blackwell KT. Modelling the molecular mechanisms of synaptic plasticity using systems biology approaches. Nat Rev Neurosci. 2010;11:239–251. doi: 10.1038/nrn2807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larson J, Wong D, Lynch G. Patterned stimulation at the theta frequency is optimal for the induction of hippocampal long-term potentiation. Brain Res. 1986;368:347–350. doi: 10.1016/0006-8993(86)90579-2. [DOI] [PubMed] [Google Scholar]
- Lewis RS. Store-operated calcium channels: new perspectives on mechanism and function. Cold Spring Harb Perspect Biol. 2011;3:ii. doi: 10.1101/cshperspect.a003970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li YX, Rinzel J. Equations for InsP3 receptor-mediated [Ca2+]i oscillations derived from a detailed kinetic model: a Hodgkin–Huxley like formalism. J Theor Biol. 1994;166:461–473. doi: 10.1006/jtbi.1994.1041. [DOI] [PubMed] [Google Scholar]
- Lisman J. A mechanism for the Hebb and the anti-Hebb processes underlying learning and memory. Proc Natl Acad Sci U S A. 1989;86:9574–9578. doi: 10.1073/pnas.86.23.9574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lisman JE. Three Ca2+ levels affect plasticity differently: the LTP zone, the LTD zone and no man's land. J Physiol. 2001;532:285. doi: 10.1111/j.1469-7793.2001.0285f.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Losonczy A, Magee JC. Integrative properties of radial oblique dendrites in hippocampal CA1 pyramidal neurons. Neuron. 2006;50:291–307. doi: 10.1016/j.neuron.2006.03.016. [DOI] [PubMed] [Google Scholar]
- Losonczy A, Makara JK, Magee JC. Compartmentalized dendritic plasticity and input feature storage in neurons. Nature. 2008;452:436–441. doi: 10.1038/nature06725. [DOI] [PubMed] [Google Scholar]
- Lujan R, Nusser Z, Roberts JD, Shigemoto R, Somogyi P. Perisynaptic location of metabotropic glutamate receptors mGluR1 and mGluR5 on dendrites and dendritic spines in the rat hippocampus. Eur J Neurosci. 1996;8:1488–1500. doi: 10.1111/j.1460-9568.1996.tb01611.x. [DOI] [PubMed] [Google Scholar]
- Lytton J, Westlin M, Burk SE, Shull GE, MacLennan DH. Functional comparisons between isoforms of the sarcoplasmic or endoplasmic reticulum family of calcium pumps. J Biol Chem. 1992;267:14483–14489. [PubMed] [Google Scholar]
- Magee JC, Johnston D. Characterization of single voltage-gated Na+ and Ca2+ channels in apical dendrites of rat CA1 pyramidal neurons. J Physiol. 1995;487:67–90. doi: 10.1113/jphysiol.1995.sp020862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manita S, Miyazaki K, Ross WN. Synaptically activated Ca2+ waves and NMDA spikes locally suppress voltage-dependent Ca2+ signalling in rat pyramidal cell dendrites. J Physiol. 2011;589:4903–4920. doi: 10.1113/jphysiol.2011.216564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayer ML, Westbrook GL. Permeation and block of N-methyl-D-aspartic acid receptor channels by divalent cations in mouse cultured central neurones. J Physiol. 1987;394:501–527. doi: 10.1113/jphysiol.1987.sp016883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meldolesi J, Pozzan T. The endoplasmic reticulum Ca2+ store: a view from the lumen. Trends Biochem Sci. 1998;23:10–14. doi: 10.1016/s0968-0004(97)01143-2. [DOI] [PubMed] [Google Scholar]
- Migliore M, Hoffman DA, Magee JC, Johnston D. Role of an A-type K+ conductance in the back-propagation of action potentials in the dendrites of hippocampal pyramidal neurons. J Comput Neurosci. 1999;7:5–15. doi: 10.1023/a:1008906225285. [DOI] [PubMed] [Google Scholar]
- Mikoshiba K. Inositol 1,4,5-trisphosphate IP3 receptors and their role in neuronal cell function. J Neurochem. 2006;97:1627–1633. doi: 10.1111/j.1471-4159.2006.03985.x. [DOI] [PubMed] [Google Scholar]
- Nakamura T, Barbara JG, Nakamura K, Ross WN. Synergistic release of Ca2+ from IP3-sensitive stores evoked by synaptic activation of mGluRs paired with backpropagating action potentials. Neuron. 1999;24:727–737. doi: 10.1016/s0896-6273(00)81125-3. [DOI] [PubMed] [Google Scholar]
- Nakamura T, Lasser-Ross N, Nakamura K, Ross WN. Spatial segregation and interaction of calcium signalling mechanisms in rat hippocampal CA1 pyramidal neurons. J Physiol. 2002;543:465–480. doi: 10.1113/jphysiol.2002.020362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakamura T, Nakamura K, Lasser-Ross N, Barbara JG, Sandler VM, Ross WN. Inositol 1,4,5-trisphosphate (IP3)-mediated Ca2+ release evoked by metabotropic agonists and backpropagating action potentials in hippocampal CA1 pyramidal neurons. J Neurosci. 2000;20:8365–8376. doi: 10.1523/JNEUROSCI.20-22-08365.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayanan R, Dougherty KJ, Johnston D. Calcium store depletion induces persistent perisomatic increases in the functional density of h channels in hippocampal pyramidal neurons. Neuron. 2010;68:921–935. doi: 10.1016/j.neuron.2010.11.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayanan R, Johnston D. Long-term potentiation in rat hippocampal neurons is accompanied by spatially widespread changes in intrinsic oscillatory dynamics and excitability. Neuron. 2007;56:1061–1075. doi: 10.1016/j.neuron.2007.10.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayanan R, Johnston D. The h current is a candidate mechanism for regulating the sliding modification threshold in a BCM-like synaptic learning rule. J Neurophysiol. 2010;104:1020–1033. doi: 10.1152/jn.01129.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neves SR, Iyengar R. Models of spatially restricted biochemical reaction systems. J Biol Chem. 2009;284:5445–5449. doi: 10.1074/jbc.R800058200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishiyama M, Hong K, Mikoshiba K, Poo MM, Kato K. Calcium stores regulate the polarity and input specificity of synaptic modification. Nature. 2000;408:584–588. doi: 10.1038/35046067. [DOI] [PubMed] [Google Scholar]
- Park CY, Shcheglovitov A, Dolmetsch R. The CRAC channel activator STIM1 binds and inhibits L-type voltage-gated calcium channels. Science. 2010;330:101–105. doi: 10.1126/science.1191027. [DOI] [PubMed] [Google Scholar]
- Park MK, Choi YM, Kang YK, Petersen OH. The endoplasmic reticulum as an integrator of multiple dendritic events. Neuroscientist. 2008;14:68–77. doi: 10.1177/1073858407305691. [DOI] [PubMed] [Google Scholar]
- Pin JP, Duvoisin R. The metabotropic glutamate receptors: structure and functions. Neuropharmacology. 1995;34:1–26. doi: 10.1016/0028-3908(94)00129-g. [DOI] [PubMed] [Google Scholar]
- Poirazi P, Brannon T, Mel BW. Pyramidal neuron as two-layer neural network. Neuron. 2003;37:989–999. doi: 10.1016/s0896-6273(03)00149-1. [DOI] [PubMed] [Google Scholar]
- Prakriya M, Feske S, Gwack Y, Srikanth S, Rao A, Hogan PG. Orai1 is an essential pore subunit of the CRAC channel. Nature. 2006;443:230–233. doi: 10.1038/nature05122. [DOI] [PubMed] [Google Scholar]
- Pyapali GK, Sik A, Penttonen M, Buzsaki G, Turner DA. Dendritic properties of hippocampal CA1 pyramidal neurons in the rat: intracellular staining in vivo and in vitro. J Comp Neurol. 1998;391:335–352. doi: 10.1002/(sici)1096-9861(19980216)391:3<335::aid-cne4>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]
- Rizzuto R, Pozzan T. Microdomains of intracellular Ca2+: molecular determinants and functional consequences. Physiol Rev. 2006;86:369–408. doi: 10.1152/physrev.00004.2005. [DOI] [PubMed] [Google Scholar]
- Rose CR, Konnerth A. Stores not just for storage: intracellular calcium release and synaptic plasticity. Neuron. 2001;31:519–522. doi: 10.1016/s0896-6273(01)00402-0. [DOI] [PubMed] [Google Scholar]
- Ross WN. Understanding calcium waves and sparks in central neurons. Nat Rev Neurosci. 2012;13:157–168. doi: 10.1038/nrn3168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabatini BL, Oertner TG, Svoboda K. The life cycle of Ca2+ ions in dendritic spines. Neuron. 2002;33:439–452. doi: 10.1016/s0896-6273(02)00573-1. [DOI] [PubMed] [Google Scholar]
- Shah MM, Hammond RS, Hoffman DA. Dendritic ion channel trafficking and plasticity. Trends Neurosci. 2010;33:307–316. doi: 10.1016/j.tins.2010.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shibata R, Nakahira K, Shibasaki K, Wakazono Y, Imoto K, Ikenaka K. A-type K+ current mediated by the Kv4 channel regulates the generation of action potential in developing cerebellar granule cells. J Neurosci. 2000;20:4145–4155. doi: 10.1523/JNEUROSCI.20-11-04145.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shouval HZ, Bear MF, Cooper LN. A unified model of NMDA receptor-dependent bidirectional synaptic plasticity. Proc Natl Acad Sci U S A. 2002;99:10831–10836. doi: 10.1073/pnas.152343099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sneyd J, Keizer J, Sanderson MJ. Mechanisms of calcium oscillations and waves: a quantitative analysis. FASEB J. 1995;9:1463–1472. doi: 10.1096/fasebj.9.14.7589988. [DOI] [PubMed] [Google Scholar]
- Sourdet V, Russier M, Daoudal G, Ankri N, Debanne D. Long-term enhancement of neuronal excitability and temporal fidelity mediated by metabotropic glutamate receptor subtype 5. J Neurosci. 2003;23:10238–10248. doi: 10.1523/JNEUROSCI.23-32-10238.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stutzmann GE, Mattson MP. Endoplasmic reticulum Ca2+ handling in excitable cells in health and disease. Pharmacol Rev. 2011;63:700–727. doi: 10.1124/pr.110.003814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verkhratsky A. Physiology and pathophysiology of the calcium store in the endoplasmic reticulum of neurons. Physiol Rev. 2005;85:201–279. doi: 10.1152/physrev.00004.2004. [DOI] [PubMed] [Google Scholar]
- Vig M, Peinelt C, Beck A, Koomoa DL, Rabah D, Koblan-Huberson M, Kraft S, Turner H, Fleig A, Penner R, Kinet JP. CRACM1 is a plasma membrane protein essential for store-operated Ca2+ entry. Science. 2006;312:1220–1223. doi: 10.1126/science.1127883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Deng X, Mancarella S, Hendron E, Eguchi S, Soboloff J, Tang XD, Gill DL. The calcium store sensor, STIM1, reciprocally controls Orai and CaV1.2 channels. Science. 2010;330:105–109. doi: 10.1126/science.1191086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanabe S, Hoffman DA, Migliore M, Johnston D. Dendritic K+ channels contribute to spike-timing dependent long-term potentiation in hippocampal pyramidal neurons. Proc Natl Acad Sci U S A. 2002;99:8366–8371. doi: 10.1073/pnas.122210599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weaver AK, Olsen ML, McFerrin MB, Sontheimer H. BK channels are linked to inositol 1,4,5-triphosphate receptors via lipid rafts: a novel mechanism for coupling [Ca2+]i to ion channel activation. J Biol Chem. 2007;282:31558–31568. doi: 10.1074/jbc.M702866200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao C, Wang L, Netoff T, Yuan LL. Dendritic mechanisms controlling the threshold and timing requirement of synaptic plasticity. Hippocampus. 2011;21:288–297. doi: 10.1002/hipo.20748. [DOI] [PubMed] [Google Scholar]


