Out-of-atlas likelihood estimation using multi-atlas segmentation

Abstract

Purpose: Multi-atlas segmentation has been shown to be highly robust and accurate across an extraordinary range of potential applications. However, it is limited to the segmentation of structures that are anatomically consistent across a large population of potential target subjects (i.e., multi-atlas segmentation is limited to “in-atlas” applications). Herein, the authors propose a technique to determine the likelihood that a multi-atlas segmentation estimate is representative of the problem at hand, and, therefore, identify anomalous regions that are not well represented within the atlases.

Methods: The authors derive a technique to estimate the out-of-atlas (OOA) likelihood for every voxel in the target image. These estimated likelihoods can be used to determine and localize the probability of an abnormality being present on the target image.

Results: Using a collection of manually labeled whole-brain datasets, the authors demonstrate the efficacy of the proposed framework on two distinct applications. First, the authors demonstrate the ability to accurately and robustly detect malignant gliomas in the human brain—an aggressive class of central nervous system neoplasms. Second, the authors demonstrate how this OOA likelihood estimation process can be used within a quality control context for diffusion tensor imaging datasets to detect large-scale imaging artifacts (e.g., aliasing and image shading).

Conclusions: The proposed OOA likelihood estimation framework shows great promise for robust and rapid identification of brain abnormalities and imaging artifacts using only weak dependencies on anomaly morphometry and appearance. The authors envision that this approach would allow for application-specific algorithms to focus directly on regions of high OOA likelihood, which would (1) reduce the need for human intervention, and (2) reduce the propensity for false positives. Using the dual perspective, this technique would allow for algorithms to focus on regions of normal anatomy to ascertain image quality and adapt to image appearance characteristics.

INTRODUCTION

The ability to detect abnormalities and anomalies in medical images plays a critical role in the detection of diseases and pathologies as well as maintaining image quality assurance. A common way to detect abnormalities or anomalies is through the use of a normal template (or atlas) and finding deviations from that template in order to determine the likelihood of an abnormality.^{1, 2, 3, 4, 5, 6} However, the ability to discover these deviations relies upon the definition of meaningful structure within a target image so that inference can be made about the underlying anatomy. Thus, segmentation plays a critical role in the discovery and quantification of abnormalities and anomalies in medical images.

In multi-atlas segmentation,^{7, 8} multiple atlases are separately registered to the target and the voxelwise label conflicts between the registered atlases are resolved using label fusion. In general, there are two primary fields of study in label fusion: (1) voting-based strategies which include a majority voting^{7, 9, 10, 11} and weighted voting strategies^{12, 13, 14, 15, 16, 17, 18} and (2) statistical fusion strategies based upon simultaneous truth and performance level estimation (STAPLE) (Ref. ¹⁹) and the proposed extensions.^{8, 20, 21, 22, 23, 24, 25, 26, 27, 28} Multi-atlas segmentation has been shown to be highly robust across an extraordinary range of potential applications (e.g., segmentation of the thyroid,^{27, 28} hippocampus,¹⁵ neonatal brain anatomy,²⁹ and the optic nerve³⁰).

Nevertheless, there are two primary concerns that limit the generalizability of multi-atlas segmentation. First, we are limited to structures that are represented by the atlases—multi-atlas segmentation cannot be used to segment structures that are not present on the available atlases. Second, we are limited to structures that are anatomically consistent across potential target subjects. For example, regardless of whether there are atlases available, a direct multi-atlas segmentation procedure cannot be used to segment malignant gliomas in the human brain as tumor characteristics (e.g., location, size, shape) are widely varying across a given target population. As a result, the potential scope of multi-atlas segmentation applications is limited, particularly in the case of anatomical abnormalities (e.g., the detection of highly varying pathologies) and quality control (e.g., the detection of imaging and quality-based artifacts). We enumerate this problem as the fact that multi-atlas segmentation is limited to “in-atlas” applications (e.g., applications where the atlases are anatomically and structurally indicative of the target image).

Herein, we propose a technique to estimate the out-of-atlas (OOA) likelihood for every voxel in the target image (Fig. 1). The OOA approach provides an intuitive and fully general abnormality/outlier detection framework that (1) overcomes several of the current limitations with multi-atlas segmentation and (2) has the potential to dramatically increase the scope of potential multi-atlas-based applications.

Figure 1.

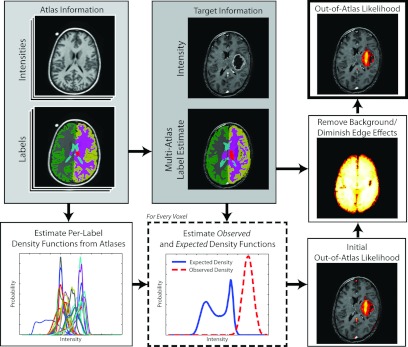
Flowchart demonstrating the out-of-atlas likelihood estimation procedure. First the provided atlas information is used to both (1) perform a multi-atlas segmentation estimate of the target image, and (2) estimate the per-label density functions. Next, these per-label density functions and the target information are used to estimate the observed and expected density functions. These two density functions are then used to construct a voxelwise estimate of the out-of-atlas likelihood. Finally, the background and edge effects are diminished through a postprocessing smoothing step.

This manuscript is organized as follows. We begin by deriving the theoretical basis and the model parameters for the proposed OOA likelihood estimation framework. Next, using a collection of manually labeled whole-brain datasets, we demonstrate the efficacy of the proposed framework on two distinct applications. First, we demonstrate the ability to detect malignant gliomas in the human brain—an aggressive class of central nervous system neoplasms. For this application, we both quantitatively and qualitatively assess the accuracy of the proposed algorithm and demonstrate its sensitivity to the various model parameters and initializations. Second, we demonstrate how this OOA likelihood estimation framework can be used within a quality control context for diffusion tensor imaging (DTI) datasets. Using a clinically acquired dataset, we qualitatively demonstrate that we can detect large-scale quality control issues (e.g., aliasing, shading artifacts) within the proposed estimation framework.

OUT-OF-ATLAS LIKELIHOOD ESTIMATION THEORY

In the following presentation of theory we derive the theoretical basis for the OOA likelihood estimation framework and provide a brief overview of the model parameters and initialization procedure.

Problem definition

Consider an image of N voxels with unknown target labels T, T_i ∈ {0, 1} (i.e., 0: “in-atlas” and 1: “out-of-atlas”). R registered atlases (or “raters” in common fusion terminology) each provide an observed delineation of all N voxels exactly once. The set of labels on these atlases, L, represents the set of possible values that an atlas can assign to all N voxels. Let D be an N × R matrix that indicates the label decisions of the R registered at all N voxels where each element D_ij ∈ {0, 1, …, L − 1}. Let A be another N × R matrix that indicates the associated postregistration atlas intensities for all R atlases and N voxels where $A_{ij}\in \mathbb{R}$. Finally, let $\mathit{I}:I_i\in \mathbb{R}$ be the N-vector representing the target intensities, and let Ψ: Ψ_i ∈ L be the N-vector representing the multi-atlas segmentation estimate of the target image.

Construction of the expected intensity distributions

We define the expected intensity distribution as the approximate semilocal intensity distribution that would be observed given the provided atlas label-intensity relationships and the multi-atlas segmentation estimate at each voxel on the target image. Herein, we define the “semilocal neighborhood” to be a predefined collection of voxels surrounding and including the directly corresponding voxel in the common atlas-target coordinate space. This expected intensity distribution is approximated by summing the observed label-intensity relationships from the atlases across the multi-atlas segmentation estimate of the target within the semilocal neighborhood around the current voxel of interest. Thus, the first step is to construct the label-intensity relationships that can be inferred from the provided atlas information. In other words, we need to construct p(γ|Ψ_i = l) which represents the probability of all possible intensities given that the estimated label is l. Note that this distribution is a global measure with respect to each individual label which limits the impact of shading artifacts and spatial inhomogeneities. We infer this distribution fully from the atlas intensities and labels using a nonparametric Kernel density estimation (KDE) approach:

$$p\left(\gamma {|\Psi }_i=l\right)=\frac{{\sum }_j{\sum }_{i:D_{ij}=l}K\left(\frac{\gamma -A_{ij}}{h}\right)}{h{\sum }_j{\sum }_i\delta (D_{ij},l)},$$ (1)

where γ is all possible intensities, K is a standard Gaussian kernel, and h is the bandwidth associated with the Gaussian kernel, and δ is the Kronecker delta function. Given Eq. 1, which is an estimation of the complex label-intensity relationships inferred from the atlases, the expected intensity distribution within a semilocal neighborhood can then be estimated using the multi-atlas segmentation estimate of the underlying target image:

$$p_i^E\left(\gamma \right)=\frac{1}{Z_i^E}\sum _{i^{\prime }\in {\mathcal{N}}_i}p\left(\gamma {|\Psi }_{i^{\prime }}\right),$$ (2)

where ${\mathcal{N}}_i$ is the semilocal neighborhood surrounding the target voxel i and $Z_i^E$ is the partition function that enforces that $p_i^E\left(\gamma \right)$ is a valid probability density function across all potential image intensities. In other words, $Z_i^E$ enforces the constraint that

$${\int }_{-\infty }^{+\infty }{p}_i^E\left(\gamma \right)d\gamma =1.$$ (3)

As an aside, depending on the processing techniques and imaging characteristics, the expected intensity-label distributions may or may not change as a result of the registration procedure. Assuming they do not change as a result of the registration, these distributions could be directly calculated prior to the registration. Additionally, if a very large number of representative atlases were provided these distributions could be fixed regardless of the desired target image and we could have high confidence in their accuracy. Here, we calculate the distributions after registration for two primary reasons: (1) the intensity normalization procedure provides a mechanism for accounting for the variability of the intensity characteristics between the targets (e.g., as a result of the contrast enhancement), and (2) the calculation of these distributions only minimally affects the computation time of the approach.

Construction of the observed intensity distributions

We define the observed intensity distribution at a given target voxel as simply the KDE of the intensities within a semilocal neighborhood surrounding the current voxel of interest on the target image. The observed intensity distribution is approximated using a similar approach to Eq. 1:

$$p_i^O\left(\gamma \right)=\frac{{\sum }_{i\in {\mathcal{N}}_i}K\left(\frac{\gamma -I_i}{h}\right)}{h\left|{\mathcal{N}}_i\right|},$$ (4)

where K and h are defined in the same way as Eqs. 1, 2, and $\left|{\mathcal{N}}_i\right|$ is the cardinality of the set ${\mathcal{N}}_i$ (i.e., the predefined semilocal neighborhood surrounding the current voxel of interest).

Estimation of the voxelwise out-of-atlas likelihood

We define the out-of-atlas likelihood as the voxelwise difference between the expected and the observed intensity distributions. There are several potential techniques that could be used to capture the difference between these two density functions [e.g., Kullback–Leibler (KL) divergence³¹]. Due to the proposed formulation of the expected/observed distributions, we found that the KL divergence did not provide an appropriate mechanism for capturing OOA likelihood. As seen in Eq. 1, the expected distribution can be viewed as a global measure of the intensity-label relationships within the atlases. Given its global nature, we would not expect the observed distribution to match exactly at a semilocal level. Rather, we would expect the observed distribution to be fully “covered” by the expected distribution. As a result, we found that the best way to capture the difference between these distributions is by integrating over the intensities by which $p_i^O\left(\gamma \right)$ is greater than $p_i^E\left(\gamma \right)$ (i.e., the intensities for which the observed probabilities are greater than the expected probabilities). Mathematically, this quantity is defined as

$$\begin{array}{ccc}\hfill p\left(T_i=1\right)& =& {\mathcal{L}}_i={\int }_{-\infty }^{+\infty }I\left(p_i^O\left(\gamma \right)>p_i^E\left(\gamma \right)\right)\hfill \\ & & \times \left[p_i^O\left(\gamma \right)-p_i^E\left(\gamma \right)\right]d\gamma \hfill \end{array}$$ (5)

where ${\mathcal{L}}_i$ represents the OOA likelihood at target voxel i, and I(·) is the indicator function. This formulation of the OOA likelihood has several benefits. First, it is guaranteed that the value of ${\mathcal{L}}_i\in [0,1]$ given that $p_i^O\left(\gamma \right)$ and $p_i^E\left(\gamma \right)$ are properly normalized density functions. Second, this formulation has an easily understood probabilistic interpretation where ${\mathcal{L}}_i=1$ indicates an out-of-atlas likelihood of unity, and ${\mathcal{L}}_i=0$ indicates an out-of-atlas likelihood of zero.

Model parameter initialization, and implementation details

There are two primary model parameters that need to set in order to use the OOA likelihood estimation framework: (1) the neighborhood structure, ${\mathcal{N}}_i$, and (2) the bandwidth for the KDE formulation. First, for all presented experiments we used an approximately 11 × 11 × 11 mm window centered at the target voxel of interest for all voxels within the neighborhood structure. For cases where this window size resulted in fractional number of voxels in a given direction, the number of voxels was rounded appropriately. It is important to note that, in general, large semilocal neighborhoods result in more accurate OOA likelihood estimations. However, as the neighborhood size increases, so does the computation time of the algorithm. Thus, we found that an 11 × 11 × 11 mm window was consistently large enough to decrease the effects of local noise, but still small enough to maintain a reasonable runtime. Second, unless otherwise noted, the bandwidth parameter, h, was set to 1.0. Note that this parameter is inherently related to the variance of the observed data, and, thus, a function of the intensity normalization process.

Additionally, one extremely important aspect of this algorithm is the way in which the multi-atlas segmentation estimate is acquired. For all presented experiments, all atlases were registered to the target image using a pairwise registration procedure (i.e., all atlases were independently registered to the target). After registration, the intensities between the target and the atlas images were normalized in a two-step process. First, both the target and the registered atlas images were normalized so that the intensities are distributed as a unit Gaussian distribution within the brain region (defined by the union of the nonbackground registered atlas labels). Second, a second order polynomial was fit to each atlas by finding a least squares solution for the polynomial coefficients that map the mean of each label on the target (via an initial majority vote) to the corresponding labels on the atlases. The registered atlases were then fused using nonlocal STAPLE (NLS).^{27, 28} For all presented experiments, NLS was initialized with performance parameters equal to 0.95 along the diagonal and randomly setting the off-diagonal elements to fulfill the required constraints. For all presented results, the voxelwise label prior was initialized using the probabilities from a “weak” log-odds majority vote (i.e., decay coefficient set to 0.5),¹⁴ the search neighborhood, ${\mathcal{N}}_s\left(i\right)$, was initialized to an 11 × 11 × 11 mm window centered at the target voxel of interest, and the patch neighborhood, ${\mathcal{N}}_p(·)$, was initialized to a 3 × 3 × 3 mm window. The values of the standard deviation parameters, σ_i and σ_d, were set to 0.1 and 3, respectively. Consensus voxels were ignored during the estimation process. Convergence of NLS was detected when the average change in the trace of the performance level parameters fell below 10⁻⁴. For a full derivation of NLS and additional details on NLS initialization, we refer the reader to Refs. ²⁷ and ²⁸.

Finally, there are a couple of important implementation details that need to be discussed. First, the OOA likelihood, ${\mathcal{L}}_i$, was only calculated on voxels for which the multi-atlas segmentation estimate was nonbackground. Background voxels were ignored because (1) as both of our empirical experiments are for whole-brain analysis, it is assumed that we are only interested in abnormalities that take place within the brain region and (2) it dramatically decreases the runtime of the algorithm. Second, a postprocessing step that decreased the potential edge effects on the image was performed. Due to the fact that we are ignoring background voxels, it is possible that undesired likelihood estimates could be achieved along the boundaries between background and nonbackground voxels. To alleviate this problem, we multiplied the final OOA likelihood estimate by an inverse log-odds estimate [decay coefficient set to 1.0 (Ref. ¹⁴)] of the background label (see Fig. 1 for a visual representation of this process). While this edge correction step limits the ability of the approach to detect accurate abnormalities along the edge of the brain, it increases the accuracy of the approach within the brain and limits the effects of minor boundary errors in the multi-atlas segmentation. If a desired application requires the inclusion of the boundary of the brain (or is outside the brain entirely) then this step would certainly not be desirable.

METHODS AND RESULTS

We present two starkly different whole-brain empirical experiments in order to assess the efficacy of the proposed OOA likelihood estimation framework. For our first experiment, we both quantitatively and qualitatively assess the ability of our framework to detect malignant gliomas in the human brain based on clinically acquired MRI data. Additionally, we provide insight into the sensitivity of the proposed framework with respect to the KDE bandwidth parameter and the accuracy of the multi-atlas segmentation estimate. For our second experiment, we provide a qualitative example for how this OOA model could be used to provide a quality control framework for acquired DTI images and demonstrate the type of imaging artifacts and quality control metrics that could be performed.

Multi-atlas data

The collection of whole-brain atlases used in the following experiments is a collection of 15 T1-weighted magnetic resonance (MR) images of the brain as part of the open access series of imaging studies (OASIS) (Ref. ³²) dataset. These data were expertly labeled courtesy of Neuromorphometrics, Inc. (Somerville, MA) and provided under a nondisclosure agreement. A refined dataset (using the OASIS brains and a subtly revised labeling protocol) has recently been made available as part of the MICCAI 2012 workshop on multi-atlas labeling. These data are available at the following URL: https://masi.vuse.vanderbilt.edu/workshop2012/ or directly from Neuromorphometrics. For each atlas, a collection of 26 labels (including background) were considered: ranging from large structures (e.g., cortical gray matter) to smaller deep brain structures. Note that all of the cortical surface labels were combined to form left and right cortical gray matter labels (see Ref. 28) for a description of the simplified label set). All images are 1 mm isotropic resolution.

Detection of malignant gliomas

Thirty preoperative gadolinium-enhanced T1-weighted brain MRI scans based on varied (but standard of care) imaging protocols with malignant gliomas were obtained in anonymous form under Institutional Review Board (IRB) approval. On average, the resolution of each of the patient image is 0.45 × 0.45 × 3 mm. All subjects exhibited high grade gliomas (WHO grade III) with an average tumor volume of 29.67 ± 20.18 cm³. The corresponding “ground truth” labels associated with each of the tumor regions were manually drawn by an experienced anatomist using the Medical Image Processing And Visualization software.³³

For each target image, all pairwise affine registrations between the 15 labeled atlases and the target image were performed using FLIRT (FMRIB, Oxford, UK). Note that nonrigid registration was not performed due to the highly variable imaging characteristics of the malignant gliomas on the target subjects. Nevertheless, due to relatively small tumor-to-brain size ratio, the global affine registration procedure consistently provided enough correspondence to result in acceptable multi-atlas segmentations. Using an implementation in C, the OOA likelihood estimation procedure took less than two hours for each target brain. We assess the quantitative accuracy of the proposed approach by analyzing the positive predictive value (PPV), negative predictive value (NPV), and the corresponding receiver operating characteristic (ROC) associated with each target image for varying threshold values of the estimated OOA likelihood. All quantitative results are presented in reference to the corresponding manual labels. Additionally, we present the sensitivity of the approach to the KDE bandwidth parameter, and various multi-atlas label fusion approaches.

Glioma detection results

The quantitative results (Fig. 2) demonstrate the ability of the proposed framework to detect large-scale abnormalities in the human brain. The proposed framework can consistently and reliably declare voxels to be cancerous in terms of increasing declaration threshold [Fig. 2a]. For a declaration threshold above approximately 0.7 the resulting PPV was equal to unity (i.e., all voxels declared to be OOA were cancerous voxels). To support these PPV values, the NPV values [Fig. 2b] show that, despite increasing the threshold, the negative predictive value remains over 0.97. The per-subject ROC curves [Fig. 2c] confirm that this performance is consistent across the target population with an average area under curve (AUC) value of greater than 0.95. Qualitative results (Fig. 3) support the quantitative accuracy. While the resulting likelihood estimates are far from perfect (e.g., “holes” in the likelihood estimates), it is evident that the proposed framework is consistently detecting the cancerous regions. The representative example in the fifth column represents the worst-case of the considered subjects, and it is shown that while none of the images has an OOA likelihood of greater than 0.6, the values greater 0.3 are outside of the “core” of the glioma. Note that this example is represented by the outlier case in Fig. 2c. Due to the known issues with strict ROC analysis,^{34, 35} we provide additional quantitative evaluation for the glioma detection (Table 1) in which we present the false negative rate (FNR), false positive rate (FPR), and dice similarity coefficient (DSC) (Ref. ³⁶) for declaration thresholds of 0.2 and 0.3 on the OOA likelihood estimates. Interestingly, despite the relatively small size of the gliomas, the FNR for both thresholds is consistently below 20% which is a strong indicator that we are largely capturing the extent of the tumor's core. Likewise, the FPR consistently remains below 10% which supports the qualitative results seen in Fig. 3. Finally, the mean DSC values for both thresholds are above 0.5. This distribution of DSC values is perhaps surprisingly high considering the fact that the proposed model is not a segmentation algorithm in a traditional sense as it makes no assumptions about tumor size, location, appearance, or morphology.

Figure 2.

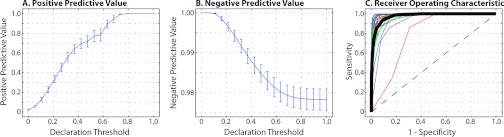
Quantitative results for the detection of malignant gliomas across 30 target subjects. The positive and negative predictive values for varying declaration thresholds can be seen in (a) and (b), respectively. The “declaration threshold” indicates the threshold probability for which we declare a voxel to be anomalous (in this case, a cancerous voxel). Finally, the per-subject ROC curves can be seen in (c) in the various thin lines, with the mean ROC curve across the subjects represented with the thick black line.

Figure 3.

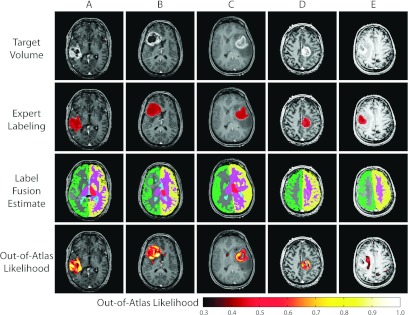
Qualitative results for the detection of malignant gliomas. Five representative examples are presented. For each example, the target volume, expert labeling, label fusion estimate, and the out-of-atlas likelihood are presented. The first four examples represent cases where the tumor region is correctly identified. The last example represents the outlier case [seen in Fig. 2c] in which the cancerous region was almost completely missed.

Table 1.

Quantitative glioma detection accuracy for varying OOA likelihood declaration thresholds.

Declaration threshold	False negative rate	False positive rate	Dice similarity coefficient
0.2	0.0670 ± 0.0230	0.0901 ± 0.0230	0.5266 ± 0.2094
0.3	0.1522 ± 0.0333	0.0417 ± 0.0310	0.5470 ± 0.2220

The OOA approach is not particularly sensitive to the bandwidth parameter (Fig. 4), with the optimal setting being approximately 1.0. Note that this value is not particularly surprising as the atlas and target images were normalized to a unit Gaussian distribution as part of the preprocessing steps. The qualitative results in Figs. 4b, 4g demonstrate the effect of the various bandwidth values. For values that are too small (e.g., 0.5) largely normal regions of the anatomy are declared OOA, while, for values that are too large (e.g., 1.5), the OOA likelihoods are not strict enough and fail to discover a large portion of the malignant glioma. Fusion of multiple atlases consistently outperforms using the best individual atlas (in terms of the mean ROC curve across the target population—Fig. 5). NLS (which utilizes the intensity information of the atlas–target relationships) consistently results in more accurate labels, and, thus, more accurate OOA likelihood estimates than traditional STAPLE and a majority vote fusion approaches. While a slight deviation from the focus of this manuscript, Fig. 5 demonstrates (1) the importance of using multiple atlases, and (2) the quality of the underlying OOA likelihood estimation is tightly coupled to the quality of the structural representation of the target.

Figure 4.

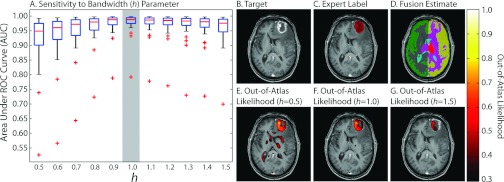
Sensitivity of the approach to the bandwidth parameter. The spread of AUC values across the 30 subjects for various bandwidth values is seen in (a). Note that the optimal value is approximately 1.0, which is not surprising given the intensity normalization procedure. (b)–(g) Qualitative results are presented with various out-of-atlas likelihood estimations for varying bandwidth values presented in (e)–(g).

Figure 5.

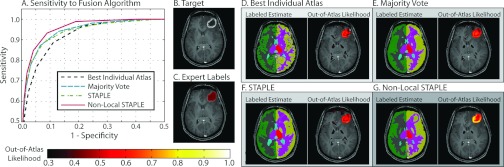
Sensitivity of the approach to the label fusion algorithm. A comparison is made between four different fusion approaches: (1) best individual atlas, (2) majority vote, (3) STAPLE, and (4) nonlocal STAPLE. Nonlocal STAPLE provides both quantitatively and qualitatively the best results due to the fact that it incorporates both label and intensity information into the fusion process. Note that all of the multi-atlas fusion approaches outperform the best individual atlas which highlights the importance of using multiple template images to account for atlas bias.

DTI quality control

For our second experiment, we demonstrate the ability of the proposed algorithm to be used in a DTI quality control framework. Here, a collection of 11 subjects consisting of both a T1-weighted image and corresponding DTI images were retrieved from an ongoing study in anonymous form under IRB approval. The T1-weighted images were oriented axially and consisted of 170 × 256 × 256 voxels at 1.0 mm isotropic resolution. The DTI images contained a single B₀ image and 92 diffusion weighted images, with all images consisting of 96 × 96 × 52 voxels and 2.5 mm isotropic resolution mm. Due to the difficulty in acquiring consistent and robust DTI images, several of the images within these datasets exhibit problems in terms of image quality (e.g., various degrees of aliasing and shading artifacts).

We employed a two-tier multi-atlas segmentation framework to obtain labels for the DTI images (Fig. 6). The 15 atlases were registered to the T1-weighted subjects in a pairwise fashion using the SyN nonrigid registration algorithm³⁷ and the corresponding label observations were fused using NLS. Next, the T1-weighted labels were then transferred to the corresponding B₀ image using an intrasubject rigid registration. Finally, each of the diffusion weighted images was rigidly registered to their corresponding B₀ image to account for patient movement and to obtain consistent labels for all of the images within each DTI dataset. To assess DTI quality, five of the resulting DTI images were chosen as “atlases” so that the OOA likelihood estimation framework could be applied to the remaining six subjects. Note that the B₀ images were normalized to one another using the previously described intensity normalization process and each of the diffusion weighted images were normalized to their corresponding B₀ images in order to obtain consistent intensity values across subjects. For all presented results, the OOA likelihood estimation was completed in less than one hour.

Figure 6.

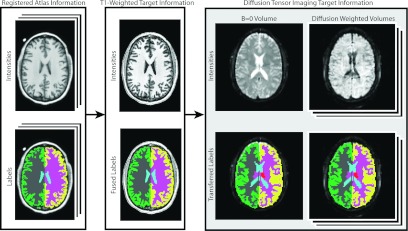
Flowchart demonstrating the multi-atlas labeling process for the DTI study. First, the provided atlases are used to label each subject's T1-weighted image. Next, this label information is transferred to all of the DTI datasets via an intrasubject rigid registration. Note that all of the diffusion weighted volumes were rigidly registered to their associated B₀ volume to account for patient movement.

DTI results

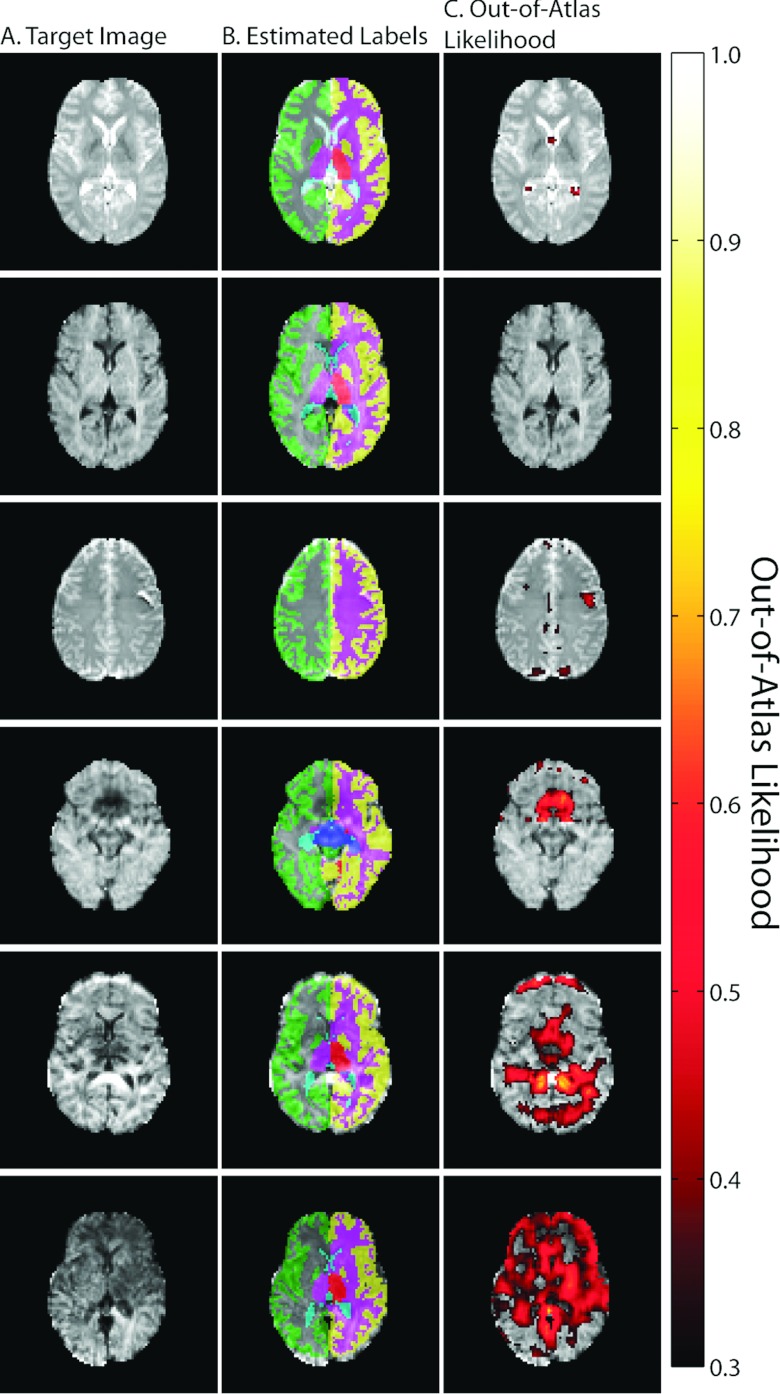
Qualitative results for this DTI quality control experiment are presented in Fig. 7. Here, we show example slices for the six subjects that exhibit varying degrees of image quality issues. The first two examples (the top two rows) represent well controlled datasets and this is supported by the lack of any OOA likelihoods greater than 0.3. The example in the third row represents a B₀ image that exhibits an aliasing issue. Here, the OOA likelihood estimate catches this aliasing issue and indicates this anomalous behavior in the appropriate image location. The final three exemplars (the bottom three rows) represent diffusion weighted images that exhibit varying degrees of aliasing and shading artifacts. For example, the example in the bottom row represents an example that has severe shading artifacts across more than half of the image. The proposed algorithm clearly detects this large-scale issue and provides consistently high OOA likelihoods across the observed slice.

Figure 7.

Qualitative results for the quality control framework for DTI images. Six representative examples are presented demonstrating the gamut of potential image qualities in the provided dataset. The first two examples (top two rows) represent examples where no abnormalities are present and the out-of-atlas likelihood estimate supports this observation. The final four examples demonstrate images with varying degrees of aliasing and shading artifacts, and the out-of-atlas likelihood estimate consistently detects and localizes these image quality issues.

While the presented results represent a purely qualitative assessment of DTI quality control, the proposed framework presents numerous opportunities for large-scale DTI quality control—a subject of increasing prevalence and importance.^{38, 39, 40} For example, if the OOA likelihoods are aggregated over subjects/diffusion weighted volumes, one could quantify the OOA likelihood for a given subject/image for fully automated quality control. Additionally, due to the huge amount of data within a single DTI dataset, the proposed framework could provide a mechanism for localizing the regions/slices of high artifact likelihood. This could dramatically lessen the need for large-scale manual inspection and provide a mechanism for quickly quantifying quality control metrics within an existing DTI quality control framework. While further validation is certainly warranted (e.g., using the existing quality control metrics⁴¹), the results in Fig. 7 indicate that the proposed general OOA likelihood estimation framework provides a promising avenue of continuing research.

DISCUSSION

The proposed OOA framework extends the multi-atlas labeling paradigm to be sensitive to abnormalities present in the medical images. Previous work on the problem of abnormality detection has primarily relied on a single atlas (or template) (Refs. ¹ and ⁶) and, as a result, has been largely dependent on highly representative atlas characteristics (e.g., intensity/morphological properties, differences in contrast enhancement). Moreover, previous abnormality detection algorithms have been highly tuned for specific applications (e.g., brain tumor segmentation,^{1, 2, 3, 6} lung nodule detection, and⁴ intestinal abnormalities⁵). The proposed method provides a fully general framework that (1) uses multiple normal atlases to limit the inherent bias of using a single atlas and avoid the need for nonrigid registration, and (2) can be used in a large number of potential applications.

Despite the promise of the OOA likelihood estimation framework, there are limitations to the proposed approach. First, we use a collection of normal (nongadolinium enhanced) T1-weighted atlases and use them to assess images that were acquired using clinical imaging protocols (e.g., differing imaging sequence). As a result, the ability to intensity normalize these images is limited and we are forced to limit ourselves to applications where the intensity profile of the desired abnormality is dramatically different than normal anatomy (e.g., malignant gliomas). The use of the proposed framework for the detection of more subtle anatomical pathologies would be inherently limited unless the atlases were constructed using the appropriate imaging characteristics. Additionally, we used a global intensity normalization procedure that, for the provided examples, has consistently resulted in robust normalized intensities. However, if (1) the size of the tumor region is particularly large, or (2) the contrast enhancement results in highly nonlinear mapping of the image intensities, the considered intensity normalization procedure could result in undesired intensity mappings. Thus, for more complicated OOA likelihood estimation procedures (e.g., intermodality modeling) different, less intensity-dependent techniques may be desirable to calculate the difference between the expected and observed distributions (e.g., correlation coefficient, mutual information).

Along the same lines, the proposed framework is limited in its ability to detect anomalies that have similar intensity profiles to normal anatomy. For example, differentiating between areas with edema and normal gray matter (e.g., Fig. 3) represents a limitation within the proposed framework as the edema regions “look like” normal gray matter from an intensity perspective. Thus, incorporation of more sophisticated comparison techniques (e.g., local difference estimation, entropy of the joint atlas-target histogram) and/or feature vectors would be a promising area of investigation. Direct modeling of texture and shape characteristics into the OOA model, for example, could improve the potential applications by which the model could be applied. Additionally, direct incorporation of label constraints (e.g., topology, symmetry across the cerebral hemispheres) could enable the OOA likelihood estimation framework to use both intensity and label information simultaneously. Regardless of the approach, however, the proposed framework provides a natural mechanism for estimating local OOA likelihoods by utilizing robust multi-atlas segmentations.

In conclusion, the out-of-atlas likelihood estimation framework shows great promise for robust and rapid identification of brain abnormalities and imaging artifacts. Using only weak dependencies on anomaly morphometry and appearance, we demonstrate the ability to (1) detect malignant gliomas on T1-weighted images and (2) identify quality control issues for DTI images. We envision that this approach would allow for application-specific algorithms to focus directly on regions of high OOA likelihood, which would (1) reduce the need for human intervention, and (2) reduce the propensity for false positives. Alternatively, this technique may allow for algorithms to focus on regions of relatively normal anatomy to ascertain image quality or model/adapt to image appearance characteristics.