Normalization is a general neural mechanism for context-dependent decision making

Abstract

Understanding the neural code is critical to linking brain and behavior. In sensory systems, divisive normalization seems to be a canonical neural computation, observed in areas ranging from retina to cortex and mediating processes including contrast adaptation, surround suppression, visual attention, and multisensory integration. Recent electrophysiological studies have extended these insights beyond the sensory domain, demonstrating an analogous algorithm for the value signals that guide decision making, but the effects of normalization on choice behavior are unknown. Here, we show that choice models using normalization generate significant (and classically irrational) choice phenomena driven by either the value or number of alternative options. In value-guided choice experiments, both monkey and human choosers show novel context-dependent behavior consistent with normalization. These findings suggest that the neural mechanism of value coding critically influences stochastic choice behavior and provide a generalizable quantitative framework for examining context effects in decision making.

A fundamental question in neuroscience is how the brain represents behaviorally relevant variables. Neural coding is governed by a small number of canonical computations implemented in diverse circuits and mechanisms, a prominent example being divisive normalization, in which the initial input-driven activity of a neuron is divided by the summed activity of a large pool of neighboring neurons. Originally proposed to explain nonlinear responses in primary visual cortex (1), divisive normalization has been widely observed in sensory systems and characterizes responses including contrast gain control in the retina and thalamus (2, 3), surround suppression in the middle temporal area (4, 5), ventral stream responses to multiple objects (6), and gain control in auditory cortex (7). Normalization also explains neural activity underlying higher-order processes such as multisensory integration (8) and visual attention (9). This ubiquity may reflect the role of normalization in generating normative coding efficiency via processes such as gain control, feature invariance, and redundancy reduction (10–12).

Recent neurophysiological evidence shows that such normalization processes extend beyond sensory areas to higher-order cortical areas involved in decision making. In parietal and premotor cortex, neurons specifying individual actions are strongly modulated by the value of those actions (13–16). Importantly, this value representation is encoded in a normalized form: Firing rates are increased by increases in the value of the represented action and suppressed by increases in the value of alternative actions (17–19). Such normalization, however, introduces an inherent context dependence in neural coding. In the visual system, normalization underlies contextual modulation of activity by extrareceptive field stimuli, for example surround suppression in visual cortical neurons (12, 20). In decision-related areas, normalization produces an analogous context dependence, where the neural representation of the value of an option is explicitly dependent on the value of other available alternatives. Although the nature of value representation is closely tied to the decision process, the behavioral implications of value normalization are unknown.

Here we develop a model of decision making derived directly from neurophysiologically observed value normalization (17) and show that it predicts a unique form of context-dependent choice behavior. A fundamental assumption of many traditional rational theories of choice is that the context-independent value of options guides decision making (21, 22); how a chooser decides between any two options should not depend on the number or quality of other options, a property known as independence of irrelevant alternatives, or IIA (23). However, at an empirical level it is known that context can profoundly affect choice behavior in species ranging from insects to birds to humans (24–28). Various explanations have been proposed for specific context effects, but to date no general model rooted in specific physiological data exists for context-dependent choice.

We show here that the normalization model predicts significant context-dependent rationality violations in computational simulations, driven by normalized scaling of value-coding neural activity. These simulations provide a quantitative examination of qualitative predictions about the effects of normalization on decision making (17, 29). Furthermore, we examine human and monkey behavior under conditions in which the model specifically predicts context-driven distortions of choice behavior. These findings demonstrate a direct link between divisive normalization and behavior and suggest that normalization is a fundamental feature of cortical computation beyond the sensory domain.

Results

Forms of Value Representation.

Value-related neural activity has been observed in multiple brain areas underlying decision making, for example in areas linked to action selection. Such value coding is presumably critical to the decision process, providing the appropriate decision values for action selection. Many initial studies have interpreted this activity in terms of an absolute value code, for example:

where the mean firing rate representing the value of option i is postulated to be a function of that option value alone. However, recent experiments suggest that these brain areas, including portions of premotor and parietal cortex, use a relative value code (17–19). We have recently demonstrated that relative value representation in parietal cortex is specifically implemented by the classic divisive normalization algorithm (17), in which each option value is transformed into a mean firing rate:

where V_i is the value of the option under consideration, the index j is summed over all available options, and the parameters K, σ_H, and w represent gain, semisaturation, and weight terms, respectively. The critical feature of this representation is the presence of all option values in the denominator, which mediates the relative nature of the value coding.

Model of Normalized Value Coding and Choice.

A fundamental prediction of many rational theories of choice is that the relative preference of a chooser between any two options should be unaffected by choice context. A prominent example is the choice axiom of Luce, an instantiation of IIA (23). This requires that the ratio of stochastic choice probabilities for two given, or target, options (p₁/p₂) should be independent of the presence or value of a third, or distracter, option. Our simulations reveal, however, that the combination of normalized value coding and variability alone produces context-dependent choice behavior.

We modeled stochastic choice behavior with a simple algorithmic simulation comprising three components: value representation to transform each option value into a firing rate, stochastic variability to model noise in the coding process, and option selection to implement choice (Fig. 1A). For each option i, a mean firing rate μ_i was calculated from the option value and the values of other alternatives using Eq. 2, thus implementing normalization. Note that because value is quantified in arbitrary units, the gain term K was set to reproduce realistic firing rates [∼75 spikes per second (sp/s)]. For simplicity, the semisaturation and weight terms were set to standard fixed values (Materials and Methods).

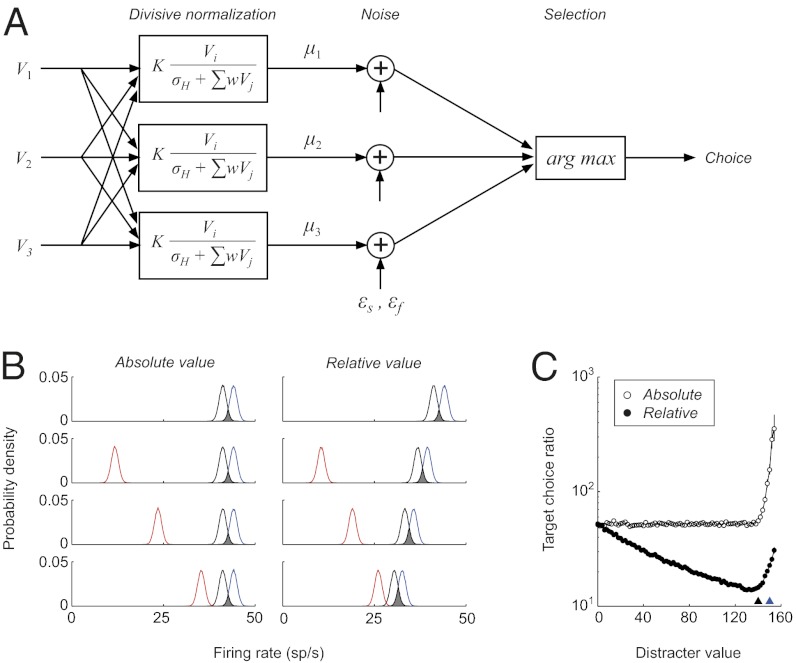
Fig. 1.

Model of normalized value coding in stochastic choice. (A) Structure of the trinary-choice model. Value inputs (V₁,V₂, and V₃) were converted into mean firing rates (μ) representing each choice option and variability was introduced as noise terms added to the mean firing rates. In a given trial, the option with the maximum firing rate was designated as the chosen option. (B) Example difference between absolute and relative value-coding representations. Each curve shows the probability density function of the neural activity associated with one of three choice options. Under relative value coding, increasing distracter value (red) reduces the distance between target option distributions and decreases the relative choice ratio for the better target. Relative value parameter settings: K = 100, σ_H = 50, w = 1, σ_fixed = 1, S = 0. (C) Two forms of context dependence in stochastic choice behavior. Points show relative choice ratio between two targets (V₁ = 150 and V₂ = 140, arbitrary units) as a function of distracter value under absolute or relative value coding (error bars, bootstrap 95% CI).

To introduce structured trial-to-trial variability into the model, we added two forms of noise to each mean firing rate: a fixed noise term (ε_f), drawn from a zero-mean Gaussian distribution with fixed variance σ²_fixed, and a mean-scaled noise term (ε_s), a class of noise commonly observed in cortical neurons that increases as mean firing rate increases (30, 31). Mean-scaled noise was drawn from a zero-mean Gaussian distribution with variance Sμ_i, where the parameter S controls the degree of mean scaling. Both types of noise were included to avoid assumptions about the specific form of variability; the magnitude of each term was varied independently to examine their relative contribution to model behavior (SI Materials and Methods). In each simulated trial, option selection was implemented by simply choosing the option with the highest postnoise activity in that trial. This procedure produces stochastic choice governed by the values of the offered options and the noise terms.

To demonstrate the critical nature of value coding representations, we show in Fig. 1B example choice simulations under either absolute or normalized value coding. We use the term “distracter” to denote a low-valued alternative that is eligible for selection; the critical issue is how distracter value affects relative target choice. In a traditional absolute value representation, relative preference between two fixed target options (V₁ = 150 and V₂ = 140, arbitrary units) remains constant as distracter value increases (V₃ = 0, p₁/p₂ = 53.3, bootstrap confidence interval [CI], [51.2, 55.8]; V₃ = 120, p₁/p₂ = 52.9, bootstrap CI [50.5, 55.3]). In a relative value representation, however, the mean firing rate of each option depends on the values of the other options. As distracter value (red) increases, divisive scaling decreases the distance between the target option firing rates (black and blue). The resulting increase in overlap between firing rate distributions decreases the relative preference of the chooser for the better target option (V₃ = 0, p₁/p₂ = 51.7, bootstrap CI [49.3, 54.0]; V₃ = 120, p₁/p₂ = 15.8, bootstrap CI [15.3, 16.2]).

Examined as a function of distracter value, normalized value coding produces a consistent decrease in relative target choice (p₁/p₂) that is absent under absolute value coding (Fig. 1C). Notably, a second type of context dependence emerges in both value representations when distracter values approach the target values (black and blue triangles): Increasing the value of the distracter increases the relative preference of the model for the better target option. This effect is driven by choices captured by the distracter option, which selectively competes with the lower-valued target option. Thus, under normalization context dependence is biphasic: Effective choice consistently decreases until distracter competition counteracts the effect of divisive scaling and offsets the normalization-induced decrease in relative target preference.

Context Dependence in Simulated Choice Behavior.

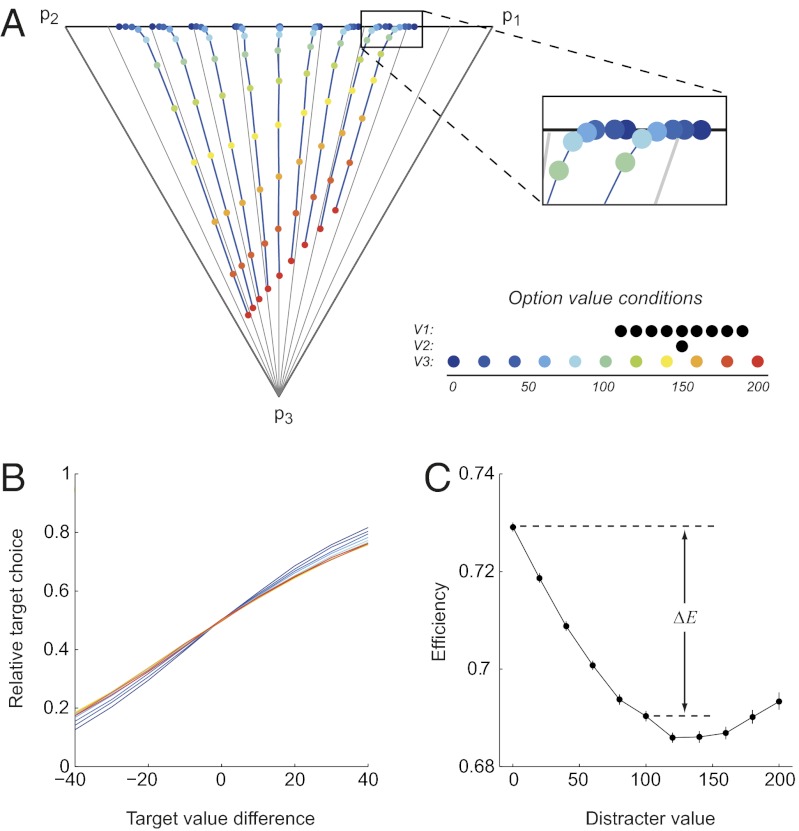
To examine trinary-choice behavior in detail, we simulated choice while varying both target value differences and distracter value under a range of noise parameters. Fig. 2A shows example data for a specific set of noise parameters (σ_fixed = 8, S = 0). In this simplex plot, each point represents how the average choice behavior for a given set of value conditions is divided between the three options, color-coded by distracter value (probability for a given option increases linearly with distance to its vertex). Notably, choice behavior as a function of distracter value for a given pair of target values (blue lines) differs markedly from the constant relative preference assumption (straight gray lines) of rational choice theory (23).

Fig. 2.

Relative value coding generates context dependence in model choice behavior. (A) Example trinary-choice behavior. Each point in the simplex plot represents average choice behavior for a given triplet of value conditions, color-coded by distracter value (V₃). The choice probability of a given option is represented by the linear distance between its associated vertex and the opposite edge; for example, a point at the bottom vertex would represent 100% choice of option 3 (p₁ = 0, p₂ = 0, p₃ = 1) and a point in the midpoint of the top edge would represent 0% choice of option 3 (p₁ = 0.5, p₂ = 0.5, p₃ = 0). The legend shows the different value conditions, with each trial using a single value triplet (V₁, V₂, and V₃). Choice behavior under fixed target-value pairs (V₁ and V₂) are connected with blue lines and deviate markedly from the linear constant relative ratio lines predicted by rational-choice theory (gray lines). Example simulation parameters: K = 100, σ_H = 50, w = 1, σ_fixed = 8, S = 0. (B) Context-dependent relative target choice functions. Lines are color-coded by distracter value, as in A. (C) Relative target choice efficiency plotted as a function of distracter value. Efficiency is defined as the average choice probability for the better target across all target-value differences, a quantity that varies inversely with stochasticity. To quantify the normalization-driven context dependence, we measured the decrement in efficiency (−ΔE) between V₃ = 0 and V₃ = 100.

Fig. 2B summarizes this data as relative choice probabilities between the two targets, segregated by distracter value. In contrast to the constancy of relative preference predicted by IIA, these stochastic choice curves are shallower at higher distracter values. To quantify this stochasticity, we computed for each choice function the average efficiency (E), which ranges from 0.5 (random chooser) to 1 (perfect chooser) and varies inversely with stochasticity. Consistent with the previous example, the effect of distracter value on efficiency is biphasic (Fig. 2C). Importantly, the primary normalization-driven decrease in choice efficiency persists across a broad range of noise levels (SI Results and Fig. S1) and normalization parameters (SI Results and Fig. S2).

Because normalized value coding incorporates the value of all available alternatives in the suppressive term, this mechanism should also generalize to set-size context effects. In simulations with target options and a varying number of low-valued distracters, we found that relative choice behavior between targets consistently decreases as the number of distracters increases (Fig. S3). Notably, set-size-driven context effects are larger than those seen in trinary choice because larger numbers of small-valued distracters increase the overall divisive scaling term without directly competing for selection.

Context Dependence in Monkey Choice Behavior.

To test the predictions of the normalization model in empirical choice behavior, we examined monkey decision making in a simple trinary-choice task. Sessions were conducted in a block design; in each block, monkeys first learned the value associated with each of three different locations presented individually in instructed trials. In subsequent choice trials, the animals were presented with cues in the three locations simultaneously and were free to choose their preferred option. Both the target configuration and the value assignments were chosen randomly for each block (two monkeys, 598 blocks). Consistent with value-guided decision making, the monkeys distributed their choices according to the reward magnitudes (p_high-target = 69.3%, p_low-target = 27.0%, and p_distracter = 3.7%, excluding trials where the two targets were of equal value).

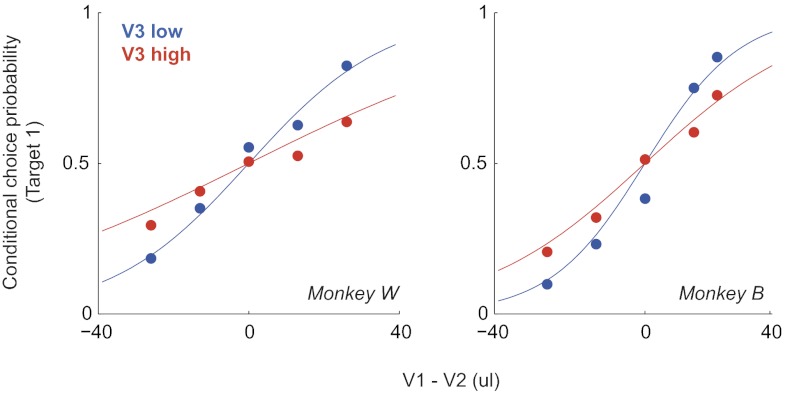
To quantify context dependence, we examined choice behavior between two high-value targets at two different distracter values (Fig. 3). Strong value dependence was observed in the relative choice behavior between targets, as evident in logistic functions fit to the choice data and the difference between the values of the two targets (logistic slope parameters: Monkey W, α = 0.039, 95% CI [0.036 0.043]; Monkey B, α = 0.061, 95% CI [0.058 0.064]). More importantly, although the distracter was almost never chosen, its value had a strong effect on choice. In both monkeys, relative choice curves were steeper in the presence of a low- (Monkey W, α = 0.055, 95% CI [0.050 0.060]; Monkey B, α = 0.080, 95% CI [0.074 0.085]) versus a high-value distracter (Monkey W, α = 0.025, 95% CI [0.020 0.029]; Monkey B, α = 0.046, 95% CI [0.042 0.050]). Thus, the magnitude of a low-value distracter, an option that was essentially never chosen, nevertheless profoundly affects the efficiency of choice behavior. This effect resulted in a significant decrement in reward outcome: On average, at the largest value differences, the rate of correct decisions decreased from 84.4 to 69.1% (pooled data; P < < 0.001, binomial proportion test).

Fig. 3.

Context dependence in monkey value-guided choice. Context-dependent behavior in a trinary-choice task. Points show average relative choice behavior between the two high-value target options in the presence of a low- (blue) or high- (red) value distracter. Curves plot logistic functions fit to the conditional choice data (either target chosen).

Context Dependence in Human Choice Behavior.

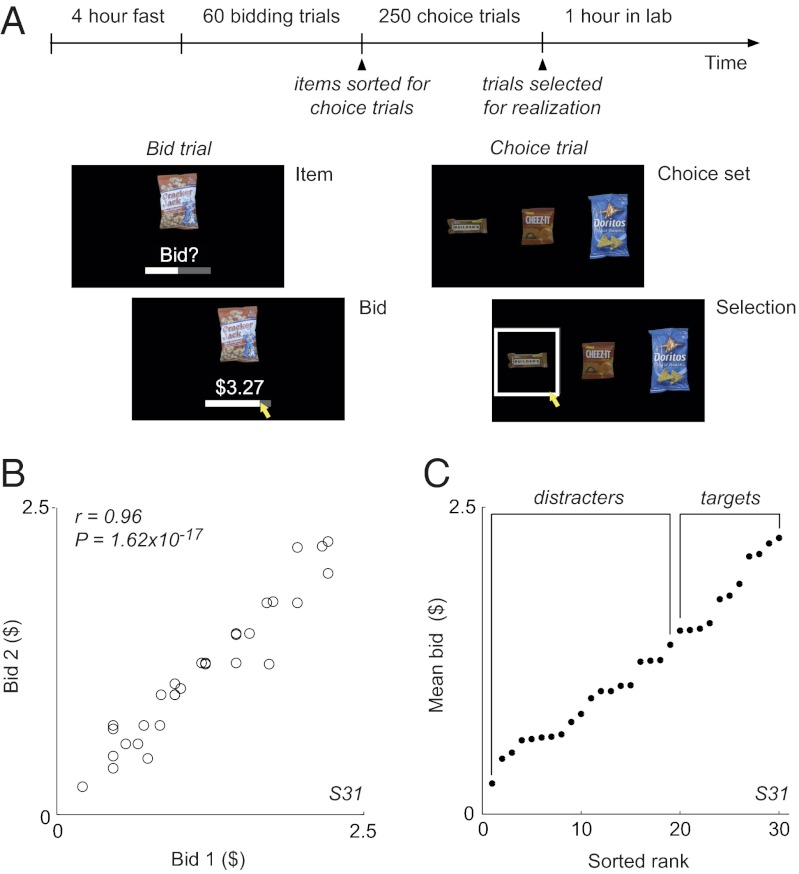
To date, examples of context dependence in the human literature primarily involve higher-order complexities in the decision process, such as the relative weighting of different option attributes. However, the normalization model suggests that context dependence can arise out of the fundamental coding mechanism of valuation itself. To test this hypothesis, we examined choice behavior in human subjects performing a two-stage valuation and choice task involving common snack-food items (Fig. 4A). In each bid trial, subjects viewed a single item and reported their maximum willingness to pay ($0–$4). If implemented, realization of one of these trials was conducted at the end of the experiment via an auction procedure designed to elicit subjects’ true valuations (32) (Becker–DeGroot–Marschak auction, SI Materials and Methods). Subjects completed 60 bid trials with two repetitions for each of 30 items. Consistent with an elicitation of stable underlying valuations, individual item bids were strongly correlated across repetitions, as shown for an example subject (Fig. 4B; r = 0.96, P = 1.62 × 10⁻¹⁷) and quantified across the population (mean correlation r = 0.87; P = 3.13 × 10⁻³⁶, t test).

Fig. 4.

Human choice behavior experiment. (A) Trinary-choice task. In each bid trial, subjects indicated the maximum price they would pay for a snack-food item. Subjects completed two bid trials for each of 30 food items. In each choice trial, subjects were presented with three food items and selected the one they most preferred. (B) Example bid data. Consistent with a stable valuation, subjects’ bids for individual items were highly correlated across repetitions (example subject: r = 0.96, P = 1.62 × 10⁻¹⁷; population: mean r = 0.87, P = 3.31 × 10⁻³⁶, t test). (C) Example bid distribution and choice-set construction. The 10 highest-valued items were assigned to be target items; 10 distracter items were sampled evenly from the 20 lowest-valued items.

We examined in subsequent choice trials how trinary-choice behavior depended on distracter valuations. For each subject, we selected a subset of 10 high-value items and 10 low-value items based on their individual mean valuations (targets and distracters, respectively; Fig. 4C). We then constructed 250 different trinary-choice sets pairing a range of single distracters with different target pairs, allowing us to examine how distracter value modulates choice efficiency. Consistent with value-guided decision making, overall choice behavior was governed by the values extracted from bid trials (population choice probabilities: high-value target 60.5%, low-value target 33.3%, and distracter 6.2%).

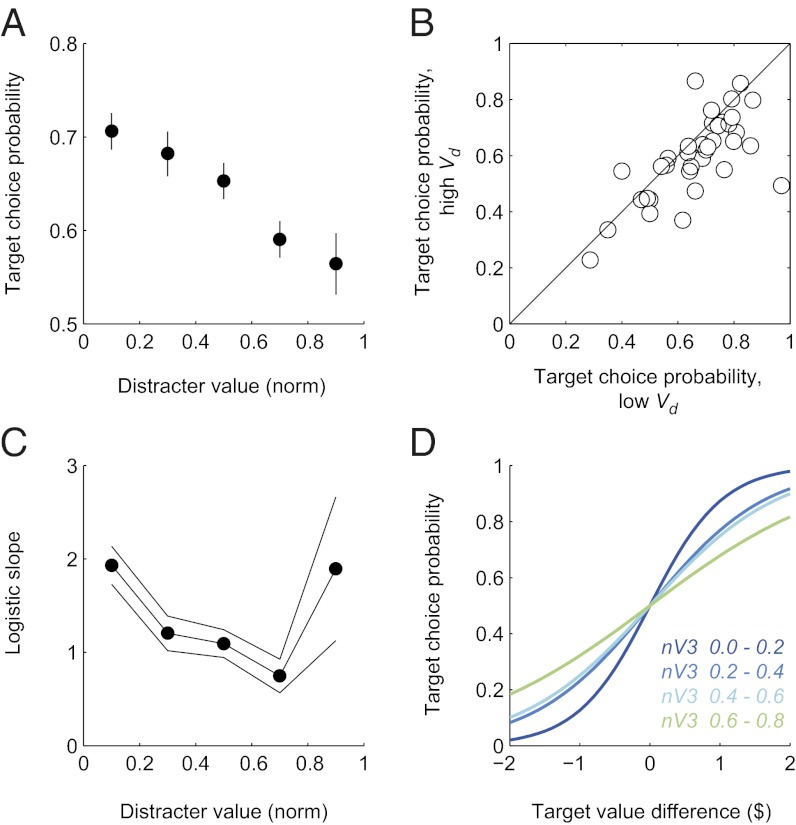
To examine context dependence across the subject population, we normalized distracter value relative to the target pair with a metric that ranges from 0 (small value) to 1 (large value). As predicted by the normalization model, relative choice of the better target consistently decreased as distracter value increased (Fig. 5A), with strong correlation between conditional choice probability and normalized distracter value (r = −0.80, P = 0.006). This effect exists across the population of subjects, as was evident when we examined individual conditional target choice under conditions of low versus high distracter value (Fig. 5B; mean difference in target choice 0.064, P = 0.0019, t test).

Fig. 5.

Context dependence in human value-guided choice. (A) Choice behavior varies with distracter value. Points show relative choice probability of the higher-value target as a function of normalized distracter value averaged across the subject population (error bars, binomial CI). Target choice probability is significantly dependent on distracter value (r = −0.80, P = 0.006). (B) Individual subject choice behavior depends on distracter value. Each point shows the average relative choice of the better target option in high- versus low-distracter-value trials. Individual subjects’ choices were classified as high or low according to normalized distracter value. (C) Biphasic effect on choice efficiency. Points show the population logistic function slope parameter as a function of normalized distracter value (lines, 95% CI of the parameter estimation). (D) Context-dependent choice curves. Curves show logistic functions fit to the population data, color-coded by distracter value for the range of decreasing efficiency (0–0.8). As distracter value initially increases from low magnitudes, the choice functions grow shallower and choice grows increasingly inefficient.

To examine this effect parametrically, we performed a generalized linear regression of the form

quantifying the effect of the target values (V₁ and V₂) and normalized distracter value (normV₃) on conditional choice behavior across the aggregate population data. This analysis showed that choice of the better target depended on the values of the target options, consistent with value-guided decision making (β₁ = 0.88, P = 1.2 × 10⁻⁵²; β₂ = −1.01, P = 4.5 × 10⁻⁵⁸); the larger the difference in the value of the two targets, the more likely the subject was to choose the better target. More importantly, the likelihood that a subject chose the best target depended significantly on the value of the distracter, with target choice decreasing as distracter value increased (β₃ = −0.42, P = 2.1 × 10⁻⁷).

In addition to the general decrease in choice efficiency with rising distracter value, model simulations predicted a biphasic response at high distracter value. To examine this in detail, we fit logistic choice functions to the population data, segregated by normalized distracter value. This analysis revealed a clear biphasic profile in empirical context dependence (Fig. 5C): The logistic slope parameter consistently decreased for the majority of the range of distracter values (normV₃ 0–0.8) but increased as distracter values approached the value of the target pairs (normV₃ 0.8–1.0). Fig. 5D plots the effective choice functions corresponding to these fits (distracter value range 0.0–0.8 shown for clarity). We confirmed this biphasic effect by repeating the generalized linear regression on low- versus high-valued distracters: Low distracter values (normV₃ < 0.8) decreased the efficiency of target choice (β₃ = −0.54, P = 1.2 × 10⁻⁸), whereas sufficiently high distracter values (normV₃ > 0.8) had the opposite effect (β₃ = 0.42, P = 0.001). In simulation, this increase in relative choice at high distracters is driven by the selective competition between the distracter and lower-valued target; consistent with this mechanism, distracters are chosen much more frequently when distracter value increases choice inefficiency (normV₃ < 0.8: 4.3%; normV₃ > 0.8: 20.0%).

Discussion

Context-dependent choice behavior is of particular interest in economics because it violates one of the fundamental assumptions of many rational-choice theories, namely, that decisions reflect absolute valuations assigned to individual options. The predominant examples of context-dependent choice behavior involve attribute-based decisions, where the exact nature of the effect depends on the relative position of the options in multidimensional attribute space (26, 27, 33). Although various mechanisms have been proposed for such effects (34, 35), these models typically rely on higher cognitive processes, such as attentional switching between dimensions or differential weighting of attributes, as explanations. Our results provide a different mechanism for context dependence that arises from the fundamental nature of value representation in the neural circuits implementing the decision process. We have not attempted to specifically address multiattribute context phenomena here; such effects likely involve higher-order processing in areas such as prefrontal cortex and are beyond the current scope of our model. However, we note that related normalization processes in circuits coding for specific attributes may play an important role (36).

These findings demonstrate context-dependent choice driven by the values of the choice options alone. Moreover, the biphasic nature of the contextual influence argues for careful consideration of the underlying valuations when examining such effects: At low values, distracters decrease target choice efficiency via normalization; however, at higher values, distracters increase efficiency by being selected, reducing or even reversing the overall effect. In addition to trinary-choice effects, the normalization model predicts a decrement in choice inefficiency with increasing set size, a well-documented phenomenon in behavioral experiments and empirical data (37–39). Although limitations in information processing capacity and potential postchoice dissatisfaction may be involved, the normalization model predicts that set-size effects can arise directly from the nature of the neural representation of value.

Our results suggest that normalized value coding in decision circuits has a direct influence on choice behavior. In the lateral intraparietal area (LIP), neurons represent saccade value in a normalized form, relative to the values of all available saccades (17, 19). Reach-related neurons in dorsal premotor cortex also encode a relative value representation across potential actions (18), suggesting a similar value coding in other effector systems. Moreover, normalization across option values is consistent with a number of other previous neurophysiological studies. In perceptual decision-making tasks, the activity of LIP neurons covaries with the accumulated sensory evidence (40, 41) and has been proposed to reflect the logarithm of the likelihood ratio (logLR) favoring a particular outcome (42). With fixed rewards, relative value varies monotonically with logLR, suggesting that probabilistic information can be implemented via a divisive normalization computation. Consistent with the predicted effect of set size, LIP neurons recorded during perceptual decision making show lower activity during target presentation and motion viewing with four targets versus two targets (43); a similar mechanism may underlie the effect of choice set size and target uncertainty in the superior colliculus (44, 45).

In our model, context dependence arises from two critical elements: normalization and stochasticity in value representation. Normalization during decision making drives a rescaling of neural activity driven by the value of all choice options, implementing a relative value code. Although we included a semisaturation term in the normalization algorithm to match neurophysiological observations, this parameter is not required for context dependence (SI Results); the crucial term is the value summation in the normalization denominator. In addition to normalization to the immediate choice set, the brain also displays normalization to the recent history of rewards (46–48). In theory, temporal normalization can also generate context dependence (29), but the consequences of such adaptation in value coding and potential interaction with choice circuit normalization remain currently unknown. Importantly, the normalization model provides a testable hypothesis of causality: Disrupting value normalization should reduce the magnitude of context-dependent choice inefficiency. Although the biophysical basis of value normalization has not been identified, potential candidate mechanisms such as feedforward or feedback inhibition offer attractive targets for further research. In our simulations, noise is also required for context dependence, mediating changing stochasticity as firing rates are scaled by normalization; notably, significant effects were observed with both rate-dependent and fixed variability. Given the importance of neural variability in our model and evidence that such variability can be strongly modulated (49), examining the nature of noisy neural codes in decision making is an important area for future work.

In summary, we report here a class of anomalous choice behavior predicted by a normalization-based decision model and confirmed in empirical choice data. This neural choice model derived from physiological measurements makes validated economic predictions, including context dependence independent of attribute-based choice and contextual set-size effects. These findings suggest that the divisive scaling documented in value coding plays a critical functional role in decision making and underscore the importance of incorporating normalization processes in the interpretation of decision-making activity and behavior.

Materials and Methods

Model.

To obtain divisively normalized relative value coding, the mean firing rate μ_i representing each option was calculated from Eq. 2. This fully parameterized relative value code replicates the normalized functional form observed in parietal recordings (17) but reduces with the appropriate parameter settings to an absolute value code (σ_H = 1, w = 0). Note that the full neurophysiological model originally included a baseline parameter to accommodate situations with no target in the receptive field; because this parameter is empirically small and does not apply to the choice situations examined here, it has been omitted for the sake of simplicity. For the primary analyses using normalized value codes, K was set to produce firing rates of 75 sp/s with a single option choice set; using different gain terms results in qualitatively similar results. The semisaturation constant σ_H was set to a fixed value of 50 for the primary simulations, but the specific effects of varying this parameter was explored in further simulations.

To introduce variability, two sources of noise were added independently to each mean firing rate to obtain an option value for each alternative:

ε_f implements fixed noise and is drawn from a zero-mean normal distribution with a fixed variance σ²_fixed, independent of mean firing rate. ε_s implements mean-scaled noise and is drawn from a zero-mean normal distribution with a variance that is linearly dependent on the mean firing rate, where the parameter S controls how the variance scales with the mean. The effects of noise on choice behavior were examined by independently varying the parameters σ²_fixed and S.

Simulation Conditions and Analysis.

To examine the effect of distracter value, we simulated trinary-choice behavior between two target items (V₁ = {100, 110, …, 200} and V₂ = 150) and a distracter item (V₃ = {0, 20, …, 200}). In these simulations, value is dimensionless and the gain term K controls the magnitude of the mean firing rates. For the relative value simulations, K was set to 100 sp/s to produce realistic mean firing rates.

Relative choice behavior was quantified as the conditional choice probability of option 1 over option 2 when either is chosen:

where c₁ and c₂ indicate the absolute number of choices for options 1 and 2, respectively. To quantify choice stochasticity, we calculated the average efficiency (E) for each choice function over all V₁ and V₂ options, where

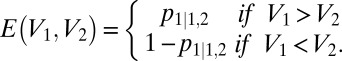Note that E varies inversely with stochasticity and ranges from 0.5 (random chooser) to 1 (perfect chooser) and ignores conditions where V₁ = V₂. To quantify normalization-driven changes in context dependence, we calculated the magnitude of the decrement in average efficiency (−∆E) between low- (V₃ = 0) and high- (V₃ = 100) valued distracters.

Human Choice Behavior Experiment.

Forty healthy volunteers (21 female, ages 18–43 y) with normal or corrected-to-normal vision participated in the experiment after giving informed consent. All procedures were approved by the University Committee on Activities Involving Human Subjects of New York University. Subjects were instructed to fast for 4 h before the experimental session and informed that they would have to remain for 1 h after the completion of the session, during which the only food they could consume was any food items received from the experiment. In addition, they were instructed that one trial would be randomly selected from all of the trials in the experiment for realization at the end of the experiment, and they received a detailed explanation of the auction procedure for realization. Each subject was initially endowed with $4 for use in the bid trials. SI Materials and Methods gives a full description of task and realization procedures.

Choice Behavior Analysis.

To examine the effect of distracter value on choice behavior across different subjects with different ranges of bid prices, we quantified a normalized distracter value:

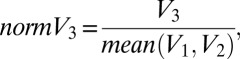where V₁, V₂, and V₃ are the mean bid values for the high target, low target, and distracter items in a given trial, respectively. This metric ranges from 0 to 1 and allows comparison of distracter values across subjects for population analyses. To quantify the effect of value on conditional choice data, we performed a generalized linear regression on data from the trials in which either target was chosen (n = 9,381 trials). Regression was performed using the binomial distribution and a logit link function; predictors were the values of the two target options and the normalized value of the distracter option.