Spectroscopic evidence for Fermi liquid-like energy and temperature dependence of the relaxation rate in the pseudogap phase of the cuprates

Abstract

Cuprate high-T_c superconductors exhibit enigmatic behavior in the nonsuperconducting state. For carrier concentrations near “optimal doping” (with respect to the highest T_cs) the transport and spectroscopic properties are unlike those of a Landau–Fermi liquid. On the Mott-insulating side of the optimal carrier concentration, which corresponds to underdoping, a pseudogap removes quasi-particle spectral weight from parts of the Fermi surface and causes a breakup of the Fermi surface into disconnected nodal and antinodal sectors. Here, we show that the near-nodal excitations of underdoped cuprates obey Fermi liquid behavior. The lifetime τ(ω, T) of a quasi-particle depends on its energy ω as well as on the temperature T. For a Fermi liquid, 1/τ(ω, T) is expected to collapse on a universal function proportional to (ℏω)² + (pπk_BT)². Magneto-transport experiments, which probe the properties in the limit ω = 0, have provided indications for the presence of a T² dependence of the dc (ω = 0) resistivity of different cuprate materials. However, Fermi liquid behavior is very much about the energy dependence of the lifetime, and this can only be addressed by spectroscopic techniques. Our optical experiments confirm the aforementioned universal ω- and T dependence of 1/τ(ω, T), with p ∼ 1.5. Our data thus provide a piece of evidence in favor of a Fermi liquid-like scenario of the pseudogap phase of the cuprates.

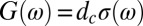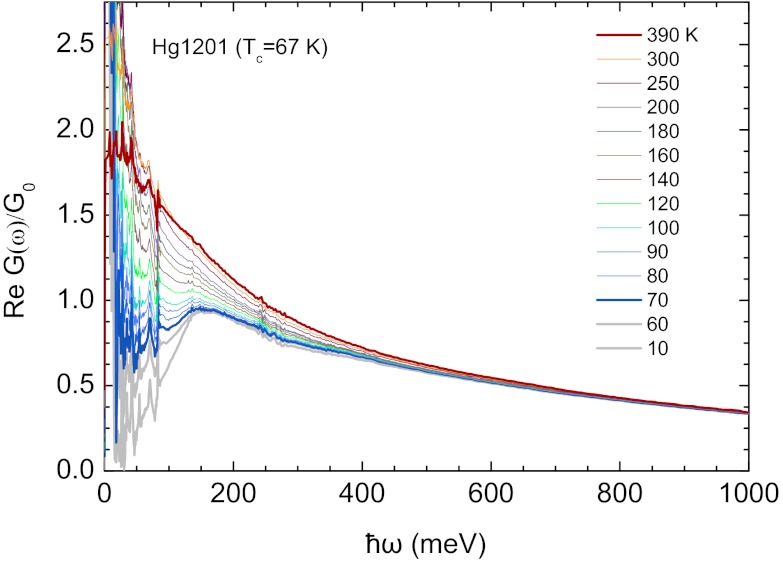
The compound HgBa₂CuO_4+δ (Hg1201) is the single-layer cuprate that exhibits the highest T_c (97 K). We therefore measured the optical conductivity of strongly underdoped single crystals of Hg1201 . Here we are interested in the optical conductivity of the CuO₂ layers. We therefore express the optical conductivity as a 2D sheet conductance , where d_c is the interlayer spacing. The real part of the sheet conductance normalized by the conduction quantum 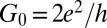is shown in Fig. 1. As seen in the figure, a gap-like suppression below 140 meV is clearly observable for temperatures below T_c and remains visible in the normal state up to ∼250 K. This is a clear optical signature of the pseudogap. We also observe the zero-energy mode due to the free charge carrier response, which progressively narrows upon lowering the temperature. In materials where the charge carrier relaxation is dominated by impurity scattering, the width of this “Drude” peak corresponds to the relaxation rate of the charge carriers. Relaxation processes arising from interactions have the effect of replacing the constant (frequency-independent) relaxation rate with a frequency-dependent one. The general expression for the optical conductivity of interacting electrons is then

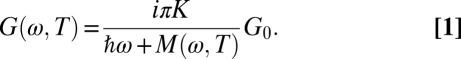Fig. 1.

Optical sheet conductance of underdoped Hg1201 (T_c = 67 K). Temperatures from 10 to 390 K. Data below T_c are shown in gray.

The spectral weight K corresponds to minus the kinetic energy if the frequency integration of the experimental data is restricted to intraband transitions. The effect of electron–electron interactions and coupling to collective modes is described by the memory function 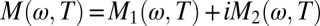, where 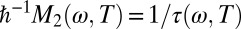represents the dynamical (or optical) relaxation rate in the case of a Fermi liquid.

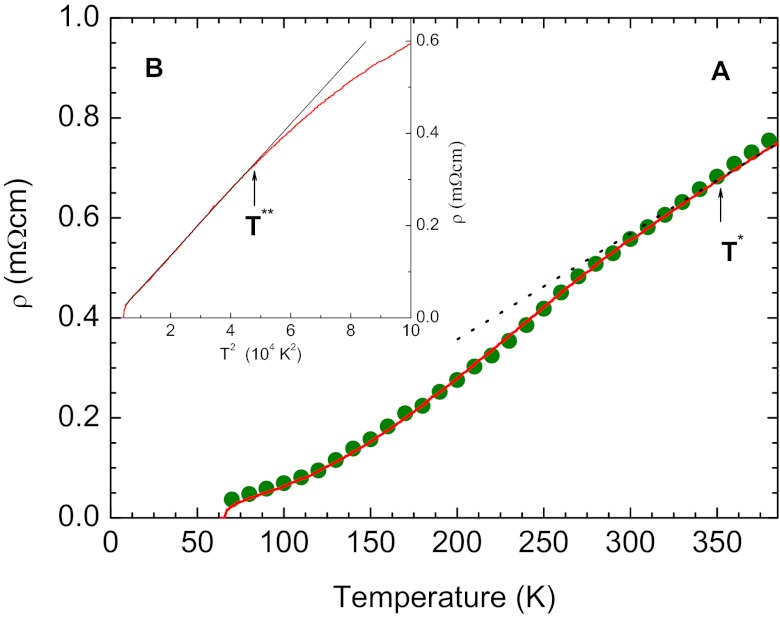
The zero frequency limit of the optical conductivity of Fig. 1 corroborates the recently reported temperature dependence of the dc resistivity (1) as shown in Fig. 2. Because K is practically temperature independent in the normal state (2), the low-temperature T² dependence of the resistivity is due to the quadratic temperature variation of 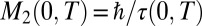. The infrared data confirm that Hg1201 exhibits the lowest residual resistance among the cuprates and a change to a linear temperature dependence above T* associated with the sudden closing of a pseudogap (3, 4). Fig. 2B shows this as a clear departure from the T² curve at ∼5 × 10⁴ K². The dc transport data, owing to the higher precision, allow for Hg1201 crystals of the same composition and doping to identify T* ∼ 350 K as the temperature above which the resistivity has a linear temperature dependence, and T** ∼ 220 K as the temperature below which the temperature dependence is purely quadratic. Finally, superconducting fluctuations become noticeable at 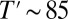K.

Fig. 2.

dc resistivity of underdoped Hg1201 (T_c = 67 K). Inverse optical conductivity extrapolated to zero frequency (green circles) compared with measured dc resistivity (1) (solid red line) of a sample of the same composition and doping (A). The dashed black curve is a T-linear fit to the resistivity data above 350 K. (B) Same dc resistivity data as a function of T², shown with a T² fit to the data below 220 K. Definitions and values for T* and T** of ref. 1 are used.

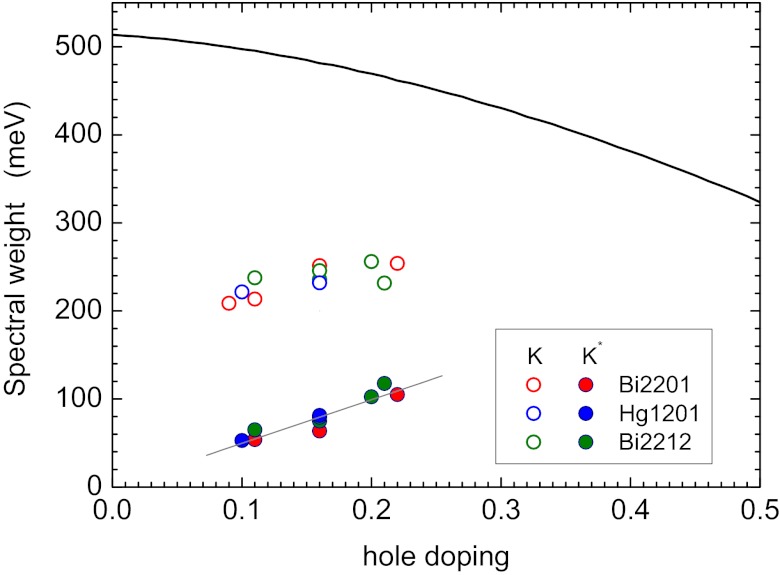
The doping dependences of K and of the coherent spectral weight, defined as K*=K/(1+M₁(ω,T)ℏω)|_ω=0, are summarized in Fig. 3 for a number of hole-doped cuprates. The theoretical values of K based on the band parameters obtained from local density approximation (LDA) ab initio calculations are about a factor of 2 larger than the measured values, which is due to strong correlation predicted by the Hubbard model for 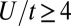(6). K decreases when the hole doping decreases, but does not extrapolate to zero for zero doping in accordance with the analysis of Comanac et al. (7). In contrast, the coherent spectral weight K* is proportional to the hole doping x: K = xK⁰, where 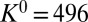meV, in agreement with the trend observed for La_2−xSr₂CuO₄ (8) and YBa₂Cu₃O_7−δ (9). This provides strong evidence that a Mott insulator is approached as the doping is reduced. It cannot be determined from these data whether this occurs because (i) the quasi-particle residue is gradually suppressed (10, 11) or (ii) the Fermi surface arcs shrink to zero without vanishing of the nodal spectral weight (12, 13).

Fig. 3.

Conduction band spectral weight per CuO₂ layer for a large number of cuprate superconductors. Closed symbols: coherent spectral weight K*. The gray line is a linear least-squares fit, K* = 496x, where x is the nominal hole doping. Open symbols: total spectral weight, K. Data are presented for Hg1201 with 10% doping (see Supporting Information). For the other materials see table 1 in ref. 5. The black solid curve represents K calculated from ab initio band parameters for Hg1201 (Supporting Information). For the Bi₂Sr₂CuO_6+δ (Bi2201) sample with hole doping below 0.10, K* could not be calculated, because in this case we obtain 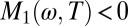for 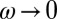, possibly due to disorder.

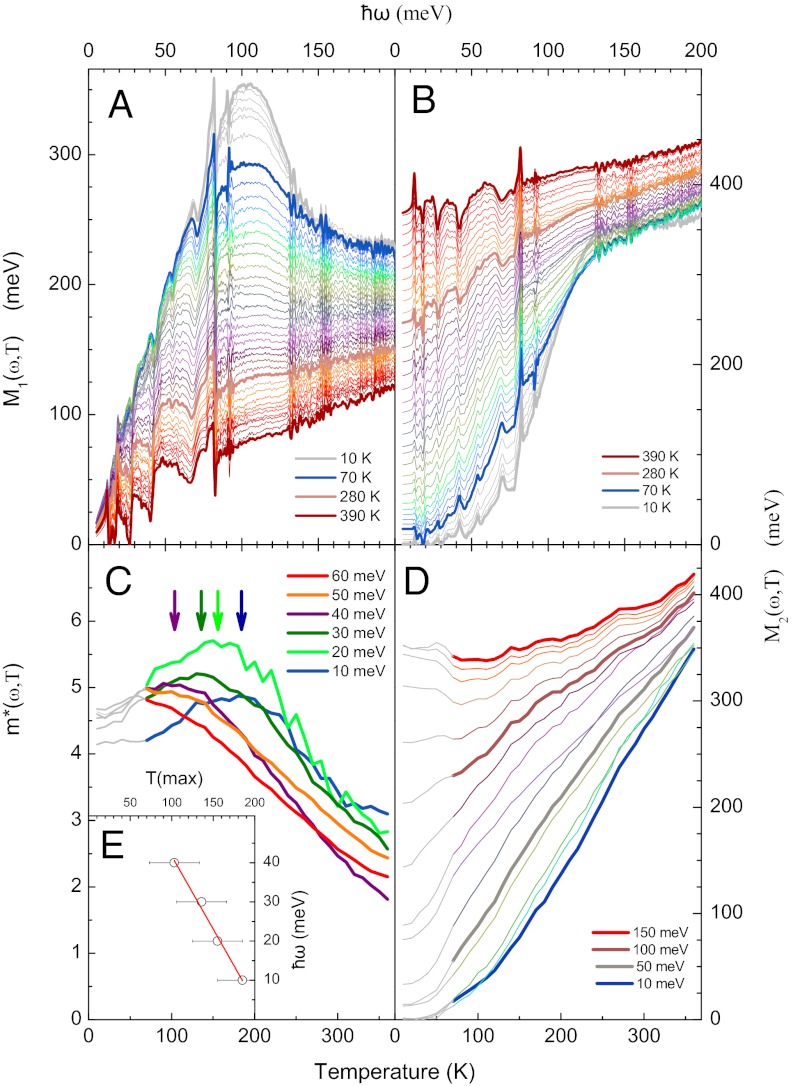
The real and imaginary parts of the memory function of underdoped Hg1201 with 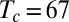K are shown in Fig. 4 for temperatures from 10 to 390 K. 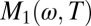has a linear slope extrapolating to ω = 0, which becomes less steep at higher temperatures. The maximum at ∼105 meV erodes gradually as temperature increases, but a residue of this structure remains visible even at 390 K. In Fig. 4E we show a plot of the frequency- and temperature-dependent mass enhancement factor 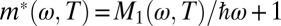. Above 60 meV 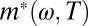is a monotonously decreasing function of temperature. For ω that is not too large, 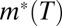is, roughly speaking, a plateau at low temperature, with a weak maximum at T(max) followed by a linear-like decrease at higher temperature. T(max) increases when ω decreases and for 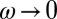extrapolates to 212 K ∼ T**, indicating another way of identifying T**. The increase of 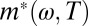from about 3 at 390 K to 5 at T**, taken together with the strong temperature dependence of 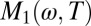near its maximum at 105 meV, indicates that the charge carriers become increasingly renormalized when the temperature decreases. Our results also corroborate the observation in ref. 14 that the integrated optical conductivity does not decrease when T decreases, so that no opening of an optical pseudogap is seen when, at T*, part of the Fermi surface is removed by a pseudogap, despite the emergence at this temperature of a novel ordered state with two Ising-like magnetic collective modes at 54 and 39 meV as observed with inelastic neutron scattering (15).

Fig. 4.

Optical self-energy as a function of frequency and temperature. (A) Real and (B) imaginary part of the memory function as a function of ℏω for underdoped Hg1201 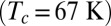. Spectra are shown in 10-K intervals for temperatures from 10 to 390 K. Thick lines are used to highlight the 10-, 70-, 280-, and 390-K data. (C) Effective mass 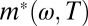as a function of temperature for selected values of ℏω in 10-meV intervals from 10 to 60 meV. (D) Relaxation rate 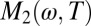as a function of temperature for selected values of ℏω in 10-meV intervals from 10 to 150 meV. Thick lines are used to highlight the data at selected energies. In C the approximate temperatures of the maxima T(max) are indicated with an arrow for ω with the corresponding color. (E) shows the same T(max) versus ω. The solid line is a linear fit, which extrapolates to 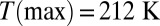for 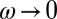. All data in the superconducting state are in gray. The temperature range (370 K) of C and D is chosen to match the frequency range of A and B (200 meV) according to the scaling relation .

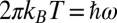Turning now to the dynamical relaxation rate 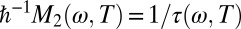, we observe from Fig. 4 that its frequency dependence exhibits an upward curvature for all temperatures. Also, the temperature dependence has a T² component at the lowest frequencies. Earlier indications for T² dependence of the scattering rate came from the dc 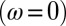resistivity (1, 16, 17). For frequencies above 50 meV this component is either absent or completely masked by the onset of superconductivity (gray segments of the temperature traces). 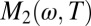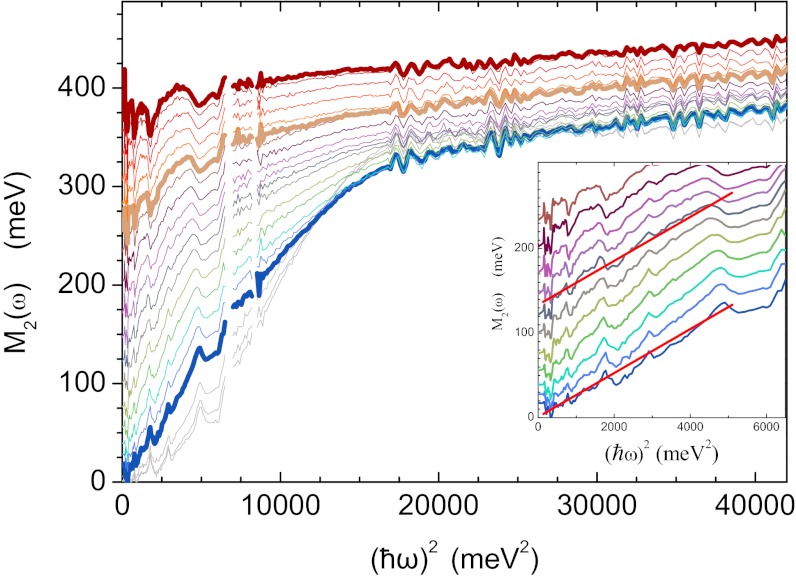Although has no maximum as a function of temperature, the curves have an inflection point which shifts from roughly 200 to 100 K when the frequency is raised from 10 to 50 meV. The saturation of 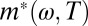and the merger of the resistivity with a T² dependence indicate that the system enters a Fermi liquid-like state at ∼200 K. We notice that at temperatures above T_c the initial rise is given by a linear slope as a function of ω² (Fig. 5, Inset). For an ideal Fermi liquid, 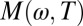in the relevant range of ω and T is, to a good approximation,

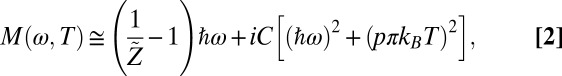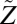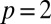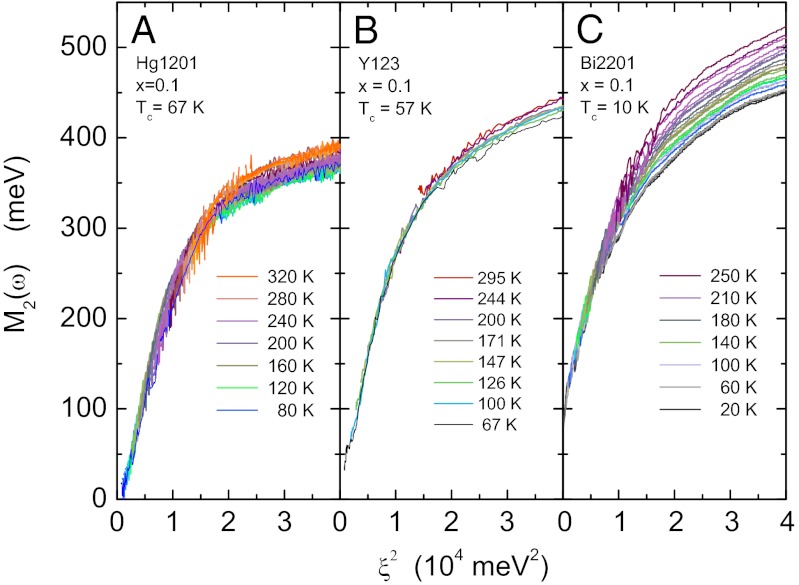
where is proportional to the quasi-particle residue, C is a constant with units of inverse energy, and (ref. 18 and Supporting Information). To check possible Fermi liquid characteristics of the data, we introduce a single parameter ξ defined as 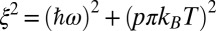, and we investigate M₂ as a function of ξ. As shown in Fig. 6 for three underdoped cuprate materials [Hg1201, ortho-II Y Ba₂Cu₃O_6.5 (Y123) (ref. 19), and Bi2201 (ref. 20)] with hole concentration 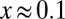, the M₂ data of the normal state collapse in the low-energy range on a single scaling curve for 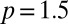. This value of p was obtained by searching for the best scaling collapse for 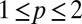in steps of 0.1 (Supporting Information). Comparing the functional form of 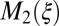for these three materials, we make the following observations: (i) Going from Hg1201 to Bi2201 (Fig. 6, Left and Right, respectively) in this plot, the residual 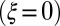value of 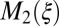increases from 0 to about 80 meV. Indeed, it is generally thought that the relatively low values of T_c in single-layer Bi2201 have to do with strong scattering by disorder (1, 21). (ii) We also notice that in the case of Bi2201 some negative curvature appears at the lowest energies, which is an indication that the Fermi liquid characteristics are affected to some extent, and appear to be relatively fragile with respect to disorder. (iii) The implications of the loss of scaling above 100 meV in the Bi2201 data are not entirely clear. In principle there is no reason to expect scaling, because this is clearly beyond the range of “universal” Fermi liquid behavior. However, the single-parameter scaling seems to persist into this regime for the other two materials (Y123 and Hg1201), leading to the speculation that impurity scattering also contributes to the disappearance of scaling above 100 meV for the Bi2201 sample.

Fig. 5.

Dynamical relaxation rate of underdoped Hg1201. Imaginary part of the memory function of underdoped Hg1021 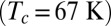for temperatures between 10 and 390 K in 20-K steps as a function of ω². Thick lines are used to highlight the 70-, 280-, and 390-K data. (Inset) Zoom of the low-ω range showing a linear fit; temperatures are from 70 to 270 K in 20-K steps.

Fig. 6.

Collapse of the frequency and temperature dependence of the relaxation rate of underdoped cuprate materials. Normal state 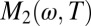as a function of 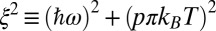with 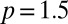. (A) Hg1201 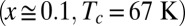. (B) Y123 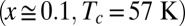, spectra by Hwang et al. (19) (digitized data of Fig. 6 represented here as a function of ξ²). (C) Bi2201 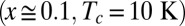; data of van Heumen et al. (20) represented here as a function of ξ². The data displayed in A and C are in 10-K intervals with color coding indicated for temperatures in 40-K steps. In between these steps the color evolves gradually as a function of temperature. In B the color coding is given for all temperatures displayed.

The most important observation borne out by these data is that the frequency dependence of 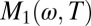and 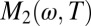follows by and large the behavior expected for a Fermi liquid: At low frequencies and temperatures 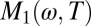is indeed a linear function of ω, and 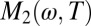scales with 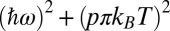. Other hints at possible Fermi liquid behavior came from the recent discovery of quantum oscillations at low temperature and high magnetic field in underdoped YBa₂Cu₃O_6+δ (13) and YBa₂Cu₄O₈ (22), from the observation of the Fermi–Dirac statistics underlying the quantum oscillations (23), and from the two-fluid analysis (24) of NMR data (25). We note that recent theories (e.g., refs. 26–28) have emphasized the possible relevance of Fermi liquid concepts––or a hidden form of these in the superconducting regime (29)––to the metallic state of hole-doped cuprates. Our experimental observations provide a strong incentive for further theoretical work in this direction. We highlight two striking aspects of the data: (i) The slope 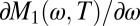for 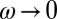decreases significantly as a function of increasing temperature; and (ii) 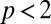. We speculate that these issues are related to the progressive filling-in of the pseudogap as a function of increasing temperature. Already in a two-fluid picture of a nodal Fermi liquid in parallel to an antinodal liquid, nonuniversal features (for Fermi liquids) are introduced in the optical conductivity, because the properties at the Fermi surface change gradually from Fermi liquid at the nodes (30) to strongly incoherent and pseudogapped at the hot spots near the antinodes (31). In fact, also in other compounds p is found to be different from 2 (32–34). Recently, Maslov and Chubukov interpreted this as a combination of Fermi liquid scattering and an additional source of elastic scattering from magnetic moments or resonant levels (35).

Theoretically, it is expected that the T²- and ω² dependence of 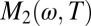is limited to ℏω and pπk_BT lower than some energy scale ξ₀, which in the context of single-parameter scaling behavior of a Fermi liquid is proportional to the effective Fermi energy. Electronic correlations strongly reduce this energy scale compared with the bare Fermi energy. For most materials the issue of the Fermi liquid-like frequency dependence of 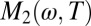has remained largely unexplored. This is related to the difficulty that in cases such as the heavy fermion materials where this type of coupling dominates, the range of Fermi liquid behavior is smaller than 10 meV, making it particularly difficult to obtain the required measurement accuracy in an infrared experiment. Clean underdoped cuprates present in this respect a favorable exception because, as can be seen from Figs. 5 and 6, the relevant energy scale ξ₀ is about 100 meV for a doping level around 10%. Above this energy, 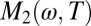crosses over to a more linear trend as a function of both ω and T. This suggests that in cuprates the range of applicability of Fermi liquid behavior is limited by a different scattering mechanism that develops at high T and high ω as the pseudogap gets filled.

The ξ²-dependence of the relaxation rate can be understood as follows: An electron at a distance ξ above the Fermi energy can, as a result of electron–electron interactions, decay to a final state ξ−Ω by creating an electron–hole pair of energy Ω. The density of states of electron–hole pairs is the spin (charge) susceptibility 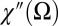, where spin (charge) refers to electron–hole pairs carrying (no) net spin. 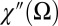can be strongly renormalized, but the property that 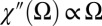in the limit 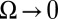is generic for Fermi liquids (24). Integration of the susceptibility multiplied with the interaction vertex 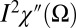over all possible decay channels from zero to ξ leads us to conclude that indeed 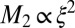, as reported experimentally in the present article. In this description the cross-over ξ₀ corresponds to the energy where is truncated, leading to a leveling off of M₂ for 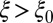. The strong temperature dependence of 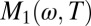is also a natural consequence of this description; it was shown in ref. 36 that, in leading orders of temperature, 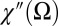of a correlated Fermi liquid decreases as a function of temperature.

In summary, we have shown from optical spectroscopy measurements that the ungapped near-nodal excitations of underdoped cuprate superconductors obey Fermi liquid behavior when materials with reduced amount of disorder are considered. This observation, which is at variance with some established paradigms, provides leads toward understanding of the metallic state and high-temperature superconductivity in these materials.

Materials and Methods

Sample Preparation.

Single crystals were grown using a flux method, characterized, and heat treated to the desired doping level as described in refs. 37 and 38. The conductivity data in Fig. 1 are of a sample which has an onset critical temperature of 67 K and a transition width of 2 K. The crystal surface is oriented along the a–b plane with a dimension of about 1.51 × 1.22 mm². Hg1201 samples are hygroscopic. Therefore, the last stage of the preparation of the sample surface is done under a continuous flow of nitrogen, upon which the sample is transferred to a high-vacuum chamber (10⁻⁷ mbar) within a few minutes. Before each measurement the surface is carefully checked for any evidence of oxidation.

Comparison with dc Resistivity.

Transport measurements have been performed using the four-terminal method. Due to the irregular shape of the cleaved samples the absolute value of the dc resistivity can only be determined with about 20% accuracy. However, we obtained very high relative accuracy of the temperature dependence of the dc resistivity, as seen from identical temperature dependences of samples of the same composition and doping, regardless of having significantly different dimensions and shapes. An independent check of the dc resistivity was obtained from the 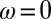limit of the experimental infrared optical conductivity (Fig. 2). The dc resistivity had to be scaled by a factor of 0.66 to match the optical data, most likely due to the aforementioned influence of the irregular shape of the crystals on the absolute value of the measured dc resistances. The excellent match of the two temperature dependences demonstrates the high quality of both dc resistivity and optical conductivity data.