Atomic-level description of ubiquitin folding

Abstract

Equilibrium molecular dynamics simulations, in which proteins spontaneously and repeatedly fold and unfold, have recently been used to help elucidate the mechanistic principles that underlie the folding of fast-folding proteins. The extent to which the conclusions drawn from the analysis of such proteins, which fold on the microsecond timescale, apply to the millisecond or slower folding of naturally occurring proteins is, however, unclear. As a first attempt to address this outstanding issue, we examine here the folding of ubiquitin, a 76-residue-long protein found in all eukaryotes that is known experimentally to fold on a millisecond timescale. Ubiquitin folding has been the subject of many experimental studies, but its slow folding rate has made it difficult to observe and characterize the folding process through all-atom molecular dynamics simulations. Here we determine the mechanism, thermodynamics, and kinetics of ubiquitin folding through equilibrium atomistic simulations. The picture emerging from the simulations is in agreement with a view of ubiquitin folding suggested from previous experiments. Our findings related to the folding of ubiquitin are also consistent, for the most part, with the folding principles derived from the simulation of fast-folding proteins, suggesting that these principles may be applicable to a wider range of proteins.

Understanding the principles that govern protein folding, the self-assembly process that leads from an unstructured polypeptide chain to a fully functional protein, has been one of the major challenges in the area of physical biochemistry over the last 50 years. Naturally occurring proteins typically fold on timescales ranging from milliseconds to minutes, but as our understanding of the principles of protein folding has improved, a number of fast-folding proteins that fold on the microsecond timescale have been engineered and characterized (1–12). The design of such fast-folding proteins was in part intended to narrow the gap between the timescales of protein folding and the timescale accessible to physics-based atomistic molecular dynamics (MD) simulations, thus enabling fruitful combinations of experiments and simulations to study the mechanisms of folding (13–18). We recently studied 12 fast-folding proteins using equilibrium MD simulations, for example, with the aim of elucidating general principles underlying the folding of these proteins (19). The folding of these proteins was found to be a relatively sequential process that follows a few paths, in which the order of formation of native structure is correlated with relative structural stability in the unfolded state. The extent to which these observations pertained to fast-folding proteins only or to protein folding more generally, however, was unclear. Here we address this question by applying the same methodology and physics-based force field used in our previous investigation of fast-folding proteins to the study of ubiquitin, a naturally occurring protein known to fold on a millisecond timescale.

Ubiquitin is a 76-amino-acid-residue long, highly conserved (20) protein that is found in all eukaryotic organisms (21) and plays a fundamental role in the process of proteasome-mediated protein degradation (22–25). The so-called “ubiquitin fold” is characterized by a complex topology consisting of a five-stranded β sheet, an α helix, and a short 3₁₀ helix (26). Ubiquitin has no prosthetic groups or disulfide bonds, is highly soluble, and is thermostable (T_M > 360 K) (27–28), making it an ideal target for experimental folding studies. The N and C termini form consecutive strands in the β sheet and are in close contact, a common feature in two-state folders (29); indeed, early investigations established that ubiquitin folds on the millisecond timescale with an apparent two-state behavior (30–33), but later studies suggested that additional on- or off-pathway intermediates may be populated depending on the experimental conditions (34–42). A protein engineering Φ-value analysis of ubiquitin folding is consistent with a transition state ensemble (TSE) characterized by a well-defined folding nucleus localized in the N-terminal region of the protein and encompassing the helix and first two β strands (43, 44). The third, fourth, and fifth β strands, which are in the C-terminal region of the protein, have low Φ-values. This originally prompted the suggestion that they are unstructured in the TSE, although a subsequent computational analysis of the experimental Φ-values suggested that strands β3 and β4 may be partially formed, and may adopt a native-like topology in the TSE (45). An extensive Ψ-value analysis of ubiquitin folding is also consistent with a more diffuse TSE, as indicated, for example, by high Ψ-values between strands β3 and β4 (43, 46).

To date, ubiquitin’s relatively slow folding rate has impeded efforts to characterize its folding process through physics-based atomistic MD simulations. Previous simulation studies of ubiquitin folding have for the most part used coarse-grained representations (47) or “native-centric” topology-based potentials (48). Using physics-based, atomistic force fields and simulations on the nanosecond timescale, the fast-collapse phase preceding the folding process has been analyzed by rapid low-temperature quenching of unfolded-state structures generated in high-temperature simulations (49), while the process of ultrafast unfolding in out-of-equilibrium conditions has been described by performing simulations at high temperature (50–53) or under tensile load (54–56).

Here we report the results of unbiased, all-atom MD simulations of ubiquitin performed close to its melting temperature, in which we observe spontaneous and reversible folding to the native structure. These simulations allow a detailed characterization of key elements of the pathway, kinetics, and thermodynamics of ubiquitin folding. We compare these results with those we previously obtained for fast-folding proteins. We find that the same general principles appear to govern the folding of both fast-folding proteins and ubiquitin, suggesting that these principles may be more generally applicable across a broader range of proteins.

Methods

Eight MD simulations of ubiquitin were performed on a special-purpose machine, Anton (57), using the CHARMM22* force field (58) modified to reproduce the correct balance between the cis and trans isomers observed at proline residues in extended simulations at high temperatures (SI Text). Six of these simulations were initiated in the folded state [Protein Data Bank (PDB) ID code 1UBQ] (26) and two in an extended, unfolded state. Four systems starting from the folded state were solvated in a 58-Å box containing 5,581 TIP3P (three-point water model) (59) water molecules. To check for the presence of system size–related artifacts, two additional simulations starting from the folded state and two simulations starting from the unfolded state were performed in a larger 66-Å box containing 8,535 water molecules. The protein interacted with its periodic image in 9% of the frames in the small-box simulations and in 2% of the frames in the large-box simulations (an interaction is here defined as any pair of heavy atoms that are within 5 Å of each other). The simulations performed in the larger and smaller boxes behaved comparably; in particular, the radius of gyration of the unfolded state, which is expected to be very sensitive to finite-size artifacts, has similar probability distributions in the two sets of simulations (Fig. S1). Nonbonded interactions were truncated to 10.5 Å, and the Gaussian Split Ewald (GSE) method was used to account for long-range electrostatic interactions (60). Preliminary tests performed without an Ewald method and using a simple shifted-force truncation of the electrostatic interactions (61) gave good results for the folded state (Results and Discussion), but did not accurately describe the unfolded state, which became very compact (SI Text), with an average radius of gyration similar to that of the folded protein; this observation is similar to other recent findings (62). To further increase computational efficiency in the simulations, we modified all of the hydrogen and water oxygen masses (H, 4 Da; O_w, 10 Da); this allowed us to integrate the equations of motion using a reference system propagator algorithm (RESPA) scheme (63) with an inner time step of 5 fs and an outer time step of 10 fs (64). While this modification slightly alters water properties (64), we verified that this setup does not have any substantial effect on the folding kinetics or the thermodynamics of a previously well-characterized protein (SI Text). The ubiquitin systems were first equilibrated in the NPT (constant pressure) ensemble for 2 ns, and they were subsequently run in the NVT (constant volume) ensemble at 390 K by coupling to a Nose–Hoover thermal bath (65, 66) with a relaxation time of 2 ps. To test the ability of the force field to describe the folded protein, a preliminary 1-ms simulation of the native state of ubiquitin at 300 K was performed using standard CHARMM22* (58), normal atomic masses, an integration time step of 2.5 fs, and a shifted-force treatment of the electrostatics (61).

The trajectories of the eight folding simulations were analyzed in combination, as described previously (19). Dual cutoffs of 1.3 and 6.5 Å on the Cα RMSD of residues 2–45/65–69 were used to assign transition paths (19, 67). Φ-values from MD simulations are commonly calculated from computational models of the TSE through an analysis of the fraction of native contacts that are formed (68). This approach, however, assumes a two-state behavior and requires an accurate model for the TSE. Here we instead calculate Φ-values for 26 point mutations from the folding and unfolding rates obtained from Langevin Dynamics simulations performed along a suitably optimized one-dimensional reaction coordinate, obtained here through optimization (69) of a linear combination of the Q-values (70) of the individual residues. This approach does not require an accurate determination of the TSE and can account for the effect of point mutations on the stability of metastable intermediate states, as long as they are captured by the reaction coordinate. A control calculation performed using a different P value–based reaction coordinate (71) shows that the calculated values are robust with respect to the choice of reaction coordinate, as long as it describes the folding transition reasonably well. The diffusion coefficient along the optimized reaction coordinate was assumed to be independent of the mutation and was estimated from the wild-type MD simulations using a maximum-likelihood approach and a lag time of 10 ns (72). The free-energy surface of the mutants was estimated using a contact approximation and assuming that the energy of each native contact was 0.06 kcal⋅mol⁻¹ (73). The relevant metastable states on the ubiquitin free-energy landscape were identified with a kinetic-clustering analysis of the autocorrelation functions of 400 Cα–Cα contacts (71).

Results and Discussion

Native State of Ubiquitin in CHARMM22*.

As a first step of the investigation, we performed a 1-ms simulation of the native state of ubiquitin at 300 K. The protein turned out to be remarkably stable during the entire simulation, making several reversible transitions between a small number of distinct states. The average structure in the most populated state (population ∼70%) has a Cα RMSD of only 0.5 Å from the X-ray structure (PDB ID code 1UBQ, excluding the flexible C-terminal tail). The second-most populated state (∼20%) is very similar to the dominant conformation, but differs locally around residues 50–54 (the Cα RMSD from 1UBQ is 0.9 Å when excluding the tail); a conformational switch in this region of ubiquitin has previously been observed in experiments (74, 75). In the remaining 10% of the structures, the α helix is partially frayed at its C terminus; similar unfolding of the C-terminal end of the helix has been observed in experiment both at high pressure (76) and in a mutant in which the helix C-cap has been removed (77), suggesting that ubiquitin may undergo such motion, although the force field appears to overestimate its population. We conclude that the force field provides a reasonable description of the folded state of ubiquitin, although it seems to slightly underestimate the stability of the α helix in the context of the folded state.

Equilibrium Reversible-Folding Simulation of Ubiquitin.

We performed eight simulations of ubiquitin at 390 K starting from native or extended conformations. This temperature was chosen as we expected it to be a reasonable compromise between remaining close enough to the melting temperature of ubiquitin around neutral pH (which we estimated to be in the 370-K range; due to the high stability of ubiquitin, most calorimetric experiments are performed under highly acidic conditions) (27) and observing a sufficient number of folding/unfolding events in ∼8 ms of simulation. Six simulations were started from the native state, and two were started from extended, unfolded conformations. Unfolding was observed in all simulations that began in the native state (average unfolding time of 240 ± 90 µs), and in two cases reversible folding/unfolding was observed (average folding time 3 ± 2 ms; Fig. 1A). The unfolded protein repeatedly assumed extended conformations, with RMSDs of >30 Å from the native structure and without native secondary structure or long-range native contacts; this makes clear that the protein indeed transitioned between the folded and unfolded basins. No folding events were observed in the two simulations initiated in the unfolded state; this observation is not unexpected, since the folding time of ubiquitin that we calculated (3 ms) is more than twice the combined length of these two simulations (1.2 ms). A total of two folding and eight unfolding events were collected in 8 ms of aggregated simulation time (Table S1). The calculated melting temperature (372 ± 4 K) and heat capacity (1.1 ± 0.5 kcal⋅mol⁻¹⋅K⁻¹) for folding at 390 K are consistent with the experimental estimates of >360K and 1.3 ± 0.2 kcal⋅mol⁻¹⋅K⁻¹ (27), while the calculated folding enthalpy at the melting temperature (13 ± 9 kcal⋅mol⁻¹) is substantially smaller than the experimental value of several tens of kcal·mol⁻¹ (27), as has already been observed in computational folding studies of a number of other proteins (19, 58).

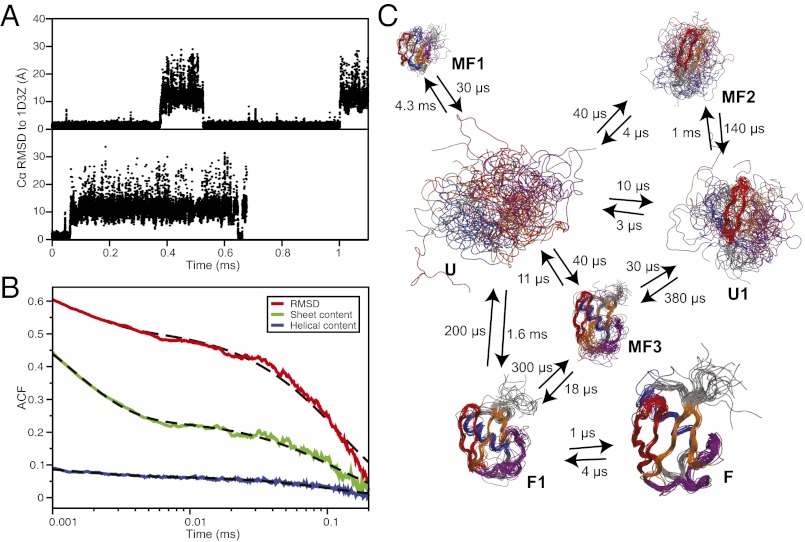
Fig. 1.

Equilibrium folding simulations of ubiquitin. (A) Traces of the Cα RMSD (for residues 2–71) from the native structure for the two simulations where reversible folding is observed. (B) Autocorrelation function of the Cα RMSD (red), the number of helical residues (blue), and the number of residues in β sheets (green). The dashed black lines are biexponential fits to the autocorrelation functions with characteristic times of ∼1.5 µs and ∼120 µs. (C) Kinetic model of the folding free-energy surface. For each state, 20 random structures are displayed, superimposed using Theseus (91), and scaled according to state population. Hairpin 1 is colored in red, hairpin 2 in orange, the α helix in blue, and the C-terminal loop containing the 3₁₀ helix and the fifth β sheet in purple. The kinetic model was obtained from an eight-state fit to the time autocorrelation function of 400 random Cα–Cα contacts (71). A higher number of states results in negligible improvement on the quality of the fit. The transition times, modified to enforce detailed balance (92), are also reported here. Two unstructured unfolded-state clusters were generated by the fitting procedure and are here merged in a single state (U) to simplify the representation.

Most of the amplitude of the microsecond-timescale relaxation of the RMSD from the native structure or the secondary structure content (a proxy for the IR signal intensity observed experimentally) (40, 42) can be described as a single exponential decay with a characteristic timescale of 0.12 ms (Fig. 1B). This timescale is in agreement with the relaxation time calculated from the folding and unfolding rates (0.2 ± 0.1 ms) and with the experimental observation that ubiquitin essentially behaves as a two-state folder on the millisecond timescale (33). A more direct quantitative comparison between simulated and experimental folding timescales is impractical: ubiquitin’s high thermal stability makes it difficult to perform experiments above the folding transition temperature without lowering it by using destabilizing conditions (e.g., the presence of a denaturant or low pH). Despite largely behaving as a two-state system, a cluster analysis (71) allows the identification of a number of metastable states that interconvert on the microsecond timescale or slower (Fig. 1C). In addition to the disordered unfolded state (U), in which the interconversion between different structures is fast, the analysis reveals a few misfolded states (MF1–3) that persist on the microsecond timescale. These states typically feature a substantial amount of nonnative β sheet and have a total population of a few percent. In state MF3, a near-native conformation is reached with a Cα RMSD of less than 2 Å from the native structure. This misfolded state is unstable, unfolding after 10 µs.

To provide a coarse-grained description of the folding mechanism of ubiquitin, supplementing the macrostate definitions above, we optimize a one-dimensional reaction coordinate based on a linear combination of the Q-values of individual residues (69). The folding free-energy landscape projected along this reaction coordinate reveals a 5 kcal⋅mol⁻¹ free-energy barrier that separates the two main folded and unfolded state basins (Fig. 2). Most of the states identified in the clustering analysis also appear as separate local minima on the one-dimensional free-energy surface, which lends additional support to the robustness of both analyses, although some states appear to be merged with others in this projection. Overall, the free-energy profile conforms to a funnel-like landscape in which the configurational entropy (here roughly approximated by the contact order) decreases as contacts are formed (78, 79), and there is a strong correlation between the enthalpy of the system and the number of native contacts formed (SI Text and Fig. S2).

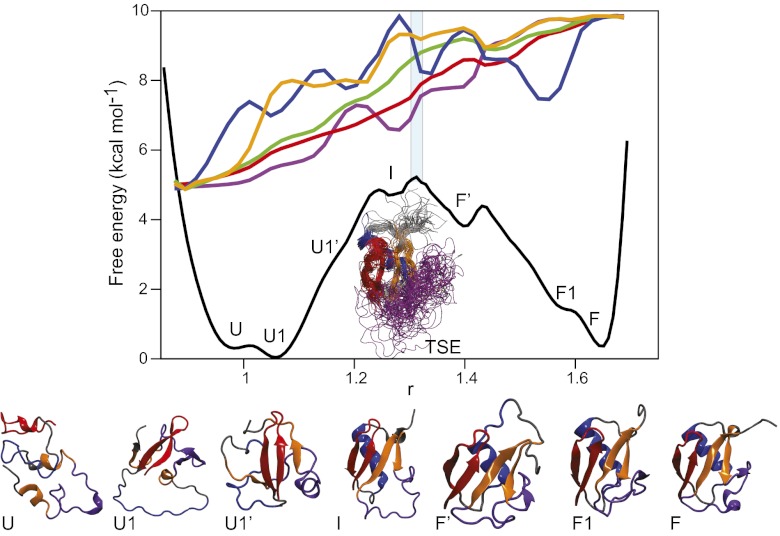
Fig. 2.

Folding free-energy surface of ubiquitin. The folding free-energy surface of ubiquitin projected along an optimal one-dimensional reaction coordinate. Representative structures for each basin on the folding free-energy surface are reported in a cartoon representation colored according to the scheme of Fig. 1. Basin U corresponds to the completely unstructured protein, while basin F corresponds to the native-state structure (average Cα RMSD from the X-ray structure, 0.8 Å). The letter codes of the macrostates determined in the kinetic clustering analysis of Fig. 1 are used to identify the corresponding basins observed in the one-dimensional projection. Some of the basins are not observed in the macrostate analysis because their population is too low (state I) or because they exchange too rapidly with other states (states F′ and U1′). The average values of a number of structural properties (blue, number of helical residues; orange, number of sheet residues; green, Cα RMSD; purple, contact order; red, fraction of native contacts) are also reported as a function of the reaction coordinate. To facilitate the comparison between different properties, all of the structural properties have been normalized so that they have the same values in the unfolded state U and in the folded state F.

Two distinct states can be clearly identified in the unfolded region: one in which hairpin 1 is formed (state U1 in Figs. 1 and 2, 60% occupancy) and one in which it is not (state U in Figs. 1 and 2, 40% occupancy). Experimental studies of the urea-denatured state of ubiquitin have shown that although the protein mostly behaves as a fully random chain overall, hairpin 1 forms a substantial amount of residual structure (80). Another low-population folding intermediate is also present near the top of the barrier (state I in Fig. 2), where most of the sheet and part of the helix are formed, but the packing of the secondary-structure elements is still not completely native. This state was not identified in the clustering analysis because its population is too low and its relaxation rate too fast to provide a sizable contribution to the microsecond-timescale autocorrelation functions. At least three states can also be identified in the folded basin: one corresponding to the native structure (state F in Figs. 1 and 2), one in which the C-terminal loop is unstructured (state F1 in Figs. 1 and 2), and one in which the C-terminal part of the helix is melted (state F′ in Fig. 2). State F′ corresponds to the state that is also observed in the native-state simulation at 300 K, while state F1 is consistent with the folding intermediate postulated on the basis of T-jump IR experiments (40). Folding and unfolding events invariably involve transitions between state F1 and the unfolded state (Fig. 2) and have an average duration of 1.7 µs.

Analysis of the transition paths (Fig. S3) reveals that, at a coarse level of resolution, all transitions essentially follow the same sequence of events (81), with hairpin 1 templating the formation of the β sheet and of part of the helix, followed by consolidation of the C-terminal loop, which includes the 3₁₀ helix and the fifth strand of the β sheet. We find some variability in the amount of helix that is formed at the transition state: while a substantial amount of helix is invariably present, the full helix may form both before and after the transition state. In this respect, state F′ does not appear to be necessarily on the folding pathway, since in the cases where the full helix is formed early in the folding pathway, the native state F can be reached directly from state U1′. The last folding step, involving formation of the 3₁₀ helix and of the fifth β strand, occurs (at least at the temperature of the simulations) on the folded side of the barrier, while the rest of the β sheet and most of the α helix are essentially formed at the transition state. In this respect, the transition state in simulation could be described as “late,” as most of the native-state topology is already consolidated at this stage. Indeed, we estimate the contact order in the TSE to be roughly 60% of the native state and the number of native contacts to be roughly 70% (Fig. 2), values that are consistent with those typically observed experimentally for a number of proteins (82, 83). Overall, our observations are in good agreement with experiments, which also suggest a rather homogeneous folding pathway for ubiquitin (84), with an order of events similar to that observed in our simulations (80, 85–87). This pathway is rather different from the pathway observed in simulations in which ubiquitin is unfolded by applying tensile stress to its N and C termini. In such simulations, the first event on the unfolding pathway is the rupture of the hydrogen bonds connecting hairpins 1 and 2 (54) followed by the melting of hairpin 1 (55).

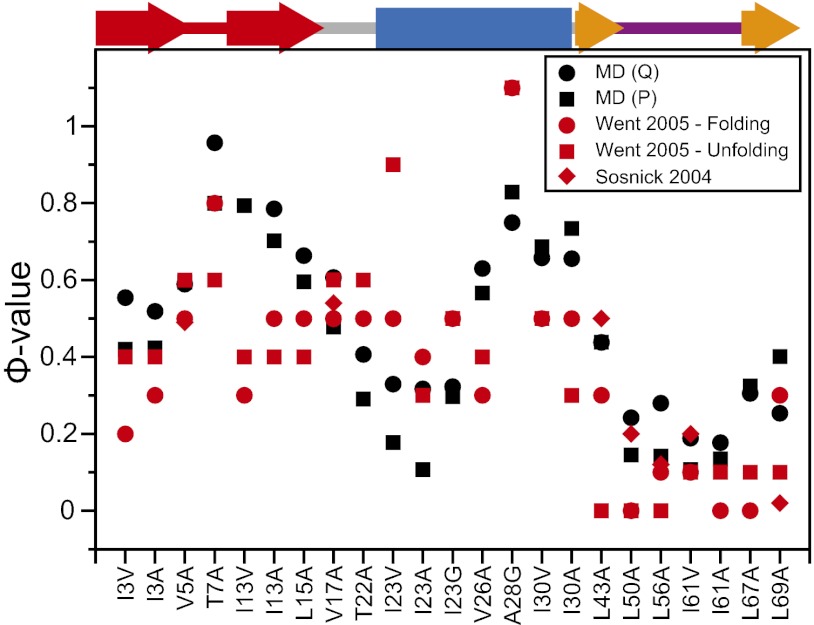
We used a contact-based approximation to estimate the changes in the free-energy surface upon mutation of individual residues. Assuming that a small point mutation has no influence on the diffusion coefficient along the optimized reaction coordinate, we can then estimate the change in the folding and unfolding rates upon mutation and thereby calculate Φ-values the same way we would experimentally. The calculation was repeated for two different reaction coordinates, and the results were found to be robust with respect to the choice of reaction coordinate. The Φ-values calculated in this way (Fig. 3) are in good agreement with those measured experimentally, with high Φ-values in the first three β strands and in the C-terminal part of the α helix, which are part of the initial folding nucleus (88), and low Φ-values for the C-terminal part of the protein. The most notable exceptions are the Φ-values calculated for residue 23, located at the beginning of the α helix, which are lower than those observed experimentally, and the Φ-values calculated for residues 13 and 67, located in strands β1 and β3, which are higher. The exception in the helix is consistent with our observations that, in some of the folding transitions, part of the helix is unstructured in the transition state and that, in the native simulation, the C-terminal part of the helix appears to be slightly less stable than observed in experiments. The slightly higher Φ-value measured for residues 13 and 67 may reflect the presence of a larger amount of β structure in the simulation TSE to compensate for the reduced helix stability. We suggest that this effect might be observed experimentally by measuring Φ-values for these residues in the presence of mutations that destabilize the C-terminal part of the helix. Only a few of the Φ-values are close to either 0 or 1, with the majority being fractional, both in simulation and in experiment. Fractional Φ-values can be ascribed to the presence of multiple folding routes with distinctly different transition states or to partial formation of native structure in a more well-defined transition state. The TSE identified in our reaction-coordinate analysis appears to be structurally rather homogeneous (Fig. 2). On the other hand, we note that several residues form only a fraction of their native contacts at the transition state, despite achieving a fairly native conformation; one example is the fourth β strand, which in both simulation and experiment has relatively low Φ-values despite being well structured in the TSE (Fig. 2).

Fig. 3.

Calculated and experimental Φ-values. The Φ-values for folding were calculated from the simulation using the contact approximation (Methods) and a Q-based reaction coordinate (black circles). For comparison, Φ-values were also calculated using a different P-based reaction coordinate (black squares) (71). Experimental values from Went et al. (red circles and squares) (44) and Sosnick et al. (red diamonds) (43) are reported for comparison. The native secondary structure is reported at the top of the graph (color scheme as in Fig. 2). The Φ-values for large hydrophilic or charged residues were also calculated, but they were found to deviate substantially from experiment, most likely because of a failure of the simple contact approximation, and are not reported here.

A central motivation for this work was to compare the folding mechanism of a naturally occurring protein with those of faster-folding proteins that have previously been characterized using the same approaches. Analysis of the transition paths for the folding and unfolding of ubiquitin indicates that, as is the case for faster-folding proteins, the native-state topology and secondary structure tend to form before the majority of long-range contacts (here defined as contacts between residues that are more than seven residues apart in sequence) are consolidated (Fig. 4 A and B). This is also consistent with our observation that the fraction of native contacts formed in the transition state region is slightly larger than the relative contact order (Fig. 2), indicating that the contacts formed after the transition state are mostly long range. In agreement with our previous observations, we also find that the sequence of events appears to be largely dictated by the local “nativeness” of the unfolded state. In particular, the residues in the β sheet, which have a high propensity to form β strands in the unfolded state, reach the native conformation early on the transition path. The helix residues (25–35) are a notable exception to this trend; they have a relatively low propensity to form helices in the unfolded state, yet the helix is formed quite early on the transition path (Fig. 4C). Overall, these results suggest that the general principles governing the folding of fast-folding proteins also apply to ubiquitin, and potentially to other naturally occurring proteins, although the correlation between the order of events on the transition path and the probability of forming native structure in the unfolded state may be weaker.

Fig. 4.

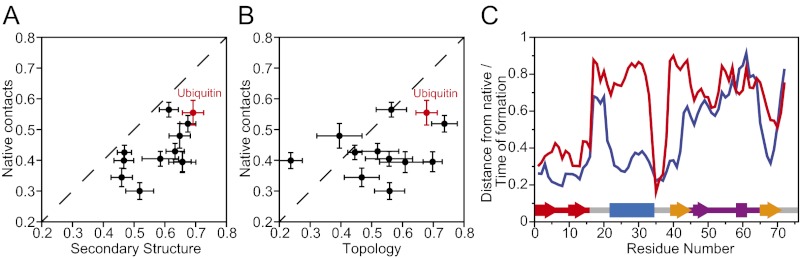
Global order of events in ubiquitin folding. (A) Relative formation order of the secondary structure and the long-range native contacts, as calculated from the integral over the transition path (19). The integrals calculated for several fast-folding proteins (19) are also reported on the same graph for comparison. (B) Same as A, but here reporting the relative formation order of native topology (93, 94) and long-range native contacts. (C) For each residue, the probability of forming local native structure in the unfolded state (red) is reported together with the order of formation of native structure along the transition path (blue) (19); Fig. S3 shows a comparable analysis of the order of events for individual folding pathways. The secondary structure of ubiquitin is reported at the bottom of the graph for comparison.

Assuming a two-state folding behavior, the prefactor for folding can be estimated from the average transition path time (1.7 µs) using Kramers’ theory (89). The calculated value of 3.5 µs, consistent with a folding time of ∼3 ms and an activation barrier of ∼5 kcal⋅mol⁻¹ (Fig. 2), is similar to the value obtained for the 73-amino-acid-residue three-helix bundle, α3D (3 µs) (19); despite having a similar size and stability, however, this protein folds two orders of magnitude faster than ubiquitin. According to current theories based on statistical analysis of folding rates (90), this difference originates from the more complex topology of ubiquitin, as reflected by its high contact order (15% compared with 9% for α3D). Indeed, while ubiquitin forms a slightly larger number of contacts in the transition state and while, accordingly, the enthalpy of the transition state is slightly lower (−28 kcal⋅mol⁻¹ for ubiquitin compared with −23 kcal⋅mol⁻¹ for α3D), the combined configurational- and solvent-entropic cost for forming these contacts is higher, and thus ubiquitin has a higher folding free-energy barrier of ∼5 kcal⋅mol⁻¹ (Fig. 2) compared with only ∼1.5 kcal⋅mol⁻¹ for α3D (19).

Conclusion

We have examined the folding mechanism of human ubiquitin through extensive MD simulations using a physically realistic model. Overall, our simulations reveal a mechanism of folding that is consistent with a large body of experimental data. Although ubiquitin folds much more slowly than a set of 12 fast-folding proteins that we previously characterized (19), our analysis reveals that the principles that govern the folding of those 12 proteins also appear to hold for ubiquitin. Experimental and computational studies of small, engineered fast-folding proteins thus appear to be able to provide important information about mechanisms of protein folding in general, including for naturally occurring proteins.