Testing for improvement in prediction model performance

Abstract

New methodology has been proposed in recent years for evaluating the improvement in prediction performance gained by adding a new predictor, Y, to a risk model containing a set of baseline predictors, X, for a binary outcome D. We prove theoretically that null hypotheses concerning no improvement in performance are equivalent to the simple null hypothesis that Y is not a risk factor when controlling for X, H₀: P (D = 1|X, Y) = P (D = 1|X). Therefore, testing for improvement in prediction performance is redundant if Y has already been shown to be a risk factor. We also investigate properties of tests through simulation studies, focusing on the change in the area under the ROC curve (AUC). An unexpected finding is that standard testing procedures that do not adjust for variability in estimated regression coefficients are extremely conservative. This may explain why the AUC is widely considered insensitive to improvements in prediction performance and suggests that the problem of insensitivity has to do with use of invalid procedures for inference rather than with the measure itself. To avoid redundant testing and use of potentially problematic methods for inference, we recommend that hypothesis testing for no improvement be limited to evaluation of Y as a risk factor, for which methods are well developed and widely available. Analyses of measures of prediction performance should focus on estimation rather than on testing for no improvement in performance.

1. Introduction

Prediction modeling has long been a mainstay of statistical practice. The field has been re-energized recently due to the promise of highly predictive biomarkers identified through imaging and molecular biotechnologies. Accordingly, there has been renewed interest in methods for evaluating the performance of prediction models. In particular, statisticians have been examining methods for evaluating improvement in performance that is gained by adding a novel marker to a baseline set of predictors.

For example, novel markers for predicting risk of breast cancer beyond traditional factors in the Gail model [1, 2] include breast density [3, 4] and genetic polymorphisms [5, 6, 7]. For cardiovascular outcomes, numerous studies have been performed in recent years to evaluate candidate markers for their capacities to improve upon factors in the standard Framingham risk score [8]. Tzoulaki et al. [9] recently performed a meta-analysis of 79 such published studies.

A typical approach to analysis is to first determine the statistical significance of an observed association between the novel marker, Y, and the outcome, D, controlling for the baseline predictors that we denote by X. The p-value is usually derived from regression modeling techniques. If the contribution of Y to the risk model is found to be statistically significant, the second step in the typical approach is to test a null hypothesis about improvement in prediction performance for the model that includes Y in addition to X compared with the baseline model that includes only X. The most popular statistic for testing improvement in prediction performance is the change in the area under the receiver operating characteristic (ROC) curve [9]. Alternate measures are also used, including risk redistribution metrics [10, 11] and risk reclassification metrics [12, 13, 14, 15, 16].

In this paper we question the strategy of testing the null hypothesis about no improvement in prediction performance after testing the statistical significance of Y in the risk model. Our main theoretical result is that the null hypotheses are equivalent. This implies that if Y is shown to be a risk factor, the prediction performance of the model that includes Y cannot be the same as the performance of the baseline model, and there is no point to a second, redundant hypothesis test.

In Section 2 we prove our main result that the null hypothesis about Y as a risk factor can be expressed equivalently as a variety of null hypotheses about the improvement in performance of the expanded model compared with the baseline model. In Sections 3 and 4 we consider the choice of methodology for testing the common null hypothesis. We recommend use of standard statistics derived from regression modeling of the risk as a function of X and Y. This recommendation is based partly on the superior power achieved with likelihood based tests, but also on the new finding corroborated by other recent reports in the literature [14, 17, 18], that standard hypothesis testing methods to compare performances of nested models appear to be invalid. We emphasize that estimation of the increment in prediction performance is more important than testing the null hypothesis of no improvement. The results are discussed in Section 5 in the context of a real dataset concerning risk of renal artery stenosis as a function of baseline predictors and a biomarker, serum creatinine.

2. Equivalent Null Hypotheses

Suppose that the outcome is binary, D = 1 for cases or D = 0 for controls, which could represent occurrence of an event within a specified time period, say breast cancer within 5 years. Let risk(X) = P(D = 1|X) and risk(X, Y) = P(D = 1|X, Y) be the baseline and enhanced model risk functions respectively, which we assume have absolutely continuous distributions. To evaluate the incremental value of Y for prediction over use of X alone, the first step is often to test the null hypothesis

$$H_0:\text{risk}(X,Y)=\text{risk}\left(X\right).$$ (1)

We use subscripts (X, Y) and X to indicate entities relating to use of risk(X, Y) and risk(X), respectively. For example, ROC_(X,Y) is the ROC curve for risk(X, Y) while ROC_X is the ROC curve for risk(X). The ROC curve for W is a plot of P(W > w|D = 1) versus P(W > w|D = 0) and it is a classic plot for displaying discrimination achieved with a variable W [19] (Chapter 4). To test if discrimination provided by risk(X, Y) is better than that provided by risk(X), one could test

$$H_0:{\text{ROC}}_{(X,Y)}(\cdot )={\text{ROC}}_X(\cdot ).$$ (2)

In ROC analysis the area under the ROC curve (AUC) is typically used as the basis of a test statistic. Then the null hypothesis is more specifically stated as

$$H_0:{\text{AUC}}_{(X,Y)}={\text{AUC}}_X.$$ (3)

In the ROC framework another approach is to assess if, conditional on X, the ROC curve for Y is equal to the null ROC curve [20]. This is particularly relevant when controls are matched by design to cases on X [21]. The corresponding null hypothesis is

$$H_0:{\text{ROC}}_{Y\mid X}\left(f\right)=f,f\in (0,1)\forall X.$$ (4)

Several authors have proposed alternatives to ROC analysis for comparing nested prediction models. The predictiveness curve displays the distribution of risk as the risk quantiles [10, 22, 23]. We write the cumulative distribution of risk as F_(X,Y)(p) = P(risk(X, Y) ≤ p) and F_X(p) = P(risk(X) ≤ p). One can test if the risk distributions based on X or on (X, Y) are different by testing the null hypothesis

$$H_0:F_{X,Y}(\cdot )=F_X(\cdot ).$$ (5)

Another view is to consider the risk distributions in the case population (denoted with superscript D) and in the control population (superscript D̄), separately. We could test

$$H_0:F_{(X,Y)}^D(\cdot )=F_X^D(\cdot )\text{and}{F}_{(X,Y)}^{\stackrel{‒}{D}}(\cdot )=F_X^{\stackrel{‒}{D}}(\cdot )$$ (6)

The integrated discrimination improvement statistic is a summary measure based on the difference in average risks between cases and controls, MRD = E(risk(·)|D = 1) − E(risk(·)|D = 0). The MRD has many interpretations, for example as the proportion of explained variation, as an R² statistic, as Yates slope, and as an average Youden’s index [14, 24, 25]. Pencina and others [12] define the integrated discrimination improvement (IDI) as IDI = MRD_(X,Y) − MRD_X and propose testing H₀: IDI = 0. That is, they propose testing

$$H_0:{\text{MRD}}_{(X,Y)}={\text{MRD}}_X.$$ (7)

Another interesting summary of the difference between the case and control risk distributions concerns proportions with risk above the average population risk, ρ = P(D = 1). The above average risk difference is AARD = P(risk(·) > ρ|D = 1) − P(risk(·) > ρ|D = 0). Like the MRD, the AARD has multiple interpretations and relates to existing measures of prediction performance. The AARD is the continuous net reclassification index (NRI (>0), defined below) [13] for comparing a risk model with the null model that has no predictors in which all subjects are assigned risk P(D = 1) = ρ. The AARD is also equal to the two-category NRI for comparing a model with the null model when the two risk categories are defined as: low risk ‘risk≤ρ’ and high risk≡‘risk> ρ’. The AARD can also be considered as a measure relating to the risk distribution in the population, F in equation (5). In particular Bura and Gastwirth [26] defined the total gain statistic as the area between the predictiveness curve for risk(·) and the horizontal line at ρ, which is the predictiveness curve for the null model. Gu and Pepe [25] showed that the standardized total gain, total gain/2ρ(1 − ρ), is AARD. One can compare the performance of two risk models by evaluating the AARD values and testing the null hypothesis

$$H_0:{\text{AARD}}_{(X,Y)}={\text{AARD}}_X$$ (8)

The medical decision making framework has also been used to compare risk models. Vickers and Elkin [27] suggested use of decision curves that plot the net benefit, $NB\left(t\right)\equiv \rho P\left(\text{risk}\right(\cdot )>t\mid D=1)-(1-\rho )\frac{t}{1-t}P\left(\text{risk}\right(\cdot )>t\mid D=0)$ against t, the risk threshold. One could envision testing the equality of decision curves

$$H_0:{\text{NB}}_{(X,Y)}(\cdot )={\text{NB}}_X(\cdot )$$ (9)

to compare performance of a model that includes Y with one that does not. Baker [28, 29] suggests standardizing the net benefit by the maximum possible benefit resulting in a relative utility measure. Testing equality of relative utility curves is the same as testing equality of decision curves in (9).

Risk reclassification methodology is yet another approach to comparing risk models. In this framework, for each individual indexed by ı, risk(X_ı, Y_ı) is compared directly with risk(X_ı). The NRI statistic is a risk reclassification measure that has gained tremendous popularity since its introduction by Pencina and colleagues in 2008 [12]. The continuous NRI [13] is defined as

$$\text{NRI}(>0)=2\left\{P\right[\text{risk}(X,Y)>\text{risk}\left(X\right)\mid D=1]-P[\text{risk}(X,Y)>\text{risk}\left(X\right)\mid D=0\left]\right\}$$

The final null hypothesis that we consider testing is

$$H_0:\text{NRI}(>0)=0$$ (10)

Our key result is that all of the null hypotheses in equations (1) through (10) are equivalent. The only condition required for this equivalence is that the distributions of risk(X) and risk(X, Y) are absolutely continuous. Before stating the main theorem we state a result used to prove the theorem, a result that is important in its own right.

Result 1

$${\text{ROC}}_{(X,Y)}\left(f\right)\ge {\text{ROC}}_X\left(f\right)\forall f\in (0,1)$$

Proof

A fundamental result from decision theory is that decision rules of the form ‘risk(X, Y) > c’ have the best operating characteristics in the sense that when c is chosen to yield a false-positive rate f, f = P(r(X, Y) > c(f)|D = 0), the corresponding true-positive rate t = P(r(X, Y) > c(f)|D = 1) cannot be exceeded by the true positive rate of any other decision rule based on (X, Y) that has the same false positive rate f (see Green and Swets [34]). This result follows from Neyman-Pearson [32] and is discussed in detail in McIntosh and Pepe [33].

It follows that the ROC curve for risk(X, Y) is at least as high at all points as the ROC curve for any other function of (X, Y). In particular, the ROC curve for the function risk(X) cannot exceed the ROC curve for risk(X, Y), namely, ROC_(X,Y)(·), at any point.

Theorem 1

The following null hypotheses are equivalent

Proof

That $H_0^1$ implies each of $H_0^2-H_0^{10}$ is obvious. Therefore we focus on showing that each of $H_0^2-H_0^{10}$ imply $H_0^1$. We start with $H_0^7$ and work in reverse order through $H_0^6$, $H_0^5$, …, $H_0^2$. Then we show $H_0^8$, $H_0^9$, $H_0^{10}\Rightarrow H_0^1$.

1. $H_0^7$ implies $H_0^1$

   Pepe, Feng and Gu [24] write

   $${\text{MRD}}_{(X,Y)}-{\text{MRD}}_X=\left\{\text{var}\right(\text{risk}(X,Y))-\text{var}(\text{risk}\left(X\right)\left)\right\}∕P(D=1)P(D=0),$$

   and because E(risk(X, Y)) = E(risk(X)) = Prob(D = 1) it follows that

   $$\begin{array}{cc}\hfill \text{var}\left(\text{risk}\right(X,Y\left)\right)-\text{var}\left(\text{risk}\right(X\left)\right)& =E{\left(\text{risk}\right(X,Y\left)\right)}^2-E{\left(\text{risk}\right(X\left)\right)}^2\hfill \\ \hfill & =E{\left(\text{risk}\right(X,Y\left)\right)}^2-2E{\left(\text{risk}\right(X\left)\right)}^2+E{\left(\text{risk}\right(X\left)\right)}^2.\hfill \end{array}$$
   Since E{risk(X, Y)|X} = risk(X) we have E(risk(X)risk(X, Y)) = E(risk(X)E(risk(X, Y)|X)) = E(risk(X))². Therefore

   $$\begin{array}{cc}\hfill \text{var}\left(\text{risk}\right(X,Y\left)\right)-\text{var}\left(\text{risk}\right(X\left)\right)& =E{\left(\text{risk}\right(X,Y\left)\right)}^2-2E\left(\text{risk}\right(X\left)\text{risk}\right(X,Y\left)\right)+E{\left(\text{risk}\right(X\left)\right)}^2\hfill \\ \hfill & =E{\left\{\text{risk}\right(X,Y)-\text{risk}(X\left)\right\}}^2\hfill \end{array}$$

   Therefore if MRD_(X,Y) − MRD_X = 0 it follows that E{risk(X, Y) − risk(X)}² = 0 and so risk(X, Y) = risk(X) with probability 1. That is, $H_0^1$ follows.

2. $H_0^6$ implies $H_0^1$

   Equality of the case specific distributions implies that the case specific means are equal: E(risk(X, Y)|D = 1) = E(risk(X)|D = 1). Similarly E(risk(X, Y)|D = 0) = E(risk(X)|D = 0). Therefore, $H_0^6$ implies $H_0^7$ which we have shown implies $H_0^1$.

3. $H_0^5$ implies $H_0^1$

   The case specific distribution of risk can be derived from the population distribution of risk using Bayes’ theorem [30].

   $$\begin{array}{cc}\hfill P\left(\text{risk}\right(\cdot )=r\mid D=1)& =\frac{P(D=1\mid \text{risk}(\cdot )=r)P\left(\text{risk}\right(\cdot )=r)}{P(D=1)}\hfill \\ \hfill & =rP\left(\text{risk}\right(\cdot )=r)∕P(D=1)\hfill \end{array}$$

   A similar argument applies to the control specific distributions. Therefore equality of population risk distributions in $H_0^5$ implies equality of case and control specific risk distributions in $H_0^6$ which in turn implies $H_0^1$.

4. $H_0^4$ implies $H_0^1$

   $H_0^4$ states that, conditional on X, the distributions of Y in the case and control populations are equal:

   $$P(Y\mid D=1,X)=P(Y\mid D=0,X)=P(Y\mid X)$$
   Using Bayes’ theorem it follows that

   $$\frac{P(D=1\mid Y,X)P(Y\mid X)}{P(D=1\mid X)}=P(Y\mid X)$$

   and so P(D = 1|Y, X) = P(D = 1|X). That is $H_0^1$ holds.

5. $H_0^3$ implies $H_0^1$

   Huang and Pepe [31] derived the one-one mathematical relationship between the ROC curve for risk(·) and the predictiveness curve which characterizes the risk distribution. Therefore equality of ROC curves for risk(X, Y) and risk(X) implies equality of the risk distributions, $H_0^5$, which in turn implies $H_0^1$.

6. $H_0^2$ implies $H_0^1$

   We now show that equality of AUCs for risk(X, Y) and risk(X) implies equality of the ROC curves, i.e. $H_0^2\Rightarrow H_0^3$, from which $H_0^1$ follows. This follows from Result 1 that states ROC_(X,Y)(·) ≥ ROC_X(·). If the areas under ROC_(X,Y)(·) and ROC_X(·) are equal, Result 1 implies that the functions must be equal at all points. That is $H_0^3$ must hold.

7. $H_0^8$ implies $H_0^1$

   In the Appendix, Theorem A.1 considers the entity ${\text{ROC}}_{(X,Y)}\left(t_{(X,Y)}^{\rho }\right)-t_{(X,Y)}^{\rho }$ where $t_{(X,Y)}^{\rho }\equiv P\left(\text{risk}\right(X,Y)>\rho \mid D=0)$. But, by definition of $t_{(X,Y)}^{\rho }$ and the ROC curve, we recognize ${\text{ROC}}_{(X,Y)}\left(t_{(X,Y)}^{\rho }\right)=P\left(\text{risk}\right(X,Y)>\rho \mid D=1)$. Therefore Theorem A.1 states that if P(risk(X, Y) > ρ|D = 1) − P(risk(X, Y) > ρ|D = 0) = P(risk(X) > ρ|D = 1) − P(risk(X) > ρ|D = 0) it follows that ROC_(X,Y)(t) = ROC_X(t) ∀ t. That is, $H_0^8$ implies $H_0^3$, which in turn implies $H_0^1$.

8. $H_0^9$ implies $H_0^1$

   If NB_(X,Y)(t) = NB_X(t) ∀ t, then in particular we have equality at t = ρ: NB_(X,Y)(ρ) = NB_X(ρ). Recall that NB(t) is defined as

   $$\text{NB}\left(t\right)=\rho P(\text{risk}>\rho \mid D=1)-(1-\rho )\frac{t}{1-t}P(\text{risk}>\rho \mid D=0)$$

   so at t = ρ we have

   $$\text{NB}\left(\rho \right)=\rho \text{AARD}.$$

   Therefore $H_0^9$ implies $H_0^8$, which in turn implies $H_0^1$.

9. $H_0^{10}$ implies $H_0^1$

   We show below that P(risk(Y) > ρ|D = 1) ≥ P(risk(Y) > ρ|D = 0). An analogous proof that conditions each component on X implies that

   $$0\le P\left(\text{risk}\right(X,Y)>\text{risk}(X)\mid D=1,X)-P\left(\text{risk}\right(X,Y)>\text{risk}(X)\mid D=0,X).$$
   But

   $$\begin{array}{cc}\hfill \text{NRI}(>0)& =2\left\{P\right(\text{risk}(X,Y)>\text{risk}\left(X\right)\mid D=1)-P(\text{risk}(X,Y)>\text{risk}\left(X\right)\mid D=0\left)\right\}\hfill \\ \hfill & =2E\left\{P\right(\text{risk}(X,Y)>\text{risk}\left(X\right)\mid D=1,X)-P(\text{risk}(X,Y)>\text{risk}\left(X\right)\mid D=0,X\left)\right\}\hfill \end{array}$$
   So if NRI(> 0) = 0 it follows that for all X with probability 1 we have

   $$P\left(\text{risk}\right(X,Y)>\text{risk}(X)\mid D=1,X)-P\left(\text{risk}\right(X,Y)>\text{risk}(X)\mid D=0,X)=0$$

   The corollary to Theorem A.1 in the Appendix then implies that the ROC curve for Y conditional on X is the null ROC curve. That is, for all X with probability 1, ROC_Y|X(f) = f ∀ f.

   In other words $H_0^4$ holds, which in turn implies $H_0^1$.

   To complete the proof we need to prove our assertion that P(risk(Y) > ρ|D = 1) ≥ P(risk(Y) > ρ|D = 0). Using Bayes’ theorem this can be restated as

   $$\frac{P(D=1\mid \text{risk}(Y)>\rho )}{P(D=1)}\ge \frac{P(D=0\mid \text{risk}(Y)>\rho )}{P(D=0)}$$

   $$\frac{a}{b}\ge \frac{1-a}{1-b}$$

   But this holds because we have a ≥ b, implying that 1 − a ≤ 1 − b, from which it follows that a/b ≥ 1 ≥ (1 − a)/(1 − b).

Theorem 1 is a mathematical result involving the functions risk(X, Y) and risk(X) and performance measures that are functionals of them. No modeling of the risk functions is assumed. No data sampling is involved in Theorem 1. In the next sections we consider practical implications of Theorem 1 for data analysis in which models for risk(X, Y) and risk(X) may be fit to data.

3. Properties of Hypothesis Testing Procedures

The equivalence of the various null hypotheses in Theorem 1 should not be confused with the equivalence of different hypothesis tests. Two tests can have the same null hypothesis but still be different tests and give different results on a dataset because they are based on different test statistics with different statistical properties. However, it does not make sense to test the same null hypothesis twice — a single test should be chosen. How does one choose the statistical test for the null hypothesis of no incremental predictive value?

There are many possible choices. Here we focus on the choice between a test for the coefficient for Y in a regression model of the risk function risk(X, Y) and the change in the AUC for the ROC curves associated with estimated risk functions, risk(X) and risk(X, Y). To make the discussion concrete, we consider the likelihood ratio test for β_Y, which is the coefficient for Y in a model for risk(X, Y), and a test based on the difference $\Delta \widehat{\text{AUC}}={\widehat{\text{AUC}}}_{(X,Y)}-{\widehat{\text{AUC}}}_X$ where $\widehat{\text{AUC}}$ is calculated with the empirical distributions of the fitted values for the risk function in subjects with D = 1 and D = 0.

3.1. Testing the regression coefficient has highest power

When the data are independent identically distributed observations, the likelihood ratio test is asymptotically the most powerful test for testing $H_0^1-H_0^{10}$, and so, at least in this classic setting, the test based on β_Y is to be preferred. We see the power advantage demonstrated in the second row of the simulation results in Table 1 where the procedure based on $\Delta \widehat{\text{AUC}}$ is fixed to have size equal to the nominal level of 0.05. It is also instructive to consider the special case where there are no baseline covariates. In that setting $\Delta \widehat{\text{AUC}}$ is equivalent to the nonparametric two-sample Wilcoxon statistic while ${\widehat{\beta }}_Y$ from a linear logistic risk model is asymptotically equivalent to the difference in means and so is equivalent to a two-sample Z-statistic. The Z-test is well known to have superior performance compared with the Wilcoxon test for normal data. That is, testing using ${\widehat{\beta }}_Y$ is well known to be superior to testing using $\Delta \widehat{\text{AUC}}$ for normally distributed data and no baseline covariates.

Table 1.

Performance of two-sided nominal 0.05 level tests. Tests are based on the likelihood ratio for β_Y , the regression coefficient for Y in the risk model logit risk(X, Y) = β₀ + β_XX + β_YY and on $\Delta \widehat{\text{AUC}}={\widehat{\text{AUC}}}_{(X,Y)}-{\widehat{\text{AUC}}}_X$. Tests based on $\Delta \widehat{\text{AUC}}$ were: ‘adjusted’ if regression coefficients were estimated in each bootstrap resampled dataset; and ‘standard’ if bootstrap resampling (bootstrap) or DeLong standard error (se) calculation used fitted values $\widehat{\text{risk}}(X,Y)$ and $\widehat{\text{risk}}\left(X\right)$ derived from the original dataset. Data were simulated with X, Y ~ N(0, 1) in controls, X ~ N(0.74, 1) in cases, Y ~ N(0, 1) in cases under the null and Y ~ N(0.37, 1) or Y ~ N(0.74, 1) in cases under the alternative. 1000 simulations for each scenario and 1000 bootstrap samples per analysis.

Test Statistic	Size(βY = 0)		Power (βY = 0.37)		Power (βY = 0.74)
	n0 = nD̄ = 50	nD = 100,nD̄ = 900	nD = nD̄ = 50	nD = 100,nD̄ = 900	nD = nD̄ = 50	nD = 100,nD̄ = 900
LR(βY)††	0.051	0.052	0.415	0.909	0.933	1.000
$\Delta \widehat{\text{AUC}}-\text{size}\text{fixed}$ †	0.050	0.050	0.256	0.799	0.775	1.000
$\Delta \widehat{\text{AUC}}-\text{se-standard}$	0.000	0.002	0.039	0.280	0.356	0.988
$\Delta \widehat{\text{AUC}}-\text{bootstrap-standard}$	0.000	0.002	0.047	0.291	0.365	0.988
$\Delta \widehat{\text{AUC}}-\text{bootstrap-adjusted}$	0.012	0.014	0.183	0.666	0.692	0.999

^†The rejection thresholds for this test were chosen using the null distribution calculated from 50,000 simulated datasets. In practice the null distribution is unknown so this test cannot be applied.

^††Results are shown for the likelihood test. Almost identical results were obtainedwith the Wald test, which is asymptotically equivalent to the likelihood ratio test.

3.2. Standard tests of performance measures may not be valid

From a practical point of view, there are additional issues that make the likelihood ratio test more desirable than the $\Delta \widehat{\text{AUC}}$ test. In particular, procedures for fitting risk regression models and for testing coefficients in regression models are highly developed. In contrast, surprisingly little work has been done regarding properties of tests that are based on estimates of performance improvement measures. The typical approach to testing with $\Delta \widehat{\text{AUC}}$ uses the fitted values for risk(X, Y) and risk(X) as data inputs to a test of equal AUCs for two diagnostic tests such as the DeLong test [35] or the resampling based test [39]. The fact that the coefficients in the fitted values are estimated from the data is ignored in these testing procedures.

We used simulation studies to investigate the properties of these tests in a simple scenario. We generated data for X and Y as independent and normally distributed with standard deviation 1 in cases (D = 1) and controls (D = 0). The mean of X was 0.74 in cases and 0 in controls yielding an AUC of 0.7 for the baseline risk model. The mean of Y was 0 in cases and in controls under scenarios simulating the null setting for evaluating size, while the means were 0.37 or 0.74 in cases and 0 in controls under scenarios simulating the alternative setting for evaluating power. We see from the third and fourth rows in Table 1 that standard tests ignoring sampling variability in the estimated risk regression coefficients are extremely conservative. Both the DeLong test [35] that uses the normal approximation with a standard error formula and the test using percentiles of the bootstrap distribution [39] have size less than .005 with sample sizes as large as 100 cases and 900 controls. The problem is due to estimating the coefficients in the nested models since the same tests comparing X alone to another independent marker with equal performance were not conservative with comparable sample sizes (data not shown). Demler et al. [18] recently provided some theoretical arguments for poor performance of the DeLong test. Tests using $\Delta \widehat{\text{AUC}}$ standardized by the bootstrap variance had similar properties (data not shown).

We implemented an alternative version of the $\Delta \widehat{\text{AUC}}$ test in the hope that acknowledging sampling variability in the estimated regression coefficients would lead to a test with correct size. This approach used the bootstrap, rejecting the null hypothesis if the 2.5^th percentile of the bootstrap distribution exceeded 0. In these simulations we resampled observations from the original dataset, fit the risk models, and calculated $\Delta \widehat{\text{AUC}}$ for each resampled dataset. Results are shown in line 5 of Table 1 as $\Delta \widehat{\text{AUC}}-\text{adjusted}$. These tests were less conservative than procedures not adjusting for variability in regression coefficients but remained conservative nevertheless. Therefore, simply acknowledging variability of the estimated regression coefficiences in the bootstrap procedure does not rectify the problem. Rather, it appears that estimating the regression coefficients leads to non-normality of the distribution of $\Delta \widehat{\text{AUC}}$ under the null, which in turn invalidates use of the bootstrap procedure. This non-normality was reported previously for the $\Delta \widehat{\text{AUC}}$ statistice [18]. Kerr et al [40] found a similar phenomenon for the IDI statistic under the null.

We conclude that all currently available procedures for testing incremental value based on $\Delta \widehat{\text{AUC}}$ in the full dataset are unacceptably conservative in the classic scenarios we studied. From Table 1 we observe that as a consequence they have extremely low power compared with the likelihood ratio test for β_Y.

Note that a simple split sampling approach can yield valid inference about ΔAUC. In particular, if the dataset is split into a training set where the risk models are fit, and a test set where fitted values are calculated, standard methods for inference about ΔAUC can be applied in the test set using those fitted values because they are fixed functions of the test set observations. However, the power of this split sample ΔAUC approach is compromised by the reduced sample size of the test set relative to the full dataset. The power will be much lower than that of a test based on β_Y that uses the entire dataset.

4. Recommendations for practice

When risk functions fit a dataset reasonably well, Result 1 and Theorem 1 hold approximately in the data. There are at least two important implications of these results and of the simulation results described earlier for practical data analysis.

1. If parametric risk models are employed and if there are no over-fitting issues that could invalidate inference, one should use likelihood based methods for testing if coefficients associated with Y are zero in order to test the null hypothesis of no performance improvement. The rationale is that likelihood based procedures have optimal power and that highly developed, well performing methods for inference are available.

2. If risk models are fit using alternatives to parametric models, Theorem 1 implies that methods to test $H_0^1$: risk(X, Y) = risk(X) can be based on performance measures mentioned in Theorem 1, such as AUC_(X,Y) − AUC_X or IDI or AARD_(X,Y) − AARD_X or NRI(> 0). However, we need to develop valid methods for inference about these performance measures under the null hypothesis before we can implement such hypothesis testing procedures.

The estimated risk model, $\widehat{\text{risk}}\left(X\right)$, is considered to fit the data well if, within subgroups S_X defined by X, the frequency of events, $\widehat{P}(D=1\mid X\in S_X$, is approximately equal to the average estimated risk:

$$\widehat{P}(D_i=1\mid X_i\in S_X)\approx \text{Average}\left(\widehat{\text{risk}}\right(X_i)\mid X_i\in S_X).$$

This is also called good calibration of the model $\widehat{\text{risk}}\left(X\right)$. Similarly the fitted model for risk(X, Y) is considered well calibrated if

$$\widehat{P}(D_i=1\mid (X_i,Y_i)\in S_{(X.Y)})\approx \text{Average}\left(\widehat{\text{risk}}\right(X_i,Y_i)\mid (X_i,Y_i)\in S_{(X,Y)})$$

where S_(X,Y) denotes a subset of observations defined by X and Y. It is our opinion that risk models should be shown to be well calibrated in the dataset before proceeding to evaluate their prediction performances. Poorly calibrated models, by definition, are known to misrepresent the risk functions in the population and are therefore inappropriate as risk calculators for use in practice. Consequently the prediction performance of poorly calibrated models is not important. There is a large literature on methods to estimate well fitting models and to evaluate calibration. See for example textbooks by Harrell (2001) and Steyerberg (2010) [36, 37]. The focus of this paper is on settings where the dimensions of X and Y are low. Ensuring good calibration is tenable when X and Y are low dimensional.

Overfitting is a concern primarily when the number of predictors is large. Overfitting yields estimated risks that are likely to be biased towards values more extreme than the true risks. Techniques such as penalized likelihood can be used to address this issue. Another approach is to use a subset of the data to reduce the dimensions of X and Y to one before fitting and evaluating risk models for X and (X, Y) in the remaining data. We demonstrate this approach in the context of an example in Section 5.

In summary, if one employs parametric risk models, our recommendation is to ensure the use of well calibrated models and to base hypothesis testing on β_Y rather than on ΔAUC. Current procedures based on ΔAUC do not have correct size. Kerr et al [40] found similar problems for the IDI statistic under the null. It is possible that new approaches to testing based on ΔAUC could be developed to properly account for estimation of the risk values and thereby yield appropriately sized tests. However, even if such procedures were developed, we have argued and observed in Table 1 (line 2) that tests based on β_Y are still likely to be more powerful, at least when likelihood based procedures are used to estimate parameters in the risk models. Therefore testing based on β_Y would still be the better choice.

More important than testing if there is any increment in prediction performance is estimating the size of the gain in performance. The sizes of the regression coefficients for Y and X in risk(X, Y) are not sufficient because prediction performance depends on the population distribution of the predictors (X, Y) in addition to the conditional probability function P(D = 1|X, Y) = risk(X, Y). A variety of measures to quantify the prediction performance of a risk model were described in Section 2 and a comparison of the measures calculated with risk(X) and risk(X, Y) constitutes the corresponding increment in performance due to Y. The field of risk prediction however has not yet settled debates about which are the best measures for quantifying performance increment and we do not debate this question further here. Our recommendation is to focus on estimating a compelling measure of increment in prediction performance. Any testing should be limited to testing whether Y is a risk factor when controlling for X in a regression model.

We note that one further implication of Theorem 1 is that if Y is found to be statistically significant as a risk factor at the α-level, then 0 should be excluded from confidence intervals for changes in AUC, MRD and AARD statistics and for the NRI (> 0) statistic. The effect on confidence interval coverage probabilities caused by excluding 0 when H₀ is rejected is a subject for future study. Nevertheless the practice seems intuitively reasonable and provides internal consistency for data analysis results.

5. Application to a Renal Artery Stenosis Dataset

Diagnosis of stenosis in the renal artery involves a risky surgical procedure and is only undertaken for patients deemed likely to have a positive finding. The risk of having renal artery stenosis is estimated from clinical data in order to guide decisions about undergoing invasive surgery for definitive diagnostic procedures. Data for 426 patients who were surgically assessed for renal stenosis were reported by Janssens and others [41]. We consider the improvement in prediction performance that is gained by adding serum creatinine to the baseline predictors.

We randomly chose one third of the observations (n = 142; 33 of the 98 cases and 109 of the 328 controls) as a training set to generate a baseline risk predictor X that is a combination of the candidate clinical variables. Using linear logistic regression we found that age, body mass index (BMI) and abdominal bruit (bruit) were highly significantly associated with renal stenosis but that gender, hypertension and vascular stenosis were not. We refit the model including only age (in years), BMI (kg/m²) and bruit (yes=1, no=0) to derive the linear combination

$$X=0.87\times \text{age}-0.27\text{BMI}+1.39\times \text{bruit}-1.99.$$

We then evaluated the performances of risk models based on this one-dimensional predictor X and on the combination of X and Y = log (serum creatinine) using the remaining two thirds of the data (n = 284), the evaluation dataset.

Linear logistic models were fit in the evaluation dataset:

$$\text{Baseline}:\mathrm{logit}P(D=1\mid X)={\alpha }_0+{\alpha }_{1}X$$

$$\text{Enhanced}:\mathrm{logit}P(D=1\mid X,Y)={\beta }_0+{\beta }_{1}X+{\beta }_{2}Y.$$

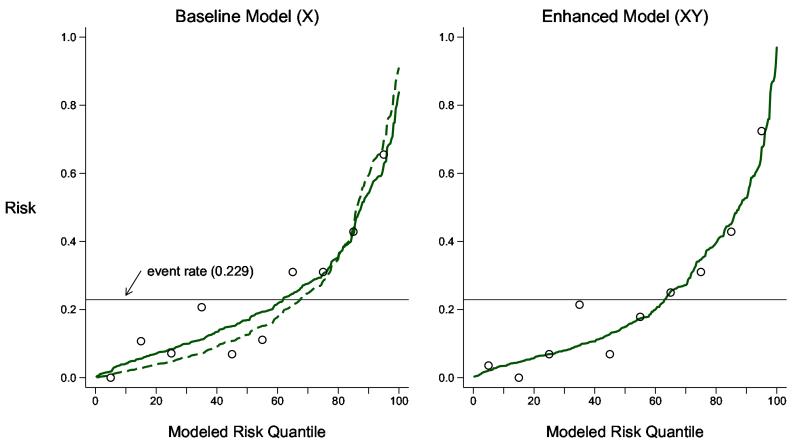
The predictiveness curves in Figure 1 show that these models are well calibrated to the evaluation study cohort since observed event rates in each decile of modeled risk (shown as open circles) are approximately equal to the average modeled risks (shown as the points on the solid predictiveness curves). Hosmer-Lemeshow goodness of fit statistics [10, 38, 43] do not provide any evidence against the null of good calibration (p-values of 0.42 for the baseline model, risk(X), and 0.51 for the enhanced model, risk(X, Y)).

Figure 1.

Predictiveness curves to assess calibration of baseline and enhanced risk models for renal artery stenosis in the evaluation dataset (n = 284). Shown are the modeled risk quantiles (as curves) and the observed event rates within each decile of modeled risk (as open circles). Hosmer-Lemeshow statistics corresponding to the plots have p-values equal to 0.43 (baseline model) and 0.51 (enhanced model). The quantiles of the risk function fitted in the one-third dataset used to generate X is also shown as the dashed curve and appears steeper than the model recalibrated in the evaluation dataset.

As an aside we also calculated risk estimates in the evaluation dataset using the model for risk(X) originally fit in the one-third dataset that generated X. The dashed predictiveness curve in Figure 1 shows that the original model does not fit the evaluation dataset. There is evidence that the original model suffers from over-fitting since the risk quantiles are more extreme than the observed event rates within each decile of X. One can think of the model for risk(X) fit in the evaluation dataset as a recalibrated version of the original model fit in the one-third dataset. This approach has been previously described. See, for example, van Houwelingen [44]. Recalibrating the risk model is a step missing from the usual split sample approach that simply evaluates the performance of the original model fit in the training dataset. If that model is over fit, however, we have argued that its prediction performance is not of interest as the risk estimates derived from it are biased towards extreme values. We recommend recalibration before evaluating prediction performance in the evaluation set.

Consider now the comparison between the risk functions risk(X) and risk(X, Y) in the evaluation dataset.

The likelihood ratio test for H₀: β₂ = 0 is highly significant with p = 0.0003 (Table 2). According to Theorem 1 we can conclude that prediction model performance is improved by addition of Y to the model. Nevertheless we implemented tests based on ΔAUC as well to compare inference. The test for equality of AUCs is also significant but with much weaker p-value, p = 0.034, using the DeLong variance formula and p = 0.026 using percentiles of the bootstrap distribution. Recall that these tests do not acknowledge variability in the estimated regression coefficients (${\widehat{\beta }}_1$, ${\widehat{\beta }}_2$) and are extremely conservative. Bootstrapping that incorporated refitting the risk model in each resampled dataset is also not valid according to our simulations. It yielded p-value= 0.07, which was even more conservative in contrast to results of our simulation study. In accordance with our recommendation in Section 4, the test based on β₂ yielded the strongest evidence against H₀ that prediction performance is not improved by including serum creatinine as a predictor.

Table 2.

Logistic regression models for risk of renal artery stenosis fit to data for 284 patients. The addition of Y = log(serum creatinine) to a model including the baseline covariate X is assessed. Also shown are results for a model including Y* = Y + ε where ε ~ N(0, 1) random variable. Log odds ratios are displayed along with standard errors and p-values calculated with likelihood ratio tests.

	Intercept	X	Y or Y*
Baseline Model (X)
coefficient	−0.12	0.76	–
se	0.21	0.12	–
p-value	0.56	<0.001	–
Enhanced Model (X, Y)
coefficient	−0.32	0.67	0.62
se	0.22	0.12	0.18
p-value	0.15	<0.001	<0.001
Enhanced Model (X, Y*)
coefficient	−0.19	0.73	0.31
se	0.21	0.12	0.12
p-value	0.38	<0.001	0.006

We repeated the analysis using a weaker marker, Y*, for illustration. Here Y* = Y + ε where ε is a standard normal random variable, adding noise to Y. In this analysis the coefficient for Y* is highly statistically significant (p = 0.006 with the likelihood ratio test, Table 2) while the standard tests based on ΔAUC are not (p = 0.21 using either the DeLong variance formula or using percentiles of the bootstrap distribution). The bootstrapped adjusted ΔAUC test that refits the models in each bootstrap sample is not significant either, p = 0.28. Again, this supports our recommendation for testing the null hypothesis of no performance improvement on the basis of the regression coefficient for Y in the enhanced risk model, risk(X, Y).

Estimates of prediction performance are shown in Table 3 for the baseline and enhanced risk models. Confidence intervals were calculated using 2.5^th and 97.5^th percentiles of bootstrap distributions with models refit in each bootstrapped dataset. We estimated that the area under the ROC curve increased from 0.78 to 0.81 with addition of serum creatinine. We also considered a point on the ROC curve. In particular, setting the risk threshold so that 80% of the cases are sent for the invasive diagnostic renal arteriography, we find that the proportion of controls who unnecessarily undergo the procedure, denoted by ROC⁻¹(0.8) in Table 3, decreases from 0.36 to 0.33. Note that Pfeiffer and Gail [42] recommend calculating the percent needed to follow (PNF) that is a simple function of ROC⁻¹(f): PNF(f) = ρf + (1 − ρ)ROC⁻¹(f). Therefore the PNF decreased from 0.46 to 0.44. The IDI statistic is the change in the MRD statistic and is calculated as 0.05 while the conceptually similar change in the AARD is 0.014. The continuous-NRI statistic is NRI(> 0) = 0.45. Note that the NRI is measured on a scale from 0 to 2, unlike most other measures that are restricted to (0,1). We calculated the net benefit using a risk threshold of 0.25. This threshold implicitly assumes that the net benefit of diagnosis for a subject with renal artery stenosis is 3 times the net cost of the diagnostic procedures for a subject without stenosis since the cost-benefit ratio = risk threshold/(1-risk threshold) [27]. The maximum possible benefit of a risk model in this population would be that associated with diagnosing all 67 (24%) subjects who have renal stenosis and not sending any controls for the diagnostic procedure. We calculate that the net benefit is 35.4% of maximum with use of the baseline model and 40.5% of maximum with use of the model that includes serum creatinine. We see that 95% confidence intervals for most measures of improvement in performance exclude the null value of 0. The bootstrap confidence interval for the change in AARD was modified to exclude values ≤ 0 because the null hypothesis H₀: β₂ = 0 was rejected, implying that the null hypothesis H₀: ΔAARD = 0 is also rejected.

Table 3.

Performance of baseline and enhanced models for prediction of renal artery stenosis and performance improvement with 95% confidence interval calculated with 1000 bootstrap samples.

Performance Measure		Baseline Model X	Enhanced Model (X, Y)	Performance Improvement†
ROC Area	AUC	0.78	0.81	0.03 (0.01,0.07)
FPR at TPR=0.8	ROC−1(0.8)	0.36	0.33	−0.03 (−0.26,0.07)
Mean Risk Difference	MRD	0.20	0.25	0.05* (0.011,0.116)
Above AverageRisk Difference	AARD**	0.43	0.47	0.014(0,0.11)
Continuous NRI	NRI (> 0)	—	—	0.45 (0.17,0.79)
Net Benefit at 0.25	NB (0.25)	8.1%	9.3%	1.2% (−1.6%,3.4%)

^†Performance improvement is defined as the difference between the measure for the enhanced model and that for the baseline model for all measures except for the NRI.

^*Also known as the IDI statistic.

^**Also known as the Total Gain statistic.

6. Discussion

The main result of this paper is that the common practice of performing separate hypothesis tests, for the coefficient of Y in the risk prediction model and for the change in performance of the model, is literally testing the same null hypothesis twice. Vickers et al. [17] make a heuristic argument for this point. We have proven the result with formal mathematical theory. Testing the same null hypothesis in multiple ways is poor statistical practice and should be replaced with a more thoughtful strategy for analysis that employs a single test of the null. Arguments in favor of basing the single test on the regression coefficient for Y in a risk model include: (i) such tests are most powerful asymptotically; and (ii) techniques are well developed and widely available for performing such tests. This strategy relies on employing risk models that are well calibrated in the data. We have argued that good calibration is a crucial aspect of risk model assessment. If necessary models should be recalibrated to the population of interest prior to assessing model performance. We demonstrated this in the renal artery stenosis dataset.

The split sample recalibration approach that we employed fit a risk model to the baseline predictors U = (U₁, …, U_K) to derive a univariate score that we denoted by X = Σγ_kU_k. We then fit and evaluated models for risk(X) and risk(X, Y) in the evaluation dataset. Note that the model risk(X, Y) = P(D = 1|X, Y) should not be interpreted as a model for risk(U, Y) = P(D = 1|U₁, …, U_K, Y). The former fixes the combination of {U₁, …, U_K} considered in joint modeling with Y and therefore may be less predictive than r(U, Y) that allows the contributions of {U₁, …, U_K} each to vary in the presence of Y. That is, our strategy that evaluates risk(X, Y) rather than risk(U, Y) might lead to a somewhat pessimistic assessment of the incremental value of Y over the baseline prediction model risk(X) = P(D = 1|X) = P(D = 1|U₁, …, U_K). The advantage of our approach is that it offers a way around calibration and performance assessment problems associated with over fitting, but admittedly a potentially pessimistic evaluation of incremental value is a possible downside of this approach.

After testing if there is any improvement in prediction performance, the next task is to estimate the extent of improvement achieved. How to quantify the improvement in performance is a topic of much debate in the literature. A multitude of metrics exist, including ΔAUC, ΔMRD, ΔAARD, approaches based on risk reclassification tables [13, 15, 16], approaches based on the Lorenz curve [42] and approaches based on medical decision making [7, 27, 29, 45]. This paper does not seek to provide guidance on the choice of measure, but we emphasize that estimating the magnitude of improvement is far more important than testing for any improvement. Moreover, if hypothesis testing based on performance measures is employed, it should be with regard to a null hypothesis concerning minimal improvement, H₀: performance improvement ≤ minimal, rather than any improvement, H₀: performance improvement = 0. The exercise of setting standards for minimal improvement may have the added benefit of helping us to choose a clinically relevant measure of performance improvement.

Appendix

We use the following notation

$$t_X^{\rho }\equiv 1-F_X^{\stackrel{‒}{D}}\left(\rho \right)=P\left(\text{risk}\right(X)>\rho \mid D=0)$$

$$t_{(X,Y)}^{\rho }\equiv 1-F_{(X,Y)}^{\stackrel{‒}{D}}\left(\rho \right)=P\left(\text{risk}\right(X,Y)>\rho \mid D=0)$$

We also assume that the distributions of risk(X, Y) and risk(X) are absolutely continuous. This implies that their ROC curves have second derivatives.

Theorem A.1

$$\begin{array}{cc}\hfill & {\text{ROC}}_{(X,Y)}\left(t_{(X,Y)}^{\rho }\right)-t_{(X,Y)}^{\rho }={\text{ROC}}_X\left(t_X^{\rho }\right)-t_X^{\rho }\hfill \\ \hfill & \Rightarrow {\text{ROC}}_{(X,Y)}\left(t\right)={\text{ROC}}_X\left(t\right)\forall t\hfill \\ \hfill & \text{and}{t}_{(X,Y)}^{\rho }=t_X^{\rho }\hfill \end{array}$$ (A.1)

Proof

For W = risk(X) or W = risk(X, Y) it is well known that ROC_W (t) − t is a concave function (Pepe 2003, page 71 [19]). Therefore ROC_(X,Y)(t) − t has a unique maximizer. Moreover, the maximizer occurs when ${\text{ROC}}_{(X,Y)}^{\prime }\left(t\right)=1$. Arguments below in the proof of Corollary A.1 show that this implies ROC_(X,Y)(t) − t is maximized at $t_{(X,Y)}^{\rho }$.

Since ROC_(X,Y)(t) ≥ ROC_X(t) ∀ t, we have

$${\text{ROC}}_{(X,Y)}\left(t_X^{\rho }\right)-t_X^{\rho }\ge {\text{ROC}}_X\left(t_X^{\rho }\right)-t_X^{\rho }$$

and equation (A.1) implies therefore that

$${\text{ROC}}_{(X,Y)}\left(t_X^{\rho }\right)-t_X^{\rho }\ge {\text{ROC}}_{(X,Y)}\left(t_{(X,Y)}^{\rho }\right)-t_{(X,Y)}^{\rho }.$$

It follows that $t_X^{\rho }=t_{(X,Y)}^{\rho }$ because, as noted above, ROC_(X,Y)(t) − t has a unique maximizer at $t_{(X,Y)}^{\rho }$. This also implies by equation (A.1) that ROC_(X,Y)(t^ρ) = ROC_X(t^ρ) where we now use the notation t^ρ for the common value of $t_{(X,Y)}^{\rho }$ and $t_X^{\rho }$.

Next we show that ${\text{ROC}}_X^{\prime }\left(t\right)\le {\text{ROC}}_{(X,Y)}^{\prime }\left(t\right)$ when t < t^ρ. To show this we suppose that ${\text{ROC}}_X^{\prime }\left(t\right)>{\text{ROC}}_{(X,Y)}^{\prime }\left(t\right)$ for some t < t^ρ and show a contradiction by constructing decision rules based on (X, Y) that have an ROC curve exceeding ROC_(X,Y) on a subinterval of (0, t^ρ). If ${\text{ROC}}_X^{\prime }\left(t\right)>{\text{ROC}}_{(X,Y)}^{\prime }\left(t\right)$ at some point t, by continuity of ${\text{ROC}}_X^{\prime }$ and ${\text{ROC}}_{(X,Y)}^{\prime }$ we have ${\text{ROC}}_X^{\prime }\left(t\right)>{\text{ROC}}_{(X,Y)}^{\prime }\left(t\right)$ on an interval (a, b) ⊂ (0, t^ρ). Let r^a denote the risk threshold corresponding to the false positive rate a and consider the family of decision rules that classify positive if {‘$\text{risk}(X,Y)>r_{(X,Y)}^a$’ or [‘$\text{risk}(X,Y)<r_{(X,Y)}^a$ and $\text{risk}\left(X\right)<r_X^a$ and risk(X) > k]’ for $k>r_X^b$}. These decision rules vary in K. They have an ROC curve equal to ROC_(X,Y)(t) at t = a and ROC derivative equal to ${\text{ROC}}_X^{\prime }$ which we assume is higher than ${\text{ROC}}_{(X,Y)}^{\prime }$ over (a, b). Therefore this ROC curve exceeds ROC_(X,Y) over (a, b). But this is impossible because the Neyman-Pearson lemma implies that ROC_(X,Y)(t) is optimal at all t. In particular ROC_(X,Y)(t) ≥ ROC_X(t) at all t. Therefore we cannot have ${\text{ROC}}_X^{\prime }\left(t\right)>{\text{ROC}}_{(X,Y)}^{\prime }\left(t\right)$ for any t < t^ρ.

Recall from above that

$$0={\text{ROC}}_{(X,Y)}\left(t^{\rho }\right)-{\text{ROC}}_X\left(t^{\rho }\right)={\int }_0^{t^{\rho }}\left({\text{ROC}}_{(X,Y)}^{\prime }\right(t)-{\text{ROC}}_X^{\prime }(t\left)\right)dt.$$

But having shown that the integrand is ≥ 0, we must conclude that the integrand is 0,

$${\text{ROC}}_{(X,Y)}^{\prime }\left(t\right)={\text{ROC}}_X^{\prime }\left(t\right)\forall t<t^{\rho }.$$

Moreover equality of ROC_(X,Y)(t) and ROC_X(t) at t = 0 and at t = t^ρ implies

$${\text{ROC}}_{(X,Y)}\left(t\right)={\text{ROC}}_X\left(t\right)\forall t<t^{\rho }.$$

Similar arguments show that ROC_(X,Y)(t) = ROC_X(t) ∀ t > t^ρ.

Corollary A.1

Let ROC_ω(·) be the ROC curve for the risk function risk(ω) = P (D = 1|ω). We show that

$$\begin{array}{cc}\hfill & {\text{ROC}}_{\omega }\left(t_{\omega }^{\rho }\right)=t_{\omega }^{\rho }\hfill \\ \hfill & \Rightarrow {\text{ROC}}_{\omega }\left(t\right)=t\forall t\in (0,1)\hfill \end{array}$$ (A.2)

Proof

ROC_ω(t) − t is maximized at the point where ${\text{ROC}}_{\omega }^{\prime }\left(t\right)=1$. Bayes’ theorem implies that

$$\mathrm{logit}P(D=1\mid \text{risk}(\omega )=r)=\mathrm{logit}\rho +\log {\text{ROC}}^{\prime }(t_{\omega }^{r)}$$

where $t_{\omega }^r=P\left(\text{risk}\right(\omega )>r\mid D=0)$. When ${\text{ROC}}^{\prime }\left(t_{\omega }^r\right)=1$ therefore, P(D = 1|risk(ω) = r) = ρ. That is, the point that maximizes ROC_ω(t) − t is $t_{\omega }^{\rho }$. We write

$$\sup \mid {\text{ROC}}_{\omega }\left(t\right)-t\mid ={\text{ROC}}_{\omega }\left(t_{\omega }^{\rho }\right)-t_{\omega }^{\rho }$$ (A.3)

but (A.2) then implies that sup|ROC_ω(t) − t| = 0. In other words (A.2) implies ROC_ω(t) = t ∀ t ∈ (0, 1). Note that equation (A.3) also follows from the fact that both sides of (A.3) were show to equal the standardized total gain statistic (see equations (6) and (7) of Gu and Pepe [25]).