Genome-Wide Association Mapping With Longitudinal Data

Abstract

Many genome-wide association studies have been performed on population cohorts that contain phenotype measurements at multiple time points. However, standard association methodologies only consider one time point. In this paper, we propose a mixed-model-based approach for performing association mapping which utilizes multiple phenotype measurements for each individual. We introduce an analytical approach to calculate statistical power and show that this model leads to increased power when compared to traditional approaches. Moreover, we show that by using this model we are able to differentiate the genetic, environmental, and residual error contributions to the phenotype. Using predictions of these components, we show how the proportion of the phenotype due to environment and genetics can be predicted and show that the ranking of individuals based on these predictions is very accurate. The software implementing this method may be found at http://genetics.cs.ucla.edu/longGWAS/.

INTRODUCTION

The use of genome-wide association study (GWAS) methodologies has become common practice in the analysis of complex traits. However, it is well known that the genetic variants identified for most common traits only account for a small portion of the heritability [Eichler et al., 2010; Manolio et al., 2009], implying that there are a large number of genetic associations yet to be identified. Many GWAS have been performed in cohorts, in which multiple time points are available for each individual [Aulchenko et al., 2008; Kamatani et al., 2010; Kathiresan et al., 2007; Sabatti et al., 2008]. However, current association methods only utilize one time point for each individual. This is accomplished by either selecting a single measurement [Sabatti et al., 2008] or by computing the average over all time points [Ionita-Laza et al., 2007; Kamatani et al., 2010; Kathiresan et al., 2007]. It is reasonable to assume that a method jointly considering all time points when performing association may have increased power over single time point approaches.

In this paper, we present a method for performing association mapping with longitudinal phenotypes and show that this method has increased power over single time point mapping approaches. Recently, there has been an interest in the prediction of the genetic contribution to traits using cohort data [Yang et al., 2010]. These methods utilize a single phenotype measurement for each individual and predict the genetic contribution to the phenotype by taking into account the relationships between individuals. We show that when utilizing multiple measurements, this genetic contribution can be differentiated from the environmental and error contribution and we show how each of these contributing factors can be accurately predicted. Our method utilizes a mixed effects approach to model phenotype measurements. Mixed-effects models have been used extensively for modeling correlated data and are an important tool in the analysis of longitudinal data [Harville, 1977; Laird and Ware, 1982]. This class of models has been used in the analysis of longitudinal data for twin studies [Wang et al., 2011] as well as pedigree-based family studies [de Andrade et al., 2002]. We propose a model that partitions each individual’s trait measurements into both a genetic and environmental component. We refer to the genetic component as the “genetic influence” to the trait. Similarly, we refer to the environmental contribution as the “lifestyle value.”

To evaluate our method, we first compare power with a traditional mapping procedure utilizing only one time point. Power is evaluated through an analytical approach similar to that introduced by Williams and Blangero [1999]. Using a set of individuals obtained from the Wellcome Trust Case Control Consortium (WTCCC), we show that our method has increased power over traditional approaches. Second, we evaluate the accuracy in calculating genetic influence and lifestyle values for individuals while varying the number of available time points. We show that for phenotypes heavily influenced by the environment, the accuracy in prediction of the proportion of the phenotype due to genetics and environment has large variation. However, when ranking individuals based on their predicted lifestyle values, we find that this ranking is highly concordant with the ranking obtained using the true lifestyle values. This implies that individuals may be effectively categorized by lifestyle based on these predicted values.

MATERIALS AND METHODS

LONGITUDINAL PHENOTYPES

In experiments adopting longitudinal designs, phenotype measurements are collected for each of n individuals at m time points. We expect that measurements acquired from the same individual will tend to be more correlated than those obtained from different individuals. This correlation is due to both genetic and environmental effects shared between measurements. In order to conceptualize this, we present a generative model for phenotype measurements, which is a model specifying the mathematical process by which measurements may be systematically generated.

$$y_{ij}=\mu +G_i+E_{ij}+{\epsilon }_{ij}$$ (1)

The generative model in equation (1) states that a phenotype measurement j from individual i is a function of the global phenotype mean μ, an individual-specific genetic effect G_i, a measurement and individual-specific environmental effect E_ij and an error term ε_{i j}, accounting for other unknown factors such as measurement error. The value of G_i is a function of the genetic variation for individual i, and is expected to remain constant over time as an individual’s genetic make up does not change. This assumption may not hold if there exist, for example, gene-by-environment interactions. On the other hand, the value of E_ij may vary across measurements due to changing environmental conditions. The correlation between each pair of E_ij s will depend on the magnitude of environmental change between time points as well as the degree of influence environment has over the phenotype in question. The residual terms ε_ij are expected to be independent between measurements.

TRADITIONAL APPROACH TO ASSOCIATION MAPPING

The traditional approach to association mapping considers one measurement for each of n individuals and interrogates each genetic locus individually. The traditional model is given as follows

$$y_i=\mu +{\beta }_r{x}_{ir}+{\epsilon }_i$$ (2)

x_ir represents the state of SNP r (single nucleotide polymorphism r) for individual i and β_r its coefficient [Balding, 2006]. By testing the hypothesis β_r = 0, it is determined whether SNP r influences the trait or not. We note that, with respect to the model in equation (1), the model in equation (2) has folded many terms into the residual term ε_i. This model is represented using standard vector notation as follows:

$$\mathbf{y}={\mathbf{X}}_r\beta +\mathbf{\epsilon }$$ (3)

y is a vector of all phenotype measurements and ${\mathbf{X}}_r=[\begin{array}{ll}{\mathbf{1}}_n\hfill & {\mathbf{x}}_r\hfill \end{array}]$, where x_r is a vector representing the n SNP values for SNP r, β is a vector of coefficients and 1_n is a column vector of ones. Other fixed effects may be added to X in order to account for additional confounding.

To apply this model to longitudinal data, the total set of mn measurements must be preprocessed into a set of n independent measurements. There are two common approaches taken and we refer to these as the single approach and the average approach. In the single approach, a single measurement from the set of m measurements is chosen for each individual i. In the average approach, the m measurements for each individual are averaged and the average value is used as the single phenotype measurement for that individual. Under the assumption that individuals are unrelated, both of these procedures result in a set of n independent measurements and the standard model may be applied.

MIXED EFFECTS MODEL FOR ASSOCIATION MAPPING

The traditional method for association mapping interrogates each genetic locus individually while using single time points. However, it is known that traits are often influenced by many loci and ignoring this fact may have a negative impact on association mapping results. In particular, global genetic similarities between individuals may be correlated with trait similarities and this global correlation may cause many genetic loci to appear to be associated with the trait, a problem often referred to as population structure or cryptic relatedness [Devlin et al., 2001; Voight and Pritchard, 2005]. One way to account for this structure is through the use of a variance component model, in which the global genetic relatedness, referred to as polygenic background, of individuals is accounted for by the introduction of a random variable into the simple model from equation (2) [Kang et al., 2010; Lange, 2002; Yu et al., 2006]. This model is summarized as follows.

$$y_i=\mu +{\beta }_r{x}_{ir}+u_i+{\epsilon }_i$$ (4)

The model is equivalently described in matrix notation using

$$\mathbf{y}={\mathbf{X}}_r\beta +\mathbf{Zu}+\mathbf{\epsilon }$$ (5)

The random variable u_i is assumed to be normally distributed with mean zero and variance ${\sigma }_g^2$ and the $cov(u_i,u_j)={\sigma }_g^2{K}_{ij}$, where K_ij is the kinship coefficient for individual i and j, which is a value representing their genetic relatedness. The incidence matrix Z maps measurements from each individual to the phenotype vector y, and in the case when there is only one measurement for each individual Z = I_n. This form is standard in the mixed-model literature. With this the $var(\mathbf{Zu})={\sigma }_g^2{\mathbf{ZKZ}}^{\prime }$ and $var(\mathbf{\epsilon })={\sigma }_{\epsilon }^2\mathbf{I}$. The total variance of y is then given by

$$\mathbf{\sum }={\sigma }_g^2{\mathbf{ZKZ}}^{\prime }+{\sigma }_{\epsilon }^2\mathbf{I}$$ (6)

To test the hypothesis β_r = 0 using the model in equation (5), the two variance components ${\sigma }_g^2$ and ${\sigma }_{\epsilon }^2$ must be estimated. Since there is no analytical solution, this is accomplished using a numerical search algorithm implemented in the program EMMAX [Kang et al., 2010]. EMMAX combines grid search with the Newton-Raphson algorithm, in order to find the optimal variance components ${\sigma }_g^2$ and ${\sigma }_{\epsilon }^2$ in time linear in the number of measurements, given the singular value decomposition of K. Furthermore, by assuming that each SNP only has a small to moderate effect on the phenotype, it is reasonable to assume that variance component estimates will be the same for each SNP. With this assumption it is only necessary to perform the variance component search once and thus feasible to perform the hypothesis test for each SNP within the genome.

There are many methods to compute the kinship matrix K. For a review of many standard relatedness estimators see [Oliehoek et al., 2006]. More recently, [Yang et al., 2010] proposed a method for adjusting the relatedness matrix, to account for the fact that the true causal SNPs may not be strongly correlated with the genotyped SNPs. Such issues are beyond the scope of this paper and thus we will only use the identity by state (IBS) allele sharing matrix [Kang et al., 2008]. Furthermore, these issues and the choice of kinship matrix do not affect our simulation results. In general, the methodology introduced in this paper may be utilized as long as the kinship matrix is positive semi-definite.

ASSOCIATION MAPPING WITH LONGITUDINAL DATA

The models from equations (2) and (4) do not take advantage of the availability of multiple time points and do not directly account for both genetic and environmental factors. We suggest a model that directly accounts for each term using all time points by extending the model in equation (4).

$$y_{ij}=\mu +{\beta }_r{x}_{ir}+u_i+v_{ij}+{\epsilon }_{ij}$$ (7)

The random variable v_ij is introduced to represent the contribution of the environment to the phenotype measurement (E_ij from equation (1)). The matrix version is as follows.

$$\mathbf{y}={\mathbf{X}}_r\beta +\mathbf{Zu}+\mathbf{v}+\mathbf{\epsilon }$$ (8)

We assume, without loss of generality, that the mean of the random components u and v are equal to zero and that the variance structure is as follows, where D is a known matrix representing the covariance between environmental components.

$$var\left[\begin{array}{c}\mathbf{u}\\ \mathbf{v}\\ \mathbf{\epsilon }\end{array}\right]=\left[\begin{array}{ccc}{\sigma }_g^2\mathbf{K}& 0& 0\\ 0& {\sigma }_v^2\mathbf{D}& 0\\ 0& 0& {\sigma }_{\epsilon }^2\mathbf{I}\end{array}\right]$$ (9)

With this we define the variance of y.

$$var(\mathbf{y})=\mathbf{\sum }={\sigma }_g^2{\mathbf{ZKZ}}^{\prime }+{\sigma }_v^2\mathbf{D}+{\sigma }_{\epsilon }^2\mathbf{I}$$ (10)

In general, the matrix D will depend on the level of correlation between individual time points and can be determined through estimation techniques or by fitting parametric models, such as models of the autoregressive class [Jennrich and Schluchter, 1986]. Most commonly D will take the form of a block diagonal matrix, so that environmental components between individuals will be independent. The variance of v is then given as var(v) = D = E ⊗ I, where ⊗ represents the Kronecker product of two matrices, and E is an m × m matrix representing the covariance between the set of m time points for each individual.

MISSING DATA

One complication that often arises when dealing with longitudinal data is that of unbalanced or missing data [McCulloch and Searle, 2001]. When a study is unbalanced, meaning that all individuals do not have the same number of measurements, the model notation becomes slightly more complicated. Let us consider that individual i has m_i measurements and define $\mathbf{m}=[\begin{array}{ll}{m}_1\hfill & m_2\dots m_n\hfill \end{array}]$. The incidence matrix Z will still map genetic components to measurements and its structure will be dictated by the vector m. For example, the first m₁ rows of Z will have a 1 in the first column and the second m₂ rows of Z will have a 1 in the second column and so on.

To avoid complicated notation, we suggest a simple scheme for defining the model. Define the model using m = max(m), so that the assumed number of measurements is equal to nm and the vector y has missing values. Select the measurements that are missing at each individual and remove the rows and columns of the full covariance matrices of each component (genetic, environmental, and residual error) that correspond to the indices of these entries in the vector y of size nm. The resulting covariance matrices will then correspond to a new vector ỹ, defined as the vector y with the missing values removed. Modeling fitting procedures are then readily adaptable to such matrices and hypothesis testing procedures can be easily applied.

ESTIMATING VARIANCE COMPONENTS

To fit the models in equations (5) and (8), we must estimate a set of variance components. For the model in equation (5), a linear time search algorithm based on maximum likelihood exists, which is able to identify the optimal variance components. However, no linear time method exists to find the three variance components required for the model in equation (8). Therefore, we utilize an approach suggested by [Listgarten et al., 2010], in which we use the EMMAX algorithm inside of a linear time search.

First, we rewrite the variance of y as shown in equation (11), letting ${\tau }^2={\sigma }_v^2-{\sigma }_g^2$ and $w={\sigma }_g^2/({\sigma }_v^2-{\sigma }_g^2)$. Then, given a value w between zero and one, we apply the EM-MAX search algorithm to find optimal variance components τ² and ${\sigma }_{\epsilon }^2$. If we search q different values of w, then our approach will be q times slower than EMMAX. More specifically, EMMAX has a one time computational cost of O(N³) followed by a cost of O(r N) for r search iterations, where N is the total number of measurements or the size of the vector y. In comparison, our approach will have a one time cost of O(q N³) followed by a cost of O(q r N). This is compared to the basic Newton-Raphson technique, which has a total computation cost of O(q r N³).

$$\begin{array}{l}var(\mathbf{y})={\tau }^2(w{\mathbf{ZKZ}}^{\prime }+(1-w)\mathbf{D})+{\sigma }_{\epsilon }^2\mathbf{I}\\ ={\tau }^2{\mathbf{K}}^{\ast }+{\sigma }_{\epsilon }^2\mathbf{I}\end{array}$$ (11)

Additional cost will be incurred if D has to be estimated, such as in the case when an auto-regressive model is utilized. For example, in the case where D is determined through an auto-regressive model, the total computational time would be multiplied by the size of the search space for the additional auto-regressive parameter. If the number of iterations required to optimize this parameter were O( p), then the total computational cost will be O( pq N³ + q r N).

PREDICTING LIFESTYLE VALUES AND GENETIC INFLUENCE

The realization of u is a vector of values representing the genetic contribution to the phenotype measurement. That is, u is a random variable and at the time the phenotype was measured a value for u was sampled from a multivariate distribution. This is the realized value. Just as fixed effects are estimated, the value of a random variable can be predicted using the best linear unbiased predictors (BLUPs) introduced by Henderson [1950]. The BLUP for u, denoted by ũ, is given by

$$\stackrel{\sim }{\mathbf{u}}={\sigma }_g^2{\mathbf{KZ}}^{\prime }{\mathbf{\sum }}^{-1}(\mathbf{y}-{\mathbf{X}}_r\widehat{\beta })$$ (12)

where Σ is given by equation (10). The realized value of u represents the overall genetic contribution to the phenotype for each individual. By determining the value of u_i for each individual, we are able to determine what proportion of each phenotypic measurement is due to genetics and what proportion is due to other factors, specifically fixed effects and error. This enables us to compare individuals based on the magnitude of their genetic contributions. Certain individuals may have a stronger genetic effect than others. When this large genetic effect causes phenotypes to become harmful, such as in high cholesterol, we may see this difference as indicator of increased risk. When large genetic effects lead to beneficial phenotypes, this may indicate a sort of genetic robustness, a phenomenon often referred to colloquially as having “good genes.” Therefore, we refer to the realized value of u as the genetic influence.

Just as it is possible to predict u, it is also possible to predict the realized value of v from equation (8). The realized value of v for each individual represents the environmental contribution to the phenotype. By comparing realized values of v it is possible to uncover differences in individual environment, which may be an indicator of an individual’s lifestyle. For this reason, we refer to the realized value of v as the vector of lifestyle values. When calculating the realized values for u and v, we are able to partition each phenotype measurement into genetics, environment, fixed effects and error, and give the proportion that each factor contributes.

$$\left[\begin{array}{c}\widehat{\beta }\\ \stackrel{\sim }{\mathbf{u}}\\ \stackrel{\sim }{\mathbf{v}}\end{array}\right]={\left[\begin{array}{ccc}{\mathbf{X}}^{\prime }\mathbf{X}& {\mathbf{X}}^{\prime }\mathbf{Z}& {\mathbf{X}}^{\prime }\\ {\mathbf{Z}}^{\prime }\mathbf{X}& {\mathbf{Z}}^{\prime }\mathbf{Z}+{\mathbf{K}}^{-1}{\alpha }_1& {\mathbf{Z}}^{\prime }\\ \mathbf{X}& \mathbf{Z}& \mathbf{I}+{\mathbf{D}}^{-1}{\alpha }_2\end{array}\right]}^{-1}\left[\begin{array}{c}{\mathbf{X}}^{\prime }\mathbf{y}\\ {\mathbf{Z}}^{\prime }\mathbf{y}\\ \mathbf{y}\end{array}\right]$$ (13)

The BLUPs for u and v are obtained by solving the system of equations given in equation (13) [Henderson, 1973; Mrode and Thompson, 2005], where ${\alpha }_1={\sigma }_{\epsilon }^2/{\sigma }_g^2$ and ${\alpha }_2={\sigma }_{\epsilon }^2/{\sigma }_v^2$. These solutions are obtained by maximizing the joint likelihood of y, u, and v under the assumption of normality. After solving the so-called mixed-model equations (MME), we obtain a prediction of the random variable v_ij for each individual i and time point j, as well as predictions for u_i for each individual i.

Theoretical accuracy of the random effects may be analyzed by evaluating the variance in the difference between the true and predicted effects, which are calculated by

$$var(\stackrel{\sim }{\mathbf{u}}-\mathbf{u})={\sigma }_g^2\mathbf{K}-{\sigma }_g^2{\mathbf{KZ}}^{\prime }\mathbf{PZ}{\sigma }_g^2\mathbf{K}$$ (14)

$$var(\stackrel{\sim }{\mathbf{v}}-\mathbf{v})={\sigma }_v^2\mathbf{D}-{\sigma }_v^2\mathbf{DP}{\sigma }_g^2\mathbf{D}$$ (15)

where P = Σ⁻¹ − Σ⁻¹X(X′Σ⁻¹X)⁻¹X′Σ⁻¹.

ANALYTICAL POWER FOR MIXED-EFFECTS MODELS

One common approach to evaluate methods for performing association is through the analysis of statistical power [de Bakker et al., 2005]. Although power is easily calculated analytically when assuming the model from equation (2), it is not well-known how to calculate power when using a mixed effects model. For this reason, time consuming simulations are often employed in order to estimate statistical power [Bennett et al., 2010]. Williams and Blangero [1999] introduced a likelihood-ratio based technique to compute power in variance component models used for linkage analysis. We introduce a similar derivation based on the F-test.

Let y be a vector of size n and assume that it has a normal distribution with mean Xβ and variance Σ, where X is an n × q matrix of fixed effects, β is a q × 1 vector of coefficients and Σ is an n × n covariance matrix. In order to test a hypothesis about β, we define a q × 1 matrix R, which defines a linear combination of the elements of β. For example, if X only encodes global mean and SNP, then we define $\mathbf{R}=[\begin{array}{cc}0& 1\end{array}]$, so that Rβ results in the single SNP coefficient. Given R we define the hypothesis test Rβ = r. The generalized least squares (GLS) F-statistic is then given by

$${\phi }_F=\frac{{(\mathbf{R}\widehat{\beta }-\mathbf{r})}^{\prime }{[\mathbf{R}{({\mathbf{X}}^{\prime }{\mathbf{\sum }}^{-1}\mathbf{X})}^{-1}{\mathbf{R}}^{\prime }]}^{-1}(\mathbf{R}\widehat{\beta }-\mathbf{r})}{q}$$ (16)

We show that under the alternative hypothesis Rβ = r + δ, φ_F follows an F-distribution with n − q numerator and q denominator degrees of freedom and noncentrality parameter λ (see Appendix), given by

$$\lambda ={\delta }^{\prime }{[\mathbf{R}{({\mathbf{X}}^{\prime }{\mathbf{\sum }}^{-1}\mathbf{X})}^{-1}{\mathbf{R}}^{\prime }]}^{-1}\delta$$ (17)

It is important to note that we have assumed an optimal estimate for the true covariance matrix Σ. Given the non-centrality parameter in equation (17), power is calculated as the area under the curve of the distribution defined by the noncentrality parameter that is beyond the null rejection region.

SIMULATIONS

The power gain was estimated by generating random covariance matrices for the environmental components and then by averaging analytical power over 1,000 randomly selected SNPs with minor allele frequencies in the range of 1– 5%. The expected power gain was calculated as the average power gain over 1,000 such randomly generated covariance matrices. The covariance matrices were generated by randomly selecting a vector of size m − 1 from a uniform (0,1) distribution, where m is the number of time points. The covariance between time points i and j (i > j) is then given as the (i − j − 1)th entry in this vector. We then define an m × m matrix E using this scheme and define the full environmental covariance matrix D = E ⊗ I.

Phenotypes with multiple time points were generated by sampling both genetic and environmental components from their respective multivariate normal distributions, having a mean of zero and with variance as specified in equation (9). This results in both a genetic and environmental contribution value for each individual. These values are used as the individual’s mean phenotype value to which random noise is added to generate each time point.

Random effects were predicted by fitting the model from equation (8), with only a mean effect, and then by obtaining the solution to equation (13). The environmental covariance matrix was estimated by calculating the correlation between time points using all individuals. This procedure works well, when either the genetic effect is small or the sample has little population structure. In the case where the population has a large amount of structure, we employ a simple iterative scheme. Starting with an estimate of the environmental covariance matrix calculated on the raw data, we predict the random genetic effect. This effect is regressed from the phenotype values and a new environmental covariance matrix is computed with these new phenotype values. This procedure is repeated until the environmental covariance matrix converges.

RESULTS

MULTIPLE MEASUREMENTS PROVIDE INCREASED POWER OVER TRADITIONAL APPROACHES

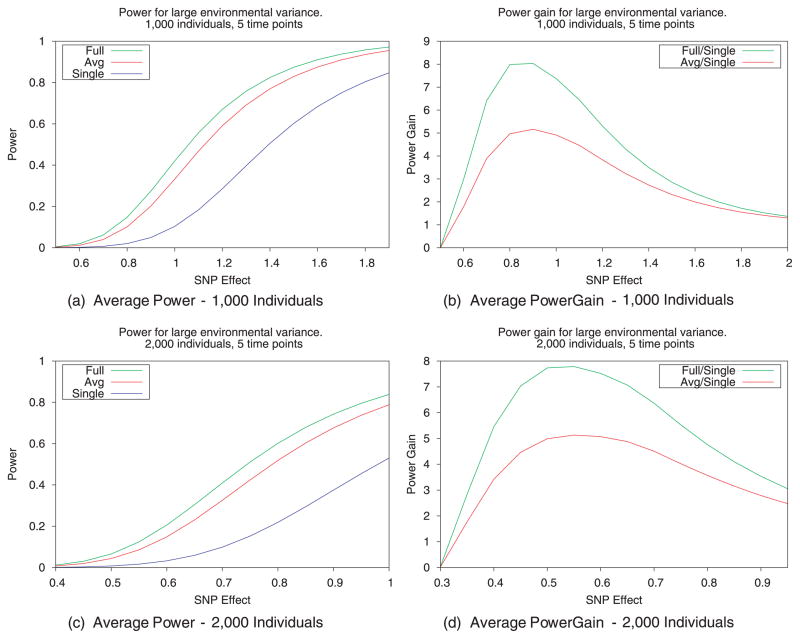
We evaluated the gain in power achieved when using the proposed method (the full method) over using an averaging approach or single approach. In the single approach, a single time point is selected for each individual, while in the average approach time point values are averaged for each individual. Power gain is evaluated by comparing the ratios of the power achieved with one method to that of the power achieved with the single approach. Figure 1 summarizes these results. Power gain was calculated for each effect size by averaging the power gain over 1,000 iterations, in which a different randomly selected environmental covariance matrix was used in the analytical calculation of power. This power was averaged over 1,000 SNPs with minor allele frequency in the range of 1–5%. All calculations assume that the environment accounts for 80% of the phenotypic variance while both the genetic background and residual error account for 10%.

Fig. 1.

Association mapping utilizing multiple measurements leads to an increase in power over traditional approaches. We compare the average power gain for the proposed full model with that of the average model (using averaged measurements for each individual). Power gain is defined as the ratio of the power of a given method to that achieved with the single approach (i.e., mapping with only one measurement for each individual) and was calculated by averaging power gain over 1,000 randomly selected SNPs with minor allele frequency (MAF) in the range of 1–5% and over 1,000 randomly selected covariance structures for the multiple measurements (m = 5). Simulations were performed with the environmental effect accounting for 80% of the variance while the genetic background and residual error accounted for the remaining 20%.

Figure 1 compares both the power curves (Figures 1A and C) and power gain (Figures 1B and D) for 1,000 and 2,000 individuals randomly selected from the WTCCC. We see that on average the full method has increased power when compared to the average and single methods. This increased power is seen more clearly in the power gain plots, which show that the full method has as much as an eightfold gain in power over the single approach, compared to a roughly 4.5-fold power gain achieved by the average approach.

MULTIPLE MEASUREMENTS ALLOW FOR THE PREDICTION OF INDIVIDUAL LIFESTYLE

Another benefit of using the full method over approaches utilizing only one time point is the ability to predict the phenotypic contribution due to environment. We evaluate this ability through simulation. We simulated phenotypes for 1,000 individuals in which the environment accounts for 80% of the variance, while genetic and error each contribute 10%. These phenotypes represent those that are largely influenced by environment. For each phenotype, we predict the environmental contribution and the proportion of the phenotype that this value accounts for. More specifically, each phenotype can be seen as a linear combination of mean, genetic contribution, environmental contribution, and error. Using random effect predictions, as summarized in the methods, we obtain predicted values for the genetic and environmental contributions at each time point. The prediction of random effects for each time point scales with the cube of the number of individuals times the number of time points. In practice, 1,000 individuals and two time points require a running time under 5 min for one phenotype, whereas the running time for 1,000 individuals with five time points is just under 50 min. However, we note that recent advances in the computational theory behind linear mixed models can serve to decrease these running times [Lippert et al., 2011].

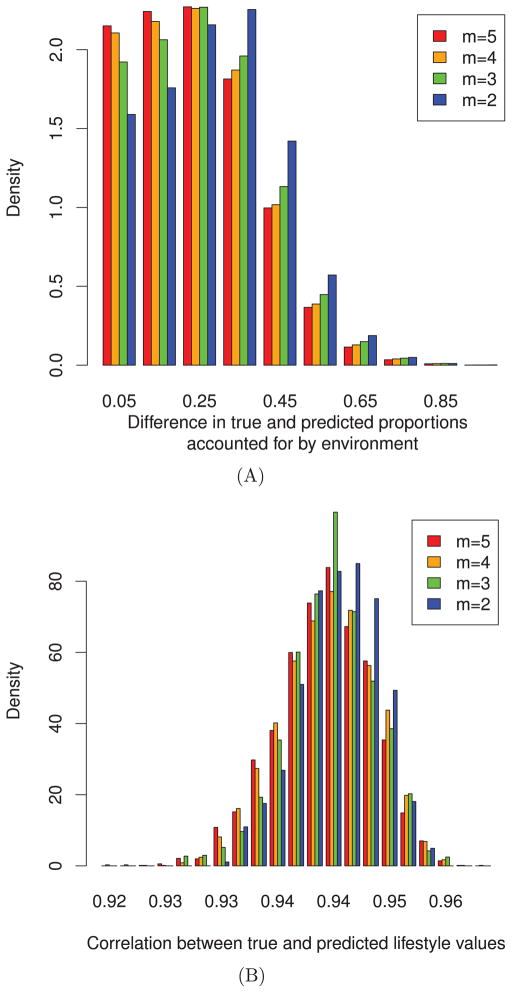
The results of this simulation are summarized in Figure 2. First, we compare the accuracy of the predictions by summarizing the difference in the true proportion of the phenotype contributed by the environmental component with that of the predicted proportion (Figure 2A) for 1,000 randomly generated environmental covariance matrices. From this plot, we see that the difference between the true and predicted proportion hovers around 25%, while increasing the number of time points available shifts this mean toward zero. Despite the high variation in accuracy, Figure 2B, showing the distribution of correlations between the true lifestyle values with the predicted, shows that on average the predictions have a rank correlation of 0.94. This indicates that although accuracy is not always high, the relative ranking of individuals based on their predicted lifestyle values is highly concordant with their true ranking. This implies that individuals may be effectively ranked based on their predicted lifestyle values.

Fig. 2.

The accuracy in prediction of lifestyle values varies, while the ranking remains consistent. For each of 1,000 iterations, lifestyle values were predicted and compared with their known true values, through simulation. Each simulation assumes 1,000 individuals and m time points. (A) Evaluates the difference between the proportion accounted for by the environment as determined by the true lifestyle effect with that of the predicted lifestyle effect. This result indicates that the accuracy of these predictions has a high variation, but that by increasing the number of time points it is possible to obtain more accurate predictions. (B) Shows the distributions of Spearman rank correlations between the true lifestyle and predicted lifestyle values. This result indicates that the ranking of individuals based on their predicted lifestyle is highly concordant with the true lifestyle ranking.

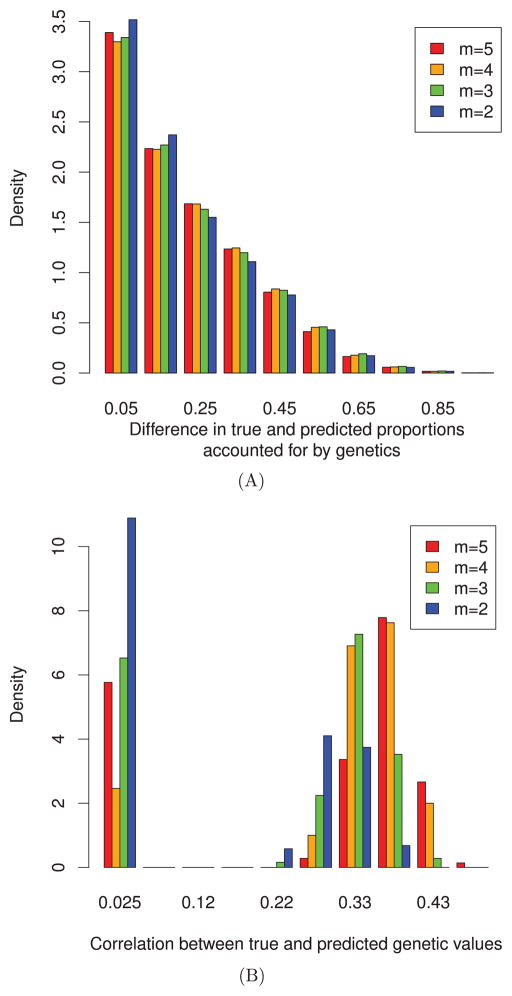
Figure 3 shows the accuracy and correlations for predicted genetic values. We find that the predicted proportions behave very similarly to that of the lifestyle values, except that the availability of additional measurements does not increase accuracy in this case. However, the correlation between the true and predicted genetic effects is on average very small and has a strange pattern. Although, we find that as the number of time points increases, the average correlation increases.

Fig. 3.

The accuracy in prediction of genetic values is similar to that of lifestyle. For each of 1,000 iterations, genetic values were predicted and compared with their known true values, through simulation. (A) Shows a very similar result to that found in lifestyle values, where the accuracy of these predictions has a high variation and has a relatively uniform distribution across different numbers of time points. However, the result in (B) is much different than that found in the lifestyle value prediction. There is not a clear pattern, although the average correlation does increase as the number of time points increases.

DISCUSSION

In this paper, we introduce a mixed-model based approach to perform association mapping in GWAS, when multiple measurements are available. We show that by utilizing multiple measurements, our method achieves increased power over methods that either select a single measurement or average measurements for individuals. Furthermore, we show that when multiple measurements for each individual are available, it is possible to differentiate the genetic contribution from the environmental contribution. We call these quantities the genetic influence and lifestyle values, respectively.

The ability to partition a phenotype into its constituents may be useful for future phenotype prediction and treatment selection. For example, some individuals might gain substantially from a decrease in dietary cholesterol when the largest part of their cholesterol is due to their intake. On the other hand, some individuals who are genetically predisposed to high cholesterol might stand to gain little from decreasing their dietary cholesterol, but instead might require medication in order to alter their overall cholesterol levels. With knowledge of the individual contributions to total cholesterol, the appropriate treatment options may be put in place in order to alter the future of the phenotype.

The previous cholesterol example extends very naturally to explain how prediction of genetic influence and lifestyle may be useful for risk prediction. For example, it may be discovered through these methods that an individual has a very large lifestyle component for cholesterol. In this case, their risk for developing cardiovascular disease may be predicted based on the magnitude and direction of this value, such that the resulting prediction may be different from that obtained by using the total level of cholesterol.

Another interesting aspect of the ability to predict lifestyle values is the subsequent ability to categorize individuals. For example, when evaluating a trait such as lung capacity, certain individuals will have decreased lung capacity due to long-term smoking, while others will have relatively normal capacity given their age and genetic makeup. This might be easily discerned by using a series of questions, but it is well-known that the truth is not always told when answering such questions. In this case, the lifestyle value may help to categorize individuals based only on their phenotype measurements and genotypes.

The model we propose is tested under a certain set of assumptions, however, the structure is very general and may work for a larger class of problems. For example, there are cases when it is not reasonable to assume that a phenotype follows a normal distribution, and a simple transformation such as log is not sufficient to obtain a normally distributed measure. For example, binary or categorical outcomes cannot be expected to follow a normal distribution. In this case, the phenotype may be modeled using a link function, such is done in logistic regression [McCulloch and Searle, 2001]. The models presented here may then be utilized in this space. Furthermore, there may be other factors to include in the model, such as gene-by-environment interactions, or even more complicated treatment-genetic-environmental interactions. Perhaps some individuals have increased variance when subjected to certain environments and certain treatments but not with others. The model presented in this paper can be used as a base to explore such conditions, which may require more complex models with additional random effects.

APPENDIX: CALCULATING POWER UNDER A MIXED EFFECT MODEL

Consider that β̂ ~ N(β, (X′Σ⁻¹X)⁻¹) from equation (16). Now consider that the hypothesis test Rβ = r, while in truth Rβ = r + δ (r = Rβ − δ). To derive a χ² statistic, we first derive a Z-score statistic for the test Rβ = r.

$$\begin{array}{l}Z={[\mathbf{R}{({\mathbf{X}}^{\prime }{\mathbf{\sum }}^{-1}\mathbf{X})}^{-1}{\mathbf{R}}^{\prime }]}^{-1/2}(\mathbf{R}\widehat{\beta }-\mathbf{r})\\ ={[\mathbf{R}{({\mathbf{X}}^{\prime }{\mathbf{\sum }}^{-1}\mathbf{X})}^{-1}{\mathbf{R}}^{\prime }]}^{-1/2}(\mathbf{R}\widehat{\beta }-\mathbf{R}\beta +\delta )\\ ={[\mathbf{R}{({\mathbf{X}}^{\prime }{\mathbf{\sum }}^{-1}\mathbf{X})}^{-1}{\mathbf{R}}^{\prime }]}^{-1/2}(\mathbf{R}(\widehat{\beta }-\mathbf{R}\beta +\delta )\end{array}$$

We know the distribution of β̂ and therefore Rβ̂; thus,

$$\begin{array}{c}{[\mathbf{R}{({\mathbf{X}}^{\prime }{\mathbf{\sum }}^{-1}\mathbf{X})}^{-1}{\mathbf{R}}^{\prime }]}^{-1/2}(\mathbf{R}(\widehat{\beta }-\beta ))~N(0,I)\\ {[\mathbf{R}{({\mathbf{X}}^{\prime }{\mathbf{\sum }}^{-1}\mathbf{X})}^{-1}{\mathbf{R}}^{\prime }]}^{-1/2}(\mathbf{R}(\widehat{\beta }-\beta )+\delta )\\ ~N({[\mathbf{R}{({\mathbf{X}}^{\prime }{\mathbf{\sum }}^{-1}\mathbf{X})}^{-1}{\mathbf{R}}^{\prime }]}^{-1/2}\delta ,I)\end{array}$$

Squaring Z, we obtain a χ² statistic. Let W = [R(X′Σ⁻¹X)⁻¹Rβ].

$$\begin{array}{l}{\phi }_c={(\mathbf{R}(\widehat{\beta }-\beta )+\delta )}^{\prime }{\mathbf{W}}^{-1}(\mathbf{R}(\widehat{\beta }-\beta )+\delta )\\ ={(\mathbf{R}\widehat{\beta }-\mathbf{r})}^{\prime }{\mathbf{W}}^{-1}(\mathbf{R}\widehat{\beta }-\mathbf{r})~{\chi }^2(q;{\delta }^{\prime }{\mathbf{W}}^{-1}\delta )\end{array}$$ (A1)

Thus, φ_c is a χ² statistic with q degrees of freedom and a noncentrality parameter of δ′W⁻¹δ. Now consider that Σ is actually unknown and that we will use an estimate Σ̂, such that $\mathbf{\sum }={\sigma }_c^2\widehat{\mathbf{\sum }}$, where ${\sigma }_c^2$ is an unknown scalar. Given this, we know that $(n-q){\widehat{\sigma }}_c^2/{\sigma }_c^2~{\chi }^2(n-q)$ and may obtain the following statistic by dividing φ_c by this quantity.

$$\begin{array}{l}{\phi }_F=\frac{{(\mathbf{R}\widehat{\beta }-\mathbf{r})}^{\prime }{[\mathbf{R}{({\mathbf{X}}^{\prime }{\widehat{\mathbf{\sum }}}^{-1}\mathbf{X})}^{-1}{\mathbf{R}}^{\prime }]}^{-1}(\mathbf{R}\widehat{\beta }-\mathbf{r})}{{\widehat{\sigma }}_c^{2}q}\\ {\phi }_F~\mathcal{F}(q,n-q,{\delta }^{\prime }{\mathbf{W}}^{-1}\delta ),\end{array}$$ (A2)

We use 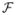(df₁, df₂, ncp) to represent the noncentral 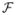-distribution with numerator degrees of freedom df₁ and denominator degrees of freedom df₂ and noncentrality parameter ncp. With optimal variance component estimates, we expect that ${\widehat{\sigma }}_c^2=1$.