Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Apr 15;3:1657. doi: 10.1038/srep01657

Scaling Effect on Unipolar and Bipolar Resistive Switching of Metal Oxides

Takeshi Yanagida 1,2,a, Kazuki Nagashima 1, Keisuke Oka 1, Masaki Kanai 1, Annop Klamchuen 1, Bae Ho Park 3, Tomoji Kawai 1,3,b
PMCID: PMC3625919  PMID: 23584551

Abstract

Electrically driven resistance change in metal oxides opens up an interdisciplinary research field for next-generation non-volatile memory. Resistive switching exhibits an electrical polarity dependent “bipolar-switching” and a polarity independent “unipolar-switching”, however tailoring the electrical polarity has been a challenging issue. Here we demonstrate a scaling effect on the emergence of the electrical polarity by examining the resistive switching behaviors of Pt/oxide/Pt junctions over 8 orders of magnitudes in the areas. We show that the emergence of two electrical polarities can be categorised as a diagram of an electric field and a cell area. This trend is qualitatively common for various oxides including NiOx, CoOx, and TiO2-x. We reveal the intrinsic difference between unipolar switching and bipolar switching on the area dependence, which causes a diversity of an electrical polarity for various resistive switching devices with different geometries. This will provide a foundation for tailoring resistive switching behaviors of metal oxides.

A resistance switching phenomenon in metal/oxide/metal sandwich structures1,2,3,4,5,6,7,8,9,10 is now opening up an intensive interdisciplinary research field in academics and industry2,3,4,11,12,13,14,15. A simplicity of the geometrical structures makes the resistance switching extremely attractive and promising for various emerging electronic applications, including ultimate high-density non-volatile memory7. The typical resistive switching device structure is illustrated in Fig. 1 (a). Fig. 1 (b) shows the microscopy image of fabricated structure (Pt/CoOx/Pt). The device comprises a polycrystalline CoOx layer sandwiched by Pt electrodes, and the details of fabrication processes and the microstructures can be seen in Method section and Supplementary S1. The reason why we have chosen a Pt electrode is that it is not necessary to consider an extrinsic effect of interfacial oxidization of electrode on the resistive switching. The resistance switching behaviors can be classified into two types including polarity dependent “bipolar switching”12 and polarity independent “unipolar switching”16 in terms of the electrical polarity required for resistance switching. In the former bipolar switching, a resistance change from high resistance state (HRS) to low resistance state (LRS) occurs at certain voltage polarity, and an inverse process from LRS to HRS at reversed voltage polarity. In contrast, in the latter unipolar switching, the switching procedures do not depend on the polarity of the voltage and current signals. Since each switching requires quite different device specifications and operations, tailoring the electrical polarity is essential toward their applications2,3,4,7. In most previous works, they have observed the occurrence of only one electrical polarity character within the range of experimental conditions16,17. Some recent works have revealed the co-existence of both unipolar and bipolar switchings. For example, Jeong et al. showed that the bipolar switching can change into the unipolar switching when increasing the compliance current18. It is however still a challenging issue to correlate the experimental variables of resistive switching devices with the type of electrical polarity because of the complexity. Here we show a scaling effect on the emergence of two electrical polarities by varying a cell area ranged from 102 to 1010 nm2. The major reason why we focus on the scaling effect is that a resistive switching is closely related to a spatial inhomogeneous phenomenon. We found that the emergence of two electrical polarities can be described as a diagram of an electric field and a cell area for resistive switching oxides including NiOx, CoOx and TiO2−x.

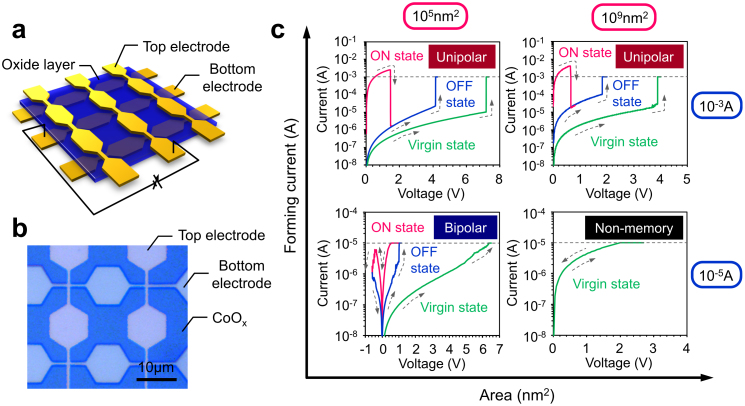
Figure 1. Schematic of typical resistive switching device, the fabricated structure of Pt/CoOx/Pt, and their typical current-voltage (I–V) data.

Figure 1

Open in a new tab

(a) Schematic of resistive switching cross-bar junction device, (b) SEM image of fabricated resistive switching devices of Pt/CoOx/Pt, (c) I–V data when varying the forming current and the cell area. Data of the forming current of 10−5 A and the cell area of 105 nm2, the forming current of 10−3 A and the cell area of 105 nm2, the foming current of 10−5 A and the cell area of 109 nm2 and the forming current of 10−3 A and the cell area of 109 nm2 are shown in the figure.

Results

Fig. 1 (c) shows the typical current-voltage (I–V) curves when varying the cell area and the upper limit of currents employed for initial forming process (hereafter called as “forming current”). The forming process is defined as an initial resistance change from a pristine sample when applying an electric field. These transport measurements were performed on Pt/CoOx/Pt structures. The details of definitions as to bipolar switching and unipolar switching in I–V data can be seen in Method section. As shown in Fig. 1(c), for the cases of 105 nm2 cell, a polarity dependent bipolar switching occurs for the forming current of 10−5A, whereas a polarity independent unipolar switching emerges for the forming current of 10−3 A. This trend significantly differs from in the cases of 109 nm2 cell. For the forming current of 10−5 A, any resistance switching behaviors are not observable, whereas unipolar switching emerges for the forming current of 10−3 A. These results highlight that two electrical polarities can coexist even within the same device, and the electrical polarity strongly depends on the cell area and the forming current.

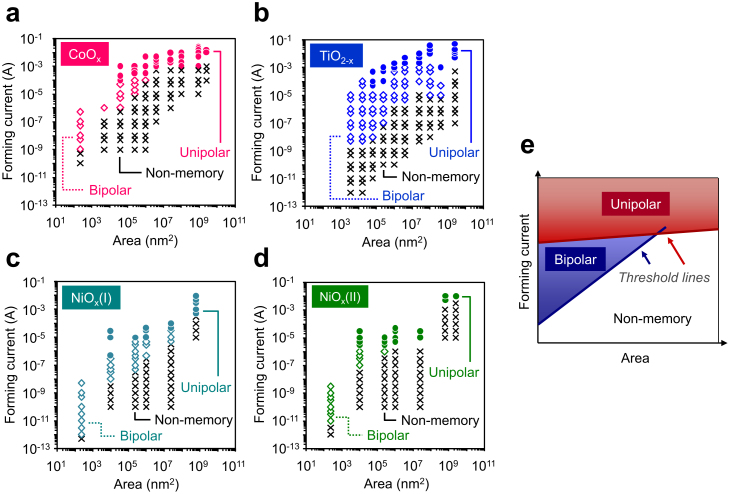
Fig. 2 (a) shows the diagram of the cell area and the forming current on the variation of two electrical polarities for Pt/CoOx/Pt devices. Non-memory behavior is mostly observed at relatively low forming current range for all cell areas. Unipolar switching behavior emerges at relatively high forming current range for relatively large cell areas. Bipolar switching behavior occurs at the middle forming current range for relatively small cell areas. Thus this diagram seems to be able to classify the occurrence of bipolar and unipolar switching. In order to examine the material dependence of the trends in Fig. 2 (a), we study resistive switching behaviors of other materials, including polycrystalline TiO2−x and two types of polycrystalline NiOxsamples which were deposited under different oxygen partial pressures. These devices are also Pt/oxide/Pt structures. The details of fabrication conditions, the microstructures and their I–V curves can be seen in Supplementary S1 and S2. Their trends as to the emergence of electrical polarity on the resistive switching behaviors are shown in Fig. 2 (b)–(d). Clearly these different materials exhibit qualitatively quite similar trend on the diagram of the cell area and the forming current in spite of the material difference. As illustrated in Fig. 2 (e), the diagram allows us to categorise the emergence of the electrical polarity for the present experimental range. In the diagram, there are two threshold lines to cause bipolar or unipolar switching when increasing the forming current. The threshold line for unipolar switching seems to be less area dependent than that for bipolar switching, resulting in the crossover of the two threshold lines in the diagram. The resultant crossover of the two lines might be able to explain why unipolar switching tends to occur for larger cell devices, as illustrated in Fig. 2 (e). Although this trend as to the existence of two threshold lines is common for different oxides employed, the quantitative differences exist due to the material dependences of two threshold lines, as seen in Figs. 2(a)–(d).

Figure 2. Diagram of a cell area and a forming current to classify the emergence of electrical polarity characteristics in resistive switching behaviors.

Figure 2

Open in a new tab

(a) Diagram as to variation of polarity characteristics in switching behaviors for CoOx. (b) Diagram as to variation of polarity characteristics in switching behaviors for TiO2−x. (c) and (d) Diagrams as to variations of polarity characteristics in switching behaviors for NiOx(1) and NiOx(2). The data of two different NiOx layers were shown when changing the deposition conditions of NiOx layers. (e) Schematic of observed scaling trends on the emergence of the two electrical polarity characteristics when varying a cell area and a forming current.

Discussion

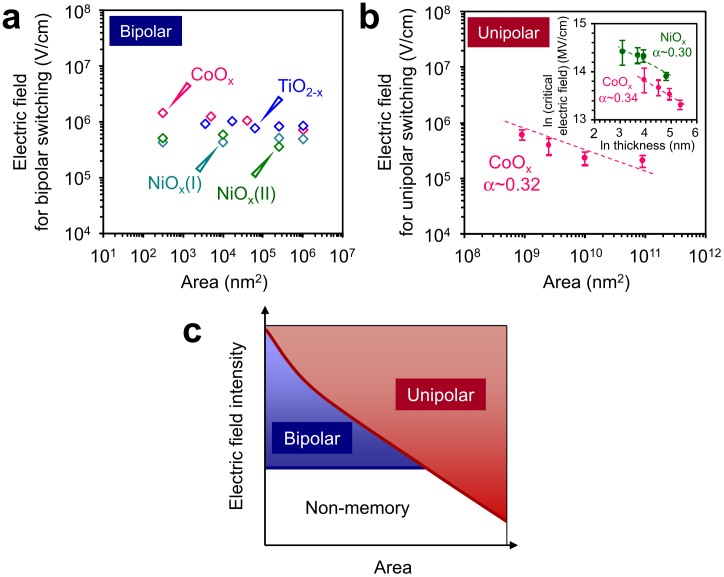
Here we discuss what essentially determines the diagram with the crossover of the two threshold lines for unipolar and/or bipolar switching in the diagram-Fig. 2 (e). The crossover indicates the different area dependences of bipolar and unipolar switching. First we consider the threshold line for bipolar switching. For the transition from non-memory to bipolar switching in Fig. 2 (a), the threshold value of operation current increases from 10−9 to 10−4 A when increasing the cell area from 102 to 106 nm2. The similar trend is also observed even for other materials as seen in Figs. 2(b)–(d). Since an electric field is an important parameter to describe an electrically induced event, we estimate an averaged electric field intensity (defined as a ratio of an applied voltage to a cross-point area) required for bipolar switching, at which a bipolar switching emerges during increasing a forming current. We have examined the effect of aspect ratio (defined as a ratio of an electrode width to an oxide film thickness) on the electric field distribution by numerical simulations and experiments, as seen in Supplementary S3. The simulations and experiments as to area dependence of resistance data demonstrate that the use of averaged electric field intensity is reasonable within our experimental range of aspect ratio. The averaged electric field data are shown in Fig. 3 (a). The electric field intensity required for bipolar switching is interestingly almost constant around 106 V/cm even varying the cell area. This trend is commonly observed for different materials. Although there is a slight variation of the critical electric field, the variation range is substantially smaller than that of the forming currents in Fig. 2. Fig. 3 (b) shows the averaged electric fields required for unipolar switching as a function of a cell area. The electric field for unipolar switching is defined as an electric field, where unipolar switching is observed when increasing a forming current. The inset shows the thickness dependence data. In the experiments, Pt/CoOx/Pt and Pt/NiOx/Pt junctions were utilized. As can be seen, the electric field required for unipolar switching increases with decreasing a cell area. The area dependence of the electric field for unipolar switching is clearly different from the trend on the electric field for bipolar switching, which is less sensitive to area size as seen in Fig. 3 (a). These trends as the electric field data can be illustrated as Fig. 3 (c).

Figure 3. Area dependence of the critical electric field required for switching.

Figure 3

Open in a new tab

Intrinsic difference between unipolar switching and bipolar switching on their area dependences. (a) Electric field data required to cause a transition from non-memory to bipolar switching for CoOx, TiO2−x and NiOx. (b) Electric field data required to cause unipolar switching for CoOx and NiOx when varying a cell area. The inset shows the thickness dependence on the electric field data. The comparisons with the model based on a soft dielectric breakdown are shown. (c) Schematic of the emergence of the two polarity characteristics in terms of a diagram between a cell area and an electric field intensity.

In order to understand the origin of the diagram with the crossover of two threshold lines, we compare the electric field intensity diagram of Fig. 3 (c) with existing models as to resistive switching phenomena. Among various models for bipolar switching2,3,4,7, a model based on an oxygen ion drift under an electric field has most successfully explained the features of bipolar switching6,12,15,19,20. Strukov and Williams have proposed that an exponential ionic drift above critical electric field causes non-volatile bipolar switching behaviors by overcoming the effect of a thermal diffusion of ions20. Clearly this model based on an electric field induced phenomenon is consistent with our experimental trends in Fig. 3, where there is a constant electric field required for bipolar switching independent of area size. In addition, the electric field values for bipolar switching in Fig. 3 are also comparable with values estimated from the model20, as shown in Supplementary S4. Thus the area-independent trend of electric fields required for bipolar switching in Fig. 3 (a) is understood in terms of an electric field required for an exponential ionic drift. As to unipolar switching, we analyse the area dependences of unipolar switching in terms of a soft dielectric breakdown model14. The critical electric field Ecr to cause a dielectric breakdown has been reported as formulas Ecr∝d−α or Ecr∝A−α (A is a cell area, d is a thickness and α is a power factor ∼0.3–0.5)21,22. As shown in Fig. 3 (b), the thickness and the cell area dependences on the critical electric field for unipolar switching can be reasonably described by the formula. Furthermore we have confirmed that other features (including Weibull distribution and irreversible trend) of forming process for unipolar switching conform to trends of a soft dielectric breakdown phenomenon21,22,23, as shown in Supplementary S5. Thus the area-dependent features of electric fields required for unipolar switching in Fig. 3(b) can be understood in terms of a size dependence of electrical breakdown strength. As a cell area tends to be smaller, the electrical breakdown strength for unipolar switching tends to increase via decreasing a probability to connect defect points within a solid. These comparisons for bipolar and unipolar switching highlight that there is an intrinsic difference between bipolar and unipolar switching on the area dependences, which in effect exhibits the crossover of two threshold lines in Fig. 2(e) and Fig. 3(c).

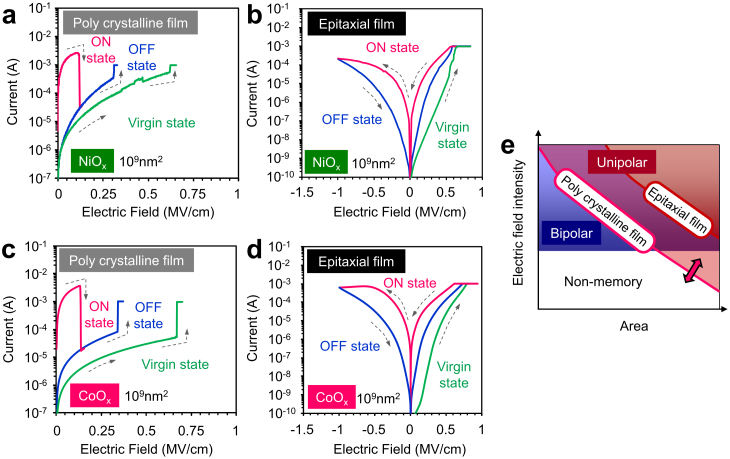
The threshold events of both switchings should depend on the switching materials and their properties. For example, the emergence of unipolar switching is strongly dependent on an electrical breakdown strength of oxide film. It is well known that an electrical breakdown strength of single crystals is higher than that of polycrystalline samples due to the lower crystal imperfections23. Fig. 4 (a)–(d) show the comparison between polycrystalline devices and single crystalline epitaxial devices on the resistive switching behaviors in the same cell area of top electrode (109 nm2) for CoOx and NiOx. The epitaxial films were grown on Nb doped-SrTiO3 substrates, and the top electrode is Pt. Further details of fabricated epitaxial samples can be seen in Supplementary S1. As can be seen in Fig. 4, polycrystalline devices show an unipolar switching, whereas single crystalline epitaxial devices exhibit a bipolar switching even for the same cell area, the same forming current and the similar electric field. Although the present epitaxial film devices are asymmetry electrode configurations, it has been reported that a NiO single crystalline film with asymmetry electrode configuration Pt(top)/NiO/Pt-Ir(bottom) exhibits the unipolar switching after thermal annealing24. In addition, many previous investigations as to single crystalline resistive switching devices have consistently demonstrated that a single crystalline film device tends to exhibit a bipolar switching rather than an unipolar switching even for relatively large cells7,12. Clearly both the present our results and previous results consistently support above our speculations based on the difference of the electric breakdown strength when varying crystallinity. Fig. 4 (e) illustrates a schematic as to the material dependence on the diagram of a cell area and an electric field. The schematic diagram highlights that manipulating the two threshold lines via controlling a property of switching layer is essential to tailor an electrical polarity of resistive switching for a desired device configuration. It is noted that the asymmetry of electrodes should also affect the emergence of bipolar switching due to the asymmetrical chemical reactivity, and our present findings might be qualitatively applicable even for such asymmetrical devices3,25. Although a quantitative prediction for the threshold lines is still challenging issue, the present concept based on the intrinsic difference between unipolar and bipolar switching on the area dependence would be a foundation to understand and tailor a variation of an electrical polarity for various geometrical small devices.

Figure 4. Comparison between an epitaxial film device and a polycrystalline device on the resistive switching behaviors.

Figure 4

Open in a new tab

(a) I–V data with the forming current of 10−3 A and the cell area of 109 nm2 for polycrystalline NiOx device. (b) I–V data with the forming current of 10−3 A and the cell area of 109 nm2 for epitaxial single crystalline NiOx device. (c) I–V data with the forming current of 10−3 A and the cell area of 109 nm2 for polycrystalline CoOx device. (d) I–V data with the forming current of 10−3 A and the cell area of 109 nm2 for epitaxial single crystalline CoOx device. (e) Diagram to explain why single crystalline device tends to exhibit a bipolar switching even for relatively large cell areas.

In conclusion, we demonstrate a scaling effect of the unipolar and bipolar switching behaviours by examining the resistive switching behaviors of Pt/oxide/Pt junctions over 8 orders of magnitudes in the area sizes. We show that the emergence of two electrical polarities can be expressed as a diagram of an electric field and a cell area. The trend is qualitatively common for various metal oxides including NiOx, CoOx, and TiO2−x. An intrinsic difference between an unipolar switching and a bipolar switching on the area dependence exhibits a diversity of an electrical polarity in resistive switching devices. We believe that the knowledge obtained herein sheds light on a strategy to tailor an electrical polarity of resistive switching behavior rather than a rule of thumb.

Methods

Pt/oxide/Pt sandwich structures were constructed as crossbar junctions on n-type Si substrate capped with a 300 nm SiO2 by utilizing a combined process of EB lithography (JEOL JSM-7001F with Nano printer SPG-724), RF sputtering (SANYU Electron SC-701HMC) and pulse-laser deposition techniques. The cell area was defined by the width of Pt electrodes, ranging from 104-1010 nm2. EB lithography and/or metal masks were utilized to define the width of electrodes. Pt electrodes were deposited by sputtering, and oxide layers, including NiOx, CoOx and TiO2−x, were formed by pulse-laser deposition method. For smallest cells below 103 nm2, junctions using oxide nanowires were used, and the details of nanowire devices can be seen in elsewhere26,27,28,29,30,31,32,33,34. The fabricated structures were evaluated by TEM (JEOL JEM-3000F) and SEM (Hitachi S-4300). See Supplementary information S1 and S2 for the details of procedures, conditions and fabricated structures. I–V data were recorded using semiconductor parameter analyser (Keithley 4200SCS) with contacts to devices made using a probe station (JANIS ST-500). During voltage sweep, the operation current (the upper limit of current range) was varied from 10−11–10-1 A. We define the occurrence of bipolar switching and unipolar switching in the I–V curves as follows. The bipolar switching is defined as the condition when we observe both the hysteresis in the I–V curves and the retained resistance difference between LRS and HRS read at 0.1 V after voltage sweep operation with the sweep rate of 8.6 V/sec after a forming process with a desired current level. We have confirmed that the used sweep rate is slow enough to exclude an effect of switching speed, as shown in Supplementary S2. The unipolar switching is defined as the condition when we observe both set (from HRS to LRS) and reset (from HRS to LRS) processes at one voltage polarity and the retained resistance difference between LRS and HRS read at 0.1 V after a forming process. Other behaviour without any observable resistance change is defined as non-memory.

Author Contributions

T.Y. designed this work and prepared the manuscript. The experiments and electrical measurements were carried out by K.N., K.O. and A.K. T.K., K.N., M.K., T.Y. and B.H.P. have analyzed the results and discussed the manuscript during the preparation. All authors discussed the results and implications and commented on the manuscript at all stages.

Supplementary Material

Supplementary Information

SUPPLEMENTARY INFORMATION

srep01657-s1.pdf (1.9MB, pdf)

Acknowledgments

This work was supported by NEXT Project. T.K. and B.H.P. were partly supported by WCU program (Grant R31-2008-000-10057-0). T.K. was supported by FIRST program.

References

  1. Hickmott M. T. Low-frequency negative resistance in thin anodic oxide films. J. Appl. Phys. 33, 2669–2682 (1962). [Google Scholar]
  2. Meijer G. I. Who wins the nonvolatile memory race? Science 319, 1625–1626 (2008). [DOI] [PubMed] [Google Scholar]
  3. Waser R., Dittmann R., Straikov G. & Szot K. Redox-based resistive switching memories- nanoionic mechanisms, prospects, and challenges. Adv. Mater. 21, 2632–2663 (2009). [DOI] [PubMed] [Google Scholar]
  4. Waser R. & Aono M. Nanoionic-based resistive switching memories. Nature Mater. 6, 833–840 (2007). [DOI] [PubMed] [Google Scholar]
  5. Strukov D. B., Snider G. S., Stewart D. R. & Williams R. S. The missing memristor found. Nature 453, 80–83 (2008). [DOI] [PubMed] [Google Scholar]
  6. Yang J. J. et al. Memristive switching mechanism for metal/oxide/metal nanodevices. Nature Nanotechnol. 3, 429–433 (2008). [DOI] [PubMed] [Google Scholar]
  7. Pershin Y. V. & Di Ventra M. Memory effects in complex materials and nanoscale systems. Adv. Phys. 60, 145–227 (2011). [Google Scholar]
  8. Di Ventra M., Pershin Y. V. & Chua L. O. Circuit elements with memory: memristors, memcapacitors and meminductors. Proc. IEEE 97, 1717–1724 (2009). [Google Scholar]
  9. Pershin Y. V., La Fontaine S. & Di Ventra M. Memristive model of amoeba's learning. Phys. Rev. E 80, 021926 (2009). [DOI] [PubMed] [Google Scholar]
  10. Chua L. O. Memristor - the missing circuit element. IEEE Trans. Circuit Theory 18, 507–519 (1971). [Google Scholar]
  11. Sawa A. Resistive switching in transition metal oxides. Mater. Today 11, 28–36 (2008). [Google Scholar]
  12. Szot K., Speier W., Bihlmayer G. & Waser R. Switching the electrical resistance of individual dislocations in single-crystalline SrTiO3. Nature Mater. 5, 312–320 (2007). [DOI] [PubMed] [Google Scholar]
  13. Kwon D. H. et al. Atomic structure of conducting nanofilaments in TiO2 resistive switching memory. Nature Nanotechnol. 5, 148–153 (2010). [DOI] [PubMed] [Google Scholar]
  14. Lee J. S. et al. Scaling theory for unipolar resistance switching. Phys. Rev. Lett. 105, 205701 (2010). [DOI] [PubMed] [Google Scholar]
  15. Oka K. et al. Dual defects of cation and anion on memristive nonvolatile memory of metaloxides. J. Am. Chem. Soc. 134, 2535–2538 (2012). [DOI] [PubMed] [Google Scholar]
  16. Strachan J. P. et al. Direct identification of the conducting channels in a functioning memristive device. Adv. Mater. 22, 3573–3577 (2010). [DOI] [PubMed] [Google Scholar]
  17. Nagashima K., Yanagida T., Oka K. & Kawai K. Unipolar resistive switching characteristics of room temperature grown SnO2 thin films. Appl. Phys. Lett. 94, 242902 (2009). [Google Scholar]
  18. Jeong D. S., Schroeder H. & Waser R. Coexistence of bipolar and unipolar resistive switching behaviors in a Pt/TiO2/Pt stack. Electrochem. Solid State Lett. 10, G51–G53 (2007). [Google Scholar]
  19. Cabrera N. & Mott N. F. Theory of the oxidation of metals. Rep. Prog. Phys. 12, 163–184 (1949). [Google Scholar]
  20. Strukov D. B. & Williams R. S. Exponential ionic drift: fast switching and low volatility of thin-film memristors. Appl. Phys. A 94, 515–519 (2009). [Google Scholar]
  21. Satoh T. & Tanaka R. Area effect and distance effect of transformer oil insulation. Aichi Denki Gihou 28, 12–17 (2007). [Google Scholar]
  22. O'Dwyer J. J. Theory of dielectric breakdown in solid. J. Electrochem. Soc. 116, 239–242 (1969). [Google Scholar]
  23. Lombardo S. et al. Dielectric breakdown mechanisms in gate oxides. J. Appl. Phys. 98, 121301 (2005). [Google Scholar]
  24. Kawai M., Ito K., Ichikawa N. & Shimakawa Y. Thermally formed conducting filaments in a single-crystalline NiO thin film. Appl. Phys. Lett. 96, 072106 (2010). [Google Scholar]
  25. Joshua Y. J., Strukov D. B. & Stewart D. R. Memristive devices for computing. Nat. Nanotech. 8, 13–24 (2013). [DOI] [PubMed] [Google Scholar]
  26. Nagashima K. et al. Effect of heterointerface on transport properties of in-situ formed MgO/titanate core-shell nanowires. J. Am. Chem. Soc. 130, 5378–5382 (2010). [DOI] [PubMed] [Google Scholar]
  27. Oka K., Yanagida T., Nagashima K., Tanaka H. & Kawai T. Non-volatile bipolar resistive memory switching in single crystalline NiO heterostructured nanowires. J. Am. Chem. Soc. 131, 3434–3435 (2009). [DOI] [PubMed] [Google Scholar]
  28. Klamchuen et al. Crucial role of doping dynamics on transport properties of Sb-doped SnO2 nanowires. Appl. Phys. Lett. 95, 053105. (2009). [Google Scholar]
  29. Nagashima K. et al. Resistive switching multistate non-volatile memory effects in a single cobalt oxide nanowire. Nano Lett. 10, 1359–1363 (2010). [DOI] [PubMed] [Google Scholar]
  30. Nagashima K. et al. Interfacial effect on metal/oxide nanowire junctions. Appl. Phys. Lett. 96, 073110 (2010). [Google Scholar]
  31. Oka K. et al. Resistive switching memory effects of NiO nanowire/metal junctions. J. Am. Chem. Soc. 132, 6634–6635 (2010). [DOI] [PubMed] [Google Scholar]
  32. Oka K. et al. Spatial nonuniformity in resistive switching memory effects of NiO. J. Am. Chem. Soc. 133, 12482–12485 (2011). [DOI] [PubMed] [Google Scholar]
  33. Nagashima K. et al. Intrinsic mechanisms of memristive switching. Nano Lett. 11, 2114–2118 (2011). [DOI] [PubMed] [Google Scholar]
  34. Nagashima K. et al. Prominent thermodynamical interaction with surroundings on nanoscale memristive switching of metal oxides. Nano Lett. 12, 5684–5690 (2012). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

SUPPLEMENTARY INFORMATION

srep01657-s1.pdf (1.9MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES