ENTROPY BASED DTI QUALITY CONTROL VIA REGIONAL ORIENTATION DISTRIBUTION

Abstract

Diffusion Tensor Imaging (DTI) has received increasing attention in the neuroimaging community. However, the complex Diffusion Weighted Images (DWI) acquisition protocol are prone to artifacts induced by motion and low signal-to-noise rations(SNRs). A rigorous quality control (QC) and error correction procedure is absolutely necessary for DTI data analysis. Most existing QC procedures are conducted in the DWI domain and/or on a voxel level, but our own experiments show that these methods often do not fully detect and eliminate certain types of artifacts. We propose a new regional, alignment-independent DTI-QC measure that is based in the DTI domain employing the entropy of the regional distribution of the principal directions. This new QC measurement is intended to complement the existing set of QC procedures by detecting and correcting residual artifacts. Experiments show that our automatic method can reliably detect and potentially correct such residual artifacts. The results indicate its usefulness for general quality assessment in DTI studies.

1. INTRODUCTION

Diffusion Tensor Imaging (DTI) has received increasing attention in the neuro-imaging community due to its ability to investigate the microstructural features, integrity and changes of white matter in normal, developing, aging and pathological human brains [1, 2]. DTI employs a “diffusion coefficient” to quantify the rate and directionality of water displacement in various brain tissues. The coefficient is estimated from a series of DWI by using several (at least six) non-collinear diffusion sensitizing gradients [3]. Using such an imaging modality in a clinical environment is difficult and can suffer from many types of artifacts as a result of either a limitation or malfunction in the hardware or software of the scanning device. In addition, severe artifacts may also originate from the source of physiological noise such as bulk head motion and respiratory motion.

Three different categories of post-processing approaches have been proposed to improve induced errors in DT-MRI. In the first category, one aims to estimate signal in MRI from a noisy signal. For instance, Tristán-Vega later proposed a DWI filtering method which was intended to take advantage of joint information from all DWIs and the correlation between them [4]. In the second category, regularization of tensor images is employed in addition to estimating the tensor [5]. Fillard. et. al. proposed a maximum-a-posterior framework estimation to couple tensor estimation and regularization to better capture information from noisy images [6]. In the third category, new diffusion tensor estimation techniques are performed from qualified DWIs where outliers are detected and removed from data set [7]. Mangin, J. et al. [7] proposed a robust DTI estimation approach, in which following eddy-current artifact correction, the weight of each data point is set to a function of the residuals of the previous iteration while iteratively doing re-weighted least-squares fitting. Artifactual data are thus given lower weights in the tensor estimation.

Despite the efforts invested in improving the DTI estimation, there is plenty of room for improvement in DTI-QC. In this paper, we propose a new approach to assess quality control of DTI and refurbish DWIs using an entropy-based measurement on the orientational distribution of principal directions. Our method is employed in a complementary process to our existing, open-source DWI-QC tool, DTIPrep [8], which detects and corrects DWI issues such as inter-slice brightness artifacts, eddy current artifacts, within-DWI and between-DWI patient motion. The orientational distribution is computed via an icosahedron subdivision based spherical histogram of the principal directions within the following regions: total brain, whole brain gray matter and whole brain white matter. Our experiments show that the proposed DTI-QC approach is especially sensitive in detecting and correcting artifacts of dominating directions of diffusion.

2. MATERIALS AND METHODS

2.1. Artifacts of dominating directions

The proposed approach is based on the assumption that standard QC procedures are ill-suited to identify artifacts that are mainly present in the DTI domain such as dominating directions of diffusion (see Fig. 1). Such artifacts can be detected visually by identifying a dominant background color tone in a colorized Fractional Anisotropy (FA) image. Fig. 1 displays an artifact free scan (with no discernible dominant color tone) alongside scans displaying artifacts of dominating directions in the colorized FA as well as the spherical PD histogram. Standard DWI-QC as well as DWI or DTI based filtering approaches cannot detect or correct such artifacts, whereas our approach is able to detect and potentially correct them.

Fig. 1.

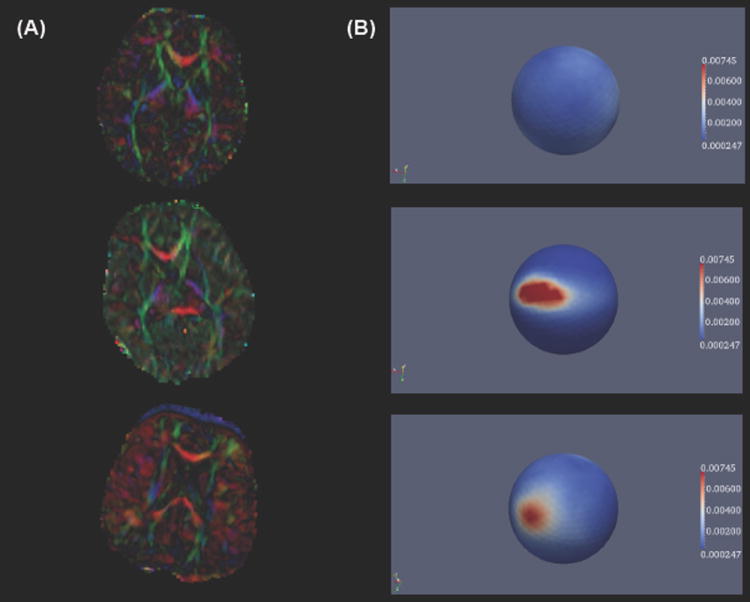
(A) Slide number 41 of artifact free scan (top) followed by scans suffering from artifact of dominant green direction (middle) and dominant red direction (bottom) in the colorized FA image. (B) Corresponding spherical histograms of the PD distribution within the entire brain region (viewpoints rotated to indicate locations of highest histogram frequency).

2.2. Overview

As the proposed QC procedure is intended to complement the existing set of DWI-QC procedures, we first apply DWI-QC using DTIPrep followed by DTI estimation via a weightedleast square fit (see Fig 2). Prior tissue segmentation masks of whole brain white matter and gray matter are used to define the regions within the PD distributions are computed. The PD distributions are represented as spherical histograms with bins defined by a quasi-uniform, icosahedron based spherical subdivision. Finally, the entropy is computed from the histogram and compared with prior training data that defines the expected range of the entropy for artifact-free scans. A leaveone- out scheme is employed to potentially correct the DWI set by excluding individual DWI images and test for optimal improvement in the entropy values.

Fig. 2.

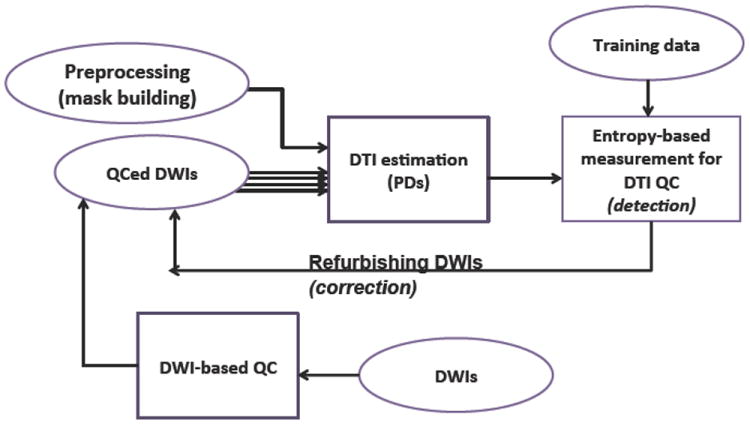
Schematic overview of the proposed DTI-QC.

2.3. Subjects

We tested our approach on two sets of data: a) 20 pediatric dataset (6-14 months of age, subjects at low or high risk of developing autism [9]) acquired with a multi-b-value (50-1000) sequence and 25 unique gradient directions, b) 26 adult datasets from a Huntington’s Disease study [10] with 3 different acquisition protocols. For both datasets, a set of artifact-free scans were first detected via visual assessment of the colorized FA, as well as manually guided streamline fiber tractography within 3D Slicer (by rater CD). For the pediatric dataset we employed 12 artifact-free scans and 8 tests scans, whereas for the adult dataset we used 14 artifact-free scans and 11 test scans. All datasets were judge by automatic and visual QC procedure to appear perfectly normal based on DWI-only QC.

2.4. Distribution of Principal Directions

In order to represent PD distribution, we employ a spherical coordinate system on which we compute the PD histogram. The spherical histogram bins are computed via a subdivision of the unit sphere. Two different subdivisions have mainly been employed in literature[11]. The first option subdivides the unit sphere based on the spherical or geographical coordinates/angles (ϕ,θ), where a rectangular grid is defined as a uniform subdivision of longitudes (ϕ) and latitudes (θ) [12]. However, such an angular coordinate grid is not optimal for the computation of spherical histograms[11], as the actual size of the subdivision face area on the unit sphere varies widely from the equatorial to polar regions. The second, common option for a spherical subdivision is the quasi-uniform icosahedron subdivision, in which the triangular faces of an icosahedron is linearly or recursively subdivided into smaller triangles whose vertices are projected to the unit sphere. While the icosahedron is uniform in spacing and area, the icosahedron subdivision is not, but can be considered a quasiuniform spherical subdivision due to the small variance in spacing and area, especially when compared to the above angular subdivision. Using an angular resolution of 5°, which leads to (360°/5°) × (90°/5°) = 1296 faces, variability in face area of an angular subdivision of the unit sphere is σ = 0.0023 with mean μ = 0.0048 and average relative error = 48% (max error 0.0076 / 150.140%). The variability in face area of the icosahedron subdivision approach computed at subdivision level 8 is σ = 0.0023, with mean μ = 0.044 and average relative error = 5.34% (max error = 35.52%). While face-wise binning could be chosen for the spherical histogram, we chose nearest-vertex based binning for the PD histogram due to its implementational simplicity. Using subdivision level 8, 812 bins are generated cover sufficient data (79832 voxels) to estimate the distribution of PD reliably.

2.5. Orientational Entropy for DTI QC

One of the goals of our orientation based DTI QC metric was to be independent to the patient’s position in the scanner or scan. We chose to use Shannon’s entropy, a concept well known from information theory [13], to summarize the PD distribution. In our application, entropy of a distribution of PDs represents the scatter and spread of dominating directions within brain regions measured independent of alignment of the spherical parametrization. Higher entropy indicates that the PDs’ distribution is more uniform. Lower entropy demonstrates clustering of the PDs’ distribution and a higher degree of such clustering is a consequence of the before mentioned artifact of dominating directions. Given the PD histogram, the proposed orientational entropy is defined as:

$$E=-\sum _{i=1}^K{p}_i\mathit{log}(p_i)$$ (1)

where K is the number of vertices/bins and p_i is the normalized frequency in the PD histogram at bin i.

Detection

In order to detect scans with unexpected value of entropy (lower values of entropy for artifacts of dominating directions), we compare a given DT scan’s entropy to values learned from a prior set of artifact-free samples. We employ z-score to categorize the quality of a DT scan into three categories: acceptable (z < 1.64/90%), suspicious (z ≥ 1.64/90%) and unacceptable (z ≥ 2.58/99%). For our experiments here, we evaluate the DTI quality within white matter, gray matter and whole brain regions.

Correction

For our correction step, we employed an iterative leave-one-out-strategy over all individual DWI images by recomputing DTI images and corresponding entropies. At each iteration, the DWI with maximal improvement is removed and all leave-one-out entropies are recomputed. This process is continued until the z-score is in acceptable range.

3. RESULTS

3.1. Detection Step

Pediatric Data

Seven of the selected test images presented with a “red” (medial-lateral) dominating direction of varying degree and one with a “green” (anterior-posterior) dominating direction. Fig. 3 plots the z-scores of the orientational entropies for all 20 images within white matter, gray matter and whole brain regions. All test images showed by at least one of the regional z-scores as classified as suspicious (indexed from 13 to 20), with z-scores correlating well with the qualitative, visual QC assessment (not shown here). These experiments surprisingly showed that the white matter z-score seems most suitable value for the detection of artifacts of dominating directions, even though visual assessment mostly focuses on gray matter areas. The dataset with the largest z-score suffers from single case with “green” dominating direction.

Fig. 3.

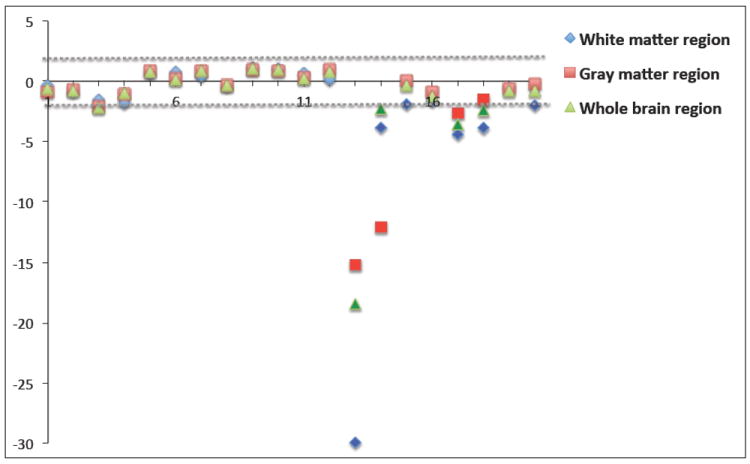
Plot of all z-scores in the pediatric data. The dashed lines represent the cutoff the suspicious category.

Adult Data

In the adult data, we chose to use a more diverse set of testing images to study whether our method can pick up other artifacts as well. While one test image suffered from “red” dominating direction artifact, others showed focused directional artifacts within the pre-frontal cortex, or general noise-related artifacts and “checkerboard” artifacts on the FA image. Our experiments show that the method is able to detect all of these artifacts only if they cover a sufficiently large area. Fig. 4 plots the z-scores of the orientational entropies for all 25 images (test images indexed 14 to 25). The presence of a dominant direction artifact in one of the sample is quite obvious. Two cases suffering from focused directional artifacts in the pre-frontal cortex can be successfully detected in the gray matter region only. Three cases with noise-related artifacts are detected at higher entropies in white matter.

Fig. 4.

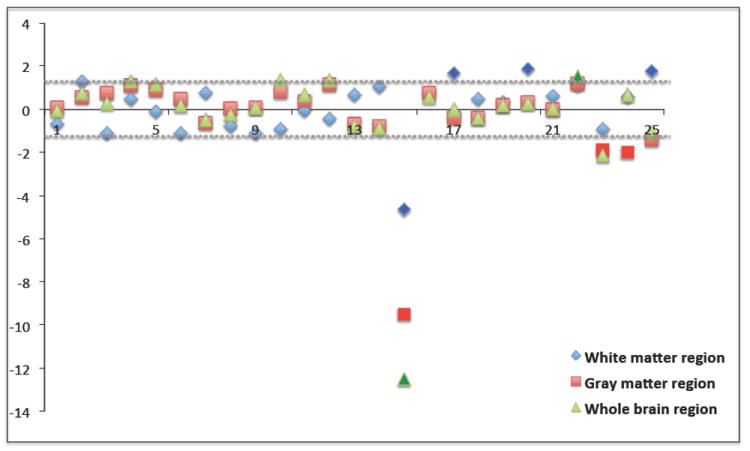
Plot of all z-scores in the adult data. The dashed lines represent the cutoff the suspicious category.

3.2. Correction

We performed the proposed correction on all cases categorized as suspicious. Fig. 5 presents an example case (pediatric case 14) that suffered from a “red” dominating direction. After correction, most of the artifactual red regions were visibly improved in contrast between different tracts with reduced artifact appearance in the colorized FA image. In order to assess the correction results quantitatively, we applied our atlasbased fiber analysis [14] before (left) and after(right) employing our correction step using the same atlas mapping. The FA profiles of genu and splenium fibers indicate that the correction results in higher FA values, which indicates an improvement in the fiber based analysis. Fig. 6 shows the assessment of a different case with a minor “red” dominating direction via fiducial fiber tractography in 3D Slicer in the splenium tract center. The tractography result of the corrected image is clearly improved. While these examples demonstrate promising correction results for DTI quality control compared with the original image, it has to be noted that many cases detected with the proposed orientational entropy were not salvageable.

Fig. 5.

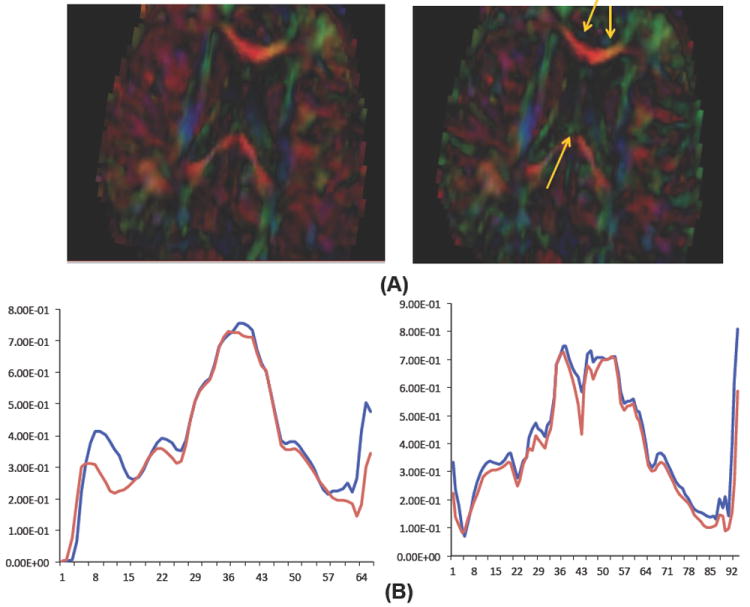
A) Improvement in contrast of cingulum and fornix fibers in corrected image(right). B) FA-profiles of genu and splenium fibers before (red) and after correction (blue).

Fig. 6.

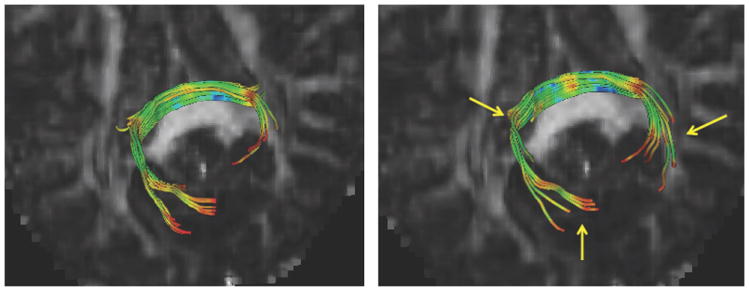
The fiber tractography of splenium of sample 20^th in Fig. 3 before (left) and after (right) our correction step.

4. DISCUSSION AND CONCLUSION

In this work, we proposed a new approach for DTI-QC which is majorly focused on detection of artifacts of dominant directions employing the entropy of regional distributions of principal directions. We tested our approach in two small-scale studies on pediatric and adult subjects. The results show that artifacts of dominant directions are successfully detected using the proposed approach. In the adult data, focused gray matter artifacts and noise-related artifacts were also successfully detected. Furthermore, we proposed a correction strategy that shows considerable promise in datasets with minor artifacts. Major artifacts have shown to be rarely salvegeable. We are currently applying this method to several large scale studies to further test the method’s usefulness in routine DWI/DTI QC procedures.