Skip to main content
PMC home page
American Journal of Epidemiology logoLink to American Journal of Epidemiology
. 2013 Jan 18;177(4):351–360. doi: 10.1093/aje/kws234

Confounding and Heterogeneity in Genetic Association Studies with Admixed Populations

Jinghua Liu, Juan Pablo Lewinger, Frank D Gilliland, W James Gauderman, David V Conti *
PMCID: PMC3626055  PMID: 23334005

Abstract

Association studies among admixed populations pose many challenges including confounding of genetic effects due to population substructure and heterogeneity due to different patterns of linkage disequilibrium (LD). We use simulations to investigate controlling for confounding by indicators of global ancestry and the impact of including a covariate for local ancestry. In addition, we investigate the use of an interaction term between a single-nucleotide polymorphism (SNP) and local ancestry to capture heterogeneity in SNP effects. Although adjustment for global ancestry can control for confounding, additional adjustment for local ancestry may increase power when the induced admixture LD is in the opposite direction as the LD in the ancestral population. However, if the induced LD is in the same direction, there is the potential for reduced power because of overadjustment. Furthermore, the inclusion of a SNP by local ancestry interaction term can increase power when there is substantial differential LD between ancestry populations. We examine these approaches in genome-wide data using the University of Southern California's Children's Health Study investigating asthma risk. The analysis highlights rs10519951 (P = 8.5 × 10−7), a SNP lacking any evidence of association from a conventional analysis (P = 0.5).

Keywords: confounding, genetic association studies, genome-wide association studies, heterogeneity, linkage disequilibrium, population stratification

Genome-wide association studies have been successful at identifying risk variants for many diseases and traits (1). Although a majority of these studies have been performed with individuals of European ancestry, the field is moving toward genome-wide association studies in more diverse populations (2). In addition to expansion to other homogeneous populations such as Chinese (3–9), Japanese (5, 10–15), and Koreans (16), genome-wide association studies among admixed populations such as African Americans (17, 18) and Hispanics (19–22) may be advantageous because of different patterns of linkage disequilibrium (LD) (23, 24). However, such admixed populations pose new challenges including the confounding due to population stratification and heterogeneity of effects due to differential LD. Genetic admixture occurs when individuals from previously distinct populations interbreed. After several generations, the genomes of the individuals in an admixed population become a mosaic composed of chromosomal segments originating from each of the ancestral populations. The ancestral origin at a particular locus is referred to as “local ancestry,” and the average of these proportions across the genome is referred to as “global ancestry.”

When the sample consists of subpopulations with various disease rates, the standard case-control analysis may result in spurious associations at any locus when allele frequencies differ among the subpopulations (25). Genomic control (26) and logistic regression (27) approaches aim to control this confounding without estimating the underlying population structures. Alternatively, latent variable approaches (28–30) and distance-based multivariate approaches (31–34) attempt to estimate population structures and then adjust for these in the association analysis. Furthermore, it has been recently suggested that correcting for individual local ancestries may be required for genome-wide association scans in admixed populations (35–39).

When testing genetic markers that are proxies for a disease causal locus, the differential LD within admixed populations can result in heterogeneity of effect estimates by local ancestry. If reliable self-identified ethnicity is available, inclusion of an interaction term between the single-nucleotide polymorphism (SNP) and ethnicity may account for the heterogeneity, and subsequent stratified analyses could be performed. However, it is unclear how appropriate this approach may be for admixed populations with variation in local ancestry or when combining an admixed population with others.

In this paper, we use graphical diagrams to clarify the mechanisms by which admixture can lead to confounding and how heterogeneity in effect estimates may arise. On the basis of these mechanisms, we investigate the source and effect of confounding and test for heterogeneity via an interaction term between SNP and local ancestry through simulations. Across all models and simulation scenarios, we focus on effect estimation, type I error, and power. Finally, we apply these models to a genome-wide association study investigating the impact of genetic variation on asthma in the University of Southern California's Children's Health Study. We discuss the overall impact of global ancestry on this analysis and identify several empirical examples where accounting for local ancestry impacts inference.

MATERIALS AND METHODS

Graphical model

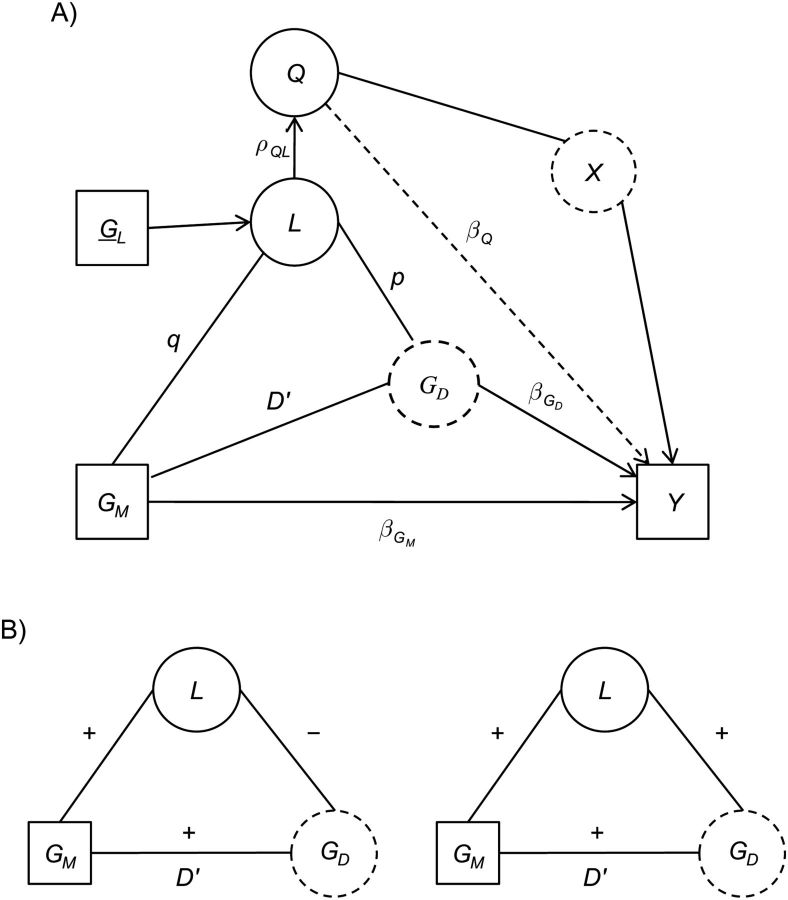
The graphical model in Figure 1A represents the relationship of several factors involved in genetic association studies among admixed populations (40, 41). Here, Y represents the outcome of interest. GM represents the SNP at a marker being tested for association with Y (with effect βGM). GD represents an unmeasured causal locus (with effect βGD ) for which we are testing GM as a proxy. X represents other causal factors that are associated with global ancestry (Q), including unmeasured environmental factors and/or unmeasured causal loci. The global ancestry is most often estimated from a subset set of markers (42–46). Alternatively, we view global ancestry as the average of local ancestries along the genome. Ancestral variation can lead to differences in allele frequencies for measured genetic variants (q) and unmeasured causal variants (p). We assume that the local ancestry at GM and GD are the same, and that there are additional SNPs (GL) that can be used to estimate local ancestry for each subject at each location.

Figure 1.

Figure 1.

Open in a new tab

A) Potential confounding paths in genetic association studies among admixed populations. Y represents the outcome of interest; GM, the single-nucleotide polymorphism at a marker locus being tested for association; L, the individual local ancestry in the immediate neighborhood of the marker locus; Q, the individual global ancestry averaged through L across the genome; X represents other causal factors, either unmeasured environmental factors or unmeasured causal loci present across the genome, that may be associated with global ancestry; and GL, the immediate neighborhood of the marker locus that is used to estimate individual local ancestry L. Squares represent observed variables. Solid circles represent unobserved variables that can be estimated. Dashed circles represent unobserved variables that cannot be estimated. B) Directions of admixture linkage disequilibrium (LD) and the LD (D′) in the parental populations. Admixture LD is represented as the path GM–L–GD.

There are paths between factors that together may lead to confounding for the relationship between the marker (GM and potentially GD) and Y. By definition, global ancestry Q is correlated with local ancestry L (ρQ,L). When there are different allele frequencies by ancestral populations at GM (variation in q), Q is thus related to GM and results in the confounding path GM–L–Q–X–Y when testing the marker locus GM. Similarly, when there are different allele frequencies at GD, there will be the confounding path GD–L–Q–X–Y if we are testing the disease locus GD or even the marker locus GM.

There are 2 components that affect the magnitude of the LD between GM and GD in an admixed population: LD within parental populations (D′) and the admixture LD (47) induced by differential frequencies between ancestral populations at both the marker and the disease locus. As shown in Figure 1B, the admixture LD is indicated as the path GM–L–GD, and the LD within the parental populations is indicated as D′. As indicated in Figure 1B, the reference alleles for GM and GD are determined, so that the correlation between these 2 loci is positive within the admixed population. Similarly, a reference local ancestry population for L can be defined, such that L is positively correlated with GM in the admixed population. Thus, the reference allele is the same in both parental populations. Given these reference definitions, when L is negatively correlated with GD (left panel), there exists an overall negative correlation between GM and GD through the path GM–L–GD. In this situation, the admixture LD is in a different direction to the LD in the parental populations. This results in a corresponding reduction in the observed magnitude of the LD in the admixed population. In contrast, when L is positively correlated with GD, there is an overall positive correlation between GM and GD through the path GM–L–GD (right panel). In this situation, the admixture LD is in the same direction as the LD in the parental populations, and the observed LD between GM and GD in the admixed population is enhanced. In addition to the scenarios discussed above, when the LD in the 2 ancestral populations is in opposite directions, the admixture LD will always enhance the LD in one ancestry while reducing the level of LD in the other. In summary, for a marker GM, admixture LD has the potential to act as an additional confounder of the GM-Y effect. For a disease locus GD, there is no such potential.

Finally, individual local ancestries may modify the marginal effect at the marker locus because of the differential LD existing across ancestral populations. That is, within a study population, the level of association between GD-GM varies across individuals as a function of L (e.g., 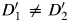Inline graphic). Thus, L acts as an effect modifier of the association between GM and Y.

Models

We use the following generalized linear models to investigate the efficiency of controlling for confounding by global ancestry and the potential impact on power by adjusting for local ancestry:

graphic file with name kws234eq1.jpg (1)
graphic file with name kws234eq2.jpg (2)
graphic file with name kws234eq3.jpg (3)

Specifically, g(μY) is a logit link for a dichotomous outcome Y conditional on the covariates included in the model, although alternative outcomes can be handled in a similar manner in the generalized linear framework. GM represents the number of variant alleles for each individual, and 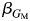Inline graphicis the corresponding marginal effect. A Wald or likelihood ratio test of 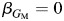Inline graphic can be used to test association. For investigating heterogeneity, we extend model 3 to include a GM × L interaction term:

graphic file with name kws234eq4.jpg (4)

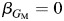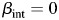Here, we use a 2-df likelihood ratio test for a joint test of Inline graphic and Inline graphic. This joint test has been shown to be nearly optimal across many different scenarios for main and interacting effects (48).

Simulations

We conduct simulations to investigate the performance of the models defined above (refer to the Web Appendix, Simulations section, available at http://aje.oxfordjournals.org/, for more details). Simulations are based on the framework represented in the graphical model (Figure 1). We simulate data based on the confounding paths and assess the type I error and power after adjusting for individual ancestries. To test the gain in power as well as the potential overadjustment by local ancestry, we include simulation scenarios that model the admixture LD. In addition, we simulate data with and without LD differences between populations to gauge the impact of heterogeneity between ancestries. In all scenarios, we generate cases for a binary disease outcome (Y) using a logistic regression model incorporating the disease locus GD and the individual global ancestry Q, with a 50% average probability for being a case. For simplicity, we assume a direct relationship of Q to Y.

Scenarios

Across all scenarios (Table 1), we vary the population-specific parameters for each ancestral population (p, q, and D′) and the causal model parameters βQ and 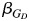Inline graphic (refer to the Web Appendix, Scenarios section, for more details).

Table 1.

Simulated Scenarios A–C

Scenario Allele Frequency Differencea SNP Effect, 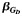Inline graphic Q Effect, βQ D′ Difference (Heterogeneity)
A 0, 0.4 None Log(3.0) None
B 0, 0.4 Log(1.2) None None
C None Log(1.2) Log(3.0) 0, 1.8
Open in a new tab

Abbreviation: SNP, single-nucleotide polymorphism.

a Allele frequencies at both the disease and the marker loci.

In scenario A, there is no genetic causal effect 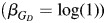Inline graphic but a strong global ancestry effect (βQ = log(3.0)). We simulate different allele frequencies between ancestral populations to investigate the efficiency of control for confounding by individual ancestries in models 2 (Y ∼ G + Q) and 3 (Y ∼ G + Q + L). In scenario B, we simulate admixture LD in the same and different directions to the LD in the original ancestral populations. Finally, in scenario C, the D′ difference between populations varies from 0 to 1.8 (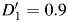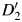Inline graphic, Inline graphic varies from −0.9 to 0.9) to gauge the impact of heterogeneity.

For each simulated scenario, we create 1,800 individuals with an equal number of individuals (NL = 600) within each local ancestry group (L = {0, 1, 2}, where L indicates the number of copies from ancestral population 1). Conditional on L and the corresponding specified parameters for allele frequency, LD, and risk, we generate GD, GM, and Q. We then probabilistically generate case status for all 1,800 individuals using a logistic regression model incorporating the disease locus GD and the individual global ancestry Q. Variables in the logistic regression model are mean centered, and there is a baseline risk of 50%, thus resulting in approximately equal numbers of cases and controls for each replicate. This simulation framework does not directly simulate potential confounding or heterogeneity by L. Rather, potential confounding and heterogeneity are induced by simulating haplotypes, global ancestry, and diseases status conditional on local ancestries as reflected in our graphical framework (Figure 1). Specifically, potential confounding is induced via the path, GM–L–Q–Y. The type I error and empirical power are calculated as the number of significant tests (α = 0.05) over 10,000 replicates.

University of Southern California Children's Health Study

The Children's Health Study is an ongoing cohort study investigating environmental and genetic influences on childhood asthma (49–51). The Children's Health Study genome-wide association study is a nested case-control study from the ongoing longitudinal Children's Health Study cohort, with approximately equal numbers of cases and controls for non-Hispanic whites and Hispanics. All Children's Health Study subjects and their parents gave informed consent, and the study was approved by the University of Southern California Institutional Review Board. In this study, we include a total of 2,839 samples from 2 self-reported ethnic groups: 1,396 non-Hispanic whites and 1,171 Hispanics. Among non-Hispanics samples, there are 595 cases and 801 controls; and there are 532 cases and 639 controls among Hispanics. We analyze the Children's Health Study data stratified by ethnicity and in a combined sample, assuming that the non-Hispanic white individuals all have 2 copies of European local ancestry at each location. Genotyping of these samples was performed at the University of Southern California Genome Center utilizing both the HumanHap550 (Illumina, Inc., San Diego, California) and the Human 610-Quad BeadChips (Illumina), and the analysis was conducted on 437,599 autosomal SNPs passing a stringent quality-control procedure. We performed several genome-wide scans on the Children's Health Study samples with additional covariates (age, gender, community of residence, and self-reported ethnicity). We estimated individual local ancestry among Hispanic samples through HAPMIX (52) (refer to the Web Appendix, Local ancestry estimation section, for more details). The average of all local ancestry estimates across the genome for each individual was used to estimate global ancestry (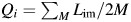Inline graphic). The estimated global ancestry is then compared with the more commonly used approach of estimating global ancestry by use of selected ancestry informative markers (42–44, 46) and the STRUCTURE program (29, 53–55) (refer to the Web Appendix, Global ancestry estimation section, for more details).

RESULTS

Simulations

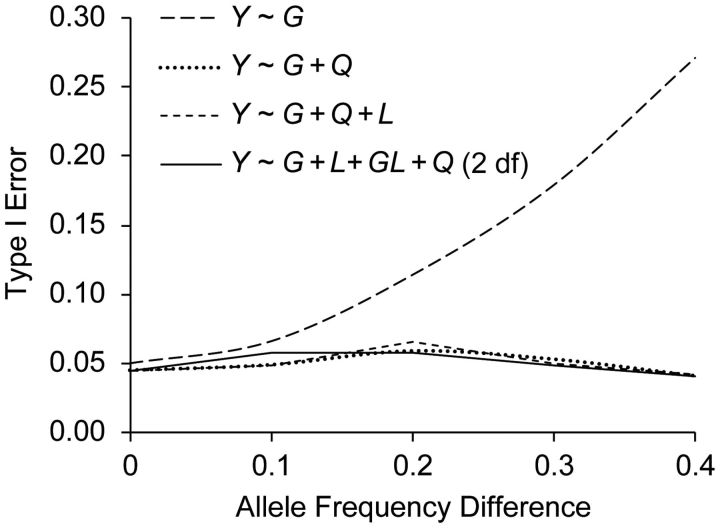
In scenario A (Figure 2), at the marker locus GM, when the allele frequency difference between ancestral populations is greater than 0.1 (account to 64% of the SNPs in the ENCODE regions as shown in Web Figure 1), the crude model has a substantially elevated type I error rate, while models 2 (Y ∼ G + Q) and 3 (Y ∼ G + Q + L) efficiently control for the confounding. The pattern is the same when testing the disease locus GD. In scenario B, there is no confounding path simulated, and all models have the correct test size (not shown). Reflecting these patterns, adjustment by global ancestry (when needed) results in an unbiased effect estimate. In contrast, there is very little impact on the effect estimate from adjustment with local ancestry. However, when the induced LD due to differential allele frequency between ancestries is in the same direction as the LD from the parental ancestries (Figure 3A), adjustment for local ancestry results in a slight loss in power. When the induced LD is in the opposite direction to the LD from the parental ancestries (Figure 3B), additional adjustment of local ancestries results in a slight increase in power. However, this decrease/increase in power is negligible for allele frequency differences of less than 0.1. When testing the disease variant directly, as opposed to a marker, we found that the pattern is the same as that shown in Figure 3A.

Figure 2.

Figure 2.

Open in a new tab

Type I error rates with and without control for confounding at the marker locus in scenario A.

Figure 3.

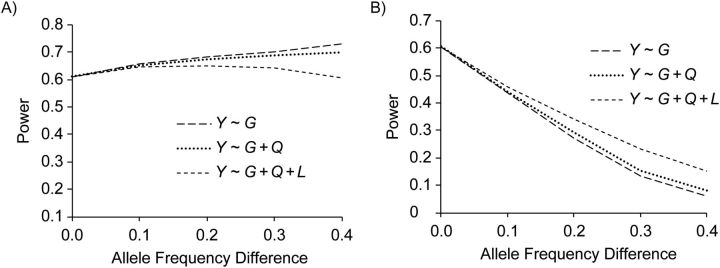
Figure 3.

Open in a new tab

Effect of adjustment by global and local ancestries on power in scenario B. A) Induced linkage disequilibrium (LD) in the same direction as the LD in the parental ancestries; B) induced LD in a different direction from the LD in the parental ancestries.

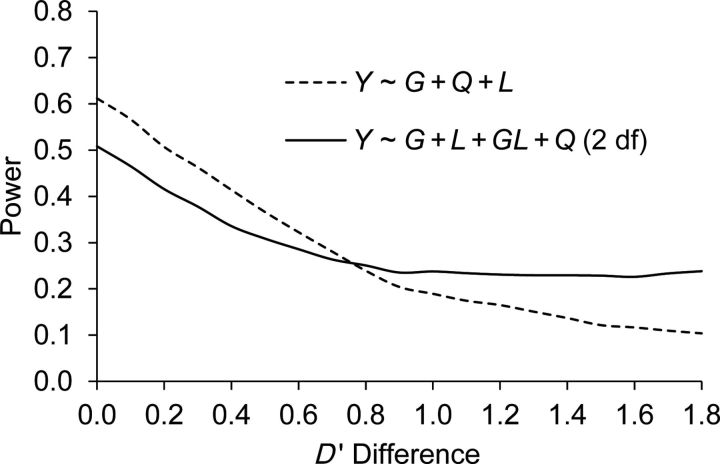
Figure 4 shows the performance of inclusion of the GM × L interaction term by comparing model 3 (Y ∼ G + Q + L) and model 4 (Y ∼ G + L + GL + Q). For tests at the marker locus GM, when the LDs between GM and GD are similar in the ancestral populations (D′ < 0.7), there is a reduction in power for the 2-df test of the joint effect of GM and GM × L from model 4. As the difference in LD increases (D′ ≥ 0.7), model 4 has similar or greater power than model 3. For testing a disease variant (D′ difference = 0), the loss in power is 0.10 for the simulated scenario.

Figure 4.

Figure 4.

Open in a new tab

Comparison of power in scenario C when there is heterogeneity due to differential linkage disequilibrium between ancestries.

Children's Health Study

When investigating the impact of confounding in the Children's Health Study (a genome-wide association study), we found that the crude analysis Y ∼ G among the combined samples of Hispanics and non-Hispanic whites results in a large overdispersion (λ1 = 1.27) that is reduced substantially with adjustment by global or both global and local ancestries in models 2 (Y ∼ G + Q) (λ2 = 1.02) and 3 (Y ∼ G + Q + L) (λ3 = 1.02). However, the overdispersion parameter is a summary across the entire genome. In the Children's Health Study data for example, about 50% of the markers have a smaller P value from model 3 (Y ∼ G + Q + L) compared with model 2 (Y ∼ G + Q). About 10% of the SNPs found to be potentially interesting (P < 0.05) from an analysis with both global and local ancestry are not noteworthy with an analysis adjusting only for global ancestry. In terms of effect estimates, among those SNPs potentially interesting (P < 0.05) from an analysis adjusting for global ancestry only, additional adjustment for local ancestry results in a 10% or greater change in the effect estimate for over 9% of the SNPs.

Figure 5 shows the P values from a genome-wide association study analysis of the combined non-Hispanic white and Hispanic populations in the Children's Health Study using models 3 and 4. The most notable SNP (rs10119122) (P = 4.5 × 10−8) from model 3 remains noteworthy with the 2-df test from model 4. There is an additional SNP (rs10519951) that lacks association with model 3 (P = 0.50) but is noteworthy with model 4 as indicated by a much smaller P value (P = 8.5 × 10−7). Table 2 provides the SNP effect estimates and corresponding P values from both models for these 2 SNPs from the ethnic-specific and combined analyses. In addition, for model 4 in the Hispanic-only analysis and the combined analysis, we present the expected genetic effect estimate within each local ancestry stratum by stratifying individuals by their estimated local ancestry at each SNP and using the stratum-specific effect estimates from model 4. For SNP rs10119122, there are similar allele frequencies across the 2 populations, and there is very little heterogeneity indicated from model 4 in Hispanics. Thus, the marginal effect estimate from model 3 in the Hispanic-only analysis Inline graphic is similar to that in the non-Hispanic estimates 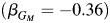Inline graphic. It is also interesting to note that, in the non-Hispanic white-only analysis, rs10119122 has an effect estimate of βGM = −0.36. 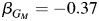For the Hispanic individuals-only analysis within the strata of individuals with 2 copies of European ancestry, the effect estimate is almost identical Inline graphic.

Figure 5.

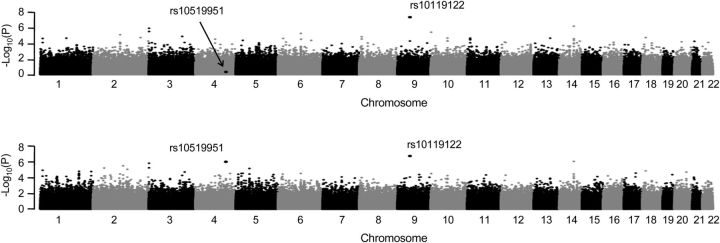
Figure 5.

Open in a new tab

Children's Health Study analysis results across models Y ∼ G + Q + L (top) and Y ∼ G + L + GL + Q (2 df) (bottom) for combined non-Hispanic white and Hispanic samples.

Table 2.

P Value and Effect Estimate for Selected Markers Across Ethnic Groups and Models in the Ongoing Children's Health Study

Marker Allele Local Strataa Non-Hispanic Whites
 Hispanics
 Combinedb
No.c Allele Frequency Model 3d
 No. Allele Frequency Model 3
 Model 4e
 No. Allele Frequency Model 3
 Model 4
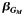Inline graphic P Value Inline graphic P Value Inline graphic P Value Inline graphic P Value Inline graphic 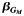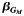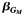P Value
rs10119122 G L ≈ 0 0 12 0.46 0.03 12 0.46 0.04
  L ≈ 1 0 410 0.60 −0.17 410 0.60 −0.17
L ≈ 2 1,372 0.66 721 0.64 −0.37 2,093 0.65 −0.37
All 1,372 0.66 −0.36 2.1 × 10−5 1,143 0.62 −0.30 1.8 × 10−3 4.7 × 10−3 2,515 0.64 −0.34 4.5 × 10−8 1.6 × 10−7
rs10519951 T L ≈ 0 0 119 0.34 −1.12 119 0.34 −1.17
L ≈ 1 0 531 0.26 −0.48 531 0.26 −0.49
L ≈ 2 1,386 0.19 510 0.19 0.16 1,896 0.19 0.18
All 1,386 0.19 0.19 7.1 × 10−2 1,160 0.24 −0.29 5.2 × 10−3 1.6 × 10−5 2,546 0.21 −0.05 5.0 × 10−1 8.5 × 10−7
Open in a new tab

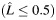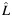a Estimated individual local ancestry. L is rounded up into 3 categorical groups: 0 Inline graphic; 1 (Inline graphic > 0.5–1.5); and 2 (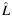Inline graphic > 1.5).

b Combined non-Hispanic white and Hispanic samples for analysis.

c Sample size within each local stratum.

d Effect estimate 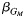Inline graphicof the single-nucleotide polymorphism marginal effect followed by the corresponding P value from model 3: Y ∼ G + Q + L.

e The expected effect estimate 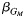Inline graphicof the single-nucleotide polymorphism effect within each local stratum followed by the 2-df test P value from model 4: Y ∼ G + L + GL + Q.

In contrast, SNP rs10519951 has very little evidence for an effect in the non-Hispanic white analysis from model 3 (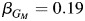Inline graphic; P = 0.07). In the Hispanic-only analysis, rs10519951 has a sizeable inverse effect on asthma from model 3 (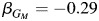Inline graphic; P = 5.2 × 10−3), and further evidence of heterogeneity by local ancestry from model 4, specifically the test for only the interaction term, has P = 1.6 × 10−5. Also, the estimates of effect are comparable between the non-Hispanic whites only (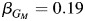Inline graphic) and the Hispanics only within the strata of individuals having 2 copies of European ancestry (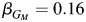Inline graphic). In the Hispanic-only analysis within the strata of individuals carrying 0 copies of European ancestry, the estimate is 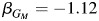Inline graphic. The contrast in estimates across strata is reflected in the more significant result from model 4 in the combined sample (P = 8.5 × 10−7).

DISCUSSION

When confounding arises through global ancestry via a path that links an external factor to the marker being evaluated, then global ancestry alone can control for the confounding. This assumes that the estimated global ancestry accurately captures the underlying factor. Previous studies have argued that adjustment for local ancestry is necessary for controlling for confounding (35, 36, 38); however, these papers simulated local ancestry as a strict confounder and did not allow for induced LD in admixed populations. Our simulations demonstrate that impact of adjustment for local ancestry is more nuanced within admixed populations. When the direction of the admixture LD is in a different direction from the LD in the parental ancestries, there is a reduction in the magnitude of the LD in the admixed population, and additional adjustment for local ancestry can increase the power to detect the true association at the marker locus. This potential gain in power, however, comes with risk: When the admixture LD is in the same direction as the LD within the ancestral population, adjustment for local ancestry will result in overadjustment. As shown in Web Figure 2, induced LD and the LD within the ancestral populations are in the same direction for about 57% of the loci in the ENCODE regions (56) (refer to the Web Appendix, ENCODE regions section, for more details).

When investigating heterogeneity-of-effect estimates by local ancestry, we found that there is also a potential loss in power by testing both the SNP main effect and the interaction via a 2-df test (Figure 4). In the ENCODE regions, about 30% of the estimated differences in D′ between the populations are greater than 0.7 (Web Figure 3). Our simulation results demonstrate that model 4 with the SNP–local ancestry interaction has greater power than the conventional model for D′ differences above 0.7. Thus, one may expect an increase in power for about 30% of the SNPs, with the remaining 70% having none or a slight reduction in power. Given this tradeoff, we believe that a genome-wide association study for discovery using only model 4 may not be the most advantageous approach. However, in practice, most investigators will first perform an analysis without an interaction term. Subsequent analyses with the interaction term included offer the potential to uncover previously unidentified regions. In such a 2-step approach, one would need to consider the impact on type I error, but for discovery and further follow-up, such impact may be negligible.

For the Children's Health Study genome-wide association study, the most notable SNP (rs10119122) from the marginal test of the SNPs remains noteworthy with the 2-df test from model 4. In contrast, SNP rs10519951, an SNP in the nuclear receptor subfamily 3, group C, member 2 gene (NR3C2), has a significant P value only from model 4 (P = 8.5 × 10−7 in the combined samples). Although rs10519951 does not reach the conventional cutoff for determining genome-wide significance for main effects (i.e., α = 5 × 10−8), the genome-wide significance level for the 2-df test that involved correlated local ancestries across the genome is unclear and is an active area of research. Such significance levels may depend on the specific admixed population investigated, beause the distribution of local ancestry for each individual across all locations in the genome will depend upon the sample. In this case, a permutation test for determining significance may be required. Whether the top SNPs are strictly significant or not, there is clear potential for additional information to be gained from including local ancestry in a test of heterogeneity. Overall for the Children's Health Study and consistent with results from ENCODE, the interaction model results in smaller P values for 35% of the SNPs across the genome. Notably, for those SNPs with a smaller P value from model 4, this change is often substantial, suggesting that a great deal of additional information may be captured by jointly considering the main and interaction terms.

When testing the disease variant, we find that adjustment for local ancestry most often results in a loss of power from overadjustment when the allele frequency is different between ancestries. Likewise, when investigating a measured causal variant in an admixed population, we find that there will be no influence of differential LD between the marker and the causal variant. Thus, the inclusion of an SNP by local ancestry interaction term will not capture any additional information, and stratified estimates across local ancestry strata should be similar. This offers a potential approach to leverage differential LD patterns in an admixed population to help identify causal variants when performing fine-scale mapping or sequencing studies (57).

In addition to capturing the heterogeneity of the SNP effect among admixed populations, it is possible that this observed effect is induced by another genetic or environmental factor that drives the observed effect modification and is correlated with self-identified ethnicity and, thus, related to local ancestry via global ancestry (i.e., X-Q-L). In order to investigate the source (environmental or genetic) of the heterogeneity, one can perform further analyses within strata by individual global ancestry and, if available, the strata of self-reported ethnicity. For SNP rs10519951, Table 3 shows that the heterogeneity captured by local ancestry is attenuated when stratifying by global ancestry or self-identified ethnicity. These results suggest that this particular observed heterogeneity is most likely due to local genetic structure and not global genetic or environmental differences.

Table 3.

Investigation of Heterogeneity for Single-Nucleotide Polymorphism rs10519951 in Combined Samples from the Ongoing Children's Health Study

Strata No. Allele Frequency β Coefficient P Value
All Combined 2,546 0.21 −0.05 5.0 × 10−1 a
Lb L ≈ 0 (Asian) 119 0.34 −1.17 8.5 × 10−7
L ≈ 1 531 0.26 −0.49
L ≈ 2 (European) 1,896 0.19 0.18
Qb Q ≈ 0.25 (Asian) 21 0.43 −0.76 2.9 × 10−2 c
Q ≈ 0.5 480 0.30 −0.35
Q ≈ 0.75 (European) 2,045 0.19 0.06
Ed Hispanics 1,160 0.24 −0.29 5.6 × 10−3 c
Non-Hispanic white 1,386 0.19 0.19
Open in a new tab

Abbreviation: SNP, single-nucleotide polymorphism.

a Conventional analysis testing of the SNP main effect only.

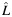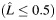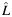b Estimated individual ancestry is rounded into 3 categorical groups when presenting the number of samples and the allele frequency within each stratum Inline graphic: 0 Inline graphic; 1 (Inline graphic > 0.5–1.5); and 2 (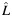Inline graphic > 1.5). Q: 0.25 (Q ≤ 0.33); 0.5 (Q > 0.33–0.66); and 0.75 (Q > 0.66).

c Two-df test of the SNP by strata interaction and the SNP marginal effect.

d Self-reported ethnicity.

We have demonstrated that one needs to consider the impact of adjustment by local ancestry in addition to the common practice of adjusting for global ancestry. Although the adjustment with local ancestry reflects the induced admixture LD within admixed populations, the impact of inclusion of local ancestry depends upon the LD patterns in the ancestral populations. Furthermore, we have also demonstrated the potential for a 2-df test of SNP main effect and SNP by local ancestry interaction to increase power when there is substantial differential LD between ancestry populations. We realize that, for most genome-wide association studies utilizing admixed populations, investigators will first scan the genome with a marginal test of association. Thus, we view analyses with the interaction term as secondary follow-up to uncover previously unidentified regions with substantial heterogeneity of SNP effect by local ancestry.

ACKNOWLEDGMENTS

Author affiliations: Department of Preventive Medicine, University of Southern California, Los Angeles, California (Jinghua Liu, Juan Pablo Lewinger, Frank D. Gilliland, W. James Gauderman, David V. Conti).

This work is supported by grants R01ES016813, P30ES007048, P01ES011627, and P30ES007048 from the National Institute of Environmental Health Sciences and by grant R01HL087680 from the National Heart, Lung, and Blood Institute.

Conflict of interest: none declared.

REFERENCES

  • 1.Hindorff LA, Sethupathy P, Junkins HA, et al. Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc Natl Acad Sci U S A. 2009;106(23):9362–9367. doi: 10.1073/pnas.0903103106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Rosenberg NA, Huang L, Jewett EM, et al. Genome-wide association studies in diverse populations. Nat Rev Genet. 2010;11(5):356–366. doi: 10.1038/nrg2760. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Garcia-Barcelo MM, Tang CS, Ngan ES, et al. Genome-wide association study identifies NRG1 as a susceptibility locus for Hirschsprung's disease. Proc Natl Acad Sci U S A. 2009;106(8):2694–2699. doi: 10.1073/pnas.0809630105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Guo Y, Tan LJ, Lei SF, et al. Genome-wide association study identifies ALDH7A1 as a novel susceptibility gene for osteoporosis. PLoS Genet. 2010;6(1):e1000806. doi: 10.1371/journal.pgen.1000806. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Hattori E, Toyota T, Ishitsuka Y, et al. Preliminary genome-wide association study of bipolar disorder in the Japanese population. Am J Med Genet B Neuropsychiatr Genet. 2009;150B(8):1110–1117. doi: 10.1002/ajmg.b.30941. [DOI] [PubMed] [Google Scholar]
  • 6.Lei SF, Yang TL, Tan LJ, et al. Genome-wide association scan for stature in Chinese: evidence for ethnic specific loci. Hum Genet. 2009;125(1):1–9. doi: 10.1007/s00439-008-0590-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Ng CC, Yew PY, Puah SM, et al. A genome-wide association study identifies ITGA9 conferring risk of nasopharyngeal carcinoma. J Hum Genet. 2009;54(7):392–397. doi: 10.1038/jhg.2009.49. [DOI] [PubMed] [Google Scholar]
  • 8.Tse KP, Su WH, Chang KP, et al. Genome-wide association study reveals multiple nasopharyngeal carcinoma-associated loci within the HLA region at chromosome 6p21.3. Am J Hum Genet. 2009;85(2):194–203. doi: 10.1016/j.ajhg.2009.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Zhang XJ, Huang W, Yang S, et al. Psoriasis genome-wide association study identifies susceptibility variants within LCE gene cluster at 1q21. Nat Genet. 2009;41(2):205–210. doi: 10.1038/ng.310. [DOI] [PubMed] [Google Scholar]
  • 10.Hiura Y, Shen CS, Kokubo Y, et al. Identification of genetic markers associated with high-density lipoprotein-cholesterol by genome-wide screening in a Japanese population: the Suita Study. Circ J. 2009;73(6):1119–1126. doi: 10.1253/circj.cj-08-1101. [DOI] [PubMed] [Google Scholar]
  • 11.Kamatani Y, Matsuda K, Okada Y, et al. Genome-wide association study of hematological and biochemical traits in a Japanese population. Nat Genet. 2010;42(3):210–215. doi: 10.1038/ng.531. [DOI] [PubMed] [Google Scholar]
  • 12.Tanaka Y, Nishida N, Sugiyama M, et al. Genome-wide association of IL28B with response to pegylated interferon-α and ribavirin therapy for chronic hepatitis C. Nat Genet. 2009;41(10):1105–1109. doi: 10.1038/ng.449. [DOI] [PubMed] [Google Scholar]
  • 13.Unoki H, Takahashi A, Kawaguchi T, et al. SNPs in KCNQ1 are associated with susceptibility to type 2 diabetes in East Asian and European populations. Nat Genet. 2008;40(9):1098–1102. doi: 10.1038/ng.208. [DOI] [PubMed] [Google Scholar]
  • 14.Yamada Y, Fuku N, Tanaka M, et al. Identification of CELSR1 as a susceptibility gene for ischemic stroke in Japanese individuals by a genome-wide association study. Atherosclerosis. 2009;207(1):144–149. doi: 10.1016/j.atherosclerosis.2009.03.038. [DOI] [PubMed] [Google Scholar]
  • 15.Yasuda K, Miyake K, Horikawa Y, et al. Variants in KCNQ1 are associated with susceptibility to type 2 diabetes mellitus. Nat Genet. 2008;40(9):1092–1097. doi: 10.1038/ng.207. [DOI] [PubMed] [Google Scholar]
  • 16.Cho YS, Go MJ, Kim YJ, et al. A large-scale genome-wide association study of Asian populations uncovers genetic factors influencing eight quantitative traits. Nat Genet. 2009;41(5):527–534. doi: 10.1038/ng.357. [DOI] [PubMed] [Google Scholar]
  • 17.Adeyemo A, Gerry N, Chen G, et al. A genome-wide association study of hypertension and blood pressure in African Americans. PLoS Genet. 2009;5(7):e1000564. doi: 10.1371/journal.pgen.1000564. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Barnholtz-Sloan JS, Shetty PB, Guan X, et al. FGFR2 and other loci identified in genome-wide association studies are associated with breast cancer in African-American and younger women. Carcinogenesis. 2010;31(8):1417–1423. doi: 10.1093/carcin/bgq128. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Hayes MG, Pluzhnikov A, Miyake K, et al. Identification of type 2 diabetes genes in Mexican Americans through genome-wide association studies. Diabetes. 2007;56(12):3033–3044. doi: 10.2337/db07-0482. [DOI] [PubMed] [Google Scholar]
  • 20.Norris JM, Langefeld CD, Talbert ME, et al. Genome-wide association study and follow-up analysis of adiposity traits in Hispanic Americans: the IRAS Family Study. Obesity (Silver Spring) 2009;17(10):1932–1941. doi: 10.1038/oby.2009.143. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Palmer ND, Langefeld CD, Ziegler JT, et al. Candidate loci for insulin sensitivity and disposition index from a genome-wide association analysis of Hispanic participants in the Insulin Resistance Atherosclerosis (IRAS) Family Study. Diabetologia. 2010;53(2):281–289. doi: 10.1007/s00125-009-1586-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Rich SS, Goodarzi MO, Palmer ND, et al. A genome-wide association scan for acute insulin response to glucose in Hispanic-Americans: the Insulin Resistance Atherosclerosis Family Study (IRAS FS) Diabetologia. 2009;52(7):1326–1333. doi: 10.1007/s00125-009-1373-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Bonilla C, Parra EJ, Pfaff CL, et al. Admixture in the Hispanics of the San Luis Valley, Colorado, and its implications for complex trait gene mapping. Ann Hum Genet. 2004;68(2):139–153. doi: 10.1046/j.1529-8817.2003.00084.x. [DOI] [PubMed] [Google Scholar]
  • 24.Gonzalez Burchard E, Borrell LN, Choudhry S, et al. Latino populations: a unique opportunity for the study of race, genetics, and social environment in epidemiological research. Am J Public Health. 2005;95(12):2161–2168. doi: 10.2105/AJPH.2005.068668. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Thomas DC, Witte JS. Point: population stratification: a problem for case-control studies of candidate-gene associations? Cancer Epidemiol Biomarkers Prev. 2002;11(6):505–512. [PubMed] [Google Scholar]
  • 26.Devlin B, Roeder K. Genomic control for association studies. Biometrics. 1999;55(4):997–1004. doi: 10.1111/j.0006-341x.1999.00997.x. [DOI] [PubMed] [Google Scholar]
  • 27.Setakis E, Stirnadel H, Balding DJ. Logistic regression protects against population structure in genetic association studies. Genome Res. 2006;16(2):290–296. doi: 10.1101/gr.4346306. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Hoggart CJ, Parra EJ, Shriver MD, et al. Control of confounding of genetic associations in stratified populations. Am J Hum Genet. 2003;72(6):1492–1504. doi: 10.1086/375613. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155(2):945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Satten GA, Flanders WD, Yang Q. Accounting for unmeasured population substructure in case-control studies of genetic association using a novel latent-class model. Am J Hum Genet. 2001;68(2):466–477. doi: 10.1086/318195. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Li Q, Yu K. Improved correction for population stratification in genome-wide association studies by identifying hidden population structures. Genet Epidemiol. 2008;32(3):215–226. doi: 10.1002/gepi.20296. [DOI] [PubMed] [Google Scholar]
  • 32.Miclaus K, Wolfinger R, Czika W. SNP selection and multidimensional scaling to quantify population structure. Genet Epidemiol. 2009;33(6):488–496. doi: 10.1002/gepi.20401. [DOI] [PubMed] [Google Scholar]
  • 33.Price AL, Patterson NJ, Plenge RM, et al. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38(8):904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
  • 34.Engelhardt BE, Stephens M. Analysis of population structure: a unifying framework and novel methods based on sparse factor analysis. PLoS Genet. 2010;6(9):e1001117. doi: 10.1371/journal.pgen.1001117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Wang X, Zhu X, Qin H, et al. Adjustment for local ancestry in genetic association analysis of admixed populations. Bioinformatics. 011;27(5):670–677. doi: 10.1093/bioinformatics/btq709. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Kang SJ, Larkin EK, Song Y, et al. Assessing the impact of global versus local ancestry in association studies. BMC Proc. 2009;3(7):S107. doi: 10.1186/1753-6561-3-s7-s107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Bryc K, Velez C, Karafet T, et al. Colloquium paper: genome-wide patterns of population structure and admixture among Hispanic/Latino populations. Proc Natl Acad Sci U S A. 2010;107(2):8954–8961. doi: 10.1073/pnas.0914618107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Qin H, Morris N, Kang SJ, et al. Interrogating local population structure for fine mapping in genome-wide association studies. Bioinformatics. 2010;26(23):2961–2968. doi: 10.1093/bioinformatics/btq560. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Shriner D, Adeyemo A, Ramos E, et al. Mapping of disease-associated variants in admixed populations. Genome Biol. 2011;12(5):223. doi: 10.1186/gb-2011-12-5-223. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Greenland S. Quantifying biases in causal models: classical confounding vs collider-stratification bias. Epidemiology. 2003;14(3):300–306. [PubMed] [Google Scholar]
  • 41.Greenland S, Pearl J, Robins JM. Causal diagrams for epidemiologic research. Epidemiology. 1999;10(1):37–48. [PubMed] [Google Scholar]
  • 42.Seldin MF, Shigeta R, Villoslada P, et al. European population substructure: clustering of northern and southern populations. PLoS Genet. 2006;2(9):e143. doi: 10.1371/journal.pgen.0020143. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Shtir CJ, Marjoram P, Azen S, et al. Variation in genetic admixture and population structure among Latinos: the Los Angeles Latino Eye Study (LALES) BMC Genet. 2009;10:71. doi: 10.1186/1471-2156-10-71. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Smith MW, Patterson N, Lautenberger JA, et al. A high-density admixture map for disease gene discovery in African Americans. Am J Hum Genet. 2004;74(5):1001–1013. doi: 10.1086/420856. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Tian C, Gregersen PK, Seldin MF. Accounting for ancestry: population substructure and genome-wide association studies. Hum Mol Genet. 2008;17(2):R143–R150. doi: 10.1093/hmg/ddn268. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46.Tian C, Plenge RM, Ransom M, et al. Analysis and application of European genetic substructure using 300 K SNP information. PLoS Genet. 2008;4(1):e4. doi: 10.1371/journal.pgen.0040004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.Smith MW, O'Brien SJ. Mapping by admixture linkage disequilibrium: advances, limitations and guidelines. Nat Rev Genet. 2005;6(8):623–632. doi: 10.1038/nrg1657. [DOI] [PubMed] [Google Scholar]
  • 48.Kraft P, Yen YC, Stram DO, et al. Exploiting gene-environment interaction to detect genetic associations. Hum Hered. 2007;63(2):111–119. doi: 10.1159/000099183. [DOI] [PubMed] [Google Scholar]
  • 49.McConnell R, Berhane K, Gilliland F, et al. Air pollution and bronchitic symptoms in southern California children with asthma. Environ Health Perspect. 1999;107(9):757–760. doi: 10.1289/ehp.99107757. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 50.Li YF, Gauderman WJ, Conti DV, et al. Glutathione S-transferase P1, maternal smoking, and asthma in children: a haplotype-based analysis. Environ Health Perspect. 2008;116(3):409–415. doi: 10.1289/ehp.10655. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 51.Navidi W, Thomas D, Stram D, et al. Design and analysis of multilevel analytic studies with applications to a study of air pollution. Environ Health Perspect. 1994;102(8):25–32. doi: 10.1289/ehp.94102s825. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 52.Price AL, Tandon A, Patterson N, et al. Sensitive detection of chromosomal segments of distinct ancestry in admixed populations. PLoS Genet. 2009;5(6):e1000519. doi: 10.1371/journal.pgen.1000519. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 53.Falush D, Stephens M, Pritchard JK. Inference of population structure using multilocus genotype data: linked loci and correlated allele frequencies. Genetics. 2003;164(4):1567–1587. doi: 10.1093/genetics/164.4.1567. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 54.Falush D, Stephens M, Pritchard JK. Inference of population structure using multilocus genotype data: dominant markers and null alleles. Mol Ecol Notes. 2007;7(4):574–578. doi: 10.1111/j.1471-8286.2007.01758.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 55.Hubisz M, Falush D, Stephens M, et al. Inferring weak population structure with the assistance of sample group information. Mol Ecol Resour. 2009;9(5):1322–1332. doi: 10.1111/j.1755-0998.2009.02591.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 56.The ENCODE (ENCyclopedia Of DNA Elements) Project. Science. 2004;306(5696):636–640. doi: 10.1126/science.1105136. [DOI] [PubMed] [Google Scholar]
  • 57.Stacey SN, Sulem P, Zanon C, et al. Ancestry-shift refinement mapping of the C6orf97-ESR1 breast cancer susceptibility locus. PLoS Genet. 2010;6(7):e1001029. doi: 10.1371/journal.pgen.1001029. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from American Journal of Epidemiology are provided here courtesy of Oxford University Press

RESOURCES