Decomposition of Variance for Spatial Cox Processes

Abstract

Spatial Cox point processes is a natural framework for quantifying the various sources of variation governing the spatial distribution of rain forest trees. We introduce a general criterion for variance decomposition for spatial Cox processes and apply it to specific Cox process models with additive or log linear random intensity functions. We moreover consider a new and flexible class of pair correlation function models given in terms of normal variance mixture covariance functions. The proposed methodology is applied to point pattern data sets of locations of tropical rain forest trees.

1 Introduction

The spatial distributions of tropical rain forest trees are influenced by many factors including e.g. spatially varying environmental conditions, seed dispersal, infectious diseases, and gap creation by hurricanes. One natural question is, loosely speaking, ‘how much of the variation’ in the spatial distribution of a tropical rain forest tree species can be attributed to each of these factors? In this paper we study methods for addressing this question with a particular focus on the contribution of the environment.

The most fundamental summaries of variation are the variances of counts of trees in bounded regions. A generalized linear mixed model (GLMM) for such counts, with a variance component for each of the sources of variation, might be a starting point for decomposing the variance. However, with this approach one loses the fine-scale information contained in extensive tropical rain forest data sets which include locations of individual trees and not just numbers of trees in certain regions (e.g. Condit, 1998). Moreover, conclusions obtained from a fitted GLMM may in general be strongly dependent on the sizes and shapes of the regions used to create the count data.

A more natural and flexible approach is to model the individual tree locations as a spatial point process (e.g. Møller and Waagepetersen, 2004) and then derive summaries of variation from a fitted spatial point process model. With this approach one can compute variances and covariances of counts in arbitrary regions and therefore recover all summaries that would be obtained from a GLMM approach. In particular, Cox processes (e.g. Møller and Waagepetersen, 2004) provide a useful framework for integrating different sources of variation.

This paper introduces a general criterion for decomposition of variance for Cox processes. The criterion is applied to specific Cox process models with either additive or log linear random intensity functions. The additive model is appealing in the context of variance decomposition but has not been well studied in the point process literature. For either model, the resulting variance decomposition depends on the assumed pair correlation function which characterizes the spatial correlation in the Cox process. It is therefore important to have a wide class of pair correlation functions to choose from. To this end we consider a new class of shot-noise Cox processes with normal variance mixture pair correlation functions. These functions are closely related to widely used counterparts in geostatistics and hence serve as a bridge to further connect the theories of geostatistics and point processes.

1.1 A tropical rain forest data example

Waagepetersen and Guan (2009) fitted so-called inhomogeneous Thomas processes to locations of three tree species, namely Acalypha diversifolia (528 trees), Lonchocarpus heptaphyllus (836 trees), and Capparis frondosa (3299 trees) that were alive in 1995 in the 1000 m by 500 m Barro Colorado Island plot (Condit et al., 1996; Condit, 1998; Hubbell and Foster, 1983). The significant covariates in the fitted Thomas models were elevation and potassium for Acalypha and Capparis and nitrogen and phosphorous for Lonchocarpus. The point patterns of tree locations and the covariate potassium are shown in Figure 1.

Figure 1.

Locations of Acalypha, Lonchocarpus, and Capparis trees and image of interpolated potassium content in the surface soil (from top to bottom).

In Section 7 we study decomposition of variance for these data sets. We moreover employ a much broader class of Cox processes than the inhomogeneous Thomas processes used in Waagepetersen and Guan (2009).

2 Background on spatial point processes

Let X be a point process on ℝ² and let N(B), for any bounded B ⊆ ℝ², denote the number of points in X ∩ B. The first- and second-order moments of the counts N(B) are determined by the intensity function ρ and the second-order product density ρ⁽²⁾ of X which are functions defined on ℝ² and ℝ² × ℝ², respectively (see Møller and Waagepetersen, 2004). More precisely,

$$\mathbb{E}N(B)={\int }_B\rho (u)\text{d}u$$

and

$$\mathbb{E}N(A)N(B)={\int }_{A\cap B}\rho (u)\text{d}u+{\int }_A{\int }_B{\rho }^{(2)}(u,v)\text{d}u\text{d}v$$

for bounded A, B ⊆ ℝ². The pair correlation function g is given by g(u, v) = ρ⁽²⁾(u, v)/[ρ(u)ρ(v)].

For a Poisson process, the counts in disjoint regions are independent and Poisson distributed. A Cox process is driven by a random intensity function Λ = {Λ(u) : u ∈ ℝ²}. Conditional on Λ = λ, the Cox process becomes a Poisson process with intensity function λ. For a Cox process, ρ(u) = Λ(u) and ρ⁽²⁾(u, v) = [Λ(u)Λ(v)].

3 Decomposition of variance

To quantify the various sources of variation in a spatial point pattern we consider the contribution of each source to the total variation of a count N(B) for a region B. According to the previous section,

$$\mathbb{V}\text{ar}N(B)={\int }_B\rho (u)\text{d}u+{\int }_B{\int }_B\rho (u)\rho (v)[g(u,v)-1]\text{d}u\text{d}v.$$ (1)

The first term on the right-hand side of (1) is the variance of N(B) for a Poisson process with intensity function ρ(·). The second term is the increase (or decrease) in variance due to possible attraction (or repulsion) between points corresponding to g > 1 (or g < 1).

For a Cox process X driven by a random intensity function Λ, we can decompose a count N(B) as N(B) = I_|Λ(B) + N̂_|Λ(B) where

$${\widehat{N}}_{\mid \mathrm{\Lambda }}(B)=\mathbb{E}[N(B)\mid \mathrm{\Lambda }]={\int }_B\mathrm{\Lambda }(u)\text{d}u$$

is the minimum mean square error predictor of N(B) given Λ and I_|Λ(B) = N(B) − N̂_|Λ(B) is an innovation process in the terminology of Baddeley et al. (2005). Then I_|Λ(B) and N̂_|Λ(B) are uncorrelated processes with

$$\mathbb{E}{I}_{\mid \mathrm{\Lambda }}(B)=0,\mathbb{C}\text{ov}[I_{\mid \mathrm{\Lambda }}(A),U_{\mid \mathrm{\Lambda }}(B)]={\int }_{A\cap B}\rho (u)\text{d}u$$

and

$$\mathbb{C}\text{ov}[{\widehat{N}}_{\mid \mathrm{\Lambda }}(A),{\widehat{N}}_{\mid \mathrm{\Lambda }}(B)]={\int }_A{\int }_B\rho (u)\rho (v)[g(u,v)-1]\text{d}u\text{d}v$$

since ℂov[Λ(u), Λ(v)] = ρ(u)ρ(v)[g(u, v) − 1]. The process I_|Λ may be viewed as a ‘nugget’ process in geostatistical terminology since I_|Λ(A) and I_|Λ(B) are uncorrelated when A and B are disjoint. The spatially correlated sources of variation causing the extra-Poisson variance in (1) enters via N̂_|Λ.

In Section 4 we model Λ in terms of a random covariate process Z. To quantify how much of the spatially structured variation is due to Z we further decompose N̂_|Λ(B) = I_|Λ,Z(B) + N̂_|Λ,Z into uncorrelated components

$${\widehat{N}}_{\mid \mathrm{\Lambda },Z}=\mathbb{E}[{\widehat{N}}_{\mid \mathrm{\Lambda }}(B)\mid Z]={\int }_B\mathbb{E}[\mathrm{\Lambda }(u)\mid Z]\text{d}u$$

and

$$I_{\mid \mathrm{\Lambda },Z}(B)={\widehat{N}}_{\mid \mathrm{\Lambda }}(B)-{\widehat{N}}_{\mid \mathrm{\Lambda },Z}(B)={\int }_B\{\mathrm{\Lambda }(u)-\mathbb{E}[\mathrm{\Lambda }(u)\mid Z]\}\text{d}u.$$

If all random variation in Λ is due to Z then arI_|Λ,Z(B) = 0. Further, arN̂_|Λ,Z(B) = 0 if Λ is independent of Z. The quantity

$$R^2(B)=\frac{\mathbb{V}\text{ar}{\widehat{N}}_{\mid \mathrm{\Lambda },Z}(B)}{\mathbb{V}\text{ar}{\widehat{N}}_{\mid \mathrm{\Lambda }}(B)}=\frac{\mathbb{V}\text{ar}{\int }_B\mathbb{E}[\mathrm{\Lambda }(u)\mid Z]\text{d}u}{\mathbb{V}\text{ar}[{\int }_B\mathrm{\Lambda }(u)\text{d}u]}$$ (2)

thus describes the proportion of the variance of ∫_B (u)du explained by Z. For sufficiently small B, R²(B) may be approximated by

$$R^2=\frac{\mathbb{V}\text{ar}\mathbb{E}[\mathrm{\Lambda }(u_B)\mid Z]}{\mathbb{V}\text{ar}\mathrm{\Lambda }(u_B)},u_B\in B$$ (3)

which in the stationary case does not depend on B. The quantity R² can also be viewed as an analogue of the R² statistic for linear regression. To see this connection, we define the expected ‘sums of squares’

$$\mathit{SSR}=\mathbb{E}{\int }_S{I}_R^2(u)\text{d}u,\mathit{SSE}=\mathbb{E}{\int }_S{I}_E^2(u)\text{d}u$$

and

$$\mathit{SST}=\mathit{SSR}+\mathit{SSE}$$

where I_R(u) = Λ̂_|Z(u) − ρ(u), I_E(u) = Λ(u) − Λ̂_|Z(u), and Λ̂_|Z(u) = [Λ(u)|Z]. Then, in the case of a stationary random intensity function Λ, the ratio SSR/SST (known as R² for linear regression) coincides with (3). We discuss our R² criterion in relation to specific models in Section 4. Note that R² is not a goodness-of-fit criterion. In particular, R² = 0 whenever Λ is independent of Z.

4 Models for rain forest data

Let X be the process that generates the point pattern of locations for a particular tree species. We assume that X is a Cox process driven by a random intensity function Λ where Λ depends on a stationary process Z = {Z(u) : u ∈ S}, Z(u) = [Z₁(u), …, Z_p(u)], of p observed covariates and a non-negative process Λ₀ = {Λ₀(u) : u ∈ S} representing unobserved sources of variation. We assume that Λ depends on Z through Z̃ = {β₀ + β_1:pZ(u)^⊤}_u∈S for some parameter β = (β₀, β_1:p) = (β₀, β₁, …, β_p) ∈ ℝ^p+1 and that Z̃ and Λ₀ are independent second-order stationary processes.

We further let ρ₀ = Λ₀(u) and $g_0(u-v)=\mathbb{E}[{\mathrm{\Lambda }}_0(u){\mathrm{\Lambda }}_0(v)]/{\rho }_0^2$. Then ρ₀ and g₀ become respectively the intensity and the pair correlation function of a Cox process driven by the random intensity function Λ₀. Note that

$$g_0(u-v)=c_0(u-v)/{\rho }_0^2+1$$ (4)

where c₀ is the covariance function for Λ₀. Moreover ${\sigma }_0^2=\mathbb{V}\text{ar}[{\mathrm{\Lambda }}_0(u)]$ is equal to ${\rho }_0^2[g_0(0)-1]$. In Section 5 we discuss parametric models for g₀ or equivalently c₀.

To quantify how much variation is due to Z, it is appropriate to model Z as a random field. However, since Z is observed, it is often convenient to base parameter estimation on X|Z where Z is then treated as a fixed quantity, see Section 6.

4.1 An additive model

Variance decomposition is straightforward for the following additive model:

$$\mathrm{\Lambda }(u)=\stackrel{\sim }{Z}(u)+{\mathrm{\Lambda }}_0(u)={\beta }_0+{\beta }_{1:p}Z{(u)}^{\top }+{\mathrm{\Lambda }}_0(u).$$ (5)

Thus, X can be considered as a superposition of two independent Cox processes with random intensity functions Z̃(u) and Λ₀. A drawback of this model is that Λ is not positive for all values of β and Z. This is probably why (5) has not attracted much interest in the point process literature; Best et al. (2000) is one notable exception. In Section 4.2 we discuss an alternative log linear model for which positivity of Λ is guaranteed.

Conditional on Z, the intensity function of X becomes

$$\rho (u\mid Z;\beta )={\rho }_0+{\beta }_0+{\beta }_{1:p}Z{(u)}^{\top }.$$

In practice, a negative estimate of the intensity function may be obtained. This did, however, not happen in our data examples (Section 7). Possible problems with fitted negative intensity functions may be mitigated by enforcing linear constraints of the type ρ₀ + β₀ + β_1:pZ(u_i)^⊤ ≥ 0 for a finite set of locations u_i e.g. including X. This is for instance possible with the R procedure constrOptim().

Further, given Z, the second-order product density and the pair correlation function become

$${\rho }^2(u,v\mid Z;\beta )=\rho (u\mid Z;\beta )\rho (v\mid Z;\beta )+c_0(u-v)$$

and g(u, v|Z; β) = 1 + c₀(u − v)/[ρ(u|Z; β)ρ(v|Z; β)].

For (5) we obtain a straightforward decomposition of the variance of Λ(u) into the sum of ${\sigma }_{\stackrel{\sim }{Z}}^2=\mathbb{V}\text{ar}\stackrel{\sim }{Z}(u)$ and ${\sigma }_0^2=\mathbb{V}\text{ar}{\mathrm{\Lambda }}_0(u)$. Hence (3) becomes

$$R^2=\frac{{\sigma }_{\stackrel{\sim }{Z}}^2}{{\sigma }_{\stackrel{\sim }{Z}}^2+{\sigma }_0^2}.$$

4.2 A log linear model

The multiplicative log linear random intensity function

$$\mathrm{\Lambda }(u)=exp[\stackrel{\sim }{Z}(u)+log{\mathrm{\Lambda }}_0(u)]={\mathrm{\Lambda }}_0(u)exp[{\beta }_0+{\beta }_{1:p}Z{(u)}^{\top }]$$ (6)

is always non-negative. This model has an appealing interpretation in terms of location dependent thinning (Waagepetersen, 2007) where X is obtained by independent thinning of a Cox process driven by Λ₀ and the probability of retaining a point at u is proportional to exp[Z̃(u)]. Hence in the tropical rain forest context, the covariates may be regarded as influencing the survival of plants in a stationary process of seedlings.

4.2.1 Intensity and pair correlation

Without loss of generality we assume in case of (6) that ρ₀ = Λ₀(u) = 1. Conditional on Z, the intensity function of X is

$$\rho (u\mid Z;\beta )=\mathbb{E}[\mathrm{\Lambda }(u)\mid Z]=exp[\stackrel{\sim }{Z}(u)],$$

the pair correlation function g(u − v|Z) = g₀(u − v) coincides with g₀, and

$${\rho }^{(2)}(u,v\mid Z)=\rho (u\mid Z;\beta )\rho (v\mid Z;\beta )+\rho (u\mid Z;\beta )\rho (v\mid Z;\beta )c_0(u-v).$$

Unconditionally, the intensity and the pair correlation function become

$$\rho (u)={\rho }_{exp\stackrel{\sim }{Z}}=\mathbb{E}exp[\stackrel{\sim }{Z}(u)]\text{and}g(u-v)=g_0(u-v)g_{exp\stackrel{\sim }{Z}}(u-v)$$

where ρ_{exp Z̃} and g_{exp Z̃} are the intensity and the pair correlation function of a Cox process with random intensity function exp[Z̃(·)].

4.2.2 Decomposition of variance

For a Cox process with random intensity function (6),

$$\mathbb{V}\text{ar}[\mathrm{\Lambda }(u)]={\sigma }_{exp\stackrel{\sim }{Z}}^2+{\sigma }_0^2[{\sigma }_{exp\stackrel{\sim }{Z}}^2+{\rho }_{exp\stackrel{\sim }{Z}}^2]$$

where

$${\sigma }_{exp\stackrel{\sim }{Z}}^2=\mathbb{V}\text{ar}\mathbb{E}[\mathrm{\Lambda }(u)\mid Z]=\mathbb{V}\text{ar}exp[\stackrel{\sim }{Z}(u)].$$

According to (3), R² becomes

$$R^2=\frac{{\sigma }_{exp\stackrel{\sim }{Z}}^2}{{\sigma }_{exp\stackrel{\sim }{Z}}^2+{\sigma }_0^2\left[{\sigma }_{exp\stackrel{\sim }{Z}}^2+{\rho }_{exp\stackrel{\sim }{Z}}^2\right]}=\frac{g_{exp\stackrel{\sim }{Z}}(0)-1}{g_{exp\stackrel{\sim }{Z}}(0)g_0(0)-1}.$$

A related approach is to consider the proportion of variance of log Λ explained by Z̃. If both Z̃ and log Λ₀ are Gaussian then (Møller et al., 1998)

$$\mathbb{V}\text{ar}log\mathrm{\Lambda }(u)=\mathbb{V}\text{ar}\stackrel{\sim }{Z}(u)+\mathbb{V}\text{ar}log{\mathrm{\Lambda }}_0(u)=log{g}_0(0)+log{g}_{exp\stackrel{\sim }{Z}}(0).$$

The proportion of variance for log Λ explained by Z then becomes

$$\frac{log{g}_{exp\stackrel{\sim }{Z}}(0)}{log{g}_0(0)+log{g}_{exp\stackrel{\sim }{Z}}(0)}$$

which is related to R² by the approximation log(x) ≈ x − 1.

5 Models for g₀

Our estimation procedure in Section 6 requires the specification of parametric models for the intensity function and the second-order product density of X|Z. Hence it remains to specify a parametric model for the pair correlation function g₀, or equivalently (cf. (4)), for the covariance function c₀ of Λ₀. A given covariance function c₀ is not necessarily a covariance function of a non-negative random field and g₀ = c₀ − 1 hence might not be a pair correlation function of a Cox process. In the literature on Cox processes, pair correlation models have therefore been obtained from explicit constructions of non-negative random fields. The two most popular constructions are log Gaussian and shot-noise fields leading to log Gaussian Cox processes (Møller et al., 1998) and shot-noise Cox processes (Møller, 2003). On the other hand, the most common examples of Neyman-Scott and Poisson-cluster processes are special cases of shot-noise Cox processes.

5.1 Log Gaussian Cox processes

A log Gaussian random field is obtained by exponentiating a Gaussian random field Y and the pair correlation function for the corresponding Cox process is simply the exponentiated covariance function of Y, i.e.

$$g_0(u-v)=exp[c(u-v)]$$ (7)

where c(u − v) = ℂov[Y (u), Y (v)] (Møller et al., 1998).

5.2 Shot-noise Cox and cluster processes

A shot-noise field is in the simplest form obtained by a sum of positive kernel functions k(· − u) scaled by a parameter ξ > 0 and centered around points u of a homogeneous Poisson point process with intensity κ > 0. A Cox process driven by a shot-noise field can equivalently be considered as a Poisson-cluster process given by a superposition of clusters where for each parent point u, a Poisson number of offspring is dispersed independently around u according to the density k(· − u). The resulting pair correlation function becomes

$$g_0(r)=1+\kappa {\xi }^2{\int }_{{\mathbb{R}}^2}k(u)k(u+r)\text{d}u.$$ (8)

Suppose g₀ is a function so that c₀(·) = g₀(·) − 1 is an absolutely integrable covariance function. Further, let k̃ denote the inverse Fourier transform of the square root of the spectral density for c₀. Then g₀ has a representation of the form (8) (see e.g. page 65 and 489 in Chilès and Delfiner, 1999) with k = k̃. However, g₀ is not a pair correlation function of a shot-noise Cox process unless k̃ is non-negative. In general for a given g₀, this property of k̃ is not easy to verify.

The usual approach in the literature on Poisson-cluster and shot-noise Cox processes (e.g. Stoyan et al., 1995; Diggle, 2003; Møller, 2003; Illian et al., 2008; Hellmund et al., 2008) is in fact to specify first k and then obtain g₀ rather than the other way around. It is, however, remarkable that in the literature on Poisson-cluster/shot-noise Cox processes essentially only two specific examples of k are considered. For the so-called modified Thomas process, k is a Gaussian density with standard deviation ω; in which case c₀ is a Gaussian covariance function

$$c_0(r)={\sigma }_0^{2}exp[-{(|\left|r\right||/\eta )}^2]$$ (9)

where ${\sigma }_0^2=\kappa {\xi }^2/(\pi {\eta }^2)$ and η = 2ω. For the Matérn cluster process, k is the density of a uniform distribution on a disc of radius r_M, say. For a Matérn process, c₀ has a less simple expression (e.g. Stoyan and Stoyan, 1995) than for the modified Thomas process but an important feature is that c₀(r) = 0 for r > r_M. Hence, the modified Thomas process and the Matérn cluster model can only produce light tailed or extremely light tailed covariance functions and this is often not appropriate e.g. for tropical rain forest data. In Wiegand et al. (2007) and Tanaka et al. (2008) more general processes are constructed using modified Thomas processes as building blocks but again only light tailed correlation structures are obtained. Tanaka et al. (2008) also consider an inverse-power type kernel k but this does not admit a closed form expression for the pair correlation function.

In the next Section 5.3 we consider a more flexible class of normal variance mixture shot-noise fields where the kernel k and the pair correlation function is given in terms of a normal variance mixture. These normal variance mixtures provide flexibility for modeling of both shape at the origin and tail behavior of the pair correlation function.

5.3 Normal variance mixtures

Our starting point for obtaining flexible kernel functions k for shot-noise Cox processes are normal variance mixtures

$$f(r)={\int }_0^{\infty }\phi (r;s)h(s)\text{d}s$$ (10)

where φ(·; s) is the density of a zero-mean two-dimensional Gaussian vector with covariance matrix sI and h is some probability density on ℝ₊. Any function of the form (10) is a positive definite function on ℝ² (e.g. Schlather, 1999). If anisotropy is required, the identity matrix I may be replaced by a suitable non-diagonal correlation matrix.

One can easily verify that if h is a convolution h = h̃* h̃ then so is f, f = k * k where

$$k(u)={\int }_0^{\infty }\phi (u;s)\stackrel{\sim }{h}(s)\text{d}s$$ (11)

which is non-negative. Hence, for the shot-noise field with kernel k we obtain c₀(r) = κξ²f(r). A wide class of covariance functions are obtained by choosing h in the class of generalized inverse Gaussian distributions (e.g. Jørgensen, 1982) which includes both gamma, inverse gamma and inverse Gaussian distributions as special cases. The resulting class of normal variance mixtures is the class of generalized hyperbolic distributions (Barndoroff-Nielsen, 1977, 1978). By Barndoroff-Nielsen and Halgreen (1977) any generalized inverse Gaussian distribution is infinitely divisible and hence any generalized hyperbolic density can be represented as a convolution. However, for a generalized inverse Gaussian density h it is not always easy to identify the convolution density h̃. We discuss below some special cases of generalized hyperbolic distributions where h̃ and hence k is explicitly known. A concise overview of multivariate generalized hyperbolic distributions is given in Sections 2.1–2.2 of Hu (2005).

5.3.1 Variance gamma/Bessel

A gamma density

$$h(s;\alpha ,\beta )={\beta }^{\alpha }{s}^{\alpha -1}exp(-\beta s)/\mathrm{\Gamma }(\alpha ),s>0,$$

with parameters α, β > 0 is a convolution of h(·; α/2, β) with itself. The densities f and k given by (10) and (11) become so-called variance gamma or Bessel densities (in the one-dimensional case an early reference is McKay, 1932). Specifically k is of the form

$$k(u)=\frac{1}{\pi 2^{{\nu }^{\prime }+1}{\eta }^2\mathrm{\Gamma }({\nu }^{\prime }+1)}{(|\left|u\right||/\eta )}^{{\nu }^{\prime }}{K}_{{\nu }^{\prime }}(|\left|u\right||/\eta )$$ (12)

where ν′ = α/2 −1, η = (2β)^−1/2, and K_ν′ is a modified Bessel function of the second kind. The covariance function for the corresponding shot-noise field becomes

$$c_0(r)={\sigma }_0^2\frac{{(|\left|r\right||/\eta )}^{\nu }{K}_{\nu }(|\left|r\right||/\eta )}{2^{\nu -1}\mathrm{\Gamma }(\nu )}$$ (13)

where ν = α − 1 and ${\sigma }_0^2=\kappa {\xi }^2/(4\pi {\eta }^2\nu )$. The resulting Matérn pair correlation function is

$$g_0(r)=1+{\sigma }_0^2\frac{{(|\left|r\right||/\eta )}^{\nu }{K}_{\nu }(|\left|r\right||/\eta )}{2^{\nu -1}\mathrm{\Gamma }(\nu ){\rho }_0^2}$$

where ρ₀ = κξ.

The smoothness parameter ν controls the shape of the pair correlation function and gives additional flexibility in the modeling. For instance, ν = 1/2 yields the exponential model

$$g_0(r)=1+{\sigma }_0^{2}exp(-|\left|r\right||/\eta )/{\rho }_0^2$$ (14)

which offers more slowly decaying correlations than the Thomas pair correlation function obtained with (9). The Gaussian covariance function (9) may be viewed as a limiting case of a Matérn covariance function when ν → ∞ (Stein, 1999, page 50).

For any fixed ν (9.7.2. in Abramowitz and Stegun, 1965)

$$K_{\nu }(x)=\frac{exp(-x)}{\sqrt{2x/\pi }}(1+O(1/x)),$$ (15)

so in the tails ||r|| → ∞, the Matérn covariance function behaves as ||r||^ν−1/2 exp(−||r||). By Corollary 2 in Yu (2011) the Matérn covariance function is log concave for ν ≥ 1/2. Moreover, by the same corollary, c₀(tr₀) is log convex as a function of t > 0 for any r₀ ∈ ℝ² when ν ≤ 1/2.

5.3.2 Cauchy

An inverse gamma density with parameters α, β > 0 is of the form

$$h(s;\alpha ,\beta )={\beta }^{\alpha }{s}^{-\alpha -1}exp(-\beta /s)/\mathrm{\Gamma }(\alpha ),s>0.$$

It is in general not easy to identify the corresponding convolution density h̃ but the case α = 1/2 is an exception. With α = 1/2 the Laplace transform of h is simply $L(t)=exp(-2\sqrt{-\beta t})$, t ≤ 0, so that h(·; 1/2, β) is a convolution of h(·; 1/2, β/4) with itself. The corresponding kernel function becomes a Cauchy density

$$k(u)=\frac{1}{2\pi {\omega }^2}{[1+{(|\left|u\right||/\omega )}^2]}^{-3/2}$$

with $\omega =\sqrt{\beta /2}$ and the covariance function becomes

$$c_0(r)={\sigma }_0^2{[1+{(|\left|r\right||/\eta )}^2]}^{-3/2}$$ (16)

with ${\sigma }_0^2=\kappa {\xi }^2/(2\pi {\eta }^2)$, and η = 2ω. The Cauchy covariance function is polynomially decreasing and hence more suitable than the Matérn model for modeling of a slowly decaying covariance. The Cauchy covariance is log concave in a neighbourhood around the origin.

5.3.3 Normal inverse Gauss

The density of an inverse Gauss distribution is given by

$$h(s;\mu ,\lambda )={\left(\frac{\lambda }{2\pi s^3}\right)}^{1/2}exp\left[-\frac{\lambda {(s-\mu )}^2}{2{\mu }^{2}s}\right]$$

with μ, λ> 0. The inverse Gauss density h(·; μ, λ) is the convolution of h(·; μ/2, λ/4) with itself. The resulting normal inverse Gauss kernel is

$$k(u)=\frac{{(\gamma /4)}^{1/2}exp(\sqrt{\gamma /4})K_{3/2}(\sqrt{\gamma /4+{(|\left|u\right||/\eta )}^2})}{{\eta }^2{\pi }^{3/2}\sqrt{2}{[\gamma /4+{(|\left|u\right||/\eta )}^2]}^{3/4}}$$

where γ = (λ/μ)² and $\eta =\mu /\sqrt{\lambda }$ and

$$c_0(r)={\sigma }_0^2\frac{K_{3/2}(\sqrt{\gamma +{(|\left|r\right||/\eta )}^2}){\gamma }^{3/4}}{K_{3/2}(\sqrt{\gamma }){[\gamma +{(|\left|r\right||/\eta )}^2]}^{3/4}}$$

where ${\sigma }_0^2=\kappa {\xi }^2{\gamma }^{1/2}exp(\sqrt{\gamma })K_{3/2}(\sqrt{\gamma })/({\eta }^2{\pi }^{3/2}\sqrt{2}{\gamma }^{3/4})$. By the asymptotic formula (15), the normal inverse Gauss covariance behaves as exp(− ||r||)/||r||² in the tails. The parameter γ may be viewed as a kind of ‘offset’ parameter for the squared distance ||r||².

Remark

The convolution representations of the Matérn and Cauchy covariance functions above are not new and were found using Fourier transforms in Matérn (1986) (see Table 1, page 30 - a detailed derivation for the Matérn class is moreover provided in Jonsdottir et al., 2011). However, these representations and the shot-noise/Poisson-cluster processes with the corresponding kernels have not been considered previously in the point process literature. Moreover, the normal variance mixture perspective leads to straightforward simulation of offspring locations when the resulting shot-noise Cox process is viewed as a Poisson-cluster process. The Matérn and the normal inverse Gauss covariance functions both have three parameters. However, the Matérn class may seem preferable since the parameter ν allows for modeling of a range of kernel and covariance shapes varying from log convex to log concave.

Table 1.

Estimates of β, ψ and R² and maximal values of the composite likelihoods CL₁ and CL₂. For each species, the first four rows in the last three columns correspond to the log linear model with Gaussian, Cauchy, Matérn and LG-Matérn covariance functions. The next four rows are for the additive model with the same covariance models. For LG-Matérn, abusing notation, ψ̂ denotes the parameter estimate for the covariance function of the Gaussian field Y. In the first column, the estimate ρ̂ is given by N(W)/|W|. The second column also shows estimates of ${\widehat{\sigma }}_{exp\stackrel{\sim }{Z}}^2$ and ${\widehat{\sigma }}_{\stackrel{\sim }{Z}}^2$.

Species	β̂1:2/CL1(β̂)	$\widehat{\psi }=({\widehat{\sigma }}_0^2,\widehat{\eta },\widehat{\nu })$	CL2(ψ̂|β̂) – C	R2
	(0.02, 0.005)	(13.7, 4.4, ∞)	27438.39	0.01
		(11.9, 4.9, –)	28744.97	0.01
	−4117.7	(8.5, 4.7, 0.69)	28507.05	0.01
Acalypha	${\widehat{\sigma }}_{exp\stackrel{\sim }{Z}}^2=0.13\times {10}^{-6}$	(2.4, 5.6, 1.02)	28675.13	0.01
	(15.5, 4.9)×10−6	(11.6×10−6, 4.1, ∞)	0	0.01
		(8.1×10−6, 5.2, –)	1724.32	0.01
ρ̂ = 1056×10−6	−4119.7	(6.1×10−6, 5.8, 0.56)	1128.50	0.02
C = −6291053.0	${\widehat{\sigma }}_{\stackrel{\sim }{Z}}^2=0.11\times {10}^{-6}$	(6.1×10−6, 5.8, 0.56)	1128.50	0.02
	(−0.03, −0.16)	(1.1, 28.4, ∞)	82006.98	0.11
		(1.8, 18.4, –)	82174.76	0.07
	−6117.6	(2.0, 14.0, 0.65)	82326.85	0.06
Lonchocarpus	${\widehat{\sigma }}_{exp\stackrel{\sim }{Z}}^2=0.45\times {10}^{-6}$	(1.1, 14.8, 0.86)	82344.08	0.06
	(−38.2, −193.3)×10−6	(1.5×10−6, 36.6, ∞)	0	0.17
		(2.1×10−6, 27.4, –)	934.78	0.12
ρ̂ = 1672×10−6	−6121.9	(2.8×10−6, 23.1, 0.41)	702.26	0.09
C = −6168628.5	${\widehat{\sigma }}_{\stackrel{\sim }{Z}}^2=0.29\times {10}^{-6}$	(2.8×10−6, 23.1, 0.41)	702.26	0.09
	(0.03, 0.004)	(0.25, 69.8, ∞)	5012.70	0.28
		(0.43, 43.1, –)	5223.48	0.18
	−19693.0	(0.76, 48.2, 0.22)	5342.78	0.11
Capparis	${\widehat{\sigma }}_{exp\stackrel{\sim }{Z}}^2=4.84\times {10}^{-6}$	(0.59, 49.7, 0.26)	5361.99	0.11
	(193.2, 24.8)×10−6	(10.0×10−6, 70.2, ∞)	0	0.29
		(15.0×10−6, 48.7, –)	285.51	0.21
ρ̂ = 6598×10−6	−19700.1	(28.8×10−6, 51.6, 0.21)	466.02	0.12
C = −5089810.54	${\widehat{\sigma }}_{\stackrel{\sim }{Z}}^2=4.06\times {10}^{-6}$	(28.8×10−6, 51.6, 0.21)	466.02	0.12

6 Parameter estimation

In practice we consider a parametric model c₀(·; ψ) for the covariance function of Λ₀ where c₀ could for instance be the Matérn covariance function (13) with $\psi =({\sigma }_0^2,\eta ,\nu )$. Given (X, Z) observed within W ⊆ ℝ², we then obtain a plug-in estimate for R² in (3) after estimating the three parameters β, ψ, and ${\sigma }_{\stackrel{\sim }{Z}}^2$ (or ${\sigma }_{exp\stackrel{\sim }{Z}}^2$).

6.1 Composite likelihood estimation

The inference about β and ψ is based on X|Z. The regression parameter β can be estimated by the first-order composite log likelihood function (CL₁) (Schoenberg, 2005; Waagepetersen, 2007)

$${\text{CL}}_1(\beta )=\sum _{u\in X}log\rho (u\mid Z;\beta )-{\int }_W\rho (u\mid Z;\beta )\text{d}u.$$ (17)

This is the log likelihood function in the case where X is a Poisson process with intensity function ρ(·|Z; β). The Berman-Turner quadrature scheme can be used to approximate the integral in (17) both for the log linear and the additive model, see e.g. Baddeley and Turner (2000).

For a Cox process specified by the log linear random intensity function (6) one may subsequently estimate ψ using minimum contrast estimation based on the K-function, see Waagepetersen (2007) and Waagepetersen and Guan (2009). However, for the additive model the K-function is not well-defined since the pair correlation function is not translation invariant (Baddeley et al., 2000). As suggested by Guan (2006) and Waagepetersen (2007), ψ can instead be estimated using a second-order composite likelihood function

$${\text{CL}}_2(\psi \mid \beta )=\sum _{u,v\in X}^{\ne }w(u,v)log{\rho }^{(2)}(u,v\mid Z;\beta ,\psi )-{\iint }_{W^2}w(u,v){\rho }^{(2)}(u,v\mid Z;\beta ,\psi )\text{d}u\text{d}v$$ (18)

based on the second-order product density where w is a weight function, see e.g. (20) and (21) below. The integral term in (18) can also be approximated by a variant of the Berman-Turner scheme. The second-order composite likelihood can be evaluated for both the log linear model and the additive model and the maximized CL₂ can be used as a criterion for model selection, see Section 7.

Instead of maximizing the right-hand side of (18) with respect to both β and ψ, a computationally simpler approach is to obtain β̂ by maximizing (17) and then ψ̂ by maximizing CL₂(·|β̂). Moreover, an equivalent version of CL₂(ψ|β̂) is given by

$${\text{CL}}_{\text{2}}^{\ast }(\psi \mid \widehat{\beta })=\sum _{u,v\in X}^{\ne }w(u,v)logg(u,v\mid Z;\widehat{\beta },\psi )-{\iint }_{W^2}w(u,v)\mathbb{C}\text{ov}[\mathrm{\Lambda }(u),\mathrm{\Lambda }(v)\mid Z;\widehat{\beta },\psi ]\text{d}u\text{d}v$$ (19)

which is obtained from CL₂(ψ|β̂) by subtracting the second-order composite likelihood of a Poisson process with intensity function ρ(·|Z; β̂). More stable convergence results were obtained using (19) instead of (18) when using a standard implementation of the Nelder-Mead algorithm for maximizing the second-order composite likelihood.

In simulation studies and applications to real data we discovered that the second-order composite likelihood estimates can be quite sensitive to the accuracy of the Berman-Turner quadrature scheme used to approximate the double integral in (19). This is especially the case when c₀ is steep at zero like for (13) with a small ν or small η. Regarding the weight function w,

$$w(u,v)=1[||u-v||\le t]/[\pi t^2]$$ (20)

is the standard choice which ensures that only t-close pairs of points are used in the composite likelihood. In the data example in Section 7 we also considered

$$w(u,v)=1[||u-v||\le t]/[\pi t^2\rho (u\mid Z,\widehat{\beta })\rho (u\mid Z,\widehat{\beta })].$$ (21)

For log linear models, this w implies a simplification of the double integral since the intensity function is eliminated from the integrand.

6.2 Estimation of environmental variances

In practice Z is observed on a grid G = {u_i}_i=1,…,M covering W. Since we assume that Z is a stationary process, simple estimators of ${\sigma }_{\stackrel{\sim }{Z}}^2$ and ${\sigma }_{exp\stackrel{\sim }{Z}}^2$ are given by

$${\widehat{\sigma }}_{\stackrel{\sim }{Z}}^2=\frac{1}{M}\sum _{u\in G}{[\widehat{\stackrel{\sim }{Z}}(u)-{\widehat{\rho }}_{\stackrel{\sim }{Z}}]}^2$$ (22)

and

$${\widehat{\sigma }}_{exp\stackrel{\sim }{Z}}^2=\frac{1}{M}\sum _{u\in G}{\left\{exp[\widehat{\stackrel{\sim }{Z}}(u)]-{\widehat{\rho }}_{exp\stackrel{\sim }{Z}}\right\}}^2$$ (23)

where

$${\widehat{\rho }}_{\stackrel{\sim }{Z}}=\frac{1}{M}\sum _{u\in G}\widehat{\stackrel{\sim }{Z}}(u),{\widehat{\rho }}_{exp\stackrel{\sim }{Z}}=\frac{1}{M}\sum _{u\in G}exp[\widehat{\stackrel{\sim }{Z}}(u)],$$ (24)

and $\widehat{\stackrel{\sim }{Z}}(u)=\widehat{\beta }Z{(u)}^{\top }$.

6.3 Discussion of theoretical properties of estimates

One may be concerned about the joint properties of the composite likelihood estimates and (22)–(24). A fully detailed asymptotic analysis is outside the scope of this paper and we here only outline the essential arguments. We may view the estimate θ̂ = (β̂, ψ̂) as a solution of an estimating equation u(θ) = 0 where u is obtained by concatenating the gradients of the log composite likelihoods (17) and (18). Note that u is conditionally unbiased, [u(θ)|Z] = 0. Moreover the estimates (22)–(24) are obtained in a simple manner from spatial averages of the form A(β̂) = Σ_u∈M f (Z(u), β̂) where f(z, β) is either βz^⊤, (βz^⊤)², exp(βz^⊤) or exp(2βz^⊤).

Under appropriate mixing conditions for Λ₀ and Z one may verify using techniques as in Waagepetersen and Guan (2009) that asymptotically (increasing window size |W|), |W|^1/2(θ̂ − θ) is distributed as u(θ)S⁻¹ for a matrix S = − du(β)/dβ and that u(θ) is asymptotically normal. Hence |W|^1/2(θ̂ − θ) is asymptotically zero-mean normal. Moreover,

$${\mid W\mid }^{1/2}(A(\widehat{\beta })-\mathbb{E}A(\beta ))={\mid W\mid }^{1/2}(A(\beta )-\mathbb{E}A(\beta ))+{\mid W\mid }^{1/2}(\widehat{\beta }-\beta )\mathbb{E}\frac{\text{d}}{\text{d}\beta }A(\beta )+o_P(1).$$

By mixing the first term on the right hand side converges in distribution to a normal distribution. It thus follows that the spatial average A(β̂) is a |W|^1/2 consistent estimate of A(β) but the replacement of β with β̂ introduces additional error in the estimation quantified by the second term in the right hand side of the above equation. This error is asymptotically independent of the error given by the first term since

$${\mathbb{C}\text{ov}}_{\theta }[A(\beta ),u(\theta )]={\mathbb{E}}_{\theta }{\mathbb{C}\text{ov}}_{\theta }[A(\beta ),u(\theta )\mid Z]+{\mathbb{C}\text{ov}}_{\theta }\{{\mathbb{E}}_{\theta }[A(\beta )\mid Z],{\mathbb{E}}_{\theta }[u(\theta )\mid Z]\}=0$$

by the unbiasedness of u(·) given Z and since A(β) is constant given Z.

To summarize, under appropriate mixing conditions, the composite likelihood estimates and the estimates (22)–(24) all become consistent and asymptotically normal.

7 Decomposition of variance for tropical rain forest data example

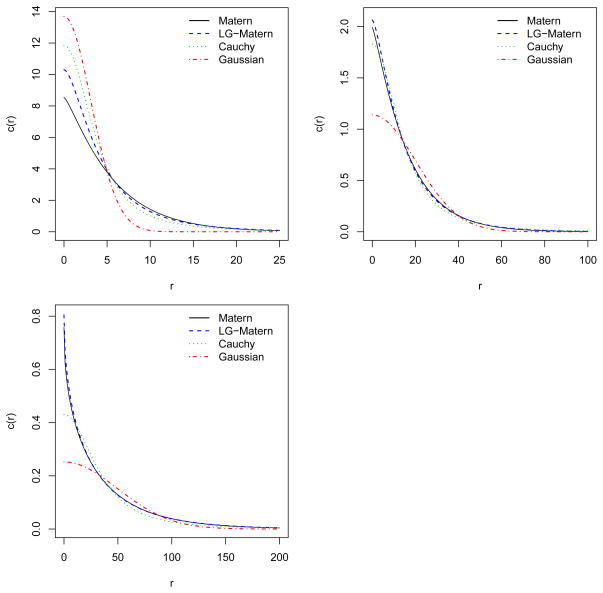
In this section we return to the data example in Section 1.1. Waagepetersen and Guan (2009) fitted inhomogeneous Thomas models with random intensity functions of the form (6) and a Gaussian covariance function (9) for Λ₀. Using the same covariates as in Waagepetersen and Guan (2009), we fit for each of the species the additive model (5) and the log linear model (6) with c₀ being the Gaussian covariance function (9), the Matérn covariance function (13), and the Cauchy covariance function (16). Note that these covariance functions have very distinct behaviors both at the origin and in the tails, see also Figure 3. As in Myllymäki and Penttinen (2009) we also consider a pair correlation function of the form (7) where Y is a Gaussian random field with a Matérn covariance function. We denote this covariance function LG-Matérn since it corresponds to the case of a log Gaussian random intensity function Λ₀. In this case ${\sigma }_0^2=exp[\mathbb{V}\text{ar}Y(u)]-1$. As measures of fit for these models, we use the maximal values of the composite likelihoods CL₁ and CL₂.

Figure 3.

The various fitted covariance functions c₀ in case of the log linear model for Acalypha (top left), Lonchocarpus (top right), and Capparis (bottom left).

Regarding the weight function w we tried both (20) and (21) with t = 125 in (18). The integrals in the composite likelihoods CL₁ and CL₂ were approximated using a Berman-Turner quadrature scheme consisting of data points and 200 × 100 dummy points over the observation window W = [0, 1000] × [0, 500]. The ranking of the models according to CL₂ did not depend on the choice of w-function (except for a single swap of ranks between Cauchy and Matérn in case of the additive model for Lonchocarpus). However, for the log linear models we in general obtained somewhat smaller estimates of ${\sigma }_0^2$ with (20) than with (21) and vice versa for the additive models. According to a model check for the best fitting log linear models (see below) the estimates obtained with (21) gave the best fit. In the following we restrict attention to the results obtained with (21).

Table 1 shows the parameter estimates, the maximal composite likelihood values, and the estimated R² for each species and model.

Considering first β_1:2 for each species, the regression parameters have similar signs and relative magnitudes for the log linear model and the additive model. However, the maximal first-order composite likelihood CL₁ is always largest for the log linear model. The fitted Z̃ are shown in Figure 2 for each species.

Figure 2.

The fitted regression term, $\widehat{\stackrel{\sim }{Z}}$, for Acalypha under the additive model and the log linear model, and for Lonchocarpus and Capparis under the log linear model (from top to bottom).

Considering CL₂ and comparing log linear and additive models for each species, the log linear models always yield the largest CL₂ values. Regarding the choice of covariance function, the best fit for Acalypha is obtained with the Cauchy covariance function while for Lonchocarpus and Capparis, the LG-Matérn covariance function performs better, followed by the Matérn covariance function. Both for the log linear and the additive models, the smallest CL₂ is obtained with the Gaussian covariance function. This suggests that the fast decaying pair correlation function obtained with the Gaussian covariance function is not suitable for the tropical rain forest data. For the additive model, the LG-Matérn and the Matérn covariance functions are almost identical because in this case ${\widehat{\sigma }}_0^2$ is small and exp(x) − 1 ≈ x when x ≈ 0.

Regarding R², the estimates vary considerably across models. However, the overall qualititative conclusion is stable: the contribution of the environment is smallest for Acalypha and largest for Capparis. This may be linked to the different modes of seed dispersal of the species, see Waagepetersen and Guan (2009). The R² obtained with the best fitting models are 0.01, 0.06, and 0.11 for Acalypha, Lonchocarpus, and Capparis.

The fitted covariance functions for the log linear models and for all species are shown in Figure 3. For all species, the Gaussian covariance function differ much from the other three covariance functions both a the origin and in the tail. For Lonchocarpus and Capparis, the fitted Matérn and LG-Matérn covariance functions appear rather similar.

We used a non-parametric estimate of the g₀-function (see e.g. Chapter 4 in Møller and Waagepetersen, 2004) as a summary statistic for model assessment and computed pointwise 90% confidence bands for this statistic using simulations from the best fitting log linear models according to CL₂. The non-parametric estimates of c₀(·) = g₀(·) − 1 and 90% pointwise confidence bands are shown in Figure 4 and do not provide evidence against the fitted models.

Figure 4.

Non-parametric estimates of c₀ (solid line) and 90% pointwise confidence bands (gray area) obtained from 100 simulations under best fitting models. The red dashed line shows mean of simulated non-parametric estimates and the blue dotted line shows the parametric estimate of c₀. Top left: Acalypha, top right: Lonchocarpus, and bottom left: Capparis.

8 Discussion

In this paper we introduced a method for decomposing variance for spatial Cox processes. As can be seen from our data analysis, the results can be sensitive to the choice of the pair correlation function. Fortunately, the flexible class of normal variance mixture pair correlation functions allow us to compare results from a wide range of pair correlation functions. We can then report results obtained with the best fitting model according to the second-order composite likelihood criterion.

Concerning the second-order composite likelihood estimation, further studies regarding numerical implementation and choice of w-function seem needed. For the Matérn model, the joint estimation of ( ${\sigma }_0^2$, η, ν) is computationally demanding and simulation studies indicate that the statistical properties of the estimates can be poor. For routine use, a more feasible approach is to maximize only with respect to ${\sigma }_0^2$ and η for each ν in a moderate collection of ν values.

The Thomas process has enjoyed much popularity in the point process literature. However, at least for the tropical rain forest data considered in this paper, it seems inferior to models with a more slowly decaying pair correlation function. For all the data examples considered, the log linear model provided a better fit than the additive model. This is perhaps not so surprising since the log linear model has an appealing interpretation in terms of survival of seedlings. On the other hand, variance decomposition is more straightforward for the additive model than for the log linear model.

Our proposed variance decomposition procedure assumes a stationary random environment. This may e.g. not be tenable for Acalypha because the fitted Z̃ in W shows a trend from right to left. Although this does not necessarily invalidate the stationarity assumption for Z̃, it at least implies that W may be too small to allow a precise estimate of the variance for Z̃. Further research is required to handle the case where Z̃ is not stationary but perhaps satisfies a weaker assumption of intrinsic stationarity.