Cerebral blood flow with [¹⁵O]water PET studies using image-derived input function and MR-defined carotid centerlines

Abstract

Full quantitative analysis of brain PET data requires knowledge of the arterial input function into the brain. Such data are normally acquired by arterial sampling with corrections for delay and dispersion to account for the distant sampling site. Several attempts have been made to extract an image-derived input function (IDIF) directly from the internal carotid arteries that supply the brain and are often visible in brain PET images. We have devised a method of delineating the internal carotids in co-registered MR images using the level-set method and applying the segmentations to PET images using a novel centerline approach. Centerlines of the segmented carotids were modeled as cubic splines and re-registered in PET images summed over the early portion of the scan. Using information from the anatomical center of the vessel should minimize partial volume and spillover effects. Centerline time-activity curves were taken as the mean of the values for points along the centerline interpolated from neighboring voxels. A scale factor correction was derived from calculation of cerebral blood flow (CBF) using gold standard arterial blood measurements. We have applied the method to human subject data from multiple injections of [¹⁵O]water on the HRRT. The method was assessed by calculating the area under the curve (AUC) of the IDIF and the CBF, and comparing these to values computed using the gold standard arterial input curve. The average ratio of IDIF to arterial AUC (apparent recovery coefficient: aRC) across 9 subjects with multiple (n = 69) injections was 0.49 ± 0.09 at 0–30 s post tracer arrival, 0.45 ± 0.09 at 30–60 s, and 0.46 ± 0.09 at 60–90 s. Grey and white matter CBF values were 61.4 ± 11.0 and 15.6 ± 3.0 mL/min/100g tissue using sampled blood data. Using IDIF centerlines scaled by the average aRC over each subjects’ injections, gray and white matter CBF values were 61.3 ± 13.5 and 15.5 ± 3.4 mL/min/100g tissue. Using global average aRC values, the means were unchanged, and intersubject variability was noticeably reduced. This MR-based centerline method with local re-registration to [¹⁵O]water PET yields a consistent IDIF over multiple injections in the same subject, thus permitting the absolute quantification of CBF without arterial input function measurements.

1. Introduction

Positron emission tomography (PET) can be used to image the distribution and kinetics of radioactive compounds of interest in the tissues of the body. In order to fully quantify the tissue kinetics from the time-activity curves (TACs) of these tissues using kinetic modeling techniques, the blood radioactivity curve or input function is necessary. Since the arterial blood is the supply for tracer to the brain, the input function is generally determined by blood sampling from an arterial catheter, which involves arterial cannulation by a trained physician followed by both serial blood draws and/or continuous blood sampling using specialized equipment. Arterial cannulation is an invasive procedure which carries a small risk (Everett et al., 2009) and may hinder study participation by patients and research volunteers. Blood sampling for the purposes of input function determination also increases the burden on research personnel both in the extra tasks during the scan and in the inherent risk of blood handling. Additionally, after blood samples are collected, corrections must then be applied for dispersion and delay between the brain and radial artery (Iida et al., 1986). To avoid arterial blood sampling, it is desirable to develop a method involving an image-derived input function (IDIF) using a blood pool visible in the PET image.

In whole body scans, large blood pools, such as the heart or major arteries, can be used to estimate this blood radioactivity curve (Choi et al., 1991, de Geus-Oei et al., 2006, Hoekstra et al., 1999, van der Weerdt et al., 2001, Watabe et al., 2001), avoiding the need to sample blood for scaling of IDIFs. In fact, multiple blood pools are often visible in the same scan. For example, de Geus-Oei et al was able to make measurements from the left ventricle, ascending aorta, and abdominal aorta in the same scans, while van der Weerdt et al was able to sample the ascending and descending aorta as well as left atrium and left ventricle. High correlations of outcome values, typically glucose metabolic rate (MRGlu), were reported without the need for partial volume correction. Van der Weerdt showed, however, that while this was true of the aorta, with MRGlu ratios (compared to radial artery sampling) of > 0.95, the left atrium and ventricle had lower ratios of ~0.80 on an HR+ scanner. Hoekstra, et al performed a visual comparison of input function shapes over different scans from the same group of patients. Individual curves were defined as acceptable if they agreed with venous data in the late portion of the curve and agreed with other curves from the same subject in the early portion of the curve. These authors determined that, on average, 85% of curves derived from the aortic arch were acceptable, whereas only 30% from the left atrium or ventricle were acceptable. In general, the aorta, with a diameter of approximately 15 mm, appears to provide a relatively robust blood pool for IDIF extraction with little or no spillover effects.

In brain PET, however, these large blood pools are not available. Efforts have therefore concentrated on the carotid arteries which are often in the field of view (FOV) of the scanner. Carotids, which have an average diameter of about 4–6 mm (Krejza et al., 2006, Terry et al., 2003), are much smaller than the blood pools used in full body IDIF methods. Thus, the use of carotids is challenging for PET scanners with intrinsic resolution of 4–5 mm. The High Resolution Research Tomograph (HRRT), a brain-dedicated, three-dimensional (3D) PET scanner, has made possible unprecedented characterization of small features with a resolution better than 3 mm (de Jong et al., 2007). Several existing IDIF methods originally proposed on lower resolution scanners have been tested on the HRRT with mixed results (Zanotti-Fregonara et al., 2011).

Carotid IDIF methods primarily differ in the method of delineation of the ROI. With a few exceptions, including Croteau et al (discussed in section 4.5) (Croteau et al., 2010), most carotid based methods rely on one or more blood samples to scale the carotid TAC. Working directly with FDG PET images, Chen et al manually delineated ROIs covering the full carotid cross section over several slices (Chen et al., 1998). Chen et al compensated for spill-in from surrounding regions by including a spill-in correction based on ROIs drawn at a distance from the carotids to represent background tissue. The spill-in and recovery coefficients were simultaneously estimated by fitting the carotid and background curves with whole blood sample data. On the other end of the spectrum, Mourik et al chose only clusters of the four hottest voxels per slice in [¹¹C]flumazenil (Mourik et al., 2008a). The resulting curve was fit to a triexponential and scaled using blood samples. Partial volume correction was handled in the reconstruction using the method described by Brix et al and Reader et al (Brix et al., 1997), (Reader et al., 2003). This involves incorporating the system point spread function into an OSEM reconstruction algorithm. While the simplicity of Mourik’s method, after implementation of the Partial Volume Correction (PVC)-OSEM, is advantageous, it has been noted to have unpredictable and large overshoots and undershoots of the input function peak (Zanotti-Fregonara et al., 2011).

A variety of other methods use different clustering techniques to preferentially select voxels likely to represent a strong carotid blood signal. Of particular relevance is the graph-based segmentation method of Parker and Feng (Parker and Feng, 2005). These authors incorporated the Mumford-Shah functional for piecewise homogeneity into the spatial segmentation of PET images based on temporal data, preprocessed with principal components analysis. This graph-based segmentation operates by iteratively merging neighboring voxels to produce hierarchical segmentations. The distance or similarity metric between neighboring segments was the Mahalanobis distance between the mean over each segment of the principal components vector. Other methods similarly combine spatial and temporal information through variations of region growing or hierarchical merging methods using a variety of similarity metrics between voxels. Such metrics include the time-weighted difference between voxel TACs (Kim et al., 2006) and local means analysis (Zanotti-Fregonara et al., 2009). While these methods take into account spatial information in evaluating voxels based on local neighborhoods in order to form continuous regions, they rely exclusively on the PET images for this information.

The use of co-registered MR images is attractive because of their superior anatomical contrast. Litton used carotid ROIs manually delineated on MR images and then applied them directly to co-registered PET images (Litton, 1997). The poor resolution of the PET camera used, though, was noted to limit the accuracy of the results. Direct measurement of CBF using MR has also been attempted using a gadolinium contrast agent to generate tissue concentration curves similar to PET TACs. Enmi et al used a method which relied on the estimation of an underlying blood input function from multiple tissue time concentration curves (Enmi et al., 2012).

We propose the use of co-registered anatomic magnetic resonance (MR) images to aid in the identification of internal carotid artery voxels in human dynamic PET data. The carotids are semi-automatically segmented in the MR images. Automatic segmentation has the potential to reduce interoperator variability as well as workload. Segmentation in MR is commonplace and is often used when defining other ROIs in brain PET. This is in contrast to automated segmentation in PET which is often considered difficult due to low signal to noise. The MR segmentations are then used to derive a centerline for each carotid. Centerlines rather than full carotids will form the basis for extraction and analysis of the IDIF since this permits the direct evaluation of carotid ROIs of varying diameter. IDIFs were determined and compared to the gold standard arterial blood sample data from [¹⁵O]water PET studies in healthy control subjects.

2. Methods and materials

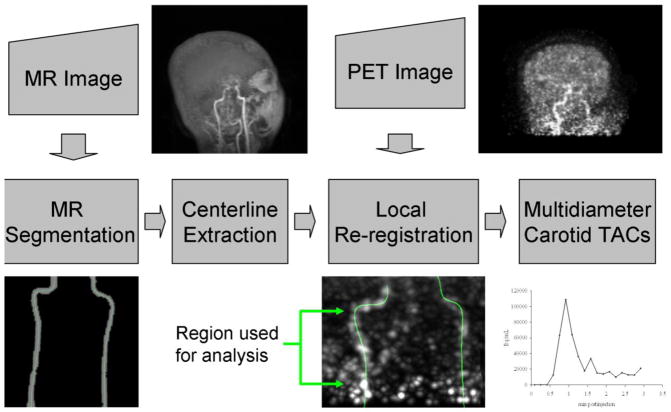
The proposed IDIF method is illustrated in figure 1. Anatomical information is derived from segmentation of the carotids in the MR image. Segmentations are reduced to centerline representations and applied to the PET images. Carotid centerlines are realigned with early PET images in which the blood pool is more visible. The re-registered centerline is used to create carotid ROIs of different diameters that are applied to the dynamic PET image set to produce TACs.

Figure 1.

Schematic of centerline IDIF method. Upper left: maximum intensity projection of the MR image used in carotid artery segmentation. Carotids are clearly visible in the center of the image. Lower left: Segmented carotids from MR image used for centerline extraction. Centerlines (indicated in color) extend from the bifurcation of the common carotid to the petrous segment. Upper right: Summed PET image over early portion of scan from tracer arrival until the trues count rate reached half its maximum value. Image was smoothed with a 2.5-mm Gaussian. Lower mid-right: PET image of carotids with centerlines superimposed. Only the region between the bifurcation and petrous segment was used for analysis. Lower far-right: Sample TAC taken by averaging values from centerline points using trilinear interpolation from neighboring voxels.

2.1. Human Subjects Measurements

Nine healthy controls received twelve [¹⁵O]water injections of ~740 MBq infused over 20 s. Data were collected in list-mode for 3 minutes per injection on the HRRT. The average number of prompts was 136 ± 30 million and the average number of delays was 57 ± 14 million. Images were reconstructed using MOLAR which includes corrections for attenuation (from transmission scan), normalization, deadtime, randoms, and scatter (Carson et al., 2004). Dynamic image sets with frame duration of 10 s were reconstructed for each injection. In addition, frames of 60 s and 90 s in duration starting when the brain trues count rate exceeded 10% of peak values were reconstructed. The 60-s image was used subsequently for whole brain registration to the MR (see below). Original PET reconstructed image dimensions were 256 × 256 × 207 with a voxel size of ~ 1.2 mm in each dimension (Qiu et al., 2010).

Subjects had an arterial catheter inserted in the radial artery for conventional input function measurement. Arterial measurements were taken using an automated system (Boellaard et al., 2001) that uses a peristaltic pump to pass blood from the arterial line through a BGO detector. These data were corrected for decay, sensitivity, deadtime, and external dispersion (Iida et al., 1986). The delay between the true input function at the brain and the blood data collected by the external detector at the radial artery was estimated as follows: The early phase of the whole brain count rate data (between −5 and 10 s after the initial rise in the brain trues rate) was fitted to a 1T compartment model with the arterial data shifted by the delay value. At this early time, clearance rate, k₂, was considered negligible so the parameters fit were K₁ and the time shift.

T1-weighted MR images were generated for each subject on a 3T scanner using an MPRAGE protocol with TR = 1500 ms, TI = 800 ms, echo time = 2.83 ms, and flip angle of 15°. Scans were typically 4–5 minutes in duration and it was assumed that there was no motion during the scan. Original MR image dimensions were 160 × 256 × 256 with a voxel size of 1 mm in each dimension.

2.2. Carotid Segmentation

Internal carotids were visually located in MR images that had been registered to PET images from the same subject (see section 2.4). A point was manually selected on each carotid at a slice just above the bifurcation of the external carotid artery. A point was also manually selected on each carotid at a slice just below the petrous segment. These four points, two for each carotid, tend to define the limits of the cervical (C1) segment of the carotids in each dimension. A rectangular bounding box was then defined, containing these four points. Additional padding of 5 1-mm voxels in each direction was added such that the cervical and petrous (C2) regions of both carotids were encompassed. Segmentation was carried out on this subimage I₀ that contained both carotids.

Assuming that voxels of the left and right carotids are more similar to each other than to background voxels, we simultaneously segmented both carotids as disjointed parts of the same ROI. The lumens of the carotids have higher intensity in their local region of the MR image, while surrounding musculature does not have many other high intensity structures. Thus, we chose the active contour model of Chan and Vese (Chan and Vese, 2001). This model minimizes the Mumford-Shah functional through use of the level set method (Sethian, 1999). Minimization of the Mumford-Shah energy results in a segmentation of an image into two regions, assuming a piecewise smooth distribution of intensities in the image. The level set method is often used for segmentation in MR and represents the final 3D surface, as the zero level set of a higher dimensional function φ. The function φ evolves over time and is defined as a signed distance function from the boundary of the 3D surface. Chan and Vese proposed the following formulation:

$$\frac{\partial \phi }{\partial t}={\delta }_{\epsilon }(\phi )\left[\mu ·\mathit{div}\left(\frac{\nabla \phi }{\mid \nabla \phi \mid }\right)-{\lambda }_1{(I_0-s_1)}^2+{\lambda }_2{(I_0-s_2)}^2\right]=0$$ (1)

Here, φ(x, y, t) has an artificial time t, and contains the boundary set {(x, y) | φ(x, y, t) = 0}, i.e., the set of points with φ = 0, at any time t. The divergence term in (1) is approximated by finite differences and updated using the method outlined in Aubert and Vese (Aubert and Vese, 1997). The segmentation boundary was initialized using spherical foreground regions three voxels in diameter located on each carotid at the 2 user-defined points. The function φ(x, y, z, t = 0) = φ₀(x, y, z) was initialized as the signed distance of each voxel to the initialization boundary. The two segmented regions of φ, the foreground and the background, take all positive and all negative values, respectively. The mean intensity at time t of the foreground is given by s₁(t) and the mean intensity of the background is given by s₂(t), which are recomputed at each iteration based on the current boundary. δ_ε is a regularized Dirac delta function. The user-defined parameters λ₁, λ₂, and μ are weights. In this implementation, λ₁ and λ₂ were set to 1, as was done by Chan and Vese. Values for μ were evaluated between 10 × 10³ and 30 × 10³ at 0.5 × 10³ increments. The optimal value was determined empirically by visually evaluating the segmentation results to minimize “leakage” into the surrounding region while still producing a connected carotid.

Every ten iterations, the boundary was extracted, comprising those voxels with φ ≥ 0, adjacent to voxels with φ < 0, and the level-set function was reinitialized to the signed distance (in voxels) from the boundary. This calculation may compromise subvoxel accuracy (Krissian and Westin, 2005) but reduces computation time. Note, however, that we do not use the carotid boundary to estimate vessel diameter; rather, we assume that the shape and position in MR space of the carotids is accurate. The iterative algorithm was stopped when subsequent reinitializations did not show any change in the position of the boundary. Note that more sophisticated vessel segmentation methods exist (for a review, see (Lesage et al., 2009)), however, the lack of vessel branching in this application and the fact that we are more concerned with application of the segmentation to PET rather than quantification and accuracy in MR suggests that this method should be sufficient.

2.3. Centerline Extraction

The next step in the algorithm is extraction of centerlines from the carotid segmentation. These vessel centerlines were modeled as cubic B-spline curves, composed of 3D cubic polynomial segments. Spline curves are commonly used in computer graphics applications. Here we use it to capture the shape of the carotids in order to transfer the segmentations to PET space. This representation also permits the easy variation in the diameter of the carotid ROI to compensate for resolution effects in the PET image. The curve is characterized entirely in 3D space by the positions of control points (P_i = [x_i, y_i, z_i]) in the 3D coordinate system of the image. For spline segment C_i, the equation of the curve is given by (2): the basis blending function, where t ranges from 0 to 1. The control points of a uniform cubic B-spline curve do not necessarily lie along the curve, but rather set the position of the basis functions that are blended to form the curve.

$$C_i(t)=\frac{1}{6}·[\left(3t^2-t^3-3t+1\right)P_{i-1}+\left(3t^3-6t^2+4\right)P_i+\left(3t^2-3t^3+3t+1\right)P_{i+1}+t^3{P}_{i+2}],t\in [0,1)$$ (2)

Centerline models were fitted to the segmentations by estimating the locations of the control points P_i that minimize the sum of the squared Euclidean distance between segmented carotid voxels and their corresponding nearest points along the B-spline curve. At all iterations, nearest points along the B-spline curve were determined by estimating the appropriate segment C_i and t value in (2) using the Newton-Raphson method. The spline curve point locations at these t values are calculated using the current estimate of the control point positions, and the appropriate distances determined. As control point positions are changed at all iterations, the nearest points along the curve and subsequently the squared distances are recalculated. The fitting process was initialized with two control points positioned at the initial seed points (see section 2.2). These first control point positions were duplicated to generate the necessary four control points used in the blending function (2). Following each fit, the number of control points was increased by inserting one additional control point midway between the last control point added and its neighbor towards the end of the spline. All control point positions were then estimated again by fitting the new spline to the segmentation. New control points were added until the reduction in the average distance of all segmented voxels to the centerline over one iteration was less than 0.01 mm. Left and right carotids were fitted separately and allowed to have different numbers of control points. Modeling the centerline curve, especially for shapes such as the carotids, has benefits over thinning or erosion of the segmented carotid calculated above in that there is less reliance on smooth and accurate boundary information. Furthermore, the estimated centerline curve is not limited to whole voxel locations (as a fully thinned centerline must still be one voxel thick), but can indicate subvoxel positions where the intensity can be interpolated from nearby voxels. Lastly, the spline representation can be resampled at any resolution as appropriate.

2.4. PET-MR Registration

MR images were stripped of bone and other nonbrain tissue using the brain extraction tool in FSL (FMRIB Analysis Group, Oxford, UK). Stripped MR brain images were registered to the 60-s PET image reconstructed from the data of the first injection in each subject. Registration was performed with a 6-parameter rigid transformation (rotation and translation) using normalized mutual information (Studholme et al., 1999). An optimized registration program, FMRIB’s Linear Image Registration Tool (FLIRT) was used to perform the registrations (Jenkinson and Smith, 2001). Additionally, each PET image from subsequent injections for a given subject was registered to the reference PET image from the first injection that had been registered to the MR image. These were registered using an affine transformation again with FLIRT. The PET images from these later injections were reconstructed again using the PET-to-PET transformations for motion correction, so that the attenuation information from the transmission scan was correct. Centerlines were initially transferred using the inverse of the PET-to-MR transformation for the first injection of each subject. Centerlines were then re-registered locally with another 6-parameter rigid transformation. Local re-registration was performed because the initial PET-to-MR registration is optimized for the whole brain. Small errors in this global registration will cause objects that are far off-center, such as the carotids, to be more misaligned.

Carotids were re-registered to early summed images. These images were reconstructed over three different periods to assess the sensitivity to this selection. All periods started when the trues count rate (prompts – delays) reached 10% of its maximum and ended when the trues count rate reached 25, 50, or 75% of its maximum. This early period was chosen for registration because of the higher contrast between the carotids and background regions. Early summed images were smoothed with a 2.5 mm Gaussian. The resulting durations equaled 5.5 ± 1.9, 12.1 ± 3.9, and 19.1 ± 6.0 s respectively. The 60-s PET image was also used for re-registration.

Re-registration was performed using an iterative search algorithm where, at each iteration, the goal was maximizing the mean of all voxel values along the sampled centerline points (under the assumption that the carotids had higher activity than the surrounding tissue). Rotation and translation parameters for the carotid registration were adjusted over a range of ±15 degrees and ±1.5 mm for the first iteration about the original position (from the PET-MR registration). A total of 7 samples were tested for each rotation and translation. Transformations from all possible permutations of 6 parameters and 7 samples were computed. At each iteration, centerlines were repositioned to the location where the interpolated mean intensity value along the centerline points was maximized. Values from the lowest five slices of the PET image were excluded due to high noise. Then, the process was repeated, starting at the new position using a sampling range of one half the previous rotation and translation ranges with the same number of samples. The algorithm was repeated until the change in the mean centerline value from the previous iteration was zero for 3 iterations. Left and right carotids were registered independently as well as jointly.

2.5. Carotid Input Function

The carotid input function was extracted by applying the centerline to dynamic images sets reconstructed with 10-s frames. The values along the centerline of each carotid were estimated by trilinear interpolation at ~ 200 sampled centerline points, spaced at intervals of 0.25 mm along the path of the centerline. For each time frame, the average value along the centerline of each carotid was estimated by defining ~200 sample points spaced at intervals of 0.25 mm along the centerline using the spline equation (2). The fine sampling was used to closely approximate the true integral over the centerline. The activity value at each sample point was determined from the image by trilinear interpolation and the centerline activity value at each frame was taken as the mean of these values.

Additional carotid ROIs were generated by first creating a regular grid with voxel dimensions equal to ¼ the dimensions of the standard PET image voxels, ~0.3 mm on each side. This subsampled grid therefore represents an interpolated version of the PET image in the area around the carotid arteries, thus more accurately accounting for the shape of the carotids than a coarse grid. A map of distances in mm from the carotid centerlines to these grid points was generated. Grid points were grouped into carotid ROIs based on distance from the centerline and therefore diameter of the ROI. Thus, this fine sampling was used to more closely approximate the true integral over each ROI. Carotid ROIs with diameters of 1 to 8 mm were created by grouping all voxels within the appropriate radius. Values at grid points were similarly interpolated from the PET image. The carotid ROI activity values were taken as the mean of the interpolated grid point values.

IDIFs were compared to the arterial input function by calculating the ratio of the areas under the curve (AUC). AUC was calculated by integrating the frame values from 0–30 s, 30–60 s, and 60–90 s post tracer arrival for the IDIF and integrating the corresponding values for the arterial input function corrected for delay as detailed above. The AUC ratio (AUCR) of the IDIF AUC to the corresponding time-shifted arterial input function AUC gives an estimate of the recovery of the gold standard arterial input function. The peak of the input function for all subjects occurred between 0 and 60 s post-arrival.

2.6. Calculation of CBF

Cerebral blood flow (CBF) was calculated using the autoradiographic method of Herscovitch, et al (Herscovitch et al., 1983). The fully sampled input function from the automated blood counter, with 1-s time resolution, was used to generate the theoretical CBF vs. activity relationship for 60- and 90-s periods starting at tracer arrival using the convolution equation. A partition coefficient of 0.80 mL/g and a density for tissue of 1.05 g/mL were used. The CBF vs. activity curves were fitted with a 4^th order polynomial. Flow values for the voxels of the 60- and 90-s frames were calculated by applying the polynomial to the activity from the reconstructed frames. Flow images were also generated using the image-derived input functions for the centerline and carotid ROIs. The IDIF curves were used in the same fashion to create CBF vs. activity plots for the 60- and 90-s duration frames.

CBF values were calculated for grey matter, white matter, and the whole brain. Since these data included various activation paradigms in which different visual cues were given to the subjects, motor and visual regions were masked from the CBF images. Grey matter was defined by segmentation of a co-registered MR image using the FAST tool in the FSL software (Zhang et al., 2001). White matter regions were defined using a centrum semiovale region defined on an MR template.

2.7. IDIF scaling

To correct the IDIFs for partial volume effect, we determined a multiplicative scale factor to be applied to the IDIF that would produce the best match to the theoretical CBF vs. activity relationship based on the arterial blood data. CBF vs. PET activity curves were generated using the image-derived input functions over the range of flow values present in the CBF image calculated using the arterial input function. A minimum flow value of 3 mL/min/100g was set. The image-derived input functions were multiplied by a scale factor to produce a group of corresponding scaled CBF-activity curves. The mean-squared-difference between the scaled CBF-activity curves and the CBF-activity curve created using the automated blood counter input function was minimized to determine the ideal scale factor. This mean-squared difference was weighted using a histogram of the flow values using either the 60-s or 90-s duration frame depending on which period was being analyzed and the blood sampled data. The use of the histogram ensured that value ranges which corresponded to a greater number of voxels were more closely fit. The IDIF scale factor SF was determined as follows: Let C_A(F) be the predicted tissue activity for a scan of specific duration, here either 60 or 90 s, for blood flow of F using the arterial input function. Let C_I(F) be the predicted tissue activity for blood flow of F using the IDIF. Since scaling of the input function produces a direct scaling of the tissue response, we chose SF to minimize the difference in predicted tissue values as a function of flow as follows:

$$\sum _i{w}_i{\left(C_A(F_i)-{\mathit{SFC}}_I(F_i)\right)}^2$$ (4)

where F_i is a set of flow values chosen for each scan ranging from 3 mL/min/100g to the maximum brain flow value in the CBF image derived from the blood sampled. The weighting terms, w_i, were derived from the histogram of the CBF values created using the blood sampled input function. In this way, SF is chosen to give a best overall match to blood-derived CBF values using scaled IDIF values.

Scale factors were calculated for each injection for the 60- and 90-s duration frames. Mean scale factors were calculated for each subject (subject-specific scale factor, SSSF) for each duration. The inverse of this scale factor, in the absence of spill-in, is the true recovery coefficient. Here, we refer to it as the apparent recovery coefficient (aRC). The image-derived input functions for all injections in each subject were rescaled using each SSSF and CBF values were calculated using the rescaled IDIFs. CBF was also calculated from IDIFs using a global scale factor (GSF), computed by averaging the SSSF across all subjects.

An alternative strategy to deriving scale factors would be to use the AUCR directly. The aRC calculated using CBF was compared to the AUCR derived directly from the IDIF. The percent difference between the aRC and the AUCR was calculated for each injection and the mean and SD was tabulated.

3. Results

3.1. Segmentation and Centerline Extraction

An optimal μ value (1) was not found that consistently produced satisfactory carotid segmentations for all subjects. Segmentations were chosen where both user-defined seed points were included in a continuous segmentation foreground. Segmentations were visually gauged to minimize leakage, i.e., when background voxels were incorrectly labeled as foreground. Attempts to extend the segmentation through the petrous segment (C2) to the circle of Willis had mixed results, i.e., the incidence of leakage increased when attempts were made to segment a larger portion of the carotid. Values for μ in the chosen segmentations varied between 10 × 10³ and 25 × 10³.

Segmented images were cropped to exclude transverse slices above or below the seed points before centerline extraction (see figure 1). Average sizes of the segmented regions were 902 ± 410 mm³. Centerlines were then determined using an average of 6.4 ± 1.0 knots. The ratio of the number of knots in the left vs. right carotid of the same subject was 0.95 ± 0.12. The average length of all carotids was 51 ± 14 mm along the spline centerlines. The volume of the segmented regions was divided by the average length to calculate the apparent diameter. Assuming a circular cross-section, the average diameter was 4.8 ± 1.2 mm, which is consistent with average values in literature.

3.2. Re-registration

AUCR was used to evaluate registrations from different early periods and results are shown in figure 2. Using short time-interval images, i.e., images from data up to 25, 50, and 75% of the maximum count rate, the AUCR from separate re-registrations was ~ 0.5, with standard deviation of ~ 0.09. AUCR values were similar for 0–30, 30–60 and 60–90 second periods post tracer arrival. Re-registration of the carotid centerlines using the longer early image (0–60 s post-arrival) resulted in larger variability in AUCR across subjects and a significant difference between the AUCR values over different periods. This is likely due to misregistration of the carotid centerline onto background tissue. Registrations using early images with durations reaching 50% of the maximum count rate were used for the remainder of the results.

Figure 2.

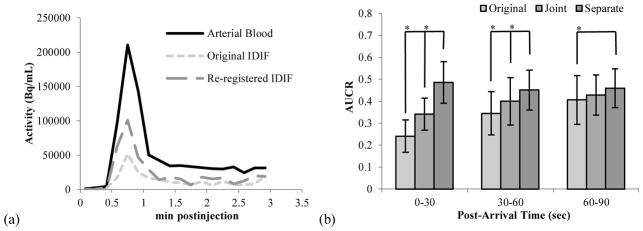
(a) Typical IDIF (mean of left and right carotids) compared to arterial sampled input function.

(b) Area under the curve ratio (AUCR) of the carotid centerlines (n=69) for 0–30, 30–60, and 60–90 s post-arrival. Three registrations were used: Original: centerlines were placed according to the original PET-MR registration. Joint: left and right carotids were registered together using a 6-parameter rigid transformation, maintaining their relative positions. Separate: left and right carotids were registered independently. Mean and standard deviations were calculated across all studies.

Re-registration of the carotid centerlines to the PET data moved the centerline 4.3 ± 3.0 mm and 5.0 ± 3.1 mm from their original positions when using joint or separate carotid re-registrations, respectively. Both joint and separate carotid re-registration increased AUCR over the AUCR when using the original PET-to-MR registration as shown in figure 2(b). The AUCR for the separate re-registration was significantly higher than that of the original and joint carotid re-registration groups (p < 0.005). Using the original transformation, later periods have higher AUCR, as seen in figure 2(b). A higher late AUCR suggests spill-in effects in the carotid centerline. Since this effect is reduced by the re-registration, it suggests that the original registration misplaced the centerline over tissue near the carotid. As can be seen in figure 2(b), we found that the IDIF/AIF ratio, or AUCR, after appropriate re-registration, is constant over the first 90 s of the scan.

AUCR for the left and right carotids were compared within each subject, results are tabulated in table 1. In two subjects, left and right carotids were significantly different. This may indicate an anatomical difference or a failure of the segmentation or registration algorithms.

Table 1.

Centerline Area under the curve ratio (AUCR) for 0–60 s period post tracer arrival.

Subject	Left	Right
1	0.47±0.05	0.43±0.06
2	0.57±0.09	0.58±0.09
3	0.42±0.07	0.47±0.05
4	0.48±0.06	0.46±0.05
a5	0.51±0.11	0.36±0.08
6	0.53±0.04	0.53±0.04
7	0.40±0.06	0.44±0.02
a8	0.38±0.06	0.52±0.13
9	0.46±0.06	0.49±0.06

^aLeft and right values significantly different.

3.3. Cerebral Blood Flow and Apparent Recovery Coefficient

The IDIF scale factors and aRCs described in section 2.7 were calculated across all studies for the centerline and carotid ROIs based on the centerline. Apparent recovery coefficients were calculated in two ways, one based on AUCR and one based on CBF values. The calculated aRCs using the CBF model were entirely consistent with the AUCR derived from direct comparison of the IDIF to arterial blood sample data. Specifically, the mean AUCR from the two methods were 0.47 ± 0.08 and 0.47 ± 0.07, with a percent difference across subjects of 3 ± 8 %. Figure 3a shows the CBF derived aRC as a function of the carotid ROI diameter used. Increasing the diameter from just the centerline to 8 mm results in a decrease in the aRC. This is as expected due to a greater partial volume effect.

Figure 3.

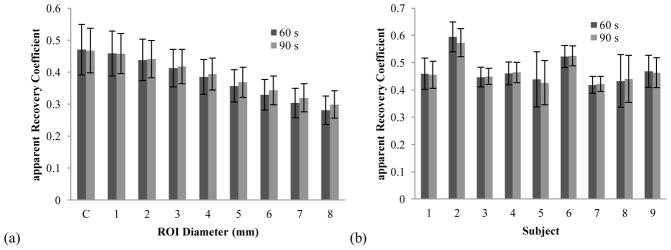
(a) Apparent recovery coefficient (aRC) for image derived input function as determined by CBF calculation, C = centerline (n=69). Carotid ROIs were increased in diameter from the centerline to 8 mm in diameter. (b) Average aRC of centerlines calculated for each individual subject. As can be seen aRC varied between subjects.

At the centerline, aRC estimated with both 60- and 90-s of data were nearly equal, paralleling the AUCR results. As ROI diameter increased, aRC estimated using 90 s of data exceeded aRC estimated using 60 s of data as seen in figure 3(a). Late in the scan, background tissue will have higher activity, so the higher aRC observed with a large ROI when using 90 s of data can be attributed to spill-in from the surrounding background tissue.

When the centerline data are displayed by subject (figure 3(b)), the between-subject variability of aRC results is shown. Note that variability within subject is generally low with the exception of the two subjects with significant differences between left and right carotids (table 1). The within-subject results for the AUCR mirrored the aRC results derived from the CBF model. The aRC of the centerline is expected to depend on the size of the carotid, which will vary across subjects according to age, genetics, and health conditions.

Using the average scale factor across injections for each subject (subject-specific scale factor, SSSF), the individual IDIFs were scaled and the corresponding CBF calculated. Application of the SSSF produces a CBF value close to that calculated using the corresponding blood derived curve (table 2).

Table 2.

CBF values using different input functions with 60 s of data. All values in mL/min/100g, (n=69).

Input Function ROI	Grey Matter	White Matter
Blood Derived	61.4 ± 11.0	15.6 ± 3.0
Subject-specific scale factor (SSSF)
Centerline	61.3 ± 13.5	15.5 ± 3.4
1 mm Diameter ROI	61.3 ± 13.2	15.5 ± 3.4
5 mm Diameter ROI	61.2 ± 11.9	15.6 ± 3.1
Global scale factor (GSF)
Centerline	60.3 ± 11.3	15.3 ± 3.0
1 mm Diameter ROI	60.2 ± 10.2	15.3 ± 2.8
5 mm Diameter ROI	60.1 ± 8.4	15.4 ± 2.3

Values for CBF in grey and white matter were similar to results from literature. The use of the IDIF with SSSF increased variability of the CBF results compared to the radial artery input function. As can be seen in table 2, though, this increase is not large.

A single global scale factor (GSF) was estimated from the mean aRC across all subjects which was 0.47 ± 0.07, 0.46 ± 0.07, and 0.36 ± 0.05, for centerline, 1-mm, and 5-mm diameter ROIs, respectively. This represents a population based scale factor rather than a specific factor for each subject. This single factor was used to correct the IDIFs from all subjects, and the resulting CBF values are shown in table 2. Not surprisingly, the mean CBF values were not changed.

It is of interest, however, to examine the within- and between-subject variability. We calculated the mean squared differences between the global mean CBF values for grey and white matter and the mean grey and white CBF values for each subject. This was calculated both when using the SSSF and the population derived GSF to scale the IDIF and calculate CBF values. The square root of the mean squared differences, i.e., standard deviations, are shown in table 3 under the columns for Between-subject variability. We also calculated the mean squared differences between each subject’s mean CBF values and the CBF values for each injection in that subject to evaluate within-subject variability. Table 3 shows the square root of these mean squared differences, i.e., standard deviations, under the columns for Within-subject variability.

Table 3.

Between- and within-subject variability in CBF (60-sec scan) using different input functions. SSSF = subject-specific scale factor. GSF = Global scale factor. Units are mL/min/100g.

Input Function ROI	Grey Matter		White Matter
	Between	Within	Between	Within
Blood Derived	10.7	4.6	2.9	1.3
SSSF Centerline	10.8	9.4	2.9	2.2
SSSF 1 mm	10.9	8.8	2.9	2.1
SSSF 5 mm	10.9	6.4	2.9	1.6
GSF Centerline	7.3	9.6	2.3	2.2
GSF 1 mm	6.3	8.8	2.1	2.1
GSF 5 mm	6.5	6.1	2.0	1.5

In comparing CBF results with SSSF vs. blood data, the between-subject variability (BSV) was unchanged; this is expected since a single SSSF was derived per subject to match the blood-derived data, thus the mean CBF per subject was unchanged. However, the within-subject variability (WSV) with the centerline ROI increased substantially, presumably due to noise in the IDIF, and/or variability in the centerline registrations. The average of the coefficients of variation within each subject when using blood data was ~ 7% for both grey and white matter. This value was approximately 14% when using the IDIF, using the SSSF. The same effects on within-subject variation were seen for the population based GSF.

Increasing the diameter of the ROI resulted in decreased WSV when using both the SSSF and the GSF as can be seen in tables 2 and 3. Increased ROI size reduced noise in the IDIF by increasing the number of voxels sampled. Using the largest diameter ROIs, WSV approaches the level observed when using radial artery blood data. It is important to note though that when using the large ROIs, spillover is pronounced, as seen in figure 3(a).

When using the GSF, interestingly, the BSV dropped to a value noticeably lower than that of the blood-derived data. This suggests that some of the BSV in the blood data is due to subject-specific biases in those measurements, such as interindividual variation in dispersion. Further, the magnitude of these errors is larger than the interindividual variation produced by the IDIF, such as errors in the centerline shape or varying recovery coefficient due to individual differences in carotid anatomy. In other words, the intersubject variability in aRC (figure 3(b)) may be attributed more to the blood measurements, the presumed gold standard, than to the IDIF.

4. Discussion

This study presents a new method that successfully characterizes the carotid ROI in PET images utilizing anatomical MR information for the purpose of quantification of cerebral blood flow with [¹⁵O]water. Carotids were segmented in a semi-automated fashion using the level set method from high-resolution anatomic MR images. Carotid centerlines modeled as cubic splines were extracted from these segmentations and used as the basis for carotid ROIs of varying diameter. These centerlines were used in a local re-registration of the carotid arteries in PET images that had been previously registered to the relevant MR images using the skull-stripped brain. IDIFs were extracted by interpolating the values in the PET image at points along the centerline and in various diameter carotid ROIs. These IDIFs as well as gold standard blood data drawn from the radial artery were used in the autoradiographic CBF model and a scale factor for the IDIFs was estimated to match the CBF values. Results using the subsequently scaled IDIFs indicate that our centerline IDIF method introduces some additional within-subject variability in CBF but remains highly consistent within each subject. Using a global scale factor, we have demonstrated reduced intersubject variability, presumably by avoiding errors in the arterial blood measurements. Thus, this methodology provides a completely bloodless approach to derive an IDIF from [¹⁵O]water IDIF for use in calculating CBF.

4.1 Carotid Identification in MR Images

In this work, carotids were identified from T1-weighted MR images. Carotids have previously been successfully segmented in a semi-automatic fashion in these images. Methods have been developed to remove bright blood vessels from T1-weighted brain MR images in order to facilitate analysis of grey and white matter volumes (Penumetcha et al., 2008). Blood appears bright in MPRAGE images due to its flow through the scan volume. Tissues scanned with gradient echo sequences will have their magnetizations partially saturated during the scan. Blood flowing into the scan volume is unsaturated and has full longitudinal magnetization before the excitation pulse, therefore appearing bright in the image. While carotids are easily visualized in T1-weighted images, the boundaries are blurred due to the partial volume effect, resulting in a gradient of intensity values rather than a sharp delineation. Therefore, in this study we used the MR to find the centerline of the carotids, but not to define their exact borders.

MR images were not corrected for motion during the scan. Subject motion during the MR scan could cause errors in the position of the carotid arteries, however, this error would be compensated by the reregistration step between the MR-derived centerlines and the PET image of the carotid arteries. Subject motion could also distort the shape of the carotids in the MR images. Using the centerline of the segmented carotids rather than using the entire segmented region may lessen the effect of motion artifacts. However, such motion would likely degrade the centerline signal by incorporating off center regions of the carotid with greater PVE. This would lower the aRC for that particular subject.

4.2 Segmentation

In the level-set segmentation, the parameter μ used was proposed by Chan and Vese as a means to regularize the process based on the size of the segmentation boundary. We allowed the μ value to be different for different subjects, preferring to visually confirm the quality of the segmentation in the absence of a gold standard to which to compare the results. As can be seen in (1), μ scales the weight of the φ image divergence term against the λ–weighted intensity term. Differences in the intensity distribution of the image as it pertains to carotid delineation could affect this intensity term and thus the optimal weight μ on the divergence term. Rescaling of the MR values around the carotids to a common range may produce a more consistent μ value. Modifying the Chan-Vese energy model with additional terms may also improve results by further constraining the solution based on assumptions about the carotids. This could involve terms taking into account high intensity background regions that might confound the basic two-region Chan-Vese model. For example, Scherl et al. introduced an additional background region to model high-intensity calcifications visible in CT angiography images and a regularization term based on a preliminary estimate of the lumen intensity (Scherl et al., 2007).

In this analysis, to minimize spillover, the carotid data were limited to a region away from the brain. This meant that portions of the carotid, i.e., the petrous segment (C2), were not used since it was likely to have significant spillover from high activity brain regions making it potentially unsuitable for IDIF extraction. A more extensive segmentation of the carotid, though, may be useful for investigating spillover effects and the level of consistency of the IDIF signal in different regions of the carotid. Additionally, a larger carotid region may improve re-registration.

4.3 IDIF Calculation

Local re-registration of the MR-based centerline to the PET images improved results, demonstrating some misalignment of the carotids when using a transformation based solely on a brain registration. This can be explained by the fact that the carotids are essentially beyond the edge of the region used for the original registration. Furthermore, their small size means that even small errors in registration will lead to large partial volume errors. The need for a separate re-registration for left and right carotids was not expected. This difference may indicate a subtle scale distortion between the high-resolution MR and PET images. Alternatively, errors in the segmentation or subsequent centerline modeling might result in altered positioning of one of the centerlines. Carotid flexion, or warping of the carotid shape due to neck position, could also contribute to errors in registration, though this is less likely in sections of the carotid close to the brain. Ultimately, the effect of re-registration suggests that a method that relies on anatomical information must be especially cognizant of positioning errors whether arising from misregistration as well as from subject motion.

The re-registration method requires that there is an identifiable period during the PET scan for which the carotid arteries have much higher intensity than surrounding background. This is often true in the earliest period of a scan. Since the carotid shape information is derived from the MR, the PET image can be noisy due to the low count rate in these early frames, as was observed in the [¹⁵O]water studies used here for centerline re-registration. Smoothing of the images, which would obscure boundary information, might be useful to improve the positioning of the centerline, although final IDIF values should then be obtained from original unsmoothed images

IDIFs here were calculated using 10-sec frames. In principle, shorter frame durations might be desirable, as it should better characterize the input function shape. Alternatively, shorter frames obviously have higher noise. For example, 5-s frames had an average number of noise equivalent counts (NEC) over the first 60 s between ~ 300 × 10³ and ~ 700 × 10³ NEC. Previous studies have demonstrated a slight bias in OSEM reconstruction in such low-count frames (Planeta-Wilson et al., 2009). To further evaluate this effect, we compared CBF calculated using arterial blood data sampled at 1 s intervals and blood data resampled by averaging over 10 s intervals. Grey matter CBF was 62.4 ± 11.2 and white matter CBF was 15.7 ± 3.1, when using 10-s sampling. These results are essentially identical to the 1-s sampling results and demonstrate that 10-s frames are sufficient for calculating CBF when using 60 s of data.

4.4 IDIF Scaling and Partial Volume Effect

The centerline IDIFs used here underestimated the arterial input functions by ~50%, as measured by the AUCR and aRC. With an expected resolution of better than 3 mm on the HRRT, we anticipated higher centerline recovery coefficients. Using an average carotid diameter of 5 mm, we created images with carotid ROIs based on one of the extracted centerlines. Smoothing the image with successively larger Gaussian filters, we measured the aRC at the known centerline and compared it to our results. Our mean centerline aRC of 0.47 corresponded to a 5.0 mm Gaussian filter, i.e., the apparent image resolution at the carotids is ~5 mm. While this value for the apparent image resolution seems high, our AUCR and thus aRC results were similar to other IDIF results published for the HRRT. The measured aRC is based on application of a CBF model to the IDIF data. Since the goal here was measurement of CBF, optimizing the weighting for CBF should produce most favorable results. This is especially true in light of the possible errors in the gold standard blood sampling measurements which we may have avoided with IDIF. However, it is noteworthy that IDIF scaling based on the CBF model was nearly identical to what would have been calculated using the AUCR directly. This supports the consistency and validity of the results, although this good agreement may also be due to the fact that the CBF model incorporates the integral of the input function.

In comparison to other methods, this centerline approach may be most comparable to the method of Mourik et al that uses clusters of voxels having the maximum value per slice in the carotid region. Mourik et al reported similar AUCRs of 0.44 ± 0.19 in their peak and 0.57 ± 0.22 in their tail periods on the HRRT when reconstructing with an OSEM algorithm without partial volume correction (Mourik et al., 2008b). Their study though was conducted with [¹¹C]flumazenil. Here, with [¹⁵O]water, the AUCR values were 0.49 ± 0.09 in the 0–30 s period (peak rising), 0.45 ± 0.09 in the 30–60 s period (peak falling), and 0.46 ± 0.09 in the 60–90 s (tail) period, i.e., recovery was nearly constant over time after re-registration. This may indicate that, with a centerline ROI, spill-in effects are less noticeable when the ROI is properly centered. If so, however, this would suggest a small PVE, and again higher aRC values would be expected. It is also possible that spill-in is affecting the late AUCR and is not apparent because of a balancing effect on the early AUCR. For example, the early AUCR may be higher due to less dispersion in the IDIF than in the arterial input function, since the correction for dispersion used here did not correct for dispersion internal to the body.

The partial volume effect was clearly demonstrated through the use of the centerline model with which coaxial ROIs of increasing diameter were easily constructed. The smooth reduction in aRC with increasing diameter is indicative of the partial volume effect. With accurate partial volume correction, one would expect to eliminate this dependency on size of the ROI and would also expect better recovery of the peak TAC value. In figure 3(a), increasing diameter is shown to correspond to an increase in the aRC when using 90 s of data relative to using 60 s of data. This is in agreement with the expectation that spill-in during late scan times would artificially inflate the IDIF.

Other reconstruction-related factors may also introduce inaccuracies, producing lower aRC values than expected. The reconstructions here used an isotropic Gaussian PSF (2.5 mm FWHM), and it is likely that higher accuracy would be obtained with a more accurate, spatially varying point-spread function (Jian et al., 2011). Another potential factor is the presence of low-count biases in the short early frames, causing IDIF underestimation. Additionally, OSEM reconstructions are generally run to a predetermined number of iterations, even though convergence is object-dependent. Increasing the number of iterations, one would expect improved resolution and higher recovery coefficient, especially with a PSF reconstruction. In simulations of carotid PET images including randoms and scatter, centerline AUCR continued to rise when the number of iterations was increased beyond the standard protocols. In simulation, we achieved an aRC of > 0.5 in 15 effective iterations, i.e., iterations × subsets, and an aRC of > 0.8 at the centerline in 60 effective iterations, which was used for the human data. Thus, when the data and the reconstruction model are perfectly matched, the expected high aRC values can, in fact, be obtained. Therefore, this suggests that that there may be inconsistencies between the data and reconstruction that have a large effect on carotid quantification.

Another factor potentially contributing to bias is derived by the specific implementation of the OSEM algorithm in MOLAR, related to the position of the carotids at the edge of the axial FOV. Sensitivity in the PET scanner is not uniform throughout the FOV. In our OSEM reconstruction (Carson et al., 2004), we estimate the sensitivity image (Q) by undersampling the 4.5 billion possible LORs. This method is used to correct for dynamic changes in sensitivity due to subject motion. Standard practice for brain reconstructions chooses a Q LOR sample size proportional to the counts in each reconstructed frame. The peak of the input function curve as well as the period during which the carotids are most visible are both early in the scan when the count rate is relatively low, but concentrated at one edge of the FOV. Standard sensitivity image sampling techniques place the LORs uniformly without regard to the probability of counts occurring on that LOR. Thus, it is possible that these reconstruction parameters may have higher noise and bias in the carotid region. Thus, an optimized Q sampling paradigm, like that described by Qi et al, may improve results with our carotid centerline method (Qi, 2006).

Thus, the aRC values of ~0.5 appear to be the result of the partial volume effect, made worse by a variety of reconstruction-related factors including object- and iteration-dependent resolution of OSEM, accuracy of the PSF model, low-count bias, and the method for calculation of the sensitivity image in the OSEM reconstruction.

4.5 Partial Volume Correction

Implementing a partial volume correction would require accurate information regarding the diameter of the carotid as well as the point spread function of the HRRT. Croteau et al estimated the relationship between diameter, measured in PET and CT images, and recovery coefficient using phantom experiments (Croteau et al., 2010). The authors used manual measurements of the carotid diameter on both PET images and co-registered CT images to lookup the appropriate recovery coefficient and scale the IDIF without the use of blood samples. Zanotti-Fregonara applied this method substituting MR images to measure the carotid diameters (Zanotti-Fregonara et al., 2011). Carotid segmentations could be used to simultaneously make estimates of the carotid diameter. Both studies demonstrated that this method was highly sensitive to variations in the diameter measurement.

An alternative to predetermining the diameter would be estimating it in the PET images directly in the manner of Asselin et al (Asselin et al., 2004). This approach also requires characterization of the point spread function or recovery coefficient vs. diameter curve for the particular scanner in use. This characterization itself may prove problematic. Resolution using an OSEM reconstruction is dependent on a number of factors including object contrast. Accurately predicting the recovery coefficient may require realistic modeling of the background activity.

Many more general approaches exist for the problem of partial volume correction in both PET and MR images. In particular, some methods, e.g., (Bousse et al., 2012) rely specifically on anatomical MR information in order to correct PET emission images. The method of Bousse et al uses the MR anatomical information to generate a hidden Markov information layer in between the observed data and the reconstructed image. For an excellent review of the topic of partial volume correction specifically with regard to emission tomography see Erlandsson, et al (Erlandsson et al., 2012)

4.6 Non-invasive CBF

The high within-subject consistency of CBF values using the centerline method suggests that it could be used in a completely bloodless manner, once the relevant scale factor has been determined. This value can be estimated from a population scanned on the same scanner for which arterial blood sample data are available for comparison.

For a given subject population, once an average aRC is determined, we would expect to measure CBF accurately on average for the population using a global scale factor (GSF), with added intrasubject variability (table 3) due to noise in the IDIF. While the CBF measured for a particular subject may not be absolutely correct using this method, multiple CBF values could be compared in a relative manner. This is suitable for CBF studies since generally, activation under different test conditions is being studied rather than the absolute CBF value.

The lower between-subject variability observed when using the GSF suggests that we may have avoided some types of error by using the IDIF. Blood sampled data are collected from the radial artery and must be correct for delay by the method outlined in section 2.1 as well as for dispersion (Iida et al., 1986). Iida et al reported that the dispersion time constant for external dispersion could be affected by the specific patient’s blood and that this between subject variability would be a dominant error in the dispersion correction. Iida et al also demonstrated that dispersion correction errors would result in errors when calculating CBF by the autoradiographic method. Since the carotid IDIF does not have an external transit component, both delay and external dispersion errors should be avoided. We believe this is demonstrated by the decreased between-subject variability. Of course, the IDIF method achieves this tradeoff with somewhat increases within-subject variability.

Different populations would require different aRC scale factors. Carotid diameter is affected by age and pathology with older patients generally having larger diameter arteries (Terry et al., 2003). A larger caliber artery should be less affected by the partial volume effect and thus have a larger region at its center with similar values. At the same time, older patients are also more likely to have carotid occlusions due to pathology. If a markedly different distribution of carotid diameters is expected, for example in an elderly population or due some pathology such as hypertension, a GSF may be estimated for this population.

The selection of the size of the carotid ROI will be influenced both by the population characteristics and the study design. As seen in tables 2 and 3, increased ROI size produces decreased WSV. However, this decrease in noise is countered by an increase in partial volume effect and lower aRC values (figure 3(a)). Therefore, if lowering WSV should be prioritized over bias due to the PVE, a larger ROI should be chosen. Conversely, a centerline ROI is less affected by PVE, although it comes at a cost of increased noise and within-subject variability.

4.7 Application to other tracers

This method should, in principle, be applicable to other tracers, so long as there are early PET images with clear definition of the carotids. Ideally, a centerline derived from the patient MR should be equally applicable for different tracers so long as the associated aRC is known. There are, of course, major caveats for this idea. First, the magnitude of spill-in to the carotid region at later times is likely to be much greater for other tracers than for [¹⁵O]water, which tends to equilibrate equally between tissue and blood. Also, due to the need to measure the input function for longer times, highly accurate motion correction, such as with the Vicra system (Jin et al., 2009), is required. Here, the method estimated the scale factor based on the final outcome measure of CBF. Calculation of the CBF involves integration of the input function curve, thus the AUCR values were particularly relevant. When utilizing other kinetic models, the integral of the curve may be less relevant. Thus, for other tracers, a different approach to scale or adapt the IDIF may be useful, e.g., a method based on scaling to a population-average input function. Finally, of course, most tracers produce radioactive metabolites in the blood in vivo, so a correction to the IDIF for parent tracer fraction will be needed, either based on population averages or actual blood samples.

4.8 Application to other scanner systems

This method was developed on the HRRT which has superior resolution to most other human brain scanners. With simultaneous PET-MR, we would expect elimination of the registration error of the carotid arteries assuming that there was no patient motion between the MR and PET scans. While the lower resolution of PET-MR and scanners such as the HR+ would result in a lower recovery coefficient, this would provide IDIFS similar to our result when using a carotid ROI of larger diameter. In that case, we expect that an appropriate scale factor could be estimated for use with the lower recovery coefficient. However, as illustrated in figure 3(a), larger diameter carotid ROIs might increase spill-in effects late in the scan. Furthermore, the HRRT is particularly suited to carotid IDIF methods because of the greater axial FOV which affords better imaging of the carotid arteries simultaneously with the brain.

5. Conclusion

The results of this study confirm that MR-derived carotid regions can be applied to PET data with appropriate re-registration for the purposes of IDIF extraction. Centerline IDIFs showed an apparent recovery coefficient of ~ 0.5, lower than might be expected due only to the partial volume effect; this value is attributed to a number of reconstruction-related effects. Nevertheless, it is possible to derive a consistent IDIF for a subject across injections and scans when an appropriate scale factor is used to correct the IDIF. For this study, we demonstrated that the use of a fixed global recovery coefficient (GSF) results in CBF values from a centerline IDIF with increased within-subject variability. Importantly, between-subject variability in CBF was reduced compared to the gold standard arterial input function data, suggesting that some subject-specific errors associated with radial artery blood measurements may have been avoided by the IDIF method. We conclude that noninvasive absolute CBF measurements can be performed with high resolution PET using an MR-based carotid centerline method with a fixed recovery coefficient.