Quantifying the roles of cell motility and cell proliferation in a circular barrier assay

Abstract

Moving fronts of cells are essential features of embryonic development, wound repair and cancer metastasis. This paper describes a set of experiments to investigate the roles of random motility and proliferation in driving the spread of an initially confined cell population. The experiments include an analysis of cell spreading when proliferation was inhibited. Our data have been analysed using two mathematical models: a lattice-based discrete model and a related continuum partial differential equation model. We obtain independent estimates of the random motility parameter, D, and the intrinsic proliferation rate, λ, and we confirm that these estimates lead to accurate modelling predictions of the position of the leading edge of the moving front as well as the evolution of the cell density profiles. Previous work suggests that systems with a high λ/D ratio will be characterized by steep fronts, whereas systems with a low λ/D ratio will lead to shallow diffuse fronts and this is confirmed in the present study. Our results provide evidence that continuum models, based on the Fisher–Kolmogorov equation, are a reliable platform upon which we can interpret and predict such experimental observations.

1. Introduction

Spatial spreading of cell populations, characterized by moving fronts, is essential for development [1], tissue repair [2,3] and disease progression [4]. Many kinds of experimental observations can be made to characterize cell spreading, including measuring front speed [2,3], recording time-lapse observations [1] or measuring properties of various subpopulations [5,6].

The formation of moving cell fronts can be thought of as an emergent population-level outcome driven by individual-level properties of cells within the population [7]. For such a system, it is relevant to ask whether we can predict how differences in cell behaviour, such as a change in the relative frequency of motility and proliferation events, affects the emergent properties. This is important if we consider designing intervention strategies aimed at manipulating the front speed [8]. To design such interventions, we must first be able to identify, and quantify, the various components of cell behaviour that lead to moving fronts so that we can begin to understand how to manipulate these components to obtain a particular outcome.

The standard continuum model used to represent cell spreading is

1.1

where 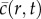is the cell density, D is the cell diffusivity (random motility coefficient), λ is the intrinsic proliferation rate and K is the carrying capacity density [9,10]. In one-dimensional Cartesian geometry, equation (1.1) simplifies to the Fisher–Kolmogorov equation [11], which has constant shape travelling wave solutions, 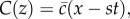moving at constant speed s [2,3,9]. The front speed approaches 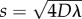as t → ∞ for initial conditions with compact support [9]. Variations of the Fisher–Kolmogorov equation, incorporating directed motility [12] or nonlinear diffusion [13,14], also have travelling wave solutions and different relationships between the wave speed and the model parameters can be derived for these generalizations. Other options for modelling cell spreading processes include using discrete approaches that are related to equation (1.1) in an appropriate limit [15]. Discrete models have the advantage that they produce discrete stochastic data that are similar to experimental images and movies [16], as well as having a formal mathematical relationship with continuum models, such as equation (1.1) [15,17,18].

Many choices of λ and D in the Fisher–Kolmogorov equation give the same asymptotic front speed, 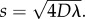This property was demonstrated by Maini et al. [2,3], who measured the front speed in a scrape assay and showed that several reasonable choices of λ and D could be used to match the front speed. Other approaches to identifying parameters have used measurements of the cell density profile, 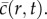For example, Sengers et al. [19,20] fitted the solution of a reaction–diffusion equation to experimental density profiles to match the experimental data [19,20]. Similarly, Sherratt & Murray [10] studied a wound-healing experiment and chose the parameters in two different reaction–diffusion equations so that both models predicted the observed closure rates. The disadvantage of fitting the solution of mathematical models to cell density information alone is that this does not necessarily ensure that the parametrized model can make independent predictions. One way to overcome this is to collect different types of experimental data so that the process of model calibration can be separated from the process of model prediction.

In addition to making experimental observations of the position of a moving front of cells, here we study the shape of the moving front to understand how the relative roles of cell motility and cell proliferation affect these details. We study the details of the leading edge since the shape of the moving front is thought to have clinical implications. For example, in the context of glioma invasion, Swanson et al. [4] discuss the difference between shallow-fronted tumours (low λ/D ratio) and sharp-fronted tumours (high λ/D ratio) [4]. These differences are relevant when considering surgical removal since the boundary between the tumour tissue and normal tissue is increasingly difficult to detect as the front becomes more diffuse [4,21]. The shape of the leading edge is also of interest in the context of melanoma progression where visual inspection of the invading cancer, including the details of the leading edge, is thought to provide important information about the aggressiveness of the tumour [22].

In this work, we investigate how cell motility and proliferation control the position and shape of the leading edge of a two-dimensional cell spreading system. Using a circular barrier assay, we perform experiments that provide independent estimates of D and λ. We then make separate modelling predictions with regard to the position and shape of the leading edge. We investigate how the relative roles of motility and proliferation affect the spreading by performing two parallel sets of experiments. In the first, we consider cell spreading driven by motility without proliferation, whereas in the second we consider cell spreading driven by combined motility and proliferation. All experimental observations are repeated at three different initial cell densities.

2. Experimental methods

2.1. Cell culture

Murine fibroblast cells (3T3 cells) were cultured in Dulbecco's modified Eagle medium (Invitrogen, Australia) with 5 per cent foetal calf serum (FCS; Hyclone, New Zealand), 2 mM l-glutamine (Invitrogen) and 1% v/v penicillin/streptomycin (Invitrogen) in 5 per cent CO₂ at 37°C. Monolayers of 3T3 cells were cultured in T175 cm² tissue culture flasks (Nunc, Thermo Scientific, Denmark).

2.2. Barrier assay

We use a barrier assay since several studies claim that they are more reproducible than a scrape assay [23,24]. Metal–silicone barriers, 6 mm in diameter (Aix Scientifics, Germany), were cleaned, sterilized, dried and placed in the centre of a 24-well tissue culture plate with 500 μl culture medium. Each well in the tissue culture plate has a diameter of 15.6 mm. The plate was placed at 37°C in a humidified incubator at 5 per cent CO₂ for 1 h to allow the barriers to attach to the surface of the tissue culture plate. Cells were lifted just prior to confluence using 0.05 per cent trypsin (Invitrogen). Viable cells were counted using a trypan blue exclusion test and a haemocytometer.

Three different densities of cell suspension were used: 5000, 10 000 and 30 000 cells/100 μl. The cell suspension was carefully introduced in the barrier so that the cells were approximately evenly distributed. Once seeded, the tissue culture plate was placed in an incubator. Mitomycin-C (Sigma-Aldrich, Australia), an inhibitor of cell proliferation, 10 μg ml⁻¹, was added to some cell solutions for 4 h. After allowing the cells to attach for 1 h, the barriers were removed and the cell layer was washed with serum-free medium (SFM; culture medium without FCS) and replaced with 0.5 ml of culture medium. The attachment time was varied; we found 1 h was sufficient to prevent cells washing off the plate when the cell layer was washed with SFM. Plates were incubated at 37^oC, 5 per cent CO₂, for four different times, t = 0, 24, 48 and 72 h. Each assay, for each initial density, was repeated three times (n = 3).

2.3. Cell staining

Two staining techniques were used to analyse these experiments.

• (i) Population-scale images were obtained by fixing the cells with 10 per cent formalin, followed by 0.01 per cent crystal violet (Sigma-Aldrich). The stain was rinsed with phosphate-buffered saline (Invitrogen), and the plates were air-dried. Images were taken on a stereo microscope with a Nikon digital camera (DXM1200C).

• (ii) Individual-scale images were obtained by fixing the cells with 10 per cent formalin, then made permeable using ice-cold 70 per cent ethanol and the nucleus stained with propidium iodide (PI), 1 mg ml⁻¹ (Invitrogen). Images were taken using a Laborlux fluorescence microscope with a Nikon digital camera (DXM1200C) at 100× magnification. Overlapping images were taken to reconstruct both horizontal and vertical transects through the spreading population.

2.4. Image analysis

The average cell diameter, Δ, was estimated using Leica LAS AF Lite software (electronic supplementary material, data). All other image analysis was performed using customized software written with Matlab's Image Processing Toolbox (v. 7.12) [25] (see the electronic supplementary material, data). In summary, to estimate the location of the leading edge of the spreading populations, edge detection and image segmentation algorithms were used to identify and isolate the entire cell population from the background of the image. To count cell numbers in the PI-stained images, we assumed that each cell corresponds to a distinct identifiable region in the image. Each cell was automatically identified. For some images, at high cell density, we found that a relatively small number of cells had to be manually identified and counted.

3. Modelling methods

3.1. Discrete model

An interacting random walk model with proliferation is used to simulate the experiments. The model is interacting in the sense that it permits only one agent to occupy each lattice site so that the model incorporates volume exclusion and finite-size effects [15,17,18,26]. We take the most straightforward modelling approach by implementing the discrete model on a two-dimensional square lattice with spacing Δ. We could use a more sophisticated lattice-based [27,28] or lattice-free [16,29,30] modelling approach; however, given that this is the first time that a mathematical model has been used to separately quantify the parameters governing cell migration and cell proliferation in a barrier assay, it is reasonable to take a parsimonious modelling approach. In our discrete simulations, each site is indexed (i, j), where i, 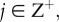and each site has position (x, y) = (iΔ, jΔ). A random sequential update method [31] is used to perform the simulations. If there are N(t) agents at time t, during the next time step of duration τ, N(t) agents are selected at random and given the opportunity to move with probability 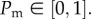The random sequential update method means that not all the N(t) agents are always selected in every step, and sometimes a particular agent will be selected more than once per time step. Our experiments indicate that the initially circular region maintains a circular shape (§4); therefore, we implement an unbiased mechanism where an agent at (x, y) attempts to step to (x±Δ, y) or (x, y ± Δ) with equal probability. Once the N(t) potential motility events have been assessed, other N(t) agents are selected at random and given the opportunity to proliferate with probability 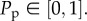We model proliferation with an unbiased mechanism whereby a proliferative agent at (x, y) attempts to deposit a daughter agent at (x±Δ, y) or (x, y±Δ), with each target site chosen with equal probability. Potential motility and proliferation events that would place an agent on an occupied site are aborted [15,17,18].

In the kth identically prepared realization, the occupancy of site (i, j) is denoted 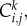with 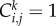for an occupied site, and 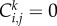for a vacant site. If the average occupancy of site (i, j), evaluated for M identically prepared realizations, is 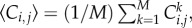the corresponding continuous density, 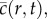is governed by equation (1.1) [15] with K = 1, where 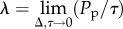and 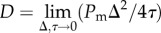[15]. Here, 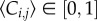is equivalent to 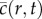as M becomes sufficiently large, provided that the ratio P_p/P_m is sufficiently small. This mathematical relationship allows us to use the averaged data from the discrete model and the solution of equation (1.1) interchangeably, provided that P_p/P_m is sufficiently small. We do not discuss this equivalence here since it has been analysed, in detail, previously [15].

To interpret our experimental data using equation (1.1), we obtain numerical solutions (see the electronic supplementary material, data) of

3.1

which is equivalent to equation (1.1) in an axisymmetric geometry where the dimensional cell density, 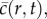has been scaled relative to the carrying capacity density, 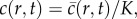with 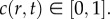Numerical solutions are obtained on 0 ≤ r ≤ 7800 μm, with zero flux boundary conditions at r = 0 and at r = 7800 μm. The initial condition for all numerical solutions is given by

3.2

where c₀ is the initial density of cells inside the barrier.

4. Results

4.1. Cell motility estimates

Images of individual cells were acquired, and Leica software was used to obtain measurements of the diameter of cells (n = 15), giving 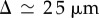(see the electronic supplementary material, data).

In our initial analysis, we assume that there is no proliferation. Assays were conducted using three different initial cell densities by placing 5000, 10 000 or 30 000 cells inside the barriers after mitomycin-C pretreatment. Each experiment, at each initial density, was repeated three times (n = 3). Snapshots in figure 1 show that the spreading population maintains an approximately circular shape. We used image analysis software (see §2 and electronic supplementary material, data) to quantify the increase in size of the region enclosed by the leading edge of the spreading population. The location of the leading edge, determined by our image analysis software, is superimposed in figure 1a–d. We converted the area estimates into an equivalent circular diameter, d, giving d = 6.08, 6.60, 7.06 and 7.54 mm after t = 0, 24, 48 and 72 h, respectively. Equivalent results for the experiments where 5000 and 30 000 cells were placed in the barriers are given in the electronic supplementary material, data.

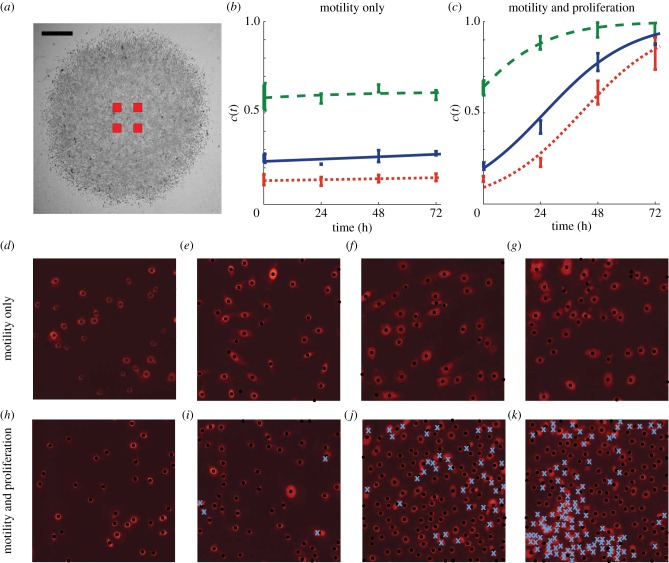
Figure 1.

Experimental images in (a–d) show a barrier assay where 10 000 cells were initially placed uniformly within the barrier after pretreatment with mitomycin-C. Images in (a–d) correspond to t = 0, 24, 48 and 72 h, respectively. The black (solid) line indicates the position of the leading edge detected by the image analysis software. The area enclosed by the leading edge was converted to an equivalent circular diameter giving d = 6.06, 6.60, 7.06 and 7.54 mm in (a–d), respectively. Images in (e–h) correspond to snapshots from the discrete model on a 624 × 624 lattice with Δ = 25 μm. Simulations were performed by initially placing 10 000 agents uniformly inside a circular region of diameter 6.0 mm, and the system evolved with P_m = 1, P_p = 0 and τ = 0.09191 h. The leading edge of the simulated spreading population is shown by the black (solid) line. Here, D was chosen so that the area enclosed by the leading edge of the simulated population is, on average, equal to the area enclosed by the leading edge of the population in the corresponding experimental images. The dashed curves in (a–h) correspond to the c(r,t) = 0.017 contour of the numerical solution of equation (3.1) with λ = 0 and D = 1700 μm² h^–1. The scale bar corresponds to 1.5 mm. (Online version in colour.)

To model this spreading behaviour, we used the discrete model with Δ = 25 μm, P_p = 0 and P_m = 1. Simulations were performed on a lattice of size 624 × 624, whose dimensions were chosen so that the width of the lattice was equal to the 15.6 mm diameter of wells in the 24-well plate, 15 600/25 = 624. To initialize the simulations, agents were placed uniformly inside a circle of diameter 6.0 mm. The centre of the circle was placed at the centre of the lattice, which is equivalent to placing the 6.0 mm barrier in the centre of the 15.6 mm well. The circular region representing the barrier has a diameter of 6000/25 = 240 lattice sites, containing π(240)²/4 ≈ 45 239 lattice sites. To model the three different initial cell densities, simulations were initiated by placing either 5000, 10 000 or 30 000 agents uniformly, at random, across these 45 239 lattice sites. Zero flux boundary conditions were imposed, and the model was used to perform simulations until t = 0, 24, 48 and 72 h.

To calibrate the discrete model, we performed simulations of each experiment with P_m = 1, which gives, on average, an isolated agent an opportunity to undergo a motility event during each time step. We systematically varied the duration of the time step τ [32], which is equivalent to varying D. For 25 different values of D in the range 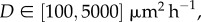each experiment was simulated three times (n = 3), and the image analysis software was used to locate the position of the leading edge in the discrete snapshots in exactly the same way that the leading edge was located in the experimental images. This gave us an estimate of the area enclosed by the leading edge for the simulated spreading populations at t = 24, 48 and 72 h, allowing us to find an optimal value of D to match the experiments (see the electronic supplementary material, data). Results in figure 1e–h show snapshots from a single realization of the calibrated discrete model together with the leading edge. Similar results were obtained for the experiments with 5000 and 30 000 cells (see the electronic supplementary material, data). In summary, we found estimates of the diffusivity to be D = 1500, 1700 and 2900 μm² h^–1 for the 5000, 10 000 and 30 000 cell experiments, respectively.

We also quantitatively model the spreading behaviour in figure 1 using equation (3.1). One way to do this is to solve equation (3.1), using our estimates of D with λ = 0, and choose a particular contour of the solution, c(r, t) = c*, that matches the average spreading observed in the experiments. Choosing c* = 0.017 matches the experimental measurements (see the electronic supplementary material, data). To demonstrate the efficacy of our approach, we superimpose the c* = 0.017 contour of the solutions of equation (3.2) on the images in figure 1. Equivalent results for the 5000 and 30 000 experiments are summarized in the electronic supplementary material, data.

Our approach to estimate D used the image analysis software to calibrate the discrete model. Using our estimates of D, we chose the contour of the solution of equation (3.2), with λ = 0, so that the position of the leading edge, determined by the image analysis software, matched the solution of equation (3.2). Without the image analysis software, it is not obvious how to interpret the image data in figure 1 using the solution of equation (3.2), since we do not know in advance which contour of the solution corresponds to the leading edge of the spreading populations. Here, we overcome this by applying the same image analysis technique to both the experimental images and the discrete snapshots.

4.2. Cell proliferation estimates

Previously, we assumed that mitomycin-C pretreatment prevents cell proliferation [33,34], and we now test this by quantifying the observed proliferation rate in the experiments. Assays were performed in triplicate (n = 3) for each initial cell density of 5000, 10 000 and 30 000 cells. We used PI staining and higher magnification images to identify the nucleus of individual cells allowing us to estimate the temporal changes in the cell density in the central region of the assay. In each experimental replicate, we recorded snapshots of four square subregions of dimension 400 × 400 μm. This means we analysed 16 square subregions for each initial density. The approximate location of the subregions is shown in figure 2a, confirming that they were located away from the leading edge so that the cells were approximately uniformly distributed within each subregion.

Figure 2.

Proliferation in the barrier assay was quantified by counting the number of cells in four different subregions in each experimental replicate. The relative size and approximate location of the subregions are shown in (a), where the scale bar corresponds to 1.5 mm. The number of cells in the subregions were counted, and the corresponding time evolution of the mean scaled cell density is shown in (b,c), with error bars indicating one standard deviation from the mean. Dotted, solid and dashed curves in (b,c) correspond to appropriately parametrized logistic growth curves for the experiments where 5000, 10 000 and 30 000 cells were placed initially in the barrier, respectively. Images in (d–g) show four subregions of dimensions 400 × 400 μm for the experiment where 5000 cells were initially placed inside the barrier after pretreatment with mitomycin-C. The images in (d–g) correspond to t = 0, 24, 48 and 72 h, respectively. The PI staining highlights each cell nucleus. Black dots indicate cells that were automatically identified using the image analysis software. Results in (h–k) show equivalent images from an experiment without mitomycin-C pretreatment. The crosses in (i–k) indicate cells that were manually counted. (Online version in colour.)

Images in figure 2d–g show snapshots of the cells in a central subregion after mitomycin-C pretreatment, indicating that the number of cells does not change significantly with time. These images indicate that the size of the cell nucleus appears to increase with time; however, it is unclear whether the size of the cells also increases with time as the PI staining highlights the cell nucleus rather than the cell cytoplasm. Images in figure 2h–k show an identically prepared experiment without mitomycin-C pretreatment where the number of cells increases dramatically with time, and there is no obvious change in the size of the cell nucleus.

To quantify the differences between figure 2d–g and figure 2h–k, we plot the non-dimensional cell density in figure 2b,c by approximating the carrying capacity density to be K = 1.6 × 10⁻³ cells μm^–2, which is the maximum packing density of circular disc-like cells with diameter 25 μm on a two-dimensional square lattice. The cell density in the experiments without mitomycin-C pretreatment increased rapidly. To quantify the growth, we note that equation (3.2) can be simplified when the cell density, c(r, t), is spatially uniform so that locally we have c(r, t) = c(t). Under these conditions, equation (3.2) simplifies to the logistic equation

4.1

which has the solution

4.2

where 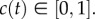We used a line search to choose the optimal value of λ that minimized the least-squares error between our measurements, in figure 2b,c, and the solution of the logistic equation (see the electronic supplementary material, data). This gave λ = 0.0561 h⁻¹ for the experiment with 5000 cells without mitomycin-C pretreatment and λ = 0.0016 h⁻¹ for the equivalent experiment with mitomycin-C pretreatment, confirming that mitomycin-C pretreatment prevented proliferation and justifies our modelling assumption in figure 1, where we set P_p = 0. Equivalent measurements were repeated for the experiments with 10 000 and 30 000 cells, and the relevant logistic growth curves are superimposed in figure 2b,c. For these experiments, we found λ = 0.0552 h⁻¹ for the 10 000 cell experiment without mitomycin-C pretreatment, and λ = 0.0021 h⁻¹ for the equivalent experiment with mitomycin-C pretreatment. Similarly, our results indicate λ = 0.0594 h⁻¹ for the 30 000 cell experiment without mitomycin-C pretreatment, and λ = 0.0026 h⁻¹ for the 30 000 cell experiment with mitomycin-C pretreatment.

4.3. Position of the leading edge

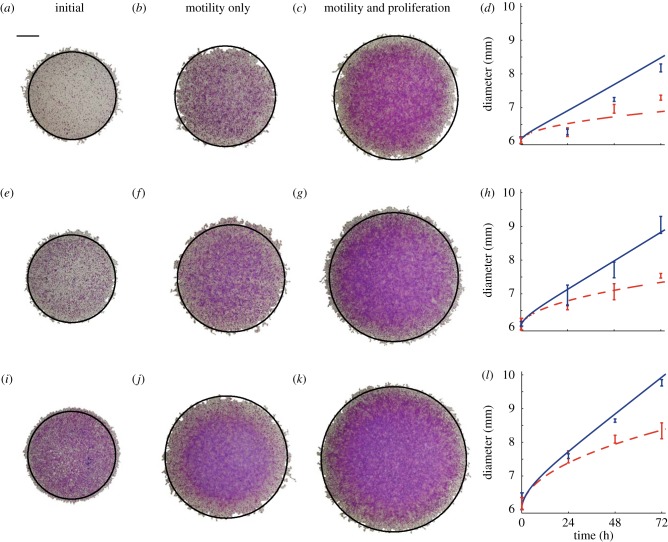
We now test whether our estimates of D and λ lead to accurate predictions of the time evolution of the position of the leading edge of the spreading populations. Experimental images in figure 3 show the distribution of cells at t = 0, and compare the distribution after 72 h both with and without mitomycin-C pretreatment. The extent of the spreading is significantly larger in the proliferative populations. To quantify these differences, we make predictions using equations (3.1) and (3.2) with c₀ chosen to approximate the different initial cell densities. For the experiments with 5000 cells, initially we have c₀ = 5000/45 239 ≈ 0.11; similarly for 10 000 and 30 000 cells initially we have c₀ ≈ 0.22 and c₀ ≈ 0.66, respectively. Using these initial conditions, and our estimates of D, we solved equation (3.2) with λ = 0 to match the experiments where proliferation was suppressed, and we superimpose the c(r, t) = 0.017 contour of the solution at t = 72 h onto the images in the second column in figure 3. For the same initial conditions, we used the previously determined values of D and λ to solve equation (3.2), and the relevant contours are superimposed in the third column of figure 3. A visual comparison of the experimental images and the numerical solutions of equation (3.2) in figure 3 indicates that the modelling prediction of the position of the leading edge accurately captures the observed spreading. The comparison of the modelling and experimental results in figure 3 involved no calibration, indicating that our modelling framework can make reasonably accurate predictions of the experimental observations.

Figure 3.

The position of the leading edge was determined by analysing experimental images for the experiments with (a–d) 5000, (e–h) 10 000 and (i–l) 30 000 cells initially. Images are shown at t = 0 (a,e,i), at t = 72 h for the experiments with mitomycin-C pretreatment (b,f,j) and at t = 72 h for the experiments without mitomycin-C pretreatment (c,g,k). In each image, the c(r,t) = 0.017 contour of the relevant solution of equation (3.1) is superimposed in black (solid) on the spreading population and the scale bar represents 1.5 mm. Results in (d), (h) and (l) show the mean diameter (n = 3) calculated from experimental images at t = 0, 24, 48 and 72 h, with the error bars representing one standard deviation from the mean. The curves in (d), (h) and (l) represent the time evolution of the position of the c(r,t) = 0.017 contour of the relevant solution of equation (3.1). The solid curves correspond to spreading driven by combined motility and proliferation, whereas the dashed curves correspond to spreading by motility only. The numerical solution of equation (3.1) corresponds to δr = 1.0 μm, δt = 0.005 h and ε = 1 × 10⁻⁶. (Online version in colour.)

We analysed the remaining images at t = 0, 24, 48 and 72 h, using the same procedure, to produce equivalent results shown in the fourth column of figure 3. For each experiment, we superimpose the predicted diameter of the spreading population using the c(r, t) = 0.017 contour of the relevant solution of equation (3.2). Comparing the partial differential equation solution with the experimental results illustrates that the modelling framework reliably predicts the observed spreading patterns. The match between the modelling prediction and the experimental measurements improves as the initial numbers of cells increases, which could indicate that our parameter estimates are more reliable for the experiments with larger numbers of cells present.

For all experimental conditions in figure 3, we observe that cell spreading driven by combined motility and proliferation occurs faster than in the equivalent experiment without proliferation. We observe a separation of time scales in the data as the difference between the diameter for the experiments with combined motility and proliferation, and the experiments without proliferation are minimal at relatively short times, t < 24 h. Over longer time scales, the influence of proliferation is more pronounced. For example, with 30 000 cells initially, the diameter of the proliferative spreading population is very similar to the diameter of the non-proliferative spreading population at t = 24 h. Conversely, the diameter of the experiment with proliferation is approximately 1.5 mm larger than the diameter of the equivalent experiment without proliferation after t = 72 h. These differences indicate that cell migration takes place over a relatively short time scale, whereas proliferation takes place over much longer time scales. With our estimates of D and λ, the corresponding ratio P_p/P_m in the discrete model is P_p/P_m ≈ 2 × 10⁻³, indicating that, on average, an isolated uncrowded cell will undergo approximately 500 motility events for each proliferation event. Since 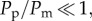the effects of proliferation in the discrete simulations, or equivalent solutions of equation (3.1), will be insignificant over relatively short time scales.

Our estimates of D and λ allow us to predict the long-term front speed for the proliferative populations. Formally, equation (3.1) does not support travelling wave solutions [9,35]. However, the asymptotic result for the Fisher–Kolmogorov equation is approximately valid in an axisymmetric radial geometry for sufficiently large r [9]. For our parameter estimates, the mean front speed predicted by the Fisher–Kolmogorov equation, 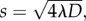is s = 18.3 (16.3–24.6), 19.4 (13.8–22.1) and 26.2 (23.0–31.7) μm h^–1, for the results with 5000, 10 000 and 30 000 cells placed initially in the barrier, respectively. Here, the uncertainty in the prediction of s was estimated using our estimates of the uncertainty in D and λ (see the electronic supplementary material, data). To test this prediction, we fitted a straight line to the mean data in figure 3d,h,l, describing the time evolution of the diameter of the spreading proliferative populations, giving s = 15.7 (15.0–16.5), 20.1 (18.7–21.6) and 23.6 (23.0–24.1) μm h^–1 for the results with 5000, 10 000 and 30 000 cells placed initially in the barrier, respectively. The uncertainty in s was calculated by fitting straight lines to the mean data at t = 0 and the upper and lower bound, defined by the error bars in figure 3d,h,l, at t > 0. Given that our experiments are made over relatively short time scales in an axisymmetric radial geometry, it is remarkable that the Fisher–Kolmogorov prediction is relatively accurate. We also note that front speed measurements can depart from the Fisher–Kolmogorov result owing to the effects of stochastic fluctuations [36,37], which we have not quantified, but could be measured in future experimental investigations.

4.4. Shape of the leading edge

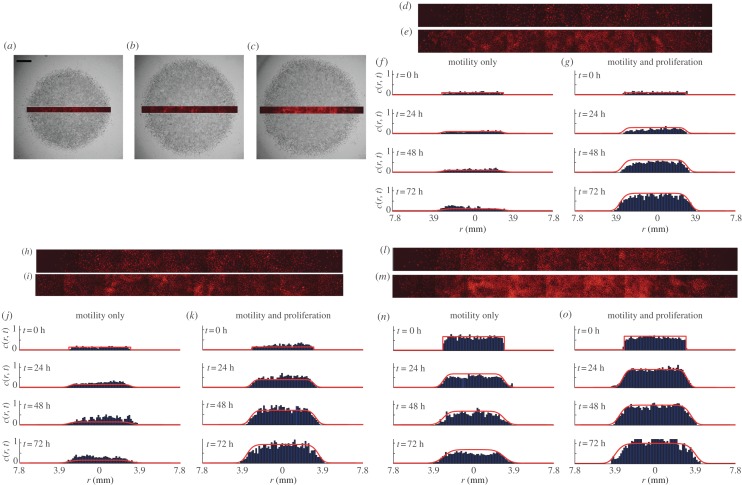
We now present measurements and modelling of the cell density profiles across a transect of the spreading population. Snapshots in figure 4a–c show the population-scale crystal violet-stained images superimposed with a PI-stained transect to illustrate how the transect data correspond to the images in figure 3.

Figure 4.

(a–c) Snapshots of the entire spreading cell population (grey scale) are compared with the corresponding PI-stained transect after 72 h without mitomycin-C pretreatment for experiments with 5000, 10 000 and 30 000 cells initially placed in the barrier, respectively. Images in (d,e), (h,i) and (l,m) show pairs of PI-stained transects after 72 h for experiments with 5000, 10 000 and 30 000 cells, respectively. Images in (d), (h) and (l) correspond to mitomycin-C pretreated experiments, and images in (e), (i) and (m) correspond to experiments without mitomycin-C pretreatment. Histograms in (f,g), (j,k) and (n,o) show the time evolution of the cell density across the transect for the experiments with 5000, 10 000 and 30 000 cells, respectively. Histograms are shown at t = 0, 24, 48 and 72 h, as indicated. The solid curves in (f,g), (j,k) and (n,o) correspond to the relevant solutions of equation (3.1). The initial condition is given by equation (3.2), and results in (f,g), (j,k) and (n,o) correspond to c₀ = 0.11, 0.22 and 0.66, respectively. The numerical solution of equation (3.1) corresponds to δr = 1.0 μm, δt = 0.005 h and ε = 1 × 10⁻⁶. (Online version in colour.)

To quantify the spatial distribution of cells, we divided each transect into 40–60 equidistant sections, each of length 150 μm, along the transect axis. The image analysis software was used to count the number of cells in each section, and this was converted into a non-dimensional cell density, c(r, t), which was used to construct the histograms of cell density in figure 4. The histogram data at t = 0 confirm that the initial cell density is approximately uniform, which supports our previous modelling assumptions. The histogram data in figure 4 for t > 0 allow us to compare the time evolution of the cell density in those experiments where proliferation is suppressed with those where proliferation was present. These data confirm that proliferation has a relatively small influence before t = 24 h, but a far more pronounced effect by t = 72 h. These differences are most obvious in figure 4f,g, for the lowest initial density experiments. Here, we observe that the density profiles for the experiment where proliferation is suppressed remain relatively low for all time, whereas the density profiles for the corresponding proliferative experiments almost reach carrying capacity density after 72 h. The relevant solution of equation (3.2) is superimposed on each histogram in figure 4. These solutions reflect the key differences between the six sets of experiments, thereby confirming that the key features of these experiments can be captured, relatively accurately, by our modelling framework.

The histogram data in figure 4 enable us to compare how the balance of motility and proliferation controls the shape of the leading edge. Previous results in figure 3d indicate that the presence of proliferation in the 5000 cell experiment drives the position of the leading edge approximately 1.5 mm further by t = 72 h than the equivalent experiment where proliferation is suppressed. The histograms in figure 4f,g confirm this and highlight a major difference in the shape of the leading edge. To emphasize the difference in shape, we re-scaled these histogram data, focusing on the details of the shape of the leading edge, over a distance of approximately 1.65 mm, in figure 5a,b. The re-scaled images confirm that cell spreading driven by combined motility and proliferation leads to relatively steep fronts, whereas cell spreading in the absence of proliferation leads to relatively shallow fronts [4]. The relevant solutions of equation (3.2) confirm that the experimental observations are consistent with differences predicted by our modelling framework. Additional results in figure 5c,d and figure 5e,f compare the shape of the leading edge at t = 72 h for the experiments initialized with 10 000 and 30 000 cells, respectively. These results also confirm that proliferative fronts are relatively steep while fronts without proliferation are relatively shallow.

Figure 5.

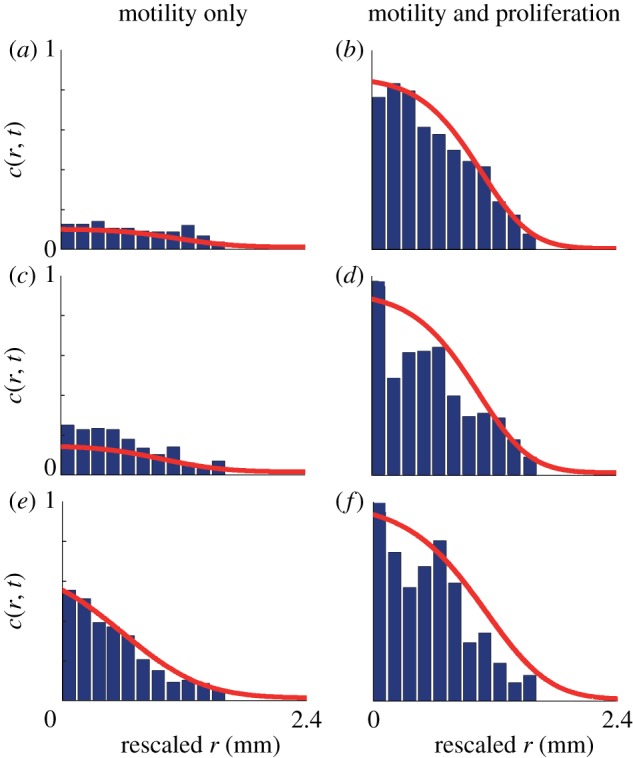
The shape of the leading edge is compared where the spreading is driven by motility alone (a,c,e) and combined motility and proliferation (b,d,f). To facilitate the comparison, in each case we shifted the radial coordinate to compare the density profiles over a distance of approximately 1.65 mm behind the leading edge. The experimental data correspond to a barrier assay with (a,b) 5000, (c,d) 10 000 and (e,f) 30 000 cells placed into the barrier initially. All data correspond to 72 h after the barrier was lifted. The solid curves are the numerical solutions of equation (3.1), with the appropriate parameter values, previously described. The numerical solution of equation (3.1) corresponds to δr = 1.0 μm, δt = 0.005 h and ε = 1 × 10⁻⁶. (Online version in colour.)

5. Discussion

Quantifying the mechanisms driving cell spreading will improve our understanding of several processes, including development [1], repair [2,3] and certain diseases [4]. Previous experimental studies have focused on measuring the front speed [2,3]. One of the limitations of measuring the front speed alone is that there are many choices of D and λ that give the same front speed according to the Fisher–Kolmogorov equation [2,3]. To address this, others have chosen model parameters to ensure that the solution of the model matches the density observations [10,19,20]. Using this kind of parameter-fitting approach alone may not allow for any independent assessment of the predictive capability of the model unless separate experimental measurements are obtained so that the calibrated model can be independently tested. One way to overcome these limitations is to intentionally alter the details of the experiment so that we can separately identify the roles of cell motility and cell proliferation. Here, we use a combination of experimental and modelling techniques to isolate the roles of motility and proliferation in a two-dimensional circular barrier assay. We characterize D and λ separately, and then make independent modelling predictions about other aspects of the experiment.

Our experiments were designed to study the differences between cell spreading-driven combined motility and proliferation, from an equivalent set of experiments where proliferation was suppressed [33]. By quantifying the differences between these experiments, we showed that mitomycin-C pretreatment caused the cell density in the central region of the assay to remain approximately constant over 72 h, whereas equivalent cells in the central region without mitomycin-C pretreatment proliferated significantly over the same time period. Using image analysis software, we showed that cell spreading is enhanced by the presence of cell proliferation.

High-magnification images of transects through the spreading population were used to reconstruct cell density profiles during each experiment. These density profiles confirmed that the proliferative experiments led to faster spreading than when proliferation was suppressed. The cell density profiles showed that the shape of the leading edge can be very different depending on whether or not cell proliferation is present. When proliferation was suppressed, we observed the formation of shallow fronts, whereas proliferative fronts are relatively steep. We also used our parametrized modelling framework to make quantitative predictions of the shape of the leading edge in each experiment and found that our modelling provided reasonable predictions. Understanding the differences between cell spreading with and without proliferation, and confirming that our modelling framework can predict these differences, is important since the shape of the leading edge of a spreading cell population is thought to have important clinical implications [4,22].

Our results highlight the need to consider the role of initial cell numbers since our estimates of D indicate a weak density dependence as we observe D = 1500, 1700 and 2900 μm² h^–1 for the experiments initialized with 5000, 10 000 and 30 000 cells, respectively. From a practical point of view, given that estimates of cell diffusivity in the literature can vary over one or two orders of magnitude [2,3,19,38], our observed variation is relatively small. Nonetheless, we do observe a consistent density-dependent mechanism for which there are several plausible explanations such as the possibility that cells produce a chemical signal (or signals) enhancing migration, or the possibility that cells modify the substrate as they migrate. For both these putative mechanisms, it is reasonable to assume that placing more cells in the barrier initially leads to enhanced migration. Although our current experimental platform was not designed to resolve these details, our results illustrate the importance of repeating barrier assays with different initial numbers of cells so that these effects can be observed and quantified.

The experimental observations reported here are relevant to current theoretical developments, where there has been active debate regarding appropriate techniques to model collective cell motility. Some observations favour models based on linear diffusion, while others favour nonlinear diffusion [2,3,10,19]. Recent theoretical developments have even suggested that it is possible to accurately model the same discrete interacting motility mechanism invoking either a linear or a nonlinear diffusion equation. These differences depend on the details of how the continuum limit is constructed [39].

Our combined modelling and experimental study illustrates how to separately quantify the effects of cell motility and cell proliferation in a barrier assay to help understand how each component contributes to cell spreading. We anticipate that designing more detailed experimental programmes will be necessary when modelling cell spreading involving cell-to-cell adhesion [18,32] or an epithelial-to-mesenchymal transition (EMT) [40]. For both these extensions, we must quantify how the cell motility is affected by cell-to-cell adhesion and how the EMT contributes to the net spreading of the population. Incorporating such details will be the subject of future research.