Context-dependent decision-making: a simple Bayesian model

Abstract

Many phenomena in animal learning can be explained by a context-learning process whereby an animal learns about different patterns of relationship between environmental variables. Differentiating between such environmental regimes or ‘contexts’ allows an animal to rapidly adapt its behaviour when context changes occur. The current work views animals as making sequential inferences about current context identity in a world assumed to be relatively stable but also capable of rapid switches to previously observed or entirely new contexts. We describe a novel decision-making model in which contexts are assumed to follow a Chinese restaurant process with inertia and full Bayesian inference is approximated by a sequential-sampling scheme in which only a single hypothesis about current context is maintained. Actions are selected via Thompson sampling, allowing uncertainty in parameters to drive exploration in a straightforward manner. The model is tested on simple two-alternative choice problems with switching reinforcement schedules and the results compared with rat behavioural data from a number of T-maze studies. The model successfully replicates a number of important behavioural effects: spontaneous recovery, the effect of partial reinforcement on extinction and reversal, the overtraining reversal effect, and serial reversal-learning effects.

1. Introduction

An animal's model of its environment is important for the purposes of prediction and control in pursuit of its goals. That environment may change gradually with time, requiring only minor behavioural adaptation, but may also change abruptly and drastically, requiring rapid and substantial revision of expectations. Insofar as an animal's environment switches between recurring, relatively stable regimes [1,2], it is adaptive for the animal to maintain separate knowledge structures corresponding to each regime in the interests of timely and appropriate behavioural adjustment. We should expect animals to learn about such environmental regimes, identify which is currently active, and adapt quickly to regime shifts by employing appropriate knowledge.

Traditional models of animal learning lack such sophistication, typically representing knowledge as a single set of ‘associations’ between representations of stimuli, responses and rewards which can be strengthened or weakened by various learning rules (see [3] for a recent review). Such simple associationist models may be adequate for gradually changing, single-regime environments but are ill-suited to the recurrent, multi-regime environments more typical of the real world and indeed many experimental settings. We therefore present a more flexible model capable of learning the characteristics of multiple regimes or ‘contexts’ and adapting its behaviour depending on its belief about the currently active context. The model captures multiple behavioural phenomena outwith the scope of more traditional animal learning models.

A simple example of the sort of behavioural sophistication difficult to capture with traditional models is observed in the serial reversal-learning paradigm. Consider a rat required to make repeated choices between left and right arms in a simple T-maze. Initially, only the left arm contains a reward and the rat increases its tendency to choose left over successive trials. If the experimenter now makes the right arm the rewarding option, the rat may initially persist in choosing left but will eventually adapt its choices so that the right arm becomes the majority choice. If the experimenter continues to repeatedly switch the reward arm in this way, the rat becomes quicker to adjust its choices up to the point where a single error trial (i.e. unrewarded choice) becomes sufficient for the rat to completely reverse preference [4–6]. Rather than suggesting a continual process of unlearning and relearning of preferences, the development of rapid behavioural switching is more naturally interpreted as a process in which the rat learns distinct knowledge structures corresponding to the different reinforcement schedules, with the rewards themselves acting as ‘contextual cues’ signalling change points between the different regimes.

In accord with this interpretation, recent modelling approaches have taken the view that animals distinguish between different environmental regimes, or equivalently, latent ‘states’ [7], ‘situations’ [7] or ‘contexts’ [8–10] assumed to underlie their varying experience. The learning problem for the animal is thus viewed in terms of a clustering or categorization process in which the animal makes inferences about the underlying structure of its environment and behaves according to its beliefs about which context is currently active [7–10]. We will use the term ‘switching models’ to refer to these clustering models to reflect their ability to ‘switch’ from assigning observations to one context to another. By contrast, we shall call ‘tracking models’ those which essentially assign all observations to a single latent context by continually updating a single set of parameters over time [11,12].

In this work, we suggest that animals make a number of key assumptions about their environment which reflect the general properties of environmental regimes and which underlie a broad range of behavioural phenomena. Firstly, the persistence assumption is simply the assumption that once a context is active, it tends to persist over time. An implication of this assumption is that animals should weight recent evidence concerning context identity more heavily than older evidence. One behavioural phenomenon that suggests that animals do indeed make this assumption is spontaneous recovery which we discuss in detail in §3.2. Secondly, the switching assumption is the assumption that although contexts generally persist, rapid shifts in context are possible. Animals' ability to rapidly adapt their behaviour to abrupt changes, for example, in reversal learning (§3.4), is consistent with this assumption. Thirdly, the recurrence assumption expresses the expectation that when the world changes, it may be to a state that has previously been experienced. Thus, previous learning may well be relevant when such switches occur (as in serial reversal learning—§3.4). Finally, the generative assumption captures the possibility that the animal may find itself in a novel situation, requiring new learning and behaviour. Previous models tend to express only a subset of these assumptions and so express certain limitations. For example, as an instance of a tracking model, the jump-diffusion model presented by Daw & Courville [11] does not allow for context recurrence and so fails to take advantage of previous learning. By contrast, the switching model of Gershman et al. [10] expresses the recurrence assumption but not the persistence assumption and so fails to capture animals' sensitivity to the temporal ordering of experience.

We therefore present a novel sampling-based Bayesian decision-making model which essentially combines the Daw & Courville [11] and Gershman et al. [10] models, thereby integrating all of the context assumptions in a simple way. Indeed, these previous models are either special cases of the model presented here [10] or very close to being a special case [11]. In turn, the current model can be derived as a limiting case of more complex hidden Markov models (HMMs) [13,14]. Additionally, by explicitly modelling action selection we move beyond classical conditioning to consider experimental findings from more complex decision-making scenarios in which an animal's observations depend on its choices. Focusing primarily on experimental results from the study of rats in simple two-alternative choice tasks, we test our model's ability to replicate a number of key behavioural phenomena. We show that the model successfully captures general features of spontaneous recovery, the effects of partial reinforcement and overtraining on reversal, and the development of rapid switching in serial reversal learning. Furthermore, we highlight some novel predictions of the model, e.g. in the multi-arm bandit setting, which differentiates it from accounts based on abstract behavioural strategies such as win–stay lose–shift (WSLS).

2. Model

We model two-alternative choice tasks in which the animal selects one of two actions on each trial and receives a reward which depends on the current reinforcement schedule. The model can be thought of as consisting of a number of distinct components (cf. [8,10]). The first component describes beliefs imputed to the animal about the general nature of its environment prior to its making any observations (the generative model). The second component describes assumptions about how the animal changes its beliefs over time in response to observations (the inference model). The third and final component describes assumptions about how the animal makes choices on the basis of its beliefs (the choice model). We outline each in turn.

2.1. Generative model

It is assumed that on each trial t there is an active reinforcement schedule or context c_t that specifies the rewards expected on performing each action a. Context is assumed to evolve according to a jump process such that on each trial there is some small probability π that the context switches, either to a previously seen or novel context. Conversely, with probability 1−π the context is assumed to remain the same as on the previous trial, i.e. c_t = c_t−1. These assumptions capture the persistence and switching properties since, once active, a context is assumed likely to be stable over multiple trials (persistence) though occasional jumps to different contexts are expected (switching). Specifically, it is assumed that context evolves according to the distribution

2.1

where CRP(c_{1 : t−1};α) denotes the mass function that would arise on context c_t if it were the case that context sequence c_{1 : t} were drawn from a Chinese restaurant process (CRP) [15,16].¹ We take concentration parameter α such that the prior conditional probability of a new context is α/(t−1+α) and the prior conditional probability of a previously seen context is n_c/(t−1 + α), where n_c is the number of observations previously attributed to context c. Thus, both recurrence and generative properties are expressed since the recurrence of previous contexts and the proposal of new contexts is permitted. In addition, the CRP implements a ‘rich gets richer’ property in which switches to contexts more frequent in the past have higher prior probability, encouraging context recurrence. The CRP is an inevitable consequence of the Dirichlet process mixture model (DPMM) [17] but here is only a component of the generative model; our model differs from the standard DPMM (and hence from [10]) in introducing the jump probability π. The effect is similar to the persistence assumptions in [13,14].

Within a context c, the distribution of action-specific rewards are summarized by parameters θ^c,a, which parametrize a simple conjugate Bayesian model (details in appendix A).

2.2. Inference model

Given the assumed generative model, the animal would like to learn the characteristics of each context and be able to identify which is currently active in order to make sensible decisions. To this end, we assume that animals aim to approximate the solution given by full Bayesian inference. We here outline a model of how animals perform this approximate inference.

While standard Bayesian calculations (appendix A) tell us how to sequentially update parameters based on the allocations of observations to contexts, we need a way of deciding how rewards are assigned in the first place. The full Bayesian solution to inferring the sequence of contexts c_{1 : t} underlying observation sequence of rewards r_{1 : t} involves the calculation of the posterior distribution p(c_{1 : t}|r_{1 : t}) over all possible context sequences of length t. Unfortunately, owing to the number of possible context sequences increasing exponentially with t, this calculation is computationally intractable and approximate inference is required. Following previous psychological models [10,11,19,20], we assume a sample-based approximation in which contexts are sequentially sampled on a trial-by-trial basis (i.e. sequential Monte Carlo; see [21] for an overview). Sampling approximations have proved to be popular in psychological modelling as they provide a way of interpolating between exact inference (in the limit, when the number of samples is infinite) and more psychologically realistic inference under limited resources (i.e. limited samples). Indeed, we take the extreme one-sample case which has previously been employed to model instabilities in individual learning curves [11] and sequential effects in category learning [19,20].

The inference process that the animal is assumed to go through in considering context identity on each trial consists of two steps. Firstly, the animal considers whether, given the observed reward, the context has ‘jumped’ (c_t ≠ c_t−1) or not (c_t = c_t−1). Secondly, the animal needs to update its beliefs about the identity of the current context.

We introduce indicator variable 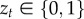to denote a jump (z_t = 1) or no jump (z_t = 0) on the current trial. Denoting by θ₀ the prior parameters of an unobserved context, and the estimated parameters of the reward distribution of action a in context c at time t, the posterior probabilities of these respective events having occured given the observed reward on the current trial r_t and previous rewards r_{1 : t−1}, contexts c_{1 : t−1} and actions a_{1 : t} are given by

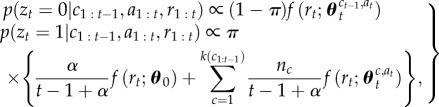2.2

where f(·) denotes the likelihood of the observed reward r_t given the action taken a_t and assumed context c, 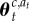denotes the associated current parameter estimates of the reward distribution, k(·) is a function that returns the number of distinct contexts in a context sequence (i.e. the number of occupied tables in the CRP) and n_c is the number of observations attributed to context c (i.e. the number of customers sitting at their designated table in the CRP). Calculation of the likelihood terms again proceeds by routine Bayesian calculation involving marginalizing out uncertainty in estimated mean and variance (appendix A, (A 7)). Drawing a sample from the distribution specified in (2.2) determines whether the animal believes that the context has jumped (z_t = 1) or remains the same (z_t = 0).

If it is decided that the context has changed, a decision needs to be made about the identity of the new context to which the current reward r_t should be assigned. This decision is resolved by using a standard CRP decision as to which context to sample

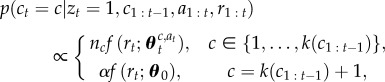2.3

where k(c_{1 : t−1}) is the number of contexts previously proposed.

2.3. Choice model

Most previous models of context learning have no choice model, either because they are focused on classical conditioning [10] or presumably as a simplifying step [9]. Exceptions are the models in [7,22] which simply assume a softmax/logit-response model. Focusing on scenarios where observations do not depend on the animal's actions, or simply avoiding the question of how actions are selected, is understandable given the difficult issue of what the choice model should be. Optimal solutions for allocating choices are unavailable for all but the simplest problems, leading to a variety of heuristic approaches (see [23] for a recent review). A popular choice of heuristic in many reinforcement learning models, as in [7,22], is the softmax function where the probability of choosing an action is a function of the predicted rewards of all available actions and an additional ‘exploration’ parameter that controls the amount of noise in the selection process. Problems with this method, in our view, include the question of how to set the exploration parameter without knowing the scale of the rewards in advance, and the fact that the point estimates for each action are all treated in the same way, despite the fact that the decision-maker has higher confidence in some of these estimates than others. In particular, it is usually more valuable in the long term to explore an action about which the decision-maker has little information than an action that has been selected many times already. A more principled approach to action selection involves tracking uncertainty in parameters and taking decisions based on hypotheses about true parameter values (cf. [24]). We therefore employ a choice scheme known as Thompson sampling [25] in which actions are selected on the basis of sampling values from probability distributions. Not only does this method take into account uncertainty about true parameter values, but also it is simple (e.g. there are no parameters to be tuned), and has been shown to perform well in computational experiments [26–28].

Under Thompson sampling, the decision-maker samples a value for each action from the posterior distribution for that action, then selects the action with the highest sampled value. This corresponds to selecting an action with the probability that it is the best action given the information so far. We note that under this scheme, if the uncertainty in the value of an (suboptimal) action increases, then the probability of selecting it also increases.

Implementing Thompson sampling within the model of this paper is straightforward. Since the reward r_t observed on the current trial is contingent on the action a_t taken, actions must be chosen on the basis of the belief about current context before observing evidence. Note that this is one practical reason for including persistence in the generative model. In particular, persistence ensures that with high probability the action selected at time t is informed by the context at time t – 1. Without persistence, as in the model of Gershman et al. [10], the action will depend not only on the current context but also on all previous contexts. The choice procedure at time t therefore proceeds as follows:

• — sample a context 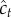according to the generative model (equation (2.1));

• — for each action 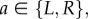sample a value 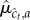from the corresponding posterior marginal 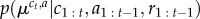(see appendix A); and

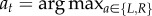
• — select 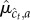to maximize the sampled value.

The full decision-making process is summarized graphically in figure 1.

Figure 1.

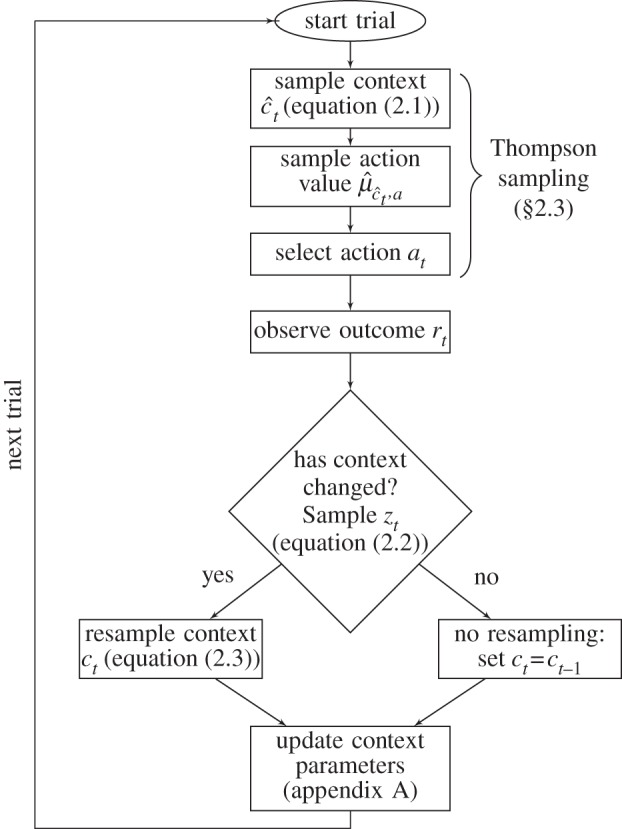
Steps of the model.

3. Results

A large amount of discrete-trial data has been gathered by psychologists studying rats in simple choice problems. We compare the behaviour of our model with rat data from T-maze experiments where choice of the different arms (left or right) result in different probabilities and/or magnitudes of reward. The data of interest are the distributions of responses between alternatives over time. Since only average choices tend to be reported in this literature, comparisons are made with model average behaviour (i.e. averages over multiple simulation runs). Rather than seeking exact quantitative fits to individual data sets, we concentrate on qualitative trends. In all simulations, we set the prior jump probability to π = 0.075 and the concentration parameter of the CRP to α = 1. Prior parameters involved in estimating the reward distributions are set to generic values and fixed across experiments (see appendix A).

3.1. Basic effects: magnitude and probability of reward

When choosing between two alternatives delivering rewards of different magnitude, animals converge to exclusive choice of the more favourable alternative. Furthermore, larger differences in magnitude lead to faster convergence (e.g. fig. 1 of [29]; also [30–32]). Similarly, if two alternatives deliver rewards with the same magnitude but with different probabilities, animals come to choose the alternative with the higher probability of reward at levels in excess of that reward probability, though generally not to the level of exclusive choice (e.g. data in [33]; see [34] for review). Again, larger differences between alternatives, this time in probability, lead to preferences developing at a faster rate [4,31].

Reproducing these behavioural patterns is a basic requirement of a model of animal decision-making and our model shows the correct trends (figure 2). As an interesting aside, the reason why exclusive choice is not seen in the model's average learning curve with probabilistic rewards (figure 2b), even for larger numbers of trials (as is the case in the 60 : 40 condition), is due to averaging over qualitatively different behaviours (not shown). While most simulation runs lead to complete absorption on the more rewarding option, some get ‘stuck’ in exclusive choice of the less rewarding arm. Other simulation runs partition trials into distinct contexts leading to behaviour more like probability matching. Such heterogeneity of choice patterns is consistent with experimental findings. Individual rats sometimes get stuck on the worse option [33], and varying choice patterns presumably helped prolong the debate regarding whether rats ‘match’ or ‘maximize’ in simple choice tasks (see [34] for review).

Figure 2.

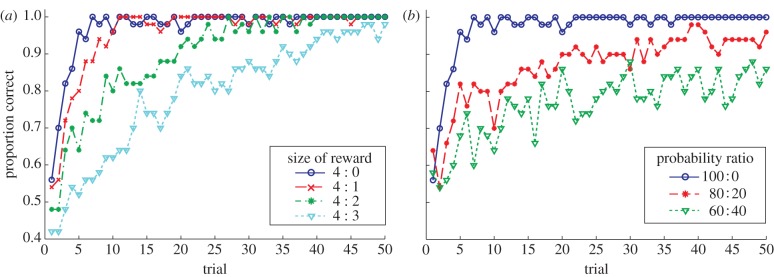
Basic effects of reward magnitude and probability on choice. Alternatives were rewarded with different magnitudes or probabilities over the course of 50 trials as indicated. (a) The alternative with the greater magnitude of reward is exclusively preferred and larger differences in magnitude lead to faster convergence. (b) The alternative with the greater probability of reward is favoured at levels above probability matching and larger differences in probability lead to faster learning (reward r = 4 for both options). Learning curves are averages over 50 simulation runs. (Online version in colour.)

3.2. Spontaneous recovery

Spontaneous recovery was first reported by Pavlov [35] in the context of classical conditioning ([36] provides a recent review). In an acquisition phase, the animal learns to perform a conditioned response (CR) following presentation of a conditioned stimulus (CS). A period of extinction follows during which the CR is no longer an appropriate response to the CS, and the animal ceases to perform the CR. If the animal is subsequently presented with the CS after a time delay, the level of CR depends on the length of the delay: with short delays, performance of the CR is minimal; as the delay is increased, the level of CR increases in a negatively accelerating fashion, though never to the level observed during acquisition [36].

We suggest that this phenomenon results from the animal's assumption that contexts are relatively stable over time. In particular, without evidence otherwise, the animal assumes that the extinction context remains active at short time delays, hence the absence of responding. However, with increasing time since extinction the animal is increasingly uncertain whether a change in context has occured. The CS therefore becomes an increasingly ambiguous cue as to whether the animal is in the acquisition context, extinction context, or possibly some other context (cf. [37]). We attribute the partial recovery of conditioned responding with time to this increasing uncertainty.

Spontaneous recovery has also been observed in instrumentally conditioned responses [38] and in choice settings [39]. To demonstrate the basic effect in our model, we present 50 trials on a 100 : 0 reinforcement schedule in which left is continuously rewarded (‘context A’) followed by 50 trials on the reversed 0 : 100 reinforcement schedule in which right is continuously rewarded (‘context B’). To test for spontaneous recovery, we probe the model's choice of action on a single trial at differing delays following the last trial of context B. Delays are modelled as a series of ‘dummy trials’ in which contexts are sampled sequentially from the generative model (equation (2.1)) with the number of samples corresponding to length of delay. For the model to behave in a way consistent with spontaneous recovery, left choices should be essentially non-existent for short delays but should increase with longer delays in a negatively accelerating fashion to some proportion. This is what is observed (figure 3).

Figure 3.

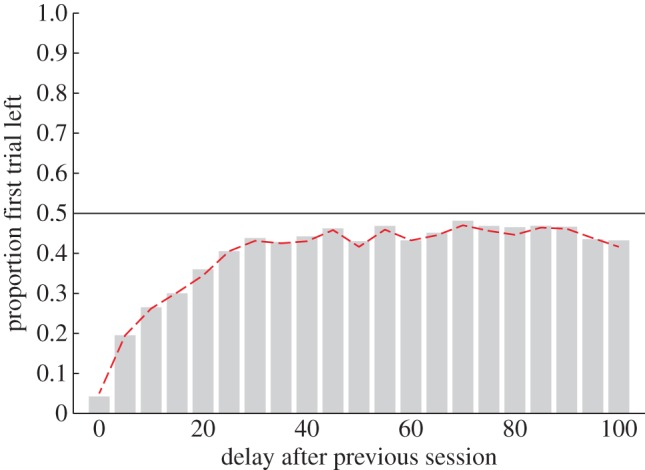
Spontaneous recovery. Bars show the proportion of simulation runs (runs = 1000) choosing the left arm on a single test trial as a function of delay (number of sequential samples from the generative model) between the end of initial training and the test trial. Training consisted of 50 trials under a 100 : 0 reinforcement schedule (left arm always rewarded; ‘context A’) followed by 50 trials under the reversed 0 : 100 schedule (right arm always rewarded; ‘context B’), with reward r = 4. Also shown is the proportion of simulation runs sampling ‘context A’ on the test trial (dashed line). (Online version in colour.)

In the model, the result arises as a natural consequence of the assumption of persistence. Initially, context B is likely to continue to be sampled due to the low prior probability π of context switching, reflected in the model continuing to favour choosing right. With further sampling, the probability of sampling a jump in context increases and so the hypothesized context is likely to ‘drift’ with time. Furthermore, the ‘rich gets richer’ property of the CRP (equation (2.3)) means that drift is more likely to be to a previously seen context (context A) than to a completely new context (figure 3, dashed line). However, in the absence of evidence, context A will not be consistently sampled, explaining why recovery is never complete. Spontaneous recovery will play a role in our consideration of serial reversal learning (§3.4).

3.3. Reversal learning

In a reversal-learning experiment, the experimenter tests an animal's ability to adapt its behaviour when the initial reinforcement schedule is reversed. For example, in the T-maze, only the left arm may initially be rewarded before switching to exclusively reward choices of the right arm. Conditioning-extinction theory traditionally assumes that adaptation of behaviour in such a scenario involves the unlearning of an initial ‘habit’ (stimulus-response association) and its gradual replacement with the reversed habit (see [40] for summary). However, reversal-learning experiments revealed a number of phenomena that are ‘paradoxical’ on such a view. These phenomena, considered next, no longer appear paradoxical when a mechanism for context-specific learning and choice is assumed.

3.3.1. Partial reinforcement effects

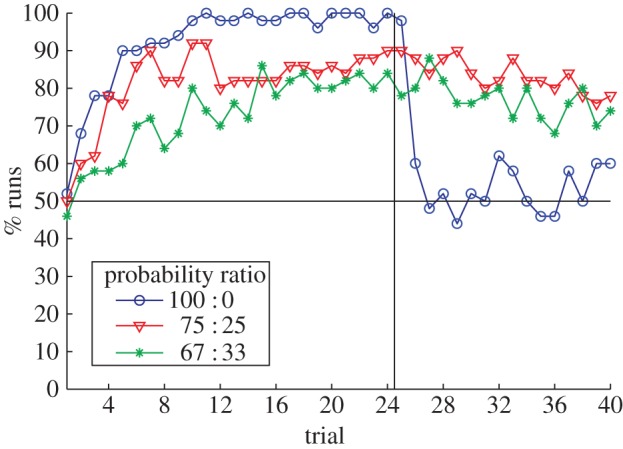
Decreasing the difference in reward probability between two choices slows not only the rate at which preference develops but also the rate of adapting choices to a subsequent reversed schedule [34,41,42]. This effect troubled the conditioning-extinction account since, on that account, partial reinforcement leads to weaker learned responses. If reversal involves unlearning of the initial response, partial reinforcement should lead to faster reversal learning, not slower. An example of the effect is seen in Brunswik's [4] classic study exploring the effect of probabilistic reinforcement schedules. Brunswik found that rats only reversed their initial preference in the case of continuous (100 : 0) rewards when run on a T-maze with different reinforcement ratios (figure 4a).

Figure 4.

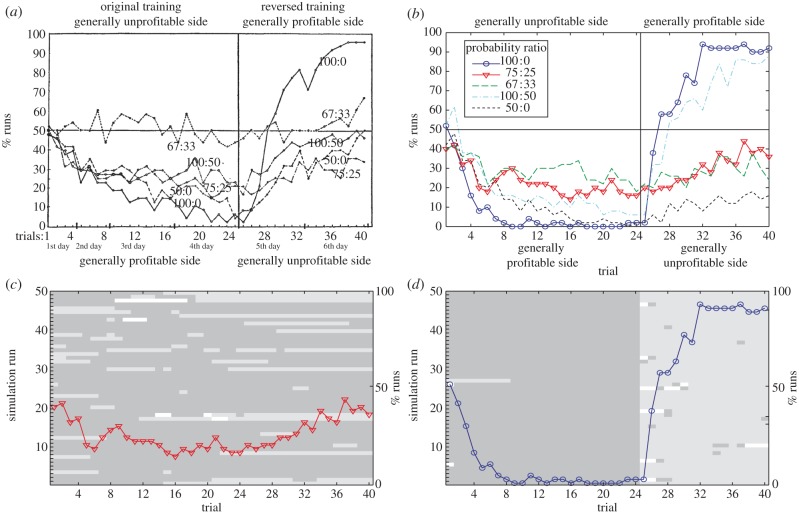
(a) Brunswik's rat data (adapted from [4]). The choices of different experimental groups (48 rats in each) in a T-maze were rewarded according to various probability ratios (100 : 0, 50 : 0, 75 : 25, 100 : 50 and 67 : 33). The reinforcement schedules were reversed after 24 trials. (b) As with Brunswik's rats, the model quickly reverses its preference of arm following reinforcement schedule reversal for the 100 : 0 case, but only slowly modulates its choice in the 75 : 25 case. The difference in behaviour arises due a tendency to assign most observations in the 75 : 25 case to a single context (c), while in the 100 : 0 case two distinct contexts are correctly inferred (d). Learning curves are averages over 50 simulation runs. In figures c,d, for each of the 50 simulation runs, we look at the sequence of contexts to which observations are assigned. Thus, for each simulation run, there is a horizontal line of small rectangles which indicates the context to which the observation on the current trial is assigned on that particular simulation run. The identity of the context is indicated by the greyscale value of the rectangles so that differences in greyscale denote assignments of observations to distinct contexts. In the 75 : 25 case, observations are either assigned to a single context, as indicated by a line with no change in greyscale, or are assigned to distinct contexts in an irregular fashion as indicated by the irregular pattern of changes in greyscale. By contrast, in the 100 : 0 case, there is a clear switch in context assignment after trial 24, when the reinforcement schedule is switched. This is reflected by the systematic change in greyscale for each simulation at this point. Reward r = 4 for all simulations. (Online version in colour.)

The results of our own version of Brunswik's experiment capture the main effect: preference reverses in the deterministic case, while it generally fails to reverse under partial reinforcement (figure 4b). Model behaviour does deviate from Brunswik's particular results in some instances. Most strikingly, the rats apparently failed to develop a preference in the 67 : 33 condition. This finding of Brunswik is somewhat surprising considering that the rat can expect to be rewarded 16 times for choice of the more favourable arm over the first 24 trials in the 67 : 33 condition, compared with 18 times in the 75 : 25 condition in which a preference does develop—a difference of only two rewards. The model also clearly reverses preference in the 100 : 50 condition and develops initial preference in the 100 : 0 condition at a faster rate than the rats. These discrepancies are trivially diminished by allowing parameters to vary between different conditions but not if we restrict ourselves to a single set of parameters for all conditions. The aim of the current work is not to fit a single data set perfectly—rats are undoubtedly more complex than our model—but such discrepancies potentially indicate where the model might be extended. For example, rats have a natural propensity to spontaneously alternate choices [43,44], a tendency not modelled here and which is relevant to the rate at which preferences develop and indeed whether a clear preference develops at all. We leave these finer points for future work.

To illustrate how the model captures the main trend, consider the difference in model behaviour under the 100 : 0 and 75 : 25 conditions. The absence of preference reversal in the 75 : 25 condition is due to a tendency to assign observed rewards to a single context, or to more than one context in a way that varies across simulation runs (figure 4c). By assigning rewards to a single context, the context's parameters are ‘relearned’, much as conditioning-extinction theory envisaged, but the process is not fast enough to lead to preference reversal. In the 100 : 0 case, observations from the two schedules are reliably assigned to distinct contexts (figure 4d). When the model samples a second context, learning starts with a new set of parameters leading to a rapid reversion to indifference between choices and ultimately to a clear preference reversal.

To understand why the model assigns observations to one or two contexts, one needs to consider the probabilities of the model inferring a change in context when the reinforcement schedule is reversed. The probability of sampling ‘no jump’ is proportional to the prior probability of no jump (a constant close to 1) multiplied by the likelihood of the current observation under the current context. In the 100 : 0 case, confidence in parameter estimates is high because of the consistency of reward outcomes. Thus, the sudden absence of reward when the schedule reverses has a very small likelihood (almost 0) under the current context, increasing the probability of sampling a jump in context. Conversely, in the partial reward case estimates are more uncertain. Thus, when reversal takes place the observed rewards may not be sufficiently unlikely under the current context to cause resampling of context. In other words, the difference in behaviour in the two cases is explained by the greater difficulty of discriminating pre- and post-reversal schedules in the partial reward condition.

This effect of partial reinforcement on reversal learning is closely related to the well-known partial reinforcement extinction effect (PREE; see [45] and references therein). The PREE traditionally describes an effect whereby partial reinforcement leads to slower extinction of a classically or instrumentally conditioned response than does continuous reinforcement. Again, conditioning-extinction theory predicts exactly the opposite. In the choice setting, an analogous effect can be demonstrated by rewarding the two options with different probabilities and subsequently withholding reward completely. As with rats tested under this procedure [46], the rate at which model choices regress to indifference between options is faster for continuous rewards (100 : 0) than for partial rewards (figure 5). The explanation for this effect in the model is the same as for the reversal case.

Figure 5.

PREE. For the first 24 trials, the two choice options have different probabilities of reward (100 : 0, 75 : 25 or 67 : 33) before rewards for both options are set to zero. The rate of regression towards indifference between options during extinction is greater in the continuous reward (100 : 0) condition than in the partial reward conditions (75 : 25 and 67 : 33). (Online version in colour.)

3.3.2. The overtraining reversal effect

Another of the paradoxical effects is the overtraining reversal effect (ORE), the observation that increasing the amount of training on an initial reinforcement schedule can increase the speed of learning a subsequent reversal [47]. For the same reason that partial reinforcement effects seemed paradoxical for traditional theories, the ORE was problematic for a view which suggested that reversal requires unlearning of an acquired habit: if overtraining leads to strengthening of a habit, this should slow acquisition of the reversed habit.

In fact, experiments following Reid's initial demonstration presented a more complex picture (see [34] for review). While some learning studies replicated the ORE [48], others found no effect of overtraining on reversal [49] and some found that overtraining did indeed slow reversal [50]. Such mixed results highlighted the critical dependence of the ORE on factors such as the size of reward and criterion of learning [51]. For example, one study involving a series of T-maze experiments found that overtraining with large rewards produced ORE while overtraining with small rewards could slow reversal [52].

The model produces behaviour consistent with all of these results since it produces different reversal outcomes as the reward size and amount of initial training on a deterministic (100 : 0) reinforcement schedule is varied (figure 6). For a relatively large reward, the number of trials to reach criterion performance in the reversed schedule is a monotonically decreasing function of the amount of training on the initial schedule (figure 6a). In contrast, for a smaller reward the number of reversal trials to criterion varies non-monotonically with the amount of training on the initial schedule: the number of reversal trials required may be larger, equal, or smaller than the number of initial training trials (figure 6b).

Figure 6.

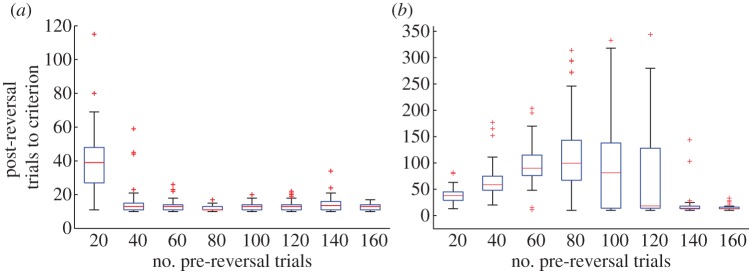
ORE. (a) Large reward (r = 1.5). Increasing the number of pre-reversal trials leads to a monotonic decrease in the number of post-reversal trials required to reach criterion. (b) Small reward (r = 0.75). Number of post-reversal trials to criterion varies non-monotonically with number of pre-reversal trials. Initially, the number of post-reversal trials required increases, but eventually the amount of pre-reversal training (≈140 trials) is sufficient to produce the ORE. Fifty simulations were run for each condition. The criterion for having learned the reversed task was at least 10 rewarded responses in the previous 12 responses. (Online version in colour.)

As with the effect of varying reward probability on reversal training, these various effects are crucially dependent on the likelihood of inferring a change in context when reversal occurs. This in turn depends on the confidence in parameter estimates at reversal. Consider first the small reward case (figure 6b) and assume that all pre-reversal observations have been assigned to ‘context A’. If the animal has only made a small number of observations before the schedule is reversed, its estimates of context A parameters may still be quite uncertain. Thus, when observations from the reversed schedule begin to be observed, the probability that they were generated by context A may not be judged sufficiently low that a change of context is inferred. In this case, the animal continues to assign observations to context A and eventually learns to reverse its behavioural preferences, but has done so by essentially ‘unlearning’ its initial preference. Thus, when all observations are assigned to a single context, greater amounts of initial training on the pre-reversal schedule lead to slower adaptation during the post-reversal phase, just as conditioning-extinction theory suggests. This explains why the number of trials to criterion initially increases for the small reward case (figure 6b, 20–60 pre-reversal trials). However, increasing the number of pre-reversal observations leads to greater confidence in parameter estimates for context A so that at some point, post-reversal observations are judged very unlikely to have been generated by context A, causing a switch in context and rapid adaptation to the new schedule (figure 6b, 140–160 pre-reversal trials). The large increase in the spread of number of post-reversal trials to criterion over the intervening training range (figure 6b, 80–120 pre-reversal trials) is due to the algorithm exhibiting a mixture of these two behaviours in this range: in some cases, the algorithm assigns all observations to a single context; in other cases, the appropriate switch in context is made. In the large reward case (figure 6a), the pattern is monotonic since even a relatively small amount of pre-reversal training is sufficient to render post-reversal observations highly improbable under the initial context.

3.4. Serial reversal learning

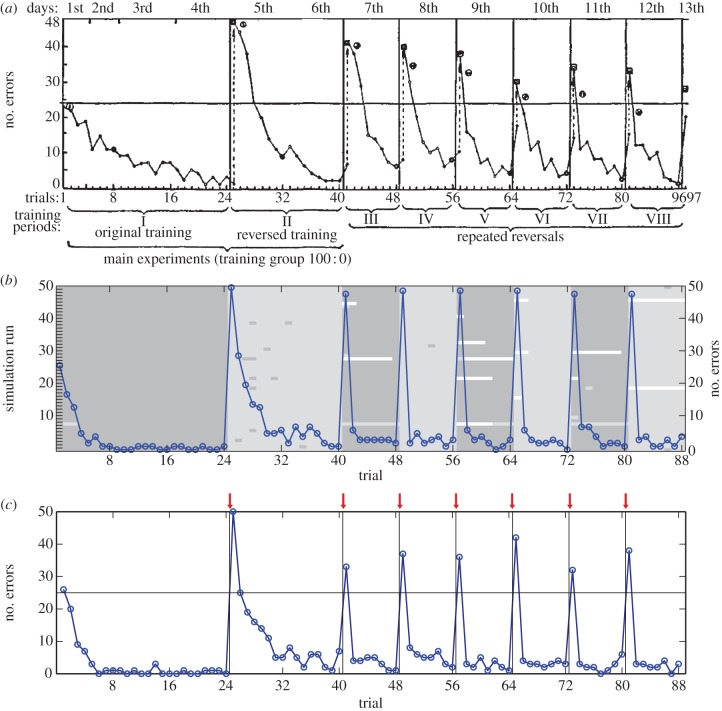
It is well known that if reinforcement contingencies are repeatedly reversed, performance progressively improves so that a single error trial at the beginning of each reversal may be sufficient for an animal to completely switch its preference to the alternative option [4–6]. A particular example, again from Brunswik [4], is reproduced in figure 7a. As previously mentioned (§1), these results are difficult to explain in terms of successive acquisitions and extinctions of choice response. A more promising explanation is that animals correctly learn that there are two reinforcement schedules or contexts involved in the task and, through progressively learning about the characteristics of each context, become increasingly reliable in their inferences about which context is currently active (cf. [9]).

Figure 7.

Serial reversal learning. (a) Brunswik's serial reversal-learning data (adapted from [4]): total number of errors (i.e. choices of the unrewarded arm) per trial for 48 rats with repeated reversal of the 100 : 0 reinforcement schedule. (b) Total number of errors for 50 simulation runs on the serial reversal-learning task. Rewards observed under the reversed and non-reversed reinforcement schedule tend to be assigned to distinct clusters in each individual run, as indicated by shading. (c) Total number of errors for 50 simulation runs on the serial reversal-learning task with the addition of temporal delays (generative model samples = 10) between reversals (as indicated by vertical black lines and arrows above graph). (Online version in colour.)

The principal trend is naturally captured by the model: the first trial of each successive reversal quickly becomes sufficient to strongly reverse preference by signalling a switch to the other context (figure 7b). Again, detailed comparison with Brunswik's [4] data does highlight certain differences, however. Firstly, the development of rapid preference switching is slower in the rats than in the model. Secondly, the rats show a progressive decrease in the number of errors on the first trial of each reversal, a phenomenon replicated in other experiments [34]. This latter trend contrasts with the relatively constant first trial error rate in the model. The possibility that this reflects the rats learning to anticipate reversals has not been supported by experiments since the probability of a first trial error has apparently never been observed to drop consistently below chance [34]. Rather, the evidence suggests that this effect arises from spontaneous recovery of the extinguished response, leading to ‘proactive interference’ between successive reversals [53]. Indeed, in most serial reversal-learning experiments such as that of Brunswik (figure 7a), reversals of reinforcement schedule tend to occur between successive days of testing. The apparent forgetting manifest in the rats' behaviour with such temporal delays between experimental sessions is therefore consistent with spontaneous recovery of the response less favoured in the most recent experimental session. Simulating temporal delays as before (§3.2) between successive reversals leads to a better match to the animal data (figure 7c) though it does not by itself capture the trend for forgetting to only gradually increase, a trend outwith the scope of the current model. Such an effect could conceivably be captured by adapting the value of the context-switch parameter π, but learning the generative model in response to experience is not addressed in this paper. Note that there is no spontaneous recovery effect following the first delay in the model since all observations have hitherto been assigned to a single context.

4. Discussion

The premise of the current work was that animals should show learning and behaviour suited to an environment in which rapid switches can occur between recurring, relatively stable behavioural regimes or contexts. We considered a number of behavioural effects consistent with animals learning the characteristics of different contexts and rapidly adjusting their behaviour to context change. Following previous work [7–10], we took a latent variable approach to modelling such capabilities, viewing the animal as categorizing its experience into a sequence of discrete underlying contexts. Furthermore, we argued that models of context learning should include a number of properties—persistence, switching, recurrence and generativity—to account for the behavioural data. The principal contributions of the current work are as follows. Firstly, we present a simple Bayesian model that integrates all of the identified context properties, not just a subset. Secondly, by incorporating a choice model, we begin to address more complex decision-making scenarios than generally tackled in previous models. Thirdly, we demonstrated the ability of the resulting model to account for a number of important choice effects, namely spontaneous recovery, the effects of partial reinforcement and overtraining on reversal learning, the PREE and serial reversal-learning effects.

4.1. Related work

The current work borrows explicity from two previous models. Firstly, our model borrows from Daw & Courville [11] both the idea of modelling the environment as a jump process and the use of single-sample approximate inference. However, Daw & Courville [11] target different behavioural phenomena than those addressed here and define a generative model over a single set of parameters rather than over distinct contexts. Their model therefore fails to take advantage of previous learning in a way that allows the development of rapid behavioural switching such as in serial reversal learning. We note that the Daw–Courville model is close to being a limiting case of the current model as α → ∞ (i.e. propose a new context whenever a jump is assumed to occur) though within-context drift would need to be added to the current model for this limiting case to be equivalent.

Secondly, our model borrows from Gershman et al. [10] an approach that allows online inference over a potentially unbounded number of contexts. However, their application of the standard DPMM to certain classical conditioning phenomena assumes a context prior that is a function of the frequency with which a context has previously occured but not the recency of its being active. In other words, Gershman et al. [10] assume that the ordering of trials is irrelevant to inferring context identity and so fail to make the persistence assumption. We have already noted (§2.3) that some form of persistence is necessary to ensure that actions are selected appropriately given recent observations. Furthermore, we addressed a particular behavioural phenomenon that suggests the inappropriateness of such insensitivity to time—spontaneous recovery (§3.2; cf. [10], p. 207). More sophisticated forms of the DPMM [54,55] can incorporate persistence but our explorations with such models suggest that they lead to difficulties with other desired context properties such as recurrence. The standard DPMM used by Gershman et al. can be recovered from the current model by setting π = 1 (i.e. a jump is assumed to occur on each trial).

A number of models similar in spirit but less directly related to the current work include those of Redish et al. [7], Fuhs & Touretzky [9], Dayan & Yu [8], Collins & Koechlin [22] and Haruno et al. [56]. The model in [7] appears to incorporate all of the assumptions that we specify but not necessarily, we argue, in the right way. For example, the persistence assumption is incorporated by selecting actions on the basis of the inferred identity of the immediately preceding context. This is actually too strong an assumption since it implies that, in the absence of evidence otherwise, an animal assumes a particular context to persist indefinitely. Again, the phenomenon of spontaneous recovery suggests that animals are more sophisticated than this. The model of Fuhs & Touretzky [9] addresses some of the same phenomena as the current work and expresses similar properties, though their batch inference scheme would be so computationally expensive in practice that we regard it as being essentially non-generative. The HMM of Dayan & Yu [8] enforces persistence between a series of contexts but assumes the number of contexts to be known as is also the case in [56]. A very recent model more complex than our own but sharing many of the same intuitions has recently been presented in [22].

The current model also has a strong relationship with Bayesian nonparametric approaches to HMMs [13,14]. Indeed, the current model is a simplifed, special case of the infinite HMM (iHMM) presented by Beal et al. [13] when certain parameters are sent to infinity meaning that transition rates are not counted and only state occupancy rates are relevant. Fox et al. [14] have modified the hierarchical Dirichlet process HMM [57] to reintroduce inertia and generalize the iHMM. Given that the current model interpolates between a number of simpler models [10,11] which have been applied to animal-learning phenomena and more complex models [13,14] which to the best of our knowledge have not, a natural direction for future research is to further probe the ability of animals to take advantage of temporal structure in their environments with an eye to further constraining the class of adequate models.

We finally note that of these related models, only Redish et al. [7] and Collins & Koechlin [22] have explicit choice models, standard softmax selection in both cases. Considering explicitly how actions are selected is a crucial step in addressing true decision-making problems in which observations depend on choices. The choice model of the current model, based on Thompson sampling, provides a simple and more principled approach to action selection.

4.2. Differential retrieval and discriminability

The assumptions embodied in our model in combination with its ability to capture a variety of learning effects naturally entail that we favour some explanations of these effects over others. Spontaneous recovery was explained by a process of ‘contextual drift’ in which repeated sampling of the most recent context due to the persistence assumption gradually allows for sampling of previous, more temporally distant contexts with time. This is concordant with ‘differential retrieval’ explanations [36] in which spontaneous recovery is taken to reflect differential retrieval of experience over time [58,59]. We note that the idea of contextual drift invoked in this case bears resemblance to ideas proposed in [60].

Our replication of the effects of partial reinforcement and amount of training on reversal is consistent with explanations based on the discriminability of reinforcement schedules. Under partial reinforcement and low amounts of pre-reversal training, uncertainty in parameter estimates led to poor detection of changes in context and a tendency to assign all observations to a single context. This ‘discrimination hypothesis’ is far from new [61,62] but continues to generate experimental work and discussion in the field [63].

Finally, reproducing the development of rapid switching of preferences in serial reversal learning relied on the model's ability to not only detect changes in context but to take advantage of previous learning by maintaining different parameters for each context. This general approach, related to the multi-task learning field [64], is to be contrasted with modelling approaches that rely on continuously adjusting a single set of parameters (what we called ‘tracking’ models) which are ill-equipped to model such effects.

4.3. Alternative approaches

We have taken the general approach that a variety of behavioural phenomena are well accounted for by assuming that animals distinguish between different environmental regimes or ‘contexts’. However, alternative explanations of the same phenomena have been proposed. One such explanation is given by two process theories [34,65,66] which assume that animals need to solve two general problems in simple choice (or ‘discrimination learning’) experiments: learning to attend to the stimulus dimension which is relevant to the current task, and learning to attach correct responses to stimuli having different values on that dimension. Thus, in a simple T-maze task, the animal must learn to attend to the relevant dimension of space (choices of one arm being generally more rewarding than choices of the other) and differentiate along this dimension in its responses (by preferentially choosing the more rewarding arm). Classically, the two learning processes are framed in terms of strengthening or weakening the relevant ‘analysers’ (i.e. amount of attention to each dimension) and responses, respectively. To see how such models might explain some of the effects considered, consider the example of the ORE (§3.3.2). Pre-reversal training is assumed to lead to strengthening of the relevant spatial analyser and attachment of appropriate responses to ‘left’ and ‘right’ dimension values. To account for the ORE, the two-process account must assume that with large amounts of training on this initial task, the strength of the relevant analyser is greater than the strength of the learned responses. Consequently, while responses are relearned following reversal, attention remains focused on the spatial dimension to some degree, leading to quicker learning in the reversed schedule. While this account seems reasonably intuitive, two immediate difficulties present themselves. Firstly, there is a clear need to explain why the strengths of attentional analysers should adapt at different rates to the motor responses. Secondly, since two process accounts have typically been framed in terms of continually adjusting a single set of attentional and response strengths, they will struggle to explain, for example, serial reversal-learning effects. As with all tracking models, prior learning fails to be retained in a sensible fashion.

An alternative to our context-learning account may also be considered in relation to the progressive improvement observed in serial reversal learning over successive reversals. Indeed, this trend is traditionally explained as reflecting acquisition of a general WSLS strategy: ‘if the previous response was rewarded then use it again; otherwise shift to the other response’ [67]. In contrast to our own account, such a rule makes no appeal to identifying an underlying context. From our point of view, the WSLS explanation is not completely satisfactory. Firstly, we are not aware of a model that clearly describes what it means to ‘develop a WSLS strategy’. Rats clearly do not start out with such a strategy for if they did, they would reverse at the same rate (i.e. after a single error trial) each time. Secondly, such a strategy fails to take advantage of possible structure in the environment. To see this, consider a three-armed bandit with arms A, B and C, and two reinforcement schedules which specify the probabilities of reward for each arm. The first schedule specifies respective probabilities (1,0,0), i.e. only choices of A get rewarded, while the second specifies probabilities (0,0,1), i.e. only C gets rewarded. These are not strictly ‘reversed schedules’, but if the rat is faced with serial alternations between them, a developing WSLS strategy presumably does not have much to say about what the rat's first choice following an error will be (e.g. the rat has been choosing A but suddenly observed a zero reward)—WSLS just says ‘shift’. Presumably, given sufficient experience, the rat knows that C is likely to be a good choice, not B. We do not know whether such experiments have been carried out, but such studies would help one to discriminate between the acquisition of relatively simple behavioural strategies and the learning of richer representations. Overall, we acknowledge that it may be difficult to distinguish between a WSLS and context-learning account of serial reversal-learning effects in the two-alternative case. However, when the environment has structure to be exploited, the latter makes more sense.

Appendix A. Estimating reward distributions

Each context–action pair is assumed to have an associated Gaussian reward distribution of unknown mean and variance. Estimation proceeds by standard Bayesian conjugate analysis independently for each context–action pair [18] such that for each context–action pair, a Normal-Gamma prior on the mean μ and precision λ (=1/σ²) is assumed

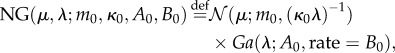where NG denotes the prior probability, and 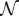and Ga denote the densities of a normal distribution and a Gamma distribution, respectively. The prior parameters θ₀ = (m₀, κ₀, A₀, B₀) are set to generic values: m₀ = 0, κ₀ = 1, A₀ = 1, B₀ = 1. For a given context–action pair (c,a), routine Bayesian calculations yield the posterior

where

A1

A2

A3

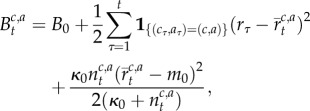A4

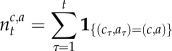A5

and

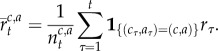A6

We denote the collection 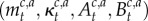as 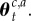Thus, estimating each context- and action-specific Gaussian distribution depends on keeping track of a number of sufficient statistics: the number of observations 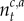assigned to a context–action pair, the mean of the observed rewards 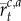assigned to each context–action pair and the context–action sum of squares Each of these quantities can be recursively updated on line in a simple manner.

To calculate the likelihood of the reward on the current trial r_t being generated from a given context c given that action a has been taken (as required for equations (2.2) and (2.3)), we marginalize out uncertainty in μ^c,a and λ^c,a to yield the likelihood term

A7

where t_ν(·;m, s²) represents a t distribution with shape parameter ν, location parameter m and scale parameter s².

Finally, as a component of Thompson sampling, we need to sample from the posterior of 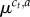conditional on c_{1 : t}, a_{1 : t−1} and r_{1 : t−1} (see §2.3). Routine Bayesian calculations [67] to marginalize λ^c,a give

A8

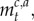
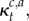
where and 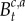are as specified earlier.