Increasing silk fibre strength through heterogeneity of bundled fibrils

Abstract

Can naturally arising disorder in biological materials be beneficial? Materials scientists are continuously attempting to replicate the exemplary performance of materials such as spider silk, with detailed techniques and assembly procedures. At the same time, a spider does not precisely machine silk—imaging indicates that its fibrils are heterogeneous and irregular in cross section. While past investigations either focused on the building material (e.g. the molecular scale protein sequence and behaviour) or on the ultimate structural component (e.g. silk threads and spider webs), the bundled structure of fibrils that compose spider threads has been frequently overlooked. Herein, I exploit a molecular dynamics-based coarse-grain model to construct a fully three-dimensional fibril bundle, with a length on the order of micrometres. I probe the mechanical behaviour of bundled silk fibrils with variable density of heterogenic protrusions or globules, ranging from ideally homogeneous to a saturated distribution. Subject to stretching, the model indicates that cooperativity is enhanced by contact through low-force deformation and shear ‘locking’ between globules, increasing shear stress transfer by up to 200 per cent. In effect, introduction of a random and disordered structure can serve to improve mechanical performance. Moreover, addition of globules allows a tuning of free volume, and thus the wettability of silk (with implications for supercontraction). These findings support the ability of silk to maintain near-molecular-level strength at the scale of silk threads, and the mechanism could be easily adopted as a strategy for synthetic fibres.

1. Introduction

Spider silk is one of the most fascinating natural materials across a multitude of scales [1–4]. It is well known that its combination of strength and toughness is unrivalled in Nature [5], and it has intrigued medical, physics and materials communities alike in attempts to exploit it [6–15]. Unlike materials science and engineering, however, Nature is seemingly not precise—biological processes are riddled with apparent ‘imperfections’ or random variations that introduce disorder to a material system. Yet, frequently, these structural or morphological features are beneficial to system performance (such as in toughening or crack mitigation mechanisms). What may first appear as a ‘mistake’ may have unknown functional value. At the same time, one of the most intriguing and attractive properties of silk is that it maintains near-molecular-level performance (in terms of strength and strain) at the macroscale [7]—performance that has yet to be matched in synthetic efforts to replicate silk. Indeed, the ultimate stress of the molecular ‘building block’ of silk has been shown almost equivalent to experimental measures of silk threads, on the order of 1–2 GPa [7,16–18], with a toughness exceeding that of Kevlar [5,19]. In contrast to silk, one of the technological challenges of carbon nanotubes, for example, is scaling-up their intrinsic nanoscale capacity [20,21], involving ingenious methods of bundling and fibre weaving to approach the full material strength [22–24]. ‘How has the spider solved this engineering problem?’ ‘Could we be missing a critical structural feature, hidden in what we perceive as a structural flaw?’ Undeniably, there is no single strategy allowing multi-scale stress transfer, and, like many biological materials [25–27], spider silk relies on a hierarchy of mechanisms to sustain strength and toughness across scales, from the nano- to macroscales [28]. In consideration of the fibril structure of silk, the question arises: can a little disorder—or structural heterogeneity—improve system performance? While the majority of past research focus has been on either the molecular (e.g. protein sequence and structure [8,9,16]) or the macroscale (e.g. silk threads [7] and spider webs [29–33]), here we look at the often overlooked intermediate structure—the bundled collection of fibrils that compose a silk fibre.

It is well known that silk, like many biological materials, features a hierarchical structure arising from a complex assembly process [28]. The molecular geometry is defined by strands of a single, repetitive protein sequence [10], resulting in hydrogen-bonded β-sheet nanocrystals embedded in a semi-amorphous protein domain [16]. These protein structures are further spun into fibrils via extrusion and shear flow to increase alignment and connectivity [18,34,35], and self-assemble into fibres to form silk threads [7]. Motivated by the two-phase composition of silk fibrils (β-crystalline regions networked with entropic/amorphous domains), prior investigations have focused on individual fibrils for characterization, linking molecular structure to homogenized behaviour [36]. For example, a recent coarse-grain study investigated size dependence of the fibrils and demonstrated that, owing to the unique constitutive behaviour of silk, small fibrils were necessary to achieve superior toughness of the molecular structure in the presence of small defects [37]. Such behaviour was only achieved provided that the fibrils were confined to dimensions below a critical length scale on the order of approximately 20–80 nm [37]. Experimental results indicate silk fibrils on the order of 20–200 nm in diameter [18,38–41], suggesting a length scale in accordance with the benefits of such nanoconfinement. Moreover, another study [42]—motivated by continuum fracture mechanics criteria—indicated that silk toughness does not depend directly on nanostructure, but rather cohesive energy density (in collusion with a modulus contribution), and the fracture mechanics characteristics depends on micrometre-scale dimensional features and attributable to its fineness. In both cases, it was concluded that bundles of small fibrils are mechanically advantageous in larger threads. While, at first glance, the fibril structure of silk may seem like a by-product of assembly, a strong mechanical effect is becoming apparent. Indeed, it is a common theme in Nature that material structures often have hidden or unknown benefits.

While recent investigations have shed insights on the spinning process, the fibrillation mechanism is inherently complex, and it is still not fully known how meso- and microscale organization develops. Previous investigations have indicated the fibrillar nature of silk, and have proposed the so-called skin–core structural model—a bundle of silk fibrils encapsulated by an outer layer [39,43–46], depicted in figure 1. The skin is thin with no discernible distinct features [44], even at failure [39], suggesting the core dominates mechanical properties. The skin—shown to contain an abundance of glycoproteins [43,46]—may play a key in the adhesion properties of silk [47,48]. That being said, few studies have explicitly considered the contribution of interfibril interactions to the response of a thread. Recent atomic force microscopy (AFM) imaging has indicated that these fibrils are not homogeneous along the axis—they are characterized by globular protrusions at regular intervals (figure 2a,b), increasing the fibril diameter over 50 per cent [41]. It has been proposed that these globules effectively form shear keys [41]. The same investigation implemented a two-dimensional finite-element model to focus on the fibril–fibril interface and the effect of heterogeneous globules/protrusions [41]. Indeed, it was shown that the globular structures resulted in non-slip kinematics, restricted fibril shearing, controlled slippage, stress transfer as well as energy dissipation [41]. An analogy was made to bone and nacre, wherein the roughness of interfaces [49] and layer bridging [50,51] results in strong and tough materials [52,53]. Little attention, however, was given to the three-dimensional thread morphology.

Figure 1.

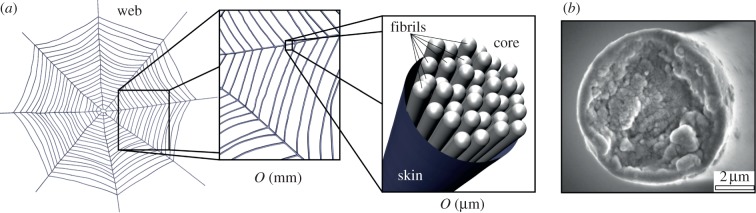
Skin–core, fibril bundle structure of spider silk. (a) Schematic of the multi-fibril core of dragline silk that constitutes a spider web, on the order of micrometres, the scale investigated here. (b) Low magnification view of fracture surfaces of Argiope trifasciata fibres showing a skin–core nanofibrillar, globular microstructure. Image from Poza et al. [39], used with permission, copyright 2002, Elsevier Inc. (Online version in colour.)

Figure 2.

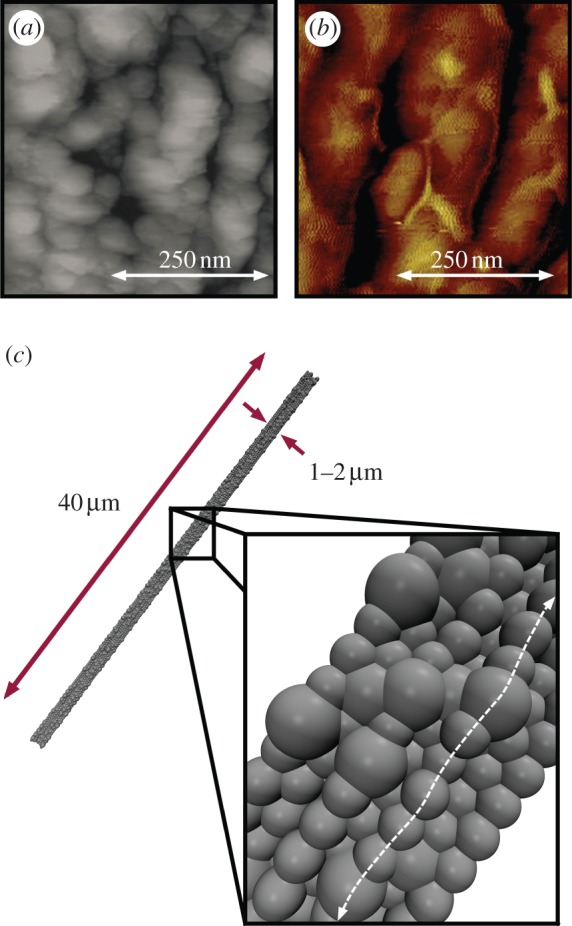
Experimental and model silk fibre cross sections. (a,b) Experimental images of fibril structure in the core region of dragline silk fibres. (a) Topographic AFM image of spider dragline silk from Nephila pilipes, from Du et al. [7], used with permission, copyright 2006 Elsevier Inc. (b) AFM image from Nephila clavipes (golden orb weaver), from Brown et al. [41], used with permission, copyright 2012, American Chemical Society. Both images depict braided bundles of fibrils on the hundreds of nanometre scale constituting the fibre's core, with irregular ‘globular protrusions’ along the fibre axis. Moreover, small voids were observed in the images, indicating potential free volume for hydration. (c) Model silk fibre consisting of aligned and bundled fibrils with random globular protrusions to mimic the observed natural structure. Here, 20% of the particle sites are designated ‘globules’ (with a diameter of 300 nm) and randomly distributed along the fibril length, with an equilibrated diameter of approximately 1.2 μm. (Online version in colour.)

Here, I exploit a coarse-grain model developed for dragline silk [32] (previously parametrized by known atomistic behaviour [9,16]) to construct a fully three-dimensional fibril bundle, with a length and diameter on the order of micrometres (figure 2c). I probe the mechanical behaviour of bundled silk fibrils with variable density of globules, ranging from ideally homogeneous to saturation of protrusions and demonstrate that fibril strength and cooperativity is enhanced by contact through low-force deformation and shear ‘locking’ between globules.

2. Methods

While the motivation here stems from the bundled structure of spider's silk, the aim is more pedagogical. Indeed, the transfer of ideas from biology is not limited to the ultimate form and function of a biological system—we are not interested in spider silk so we can fight crime like Spiderman. The benefit lies not just in the analysis of specific biological systems, but rather in a mechanistic understanding, i.e. learning from Nature. Thus, while efforts are made herein to accurately model silk, the results presented should not be considered an exact replication of dragline threads, but a platform to isolate a potentially key mechanistic phenomenon.

The goal is to develop a test specimen subject to tensile stretching to induce interfibril shear transfer (the presumed transfer mechanism of the globules). I construct a computational model used to probe the behaviour of three-dimensional silk fibres with variable material properties and random (disordered) globule distributions. While full atomistic approaches have elucidated the molecular behaviour of silk's nanostructure, the length scale associated with fibril bundles in beyond the length of atomistic resolution. That being said, a molecular dynamics (MD) approach allows efficient manipulation of constitutive behaviour, such as elasticity and contact as well as interfacial failure and large deformation. As such, I use a coarse-grain mesoscopic ‘bead-on-a-string’ model as a platform to assess silk fibril behaviour, using general MD formulations [28,32]. Experimentally, it has been demonstrated that shearing of the silk protein solution can lead to a similar bead-on-a-string assembly at the nanometre scale [54,55]. Through the total potential energy of the fibril, ϕ the energetic contributions of the model can be simply described as ϕ = ϕ_fibril + ϕ_contact, where the fibrils are represented by particle-spring chains with defined axial behaviour (ϕ_fibril) and interfibril repulsive pairwise interactions (ϕ_contact).

2.1. Fibril constitutive law and interfibril interaction(s)

While the exact behaviour of silk depends on many factors (spider species, silk type, etc.), most silks (e.g. dragline or capture silks) can be approximately characterized by hyperelastic stiffening [5,6,17,32,56]. As such, a simple potential is desired that can capture such behaviour with a minimum number of parameters. It is stressed that natural silk is intrinsically viscoelastic [57–59], dependent on strain rate (e.g. a load-dependent dynamic modulus, accumulation of non-recoverable strain, etc.). Treating silk here as an elastic material (albeit nonlinear) is consistent with previous work and simplifies the simulation approach—capturing viscoelastic effects of the natural material at such a coarse scale is not required to reflect the desired effect of the heterogeneous globules. To generalize further, although inspired by the nonlinear behaviour of silk, a simple hyperelastic constitutive law is introduced (similar to the behaviour of capture, or viscid, silks [6,56]), which can systematically be varied from a relatively stiff, brittle response (i.e. ultimate strain, ɛ_ult = 0.1), to a highly compliant, extensible response (i.e. ɛ_ult = 10.0). The governing hyperelastic material law is expressed as

2.1a

defined by three parameters: ultimate stress (σ_ult), ultimate strain (ɛ_ult) and a non-dimensional hyperelastic parameter, α. For α > 1.0, the material undergoes mechanical stiffening under extension, whereas for α < 1.0, the material undergoes softening (e.g. plasticity). Here, I assume hyperelastic stiffening and set α = 3.0 (derived by fitting the hyperelastic region of dragline silk; consistent with previous modelling [32,60,61]) and maintain a constant ultimate stress (1000 MPa) and strain (2.0 m m⁻¹)—values within the range of measured silks [56]—intended to provide benchmarks for variation in constitutive law. This results in a fibril potential of

2.1b

where l₀ is the equilibrium (stress-free) distance between particles along the fibril axis, set at 200 nm, l_ult = (1 + ɛ_ult)l₀ and r₀ is the equilibrium distance between adjacent fibrils (i.e. the diameter) that defines the cross section. I note that model parametrization is not intended to represent any particular silk, but rather an idealized mechanical model, representative of silk in general.

I next parametrize the model such that fibril–fibril interaction can be manipulated via geometrical changes alone (specifically, bulges and irregularities along the fibril length that mimic the structure of spider silk [41]). In a recent study [41], imaging indicates fibrils approximately 200 nm in diameter (which I implement as a basis fibril diameter, r₀) with globules roughly 100 nm in width and protrusions approximately 50 nm. Thus, the protrusions would roughly be equivalent to globules with a diameter of 1.50r₀. I subsequently decrease and increase the diameters (1.25r₀ and 2.00r₀, respectively) to parametrically explore the effect of globule size. While at a different scale (as silk/fibrils are species dependent), there is visual evidence supporting such a magnitude of change in globule size [7]. Again, the intent is to represent a generalized silk model, and not encapsulating any particular species. For the current model, I therefore exploit three globule sizes (r_g = 1.25r₀, 1.50r₀ and 2.00r₀) to determine the potential relation with mechanical response (figure 3a).

Figure 3.

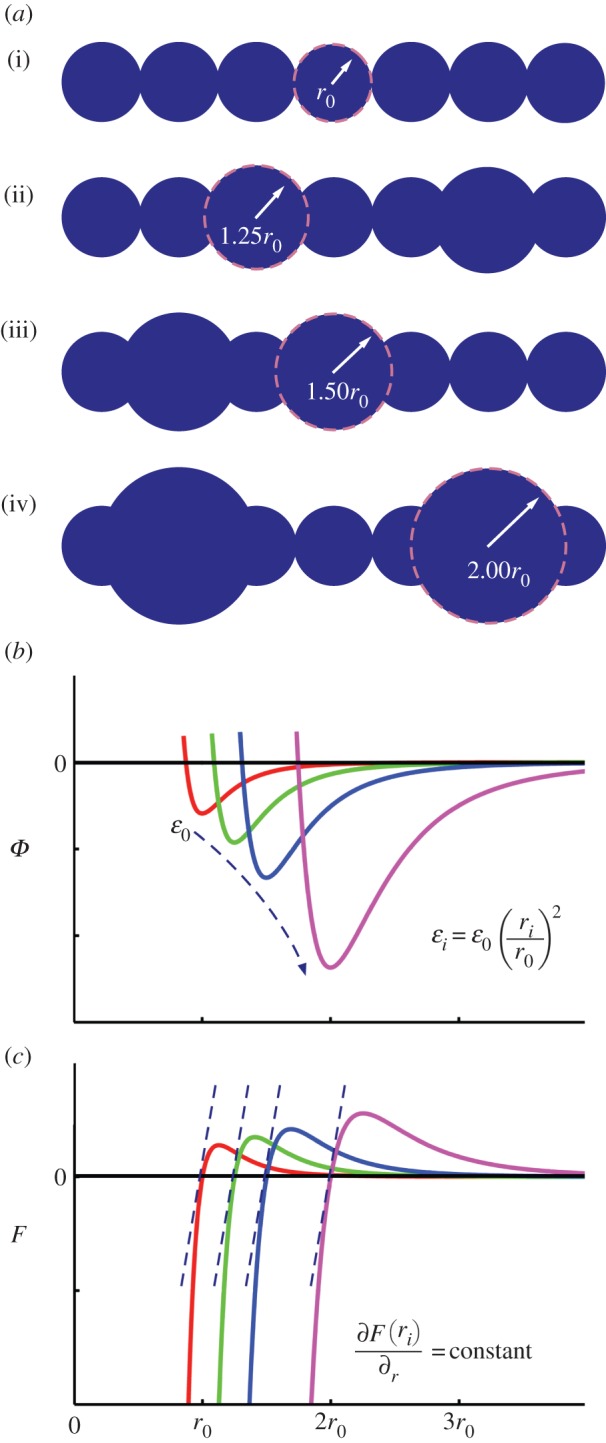
Fibril computational model. (a) Depiction of relative particulate size along the modelled fibrils, including (i) homogeneous fibril (r₀; 0%g), and three globule sizes (ii) r_g = 1.25r₀, (iii) r_g = 1.50r₀ and (iv) r_g = 2.00r₀. The globules are randomly distributed amongst all fibrils in the fibre model, with %g ranging from 5% to 50%. (b) Plot of energy versus separation for LJ 9 : 6 potential for fibril contact (ϕ_contact) depicting scaling of parameters: as r_g increases, the LJ parameter scales with ɛ_i ∝ (r_i/r₀)² to maintain constant stiffness. (c) Plot of force versus separation for LJ 9 : 6 potential, depicting equivalent small deformation stiffness for r = r₀, 1.25r₀, 1.50r₀ and 2.00r₀. (Online version in colour.)

A critical requirement is that the mechanical stiffness of the fibre remains constant, regardless of geometrical variation (e.g. equivalent material). Thus, I wish to derive a scaling law for the interaction parameters. The coarse-grain fibril–fibril interaction is governed by a classical Lennard–Jones (LJ) 9 : 6 potential,

2.2

where the input parameters are defined by ɛ (surface energy) and σ (a function of r₀ the equilibrium distance, solved by minimizing the potential function, or ∂ϕ/∂r = 0 at r = r₀). I note that setting the cut-off to r₀ limits the associated forces to the repulsive regime. From a geometrical perspective, r₀ dictates the diameter of each fibril, and is set at 200 nm (at the upper range of experimental measures, on the order of 20–200 nm [18,38–41]). To estimate the contact stiffness, I can equate the stiffness at first contact (r = r₀) of the LJ potential with the classical Hertzian force–displacement contact of two spheres, F = (4/3)KR^1/2Δ^3/2 (where F = force, K = bulk modulus, R = radius = r₀ and Δ = displacement), subject to small deformation. Assuming an initial stiffness on the order of 3 MPa [6], similar to soft polymeric materials, I attain ɛ ≈ 300 kcal mol⁻¹ (note that this modulus is intended to represent contact stiffness, and not axial stiffness). Moreover, as the potential is implemented for pure repulsion (and not adhesion), large variation in ɛ only marginally influences the measured stresses (owing to the exponential nature of the LJ 9 : 6 potential). As such, an assumption of small contact deformation is presumed valid.

I next wish to ensure the stiffness, K_g, is constant (e.g. resistance to contact deformation), regardless of defined r_g, allowing exploration of globules of various scale. Thus, I take the second derivative of the potential (first derivative of force) setting

2.3a

from which it follows 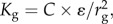where C is a constant (only the scaling law is required), or

2.3b

Thus, for geometrical variation, r₀ → r_g, I impose that K₀ = K_g, and

2.4

It follows that in order to maintain the same material stiffness through the introduction of the fibril globule (increasing the contact diameter, r₀), the energy of adhesion, ɛ, also increases (figure 3b). A summary of all model parameters is given in table 1.

Table 1.

Modelling parameters for coarse-grain silk fibre.

parameter	value	units
ultimate stress, σult	1000	MPa
ultimate strain, ɛult	2.0	m m−1
hyperelastic parameter, α	3.0	n.a.
equilibrium distance, l0	200	nm
fibril diameter, r0	200	nm
globule diameters, rg	rg = 1.25r0, 1.50r0, 2.00r0	nm
fibril contact stiffness parameter, ɛ0	300	kcal mol−1
globule contact stiffness parameter, ɛg	ɛg = ɛ0(rg/r0)2	kcal mol−1
contact distance parameters, σg	σg = (2/3)1/3r0	nm

2.2. Fibre model and mechanical testing

The fibre is initially constructed with 37 fibrils (length of 40 μm) in a hexagonal arrangement aligned along a common axis. Each fibril is generated with a random distribution of globules along its length, and consecutive particles cannot be assigned as globules to facilitate heterogeneity. I measure the heterogeneity through the percentage of globule particles (denoted %g), and construct models with 0–50% distributions in 5 per cent increments. I note, owing to the constraint on consecutive particles, 50 per cent is the maximum allowable globule distribution for the current model (in effect, greater than 50% of globules would change the fibril model to a relatively thin fibril with large protrusions to a relatively wide fibril with dispersed cavities and voids [38], which would not directly contribute to the shear transfer investigated here). For statistical variation, three random geometrical distributions were implemented for each percentage.

Upon adding globules, the material volume of the thread changes, and as a direct consequence, if one was to implement a constant cross section, addition of globules would result in a compressive pre-stress. Thus, a stress-free fibre must have a thread radius, R, sufficient to accommodate the addition of material. Moreover, assuming random and heterogeneous distribution of the globules, it is impossible to determine the necessary volume of the fibril (i.e. cross-sectional area) a priori. Here, the skin–core structure of the silk fibre is advantageous, to be used to both determine and confine the fibril bundle to an equilibrium (stress-free) radius, R_eq, for each %g distribution. The confining skin is modelled by a cylindrical elastic boundary, adjusted to provide zero stress at zero strain (i.e. control pre-stress), similar to previous mechanical assumptions regarding the role of the skin [40]. I again note that little is known regarding the physical properties of this layer. The confinement force is calculated by F = K(R−R₀)², where K is a specified force constant, R is the distance from the fibril to the centre axis of the cylinder and R₀ is the radius of the cylinder, where F = 0 for R < R₀. To attain an equilibrated structure, the cylinder decreases radius at a constant rate, and the potential energy (ϕ) of the fibre system is tracked (figure 4a). To attain a minimum energy, the cut-off for the interfibril interaction (equation (2.2)) is relaxed to 1.25r₀, allowing marginal attraction between fibrils and an energetically favourable state. The equilibrium radius, R_eq, is then taken as the minimum of the energy–radius curve (figure 4b). This process is repeated for all distributions, and for each globule size (figure 4c). As anticipated, there is a constant increase in equilibrium radii with increasing globules, but is irregular due to the random distribution. Moreover, the magnitude of the energetic minimum decreases with an increase in %g—the protrusions inhibit interaction between otherwise aligned sections of fibril. We observe that, for cases of r_g = 1.25r₀ and 1.50r₀, the increase in equilibrium radius (R_eq) is near linear, with additional globules requiring nominal increase in volume. However, the behaviour differs for r_g = 2.0r₀, where the significance is increased when a few globules are introduced (%g up to approx. 20%) and then the dependency decreases. In this case, a few interacting globules are sufficient to greatly increase the necessary volume for stress-free conditions.

Figure 4.

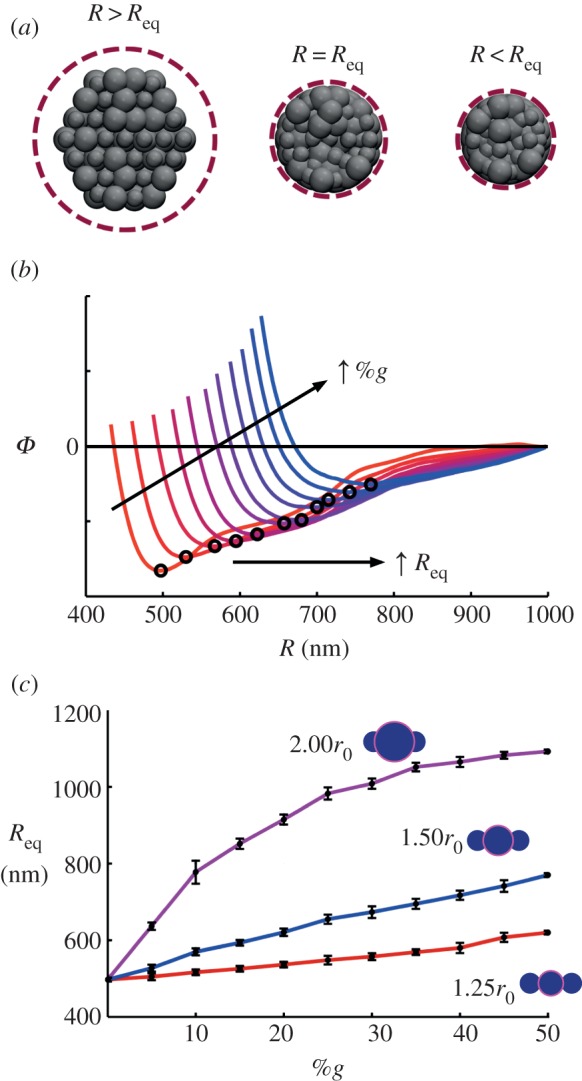
Attaining equilibrium (stress-free) fibre radii, R_eq. (a) Depiction of fibre cross section upon equilibration, subject to cylindrical compression. For a confining volume of R > R_eq, the fibrils maintain a configuration close to the initial hexagonal arrangement. To attain an equilibrated structure (R = R_eq), the cylinder decreases radius at a constant rate, and the potential energy (ϕ) of the fibre system is tracked to determine a minimum. (b) Representative plot of potential energy versus confining cylinder (e.g. fibre) radius, R, for r_g = 1.50r₀, %g from 5% to 50%. The equilibrium radius, R_eq, is then taken as the minimum of the energy–radius curve (indicated). As anticipated, there is a constant increase in equilibrium radii with increasing globules, but is irregular due to the random distribution. Moreover, the magnitude of the energetic minimum decreases with an increase in %g. (c) Results for three globule sizes, all %g distributions. Error bars indicate statistical distribution for three model samples. (Online version in colour.)

Once the equilibrium radius is attained, the cylindrical elastic boundary is fixed, acting as the constraining ‘skin’. It behoves to note that while the diameters of our threads vary from approximately 1.0 to 2.2 μm, the model is not necessarily intended to capture the complete thread (silk thread diameters range from approx. 0.5 to 8 μm [11,56,62]). Rather, the skin boundary can be considered equivalent to surrounding fibrils, of a much larger structure. As such, the stiffness parameter, K, is fitted to approximate the resistance of fibril contact (e.g. taking a Taylor expansion about r = r₀ for ϕ_contact).

Once equilibrated, each fibril model is subject to uniaxial stretching. As the desired mechanisms of stress transfer is interfibril interaction (rather than direct tension), connectivity is removed along each fibril, at alternating one-quarter and one-half fibril lengths, resulting in a discontinuous and staggered fibril arrangement (figure 5). Loading is introduced by moving the ends at a constant pulling velocity (1 m s⁻¹) and tacking the resulting virial stress, S. Virial stress is commonly used to relate to the macroscopic (continuum) stress in MD computations [63,64]. The virial stress approach allows us to determine the components of the macroscopic stress tensor, S_ij in a volume Ω, where

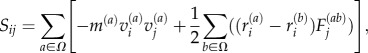2.5

which generates the six components of the symmetric stress–volume tensor, S_ij, where m^(a) is the mass of particle ‘a’, 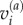and 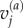are the velocities in the ith and jth vector component basis, 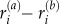denotes the distance between particle ‘a’ and atom ‘b’ along the ith vector component, whereas 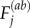is the force on particle ‘a’ exerted by particle ‘b’ along the jth vector component. To reduce random and temperature-related stress fluctuations, in addition to averaging over the representative volume, Ω, the stress is averaged further over a small timeinterval of 100 timesteps around the desired time point of stress calculation. The total stress can be calculated as σ_ij = S_ijΩ⁻¹, where Ω is taken as the dimensions of the interior portion of the fibre free from imposed boundary conditions (shown schematically in figure 5). All simulations are carried out using the molecular simulation package LAMMPS [65], implementing a microcanonical (NVE) ensemble, with temperature control through a Berendson thermostat (T = 300 K, τ = 1000 timesteps).

Figure 5.

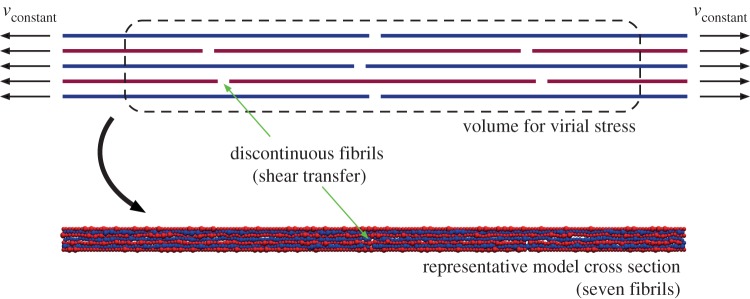
Schematic of mechanical test. Once equilibrated, each fibril model is subject to uniaxial stretching through at an applied constant pulling velocity (v_constant). Fibril connectivity is removed in an alternating, staggered arrangement to ensure stress transfer via interfibril interaction (shear transfer) rather than fibril stretching. Stress is calculated, using the virial stress of a representative interior volume to reduce boundary effects. The discontinuities are difficult to visualize in the model (see representative cross section), owing to the non-uniform particulate size and equilibrium (e.g. packed) configuration. (Online version in colour.)

3. Results

3.1. Ultimate strength

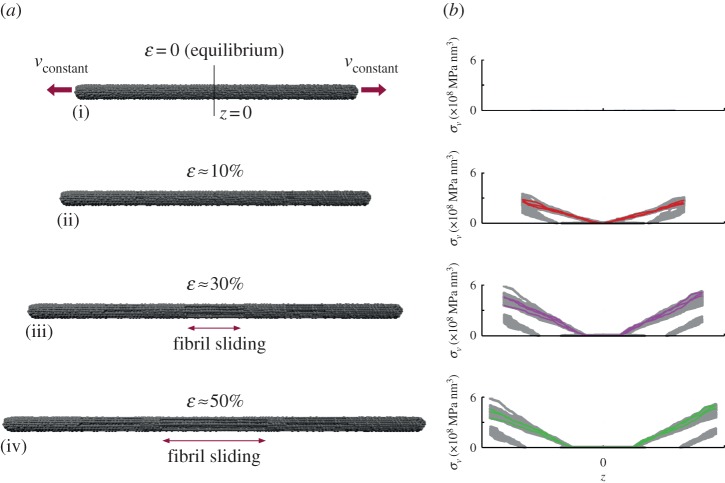
Our interest is the enhanced strength (e.g. ultimate stress) that the addition of heterogeneous globules may provide through an increased transfer of shear stress. As such, I apply uniaxial stretching to initiate fibril slippage and record the peak stress. Figure 6 depicts simulation snapshots and virial stress distributions of a representative model (r_g = 1.50r₀; 20%g). The stress depicted is the virial stress along the fibril axis, and indicates the primary stress transfer mechanism is via shear. We see a shear-lag effect, where a finite length of fibril is required to build up the stress transfer (see highlighted fibrils in figure 6 right). When stress is increasing, the slope of the stress distribution correspondingly increases (e.g. from ɛ = 10 to 30%, figure 6), until a maximum stress level is reached, and the slope distribution is maintained along the fibril, whereas the fibrils themselves slip along the fibre axis (e.g. from ɛ = 30 to 50%, figure 6). This effect can be understood through a shear-lag model [66], which predicts that the shear stress is the highest at the ends of the overlap length and drops towards the centre of the junction [66]. Because the only mechanism here is shear transfer (owing to the discontinuity of the fibrils and boundary conditions), the shear stress directly correlated with total fibre stress. As a direct result, for longer overlap lengths, the shear stress is very small in the centre of the junction. As anticipated, the short fibril lengths build up less stress owing to the shorter overlap length, whereas the interior (e.g. un-pulled) fibrils build up very little stress as they are free at their boundaries (slippage is observed during deformation). This mechanism of shear transfer has been used in the description of bone [67] as well as bundles of carbon nanotubes [68], where a soft phase (collagen and poly(methyl methacrylate), respectively) was the medium of stress transfer, similar to the long-chain molecular structure of silk fibrils. When the fibril overlap begins to decrease (i.e. complete fibril separation at ɛ = 100%), the stress correspondingly drops to zero. Extending the concept, a sufficiently long overlap length results in saturation [66], indicating an optimal fibril length, dependent on the fibril interaction. Such a length, however, is beyond the scope of this study. The intent here is not to present a rigorous theoretical model for the stress transfer (which would require additional analysis of fibril stresses), but rather illustrate the dominance of shear transfer.

Figure 6.

Mechanism of fibre deformation and fibril stress distribution. Representative model snapshots (a) of fibre subject to uniaxial deformation, 20%g and r_g = 1.50r₀ at ɛ = 0 (equilibrium; (i)), ɛ = 10% (ii), ɛ = 30% (iii) and ɛ = 50% (iv), with corresponding virial stress distribution (b). A selection of four pulled individual fibrils that initially extend one-half the fibre length is highlighted. Owing to the staggered and discontinuous fibril arrangement (figure 5), fibril sliding initiates at approximately ɛ > 10%. In the stress distributions, we see a shear-lag effect, where a finite length of fibril is required to build up the stress transfer. Shorter fibril lengths build up less stress. When stress is increasing, the slope of the stress distribution correspondingly increases (e.g. from ɛ = 10% to 30%), until a maximum stress level is reached, and the slope distribution is maintained along the fibril, whereas the fibrils themselves slip along the fibre axis (e.g. from ɛ = 30% to 50%). To determine total stress, the virial stress contributions of all fibrils are summed (equation (2.5)) and taken over the representative volume. (Online version in colour.)

To determine total stress, the virial stress contributions of each fibril are summed (equation (2.5)) and taken over the representative volume (figure 5), allowing a global representation of stress (σ) versus strain (ɛ). I note that while the loading is uniaxial tension, the stress–strain relation is not indicative of the stress–strain response of silk threads, due to the introduction of discontinuity to isolate shear transfer (the strain is a combination of fibril slippage as well as local strain). As such, the stresses and strains are predominately associated with shear transfer. A representative stress–strain plot is depicted (r_g = 1.50r₀; 20%g; figure 7a), indicating the typical stress response of nonlinear stress increases, followed by saturation and nominal decrease as the fibrils slip along the fibre axis. I note slippage initiates prior to a maximum stress, at approximately ɛ > 10 per cent, which, visually, corresponds with the onset of system softening. The curves were attained for all models (three geometrical distributions each of %g from 0 to 50% for r_g = 1.25r₀, 1.50r₀ and 2.00r₀; over 99 separate simulations in total). The mean at each %g was calculated, as well as the uncertainty, accounting for the deviation in stress and radii calculation (figure 7b). While the uncertainty is on the order of ±5%, the trends between each r_g value is clear.

Figure 7.

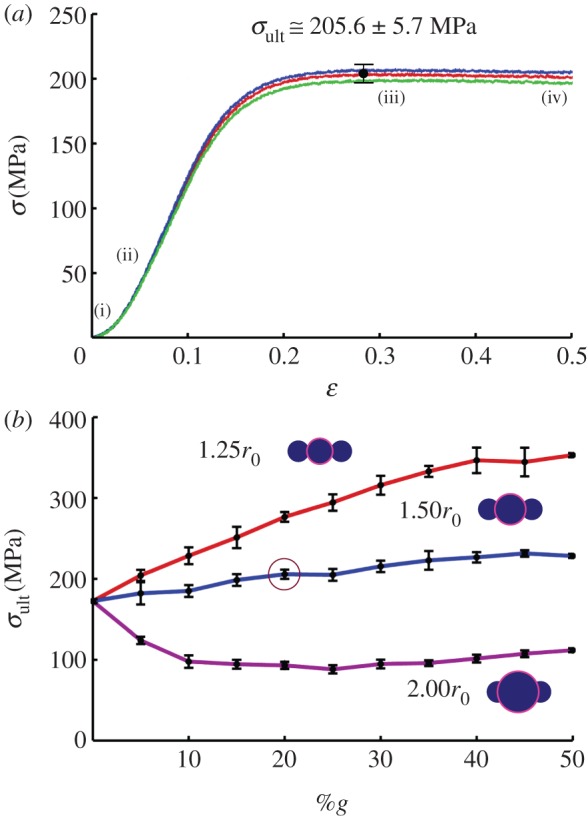
Global stress–strain response and ultimate stress. (a) Representative fibre stress (σ) versus strain (ɛ) for r_g = 1.50r₀ and 20%g. The stresses and strains are representative to the shear transfer contribution only. The typical stress response is nonlinear stress increase, followed by saturation and nominal decrease as the fibrils slip along the fibre axis. Slippage initiates prior to a maximum stress, at approximately ɛ > 10%, which visually corresponds with the onset of system softening. Three curves depict three random distributions, maximum stress taken as the mean (with the variance accounting for the uncertainty in radii determination). The indicated points (i), (ii), (iii) and (iv) correspond with the snapshots from figure 6. (b) The curves were attained for all models, and the ultimate stress (σ_ult) plotted as a function of %g (result from (a) indicated by circle). While the uncertainty is on the order of ±5%, the trends between each r_g value is clear. Addition of slightly larger fibril globules enhances interlock while only nominally increasing the require fibre volume. As a result, each additional globule enhances shear transfer, as it interlocks with an adjacent fibril, while allowing interaction between adjacent fibril sections. However, as larger globules interact (r_g = 1.50r₀ and 2.00r₀), they prevent adjacent fibril sections of nominal radius from contact, thus decreasing the total interfibril interaction and stress transfer. For the largest globules (r_g = 2.00r₀), the required volume (i.e. equilibrium radius) exceeds the benefit of fibril interlock. Addition of a few large globules must be accommodates by a large fibre radius, leaving significant unused fibril length (non-interlocking sections). (Online version in colour.)

Regardless of model, the initial case of zero globules (e.g. 0%g) is representative of a homogeneous fibre (as depicted in figure 3a–i), and allows a basis of shear transfer comparison for all models (σ_ult = 172.5 MPa). For r_g = 1.25r₀, there is an increase in ultimate stress (σ_ult) with an increase in heterogeneity (%g). Addition of slightly larger fibril globules enhances interlock while only nominally increasing the required fibre volume. As a result, each additional globule enhances shear transfer, as it interlocks with an adjacent fibril, while allowing interaction between adjacent fibril sections. The addition of 50%g results in approximately 200 per cent increase in σ_ult (from 172.5 to 363.0 MPa). Qualitatively, the same trend occurs for r_g = 1.50r₀, but with a net gain of only ≈30 per cent (from 172.5 to 228.4 MPa). The discrepancy lies in the additional spatial extension of the globules. Primarily, increasing the radius to 1.50r₀ causes an increase in required fibre volume at a much higher rate (figure 4b). This effect is compounded by the fact that, while the larger globules interact, they prevent adjacent fibril sections of nominal radius from contact, thus decreasing the total interfibril interaction and stress transfer. Finally, for r_g = 2.00r₀, we see a reversal in trend—the ultimate stress drops with an increase in heterogeneity as the required volume (i.e. equilibrium radius) exceeds the benefit of fibril interlock (a reduction in 35%, from 172.5 to 111.9 MPa). Again, the addition of a few large globules must be accommodated by a large fibre radius, leaving significant unused fibril length (i.e. non-interlocking sections). When the required radial growth decreases (%g > 20%; figure 4b), the decrease subsides and there is marginal increase in strength. In effect, enough large globules have been added, the missing space/voids are filled, and more of the fibril lengths interact. Thus, to maximize strength, relatively small globules are desired (r_g = 1.25r₀) to maximize fibril interlock of both the globules and unperturbed fibril sections. Increasing globule radius requires additional volume and decreases the total fibril interaction, which outweigh the increase in globule contact and interlock. I note the indicated ultimate stress range, from approximately 100 to 400 MPa, is about the same order of magnitude of stress reported in the aforementioned two-dimensional finite-element study [41].

3.2. Material efficiency

Beyond strength metrics alone, I next wish to quantify the material efficiency of such heterogeneous fibres, through specific strength and packing efficiency. Using specific strength (strength per density) effectively eliminates the dependence on cross-sectional area (e.g. equilibrium radius) as the same volume used for virial stress (the fibre volume, V_F) is used to calculate the effective density (ρ_eff),

3.1

where V_f refers to the fibril volume, i.e. the summation of the particulate (r₀) and globular (r_g) spheres, accounting for their overlap. The specific strength is then defined as σ_ult/ρ_eff. The results are plotted in figure 8, and depict the same qualitative trends as ultimate strength, supporting the assertion that contact and shear interlock between globules is a key mechanism in increasing strength. I note that the values attained are reflective of the component of specific strength attributed to shear stress transfer, and not the total specific strength of spider silk. The values attained (from approx. 0.1 to 0.4 MN m kg⁻¹) account for 10–40% the specific strength of silk (approx. 1.0 MN m kg⁻¹), depending on heterogeneity—a significant proportion.

Figure 8.

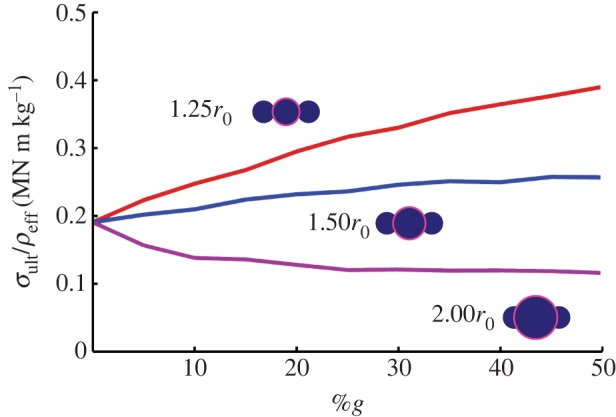
Specific strength. Determination of specific strength (strength per density; σ_ult/ρ_eff) eliminates the geometrical dependence on cross-sectional area (e.g. equilibrium radius) as the same volume used for virial stress (the fibre volume, V_F) is used to calculate the effective density (ρ_eff); see equation (3.1). Plot of specific strength versus %g depicts the same qualitative trends as ultimate strength for each r_g, supporting the assertion that contact and shear interlock between globules is a key mechanism in increasing strength. The values attained (from approx. 0.1 to 0.4 MN m kg⁻¹) account for 10–40% the specific strength of silk (approx. 1.0 MN m kg⁻¹), a significant addition regardless of %g. (Online version in colour.)

Note that the density of fibril, ρ_f, the molecular density of β-crystalline and amorphous regions, is presumed constant (here I take ρ_f = 1300 kg m⁻³ [69]). However, it was previously hypothesized that particulate size (i.e. globule radius) is correlated to spinning speed (and the crystallization of the silk proteins) [7]. Faster spinning results in larger but less dense fibrils [7]. This would vary our calculation of specific strength, decreasing the effective strength of larger globules (i.e. r_g = 2.0r₀) as the fibril density, ρ_f, decreases with an increase in r_g. That being said, such adjustments are beyond the scope of this study and would not change the qualitative trends depicted, as the silk density is presumed constant within a marginal range.

Finally, the equilibration of fibril bundles is similar to the phenomena of packing spheres (albeit the spheres are constrained to their associated linear fibril arrangement). I thus define the volume fraction, η, as a measure of packing efficiency, or

3.2

where again, V_f is the volume of the fibrils (summation of spheres), whereas V_F is the fibre volume (a cylinder with a radius R_eq). The results are plotted in figure 9a. I note the highest packing efficiency at 0%g (η ≈ 0.7), where the fibrils are the most compact owing to their uniformity. In colloidal solutions, the addition of multiple-sized particulates (e.g. polydispersity) can lead to a more efficient packing [75,76]. However, here we see that the addition of larger globules results in less efficient packing. Indeed, owing to the imposed connectivity of the particulates, they cannot arrange freely in the most efficient manner. For both r_g = 1.25r₀ and 1.50r₀, the packing efficiency is near-constant, regardless of %g (with η ≈ 0.67±0.01 and η ≈ 0.60±0.01, respectively). Maintenance of the high packing efficiency (related to fibril contact) is associated with the increasing strength with %g. For r_g = 2.0r₀, however, we see a large drop in packing efficiency owing to the large required equilibrium radius with the addition of a few globules (η ≈ 0.44 at 10%g). The subsequent addition of globules enhances the packing, effectively filling the wasted space, but the discrepancy between globule and fibril radii leads to relatively inefficient packing (and thus less fibril interaction) even at high %g (η ≈ 0.63 at 50%g).

Figure 9.

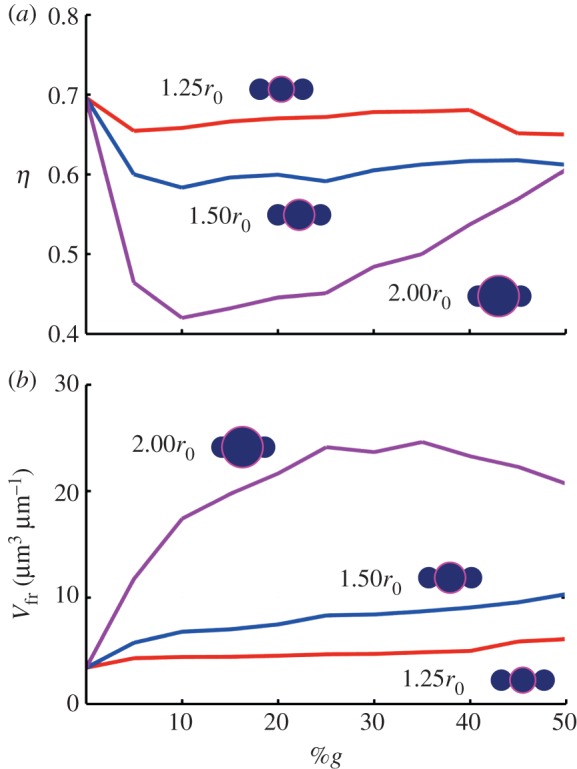
Fibril packing efficiency (η) and fibre free volume (V_fr). Beyond metrics of strength, the addition of globules also effect the geometrical character of the fibres. (a) Plot of volume fraction (η; a measure of packing efficiency; see equation (3.2)) versus %g. Note the highest packing efficiency at 0%g (η ≈ 0.7), where the fibrils are the most compact owing to their uniformity. The addition of larger globules results in less efficient packing. Indeed, owing to the imposed connectivity of the particulates, they cannot arrange freely in the most efficient manner. For both r_g = 1.25r₀ and 1.50r₀, the packing efficiency is near-constant, regardless of %g (with η ≈ 0.67±0.01 and η ≈ 0.60±0.01, respectively). For r_g = 2.0r₀, however, we see a large drop in packing efficiency owing to the large required equilibrium radius with the addition of a few globules (η ≈ 0.44 at 10%g). The subsequent addition of globules enhance the packing, effectively filling the wasted space, but the discrepancy between globule and fibril radii leads to relatively inefficient packing (and thus less fibril interaction) even at high %g (η ≈ 0.63 at 50%g). (b) Plot of free volume versus %g. Available free volume may facilitate the known process of supercontraction [70–73], whereby absorbed water leads to significant shrinkage in an unrestrained silk fibre [12,73,74]. To trigger supercontraction, solvent must penetrate the fibre, enhanced by the presence of fibril globules due to an increase in free volume (and thus exposed surface area). The free volume is normalized by the length of the fibril to attain volume per length (μm³ μm⁻¹). Correspondingly, we see large available free volume for r_g = 2.00r₀, whereas there are nominal gains for both r_g = 1.25r₀ and 1.50r₀. (Online version in colour.)

Interestingly, while the packing efficiency is greatest for the homogeneous case (e.g. 0%g), it does not result in the greatest strength (figure 7b). This can be understood as follows: once slip is initiated in shear, the homogeneity of the fibrils (i.e. the equal radius of all particles) limits any interaction between fibrils—in effect, they are free to slide past one another with limited interaction. So for the case of mechanical shear transfer only (which is reflected by this study), the homogeneous case is not the strongest. It is noted higher packing efficiency would increase adjacent fibril contact, but not necessarily interlock (and associated stress transfer). As such, any adhesion between fibrils may benefit from closer packing, in addition to the shear interlock.

3.3. Voids and free volume

Beyond mechanical interaction, the packing efficiency may also be important in terms of associated voids or free volume. This may facilitate the known process of supercontraction [70–73], whereby absorbed water leads to significant shrinkage in an unrestrained silk fibre [12,73,74], i.e. a post-tensioning mechanism controlled by wetting. Supercontraction is thought to be controlled by specific motifs in the silk proteins [71,77] and induced by the entropy-driven recoiling of molecular chains [78,79], and has a scaling effect on mechanical properties [12,70,73,74]. To trigger the proposed molecular response, solvent must penetrate the protein structure, enhanced by the presence of fibril globules due to an increase in free volume (and thus exposed surface area). While the exact function of supercontraction is still unresolved [72], for example, enabling tailored mechanical properties [80], or pre-tensioning a web [81], as examples—the mechanism appears congruent with the control of packing efficiency and associated free volume, as modelled here. As such, I quantify the free volume, defined simply as V_fr = V_F−V_f. (figure 9b), which is normalized by the length of the fibril to attain volume per length (μm³ μm⁻¹). Correspondingly, we see large available free volume for r_g = 2.0r₀, whereas there are nominal gains for both r_g = 1.25r₀ and 1.50r₀. Interestingly, using slightly larger globules (1.50r₀) can serve to increase the available free volume by 30–50% compared with r_g = 1.25r₀ for all values of %g. This is opposite to the specific strength benefits, where the smaller globules (1.25r₀) result in a strength increase of 30–50% (in comparison with 1.50r₀; figure 8). Thus, the globule size indicates a trade-off between attained strength (figure 8) or desired free volume (figure 9), which may counteract each other (i.e. supercontraction increases strength and stiffness [70,73,82] and may supersede the benefits of shear interlock alone).

4. Discussion and conclusion

Here, I study nanoscale fibril aggregations (e.g. bundles), using a simple mechanical representation—essentially a colloidal string—to capture the underlying physical mechanisms, rather than determination of exact quantitative properties. Indeed, the modelled behaviour would be physically complicated by variation in fibril contact stiffness, or adhesion between fibrils, as examples. With such assumptions, the stress quantities described should be considered only order of magnitude approximations, compatible with previous studies [41]. That being said, computational results indicate that the introduction of a little disorder, i.e. heterogeneity in fibril cross sections, can be used as a mechanism to improve fibre strength through shear interlock as well as control accessible volume (e.g. enhancing hydration and potential supercontraction). At the same time, too much disorder (e.g. large globules) has a detrimental effect on strength. Future consideration of other silk types that undergo similar spinning (such as Bombyx mori silk [83] or other fibroins [84]) may help indicate the significance of the globules owing to their different biological roles (e.g. Bombyx mori silk used in cocoons compared with dragline silk in webs). That does not mean such features could not be introduced for synthetic applications of such materials [85–87]. Extending the model, such a mechanism could be generic to any hierarchical fibrous material, including synthetic polymers or textiles. Biological systems such as collagen [41] and nacre [52] have also been shown to benefit from similar mechanisms of shear transfer. There is also some evidence for such interlock in synthetic nanomaterials [68,88,89], but the effect is coupled with molecular bonding in addition to the mechanical transfer demonstrated.

While distinct morphological ‘globules’ are considered here, the effect can be reduced to a simple mode of shear transfer, whereby the same effect can be theoretically achieved through interfibril adhesion. The benefit of the distinct globules, however, is threefold (i) mechanical interlock only rather than chemical cross-linking or adhesion, (ii) constant material throughout and (iii) no requirement of order. The final benefit—lack of order—is conducive to the manufacturing approach of Nature, beleaguered with environmental uncertainties and energetic penalties for precision. Experimental studies indicated that, in contrast to our ideal model, silk threads and fibres contain main defects that can act as stress concentrators, such as cavities [38] and tears [39], yet still maintain high strength and toughness [90]. Here, what could be considered a ‘defect’ in terms of structure is beneficial to the overall behaviour of the fibre. In terms of spacing, each model was constructed with random distributions. While the sample set was limited, there was very little variance in the results (indicated by the error bars in all plots). In such a system, the randomness was an asset to the behaviour—ordered globules (e.g. regularly spaced) are not preferable to random distributions. Here, the mechanical benefits outweigh the potential material variance—as Nature itself is not limited to strict design criteria or allowances. The key is that disorder (or randomness) can be embraced as a design strategy itself, in certain circumstances such as increasing toughness [91], and is potentially less ‘costly’ than precision (i.e. homogeneity). Note too that there is no adhesion between fibrils, merely repulsion owing to contact. An increase in interfacial surface area and interfibril adhesion owing to globules may further enhance the effect. Moreover, the interfibril interaction would be even more critical under non-axial loading (e.g. bending or torsion) where shear transfer of stresses is more dominant throughout the cross section. The fact that the globule structure can also be implicated in the phenomena of supercontraction indicates a complex assortment of cooperative interactions resulting in the performance and biological use of silk.

In addition, while the globules here are modelled with constant material stiffness (e.g. contact rigidity) such may not be the universal case. The large globules have been associated with less protein density [7], and thus increasing globule size may reduce material rigidity. Also, thread stiffness has been seen to change under dynamic loading owing to molecular reorientation [57], which would likely propagate to the globules. Dynamic effects of hydration could also potentially alter the size and mechanical character of the globules from their original state [82,92], as supercontraction results in radial swelling [45]. The randomness and heterogeneity here is only a geometrical feature, and associated variation in globule properties (either initially, owing to strain, or implicitly owing to hydration) could greatly modify the results indicated, and warrant further investigation.

It is also known that the spinning process itself has influence on the mechanical and structural properties of silk, and a previous study has indicated that a spider may have control over such globules through the speed of silk spinning [7]. In effect, faster spinning results in smaller, but more oriented crystalline nodes within a fibril and a subsequent increase in globule size as more protein chains are aggregated through alignment [7]. Thus, is can be proposed that slight variation in spinning speed can result in heterogeneous fibrils, adding another layer of mechanical control. Perhaps efforts at producing synthetic silks, such as spider duct mimicking microfluidic techniques using constant spinning speeds [93,94], can improve the final silk threads through slight variations in speed to introduce ‘disorder’ and morphological control, already achievable with existing technologies [95]. Other techniques, such as electrospinning [83,96,97] or wet-spinning [98,99] may also be used to vary fibril radial size. In addition, the mechanism that induces variance in fibril radius (and globule distribution) is due to the crystallization of the peptide sequence during assembly. The potential to artificially synthesize high-performance silk—which thus far has failed to attain biological performance [100]—requires understanding of the molecular and supramolecular assembly across all scales, and not the simple replication of protein sequences [54]. While this may not be the only route to heterogeneous fibrils, it may provide a basis for synthetic approaches. Besides manipulating crystallization, alternative means—such as the introduction of nanoparticles [101,102]—could result in equivalent globular ‘bumpiness’.

Aside from mechanics, there is also a presumed benefit to free volume, allowing water/solvent percolation throughout the silk fibre. The globule distribution can be considered similar to the polydispersity of colloidal system, and a natural by-product of thread spinning/processing. In terms of the relation with supercontraction, it has been suggested that the production of silk with different tensile properties can increase the survival ability of the spider [72,103]. Recent experimental findings indicated that protein concentration had a significant effect on fibril morphology [54], whereas active control on the properties of the fibre during spinning [18] (rather than protein sequence) would allow an efficient adaptation of the properties of silk to the environment and local requirements. As such, spider speciation and silk type would dictate the fribril/fibre structure. An interesting evolutionary biology conjecture would be whether there is correlation between environmental conditions (e.g. humid versus dry), spider speciation and the appearance of irregular globules within the fibre cross sections.

The globules effectively create heterogeneous threads, breaking the symmetry of fibrillation and increasing interfibrillar cohesion. From bulk perspective, the threads resemble amorphous or glassy (rather than ordered, or crystalline) materials. Unlike crystalline systems, the mechanical properties of structural glasses are not dominated by topological defects such as cracks. Indeed, local structural arrangements and interactions engage more material as a toughening mechanism, with a material efficiency highly dependent on size of globule and packing density. Moreover, there is evidence of cavities and voids within silk fibres, which may be related to the globules discussed here. The influence of cavities and voids is essentially the inverse problem of the current investigation—instead of additional material (i.e. globules) what are the effects of taking material away? It could be presumed that cavities and voids would both increase effective toughness (through dispersion of stress concentrations) as well as influence supercontraction (through free volume, similar to here). In effect, they add to the ‘disorder’ of the system. The full ‘story’ of silk would necessarily include these contributions.

The effect on bundled fibres materials in terms of rheology, viscoelastic effects, creep deformation and ultimate failure mechanisms is yet to be determined. Nature has evolved means to exploit the full potential of such materials [27]. Just as the fibrils exploit the full mechanical potential of the nanoscale building blocks through nanoconfinement [37], silk fibres achieve the full potential of their constitutive elements (e.g. fibrils), at a scale approaching micrometres. The shear interlocking of silk fibrils demonstrates another mechanism to quantitatively explain the role of hierarchical structures seen in silk threads, from nano- to macro [28,37]. It has been previously shown that natural silks have unique advantages in toughness, processing efficiency and environmental issues, which still make it an attractive future advanced structural material—we can thereby learn from silk, exploiting the mechanisms optimized by evolution to develop synthetic analogues. Here, the focus is on mechanical performance (specifically in shear). Advantageously, rather than relying on materials properties of fibres/fibrils, the mechanism depicted here requires only morphological manipulation and/or design and thus may be applicable to a wide range of material systems from polymer fibres [104–106] to carbon nanotube systems [23].