A stability-based mechanism for hysteresis in the walk–trot transition in quadruped locomotion

Abstract

Quadrupeds vary their gaits in accordance with their locomotion speed. Such gait transitions exhibit hysteresis. However, the underlying mechanism for this hysteresis remains largely unclear. It has been suggested that gaits correspond to attractors in their dynamics and that gait transitions are non-equilibrium phase transitions that are accompanied by a loss in stability. In the present study, we used a robotic platform to investigate the dynamic stability of gaits and to clarify the hysteresis mechanism in the walk–trot transition of quadrupeds. Specifically, we used a quadruped robot as the body mechanical model and an oscillator network for the nervous system model to emulate dynamic locomotion of a quadruped. Experiments using this robot revealed that dynamic interactions among the robot mechanical system, the oscillator network, and the environment generate walk and trot gaits depending on the locomotion speed. In addition, a walk–trot transition that exhibited hysteresis was observed when the locomotion speed was changed. We evaluated the gait changes of the robot by measuring the locomotion of dogs. Furthermore, we investigated the stability structure during the gait transition of the robot by constructing a potential function from the return map of the relative phase of the legs and clarified the physical characteristics inherent to the gait transition in terms of the dynamics.

1. Introduction

Humans and animals vary their gaits depending on their locomotion speed. Humans have walking and running gaits, whereas quadrupeds have walking, trotting and galloping gaits. A gait is a characteristic locomotion pattern that is generated over a limited range of locomotion speeds; it is described by parameters that vary discontinuously at transitions [1]. In the walk–trot–gallop transitions of quadrupeds, the relative phase between the limbs (i.e. the interlimb coordination pattern) varies [1,2]. By contrast, in the walk–run transition of humans, the relative phase between the leg segments (i.e. the intralimb (or intersegmental) coordination pattern) changes [3]. Despite such gait transitions having been investigated from various viewpoints, including mechanics, energetics, kinematics and kinetics [4–8], their underlying mechanism remains largely unclear.

In both human and animal locomotions, gait transitions exhibit hysteresis [3,5,7–12]; in other words, the gait changes at different locomotion speeds depending on whether the speed is increasing or decreasing. However, the hysteresis mechanism is also unclear. Diedrich & Warren [3] proposed a potential function to explain the hysteresis, as shown in figure 1. This potential function depends on the locomotion speed and the relative phase between the limbs (leg segments). At low and high speeds, it is U-shaped with a single attractor in the valley. By contrast, at moderate speeds, it has a double-well shape and has one attractor in each of the two valleys. Therefore, as the locomotion speed increases, a walk jumps to a trot (run) at a critical speed (indicated by the red (black) balls). However, when the locomotion speed is reduced, a trot (run) jumps to a walk at a lower critical speed (indicated by the blue (grey) balls); thus, hysteresis occurs. Diedrich & Warren examined the energy expenditure and estimated the potential function for human walk and run from metabolic energy expenditure data. They demonstrated that the walk–run transition is consistent with the properties of the potential function.

Figure 1.

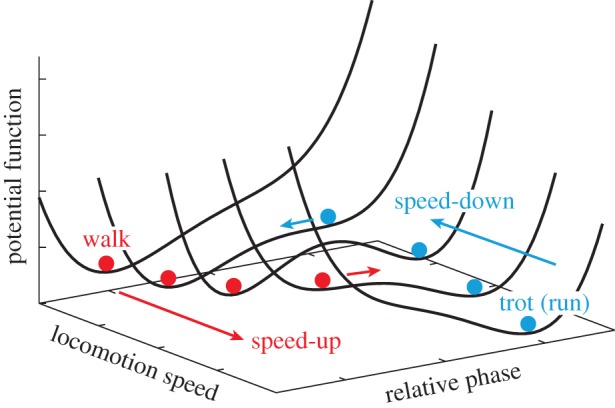
Hypothetical potential function that explains the hysteresis in the walk–trot (run) transition (adapted from [3]). (Online version in colour.)

In addition to energy expenditure, stability is a crucial factor in determining the gait [13] since, for each gait, there is a limited range of locomotion speeds in which stable locomotion occurs. It has been suggested that gaits correspond to attractors of their dynamics and that gait transitions are non-equilibrium phase transitions that are accompanied by a loss of stability [2]. The present study focuses on the dynamic stability of gaits to explain the hysteresis mechanism from a dynamic viewpoint. Specifically, if a potential function such as the one shown in figure 1 exists for locomotion speeds and gaits that explains the dynamic stability in a similar way to the Lyapunov function, it will explain the hysteresis.

So far, biomechanical and physiological studies have been independently conducted to elucidate the motions of humans and animals. Biomechanical studies mainly examine the functional roles of the musculoskeletal system, whereas physiological studies generally investigate the configurations and activities of the neural system. However, locomotion is a well-organized motion generated by dynamic interactions among the body, the nervous system and the environment. It is thus difficult to fully analyse locomotion mechanisms solely from a single perspective. Integrated studies of the musculoskeletal and nervous systems are required.

Owing to their ability to overcome the limitations of studies based on a single approach, constructive approaches that employ simulations and robots have recently been attracting attention [14–22]. Physiological findings have enabled reasonably adequate models of the nervous system to be constructed, while robots have become effective tools for testing hypotheses of locomotor mechanisms by demonstrating real-world dynamic characteristics. We have demonstrated hysteresis in a walk–trot transition using a simple body mechanical model of a quadruped and an oscillator network model based on the physiological concept of the central pattern generator (CPG) [23]. In the present study, we design a quadruped robot to examine its gaits by varying the locomotion speed. We evaluate these gait changes by measuring locomotion in dogs. Furthermore, we investigated the stability structure by constructing a potential function using the return map obtained from robot experiments and by comparing it with that proposed by Diedrich & Warren to clarify the physical characteristics inherent in the gait transition of quadruped locomotion.

2. Material and methods

2.1. Mechanical set-up of quadruped robot

Figure 2 shows a quadruped robot that consists of a body and four legs (legs 1–4). Each leg consists of two links connected by pitch joints (joints 1 and 2) and each joint is manipulated by a motor. A touch sensor is attached to the tip of each leg. Table 1 lists the physical parameters of the robot.

Figure 2.

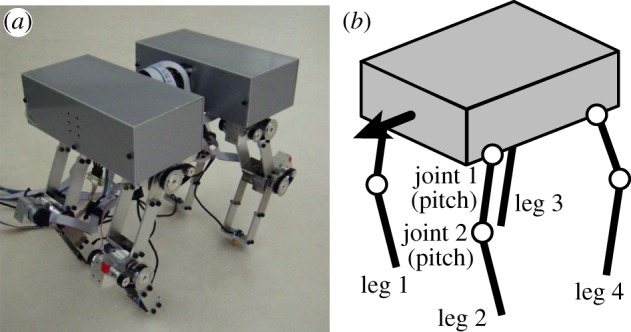
(a) Quadruped robot and (b) schematic model. (The robot body consists of two sections that are mechanically attached to each other.) (Online version in colour.)

Table 1.

Physical parameters of quadruped robot.

link	parameter	value
body	mass (kg)	1.50
	length (cm)	28
	width (cm)	20
upper leg	mass (kg)	0.27
	length (cm)	11.5
lower leg	mass (kg)	0.06
	length (cm)	11.5

The robot walks on a flat floor. Electric power is externally supplied and the robot is controlled by an external host computer (Intel Pentium 4, 2.8 GHz, RT-Linux), which calculates the desired joint motions and solves the oscillator phase dynamics in the oscillator network model (see §2.2). It receives command signals at intervals of 1 ms. The robot is connected to the electric power unit and the host computer by cables that are slack and suspended during the experiment so that they do not affect the locomotor behaviour.

2.2. Oscillator network model

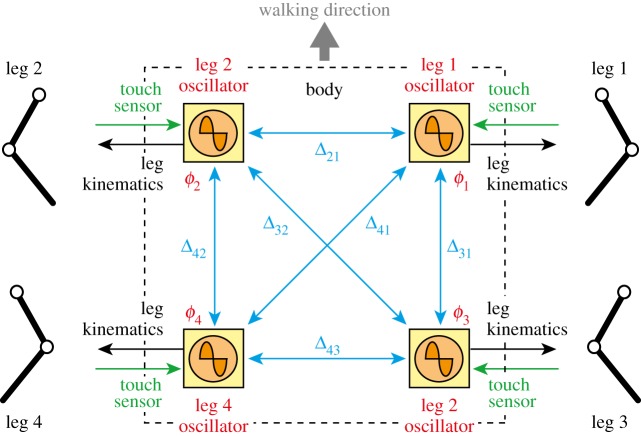
Physiological studies have shown that the CPG in the spinal cord strongly contributes to rhythmic limb movement, such as locomotion [24]. To investigate animal locomotion using legged robots, locomotion control systems have been constructed based on the concept of the CPG [16,17,19,21,22]. The CPG has been suggested to consist of hierarchical networks composed of rhythm generator (RG) and pattern formation (PF) networks [25]. The RG network generates the basic rhythm, and the PF network shapes the rhythm into spatio-temporal patterns of motor commands. We used an oscillator network model to control our robot (figure 3); it was constructed based on a two-layer network model composed of RG and PF models [23].

Figure 3.

Oscillator network model with four oscillators. The oscillators interact with each other based on the relative phase Δ_ij. The oscillator phases are modulated by touch sensor signals. The oscillator phases determine the leg joint kinematics. (Online version in colour.)

2.2.1. Rhythm generator model

We used four simple phase oscillators (leg 1–4 oscillators) to generate the basic rhythm and phase information for the corresponding leg based on commands related to the desired speed and gait. They receive touch sensor signals to modulate the rhythm and phase information. We denote the phase of leg i oscillator by ϕ_i (i = 1, … ,4, 0 ≤ ϕ_i < 2π), which follows the dynamics

2.1

where ω is the basic oscillator frequency (it has the same value for all four oscillators), g_1i is related to the interlimb coordination (see §2.2.3) and g_2i is the phase and rhythm modulation in response to touch sensor signals (see §2.2.4).

2.2.2. Pattern formation model

Recent physiological studies have shown that spinocerebellar neurons receive sensory signals from proprioceptors and cutaneous receptors and encode global information about limb kinematics such as the length and orientation of the limb axis [26,27]. We used the PF model to determine these global parameters based on the oscillator phase ϕ_i from the RG model and to produce motor torques for generating the desired kinematics.

Locomotion in humans and animals involves propelling the centre of mass forward. To achieve this, the swing limb is moved forward. When the limb touches the ground, it supports the body and produces a propulsive force from the ground. We designed a simple leg kinematics determined by the length and orientation of the limb axis in the pitch plane, which consists of the swing and stance phases (figure 4). The swing phase consists of a simple closed curve for the leg tip that includes the anterior extreme position and the posterior extreme position (PEP). It starts from the PEP and continues until the leg touches the ground. The stance phase is a straight line from the LP to the PEP. During this phase, the leg tip moves in the opposite direction to the body. The body travels in the walking direction while the leg tips are in contact with the ground.

Figure 4.

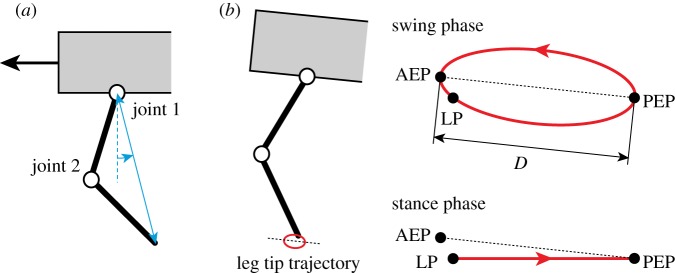
Desired joint kinematics of fore legs. (a) Length and orientation of the limb axis. (b) Leg tip trajectory consisting of swing and stance phases. The swing phase is a closed curve that includes the anterior extreme position (AEP) and the posterior extreme position (PEP). The line segment between the AEP and the PEP is parallel to the body. The stance phase is a straight line from the landing position (LP) to the PEP. When the leg lands on the ground, the trajectory changes from the swing to the stance phase. When the leg tip reaches the PEP, the trajectory moves into the swing phase. Joint 2 of the hind legs has a different bending direction from that of the fore legs. (Online version in colour.)

We denote the distance between the AEP and the PEP by D. We use T_sw and T_st for the nominal swing and stance phase durations, respectively, for the case when the leg tip contacts the ground at the AEP (LP = AEP). The nominal duty factor β, the basic frequency ω in (2.1), the nominal stride length S and the nominal locomotion speed v are, respectively, given by

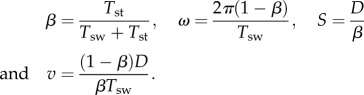2.2

In the present study, we used D = 1.0 cm and T_sw = 0.14 s and varied v by changing β through T_st in the same manner as in the motion of humans and animals [28,29], where ω and S also vary with β. We used the same values of these parameters for all the legs. Although the stride length is relatively small, we determined these parameters such that stable locomotion was generated at all locomotion speeds in the range considered in this study.

These two trajectories for the swing and stance phases are given as functions of the corresponding oscillator phase, where we used ϕ_i = 0 at the PEP and ϕ_i = ϕ_AEP (=2π(1 − β)) at the AEP. Therefore, the desired joint kinematics is given as a function of the oscillator phase and each joint is controlled by the joint torque based on PD feedback control to produce the desired kinematics.

2.2.3. Gait pattern

Since the leg kinematics is determined by the corresponding oscillator phase, the interlimb coordination pattern is determined by the relative phase between the oscillators. We denote this by the matrix Δ_ij = ϕ_i − ϕ_j (i, j = 1, …, 4, 0 ≤ Δ_ij < 2π). Since the relations Δ_ij = −Δ_ji, Δ_ij = Δ_ik + Δ_kj and Δ_ii = 0 (i, j, k = 1, …, 4) are satisfied, the gait is determined by three state variables, such as [Δ₂₁ Δ₃₁ Δ₄₃]. For example, [Δ₂₁ Δ₃₁ Δ₄₃] = [π π/2 π] is satisfied for walking, and [Δ₂₁ Δ₃₁ Δ₄₃] = [π π π] is satisfied for trotting (figure 5) [22,23,30–32].

Figure 5.

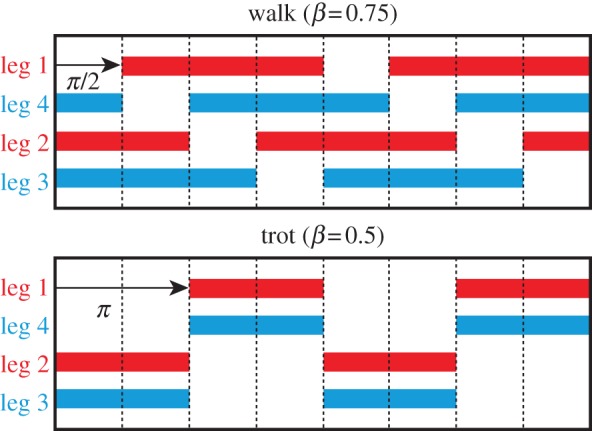
Schematic of footprint for walking (β = 0.75) and trotting (β = 0.5), where the right and left legs move in antiphase (red (black): fore legs; blue (grey): hind legs). (Online version in colour.)

Function g_1i in (2.1) manipulates this relative phase. It is given by

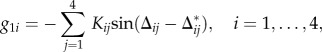2.3

where Δ_ij^* is the desired relative phase determined by the desired gait and K_ij (i, j = 1, …, 4) is the gain constant (K_ij ≥ 0). When Δ_ij is shifted from Δ_ij^* (Δ_ij = Δ_ij^* +δΔ_ij), from (2.1) we can approximately obtain

2.4

where we neglect the function g_2i. When a large value is used for K_ij, δΔ_ij quickly converges to 0 (figure 6) and we assume that Δ_ij = Δ_ij^* is satisfied.

Figure 6.

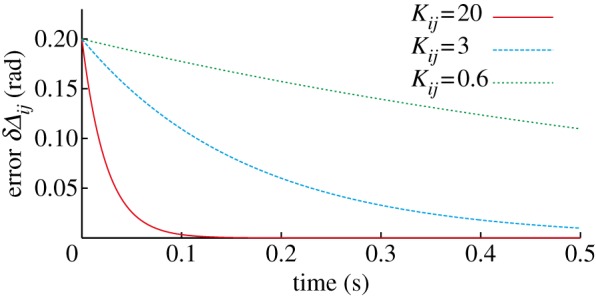
Convergence rate of the error δΔ_ij for the gain parameter K_ij (K_ji = K_ij). (Online version in colour.)

2.2.4. Phase resetting

Although the CPG can produce oscillatory signals even without rhythmic input and proprioceptive feedback, sensory feedback is required to generate adaptive and effective locomotion. Spinal cats produce locomotion on treadmills and their gait changes with the speed [24,34], suggesting that tactile sensory information influences the locomotor phase and rhythm generated by the CPG [35]. The locomotor rhythm and phase have been shown to be modulated by producing phase shift and rhythm resetting based on sensory afferents and perturbations (phase resetting) [25,36,37].

We modulated the locomotor rhythm and phase based on such a phase resetting mechanism in response to touch sensor signals using the function g_2i. When leg i lands on the ground, the phase ϕ_i of leg i oscillator is reset to ϕ_AEP. Therefore, g_2i is given by

2.5

where t_landⁱ is the time when leg i contacts the ground and 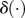denotes the Dirac delta function. The touch sensor signals not only modulate the locomotor rhythm and phase but also switch the leg movements from the swing to the stance phase, as described in §2.2.2.

2.3. Robot experiment

2.3.1. Constraints for gait

The relative phase between the oscillators determines the gait of our robot, which is produced by interactions among the oscillators (2.3) and sensory regulation by phase resetting (2.5). When we use neither (2.3) nor (2.5), the relative phase remains in the initial state and the gait does not change. When all the elements of matrix Δ_ij^* are determined based on the desired gait and large values are used for the gain constants K_ij in (2.3), the robot will establish the desired gait when the gait becomes stable. By contrast, when small values are used for K_ij, the robot can generate a different gait from the desired one due to sensory regulation through phase resetting (2.5).

The present study focuses on the gait in which the right and left legs move in antiphase. That is, we use Δ₂₁^* = Δ₄₃^* = π and a large value for K₁₂, K₂₁, K₃₄ and K₄₃ (K₁₂ = K₂₁ = K₃₄ = K₄₃ = 20). Therefore, Δ₂₁ = Δ₄₃ = π is generally satisfied so that there are two constraints for the three state variables of the gait. Under this condition, the gait is determined by the relative phase between the fore and hind legs, such as Δ₃₁. Throughout this paper, we investigate the gait based on Δ₃₁.

We also used the desired value for Δ₃₁ in which the ipsilateral legs move in antiphase; that is, Δ₃₁^* = π (Δ₄₂^* = π). This means that the desired gait is the trot. We used K₁₃, K₃₁, K₂₄ and K₄₂ for this interlimb coordination and set the other K_ij to zero. However, we used as small values as possible for K₁₃, K₃₁, K₂₄ and K₄₂ (K₁₃ = K₃₁ = K₂₄ = K₄₂ = 0.6) to minimize this influence and to allow the robot to change its gait from the desired gait through locomotion dynamics due to sensory regulation by phase resetting (2.5).

2.3.2. Experimental procedure

To examine the stability structure of the gaits dependence on the locomotion speed, we first investigated the gaits the robot generates at different speeds (see §3.1). We then slowly increased or reduced the speed using the duty factor and examined how the gait changed (see §3.2). To evaluate the gait stability, we obtained the first return map and constructed the potential function, as explained, respectively, in §2.4.1, 2.4.2 (see §3.3, 3.4). In addition to the gait stability, we also investigated the energy expenditure (see §3.2) by calculating the cost of transport μ using

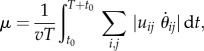2.6

where T is the gait cycle and u_ij and θ_ij are, respectively, the motor torque and rotation angle of joint j of leg i (i = 1, …, 4, j = 1,2).

2.4. Gait stability analysis

2.4.1. First return map

Under the constraints (Δ₂₁ = Δ₄₃ = π), the gait of our robot is determined by the dynamics of Δ₃₁, which is given from (2.1), (2.3) and (2.5) by

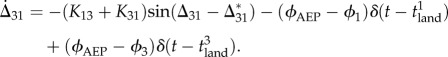2.7

Clearly, the trot is the only attractor (Δ₃₁ = Δ₃₁^*(=π)) without sensory regulation (2.5). Although regulation influences the stability, Δ₃₁ generates a stable periodic behaviour when the robot establishes a stable gait. To investigate the stability, we obtained the first return map of Δ₃₁ by plotting the relationship between Δ_31n at the foot-contact of leg 1 for the nth step and Δ_31n+1 for the next step. We can determine possible gaits and their stabilities from the intersection with the diagonal line (Δ_31n+1 = Δ_31n).

2.4.2. Potential function

To construct a potential function, we approximated the obtained return map by Δ_31n+1 = P(Δ_31n) using an polynomial, whose order we selected to reduce the error, and defined δΔ by

2.8

We consider the range 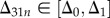and denote the integration of −δΔ from Δ₀ to Δ_31n (≤Δ₁) by

2.9

We define the potential function V by

2.10

This satisfies V > 0 for 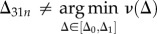. The stability is verified by

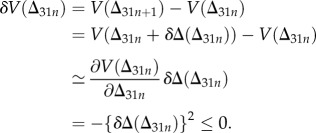2.11

This equality is satisfied only for δΔ = 0.

2.5. Empirical experiments with dogs

To evaluate the gait of our robot, we used two adult male Labrador Retriever dogs (26 and 32 kg) that had been trained as guide dogs. Reflective markers were attached to the standard bony landmarks of the fore and hindlimbs of the dogs; the humeral head, the estimated joint centre of the elbow, the distal head of the ulna, the metacarpo-phalangeal joint, and the distal phalanx of the third digit for the forelimbs; the femoral head, the estimated joint centre of the knee, the lateral malleolus, themetatarso-phalangeal joint and the tip of the third digit for the hindlimbs. Additional markers were attached to the head and the trunk. They walked on a treadmill (ITR3017, Bertec Corporation) whose speed changed between 0.5 and 2 m s⁻¹ at a rate of 0.05 m s⁻². After training them to walk on the treadmill, their motions were measured using a motion capture system (Digital RealTime System, Motion Analysis Corporation) at a sampling rate of 500 Hz.

We numbered the four limbs (limbs 1–4) in the same manner as for the robot and calculated the relative phases between the limbs from the foot contact timings to determine their gaits [13,38,39]. We denote the relative phase by Δ_ij^dog (i, j = 1, …, 4, 0 ≤ Δ_ij^dog < 2π), which is given by

2.12

where t_i^dog is the time when limb i touches the treadmill belt and T^dog is the gait cycle of limb 1.

3. Results

3.1. Dependence of walk and trot generation on speed

We first investigated the gaits that the robot generates at v = 7 cm s⁻¹ (β = 0.5) and 2.3 cm s⁻¹ (β = 0.75). We used three initial values for Δ₃₁ and investigated where Δ₃₁ converges.

Figure 7 shows Δ₃₁, plotted when leg 1 touches the ground. For v = 7 cm s⁻¹, Δ₃₁ converged to about 2.4 rad, indicating that the robot established the trot at a high speed. Although Δ₃₁ = 2.4 rad differs slightly from π rad, we considered this motion to be the trot to distinguish it from the walk described below (we discuss this difference in §4.6). By contrast, Δ₃₁ converged to about 1.6 rad for v = 2.3 cm s⁻¹, indicating that the robot performed the walk at a low speed. In other words, the robot established a different gait from the desired gait (trot) due to sensory regulation by phase resetting through locomotion dynamics.

Figure 7.

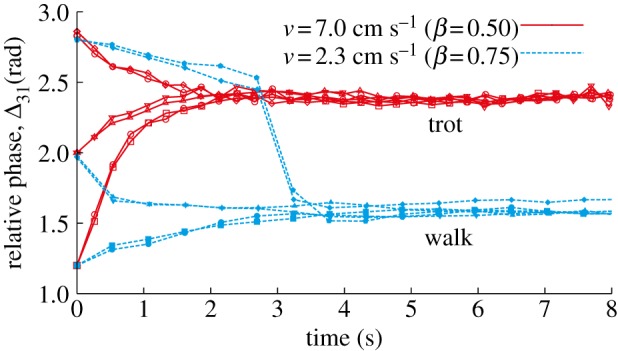
The relative phase Δ₃₁ plotted at contact of leg 1 for three initial values with v = 7 cm s⁻¹ (β = 0.5) and 2.3 cm s⁻¹ (β = 0.75). Two experimental results are shown for each initial value. For v = 7 cm s⁻¹, the relative phase converges to about 2.4 rad (trot), while it converges to about 1.6 rad (walk) for v = 2.3 cm s⁻¹. (Online version in colour.)

3.2. Hysteresis in the walk–trot transition of robot and dogs

After our robot established a stable gait, we slowly increased the locomotion speed v from 2.3 to 7 cm s⁻¹ by reducing the duty factor β from 0.75 to 0.5 or we reduced v from 7 to 2.3 cm s⁻¹ by increasing β from 0.5 to 0.75. We investigated how the gait changed through locomotion dynamics.

Figure 8a shows Δ₃₁ for six trials in which the locomotion speed was increased and reduced by β (figure 8b). Δ₃₁ varied between 2.4 and 1.6 rad, indicating that the gait changed between the walk and trot (see electronic supplementary material, movies S1–S4). When we reduced the locomotion speed, the trot transitioned to the walk at about v = 4 cm s⁻¹ (β = 0.64). By contrast, when we increased the locomotion speed, the walk changed to the trot at about v = 5.0 cm s⁻¹ (β = 0.58). This means that the gait transition occurs at different speeds depending on the direction of the speed change (i.e. hysteresis occurs). Figure 8c shows the footprint diagrams during the trot-to-walk and walk-to-trot transitions.

Figure 8.

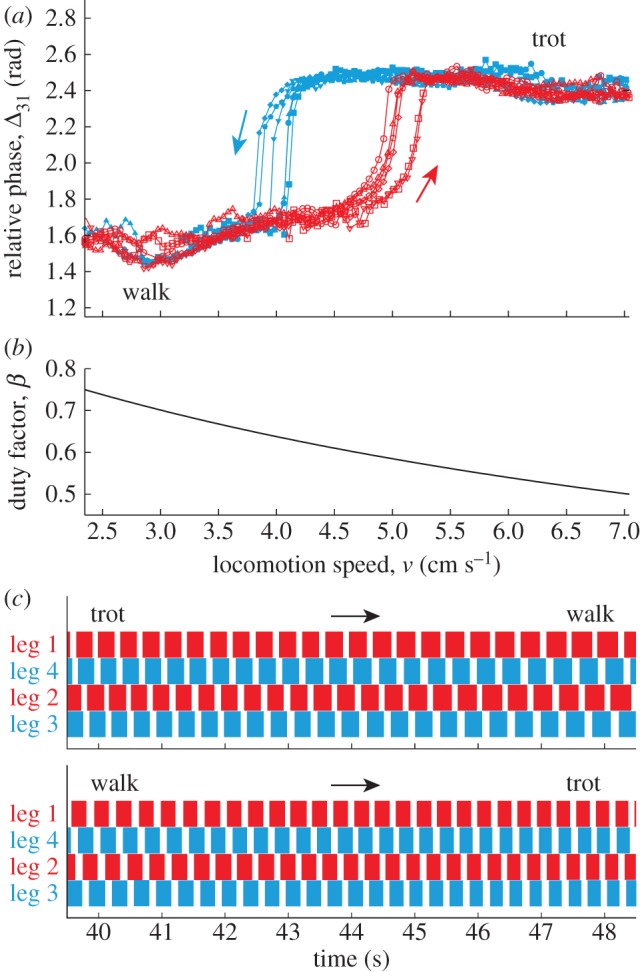
Gait transition induced by changing the locomotion speed v. (a) Relative phase Δ₃₁. Six experimental results are shown for increasing and decreasing the speed. Walk-to-trot and trot-to-walk transitions occur at different speeds and hysteresis appears. (b) Duty factor β. (c) Footprint diagrams during trot-to-walk and walk-to-trot transitions. (Online version in colour.)

Figure 9a shows the cost of transport μ/μ₀ during the gait transition, where μ₀ is the average cost for the trot using 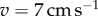. When the gait transition occurs, the cost of transport suddenly decreases. To clearly show this change, we calculated the average of μ/μ₀ over an interval of 0.5 cm s⁻¹ for each speed (bold line) and show the deviation from this average (figure 9b). The deviation increases by changing the locomotion speed in the region where the hysteresis loop exists (4–5 cm s⁻¹) and it suddenly decreases at the gait transition. This implies that the robot changes the gait to reduce the cost of transport. The cost of transport decreases more at the trot-to-walk transition than at the walk-to-trot transition, which reflects that the trot-to-walk transition occurs more rapidly than the walk-to-trot transition, as shown in figure 8a.

Figure 9.

Change in cost of transport during the gait transition. (a) Cost of transport μ/μ₀ and average cost of transport. (b) Deviation from the average. (Online version in colour.)

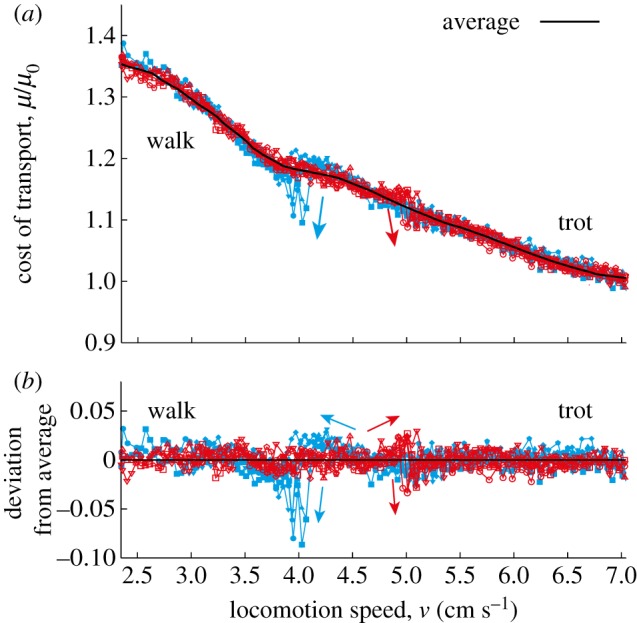
To evaluate the gait changes in the robot, we measured locomotion of dogs. Figure 10 shows the relative phases and duty factors of a dog when the belt speed was varied. The relative phases between the right and left limbs (Δ₂₁^dog in figure 10b and Δ₄₃^dog in figure 10c) remain almost antiphase. In contrast, as the speed was increased, the relative phase between the right fore and hindlimbs (Δ₃₁^dog in figure 10a) increased and the walk transitioned to the trot. When the speed was reduced, the relative phase decreased and the trot changed to the walk. The duty factors (figure 10d,e) decreased (increased) as the speed was increased (decreased). The relative phases and duty factors obtained for the walk and trot are consistent with the results of previous studies [1,40–43]. Although the transition speeds fluctuate slightly, walk-to-trot and trot-to-walk transitions occur at different speeds, indicating the occurrence of hysteresis. The results of the robot experiments are consistent with these observations. Although data are shown for only one dog, the results for the other dog exhibit similar trends.

Figure 10.

Gait transition in a dog induced by changing the belt speed. (a) Relative phase Δ₃₁^dog between the right fore and hindlimbs, (b) relative phase Δ₂₁^dog between the right and left forelimbs, (c) relative phase Δ₄₃^dog between the right and left hindlimbs, (d) duty factor of right forelimb, and (e) duty factor of left hindlimb. Six trials are shown for increasing and decreasing speed. (Online version in colour.)

3.3. First return map for various speeds

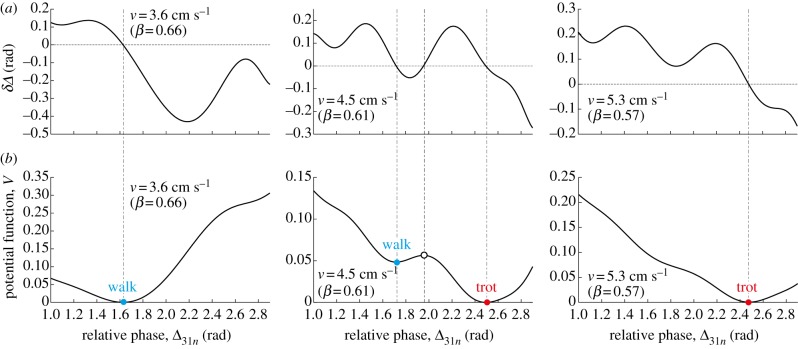
Figure 11 shows the return map obtained for various initial conditions in the robot experiment with v = 3.6 (β = 0.66), 4.5 (β = 0.61) and 5.3 cm s⁻¹ (β = 0.57). The bold lines indicate the approximated functions, where we used an eighth-order polynomial for v = 3.6 and 5.3 cm s⁻¹ and a 10th-order polynomial for v = 4.5 cm s⁻¹. When v = 3.6 cm s⁻¹, the return map shows that there is only one intersection with the diagonal line and the walk is the only attractor. However, for v = 4.5 cm s⁻¹, three intersections appear and there are two stable gaits (trot and walk) and one unstable gait between the stable gaits (indicated by the open dot). When v = 5.3 cm s⁻¹, the walk disappears due to the loss of the two intersections and the trot becomes the only attractor. The gait stability passes through the saddle-node bifurcation twice. There is a saddle-node ghost around Δ_31n = 2.5 rad for v = 3.6 cm s⁻¹ and Δ_31n = 1.8 rad for v = 5.3 cm s⁻¹.

Figure 11.

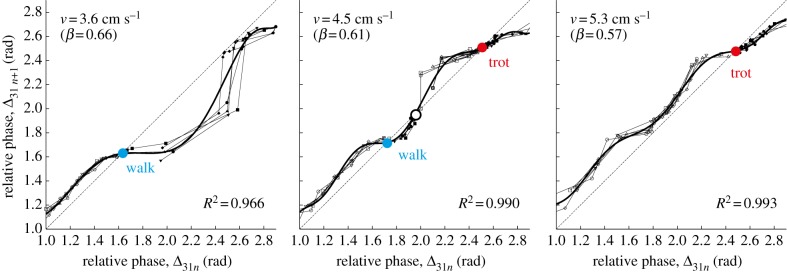
Return map of the relative phase Δ₃₁ for v = 3.6 (β = 0.66), 4.5 (β = 0.61) and 5.3 cm s⁻¹ (β = 0.57). Bold lines are approximated functions obtained using polynomials. (Online version in colour.)

3.4. Potential function for various speeds

Finally, we constructed the potential function V from the approximated return maps, where we used Δ₀ = 1.0 and Δ₁ = 2.9 rad. Figure 12a,b shows δΔ and V, respectively. When v = 3.6 and 5.5 cm s⁻¹, V is unimodal and the valley corresponds to δΔ = 0, which is the only attractor. By contrast, when v = 4.6 cm s⁻¹, V is double-well shaped and the hill and valleys correspond to δΔ = 0. The hill is a repeller and only the valleys are attractors. These potential functions obtained are consistent with the hypothetical potential function (figure 1) proposed to explain the hysteresis.

Figure 12.

(a) δΔ and (b) potential function V for v = 3.6 (β = 0.66), 4.5 (β = 0.61) and 5.3 cm s⁻¹ (β = 0.57). (Online version in colour.)

4. Discussion

4.1. Switching rhythmic motions accompanied by loss of stability

To emulate the dynamic locomotion of a quadruped, we developed a quadruped robot for the body mechanical model and used an oscillator network for the nervous system model, which was inspired from the biological systems. The robot produced the walk and trot depending on the locomotion speed and exhibited a walk–trot transition with hysteresis (figure 8). This is not because we intentionally designed the robot movements to produce the gait transition and hysteresis; rather, it is because the stability structure changes through the interaction between the robot dynamics, the oscillator dynamics and the environment.

Spontaneous switches in the coordination pattern of rhythmic human motions have been investigated from the viewpoint of a non-equilibrium phase transition in synergetics [44–46]. In this viewpoint, emerging patterns are characterized only by order parameters that have low-dimensional dynamics. In these investigations, an oscillator phase is used as an order parameter to examine the relative phase between the rhythmic motions and a potential function is used to construct the phase dynamics. Observable patterns correspond to attractors of the dynamics and the switch is accompanied by a loss of stability. The loss of stability has been measured in various experiments using theoretically based measures of stability (such as the relaxation time) to clarify the nature of the switching process. Schöner et al. [2] used a synergetic approach to investigate quadrupedal gaits and suggested that the gaits correspond to attractors of their dynamics and that gait transitions are non-equilibrium phase transitions accompanied by a loss of stability. Gait transitions could be interpreted as bifurcations in a dynamic system.

We clarified the changes in the stability structure of gaits by generating return maps (figure 11) and potential functions (figure 12). The present results show that the walk and trot produced are attractors of the integrated dynamics of the robot mechanical and oscillator network systems and that the gait stability changes twice through the saddle-node bifurcation (figure 11). These results provide dynamic confirmation of the suggestion of Schöner et al.

4.2. Clarifying stability structure using a potential function

Locomotion in humans and animals is a complex nonlinear dynamic phenomenon that involves the nervous system, the musculoskeletal system and the environment. Consequently, it is difficult to clarify stability structures inherent in the dynamics. In the switches of coordination pattern in rhythmic human motions [44–46], the relaxation time of the order parameter was measured to investigate the loss of stability from a viewpoint of the non-equilibrium phase transition, which is the time until the order parameter returns to its previous steady-state value after being disturbed close to the attractor. In our experiments, we perturbed Δ₃₁ from its steady-state value and constructed return maps from the expansion of Δ₃₁ after perturbation (figure 11). This enabled us to show the global stability of the gait dynamics.

In addition, we constructed potential functions from the obtained return maps (figure 12). This allows us to discuss the relationship with the previous study by Diedrich & Warren [3] regarding the hysteresis mechanism and further clarify changes to the stability structure due to the locomotion speed. At a low speed (v = 3.6 cm s⁻¹) and a high speed (v = 5.5 cm s⁻¹), the potential functions obtained are unimodal. On the other hand, at a moderate speed (v = 4.6 cm s⁻¹), the potential function has a double-well shape. The shapes of these potential functions are consistent with that proposed by Diedrich & Warren [3] to explain the hysteresis in the gait transition.

Hysteresis is a typical characteristic of nonlinear dynamic systems [47]. In our system, the dynamics of Δ₃₁ (2.7) contains nonlinearities such as delta functions. There is no general method for deriving a potential function (such as the Lyapunov function) for nonlinear dynamical systems to show their stability. We reduced the continuous dynamical system (2.7) to a discrete dynamical system of Δ_31n using the return map. This allowed us to construct a potential function and to clarify the stability structure. Our approach of constructing a potential function from the return map provides a useful methodology for clarifying the global stability structure of complex nonlinear dynamic systems as well as the locomotion dynamics of humans and animals.

4.3. Neural mechanism for interlimb coordination in biological systems

The cerebellum is involved in the neural mechanism for interlimb coordination [48,49]. A copy of the motor command (efference copy) is sent from the spinal CPG to the cerebellum through the ventral spinocerebellar tract (VSCT), while the sensory information is fed back to the cerebellum through the dorsal spinocerebellar tract. Purkinje cells produce the output of the cerebellum from these inputs to modulate motor commands. The locomotion of cats with selective lesions of the VSCT [50] and of mice in which the function of Purkinje cells was blocked by the targeted deletion of metabotropic glutamate receptor-subtype 1 (mGluR1) gene (mGluR1-null mutant mice) [51] and by the degeneration of Purkinje cells in Lurcher mutant mice [52] exhibited severely impaired interlimb coordination.

For a decerebrate cat walking on a splitbelt treadmill that has three moving belts (one mounted under the left forelimb, another under the left hindlimb and the third under the right forelimb and right hindlimb) [53,54], increasing the belt speed of the left forelimb induced unstable locomotor behaviour. However, after a certain number of steps, the cat generated a new stable gait. When the belt speed was returned to its original speed, the cat continued to walk with the new gait. However, after a while, the cat gradually returned to its original gait. In other words, after effects were observed in this gait adaptation. These results suggest that the cat adapted to a new environment by learning and storing a new interlimb coordination in its nervous system. Such gait adaptation was abolished by injecting with haemoglobin, a nitric oxide (NO) scavenger, or N^G-monomethyl-l-arginine (L-NMMA), a NO synthase inhibitor, which causes defects in the function of Purkinje cells [54]. In addition, similar adaptation in interlimb coordination was observed in human walking on a splitbelt treadmill [55,56] and cerebellar gait ataxia significantly impaired this adaptation [55]. Injecting an antibody of the orphan glutamate receptor δ2 (GluRδ2) into Purkinje cells in mice impaired motor learning with gait ataxia [57].

The cerebellum has been suggested to contain an internal model that plays an important role in motor learning and control [58,59]. It provides feed-forward motor commands through learning, which allows time delays associated with feedback control to be overcome and smooth and effective movements to be generated. Ito et al. [60] modelled adaptation with learning for interlimb coordination in a decerebrate cat walking on a splitbelt treadmill. They used a potential function for the relative phases between the limb movements whose minimum point corresponds to the desired relative phase. They modulated the desired relative phase to minimize the potential function to learn and store a new gait. Their model demonstrates gait adaptation in quadruped locomotion and their simulation results exhibit aftereffects in gait adaptation.

Through the robot experiments, we also generated a potential function for the relative phases between the leg movements. Its minimum point corresponds to a stable gait (figure 12). When this is stored in the control system of the robot and is used to control the interlimb coordination in a similar manner as the cerebellar function, the robot changes its gait with the locomotion speed and hysteresis appears without sensory feedback from the structure of the potential function. This is consistent with the hypothetical gait adaptation mechanism in biological systems [60]. To further understand the gait adaptation mechanism that includes aftereffects, we intend to develop a more plausible model as the learning process in the cerebellum in future studies.

4.4. Roles of sensorimotor coordination in gait generation and transition

Oscillator network models have been developed to investigate gait transitions in quadruped locomotion [2,60–62]. However, they consider only the nervous system; they do not incorporate the contribution of body mechanical systems. A nervous system model alone or a body mechanical system model alone cannot fully explain the locomotion mechanisms since neuromechanical interactions are crucial in animal locomotion [63,64]. Our results reveal that while the trot is the only attractor without sensory feedback from the robot mechanical system to the oscillator network system (phase resetting), the sensory modulation altered the gait stability and produced a different gait. This demonstrates the important contribution of the body mechanical system to gait generation.

We used phase resetting (2.5) in the sensory regulation model. This modulates the locomotor phase based on foot contact to switch the leg movements from the swing to stance phase. During locomotion, the swing leg is raised and swung forward, while the stance leg supports the body and generates a propulsive force from the ground. As the swing and stance legs play completely different roles in locomotion, adequate switching of motor commands based on foot-contact information is crucial. The phase resetting contributes to this adequate switching. This sensory regulation have generated adaptive locomotion in both rigid robots with quick responses to sensory information [65–68] and compliant musculoskeletal systems with a delay to generate muscle tension and to transmit sensory information [69–72]. In the present study, this sensory regulation contributed to adaptive gait generation at different speeds.

Taga et al. [73] conducted a pioneering study of computer simulation for human locomotion by employing a CPG model. They employed an articulated multi-link system for the body mechanical model and an oscillator network for the CPG model. They demonstrated that adaptive locomotion is established through the interaction between the body dynamics, the oscillator dynamics and the environment; they called this ‘global entrainment’. In addition, they demonstrated that the gait changes between the walking and running gait with the locomotion speed and that a gait transition with hysteresis appears. Our results reveal a gait transition with hysteresis for quadrupedal locomotion due to the interaction between the robot dynamics, the oscillator dynamics and the environment. They are consistent with Taga et al.'s results.

4.5. Determinants of gait transitions

To clarify the determinants of gait transitions, most studies have searched for a potential trigger that changes the gait. Margaria [74] and Hoyt & Taylor [6], respectively, showed that humans and horses employ gaits that minimize metabolic energy expenditure and they suggested that humans and animals switch gaits to reduce the metabolic cost of locomotion. Our results reveal that the robot changed its gait to reduce energy expenditure (figure 9). However, this does not imply that the robot selected the gait to minimize the energy expenditure, as the locomotion control system did not seek to reduce it.

Farley & Taylor [4] state that it is difficult to imagine how animals can sense metabolic cost in rapid gait transitions; rather, they consider that an another criterion (e.g. biomechanical factors) may act as the trigger. They demonstrated that the musculoskeletal force level triggered the gait transition. Griffin et al. [5] investigated the walk–trot transition based on the inverted-pendulum model and suggested that biomechanical and metabolic factors are tightly coupled at the gait transition. However, there are many conflicting reports regarding the roles of metabolic and biomechanical factors in determining gait transitions [7,75–78].

An alternative approach is based on dynamic systems analysis, as conducted in the studies of Diedrich & Warren [3], Schöner et al. [2], Ito et al. [60] and Taga et al. [73]. In this approach, gaits are viewed as the results of self-organization in complex dynamic system and gait transitions occur when the stability of a gait decreases so much that switching to a new gait improves stability [5]. The present study adopts this approach.

4.6. Limitations of our approach and future work

We used a robotic platform to investigate quadrupedal locomotion. However, there are differences between the robot and actual quadrupeds. For example, the robot is rigid and kinematically controlled by motors, whereas quadrupeds are compliant and dynamically driven by muscles. Our robot has much simpler mechanical and locomotion control systems than biological systems. In addition, we used short stride lengths for the robot. These differences cause quantitative differences in locomotion.

For example, the robot took about eight steps in the walk-to-trot transition and five steps in the trot-to-walk transition (figure 8), whereas the dog took about five steps in the walk-to-trot transition and four steps in the trot-to-walk transition (figure 10). Thus, the transition speed differs between the robot and dog. This may reflect differences in the gait stability of their dynamics; in other words, different divergence rate after a gait becomes unstable and different convergence rate to a stable gait. For the robot locomotion, we determine the convergence rate around the stable gait from the inclination of the return map at the intersection with the diagonal line. The approximate return maps in figure 11 give inclinations of 0.13 for the walk (v = 3.6 cm s⁻¹) and 0.19 for the trot (v = 5.3 cm s⁻¹), showing that the walk has a faster convergence rate than the trot. When it becomes possible to derive the return map from measuring dog locomotion in the future, this will enhance the understanding of the stability structure and the gait transition mechanism in dog locomotion.

Another important qualitative difference is in the relative phase in the trot. When the locomotion speed of the robot was increased, the relative phase Δ₃₁ changed greatly from π/2 rad (figure 8). In other words, the robot changed its gait from the walk. However, the relative phase did not reach π rad, which corresponds to the trot. This implies that the diagonal legs did not completely synchronize. This limitation may reflect that the robot did not use the spring–mass mechanism well because of the mechanical limitations [39]. This gait may be closer to the tölt [79–81], rather than the trot, which Icelandic horses often exhibit over a large range of locomotion speeds. The foot pattern of this gait is similar to the walk and the body movement is smooth. However, the bias of Δ₃₁ from π rad is so small that the diagonal legs appear synchronized during locomotion, as the footprint diagram (figure 8c) and electronic supplementary material movies show. In addition, the lateral movement of the robot body is large in the walk and is small in the trot (see electronic supplementary material, movies S1–S4), as observed in quadrupeds [82]. We confirmed this from the observation of dog locomotion.

Although the above-mentioned differences exist, our robot exhibits similar dynamic properties to quadrupeds in terms of gait generation and transition, as confirmed by the measurements of dogs (figure 10). Simple physical systems constructed by extracting the fundamentals of locomotion dynamics have enabled us to explain the essential characteristics of gait generation and have provided meaningful insights into biological sciences [14,16,23,41,83–85]. Our robot mechanical and oscillator network systems are simple since they extract the essential aspects of locomotion from biomechanical and physiological findings. The results clearly reveal the physical characteristics of the gait transition of quadruped locomotion. To further clarify the transition mechanism, we intend to develop a more sophisticated model of quadrupeds and a biologically plausible robot and to improve the experimental set-up used for the measurements of dogs (e.g. construct potential functions from measured data).