New crosslinkers for electrospun chitosan fibre mats. Part II: mechanical properties

Abstract

Few studies exist on the mechanical performance of crosslinked electrospun chitosan (CS) fibre mats. In this study, we show that the mat structure and mechanical performance depend on the different crosslinking agents genipin, epichlorohydrin (ECH), and hexamethylene-1,6-diaminocarboxysulphonate (HDACS), as well as the post-electrospinning heat and base activation treatments. The mat structure was imaged by field emission scanning electron microscopy and the mechanical performance was tested in tension. The elastic modulus, tensile strength, strain at failure and work to failure were found to range from 52 to 592 MPa, 2 to 30 MPa, 2 to 31 per cent and 0.041 to 3.26 MJ m⁻³, respectively. In general, neat CS mats were found to be the stiffest and the strongest, though least ductile, while CS–ECH mats were the least stiff, weakest, but the most ductile, and CS–HDACS fibre mats exhibited intermediary mechanical properties. The mechanical performance of the mats is shown to reflect differences in the fibre diameter, number of fibre–fibre contacts formed within the mat, as well as varying intermolecular bonding and moisture content. The findings reported here complement the chemical properties of the mats, described in part I of this study.

1. Introduction

Biopolymer micro- and nanofibre mats made from chitosan (CS) have considerable potential in biomedical applications because of their large surface-to-volume ratio, resorbability and mechanical properties, which can be carefully controlled [1]. CS is the deacetylated form of the second most abundant polysaccharide chitin (N-acetyl-d-glucosamine), which provides the exoskeletons of arthropods and crustaceans with structural integrity. CS can be electrospun either neat [2–6] from a variety of solvents, such as trifluoroacetic acid (TFA) and hexafluoroisopropanol [7], or with copolymers such as polyethylene oxide [8,9] and polyvinyl alcohol [10].

Many of the possible applications of biopolymer fibre mats, such as filtration membranes or tissue scaffolds, require that they possess good chemical stability combined with sufficient mechanical properties, such as stiffness, strength and toughness (work to failure), to survive the wet and often aggressive chemical conditions, under which they need to function. The desired property profile can be achieved via crosslinking, a process that couples functional groups, thereby stabilizing the fibre mats against dissolution.

The crosslinkers glutaraldehyde (GA) [2,4,11], genipin [12–15], hexamethylene-1,6-diaminocarboxysulphonate (HDACS) [16–18] and epoxides [19] have been widely used for CS films and hydrogels. In contrast, they have not been used for the crosslinking of electrospun fibre mats. Additionally, mechanical property measurements that compare the performance of mats stabilized with different crosslinkers have not been reported, to date.

The standard crosslinking procedure for CS fibre mats is a two-step process, in which the fibres are first spun and then crosslinked through a second process [4]. However, recently, it was shown that crosslinking can also be achieved in a single-step process, for example with GA, in which the crosslinker GA is added to the CS solution prior to electrospinning, enabling the crosslinking to occur during spinning [6].

In part I of this study, it was shown that cross-linked electrospun fibre mats could be produced with other crosslinkers, such as genipin, epichlorohydrin (ECH) and hexamethylene-1,6-diaminocarboxysulphonate (HDACS), added to the CS solution prior to spinning in the same manner as GA crosslinked mats [20]. Genipin is a plant extract of Genipa americana and Gardenia jasminoides Ellis. Genipin's crosslinking mechanism is pH-dependent; in acidic conditions genipin crosslinks CS through the opening of the dihydropyran ring of the genipin molecule by nucleophilic attack of CS amines on the olefinic carbon atom at C-3 of deoxyloganin aglycon [15]. The advantage of genipin over GA is that it is 5000–10 000 times less cytotoxic than GA, shown through in vitro studies with 3T3 fibroblasts using the MTT assay [21]. ECH is a temperature-dependent crosslinker, which at temperatures of 40°C and below binds to the NH₂ group, but above 40°C also crosslinks with primary OH groups in the CS films [11,19,22–24]. HDACS is a water-soluble and stable blocked-diisocyanate, which forms urea linkages after cross-linking with the NH₂ group of CS at basic pH [16,17]. As is the case with ECH, the crosslinking with HDACS can also be temperature-dependent.

In contrast to the previously reported crosslinking of CS fibres with GA [4,6], crosslinking of CS with genipin, ECH and HDACS during electrospinning has not been reported. Described here are the effects of these new crosslinkers, as well as the effects of post-electrospinning heat and base treatments on the fibre structure and interaction, the fibre mat morphology and their mechanical performance. Additionally, the mechanical properties stiffness, strength, strain at failure and work to failure of the electrospun mats are compared with CS mats crosslinked with GA, which have been previously reported, although not examined in detail [4].

Correlating the type of crosslinker, the mat structure and the mechanical properties is a complex undertaking. Despite a considerable body of literature concerned with the relative importance of several factors that contribute to the mechanical performance of stochastic fibrous materials, such as electrospun mats, clear correlations are still lacking [25–28]. The fibre diameter [26,27], number of fibre–fibre contacts [28,29], contact area between fibres [25,28] and fibre-to-fibre bond strength [26,27] have been noted as the most influential. They reflect the porosity, or relative density, of a mat that in turn is a measure of the stress transfer efficiency between individual fibres. The strength of a mat increases with an increase in relative density; at the same time, the probability of the presence of a critical flaw increases, on which material failure depends according to Weibull statistics [26]. In stochastic fibrous networks, the curvature of the fibres was not found to influence the number of junction points [30,31]. However, the fibre structure and molecular alignment are important and both are influenced by the draw ratio during the electrospinning process [27]. With increasing draw ratio, smaller fibres are formed and the processing creates a higher degree of molecular alignment and thereby increases mechanical properties, such as stiffness and strength. By contrast, thick fibres owing to a low draw ratio, may exhibit a core–shell structure in which the shell with more highly aligned molecules has higher properties than the more randomly organized core [27].

2. Materials and methods

Electrospun fibre mats were prepared as detailed in part I [20]. The reagents and characterization techniques are summarized below.

Medium molecular weight CS (MW = 190–310 kDa, 75% DD as specified by the manufacturer), TFA (99% ReagentPlus), GA (50 wt% in water), ECH, acetic acid (more than 99.7 + % ACS Reagent) and sodium hydroxide (NaOH) were all used as received from Sigma Aldrich, MO, USA. Genipin was purchased from Wako Chemicals USA, Inc., VA, USA. HDACS was prepared according to Welsh et al. [16]. All aqueous solutions were prepared from doubly distilled water. For density measurements, ethanol (more than 99.5%, ACS Reagent) was used as received from Sigma Aldrich.

CS solutions were prepared with 2.7% (w/v) CS in 99 per cent TFA and mixed overnight at room temperature on an Arma-Rotator A-1 (Bethesda, MD, USA). Electrospinning and crosslinking procedures were carried out as described by Schiffman & Schauer [6]. Briefly, the respective crosslinker was added to the CS–TFA solution and mixed for 2 min prior to electrospinning. Crosslinker concentrations were 0.1 wt% genipin in CS–TFA, a ratio of 10 : 1 wt% of CS to ECH and a ratio of 5 : 1 vol% of CS to HDACS. Solutions of 2.7% (w/v) CS with 1 ml of GA were prepared for comparison [6]. Crosslinker concentrations were chosen for ease of comparison with earlier studies of the authors and work reported in the literature, as detailed in part I of this study [20].

After mixing, the CS-crosslinker solution was transferred to a syringe with a 21-gauge Precision Glide needle (Becton Dickinson & Co., Franklin Lakes, NJ, USA). The syringe was placed on an advancement pump (Harvard Apparatus, Plymouth Meeting, PA, USA) and set at a distance of 100 mm from the 90 × 90 mm copper-collecting plate wrapped in aluminium foil. While the solution was advanced at a flow rate of 1.0 ml h^–1, a voltage of approximately 15.0 kV was applied between the syringe tip (positive electrode) and the collector plate (ground) with a high-voltage supply (Gamma High Voltage Research Inc., Ormond Beach, FL, USA). Electrospinning was carried out at temperatures between 23°C and 25°C and at relative humidities that ranged from 20 to 35 per cent. At least three mats of each composition were produced.

After electrospinning, the CS–ECH, CS–HDACS and as-spun CS (without crosslinker) fibre mats were subjected to either a heat or a base treatment to activate crosslinking. The temperature and duration of the heat activations were 60°C for 24 h and 120°C for 2 h for CS–ECH and CS–HDACS mats, respectively, at a relative humidity of 40 per cent. As-spun CS mats were subjected to both of these heat treatments. CS–ECH, CS–HDACS and as-spun CS fibre mats were base activated by vaporizing 10.0 ml of a 1 M NaOH solution at 23°C for 24 h in a 110 × 80 × 50 mm gas vapour chamber (VWR Scientific Products, Bridgeport, NJ, USA).

Fibre and fibre mat morphologies of the prepared electrospun samples were investigated both before and after mechanical testing with a stereomicroscope (Leica M205C, Leica Microsystems Inc., IL, USA) and field emission scanning electron microscopy (FESEM; Zeiss Supra 50VP, Carl Zeiss, NTS, Peabody, MA, USA). For FESEM imaging, samples were sputter coated with a 5 nm thick platinum–palladium layer using a Denton vacuum desk II sputtering machine (Denton Vacuum, LLC, Moorestown, NJ, USA). To determine water content differences between the fibre mats, thermogravimetric analysis (TGA) was carried out with a TGA Q50 Thermogravimetric Analyzer (TA Instruments, New Castle, DE, USA) according to the procedure detailed in part I of this study [20]. Image analysis software ImageJ, v. 1.41 (National Institute of Health, USA) was used to determine mean fibre diameters (N = 50). The average mat porosity was calculated from the mat density of three mat samples for each composition. The density measurements were based on modified ASTM D3800–99 and ASTM D891 standards using a 1 ml glass pycnometer (Thomas Scientific, Swedesboro, NJ, USA) at 25°C with ethanol as the working liquid.

The mechanical properties of the electrospun fibre mats were determined in tension with an Instron 5500R (Model 1125, Instron, Norwood, MA, USA). For testing, each mat was sectioned into 5 × 35 mm strips. These strips were mounted with adhesive tape in square paper frames with 25 × 25 mm openings to protect the samples from premature loading during sample clamping in the Instron. Prior to testing, the paper frames were cut on both vertical sides to allow for the loading of the sample at the start of the test. At least three samples were mechanically tested from each of three electrospun mats of identical composition and post-electrospinning treatment. Tests were carried out using pneumatic grips with a 5 N load cell at a strain rate of 0.02 s⁻¹. Samples were stored, conditioned and tested at 21°C and 65% relative humidity.

To convert load into stress, an effective mat thickness was calculated from the mass per unit area of the mat, assuming a density of the fibre material of 1220 kg m⁻³. Young's modulus was determined from the initial linear elastic slope of the stress–strain curve. In an effort to compare the work to failure, W_f, a property that is size-dependent, all samples were tested with the same gauge length and overall sample size (width and volume), as far as was experimentally possible. The work to failure, W_f, was determined as the area underneath the stress–strain curve. It is a measure of toughness in units of energy per unit volume.

Observation, supported by theory that models it, suggests that the dominating factor in the failure of stochastic fibrous mats is the fracture of the joints between the fibres rather than the fracture of individual fibres [25]. This is because the number of contacts between the fibres is considered too small to enable a sufficiently high stress transfer to cause individual fibres to break [26]. Frequently considered critical for the mechanical performance of stochastic fibrous mats is the number of fibre–fibre contact points, which can be calculated either per unit area or per unit volume. Eichhorn & Sampson [32] derive their equation for the number of fibre contacts per unit area, n_A, as a function of the fibre diameter, d, the mass per unit area, 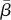, and the mass per unit length, δ:

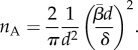2.1

The term in brackets describes the mean fibre coverage or area fraction, so that the expression can be simplified to

2.2

Toll [33] derives an expression with which the number of contact points in a fibre assembly per unit volume, n_V, can be calculated. Assuming that the fibres, which may be straight or curved, are uniform and of circular cross section, are non-aligned and slender, have a length, l, and a diameter, d, and an average fibre aspect ratio 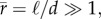he first calculates the average number of contact points per volume as a function of the fibre volume fraction, :

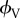2.3

where ƒ is a scalar invariant of the fibre distribution that takes the value of ƒ = π/4 and ƒ = 2/π for the case of a three- and a two-dimensional random fibre orientation, respectively. The number of fibres per unit volume is given by

2.4

This expression, multiplied by 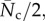because each crossing generates a contact on both of the fibres involved, yields the number of contact points per unit volume

2.5

For the calculations, below, we assume our electrospun fibre mats to represent a network with two-dimensional random fibre orientation, thus ƒ = 2/π:

A quick comparison of results obtained with both approaches is possible, when estimating the number of fibre–fibre contacts per unit volume, n_V, based on the number of fibre–fibre contacts per unit area, n_A, calculated according to Eichhorn & Sampson [32], and multiplying it with the number of layers that would form a 1 μm thick mat (assuming each layer to be one fibre diameter in thickness). For our electrospun fibre mats, we found the results to be very similar, with values according to Toll [33] differing from the estimates by a factor of 0.4–3.7.

In our analysis below, we calculate the number of fibre–fibre contacts per unit volume according to Toll [33], because we were able to experimentally determine the fibre volume fraction for the different fibre–mat compositions.

The elastic modulus of individual fibres, E_f, can, in a first-order approximation, be estimated from the mat's modulus, E, and relative density, ρ/ρ_f, which is the density of the mat, ρ, divided by the density of the solid fibre material, ρ_f [25,34]

2.6

Relative density and porosity, ɛ, are correlated as

2.7

Equation (2.6) is based on the work of Gibson & Ashby [35], who derive a correlation between the modulus of an open-cell foam, E, and the modulus of the solid, E_s, from which its fibre-like ‘struts’ are made, stating as the value for the correlation factor C = 1:

2.8

where ρ is the density of the foam, and ρ_s is the density of the solid from which the foam is made.

Zhu et al. [34] calculate a slightly smaller value of C = 2/3 in their extension of this model for open cell foams with tetrakaidecahedral cells.

This open cell foam model is based on assumptions that are valid for low densities, up to ρ/ρ_s = 0.3, because, for relative densities 0.3 < ρ/ρ_s < 0.8, the increasingly lower aspect ratio of the ‘struts’ (the fibres in our case) and end effects at the nodes, at which they are connected, become important, and because at relative densities of ρ/ρ_s > 0.8, the foam must be thought of as a solid with small spherical holes. We apply it to the electrospun fibre mats of this study, whose relative densities fall in the range of 0.25 < ρ/ρ_f < 0.65, for two reasons: because no theory exists for the relative density range 0.3 < ρ/ρ_f < 0.8 and because, empirically, the model was found to be appropriate for a variety of random fibre composites (e.g. silk cocoons, paper and non-woven cloth), whose relative density is similar to that of our samples in a study by Chen et al. [25].

3. Results

3.1. Fibre morphology

Electrospinning of crosslinked and as-spun CS resulted in mats of varying fibre morphologies. Typical mat structures are shown in figure 1, their structural properties are listed in table 1. As-spun CS fibre mats were white and composed of round, unbranched fibres. Genipin-crosslinked fibre mats (CS–genipin) were off-white to pale pink in colour and composed of unbranched, round fibres. ECH-cross-linked fibre mats (CS–ECH) were 10 min after spinning transparent and glossy and after 5 h white and opaque; their fibres were round and branched. HDACS-crosslinked fibre mats (CS–HDACS) were white with both round and ribbon-like fibres. The range in fibre diameters as a function of crosslinker and post-electrospinning treatment is listed in table 1. Post processing was found to reduce fibre diameters by nearly 50 per cent in comparison with their corresponding untreated compositions in the case of CS–HDACS and CS–ECH. However, CS–ECH mats heat-treated at 60°C exhibited an increase in fibre diameter and also an increased fibre curvature, when compared with their untreated counterparts.

Figure 1.

Scanning electron micrographs of non-treated electrospun fibre mats: (a) CS–ECH, (b) CS–HDACS, (c) CS–GA, (d) CS–genipin. Scale bar, 1 µm.

Table 1.

Structural properties of fibre mats.

material	fibre diameter d (nm)	fibre mat porosity ɛ (%)	fibre–fibre contacts per unit volume nv (1 μm−3)
CS	133 ± 71	56.7 ± 13.3	82.3
CS (heat 60°C)	312 ± 280	51.9 ± 36.6	7.86
CS (heat 120°C)	255 ± 263	58.8 ± 3.5	10.6
CS (base)	134 ± 104	43.5 ± 22.1	137
CS-genipin	358 ± 384	55.5 ± 6.8	4.45
CS–HDACS	675 ± 359	74.8 ± 22.9	0.21
CS–HDACS (heat 120°C)	285 ± 286	44.6 ± 10.6	13.7
CS–HDACS (base)	339 ± 206	60.3 ± 5.4	4.18
CS–ECH	1114 ± 590	40.3 ± 4.4	0.27
CS–ECH (heat 60°C)	871 ± 571	42.8 ± 15.3	0.51
CS–ECH (base)	394 ± 337	40.0 ± 34.1	6.07
CS–GA	112 ± 35	34.6 ± 20.7	314

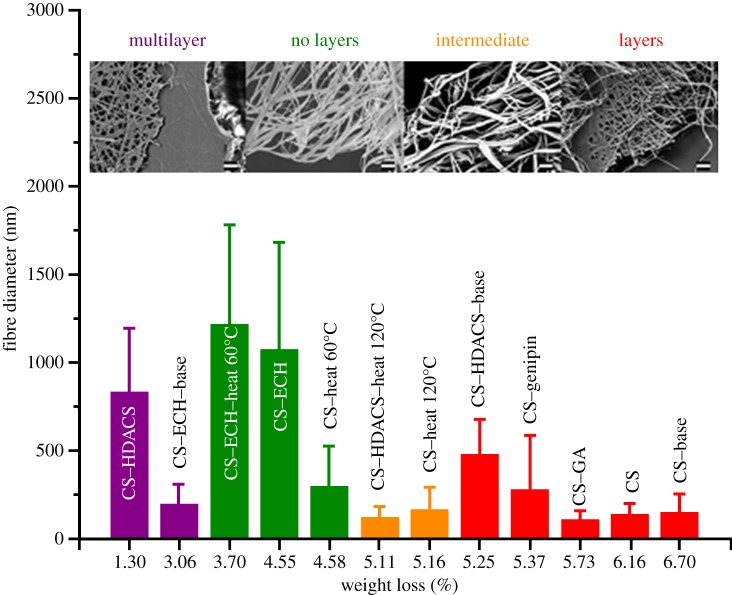
Four different mat morphologies were defined according to their structures revealed after failure. Some had distinguishable layers, others no layers, the third had a combination of the two (intermediate) and the fourth consisted of multilayers, or layers with different fibre morphologies as shown in figure 2. TGA results showed that the layered structure of the fibre mat influences the water loss of the sample more than the fibre diameter (figure 2), leading to the result that the non-layered structure had the most water loss, while the multilayered had the least.

Figure 2.

Fibre diameter plotted against the weight loss percentage for the region from 0°C to 100°C. The colours correspond to the overall structure of the fibre mats: composed of a multilayer, no layers, intermediate (or partially layered) or layers. Scale bar, 2 µm.

3.2. Mechanical properties

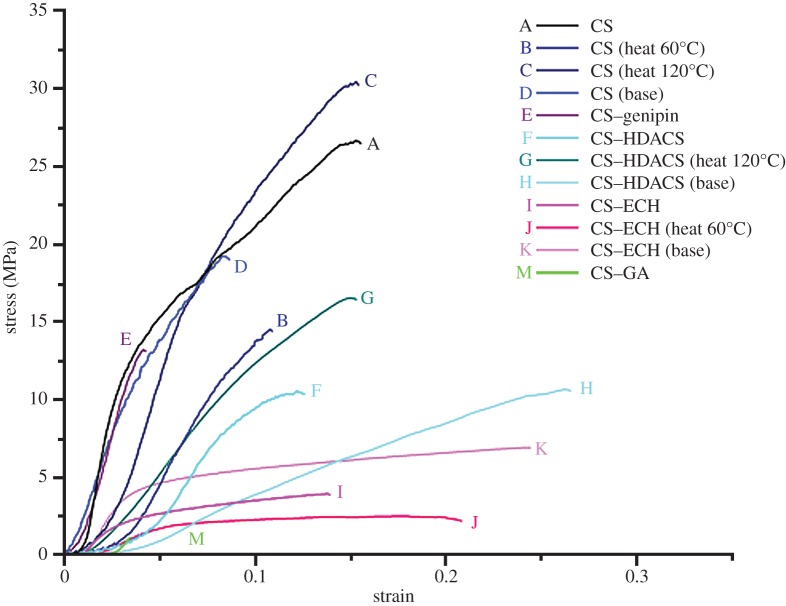
Typical stress–strain curves for all compositions are shown in figure 3; their mechanical properties are listed in table 2. According to their mechanical performance, four different groups can be identified: (i) mats B–E (CS (heat 60°C), CS (heat 120°C), CS (base), CS–genipin) are brittle, combining a high stiffness and strength with a low failure strain; (ii) mats I, J and K (CS–ECH, CS–ECH (heat 60°C), CS–ECH (base)) are highly ductile and combine both a low modulus and strength with a high failure strain, (iii) mats A, F, G and H (CS, CS–HDACS, CS–HDACS (heat 120°C), CS–HDACS (base)) fall in between the other two with intermediate stiffness, strength and failure strain; (iv) mat type M (CS–GA) is brittle, with a high modulus, but a considerably lower strength than the mats B–E. With respect to the mats overall structure, we find that the mats consisting of layers achieved the highest moduli, while those with the multilayered structure achieved the lowest.

Figure 3.

Typical stress–strain curves for all compositions and post-electrospinning treatments reveal four distinctly different patterns of mechanical performance: (i) mats B–E are brittle, combining a high stiffness and strength with a low failure strain, (ii) mats I, J and K are highly ductile, combining both a low modulus and strength with a high failure strain, (iii) mats A, F, G and H fall in between the other two with intermediate stiffness, strength and failure strain, (iv) mat M is brittle, with a high modulus, but a considerably lower strength than the mats B–E.

Table 2.

Mechanical properties of electrospun fibre mats for all crosslinkers and post-electrospinning treatments.

material	Young's modulus (MPa)	tensile strength (MPa)	strain to failure (%)	work to failure (MJ m−3)	estimated individual fibre modulus (MPa)
CS	512 ± 267	19.0 ± 6.48	18.7	2.083 ± 0.686	1956
CS (heat 60°C)	306 ± 106	20.8 ± 11.2	13.3	1.777 ± 1.495	4243
CS (heat 120°C)	361 ± 48	30.4 ± 3.22	18.7	3.261 ± 0.702	3966
CS (base)	592 ± 464	16.2 ± 4.83	7.3	0.645 ± 0.304	1398
CS-genipin	445 ± 33	17.5 ± 3.39	7.4	0.755 ± 0.471	4599
CS–HDACS	133 ± 84	9.85 ± 3.11	15.4	0.809 ± 0.461	1083
CS–HDACS (heat 120°C)	257 ± 205	13.4 ± 3.37	12.2	0.909 ± 0.542	3965
CS–HDACS (base)	101 ± 46	11.7 ± 2.78	21.2	1.383 ± 0.565	2124
CS–ECH	113 ± 106	3.58 ± 2.35	30.8	0.847 ± 0.870	72
CS–ECH (heat 60°C)	52 ± 33	1.85 ± 0.67	20.5	0.327 ± 0.194	117
CS–ECH (base)	162 ± 73	5.61 ± 1.72	17.5	0.715 ± 0.459	500
CS–GA	367 ± 160	5.30 ± 3.64	2.3	0.041 ± 0.039	2036

For easier evaluation and comparison of the mats' property profiles and to illustrate structure property correlations, four material property charts were plotted in figure 4. Their axes were chosen to be logarithmic to accommodate the large range in properties. Each data point represents at least three different tests and their standard deviations. Each ‘bubble’ circumscribes three of these datasets for each composition and treatment, resulting in at least nine tests for each condition. For easier identification, the bubbles are colour-coded: the inner fill colour refers to the composition, while the outline colour indicates the post-electrospinning treatment, or the lack thereof. The yellow fill denotes CS spun without a crosslinker, the dark blue fill denotes CS–genipin, the pink fill denotes CS–ECH, the turquoise fill denotes CS–HDACS and the green fill denotes CS–GA. The black outline denotes no post-electrospinning treatment, orange denotes heat treatment at 60°C, red denotes heat treatment at 120°C and green denotes base treatment.

Figure 4.

(a) Plotting tensile strength against Young's modulus demonstrates the range of properties. (b) Tensile strength plotted against the fibre diameter. (c) Work to failure plotted against failure strain. (d) Young's modulus plotted against the fibre diameter. The marker fill colour refers to the composition, while the outline colour indicates the post treatment, or the lack thereof. Black outline denotes no post treatment, orange denotes heat treatment of 60°C, red denotes heat treatment of 120°C and green denotes base treatment. Bubbles group all the tested samples for a given composition and treatment.

Plotting tensile strength versus Young's modulus in figure 4a reveals that the base-treated CS mats (yellow fill, green outline) have the highest Young's modulus, while the CS mats that were heat treated at 120°C (yellow fill, red outline) have the highest tensile strength. The 60°C heat-treated CS (yellow fill, orange outline), performs equally well, as does CS–genipin (dark blue fill, black outline). GA-cross-linked CS (green fill, black outline) has a similarly high modulus, but a significantly lower tensile strength. The addition of the crosslinkers ECH (pink fill, black outline) and HDACS (turquoise fill, black outline) without post-electrospinning treatment resulted in both a lower modulus and strength than that of neat CS. However, activating the crosslinkers ECH and HDACS with heat or base (see part I of this study for details) significantly increased their mechanical properties. In the case of CS–ECH, the highest modulus and strength resulted after the base treatment (pink fill, green outline), which also caused a reduction in fibre diameter by about 50 per cent (table 1). In the case of CS–HDACS, both heat and base treatments increased the tensile strength (turquoise fill with green and red outlines, respectively), but only the heat treatment also increased the modulus.

Plotting material indices on the strength–modulus plot (figure 4a), we can easily evaluate and compare the mechanical performance of the different mats. All materials on a straight line with a slope 1 have the same elastic strain, meaning they can sustain the same recoverable deflection; the materials on a straight line with slope 0.5 store the same amount of elastic energy. Materials above these lines perform better, whereas those below perform worse. Applying these criteria, we find that among the investigated crosslinkers and their respective compositions CS–HDACS with base treatment performs best with respect to both elastic deformation and elastic energy storage, providing the optimal combination of both. However, CS heat-treated at 120°C performs best, when only the elastic energy criterion is applied. Figure 4b,d shows that both Young's modulus and tensile strength increase with decreasing fibre diameter and that, as in the case of CS–HDACS and CS–ECH, the heat and base treatments resulted in a fibre diameter reduction. Using these plots, the mechanical performance of the different mats can be readily compared and the best-suited fibre mat can be selected for a given application.

The work to failure, W_f, plotted against the failure strain, ɛ_f, in figure 4c shows how a similar amount of energy per volume can be absorbed by two different mechanisms. The CS as-spun and CS 120°C heat-treated mats exhibited the highest work to failure with 3.26 ± 0.70 MJ m⁻³ and 2.08 ± 0.69 MJ m⁻³, respectively, because of their high modulus and strength at low failure strains. The high work to failure of CS–HDACS base-treated and CS–ECH of 1.38 ± 0.57 MJ m⁻³ and 0.85 ± 0.87 MJ m⁻³, respectively, resulted from their high failure strain, despite their low modulus and strength.

4. Discussion

The results of the structural and mechanical characterization show that a considerable range in mat properties can be achieved with the different crosslinkers genipin, ECH and HDACS, as well as post-electrospinning heat and base treatments. The results also revealed interesting correlations between mat structure and mechanical properties.

With respect to the average fibre diameters in the mats, we found that both the modulus and strength are inversely proportional to it. Estimating the modulus of the individual fibres based on the mat porosity according to Zhu et al. [34], we observed the same trend as in the case of the fibre mats, namely that the modulus of the individual fibre increased with a decrease in fibre diameter. The fibres had moduli that were about one order of magnitude higher than those of the mats. The observation that the fibre modulus increases with decreasing fibre diameter can further be explained by the higher draw ratio in thin fibres and a core–shell structure in the thicker ones, as described earlier.

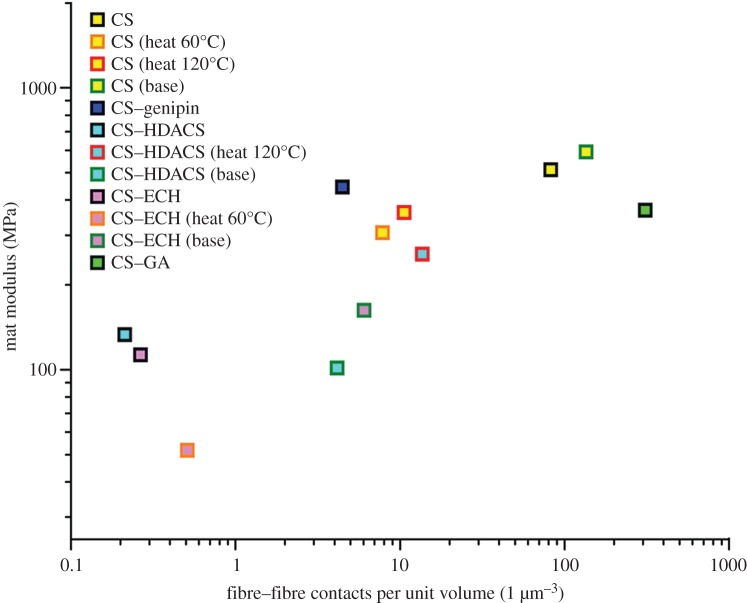
Calculating the number of fibre–fibre contacts in the mats according to Toll [33], we found the number of fibre–fibre contact points to increase with a decrease in fibre diameter (table 1). Additionally, the mats with the highest number of fibre–fibre contacts exhibited the highest stiffness (figure 5), while the more ductile mats with a lower stiffness and strength also had a smaller number of fibre–fibre contacts. Finally, the mats that exhibited the lowest stiffness, lowest strength and the highest strain to failure had the smallest number of fibre–fibre contacts. This observation suggests that the mat deformation critically depends on the number of fibre–fibre contacts. Initially, at low strains, fibres are straightened and bent between fibre–fibre contact points until load is transferred from one fibre to another, then at higher strains, the fibre–fibre bonds start to break, and as a result, the stiffness decreases while the load still increases until a maximum stress, the tensile strength, is reached.

Figure 5.

The mat modulus plotted against the fibre–fibre contacts per unit volume for all crosslinkers and post-electrospinning treatments.

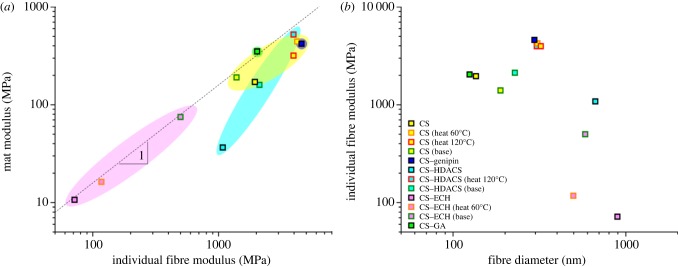
To investigate how the mat modulus scales with the modulus of the individual fibres, the two are plotted against one another in figure 6. For most crosslinkers, the mat modulus increased proportionally to that of the fibre modulus, suggesting that the mat modulus is little affected by the fibre–fibre interactions. However, in the case of CS–HDACS, CS–HDACS base-treated and CS–HDACS heat-treated at 120°C, the mat properties increased faster than those of the individual fibres, indicating that not only the fibre itself, but also the fibre–fibre interactions are affected by the HDACS and treatment.

Figure 6.

(a) The mat modulus plotted against the calculated individual fibre modulus and (b) the calculated individual fibre modulus plotted against the fibre diameter for all crosslinkers and post-electrospinning treatments.

Overall, the structure and the properties were affected by the type of crosslinker, which crosslink by different mechanisms, as shown in part I of this study [20]. Additionally, while some required the additional post-electrospinning treatments, others did not. ECH, which resulted in the lowest values of stiffness and strength, crosslinks with CS through the amines or through the hydroxyl functional groups, depending on the reaction temperature [36]. HDACS, which resulted in intermediate property values, crosslinks CS through the formation of urea linkages under both heat and base treatments. Genipin resulted in properties similar to those of the as-spun CS mats, indicating that it is not cross-linking the CS under these highly acidic conditions (TFA), but rather modifying it by forming intermediates.

5. Conclusion

The picture that emerges from the results of the combined structural and mechanical characterization of this study is that the properties of electrospun mats can be controlled over a large range through both the choice of crosslinker and post-electrospinning treatment. The different crosslinkers and treatments strongly affect the fibre diameter and through it the mat porosity and number of fibre–fibre contact points. CS electrospun neat and with carefully chosen concentrations of the crosslinkers genipin, ECH, HDACS and GA as well as with or without heat and base treatments, resulted in a library of fibre mats with a large range in properties. They had Young's moduli of 52–592 MPa, tensile strengths of 2–30 MPa, failure strains of 2–31%, and toughness (work to failure) values of 0.041–3.26 MJ m⁻³. Without post treatment, all crosslinkers, except genipin lead to a decrease in both Young's modulus and tensile strength. Genipin under the same conditions, resulted in a modulus and a tensile strength similar to that of as-spun CS. For mats with post treatment, both heat (at 60°C and 120°C) and base, Young's modulus and tensile strength increased in comparison with the untreated samples of the same composition.

What makes the electrospun CS fibre mats of this study highly attractive is their versatility. Through the careful choice of crosslinker, thermal and base treatments, structures with different fibre diameters, porosities, chemical stabilities and mechanical properties can be custom-designed, enabling the most appropriate to be selected for a given application.