Light-matter interaction in free space

Abstract

We review recent experimental advances in the field of efficient coupling of single atoms and light in free space. Furthermore, a comparison of efficient free space coupling and strong coupling in cavity quantum electrodynamics (QED) is given. Free space coupling does not allow for observing oscillatory exchange between the light field and the atom which is the characteristic feature of strong coupling in cavity QED. Like cavity QED, free space QED does, however, offer full switching of the light field, a 180° phase shift conditional on the presence of a single atom as well as 100% absorption probability of a single photon by a single atom. Furthermore, free space cavity QED comprises the interaction with a continuum of modes.

1. Introduction

Enhancing the coupling of light and matter at the level of a few photons is one of the challenges inevitable in fundamental research in quantum optics. It is likewise important in applications related to quantum information processing and quantum communication. Without any advanced measures the coupling of light and matter – especially single atoms – is inefficient under standard laboratory conditions, where optics with low numerical apertures (NA < 0.9) is typically used for focusing light onto the target to interact with. It is not surprising that there are plenty of approaches towards this issue.

One choice is employing collective effects and letting the photons interact with an ensemble of atoms [1,2]. However, this is obviously not the way to proceed when interacting with single atoms.¹ A single atom may be placed in the near field of a plasmonic antenna resulting in strong coupling between the two [3–5]. The task is then modified to coupling efficiently to the plasmonic antenna, which enhances the electric field at the position of the atom in comparison to the absence of the antenna. However, this is achieved at the cost of modifying the density of modes of the electromagnetic field [5,6]. This is an acceptable feature in some applications but not desired in all applications. Another method which also modifies the density of modes is placing the atom inside a high quality resonator. This defines the field of cavity quantum electrodynamics (cavity QED) [7–10], with seminal achievements and many impressive results.

As outlined below, a coupling between light and single atoms high enough to begin touching the strong coupling regime of cavity QED should be feasible also without modifying the free space density of modes of the electromagnetic field. The key to success is letting the radiation incident onto the atom resemble a dipole wave [11–15], since this is the mode of the electromagnetic field that maximizes the electric field at its focus [16], i.e. at the location of the atom. Several groups have been working towards this goal in recent years. The achievements made so far are reviewed in the next section and compared to the maximum values possible in free space. In Section 3 we attempt a comparison between the coupling scheme of cavity QED and the free space scenario, finding that such a comparison is partially possible but not always meaningful due to the different natures of the two schemes.

2. Experimental advances

Most of the recent experimental effort devoted to light–matter interaction in free space can be divided into two groups. The first group of experiments tackles the problem of efficient elastic scattering of a weak continuous wave (cw) laser beam [17–23]. Here, ‘weak’ means that the incident coherent state has an amplitude that is low enough to prevent an appreciable population and thus saturation of the atom's excited state. The basic layout of these experiments is depicted in Figure 1(a). The incident light mode is focused onto the atom by a lens. In the experiments cited above, the maximum numerical apertures used were NA = 0.65 [17] and NA = 0.68 [18]. The focused incident radiation drives the atomic dipole moment. This in turn radiates into the full solid angle with a radiation pattern according to its dipole character. The induced dipole moment and hence the radiation originating from the atom is the stronger the more similar the incident radiation is to the dipole wave corresponding to the atomic dipole moment.

Figure 1.

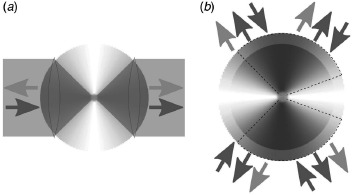
(a) Layout of recent experiments on elastic scattering of light by a single atom. The focusing optics cover less than half of the solid angle. (b) Extension of the experimental concept towards the full solid angle case. Dashed lines indicate the solid angle covered by the setup proposed in Refs. [13,26]. In both sketches the blue arrows denote the incident/focused radiation as well as its rediverging/recollimated counterpart. Light purple arrows denote the scattered radiation. The shaded areas depict the angular emission pattern of a linear dipole with white color marking zero intensity. (The color version of this figure is included in the online version of the journal.)

The induced dipole moment oscillates with a phase ψ = arctan(2Δ/Γ) − π/2 relative to the phase of the incident field at the position of the atom [24], where Δ = ω_inc − ω is the detuning between the incident radiation and the atomic transition frequency and Γ is the spontaneous emission rate. Furthermore, in the far field the rediverging incident radiation has accumulated a π/2 phase shift as compared to the value in the focus. Thus the rediverging incident radiation and the field scattered by the atom are effectively 180° out of phase for zero detuning [15,25].

In this situation, one can make different kinds of measurements. One possibility is to measure the radiation that is scattered back by the atom into the part of the solid angle covered by the focusing lens. This experiment has been performed in Ref. [23]. The power of the back-scattered radiation (i.e. the power reflected by the atom) corresponded to 0.17% of the incident power (see Table 1).

Table 1.

State of the art of coupling light and single atoms in free space.

Reference and experimental system	Year	Extinction	Reflection	Phase shift	Absorption
Wineland et al. [27] trapped ion	1987	<0.1%
Vamivakas et al. [17] quantum dot	2007	12%
Wrigge et al. [18] molecule in matrix	2008	22%
Tey et al. [19] trapped atom	2008	10%
Aljunid et al. [20] trapped atom	2009			1°
Slodicka et al. [21] trapped ion	2010	1.4%
Pototschnig et al. [22] molecule in matrix	2011	19%		3°
Piro et al. [28] trapped ion	2011				0.03%
Aljunid et al. [23] trapped atom	2011		0.17%

However, in the majority of the experiments transmission measurements where performed. In these experiments a second lens with a numerical aperture equal to the first one is used to recollimate the focused light and collect the field scattered by the atom. The phase difference between the scattered field and the recollimated incident field plays a decisive role [15,25]. The total field measured after the second lens is the superposition of the above two fields. Hence, there will be destructive interference leading to an extinction of the beam in the forward direction, with the amount of extinction depending on the detuning. Such extinction measurements where performed in Refs. [17–21]. The achieved amount of extinction is listed in Table 1. For a numerical aperture of one, i.e. focusing from half solid angle and the incident field resembling dipole radiation complete extinction in the forward direction is predicted [15]. Although substantial attenuation of the forward traveling beam has been reported, the maximum amount of extinction achieved so far is still about a factor of 5 below this optimum value.

Another way of measuring the coupling of the incident light to the atom is to measure the phase of the total field in the forward direction. This has been done in Refs. [20,22]. In Ref. [20] the setup hosting the single atom was inserted in one arm of a Mach–Zehnder interferometer. The phase shift obtained in Ref. [22] was measured by a heterodyning technique. The respective results are listed in Table 1.

In models describing the above experiments the ratio of the power scattered by the atom and the incident power plays a crucial role. This ratio can exceed unity [15,25], which might at first sight seem like a violation of energy conservation. But detailed balancing of the amount of the dipole radiation scattered by the atom and the corresponding dipole and non-dipole content of the incident radiation proves the opposite. Considering all radiation components, incoming and scattered, with the proper relative phases as well as their interference shows that the actually measurable total power equals the incident power.

The second group of experiments is devoted to the inelastic interaction of single photons with single atoms. In these experiments the aim is to bring an atom to its excited state with only a single incoming photon. Besides the already mentioned dipole characteristics, these experiments impose strict requirements on the temporal envelope of the single photon pulse. These requirements follow from a time reversal argument: The absorption of a photon by an atom in its ground state is understood as the time reversed process of spontaneous emission from the excited state [11,13,26]. Since the temporal envelope of a spontaneously emitted photon is exponentially decreasing [29], its time reversed version must have an exponentially increasing envelope. Assuming a perfect dipole radiation character of the incident photon impinging from full solid angle, a detailed calculation indeed shows that the exponentially increasing pulse brings the atom fully to the excited state [30,31].

On the experimental side, an excitation probability of a single ion of 0.03% was measured for heralded photons generated by parametric down conversion [28]. The heralding photon was spectral filtered by a resonator with a bandwidth matched to the ionic transition. A numerical aperture of NA = 0.4 was used for focusing onto the ion. Weighting the corresponding solid angle with the angular emission pattern of the driven (circular) dipole transition yields a solid angle coverage of 6%. This is the upper limit of the excitation probability achievable with the used numerical aperture, since the absorption probability is proportional to the coverage of the (weighted) solid angle [14,26]. An experiment in which the focusing optics covers 94% of the solid angle (cf. Figure 1(b)) is currently being set up [13,26,32].

There are some experiments that do not fit precisely into one of the two categories of elastic or inelastic scattering. For example, an extinction of approximately 0.1% of the laser beam used to cool a single ion was measured already in 1987 [27]. However, owing to the saturation of the ion by the cooling laser a clear distinction between elastic scattering and scattering by absorption and spontaneous (re)emission cannot be made.

Very recently, single photons emitted by single molecules using the setup of Ref. [18] were focused onto another molecule using a setup of the same kind as in the generation of the photons [33]. An extinction of 3% of the single photon stream incident onto the second molecule is reported. However, it is unclear to what extent the second molecule was brought to its excited state by a single photon.

The crucial role of the solid angle has already been highlighted above, mainly in connection with the absorption of single photons. However, a deep parabolic mirror that covers almost the entire solid angle is also beneficial in elastic scattering experiments. We highlight this circumstance by calculating the dependence of the phase shift of a monochromatic light field on solid angle, restricting the discussion to the regime of negligible saturation. In this regime the phase shift of the superposition of the electric field scattered by the atom into the solid angle cone of the recollimated incident electric field and the latter field itself is [20]

R_sc = P_sc/P is the scattering ratio on resonance, i.e. the power P_sc scattered into the full solid angle divided by the incident power P. P_sc is given by [25]

where λ is the wavelength corresponding to the wavelength of the atomic transition. E is the amplitude of the incident electric field component parallel to the atomic dipole moment at the position of the atom. The latter can be expressed as [34]

Ω_μ is the solid angle covered by the focusing optics weighted with the radiation pattern of the dipole moment μ. η is the overlap of the incident radiation with this dipole radiation pattern. η is computed on the part of the solid angle covered by the focusing optics [34]. For a dipole wave incident from full solid angle we have Ω_μ = 8π/3 and η = 1. Inserting Equation (3) into Equation (2) yields the scattering ratio on resonance

and the corresponding phase shift

For the remainder of the discussion we assume dipole radiation (η = 1). The maximum obtainable phase shift at any detuning value except Δ = 0 occurs for the full solid angle case. On resonance a phase shift of π is predicted when Ω_μ > 4π/3, i.e. for more than half of the solid angle, and zero phase shift for Ω_μ < 4π/3. For the case Ω_μ = 4π/3 one has complete extinction [15], therefore prohibiting a phase shift measurement in the forward direction under this geometry. The full solid angle case and the corresponding phase shifts for some experimental setups are illustrated in Figure 2. Also for overlaps η < 1 a π phase shift on resonance is possible, provided that Ω_μ > 4/π(3η²). This is equivalent to R_sc > 2, i.e. the power scattered into the full solid angle is more than twice the incident power. This condition can only be met for focusing optics covering more than half the solid angle.

Figure 2.

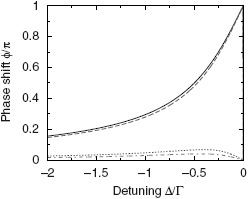
Calculated phase shift induced by a single atom for illumination with a dipole-like radiation pattern from full solid angle (solid line), using a deep parabolic mirror [26] (dashed line), a lens with NA = 0.68 [22] (dotted line) and a lens with NA = 0.55 [20] (dash-dotted line). The above solid angle and NA values correspond to values of Ω_μ/(8π/3) = 1, 0.94, 0.18 and 0.11, respectively. An overlap of η = 1 is used for all cases. (The color version of this figure is included in the online version of the journal.)

3. Attempt at a comparison with cavity QED

In cavity QED, one usually speaks of strong coupling when the coupling constant g is larger than the cavity field's decay rate κ and larger than the spontaneous emission rate Γ associated with the transition of the atom inside the cavity [10,35]. Here one has to keep in mind that the spontaneous emission rate of an atom inside a cavity may differ substantially from the free space value [36,37]. Now the question is whether the cavity QED criteria for strong coupling can be met in free space.

The relation g > κ does not seem relevant at first sight, since trivially κ is not defined in free space. However, the effective interaction time between the atom and any wave packet propagating inside the optical cavity is determined by κ⁻¹ independent of the wave packet's shape which includes continuous waves. Similarly, the interaction time in free space is given by the temporal width of a wave packet impinging onto an atom. Arguing along this line, one may just reach g = κ in free space atom-light interactions.

We now check the condition g > κ. The coupling constant g is given by [10]

with μ being the matrix element of the transition dipole moment, Ω the frequency of the atomic transition and V the quantization volume. In cavity QED V is the volume of the cavity mode. For the free space case, where we tightly focus an incident light pulse onto the atom, we make the following ansatz

which is the area of the focus with radius r_focus times the spatial length of the incident pulse. The latter is given by c₀·Δt with the speed of light c₀ and the pulse duration Δt. We express r_focus in terms of λ = 2πc₀/Ω: r_focus = β·λ. Likewise, we write the pulse duration as Δt = α/Γ, i.e. in units of the atom's excited state lifetime. Relating g to Γ we insert Equation (7) with the above definitions into Equation (6) and use the definition of the free space spontaneous emission rate Γ = μ²ω³/(3π∊₀ħc₀³) [29]. This yields

As outlined in Section 2, one example of efficient free space interaction is the absorption of an exponentially shaped single photon pulse by a single atom. Such a pulse has an effective length of Γ⁻¹ suggesting α = 1. For determining the value of β we recall that light-matter interaction in free space is maximized for dipole waves incident from full solid angle. The transverse area of a focused dipole wave that is generated by, e.g. an infinitely deep parabolic mirror can be determined with simulations of the intensity in the focal region based on a generalization of the method by Richards and Wolf [38]. As a radiation pattern incident onto the parabolic mirror we use the one for a linear dipole transition with the quantization axis parallel to the optical axis of the mirror [13]. The outcome of such a simulation is displayed in Figure 3. For comparison also the case of a finite parabolic mirror covering roughly 94% of the solid angle is shown, a mirror geometry matching the one used in Refs. [26,39]. Choosing the area at half maximum height as the spot size yields β ≈ 0.2 in both cases. This results in g ≈ 0.97Γ, i.e. the coupling constant would be almost equal to the spontaneous emission rate.

Figure 3.

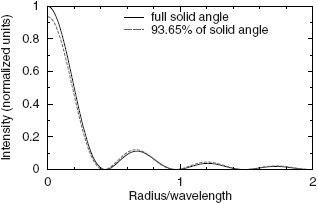
Radial intensity distribution in the focus of a parabolic mirror covering the full solid angle (solid line) and a mirror covering 93.65% of the solid angle when weighted with the emission pattern of a linear dipole oriented along the mirror axis (dashed line). (The color version of this figure is included in the online version of the journal.)

Another ansatz that does not rely on the definition of the quantization volume is the following: The coupling constant g is also called the single photon Rabi frequency [10]. In general, for a field of amplitude E that is polarized parallel to the atomic transition dipole moment the Rabi frequency is defined as [24]

We use Equation (3) to determine E and calculate the power P of the incident radiation by taking the energy of a single photon pulse and dividing it by the pulse duration Δt = α·Γ⁻¹, i.e. P = ħΩΓ/α. Inserting these values into Equation (9) and expressing μ through Γ yields

Hence, for a single photon dipole wave pulse whose effective length is the excited state lifetime (α = 1) the Rabi frequency is twice the spontaneous emission rate. The electric field based estimate for the Rabi frequency, however, should be taken with a grain of salt, because the average electric field amplitude is zero for pure Fock states.

Nevertheless it might be tempting to increase the Rabi frequency (or equivalently the coupling constant g) of a single photon pulse by reducing the pulse duration Δt. This, however, has two consequences:

• (i)The spectrum of the pulse broadens proportional to 1/Δt.
• (ii)The Rabi frequency increases proportional to

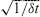
For ΔtΓ < 1 the pulse spectrum will be broader than the atomic spectrum. Consequently, in free space the probability that this single photon wave packet excites an atom will be reduced, since the pulse spectrum deviates from the atomic absorption line [30]. It is worth noting that the condition g > Δt⁻¹ – as can be inferred from the discussion of the free space equivalent to κ at the beginning of this section – prevents one from taking this route. This underlines the similarities of the figures of merit for free space and cavity systems.

Also for monochromatic continuous wave excitation the condition for the vacuum Rabi frequency Ω_r > Γ may be misleading. Under this condition the saturation parameter s = 2Ω_R²Γ⁻² is much larger than one and strong saturation results in power broadening and hence in a reduction of the atomic response on resonance. Likewise, strong saturation results in a decrease of the index of refraction, i.e. the real part of the atomic susceptibility [40]. Therefore, both the phase shift and the extinction imposed onto a cw light mode by a single atom will decrease, a scenario treated in Refs. [15,17–19,21].

For all the reasons discussed above the inequalities g, Ω_R > Γ are not the most useful criteria for indicating efficient coupling of light and single atoms in free space. We therefore suggest that the measure of the efficiency of light-matter interaction in free space is not the Rabi frequency or coupling constant in comparison to the spontaneous emission rate, but rather the efficiency of converting the power of an incident light mode into a high intensity of the field E at the location of the atom. With the intensity of a sinusoidally oscillating field given by I = ∊₀c₀E²/2 we find with the help of Equation (3)

Since the maximum effect is obtained for Ω_μ = 8π/3 and η = 1, we normalize I/P to this case and obtain the free space coupling efficiency

This free space coupling efficiency can be related to another quantity used in cavity QED, the cooperativity parameter C = g²/(2κΓ). The condition C ≫ 1 is a necessary (although not sufficient) condition for strong coupling in cavity QED [35]. As outlined in Ref. [26], C can be interpreted as a geometric quantity that is the product of the solid angle fraction Ω_μ/(8π/3) covered by the cavity mode times the average number N of round trips of a photon wave packet inside the cavity. Assuming η = 1 for the cavity mode, one can write the cooperativity parameter as C = G · N, i.e. as the free space coupling efficiency set by the cavity geometry times the number of cavity round trips.

4. Conclusion

The conclusion of this paper may be summarized as follows:

• (a)The typical condition for strong coupling in cavity QED, g > Γ, κ can be just reached in free space (g = Γ, κ), while
• (b)only in cavity QED is g ≫ Γ, κ possible.

It follows from (a) that there should be several phenomena which can be observed in both coupling schemes. And indeed, the absorption of a single photon by a single atom and the effects a single atom can have on cw beams (or coherent states) via elastic scattering belong to this class of phenomena (cf. Table 2). In both scenarios, free space QED and cavity QED, a single atom may absorb a single photon pulse, it may switch the transmission of a laser beam and it may impose a large phase shift. Corresponding experiments in cavity QED yielded phase shifts on the order of 30° [41,42] and absorption probabilities of 17%, respectively, for weak coherent state pulses [43] and for true single photon pulses produced in another cavity [44]. Extinction of a transmitted beam on resonance with the cavity and the atom has been observed as well. However, the mechanism differs substantially from the free space case. In the strong coupling regime the transmission peak of the empty cavity is split up into a doublet. This vacuum Rabi splitting [45–47] is not observable in free space. There, extinction is due to destructive interference (see the previous section) without any modification of the components of the transmission spectrum. In cavity QED the plethora of beautiful effects includes collapse and revival of the atom's excited state population [48] as well as Rabi frequency induced nonlinearities [49]. On the other hand, fundamental studies involving the – possibly structured [50] – continuum of modes are only possible in free space. In either scheme the limits of the effects possible in both coupling schemes have yet to be reached.

Table 2.

Comparison of the possible effects of a single atom on the light field in free space and in cavity QED.

Phenomenon	Cavity QED	Free space
mode spectrum	discrete/single mode	continuous
max. extinction of a cw beam	100%a	100%b
max. phase shift	180°	180°
max. absorption of a single photon	100%	100%
observation of vacuum Rabi splitting	yes	no
exponential decay	no	yes
structured continuum dynamics	no	yes

^aMechanism: vacuum Rabi splitting.

^bMechanism: destructive interference