Vowel Formant Frequency Discrimination in Cats: Comparison of Auditory Nerve Representations and Psychophysical Thresholds

Abstract

Experiment 1 derived mathematical models for estimating the neural rate representation of changes in the second formant (F2) frequency of the vowel /ε/. Models were based on linear fits to response patterns of auditory-nerve fibers with high, medium and low spontaneous rates (SRs), as characterized in previous electrophysiological studies of anesthetized cats (Le Prell et al., 1996). Simulations were run at several vowel levels in quiet and in the presence of continuous background noise. Noise levels were adjusted to produce a constant signal-to-noise ratio (S/N) of 3 dB at each vowel level. A signal detection analysis of model outputs suggested that auditory-nerve fibers with low SR provided the best rate representation of changes in F2 frequency at higher vowel levels and in background noise. Experiment 2 examined the predictions of the auditory nerve model by measuring psychophysical thresholds for F2 frequency changes (ΔF2) in cats. Behavioral tests were performed at vowel levels of 31, 51, and 71 dB in continuous background noise at S/Ns of 3, 13, and 23 dB. ΔF2 increased with decreasing S/N at each of these three vowel levels. Trends in behavioral performance corresponded well with the quality of vowel representations that are provided by high SR auditory-nerve fibers at low vowel levels and low SR fibers at moderate-to-high levels.

MANY PROPOSALS EXIST regarding the neural codes by which speech sounds are processed within the peripheral auditory system. In general, putative coding strategies are considered in terms of either phase-locked responses to temporal properties of steady-state vowels (Young and Sachs, 1979), or in terms of rate-place codes in which spectral shapes are represented by the level of activity among many fibers, each tuned to a slightly different frequency component of the complex sound (Sachs and Young, 1979; Winslow et al., 1987). Previous studies have suggested that temporal codes might provide more reliable information because for most auditory-nerve fibers, representations based on discharge rate degrade at high vowel levels (Sachs and Young, 1979) and in the presence of noise (Sachs et al., 1983; Sachs et al., 1988). A small percentage (16%) of fibers with low spontaneous rates (SR) is more resistant to the negative effects of these common conditions, which has led to the interpretation that rate responses of these neurons may be critical for speech encoding (Sachs and Young, 1979; Sachs et al., 1988; Delgutte and Kiang, 1984).

More recently, it has been shown that rate-difference measures for both low and high SR auditory-nerve fibers can also provide an adequate representation of the differences between complex spectra such as steady-state vowels (Conley and Keilson, 1995) or pinna-based spectral cues (Rice et al., 1995). The present study was conducted to compare the quality of the neural rate representation of second formant (F2) frequency changes with actual psychophysical performance. These experiments were carried out in cats because of the wealth of physiological data that are available for the species. Model simulations and behavioral thresholds were obtained using synthetic variants of the vowel /ε/, which were tested at several levels in quiet and in the presence of continuous background noise. Behavioral performance correlated best with the rate information that was conveyed by high SR fibers at low vowel levels and low SR fibers at higher vowel levels. These results support previous hypotheses that have proposed central auditory discrimination processes are enhanced by “selective listening” to peripheral neurons with complementary dynamic range properties (Winslow et al., 1987).

EXPERIMENT 1: AUDITORY NERVE SIMULATIONS FOR THE RATE REPRESENTATION OF F2 FREQUENCY CHANGES

METHODS

Experiment 1 introduces a model for the auditory nerve representation of vowel-like stimuli that is based on neural discharge rates The physiological database for these modeling efforts was obtained in six barbiturate anesthetized cats with a spectrum manipulation procedure (SMP) in which prominent spectral features of the vowel /ε/ were shifted to the best frequency (BF) of individual fibers by changing the playback sampling rate of digitized stimuli (data previously reported by Le Prell et al., 1996). This manipulation shifts the stimulus spectrum along a logarithmic frequency axis, maintaining the relative spacing of harmonic components in the sense that their ratios (e.g., F1/F2) remain constant.

The SMP was originally designed to measure vowel representation in the central nervous system where it is difficult to sample large populations of neurons within subjects but individual neurons can be studied for long periods of time (Blackburn and Sachs, 1990). As an alternative to traditional population methods, the SMP creates a rate-place vowel representation that is based on the differential responses of individual units to formant and trough features. It has been observed in recent population studies that rate-difference measures can provide a sensitive representation of changes in a vowel’s formant structure (Conley and Kielson, 1995) or pinna-based spectral cues for sound localization (Rice et al., 1995).

Linear models for predicting vowel representations in quiet were based on the physiological database of Le Prell et al. (1996). This database was comprised of 79 ANFs: 9 units were high SR fibers (>18 sp/sec), 25 units were medium SR fibers (1 – 18 sp/sec), and the remaining 15 units were low SR fibers (<1 sp/sec). Models of the effects of continuous background noise on vowel representations were investigated by sampling an additional 81 ANFs in three barbiturate anesthetized cats. In this sample, 55 units showed high SRs, 19 units showed medium SRs, and 7 units showed low SRs. The SR distributions of both physiological databases compare well to standards that have been established for cats reared under low noise conditions (Liberman, 1978).

Rate Representation of Vowels in Quiet

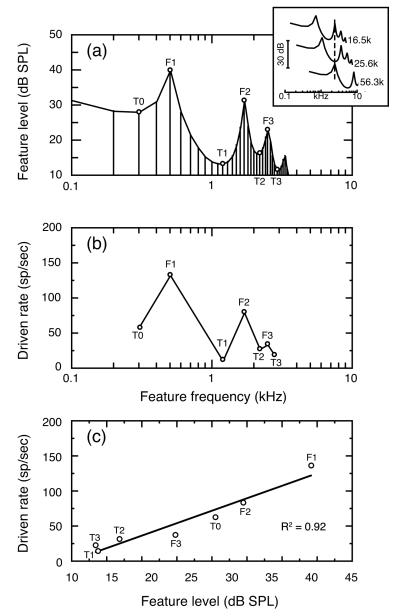
Examples of the vowel-like stimuli that were used in SMP testing are shown in Fig. 1(a). With a standard playback sampling rate of 12.8 kHz, the fundamental frequency of the prototypic stimulus was 100 Hz and formants were placed at 500, 1700, and 2500 Hz. This is the same formant structure as the standard vowel in the behavioral experiments of Experiment 2. Vowels were delivered to the ear monaurally via a closed acoustic system. To simulate the filtering effects of the head and pinna that shape the free-field stimuli of behavioral experiments, vowels used in electrophysiological experiments were digitally filtered by the cat’s head-related transfer function at 0° azimuth, 30° elevation (Weiner et al., 1966). Model simulations were performed at vowel levels ranging from 43 – 83 dB SPL. Vowel levels were computed by measuring the total power in the first 30 harmonics and are presented in dB SPL. Most energy in the vowel was contained in F1; energy above the 30th harmonic was negligible in terms of the total power of the stimulus. The vowel in Fig. 1(a) has a total power of 43 dB SPL.

FIGURE 1. Spectral manipulation procedure (SMP) for sampling auditory-nerve fiber responses to vowel-like stimuli.

(a) Amplitude spectrum of the prototypic /ε/ at a vowel level of 43 dB. Formant frequencies were placed at 500, 1700, and 2500 Hz. Individual fibers were tested with spectral features that represented three formants (F1 – F3) and four troughs (TO – T3) in the vowel’s amplitude spectrum (open symbols). These features were shifted to the unit’s BF by changing playback sampling rates (inset), (b) Rate responses obtained from a high SR auditory-nerve fiber during SMP testing with the 43 dB vowel. This analog of a population study rate-place profile was created by plotting driven rates for each test feature at the frequency location of that feature in the prototypic vowel, (c) Rate-level function produced by plotting the same rate responses according to the SPL of test features. The unit’s driven rates to different spectral features were highly correlated with feature level (R²=0.92).

The inset in Fig. 1(a) shows how the formant structure of the vowel was moved to higher frequencies by increasing the playback sampling rate to 16.5, 25.6, and 56.3 kHz. Respectively, these three sampling rates placed the vowel’s second formant (F2), second trough (T1), and first formant (F1) at 2.2 kHz (dashed vertical line). Spectral shifts of this nature were performed to align features of interest with the receptive fields of individual fibers. Each fiber was tested with seven spectral features at BF, as identified by open symbols in Fig. 1(a). These features correspond to the three formants (F1 – F3) and four troughs (T0 – T3) that characterize the amplitude spectrum of the vowel /ε/ at frequencies below 3 kHz.

The rate responses shown in Fig. 1(b) were obtained by presenting a 43 dB vowel to an auditory-nerve fiber with BF of 2.2 kHz. The fiber’s responses to each of the seven test features were averaged over 30 – 50 stimulus presentations. An SMP rate-place profile was constructed by plotting the fiber’s rate responses to each test feature at the frequency location of the feature in the natural vowel /ε/. That is, responses with F1 at BF are plotted at the normal 0.5-kHz frequency of F1 in the natural (unshifted) vowel, although the F1 feature was actually shifted to 2.2 kHz when the unit in this example was tested with the SMP procedure. This manner of data presentation aligns the rate-place profile in Fig. 1(b) with the amplitude spectrum in Fig. 1(a) and facilitates comparisons of rate responses across units with different BFs.

Auditory nerve simulations were modeled on an empirically derived database that was restricted to fibers with BFs between 0.4 – 3.0 kHz. Previous analysis of this database by Le Prell et al. (1996) has shown that BF does not influence the quality of the neural representation within this limited frequency range. The rate measure plotted in Fig. 1(b) is the unit’s driven rate to the vowel, which was calculated by subtracting spontaneous rate (SR) from the unit’s total rate during presentation of the vowel. The unit shown in this example was classified as having a high spontaneous discharge rate (>18 sp/sec). Like previous population studies of the auditory nerve (Sachs and Young, 1979), SMP testing suggests a neural representation in which vowel formants are indicated by peaks of activity among fibers with BFs near formant frequencies (Le Prell et al., 1996).

The seven spectral features used in SMP testing span a 30-dB range of levels within the vowel’s amplitude spectrum. In Fig. 1(c), the unit’s driven rate to each feature has been replotted as a function of feature level. The resulting rate-level function indicates that feature level and vowel-driven activity have a strong linear correlation (R² = 0.92). The linear relationship of response rate to feature level can be used to predict a unit’s rate responses to additional harmonics in the vowel’s amplitude spectrum, or the rate representation of variants of the vowel formant structure.

Vowel Representation in Background Noise

Effects of background noise on vowel representations were investigated at vowel levels that ranged from 33 to 73 dB in increments of 10 dB. Noise levels were adjusted to produce a fixed 3 dB signal-to-noise ratio (S/N) at each vowel level. For the calculation of S/N, vowel and noise levels are specified in terms of total power at frequencies below 3000 Hz.

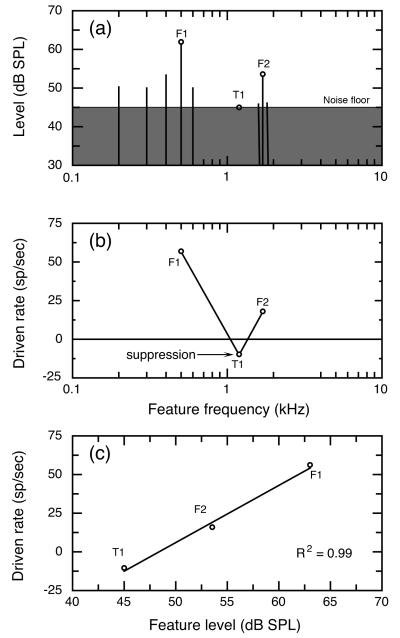
Figure 2(a) illustrates the vowel in noise stimulus condition at a vowel level of 63 dB. The amplitude spectrum of the vowel is indicated by the level of harmonic components with 100-Hz spacing; the noise spectrum is plotted in terms of noise power within 100-Hz bandwidths centered on each component. With the exception of F2, all harmonics above 700 Hz show spectrum levels near or below the noise floor. Rate responses for vowels in noise were only sampled with F1, T1, and F2 features at BF. Reducing the number of test features in this manner allowed each fiber’s rate differences to be sampled in several levels of background noise within the limited isolation period of auditory-nerve fibers.

FIGURE 2. Procedures for sampling auditory nerve responses to vowels in noise.

(a) Amplitude spectrum of a 63 dB vowel in background noise. SMP tests were performed for three spectral features (open symbols) at vowel levels ranging from 33 – 73 dB. Noise levels (shaded spectrum) refer to total power in a 100-Hz band centered on each component of the vowel spectrum. Noise levels were adjusted to maintain a constant 3 dB S/N based on total power at frequencies below 3 kHz. (b) Rate profile for a low SR fiber at a 63 dB vowel level in noise. Among low SR fibers, rate suppression (arrow) often produced T1-driven rates that fell below responses to noise alone, (c) The rate-level function for this unit shows a strong correlation between vowel-driven rates and feature level (R²=0.99).

Figure 2(b) plots the driven rates of a representative low SR fiber for each of the three test features. Here, driven rates reflect the change in discharge rate that occurs between responses to vowels in noise and responses to noise alone. For example, this unit responded to noise alone with a discharge rate of 78 sp/sec and its activity increased to 134 sp/sec when F1 was presented at BF. Thus, the unit’s F1 driven rate was 56 sp/sec. As noted for testing in quiet, peaks of activity were observed when formants F1 and F2 were placed at the unit’s BF, while minimal rates were seen with T1 at BF. For most low SR units, response rates to T1-in-noise actually fell below responses to noise alone. These negative rate changes were presumably due to suppression effects that enhance the vowel representations of low SR fibers by increasing the range of rate differences between formant-driven and trough-driven activity (Le Prell et al., 1996).

Figure 2(c) shows the driven rate of the representative low SR fiber as a function of feature level. In this plot, the level of the T1 feature has been specified as the level of the noise floor because the vowel has less energy than background noise at this feature location (Fig. 2a). As a result of noise driven activity, auditory-nerve fibers exhibit a reduced range of driven rates relative to responses in quiet (Fig. 1), even so this unit shows an excellent correlation of driven rate with feature level (R² = 0.99).

Experiment 1 used the methods described in Figs. 1 and 2 to determine linear regressions for the rate representation of the vowel /ε/ at several vowel levels and in the presence of a continuous background noise. Individual regression statistics were calculated for low, medium and high SR fibers. Signal-detection models based on these data were then developed to predict neural discrimination of changes in the vowel’s formant structure.

RESULTS

Linear Models for Vowel Representation in Quiet

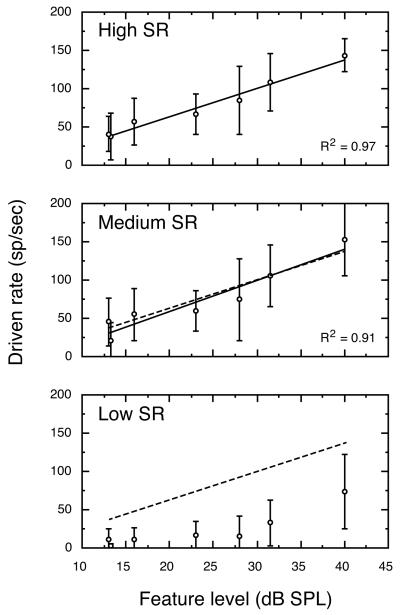
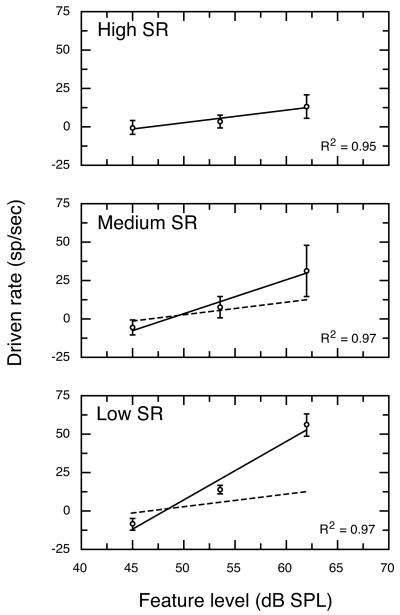
Figure 3 shows linear regressions of average driven rates for high, medium and low SR fibers at a 43 dB vowel level under quiet testing conditions. The statistics describing these linear regressions are presented in Table I. Responses of high and medium SR fibers were essentially identical at the 43-dB vowel level, as indicated by superimposing the linear regression for high SR fibers (dashed line) on the data for medium SR fibers. Low SR auditory-nerve fibers are characterized by higher and more variable thresholds than other SR classes (Liberman, 1978). As a result, low SR fibers in Fig. 3 exhibit very low driven rates to all but the most intense F1 feature. Moreover, data in Fig. 3 are slightly misleading because most low SR fibers in the database failed to respond at all under this stimulus condition. Consequently, the auditory nerve model assigns driven rates of 0 to low SR fibers at vowel levels of 43 dB and below.

FIGURE 3. Average rate-level functions for all high, medium and low SR fibers that were SMP tested at a 43 dB vowel level.

Correlation coefficients refer to the linear regression for each SR class (solid lines). For comparison, the regression for high SR fibers is plotted in all panels (dashed lines). No regression line is shown for low SR fibers because most units in this SR class failed to respond to the formant structure of a 43 dB vowel. Error bars indicate ±1 SD.

TABLE I.

Linear Regressions for Rate Responses in Quiet.

Vowel Level	Regression	High SR	Medium SR	Low SR
43 dB SPL	y-Intercept	−10.03	−21.79	No Resp.
	Slope	3.69	4.05
	R2	0.97	0.91
63 dB SPL	y-Intercept	36.95	−3.50	−60.00
	Slope	2.11	2.97	2.88
	R2	0.82	0.90	0.88
83 dB SPL	y-Intercept	64.77	17.93	−81.35
	Slope	1.17	1.78	2.52
	R2	0.87	0.75	0.78

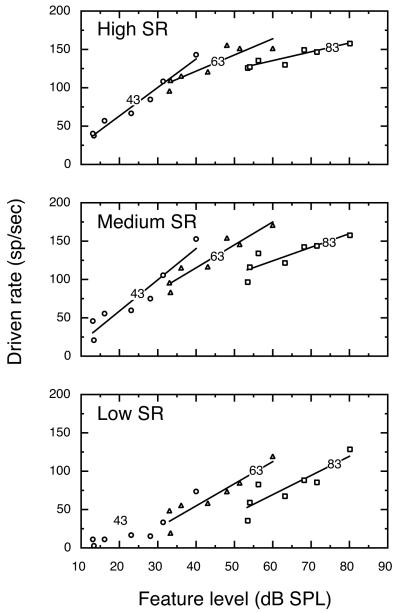
Figure 4 shows driven rates plotted as a function of feature level at vowel levels of 43, 63, and 83 dB. Separate linear regresssions (solid lines) are shown for each vowel level and SR class. The squared correlation coefficient (R²) exceeded 0.75 for all of these functions. Statistics of individual functions are presented in Table I. The effects of vowel level on discharge rates of auditory-nerve fibers fell into two distinct patterns. As shown in the upper panel of Fig. 4, high SR fibers responded to differences in feature level with changes in discharge rate at low vowel levels. The range of rate differences that were available for encoding changes in feature level diminished at higher vowel levels because of rate saturation effects (Sachs and Young, 1979; Le Prell et al., 1996). These dynamic range properties make high SR fibers better suited for the encoding of low level stimuli.

FIGURE 4. Average rate-level functions for the three SR classes at vowel levels of 43, 63, and 83 dB.

Rate responses for high SR fibers displayed good sensitivity to changes in feature level at 43 dB, but the slope of the rate-level function flattened at 83 dB because of rate saturation. In contrast, rate-level functions for low SR fibers maintained a steep slope at 83 dB. Numbers indicate vowel levels. Regression statistics are described in Table I.

As shown in the lower panel of Fig. 4, low SR fibers displayed a pattern of responding that made these units better suited for the encoding of high level stimuli. Relatively high thresholds rendered most low SR fibers insensitive at low vowel levels; whereas, large rate differences were available for encoding formant features at high vowel levels. The parallel shift shown by linear regressions for the 63 and 83 dB vowel levels indicates that driven rates of low SR fibers were minimally influenced by saturation effects at higher vowel levels. The representation of feature level by low SR fibers was enhanced under these stimulus conditions by the effects of two-tone suppression which prevented trough driven rates (data points on left-hand side of each regression) from rising to the level of formant driven rates (right-hand side of each regression). Medium SR fibers showed mixed properties of high and low SR fibers. The effects of rate saturation and two-tone suppression on the neural representation of vowel sounds are discussed in detail in Le Prell et al. (1996).

Linear Models for Vowel Representation in Background Noise

Figure 5 shows average driven rates as a function of feature level for all units that were tested at a 63 dB vowel level in background noise. Rate responses of high SR fibers exhibited a strong linear correlation of driven rate with feature level (R²=0.95), but the total range of rates available for encoding the amplitude spectrum of the vowel was reduced to less than 14 sp/sec by background noise. That is, the driven rates of these units changed by less than 14 sp/sec regardless of whether the most intense feature (F1) or the least intense feature (T1) was placed at BF. This is approximately 24% of the range of rate responses that was observed when high SR fibers were tested with the 63 dB vowel in quiet (Fig. 4). This loss of rate information has two sources. First, noise reduces the maximum difference in level between formant and trough features by approximately 10 dB because the noise floor is higher than the depth of the T1 feature. Secondly, noise-driven activity saturates and compresses the rate responses of low threshold, high SR fibers even when spectral troughs are placed at BF.

FIGURE 5. Rate representations of a 63 dB vowel in noise by high, medium, and low SR fibers.

Background noise severely reduced the range of driven rates by which high SR fibers encoded feature level differences within vowel stimuli. This dynamic range compression is particularly evident when the regression for high SR rate changes (dashed line) is compared with data obtained from low SR fibers. Figure conventions are described in Figure 3.

The lower two panels of Fig. 5 show rate responses of medium and low SR fibers to the 63-dB vowel in noise. The linear regression for high SR fibers (dashed lines) is repeated in these panels to facilitate comparisons of rate changes across SR classes. Because of their higher thresholds, medium and low SR fibers were less driven by background noise and therefore maintained a broader range of rate responses for encoding vowel stimuli. Nevertheless, these fibers displayed noise-induced rate compression. Low SR units, for example, exhibited a rate difference of 64 sp/sec between responses to the F1 and T1 features at the 63 dB vowel-in-noise condition, which represents 82% of the average change in rate that low SR fibers had available for encoding vowels under quiet testing conditions (Fig. 4). The range of rate changes by which medium and low SR fibers encode vowels in noise was augmented by suppression effects that occurred when the T1 feature was placed at BF, as indicated by the negative driven rates that were often observed for this stimulus condition. Medium and low SR fibers exhibited the enhancing influences of rate suppression at all vowel levels, but high SR fibers also showed suppression effects at 73 dB.

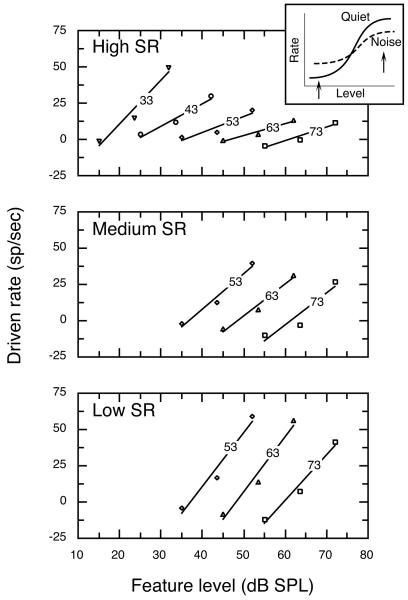
Figure 6 shows driven rates as a function of feature level for all vowel-in-noise test conditions; associated regression statistics are described in Table II. All of the regressions shown in Fig. 6 produced R² values of at least 0.89. Medium and low SR fibers were not tested below 53 dB SPL because most units in these SR classes failed to respond to any feature but F1. High SR fibers showed a rate-level function with a steep slope for the 33 dB vowel in noise condition (2.99 sp/sec/dB) which created a maximum rate difference of 51 sp/sec across the 17 dB range of feature levels that occur within the vowel-in-noise condition. A progressive flattening of rate-level functions was observed as the level of the vowel (and therefore background noise) increased. As illustrated by the inset in Fig. 6, rate compression is related to the magnitude of a unit’s response to background noise. Under quiet testing conditions, the range of rate changes available for encoding a vowel’s amplitude spectrum extends from the unit’s spontaneous rate to its maximum driven rate (solid line). Costalupes et al. (1984) have shown that this range of driven rates is reduced when noise-driven activity increases minimum rates above spontaneous activity and decreases maximum rates through short term adaptation (dashed line).

FIGURE 6. Effects of background noise on rate-level functions for high, medium and low SR fibers at vowel levels from 33 – 73 dB.

Functions for high SR fibers showed a progressive flattening at high vowel levels. In contrast, low SR fibers maintained a relatively steep slope at the highest vowel levels. Inset: Compression of rate information results from noise-driven activity that increases discharge rates to low-level trough features (left arrow) and ensuing adaptation effects that decrease rates to high-level formant features (right arrow). Numbers indicate vowel level for each function; regression statistics are presented in Table II.

TABLE II.

Linear Regressions for Rate Responses in 3 dB Signal-to-Noise Ratio.

Vowel Level	Regression	High SR	Medium SR	Low SR
33 dB SPL	y-Intercept	−49.29	Not tested	Not tested
	Slope	2.99
	R2	0.95
43 dB SPL	y-Intercept	−37.22	Not tested	Not tested
	Slope	1.55
	R2	0.96
53 dB SPL	y-Intercept	−39.53	−88.72	−137.66
	Slope	1.11	2.42	3.71
	R2	0.89	0.97	0.96
63 dB SPL	y-Intercept	−38.06	−105.76	−182.55
	Slope	0.81	2.18	3.79
	R2	0.95	0.97	0.97
73 dB SPL	y-Intercept	−58.73	−133.78	−187.00
	Slope	0.96	2.18	3.14
	R2	0.93	0.89	0.98

Rate-level functions for medium and low SR fibers displayed a 10 dB horizontal shift for each 10 dB increase in vowel level. In addition, the slopes of these functions were essentially invariant across vowel levels of 53 – 73 dB. Noise effects were less pronounced among these units because in general their thresholds were higher than those of high SR fibers. Consequently, units in the low and medium SR classes showed less noise-driven activity than high SR fibers when tested in the same level of background noise. Close inspection of rate-level functions for medium and low SR fibers in Fig. 6 does reveal a monotonic decrease in F1 response as vowel and noise levels increased. However, the decline in the driven rates elicited by formant features is offset by a similar decrease in T1 responses that is due to rate suppression. Suppression effects also produced a slight enhancement of the range of high SR rate changes at 73 dB, which is reflected by an increase in slope relative to the rate-level function at 63 dB (Table II).

Neural Representation of a Change in Formant Frequency

The linear regressions described above were used to simulate auditory nerve representations of changes in the formant structure of the vowel /ε/. Formant changes were produced by shifting the frequency of F2 above 1700 Hz, which is the frequency of this formant in the prototypic vowel. For example, the left ordinate of Fig. 7(a) compares two 43 dB vowel stimuli with differing F2 frequencies of 1700 Hz (F2₁₇₀₀) and 2000 Hz (F2₂₀₀₀). To facilitate a comparison of the formant structure of the two vowels, their discrete harmonic components (with 100-Hz spacing) are plotted as continuous amplitude spectra. Although the parameters of F1 and F3 are the same in these two vowels, moving F2 toward F3 causes an increase in level near F3 because of the properties of the cascade resonator simulation used to generate the stimuli (Klatt, 1980). These additional cues were not as prominent for smaller changes in F2. The right ordinate of Fig. 7(a) indicates the magnitude of theoretic rate responses to the two stimuli, which were calculated by applying the linear regression for high SR fibers at 43 dB to each vowel’s amplitude spectrum. It is possible to represent the spectral shape of stimuli and predicted discharge rates using the same plots because the auditory nerve model was based on a linear conversion of feature level to discharge rate.

FIGURE 7. Simulated rate responses of high SR fibers to a 300-Hz F2 frequency change at a vowel level of 43 dB.

(a) Amplitude spectra and vowel driven rates for the standard vowel /ε/ with an F2 frequency of 1700 Hz (F2₁₇₀₀, solid line) and a comparison vowel with F2 of 2000 Hz (F2₂₀₀₀, dashed line). Left ordinate indicates level of stimulus components; right ordinate, discharge rates predicted by a linear conversion of feature level-to-driven rate using the regression analysis for high SR fibers in Table I. (b) Average rate differences (d_i, upper panel) and standard deviations (σ_i, lower panel) for simulated responses to F2₁₇₀₀ and F2₂₀₀₀. (c) d’ values computed from the ratio of di to σ_i using Eq. 1. Detectable rate differences are indicated by d’ values that exceed ±1 (dashed lines).

Figure 7(b) plots simulated rate differences (d_i) as a function of unit BF. In this example, d_i reflects the difference in theoretical driven rates for the F2₂₀₀₀ and F2₁₇₀₀ vowels. The resulting rate difference profile shows peaks of about ±50 sp/sec between 1600 and 2100 Hz where different F2 frequencies create major spectral differences between the two stimuli. A potential problem with the theoretical rate representations shown in Fig. 7(b) is that auditory-nerve fiber responses to the standard vowel /ε/ were used to simulate responses to a second vowel-like stimulus with different formant structure. Unique patterns of saturation and suppression for the novel stimulus may alter the shape of rate-level functions that form the basis of the auditory nerve model. Fortunately, Conley and Keilson (1995) have used direct single-unit recording methods to characterize the auditory nerve representation of F2 changes in the vowel /ε/. Their analysis was based on rate differences that arise among a population of fibers when individual units are stimulated with different vowels. In their study, grouping high and medium/low SR fibers produced vowel rate-level functions with slopes of 2.8 and 4.0 sp/dB, respectively, at a 50-dB stimulus level. When simulated responses from low and medium SR fibers were combined (Table I), linear interpolations predicted slopes of 3.1 and 3.7 sp/dB for the same SR classes and stimulus level. Because of the similarity of these independently characterized rate-level relationships, simulated results are presumed to provide a good estimation of actual rate-difference profiles.

The quality of the neural representation that signifies a change in F2 depends not only upon the magnitude of rate differences like those shown in Fig. 7(b) but also upon the variability of responses. This relationship has been formalized in signal detection theory as the d’ statistic (Green and Swets, 1966; Macmillan and Creelman, 1991). As shown in Eq. 1, d’ is the z-transformation of an individual unit’s rate differences (d_i) for repeated presentations of two vowels (V and W). To compute d’, the standard deviation of the rate differences between two vowels (σ_i) is estimated as (see Barta, 1985, for derivation in this context).

$$d^{\prime }=\frac{d_{\mathrm{i}}}{{\sigma }_i}.$$ (1)

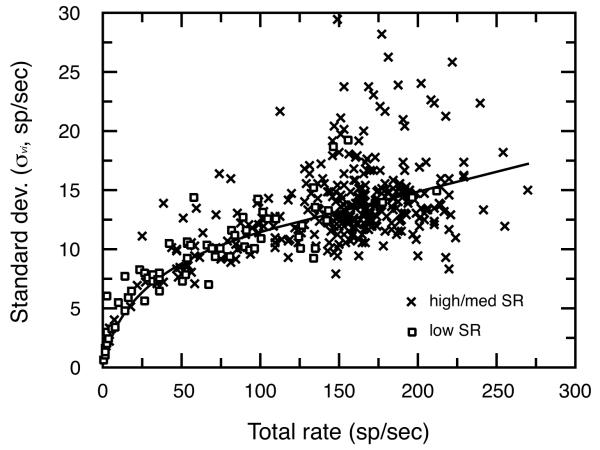
Figure 8 plots for individual fibers as a function of total discharge rate. The high sampling density and broad range of discharge rates seen in this figure were created by combining responses across all of the units, stimulus features, and vowel levels in the electrophysiological study by Le Prell et al. (1996). These data indicate that the magnitude of is proportional to total driven rates of individual fibers, and is not significantly influenced by SR. Although there is considerable variation in σ_{v i} , average values are well approximated by the product of Eq. 2 (bold line). Eq. 2 was used to derive for simulated responses after vowel driven rates were converted to total discharge rates by adding the following constant SR values: 0.5 sp/sec (low SR), 8.5 sp/sec (medium SR), and 33.0 sp/sec (high SR). These constants reflect average spontaneous rates for the three SR classes according to the database of Le Prell et al. (1996).

$${\sigma }_{vi}=1.89\times {\left(totalrate\right)}^{0.39}.$$ (2)

FIGURE 8. Changes in standard deviation (σ_vi) with total rate.

Each symbol reflects the response of a single auditory-nerve fiber. The product of Eq. 2 (solid line) was used to estimate σ_vi for simulated rate representations of vowels in quiet.

Figure 7(b) shows a plot of σ_i values that were calculated for the rate profiles in Fig. 7(a) using Eq. 2. These values vary from 10 to 20 sp/sec because of the wide range of driven rates seen in Fig. 7(a). σ_i attained peak values in the region of the F1 feature, where driven rates approached 150 sp/sec. These simulated measures approximate actual neural responses observed by Conley and Keilson (1995) whose model calculations were based on an average σ_i of 20 sp/sec at vowel levels of both 50 and 70 dB SPL. As previously discussed, the range of driven rates elicited by the amplitude spectrum of a vowel becomes compressed in the presence of continuous background noise. As a result, when tested at a constant 3 dB S/N, fibers within each SR class display a relatively uniform σ_i regardless of the level of the vowel or the test feature at the unit’s BF. Low, medium, and high SR fibers exhibited an average σ_i of 21.1, 21.5, and 24.9 sp/sec in our electrophysiological database (Le Prell, 1995). The trend toward increasing σ_i with higher SR is expected because high SR fibers show greater total discharge rates to vowels in noise than their low SR counterparts. These constant values of σ_i were used to calculate d’ values for simulations in noise.

The d’ values shown in Fig. 7(c) were produced by combining d_i and σ_i in Fig. 7(b) according to Eq. 1. The dashed reference lines in the figure indicate d’ values equal to ±1. When the d’ values extend beyond these lines, the rate increase or decrease that occurred between the two vowel stimuli exceeds one σ_i and can be considered detectable in terms of signal detection theory. In the example shown here, rate differences of this magnitude are primarily seen in the F2 frequency region where the vowels show maximal differences in formant structure. d’ values for high SR simulations reached peak values of about 4 at these frequencies. Conley and Keilson (1995) observed a similar dependence of d’ on BF, although they noted a maximum d’ of about 2.5 when testing high SR fibers at a vowel level of 50 dB SPL. In our simulations, high SR d’ values fell to about 2 at a vowel level of 63 dB SPL, which suggests a general correspondence of results obtained with the different methods of these two independent studies.

The results shown in Fig. 7(c) predict how a population of high SR fibers should respond to a change in F2 when tested at a 43 dB vowel level. One of the goals of Experiment 1 was to create a decision model that would predict behavioral discriminability of vowels by summing neural rate information across the auditory-nerve fiber array. A maximum-likelihood detector for this task was developed by Barta (1985), and recently elaborated upon by Conley and Keilson (1995). The performance of the optimal detector can be calculated from the Q statistic (Eq. 3), where d_i is the rate difference and σ_i is the standard deviation of the rate difference for the i^th fiber within the total population of auditory-nerve fibers. Q is the z-score of the probability of correct detection in a two-alternative forced choice discrimination task. For our purposes, the task involves detecting a difference in F2 frequency based on rate differences of auditory-nerve fiber responses.

$$Q=\frac{\sum _{i=1}^N{d}_i^2}{\sqrt{\sum _{i=1}^N{d}_i^2{\sigma }_i^2}}.$$ (3)

The summation in Eq. 3 must be computed across a sampling of units that reflects the actual number, SR distribution, and spatial (BF) density of fibers in the cat’s auditory nerve. To do this frequency weighting, the sums in the numerator and denominator of Eq. 3 are approximated as

$$\sum _{i=1}^N{d}_i^2\approx {\int }_{y0}^{y1}{D}^2\left(y\right)h\left(y\right)dy,$$ (4)

$$\sum _{i=1}^N{d}_i^2{\sigma }_i^2\approx {\int }_{y0}^{y1}{D}^2\left(y\right)S^2\left(y\right)h\left(y\right)dy,$$ (5)

where D(y) is a smoothed (cubic spline) continuous version of the discrete variable d_i, S(y) is a similar smoothed version of σ_i, y=log f is a log frequency scale, and h(y) is the density of auditory-nerve fibers along the cochlea in terms of the log frequency scale. h(y) is given by

$$h(y=\log f)=\frac{5000f}{0.176+0.126f},$$ (6)

which was derived from data of Keithley and Schreiber (1987), who found 5000 spiral ganglion cells/mm length of Rosenthal’s canal in the cat cochlea and provided an equation for the map of BF in terms of distance. The frequency limits of the integration in Eqs. 4 and 5 (y₀ and y₁) were set to the logarithms of 100 and 3000 Hz. Now Q can be calculated by summing separately over the SR groups using Eq. 7

$$Q=\frac{\sum _{sr}{\int }_{y0}^{y1}{P}_{sr}{D}_{sr}^2\left(y\right)h\left(y\right)dy}{\sqrt{\sum _{sr}{\int }_{y0}^{y1}{P}_{sr}{D}_{sr}^2\left(y\right)S_{sr}^2\left(y\right)h\left(y\right)dy}},$$ (7)

where the subscript sr ranges over low, medium, and high SR fibers and P_sr is the fraction of the total auditory nerve population in each SR class (P_sr = 0.61 for high, 0.23 for medium, and 0.16 for low SR fibers; Liberman, 1978).

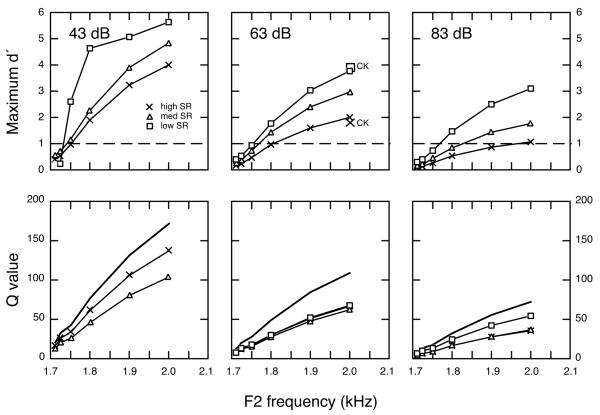
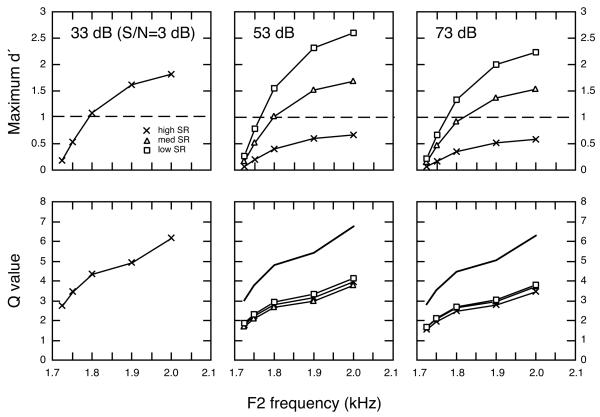
Auditory nerve responses to F2 frequency changes were simulated at several vowel levels in quiet and continuous background noise to compare representations provided by discharge rates of high, medium, and low SR fibers. In the upper panels of Fig. 9 and in Table III, the quality of these neural representations is summarized in terms of maximum d’ values for testing in quiet. These values are taken from the peaks of d’ profiles that occur at F2 frequencies (Fig. 7c). In each case, d’ values were computed from differences in rate responses to repeated presentations of the standard vowel (F2₁₇₀₀) and a comparison vowel with a higher F2 frequency. The abscissa of the figure indicates the frequency location of F2 in the comparison vowel. As noted above, most low SR fibers did not respond to the vowel’s formant structure at 43 dB. Maximum d’ values that are presented for these units reflect only the responses of the most sensitive low SR fibers (see Fig. 7, Le Prell et al., 1996). Fibers in all three SR classes displayed similar trends in their response to the 43 dB vowel. As the magnitude of F2 frequency changes grew between standard and comparison vowels, maximum d’ values increased sharply. F2 changes as small as 50 Hz produced d’ values that were greater than 1, a common criterion of detectability in signal detection theory. A 300-Hz change in F2 yielded a d’ approaching 5. These results suggest that high and medium SR fibers with BFs near the F2 frequency range provide a good representation of formant frequency changes at low levels under quiet conditions; however, rate information is also conveyed by selected low SR fibers.

FIGURE 9. Signal detection analysis of the rate representation of F2 frequency changes in quiet.

(upper panels) Maximum d’ values as a function of the F2 frequency of comparison vowels. Symbols with CK notation show maximum d’ values that were interpolated from results of Conley and Keilson (1995). Dashed lines indicate d’ of 1. (lower panels) Q statistics for the same F2 frequency changes. Q_total values (bold lines) dropped sharply with increases in vowel level.

TABLE III.

Effects of Vowel Level on Maximum d’ for F2 Changes in Quiet.

Vowel Level	2nd Formant	High SR	Medium SR	Low SR
43 dB SPL	2000	3.99	4.84	5.65
	1900	3.22	3.91	5.07
	1800	1.89	2.27	4.64
	1750	0.97	1.17	2.61
	1725	0.52	0.70	0.25
	1710	0.40	0.55	0.25
63 dB SPL	2000	1.99	2.98	3.77
	1900	1.61	2.41	3.05
	1800	0.96	1.43	1.78
	1750	0.48	0.73	0.92
	1725	0.23	0.36	0.53
	1710	0.17	0.27	0.41
83 dB SPL	2000	1.08	1.77	3.09
	1900	0.88	1.44	2.50
	1800	0.52	0.85	1.47
	1750	0.26	0.43	0.75
	1725	0.12	0.20	0.40
	1710	0.09	0.15	0.31

Simulations were also performed for high, medium, and low SR fibers at vowel levels of 63 and 83 dB. At these higher vowel levels, decreases in d_i and increases in σ_i combined to produce a decline in maximum d’ values for high and medium SR fibers. This loss of rate information was particularly apparent for high SR fibers which failed to exhibit d’ values greater than 1 for F2 changes of less than 300 Hz in the 83 dB simulation. In contrast, low SR fibers exhibited detectable rate differences for F2 changes smaller than 100 Hz. Large symbols in the 63 dB plot indicate the maximum d’ for the F2₂₀₀₀ comparison vowel for high (×) and low/medium SR fibers (square) in the population study of Conley and Keilson (1995). These data were interpolated from their results at vowel levels of 50 and 70 dB. The results of our simulations generally match their direct physiological measurements. Both simulations suggest that low SR fibers may provide the most sensitive representation of F2 frequency changes at high vowel levels.

Q values in the lower panels of Fig. 9 and in Table IV describe the combined rate representation of F2 frequency changes in quiet by all fibers with BFs of less than 3000 Hz. Data are provided for the three SR classes individually (Q_SR, lines with symbols) and in combination (Q_total, bold lines). Q_{low sr} is not shown for the 43 dB condition because the statistic is designed to reflect the combined responses of all low SR fibers, most of which were unresponsive at this low vowel level. Q_total showed a concomitant decrease with increases in vowel level that was largely due to a steep decline in the rate information provided by the high SR fibers that comprise 61% of the auditory nerve population. Contributions of low SR fibers to the Q_total statistic did not make up for the loss of high SR information because of the smaller percentage of low SR fibers (16%). Differences in Q_sr values between SR classes were smaller than differences in maximum d’ values also because of variation in the proportion of fibers within each SR class (P_sr).

TABLE IV.

Effects of Vowel Level on Q Values for Second Formant Changes in Quiet.

Vowel Level	2nd Formant	High SR	Medium SR	Low SR	Total
43 dB SPL	2000	137.8	104.7	No resp.	171.9
	1900	106.2	80.7		132.6
	1800	62.1	47.0		77.5
	1750	35.0	26.8		43.8
	1725	26.8	21.1		33.8
	1710	16.5	13.1		20.8
63 dB SPL	2000	66.9	62.3	67.8	109.2
	1900	51.6	48.0	52.2	84.2
	1800	30.3	28.2	30.5	49.4
	1750	16.8	15.7	17.3	27.5
	1725	12.5	11.9	13.5	20.6
	1710	7.7	7.3	8.3	12.7
83 dB SPL	2000	36.1	36.6	54.7	72.2
	1900	27.8	28.2	42.2	55.7
	1800	16.4	16.6	24.7	32.7
	1750	9.0	9.2	13.9	18.1
	1725	6.7	6.8	10.6	13.6
	1710	4.1	4.2	6.5	8.3

Figure 10 compares the quality of neural representations that simulate auditory-nerve fiber rate responses to vowels in continuous background noise (S/N=3 dB). Maximum d’ values are presented for vowel levels of 33 - 73 dB SPL in the upper panels of Fig. 10 and in Table V. All SR classes exhibited smaller d’ values in noise than in quiet (note scale changes between Figs. 9 and 10). High SR fibers produced maximum d’ values that exceeded signal detection thresholds of 1 (dashed lines) only when tested at 33 dB. F2 frequency changes as small as 100 Hz produced detectable rate differences at this low vowel level. Although high SR fibers failed to perform above threshold at 53 and 73 dB, low SR fibers exhibited d’ values of 1 for F2 changes of less than 100 Hz at these higher vowel levels.

FIGURE 10. Representation of F2 frequency changes in continuous background noise.

Maximum d’ values are shown in upper panels; Q statistics, in lower panels. Dashed lines in upper panels indicate d’ of 1. Q_total (bold lines) fell to values less than 7 when vowels were presented in background noise.

TABLE V.

Effects of Vowel Level on Maximum d’ for F2 Changes in Noise.

Vowel Level	2nd Formant	High SR	Medium SR	Low SR
33 dB SPL	2000	1.81	Not tested	Not tested
	1900	1.61
	1800	1.08
	1750	0.54
	1725	0.18
43 dB SPL	2000	0.94	Not tested	Not tested
	1900	0.83
	1800	0.56
	1750	0.28
	1725	0.09
53 dB SPL	2000	0.67	1.69	2.60
	1900	0.60	1.51	2.31
	1800	0.40	1.01	1.55
	1750	0.20	0.51	0.78
	1725	0.07	0.17	0.26
63 dB SPL	2000	0.49	1.53	2.65
	1900	0.44	1.36	2.36
	1800	0.29	0.91	1.59
	1750	0.15	0.46	0.79
	1725	0.05	0.15	0.26
73 dB SPL	2000	0.58	1.53	2.24
	1900	0.52	1.36	2.00
	1800	0.35	0.91	1.34
	1750	0.17	0.46	0.67
	1725	0.06	0.15	0.22

On average, the addition of background noise created a 50% decrease in maximum d’ values for all SR classes. As shown in the lower panels of Fig. 10 and in Table VI, negative effects of noise on the Q statistic were even more pronounced. For example, the Q_total for a 300-Hz F2 change at 63 dB fell from a value of 109 in quiet to less than 7 in noise. This substantial loss of rate information was due not only to a noise-induced compression of maximum d_i values but also to a decrease in the number of fibers that exhibited rate differences between vowels. The reduction in the number of contributing fibers occurred primarily at BFs that fell within the troughs surrounding F2 frequencies. Spectral differences between the standard and comparison vowels at these frequencies were a rich source of rate information in quiet (Fig. 7a), but these differences were masked by background noise (Fig. 2a). All Q functions show a steeper slope at 2.0 kHz because this F2 frequency was associated with an additional source of rate information that resulted when F3 was shifted above the noise floor by the closely spaced energy in the second formant.

TABLE VI.

Effects of Vowel Level on Q Values for Second Formant Changes in Noise.

Vowel Level	2nd Formant	High SR	Medium SR	Low SR	Total
33 dB SPL	2000	6.16	Not tested	Not tested
	1900	4.93
	1800	4.37
	1750	3.46
	1725	2.77
43 dB SPL	2000	4.44	Not tested	Not tested
	1900	3.55
	1800	3.15
	1750	2.49
	1725	1.99
53 dB SPL	2000	3.76	3.94	4.15	6.77
	1900	3.00	3.15	3.32	5.41
	1800	2.66	2.80	2.95	4.80
	1750	2.11	2.21	2.33	3.80
	1725	1.69	1.77	1.65	3.04
63 dB SPL	2000	3.21	3.74	4.20	6.41
	1900	2.57	2.99	3.36	5.12
	1800	2.28	2.65	2.98	4.54
	1750	1.80	2.10	2.36	3.60
	1725	1.44	1.68	1.88	2.87
73 dB SPL	2000	3.49	3.74	3.82	6.31
	1900	2.79	2.99	3.06	5.05
	1800	2.48	2.65	2.71	4.48
	1750	1.96	2.10	2.15	3.55
	1725	1.57	1.68	1.71	2.83

EXPERIMENT 2: BEHAVIORAL DISCRIMINATION OF SECOND FORMANT FREQUENCY CHANGES

The results of auditory nerve simulations offer insights into the neural representation of F2 frequency changes. Of particular interest are the different effects of vowel level upon maximum d’ values of low and high SR fibers and the strong negative effects of continuous background noise on vowel encoding. Behavioral thresholds for F2 frequency changes were obtained in three cats to evaluate how these changes in the quality of vowel representations related to psychophysical performance.

METHODS

Subjects

Behavioral subjects were housed in individual cages and maintained on a restricted feeding schedule. Water was provided ad libitum. Cats performed in the experimental situation for liquefied cat food, with supplemental dry cat food (10-20 g) provided on a daily basis after each experimental session. Cats were given full rations when no experimental sessions were scheduled the next day (e.g., Fridays and Saturdays). Each animal’s health was checked daily by a trained animal technician, and animals were weighed three times a week. Periodic physical examinations were performed by veterinary staff. All animal care was conducted in accordance with AALAC guidelines. Each animal had previous behavioral experience in discriminating among synthetic tokens of natural multi-formant vowels in quiet and in background noise (Hienz et al., 1996a), and in discriminating F2 frequency changes in quiet (Hienz et al., 1996b).

Apparatus

Cats were tested in a 30.5 cm × 61 cm × 43.2 cm cage constructed of 1.3-cm wire mesh. The cage was supported by 1.3-cm aluminum rods and suspended at the approximate center of a double-walled, sound-attenuating chamber (Industrial Acoustics Model 1204A) with inner dimensions of 1.8 m × 1.8 m × 2.0 m. Cats were trained to detect changes in acoustic signals presented from a free field loudspeaker placed above and toward the front of the cage. All surfaces of the chamber were covered with sound-attenuating foam. In the front of the cage at eye level was a circular, translucent stimulus light (3.8 cm in diameter) that signaled behavioral contingencies such as trial onset and offset. Above the stimulus light was a metal spout that dispensed a measured amount of liquefied cat food for the reinforcement of correct responses. To the right of and below the stimulus light, a response lever was positioned just above the floor of the cage. Cats were trained to press the response lever with the right paw. Testing sessions were monitored with a closed-circuit video system. Stimulus presentation, behavioral contingencies, and data recording were carried out automatically by a PDP11/73 computer.

Stimuli

The stimuli consisted of digitally-generated synthetic vowels (80-kHz minimum sampling frequency) which were generated using a Klatt (1980) synthesizer. The synthesis was done with a cascade synthesizer containing five formants; F₁, F₃, F₄, and F₅ were kept constant at 500, 2500, 3300, and 3750 Hz, respectively, and the fundamental (F0) was fixed at 100 Hz. Corrections for the spectrum of the glottal volume velocity and for the radiation impedance were implemented as described by Klatt (1980). The standard vowel /ε/ had a second formant of 1700 Hz (F2₁₇₀₀ in Fig. 7a). Six synthetic variants of /ε/ had F₂’s located at 1710, 1725, 1750, 1800, 1900, and 2000 Hz.

All stimuli were pre-synthesized and the digital waveforms stored for later presentation via D/A converter. Stimuli were passed through an electronic switch with rise/fall times of 20 msec, a programmable attenuator, an amplifier, and then to the speaker. Stimuli were presented through a 3-inch wide-range speaker suspended approximately 30 cm above and in front of the subject. The speaker was positioned to produce a flat frequency response (±3 dB) in the area of the cat’s head. All stimuli had a burst duration of 250 msec and were presented at a rate of 2 bursts/sec. Stimulus level was randomly varied over a 10-dB range from burst to burst to prevent the cats from attending to changes in spectrum level between vowels.

Behavioral Procedures

Cats were trained to press and hold down the lever with their right paw to produce a pulsed train of the standard vowel (F2₁₇₀₀). After a variable time of 5 to 10 sec during which the cats maintained the holding response, the stimulus train began to alternate, changing from the standard vowel to a randomly selected comparison vowel (method of constant stimuli; May et al., 1995). A release of the lever within a 1.5-sec “window” from the start of the alternating stimuli was considered a correct detection of the change in vowel sound, and was reinforced with food. Releases at any other time were considered errors and punished with a 2 – 8 sec timeout from the experimental contingencies. On 20% of all trials, false alarm rates of the subjects were measured by presenting “catch trials” during which no F2 frequency changes occurred. Releases during catch trials were also followed by a 2 – 8 sec timeout. If cats maintained the holding response for the 1.5-sec catch trial duration, a comparison vowel was presented and the subject received an additional 1.5-sec response window in which to obtain food by releasing the lever. Testing was conducted 5 days per week and each cat typically performed a minimum of 80 – 100 trials in individual sessions lasting 45 – 60 min.

Thresholds for F2 frequency changes (ΔF₂s) were measured at S/Ns of 3, 13, and 23 dB at vowel levels of 31, 51, and 71 dB SPL. Cats were tested at one stimulus condition until performance stabilized over 7 – 10 consecutive sessions. Criteria for stability was based upon: 1) at least 50 trials were obtained during each session, and 2) vowel discriminability showed no upward or downward trends across sessions (as assessed by percent correct scores and d’ values). An attempt was also made to keep average false alarm rate below 25% throughout the study. This goal was achieved in cat BU, but cats PO and TU had difficulty in maintaining false alarm rates below 25% under at least one stimulus condition.

Psychophysical thresholds were determined by summing the results of tests with each comparison vowel across the last five sessions at each stimulus condition. Psychometric functions were then constructed by plotting the combined percent correct scores as a function of the magnitude of change in F2 between the standard and comparison vowels. Correct detections (hits) for each comparison vowel were converted to d’ statistics by

$$d^{\prime }=z\left(P_{hit}\right)-z\left(P_{falsealarm}\right),$$ (8)

where z(P_hit) is the z score for the percentage of hits for the comparison vowel and z(P_{false alarm}) is the z score for the subject’s percentage of false alarms. ΔF2 was defined as the formant frequency difference corresponding to a d’ value of 1, as interpolated from the summary d’ function.

RESULTS

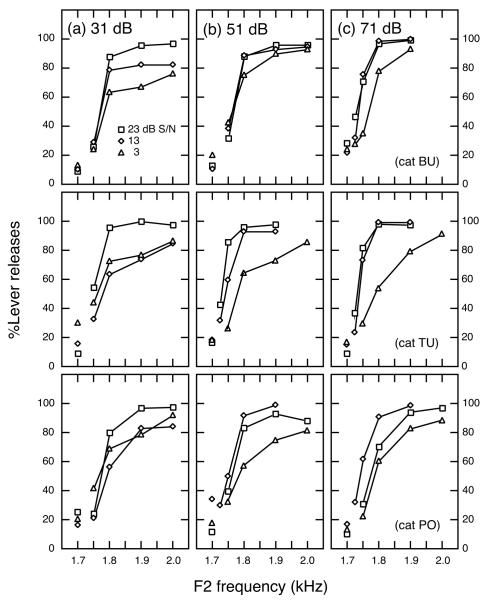
Figure 11 shows psychometric functions in which the percentage of correct releases (hits) are plotted as a function of the F2 frequencies of comparison vowels. Incorrect releases to catch trials (false alarms) are indicated by unconnected symbols at 1.7 kHz, the F2 frequency of the standard vowel. Moving from the upper to lower row of the figure, data are presented for cats BU, TU, and PO. Results of testing at three different S/Ns are shown at vowel levels of 31, 51, and 71 dB. All cats produced psychometric functions that showed greater hit rates with larger F2 changes. As the S/N decreased from 23 to 3 dB, psychometric functions became shallower in slope and asymptoted at lower performance levels.

FIGURE 11. Psychometric functions for three different S/Ns, at three vowel levels.

The percentage of correct lever releases to comparison vowels (hits) are plotted as a function of the change in F2 between standard and comparison vowels. The percentage of incorrect lever releases to catch trials (false alarms) are indicated by unconnected symbols at 1.7 kHz. (a–c) Vowel levels are 31, 51, and 71 dB. Data for cats BU, TU, and PO are shown in upper, middle, and lower rows, respectively.

Table VII summarizes ΔF2 thresholds for all subjects and stimulus conditions. Individual thresholds ranged from 35 – 92 Hz at the 31-dB vowel level, 29 – 93 Hz at the 51-dB vowel level, and 25 – 96 Hz at the 71 dB vowel level. In each case, the lower limit of the threshold range was observed in the 23 dB S/N and the upper limit in the 3 dB S/N. Figure 12(a) plots average ΔF2 thresholds at the three vowel levels as a function of S/N. Error bars encompass ±1 standard error (SE). At each vowel level, ΔF2 thresholds decreased as S/N increased. Figure 12(b) shows that false alarm rates also decreased slightly with increasing S/N, another indication that cats had greater difficulty in performing the discrimination in higher noise levels. Threshold estimates computed in terms of d’ should not be biased by false alarm rate increases of this magnitude.

TABLE VII.

Effects of Vowel Level and S/N on Behavioral Thresholds.

Vowel Level	S/N	Cat BU	Cat PO	Cat TU	Mean (SE)
31 dB SPL	23	58.1	83.4	34.6	58.9 (14.2)
	13	61.2	92.0	77.0	76.8 ( 8.9)
	3	77.9	78.2	92.0	82.7 ( 4.7)
51 dB SPL	23	60.3	53.5	29.1	47.6 ( 9.5)
	13	50.7	71.6	45.1	55.8 ( 8.1)
	3	70.4	92.9	85.9	83.1 ( 6.7)
71 dB SPL	23	45.4	61.8	25.2	44.1 (10.6)
	13	39.8	41.9	37.7	39.7 ( 1.1)
	3	79.2	81.4	96.0	85.6 ( 5.3)

FIGURE 12. (a) Second formant frequency difference thresholds (ΔF2) and (b) false alarm rates as a function of S/N, at three vowel levels.

Numerical labels indicate vowel level. Error bars show ± 1 SE.

Figure 13 shows the data of Fig. 12(a) replotted as a function of vowel level. Also shown for comparison are F2 frequency difference thresholds in quiet from a previous study (Hienz et al., 1996b) In quiet, ΔF2 thresholds drop sharply as vowel levels increase above 11 dB then remain relatively constant at higher levels. A similar trend toward smaller ΔF2s at higher vowel levels is also seen at S/Ns of 23 and 13 dB, but the threshold change occurs at higher vowel levels and is not as pronounced. No significant differences were observed between behavioral thresholds in quiet and in these two noise levels at the 71 dB vowel level. All other thresholds for testing in noise were above those obtained in quiet. The 3 dB S/N produced the highest thresholds at each vowel level. Unlike testing in high S/Ns, ΔF2 for this stimulus condition remained relatively constant across vowel levels of 31 to 71 dB.

FIGURE 13. ΔF2 as a function of vowel level, across different S/Ns.

Also shown for comparison are psychophysical thresholds obtained in quiet (dashed line: Hienz et al., 1995b). Numerical labels indicate S/N. Error bars equal ±1 SE.

DISCUSSION

Comparison of SMP Simulations with Previous Studies of Vowel Representation

Auditory nerve simulations of Experiment 1 suggest that low SR auditory-nerve fibers may provide rate information that is crucial to the neural representation of vowel-like stimuli at high SPLs and in the presence of background noise. These simulations were based on responses that were characterized in anesthetized cats with the spectrum manipulation procedure (SMP). Although SMP testing differs from traditional population studies of the neural representations of complex sounds, both sampling methods have described similar discharge patterns for responses to steady-state vowels in the cat’s auditory nerve (Sachs and Young, 1979; Le Prell et al., 1996) and anteroventral cochlear nucleus (Blackburn and Sachs, 1990; Le Prell, 1995).

Population studies of vowel representations in the peripheral auditory system are typically based on the assumption that features of the amplitude spectrum are encoded by the distribution of discharge rates at different places along the cochlear partition (Pfeiffer and Kim, 1975). In the case of steady-state vowels, rate-place profiles show peaks of activity among fibers with BFs near the frequency location of formant features and lesser discharge rates at BFs that fall within spectral troughs. A common problem with such rate representations is that rate saturation leads to a loss of differential responding to formant and trough features at higher vowel levels. Sachs and Young (1979) have shown that high SR fibers are particularly sensitive to saturation effects, but low SR fibers maintain a good representation of formant structure at vowel levels up to at least 84 dB. These patterns of responses are also seen when high and low SR fibers are tested with the SMP (Fig. 1b).

Sachs et al. (1983) observed that the range of rate changes available for encoding vowels in continuous background noise was significantly compressed relative to vowels in quiet. In their study, only fibers with BFs near the fundamental frequency or first formant of the vowel /ε/ exhibited vowel-driven rates that exceeded 25 sp/sec. In addition, fibers with BFs near trough frequencies showed negative driven rates. That is, responses to presentations of vowels in noise were less than discharge rates to noise alone. Suppression of noise-driven rates was greatest among low SR fibers. All of these major effects of background noise were also observed in our simulations (Fig. 6).

Experiment 1 used linear models of auditory-nerve fiber responses to simulate the effects of vowel level and background noise on rate representations of F2 frequency changes. As described in above, empirical response profiles of Conley and Keilson (1995) show a relatively good match to simulations in terms of rate differences, variability, and maximum d’ values. These investigators calculated Q_total statistics, although they did not report Q values for individual SR classes. Their theoretical calculations predicted a Q_total of 5 for a 10 Hz change in F2 frequency at 50 dB; Q_total dropped to a value of 0.68 for a 1 Hz change. Barta (1985) defined 0.68 as the Q_total that corresponds to the just-noticeable-difference (jnd) in frequency. Linear interpolations from simulated results at vowel levels of 43 and 63 dB (Table IV) predict a Q_total of 18 for a 10-Hz change in F2 at 50 dB. Two differences in calculation methods are likely to have contributed to larger Q values in the present study. Conley and Keilson (1995) applied a log-triangularly weighted filter to theoretical rate difference profiles which reduced the magnitude of peak rate differences. In addition, the constant standard deviation (σ_i = 20 sp/sec) used in their calculations was larger than that derived from Eq. 2, which yielded an average a σ_i of 15 sp/sec for units with BFs at F2 and a σ_i of 12 to 14 sp/sec for units with BFs at the surrounding trough features. Q statistics in both studies are consistent in that they predict jnds that are considerably less than actual behavioral thresholds (Hienz et al., 1996b).

Comparison of Behavioral Results with Other Psychophysical Studies

Close similarities exist among humans and other animals in their ability to discriminate vowel formant frequencies under quiet testing conditions. For example, Sinnott and Kreiter (1991) measured formant frequency discrimination for multiple-formant vowels in macaque monkeys, and reported thresholds of 32 – 48 Hz for formants near 1.0 and 2.0 kHz. Sommers et al. (1992) measured frequency difference thresholds in Japanese macaques for single-formant vowels, and reported an average ΔF of 23 Hz for formant changes centered at 1400 Hz. Hienz et al. (1996b) reported ΔF2s in cats that ranged from 31 to 45 Hz at 1700 Hz (summarized in Fig. 13). In all of these studies, animal psychophysical performance was only slightly below that of humans, whose ΔFs are about 1.5% of the center frequency of a vowel formant (Kewley-Port and Watson, 1994). Pfingst (1993) has also noted that monkeys and humans perform equally well when discriminating nonspectral frequency cues such as the modulation frequency of sinusoidally amplitude-modulated noise.

Vowel discrimination in cats and humans are similarly influenced by background noise. Pickett (1956) observed that background noise (S/N = −12 dB) impaired the ability of humans to distinguish among vowel pairs that differed primarily in their F2 frequencies (i-u, I-U, and e-o). Vowel pairs with different F1 frequencies were rarely confused. Hienz et al. (1996a) has shown that cats are also capable of distinguishing vowels with different F1 frequencies at a S/N of −12 dB. However, in the present study, discrimination of F2 frequency changes increased by a factor of 2 in the presence of noise at a higher S/N of 3 dB. Clearly, because formant structure may differ considerably between vowels, effects of masking noise on discrimination are determined by the frequency and level of the more salient spectral features. F2 frequency discrimination is likely to be more sensitive to background noise than F1 discrimination because F2 features are less intense than F1 features.

Similarities in vowel frequency discrimination stand in contrast to the abilities of humans and other animals to discriminate pure-tone frequency changes. Humans are uniquely able to detect small changes in tone frequency, exhibiting ΔFs of 1.1 and 3.2 Hz at 600 and 2000 Hz, respectively (Wier et al., 1977). In this same frequency range (500 to 3000 Hz), pure-tone ΔFs range from 10 – 40 Hz in birds (Sinnott et al., 1980), 10 – 60 Hz in monkeys (Sinnott et al., 1985), and 70 – 170 Hz in cats (Hienz et al., 1993). Using identical procedures to measure frequency discrimination in monkeys and humans, Sinnott et al. (1985) obtained ΔFs of 16 – 33 Hz (monkey) and 2.4 – 4.8 Hz (human) for tests at 1.0 kHz. Similarly, Pfingst (1993) reported pure-tone ΔFs of 10 – 90 Hz in monkeys and 2 – 10 Hz in humans at 1.0 kHz, and noted that there was almost no overlap in ΔFs between species. Prosen et al. (1990) have also noted that pure-tone ΔF functions of monkeys and humans are similar in shape but show almost no overlap in magnitude.

Sinnott and colleagues (Sinnott et al., 1985; Sinnott and Kreiter, 1991) have suggested that differences in pure tone and formant frequency discrimination between humans and other animals may be related to coding strategies. Among several possibilities that they discussed, the monkey auditory system may employ a rate-based code for both simple tones and complex signals such as speech sounds. Humans, on the other hand, may rely on temporal information for pure tones but use rate information for wideband sounds (e.g., vowels) because these stimuli elicit less efficient temporal coding (Horst et al., 1984). Sommers et al. (1992) proposed that Japanese macaques may discriminate formant frequency changes better than pure tone frequency changes by attending to changes in spectral shape. That is, monkeys may attend to relative intensity changes in a limited number of harmonics around the formant frequency. They suggest that this form of profile analysis is also likely to be encoded by the distribution of discharge rates along the cochlear partition. Both interpretations of the rate representation of tones and vowels in the auditory system of nonhuman animals are supported by the effects of background noise on F2 frequency discrimination in Experiment 2. When the masking effects of 3-dB S/N background noise reduced the number of harmonics exhibiting amplitude differences to only a narrowband of frequencies surrounding the second formant, ΔF2 increased to approximately 83 Hz, which is equivalent to the cat’s threshold for pure tone frequency discrimination in noise at 1 kHz (Hienz et al., 1993).

Comparison of Vowel Representations in the Auditory Nerve and Behavioral Performance

Figure 14 compares neural and behavioral ΔF2s in quiet and in background noise (3 dB S/N). For this comparison, the neural ΔF2 was defined as the change in F2 that produced rate differences equivalent to a maximum d’ of 1. These neural discrimination thresholds were derived by linear interpolation from data summarized in Table III. Additional data from Le Prell et al. (1996) were used to calculate thresholds in quiet at 23 dB SPL for high SR fibers. Because behavioral thresholds used in this comparison were obtained under free-field conditions (upper abscissa) and rate responses of auditory-nerve fibers were recorded under closed-field conditions (lower abscissa), behavioral results are shifted 12 dB relative to neural measures to compensate for free-field amplification of acoustic stimuli by the cat’s head-related transfer function (HRTF: Weiner et al., 1966). As previously mentioned, closed-field stimuli used in electrophysiological recordings and neural simulations were digitally filtered with the HRTF spectrum of a sound source at 0° azimuth, 30° elevation. After the 12-dB compensation of pinna amplification effects, vowel spectra propagating to the eardrum should approximate one another in Experiments 1 and 2.

FIGURE 14. Comparison of neural and behavioral ΔF2 thresholds at different vowel levels.

(a) Results obtained under quiet testing conditions, (b) Results obtained in continuous background noise. Behavioral thresholds corresponded well to neural thresholds predicted by d’ values of the best individual fibers. This information was conveyed by high SR fibers at low vowel levels and by low SR fibers at high vowel levels. To compensate for pinna amplification, vowel levels in free-field behavioral tests (upper abscissa) are shifted 12 dB relative to vowel levels in closed-field neural tests (lower abscissa).

Figure 14(a) compares neural and behavioral performance under quiet testing conditions. High SR fibers showed their lowest ΔF2 (52 Hz) at the 43 dB vowel level. Thresholds for these units rose steeply at higher vowel levels, exceeding 250 Hz at vowel levels of 83 dB. Most low SR fibers displayed an opposite pattern of responding; that is, they were unresponsive to 43 dB vowels and showed their lowest thresholds (55 and 68 Hz) at vowel levels of 63 and 83 dB. However, as shown in Fig. 14(a), ΔF2 thresholds of the most sensitive low SR units were as good if not better than those of high SR fibers at vowel levels down to 43 dB. High SR fibers provided the optimal rate information at 23 dB. Average behavioral ΔF2s (filled symbols) ranged from 45 to 36 Hz over free-field stimulus levels of 31 to 71 dB and corresponded reasonably well with the best neural threshold at each vowel level, regardless of SR class.

These results support previous interpretations of rate coding in the auditory periphery (Sachs and Young, 1979; Winslow et al., 1987) which suggest that the dynamic range properties of central representations are enhanced by “selectively listening” to the more sensitive high SR auditory-nerve fibers at lower stimulus levels and to the less sensitive low SR fibers at higher stimulus levels. The concept of selective listening can be applied equally to neural models based on maximum d’ values or Q statistics because both measures reflect the most salient rate-difference information that is available for a given stimulus condition. However, high SR fibers are more influential in the context of Q measures regardless of the stimulus condition because these fibers out number low SR fibers by a factor of 4.

Figure 14(b) compares neural and behavioral ΔF2 thresholds for testing in background noise (S/N = 3 dB). High and low SR fibers displayed substantial differences in their sensitivity to the negative effects of noise. High SR fibers exhibited thresholds that approached 100 Hz at the lowest vowel level (33 dB) and failed to show a detectable rate difference for F2 frequency changes as large as 300 Hz at higher vowel levels. Low SR fibers, in contrast, exhibited lower and more uniform neural thresholds (63 – 75 Hz) at vowel levels ranging from 53 – 73 dB. Average behavioral ΔF2 values also remained quite stable when measured in the 3-dB S/N condition, varying by less than 3 Hz across vowel levels of 31 – 71 dB. As observed for vowel discrimination in quiet, behavioral thresholds showed a good correspondence to the best neural representation at each vowel level. High SR fibers provided this information at low levels, but rate responses of low SR fibers were critical for the encoding of vowels in noise over a large range of stimulus levels.

Results shown in Fig. 14 suggest that optimal processing of the rate responses of single auditory-nerve fibers can yield neural performance that meets or exceeds a cat’s behavioral abilities in the F2 discrimination task. Q values show a less straightforward relationship to behavioral thresholds because small changes in F2 are capable of producing extremely large changes in discharge rates when summed across an ensemble of auditory-nerve fibers. As a result, Q_total values predict jnds of less than 1 Hz for testing under quiet conditions (Table IV) and jnds of less than 6 Hz for testing in noise (Table VI). Conley and Kielson (1995) predicted thresholds of similar magnitude in their analysis of Q_total values for the auditory nerve representation of F2 frequency changes in quiet. Other optimal processing models in which rate responses are summed across multiple auditory-nerve fibers have demonstrated neural performance well beyond that of actual psychophysical thresholds for pure-tone intensity changes (Winslow and Sachs, 1988) and frequency changes (Barta, 1985; Hienz et al., 1993).

Q values also failed to provide a consistent representation of the just-noticeable-difference in formant frequency when vowel level was changed or background noise was added to the stimulus paradigm. For example, under quiet conditions, behavioral ΔF2s at vowel levels of 43 and 83 dB corresponded to Q_total values of 42 and 16, respectively. In background noise, Q_total showed a further decline to a value of only 4. For the most part, variation in Q at the behavioral threshold was due to changes in the availability of the rate information provided by high SR fibers.

Q values for low and high SR fibers were of similar magnitude at higher vowel levels in quiet (Fig. 9) and at all tested levels in background noise (Fig. 10). However, it is important to point out that under these common stimulus conditions, Q_{high SR} reflected the summation of a large number of very small rate differences; Q_{low SR}, a small number of large rate differences. Consequently, over half of the fibers that contributed to these Q_total statistics (i.e., the 61% with high SRs) failed to achieve d’ values that would be considered detectable rate differences on an individual basis. While this distinction is unimportant in terms of optimal decision processing theory, the close correspondence between behavioral performance and neural thresholds based on maximum d’ values (Fig. 14) suggests that the decision process may be weighted toward those individual fibers showing largest rate differences.

In spite of its limitations for predicting perceptual behaviors, the Q statistic is important because it provides a quantitative description of neural information that is conveyed by the auditory nerve to the cochlear nucleus where peripheral representations are radically transformed by the variety of synaptic configurations between spiral ganglion cells and cochlear nucleus principal cells (Osen, 1969; Cant and Morest, 1984). As anatomical and electrophysiological evidence provides new insights into vowel representation by higher-order auditory neurons (Blackburn and Sachs, 1990; Le Prell, 1995), models of speech processing in the auditory periphery such as the Q statistic are likely to undergo extensive modification and elaboration. For example, low SR fibers have wide terminal fields in the anteroventral cochlear nucleus (AVCN: Fekete et al., 1984) and therefore may exert more broadly distributed post-synaptic effects than high SR fibers. Potential differences in post-synaptic effectiveness are currently ignored by the Q statistic which applies equal weight to all auditory-nerve fibers. In addition, although cochlear nucleus neurons show a localized sensitivity for excitatory and inhibitory influences (Blackburn and Sachs, 1992; Rhode and Greenberg, 1994), the Q statistic integrates rate information across the entire auditory-nerve fiber array. Maximum d’ values (an extremely “localized” rate-difference measure) provided a better prediction of the behavioral results obtained under a variety of stimulus conditions. In future studies, more sophisticated decision models that consider auditory nerve innervation patterns within the cochlear nucleus may establish even stronger links between speech processing and perception.