Mean-field interactions between nucleic-acid-base dipoles can drive the formation of the double helix

Abstract

A proposed coarse-grained model of nucleic acids demonstrates that average interactions between base dipoles, together with chain connectivity and excluded-volume interactions, are sufficient to form double-helical structures of DNA and RNA molecules. Additionally, local interactions determine helix handedness and direction of strand packing. This result, and earlier research on reduced protein models, suggest that mean-field multipole-multipole interactions are the principal factors responsible for the formation of regular structure of biomolecules.

Nucleic acids have been studied for decades since the fundamental work of Watson and Crick [1], and there is continuing interest in learning more about the structural, dynamical, and mechanical properties of these important macromolecules in relation to their biological significance and applications in nanotechnology [2]. The essential interactions appear to come from base stacking and specific base pairing [1] which, however, are difficult to attribute to a single driving force, especially when the system is treated at the detailed atomic level. To discern the dominant forces responsible for structure formation, coarse-graining (renormalization) approaches, in which several atoms are combined into a single interaction site, can be applied. An early example is the observation by Brant and Flory [3] that the experimental value of the characteristic ratio of polypeptide chains can be reproduced when representing the electrostatic interactions between peptide groups as dipole-dipole interactions.

Coarse-grained models of DNA have been developed for nucleic acids since the 1970’s [4–10] to increase the time- and size scale of simulations. Most of them implement simple harmonic [8], Morse [4], or G -like potentials [6] to describe nucleotide base-pairing and other specific long-range interactions. These approaches, however, require knowledge of the native topology of nucleic acids or their complexes with proteins. Only a few united-residue force fields designed for nucleic acids [7,9,10] have been derived based (partially or fully) on the physics of the interactions in these macromolecules.

A very successful model has been developed recently by Ouldridge and coworkers [9], in which all long-range interactions, including base pairing and stacking, are described by designed Morse-type potentials and other potentials engineered to reproduce correct dependence of base-base interactions on orientation. The energy function and parameters were derived based on a top-down design to pick out and elaborate on the essential interactions responsible for the formation of DNA structure. The model was successful in simulating DNA hybridization from separated strands and simulating the operations of DNA tweezers in unrestricted Monte Carlo runs [9].

Another very successful coarse-grained approach to predict the topology of base-base pairing of DNA and RNA molecules as well as their folding thermodynamics, termed mFold [11] and later UnaFold [12], was developed by Zucker and coworkers. This approach is based on minimizing the free energy of base pairing, the energy of each pair being computed in the context of the neighboring pairs. Prediction of secondary structure thus becomes a discrete optimization problem [11,12]. The pair free energy parameters were derived from the melting curves of model DNA and RNA systems [13].

These models provide the thermodynamics and/or dynamics of the folding of DNA and/or RNA, but they do not identify the dominant forces that govern double-helix formation of nucleic acids. Therefore, a minimal physics-based coarse-grained model of nucleic acids, named NARES-2P (Nucleic Acid united RESidue 2-Point model), is proposed here. Unlike most of earlier work [4–6,8], the respective potentials are not engineered to reproduce nucleic-acid structure, dynamics, and thermodynamics but are derived as potentials of mean force, which are approximated by generalized-cumulant terms, as in the UNRES model of polypeptide chains [14,15]. In this regard, the model is similar to a more detailed multi-center coarse-grained model of nucleic acids that we started to develop recently [10].

In the NARES-2P model, depicted in Figure 1, a polynucleotide chain is represented by a sequence of virtual sugar (S) atoms (colored red), located at the geometric center of the sugar ring, linked by virtual bonds with attached united sugar-base (B, colored green) and united phosphate groups (P, colored white). These united sugar-bases (B’s) and the united phosphate groups (P’s) serve as interaction sites.

Figure 1.

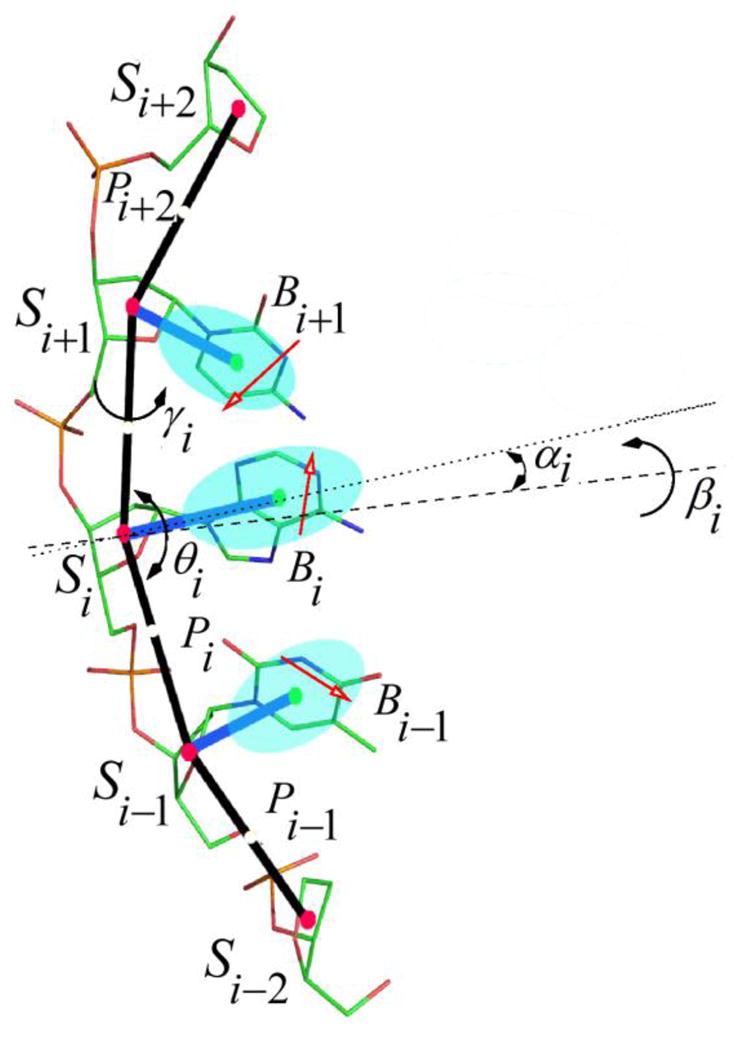
(color online) The NARES-2P model of the nucleotide chain. Solid red circles represent the united sugar groups (S) which serve as geometric points, and open white circles represent the united phosphate groups (P). Ellipsoids represent bases, with their geometric centers at the B’s (solid green circles). The P’s are located halfway between two consecutive sugar atoms. The all-atom representation is superposed on the coarse-grained representation, and dipoles are located on the bases to represent their electrostatic interaction. The electrostatic part of the base-base interactions is represented by the mean-field interactions of the base dipoles (red arrows) computed by integrating the Boltzmann factor over the rotation of the dipoles about the base axes (dotted lines). The backbone virtual-bond angles, θ, and the virtual-bond dihedral angles, γ, are indicated. The base orientation angles α and torsional angles β, that define the location of a base with respect to the backbone, are also indicated.

The NARES-2P effective energy function originates from the Restricted Free Energy (RFE) function or potential of mean force of an all-atom nucleic acid plus the surrounding solvent and counter-ions, where the all-atom energy function is averaged over the degrees of freedom that are lost when passing from the all-atom to the simplified system. The energy of the virtual-bond chain in the present NARES-2P model is expressed by eq. 1.

$$\begin{array}{l}U=w_{BB}^{GB}\sum _i\sum _{j<i}{U}_{B_i{B}_j}^{GB}+w_{BB}^{\mathit{dip}}{f}_2(T)\sum _i\sum _{j<i}{U}_{B_i{B}_j}^{\mathit{dip}}+w_{PP}\sum _i\sum _{j<i}{U}_{P_i{P}_j}+w_{PB}\sum _i\sum _j{U}_{P_i{B}_j}+\\ w_{\mathit{bond}}\sum _i{U}_{\mathit{bond}}(d_i)+w_{\mathit{ang}}\sum _i{U}_{\mathit{ang}}({\theta }_i)+w_{\mathit{tor}}{f}_2(T)\sum _i{U}_{\mathit{tor}}({\gamma }_i)+w_{\mathit{rot}}\sum _i{U}_{\mathit{rot}}({\alpha }_i,{\beta }_i)+U_{\mathit{restr}}\end{array}$$ (1)

with [16]

$$f_n(T)=\frac{exp(1)+exp(-1)}{exp\left(\frac{nT}{T_0}\right)+exp\left(-\frac{nT}{T_0}\right)}$$ (2)

where $U_{B_i{B}_j}^{GB}$ and $U_{B_i{B}_j}^{\mathit{dip}}$, U_PiPj, and U_PiBj (see section S.1 of the Supplemental Material) denote the interaction energies between the respective sites, of which $U_{B_i{B}_j}^{\mathit{dip}}$ corresponds to mean-field interactions between nucleic-acid-base dipoles, U_bond(d_i), U_ang(θ_i), U_tor(γ_i) and U_rot(α_i, β_i) denote the energies of virtual-bond stretching, of virtual-bond angle bending, of rotation about backbone virtual bonds, and of sugar-base rotamers, respectively. The U_tor(γ_i)terms provide correct right-handed chirality of the strands. The factors f_n(T) account for the temperature dependence of terms of order higher than 1 of the generalized-cumulant expansion of the RFE [15]. The term U_restr restricts the distance between the 5′ end of one chain and the 3′ end of the second chain to distances less than d_max (selected to correspond to the desired monomer concentration). The w’s are energy-term weights; in this work, all the weights were set at 2, except $w_{BB}^{GB}$ which was set at 0.5, to provide melting-transition temperatures comparable to experimental values. Detailed functional forms and parameterization of the effective energy terms in eq.1 are described in sections S.1 and S.2 of the Supplemental Material. As shown there, the $U_{B_i{B}_j}^{\mathit{dip}}$ terms have minima at base-base orientations close to those of base pairing and base stacking.

The NARES-2P model was built into the UNRES/MD platform [17], which enables canonical and replica-exchange simulations of nucleic acids to be carried out. To check if the model is able to reproduce double-helix structure, Multiplexed Replica Exchange Molecular Dynamics (MREMD) simulations of the following two DNA systems were carried out, the experimental structures of which have been determined in aqueous solution by NMR spectroscopy: the Dickerson-Drew dodecamer (DNA; 2×12 residues; PDB: 9BNA) and 2JYK (DNA; 2×21 residues), using the simulation protocol developed earlier [18]. For test purposes, the MREMD simulations were also carried out for two RNA molecules, 2KPC (RNA; 17 residues) and 2KX8 (RNA; 44 residues); the molecules are identified by their Protein Data Bank (PDB) structure names. We also ran additional MREMD simulations to assess the reproduction of folding thermodynamics and internal-loop (bubble) formation. Simulation details are included in section S.3 of the Supplemental Material. All of these systems have a simple double-helix topology without long loops, bulges, multiplexes or defects. The structures obtained from MREMD simulations with NARES-2P are compared with the respective experimental structures of the DNA and RNA test systems in Figure 2.

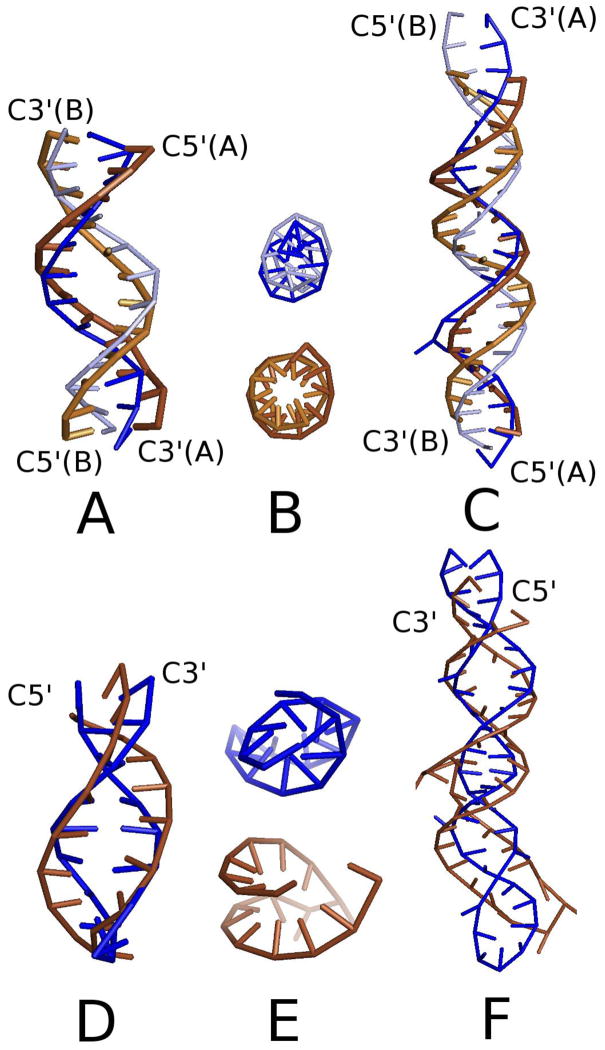
Figure 2.

(color online) Calculated ensemble-averaged structures at T = 300 K obtained in NARES-2P MREMD simulations of the molecules studied (blue sticks) compared to the respective experimental structures (light and dark brown sticks for DNA and dark brown sticks for RNA, respectively). Sticks correspond to the S…S and S…B virtual bonds. Calculated structures of 9BNA, 2JYK, 2KPC, and 2KX8 are superposed on the corresponding experimental structures and shown as side views in panels A, C, D, and F, respectively. Top views of 9BNA and 2KPC (from the C5′ ends) are shown in panels B and E, respectively, with calculated structures above and the experimental structures below. The rmsd’s over the S centers of the calculated structures averaged over all native-like clusters are 4.7 Å, 10.7 Å, 5.10 Å, and 9.8 Å for 9BNA, 2JYK, 2KPC, and 2KX8, respectively, with respect to each experimental structure. The lowest rmsd values obtained in the respective MREMD runs are 2.6 Å, 4.2 Å, 3.2 Å, and 6.0 Å for 9BNA, 2JYK, 2KPC, and 2KX8, respectively.

As can be seen from Figure 2, the calculated structures have the correct double-right-handed-helix topology. It can also be noted that, despite the early stage of development of the model, the resolution is of the order of that of the all-atom simulation; for example, after about 40 ns of canonical MD with AMBER, the sugar-center rmsd of 9BNA is 2.15 Å when starting from the experimental structure (see section S.4 of the Supplemental Material). We note that, as opposed to the all-atom simulations which were started from the experimental structure, our coarse-grained simulations were started from extended separate chains. The NARES-2P force field is now being refined for better resolution. The force field is also ergodic; canonical simulations lead to a right-handed double-helix structure. A sample canonical-folding trajectory of 9BNA is shown in Figure S-12 of the Supplemental Material.

The essential dynamics calculated from the coarse-grained canonical trajectory gives the same helix-bending principal modes as those calculated from all-atom canonical dynamics with AMBER (see section S.4 of the Supplemental Material); additionally, we found a breathing mode connected with base-pair opening which is supported by experimental data [19,20].

By comparing the calculated and experimentally determined melting temperatures, as well as standard enthalpies and entropies of folding of small DNA molecules (Table S-7 in section S.5 of the Supplemental Material), it can also be concluded that, for most of the 18 systems studied, the model reproduces the thermodynamics of folding; only the calculated melting temperatures are generally higher than the experimental values. The model also qualitatively reproduces formation of internal loops [21], often termed bubbles (pre-melting transition), in the AT-rich sequences L19AS and L33B9 studied by Zocchi and coworkers [22] and the propagation of deformation from the bubble (internal-loop) region studied by Peyrard and coworkers [23] (see section S.6 of the Supplemental Material).

As demonstrated in section S.2 of the Supplemental Material, the angular dependence of stacking and pairing orientations is encoded in the base-base interaction potentials (the $U_{B_i{B}_j}^{\mathit{dip}}$ term of eq.1). However, the backbone-torsional potential leads to preference for a right-handed twist of the strands and, consequently, it can be suspected that this potential holds single strands in a “ready-to-pair” conformation, thereby biasing the MD runs towards double-helix formation. To determine the significance of the torsional potentials, test simulations were carried out for the Dickerson-Drew duplex with w_tor = 0 (eq.1). The results are presented in Figure 3A. As shown there, double-helical structures, albeit somewhat distorted, still remain dominant. However, both right- and left-handed structures now occur, 28.5 % and 34.9 %, respectively; the rest of the sample consists of unpaired strands. This is expected because the backbone-torsional potentials are the key factor that determines chirality. Thus, switching off the torsional potentials also influenced the helical chirality. However, the torsional potential does not seem to be necessary for a double helix to form, which has also been observed by Ouldridge and coworkers [9].

Figure 3.

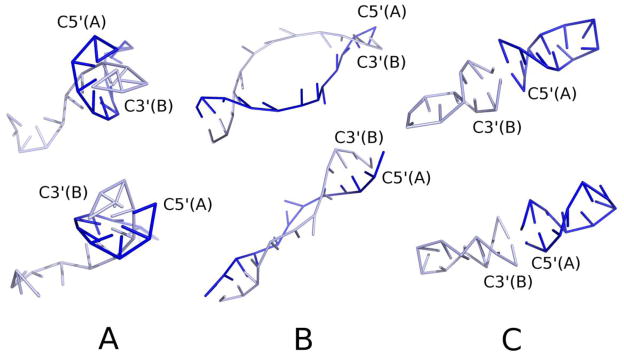
(color online) (A) (top and bottom) Right- and left-handed helical structures, respectively, of 9BNA obtained in simulations with the torsional potentials switched off (w_tor = 0 in eq.1). (B) Same for the simulations with the torsional and rotamer potentials switched off (w_tor=0 and w_rot=0 in eq.1). (C) (top and bottom) Examples of the predominant double-helical structures (right- and left-handed, respectively) obtained in simulations of this molecule with the torsional, rotamer, and virtual-bond angle potentials switched off (w_tor = 0, w_rot = 0, w_ang = 0). Each of two single strands forms a double helix which interact so that the system forms an extended double helix.

To determine how the other local interactions influence helix stability, we subsequently switched off the base-rotamer (U_rot) component and then the virtual-bond-angle (U_ang) component. The dominant conformations obtained under these conditions are shown in Figure 3B and 3C, respectively. It can be seen that the double-helical structure was also formed; however, the dominant structures obtained with w_tor=0 and w_rot=0, and the only structures obtained with w_tor=0, w_rot=0, and w_ang=0, are separate double helices, each formed from one of the two complementary strands (see Figure 3C). Nevertheless, this result demonstrates very clearly that averaged dipole-dipole interactions together with chain-connectivity constraints are sufficient to create double helices as the most stable structures. Perhaps, the difference in local-interaction pattern is the reason why DNA prefers to form inter- and RNA intra-strand double helices.

In conclusion, the results of our study strongly suggests that the mean-field interactions between nucleic-acid-base dipoles constitute a single force that accounts qualitatively for the double-helical architecture of DNA and RNA molecules and the basic features of their stability, including bubble (internal-loop) formation in the AT-rich regions. It is likely that correlation terms, that account for the coupling between base stacking and base pairing, will have to be introduced to improve the resolution of the model and also to improve the folding thermodynamics. This work, as well as a detailed parameterization of the model, are currently underway in our laboratory. Nevertheless, the symmetry of mean-field dipole-dipole interactions clearly translates to double-helix symmetry, given chain connectivity and some excluded-volume interactions ( $U_{B_i{B}_j}^{GB}$, U_PiPj, and U_PiBj) which prevent the sites from collapsing onto each other. Otherwise, the chain can be freely jointed. Local interactions, that provide backbone stiffness and chirality, decide only the form of the helix (inter- or intra-strand) and its twist (right- or left-handed). Moreover, in view of the success of our UNRES model in explaining the formation of regular protein secondary structure through mean-field interactions involving peptide-group multipoles, mean-field multipole interactions likewise seem to induce formation of ordered structures in polar biopolymer chains such as nucleic acids, and polysaccharides.

On the other hand, it should be noted that the electrostatic interactions involving phosphate-sugar units and the surrounding counter-ions and water are also crucial in the formation of nucleic-acid structure [24]. The outer phosphate groups probably provide an envelope in which the nucleic-acid bases are effectively dehydrated, which makes strong hydrogen-bonding interactions between them possible.

The energy and force calculations in the Fortran implementation of NARES-2P are parallelized, as in the Fortran implementation of UNRES [25]. Therefore, NARES-2P can be used to run simulations of large DNA and RNA molecules.