Actin Sliding Velocities are Influenced by the Driving Forces of Actin-Myosin Binding

Abstract

Unloaded shortening speeds, V, of muscle are thought to be limited by actin-bound myosin heads that resist shortening, or V = a·d·τ_on⁻¹ where τ_on⁻¹ is the rate at which myosin detaches from actin and d is myosin's step size. The a-term describes the efficiency of force transmission between myosin heads, and has been shown to become less than one at low myosin densities in a motility assay. Molecules such as inorganic phosphate, P_i, and blebbistatin inhibit both V and actin-myosin strong binding kinetics suggesting a link between V and attachment kinetics. To determine whether these small molecules slow V by increasing resistance to actin sliding or by decreasing the efficiency of force transmission, a, we determine how inhibition of V by Pi and blebbistatin changes the force exerted on actin filaments during an in vitro sliding assay, measured from changes in the rate, τ_break⁻¹, at which actin filaments break. Upon addition of 30 mM P_i to a low (30 μM) [ATP] motility buffer V decreased from 1.8 to 1.3 μm·sec⁻¹ and τ_break⁻¹ from 0.029 to 0.018 sec⁻¹. Upon addition of 50 μM blebbistatin to a low [ATP] motility buffer, V decreased from 1.0 to 0.7 μm·sec⁻¹ and τ_break⁻¹ from 0.059 to 0.022 sec⁻¹. These results imply that blebbistatin and P_i slow V by decreasing force transmission, a, not by increasing resistive forces, implying that actin-myosin attachment kinetics influence V.

Introduction

Muscle contracts when myosin heads cyclically interact with actin filaments through their ATPase reaction (1-4). With the weak-to-strong actin-binding intermediate step in the ATPase reaction, a single myosin head undergoes a discrete lever arm rotation that displaces an actin filament a distance d(5-11). A single myosin head takes one of these displacement steps every time it goes around its ATPase cycle and thus in theory can move an actin filament at a speed V = d/(τ_on + τ_off), where τ_on and τ_off are lifetimes of the A-M strong- and weak-binding states respectively.

In theory, V would increase with increasing numbers, N, of myosin heads as V = N·d/(τ_on + τ_off), but in the context of a muscle system (Fig. 1A) where many myosin heads interact with the same actin filament, the lever arm rotation of a given myosin head becomes damped by other actin-bound myosin heads that oppose actin movement (12,13), making the discrete lever arm rotation more of a force-generating than a motion-generating step. With enough myosin heads strongly bound to an actin filament, “the actin filament cannot move any faster than the heads can let go” (12), and V becomes limited by strongly-bound myosin heads that resist actin movement. It is commonly assumed that V reaches a maximum value when N = (τ_on + τ_off)/τ_on, or when

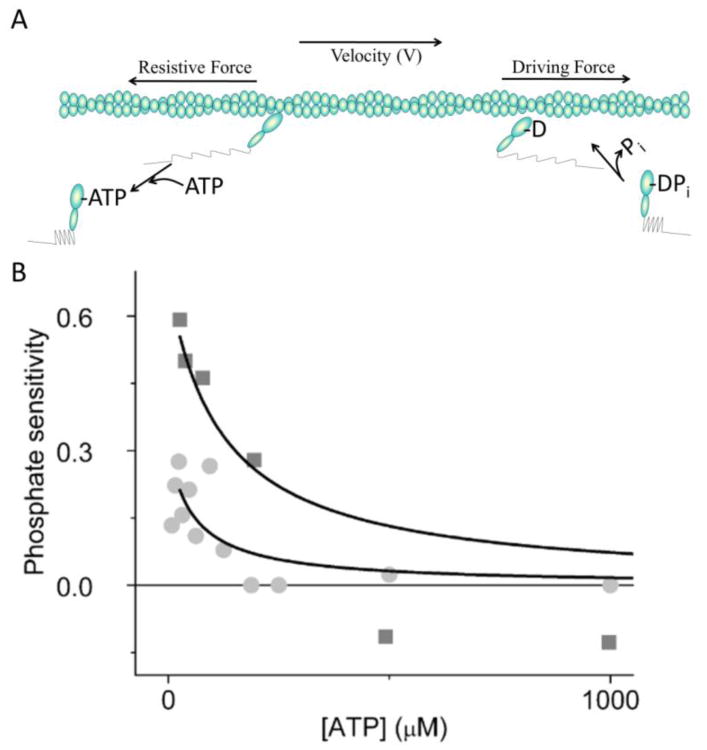
Figure 1.

Model of actin sliding velocities. (A) Driving forces (springs on right) are generated in the direction of actin movement by myosin weak-to-strong binding transitions (heads on right). These forces are opposed by resistive forces (springs on left) exerted by actin-bound myosin heads that have become negatively strained by actin sliding (heads on left). Here, the spatial separation of positively and negatively strained heads is used for illustrative purposes only. (B) The [ATP]-dependence of phosphate sensitivity (1 – V_Pi/V°) calculated from data in Amrute-Nayak et al. (20) (squares) and Hooft et al. (17) (circles), where V° is the actin sliding velocity in the absence of added P_i and V_Pi is the actin sliding velocity with added P_i.

$$V_{\mathit{\text{max}}}=\{({\tau }_{\mathit{\text{on}}}+{\tau }_{\mathit{\text{off}}})/{\tau }_{\mathit{\text{on}}}\}\cdot d/({\tau }_{\mathit{\text{on}}}+{\tau }_{\mathit{\text{off}}})=d/{\tau }_{\mathit{\text{on}}}.$$

According to this model, τ_on is the sole biochemical determinant of V_max, and thus velocities are said to be detachment limited. An additional factor, a, is sometimes included to describe the observation that V_max decreases at low myosin densities due to inefficient force transmission (39).

$$V_{\mathit{\text{max}}}=a\cdot d/{\tau }_{\mathit{\text{on}}}$$ (Eq. 1)

The goal of the present study is to determine whether inhibition of actin-myosin strong binding kinetics results in a similar decrease in a.

A myosin head can transmit forces over a relatively limited length of actin. Harris and Warshaw showed (16) that when the average spacing between myosin heads increases beyond 130 nm, the efficiency, a, with which one head transmits forces to another decreases significantly, slowing V_max (Eq. 1). Their analysis raises an important question. To achieve a maximum velocity, V_max, does the force generated by one head need to be efficiently transmitted to any actin-associated myosin head (including weakly-associated heads) or does it need to be efficiently transmitted to another strongly bound myosin head? Harris and Warshaw assume the former, but the limited ability of weak-binding heads to maintain force suggests that force transmission probably occurs between strongly bound heads. In this case, the data in Harris and Warshaw would indicate that the distance over which a myosin head can efficiently transmit force to another strongly bound myosin head is ∼130 nm·(τ_on + τ_off)/τ_on (∼2600 nm for a 5% duty ratio). Because the distance between strongly bound myosin heads increases when the rate, k_att, of actin-myosin strong binding decreases (τ_off increases), the efficiency of force transmission, a, could decrease with a decrease in k_att, resulting in a decrease in V_max and a corresponding decrease in the interhead forces generated in a motility assay.

Recent studies suggest that both τ_on and τ_off influence V (17). Specifically, Hooft et al. demonstrated that at low [ATP], in vitro actin sliding velocities, V, decrease with the addition of 30 mM phosphate, P_i, consistent with a P_i-induced increase in τ_off (per cycle) through the reversal of myosin's force-generating, weak-to-strong binding transition (18, 19). However, Brenner and colleagues argue that the inhibition of V by P_i at low [ATP] results from a P_i–induced increase in τ_on (consistent with the detachment-limited model) caused by P_i competing with ATP for the myosin active site.

To determine if P_i slows V by increasing resistance to actin sliding (i.e., increasing τ_on) or if it slows V by decreasing the driving force of weak-to-strong binding transitions (i.e., increasing τ_off), an in vitro motility assay can be used to determine the effects of P_i on the forces exerted by myosin heads along actin filaments during actin sliding (20). If P_i slows V by decreasing driving forces, then it should decrease the rate of the force-induced actin filament breaking during motility (Fig. 1A). On the other hand, if P_i slows V by increasing τ_on, P_i should increase the rate of force-induced actin filament breaking (Fig. 1A). To estimate actin filament breaking rates, Amrute-Nayak et al. (20) attempted to make these measurements by imaging fluorescently-labeled actin filaments at two time points during a motility assay. They showed that after 100 seconds of motility, filaments were on average shorter in the presence of 5 mM P_i than in the absence of added P_i. The authors inferred that P_i increases the rate of actin filament breaking, concluding that P_i slows V by increasing τ_on.

There are two potential problems with these previous experiments. First, as shown below, the rate of actin filament breaking varies with filament length, and the authors did not control for this in their study. Second, the visible pool of actin filaments changes during a motility assay due to actin filaments moving in and out of the field of view, and so actin filaments analyzed at time t = 100 sec are not the same as those analyzed at t = 0 sec. A more rigorous approach for determining the rate (τ_break⁻¹) at which actin filaments break in a motility assay is to perform a frame-by-frame analysis that detects actual actin filament breaking events. Below, we use this approach, controlling for actin filament length, to determine the effects of P_i on the rate of actin filament breaking. In contrast to the results of Amrute-Nayak et al. (20), we show that at low [ATP] the addition of P_i to a motility assay significantly decreases τ_break⁻¹. Our data imply that inhibition of V by P_i results from decreased driving forces rather than increased τ_on, supporting the hypothesis that inhibiting the forces generated in a motility assay slows actin sliding velocities.

To further test this hypothesis we examine the effects of the small molecule inhibitor blebbistatin on both V and the rate of actin filament breaking. Blebbistatin is known to slow both V and the weak-to-strong binding transition without significantly influencing actin-myosin detachment kinetics (21, 22), and it is often assumed that blebbistatin inhibits V by sequestering a non-cycling pool of myosin heads (23) that resists actin filament movement through weak actin-myosin interactions (Fig. 1A). If this were the primary mechanism by which blebbistatin slows V, we would expect blebbistatin to increase the rate of actin filament breaking. However, here we show that like with P_i, 50 μM blebbistatin slows both V and the rate at which actin filaments break, suggesting that blebbistatin slows V by decreasing force transmission in a motility assay. These results provide additional support for the hypothesis that, in addition to actin-myosin detachment kinetics, the driving force of actin-myosin binding influences actin sliding velocities. This novel perspective on muscle contraction provides potential new insights into how muscle mechanics are altered by small molecule inhibitors such as BDM and BTS (24-27), by mutations associated with muscle myopathies (28), and by regulatory proteins such as troponin and tropomyosin (29).

Experimental Procedures

Protein Purification

Fast skeletal muscle myosin was prepared from rabbit psoas as previously described (30) and stored in glycerol at -20° C. Actin was isolated from rabbit psoas (31) and stored on ice at 4° C. For in vitro motility assays, actin was incubated with tetramethylrhodamine isothiocyanate (TRITC) phalloidin overnight.

Buffers

For actin-based motility assays, myosin buffer (300 mM KCl, 25 mM imidazole, 1 mM EGTA, 4 mM MgCl₂, 10 mM DTT), actin buffer (25 mM KCl, 25 mM imidazole, 1 mM EGTA, 4 mM MgCl₂, 10 mM DTT), motility buffer (25 mM KCl, 25 mM imidazole, 1 mM EGTA, 4 mM MgCl₂, 10 mM DTT, 0.03 – 1 mM ATP, 0.5% methylcellulose, 5.8 mg/ml glucose, 0.033 mg/ml glucose oxidase, and 0.045 mg/ml catalase) were prepared. For blebbistatin experiments, we added 50 μM blebbistatin (Sigma-Aldrich, St. Louis, MO) to the motility buffer. Phosphate buffers contained a 3:2 ratio of K₂HPO₄ and KH₂PO₄ (Sigma-Aldrich, St. Louis, MO) as previously described (32). In P_i experiments ionic strength was maintained by adjusting KCl according to Fabiato and Fabiato (33).

Activity Assays

The velocity of fluorescently labeled actin filaments sliding over a bed of myosin molecules was measured using an in vitro motility assay (34, 35) at 25° C. Flow cells were prepared by attaching a nitrocellulose-coated coverslip to a microscope slide with shim spacers. Flow cells for the motility assay were treated as follows: 2 × 50 μL of 100 μg·mL^-1 myosin with a 1 min. incubation period, 2 × 50 μL of 0.5 mg·mL^-1 BSA, 2 × 50 μL of 10 μM actin with a 1 min. incubation period, 2 × 50 μL of actin buffer, and 1 × 80 μL of motility buffer. Actin filaments bound to the coverslip surface were visualized prior to addition of motility buffer so that the time elapsed between adding motility buffer and recording actin filament movement was less than 10 sec. For control experiments, actin was not immobilized specifically. The actin filaments in the control experiments were free to thermally fluctuate. For blebbistatin experiments, light exposure to blebbistatin buffer was minimized by making buffers, storing buffers, and performing experiments with minimal light (36).

Motility assays were performed using a Nikon TE2000 epifluorescence microscope with fluorescence images digitally acquired at 7.3 frames per second with a Roper Cascade 512B (Princeton Instruments, Trenton, NJ) CCD camera. We prepared at least three flow cells for each experimental condition, and for each flow cell we recorded one three-minute image sequence. For each image sequence, we analyzed actin movement using Simple PCI tracking software (Compix, Sewickley, PA) to obtain actin-sliding velocities, V. Objects were defined by applying an exclusionary area threshold to minimize background noise. Intersect filters were applied to exclude intersecting filaments. The velocities of the moving actin filaments were plotted as a histogram and fitted to a Gaussian distribution. The average velocity, V, for the field was taken from the mean of the Gaussian fit. All errors reported are standard deviation (SD).

Analysis of Actin-filament Breaking

Actin filament breaking was analyzed using Image J (NIH, Bethesda, MD). For each actin filament, the filament length and the time, τ_break, it took to break were recorded. τ_break was calculated relative to the frame of origin for a filament, defined as i) the initial frame of the image sequence for filaments fully in the field of view, ii) the frame at which the filament entered the field of view; or iii) the frame at which the filament broke from a longer filament. τ_break values for all actin filaments within a given length range were plotted in a histogram and fitted to a single exponential to determine the lifetime (τ_break) and break rate (τ_break⁻¹) using Origin (Origin Lab Corporation, North Hampton, MA). Approximately 50 – 100 filaments were analyzed per condition. Non-moving filaments were omitted from our analysis. Actin filaments appeared to break through bending rather than through a tensile pull consistent with previous studies (37).

Results

According to conventional models of muscle contraction (V = d·τ_on⁻¹), P_i and blebbistatin (both known effectors of weak-to-strong binding kinetics) slow V by altering chemical forces that resist myosin-based actin motility (Fig. 1A). Specifically, P_i has been proposed (18,20,32) to increase τ_on by competing with ATP for myosin binding (Fig. 1A), whereas blebbistatin is assumed to introduce resistive forces through weak interactions between actin and blebbistatin-sequestered, non-cycling myosin heads (Fig. 1A). An alternative hypothesis is that both P_i and blebbistatin slow V by diminishing the driving forces of strong actin-myosin binding (Fig. 1A). Here, to determine if V is slowed by altered resistive forces or altered driving forces (Fig. 1A), we measure the effects of 30 mM P_i and 50 μM blebbistatin on the rate (τ_break⁻¹) of actin filament breaking during a motility assay. An increase in τ_break⁻¹ is indicative of increased resistance to movement whereas a decrease in τ_break⁻¹ suggests a decrease in driving force (Fig. 1A).

Actin breaking is myosin-dependent

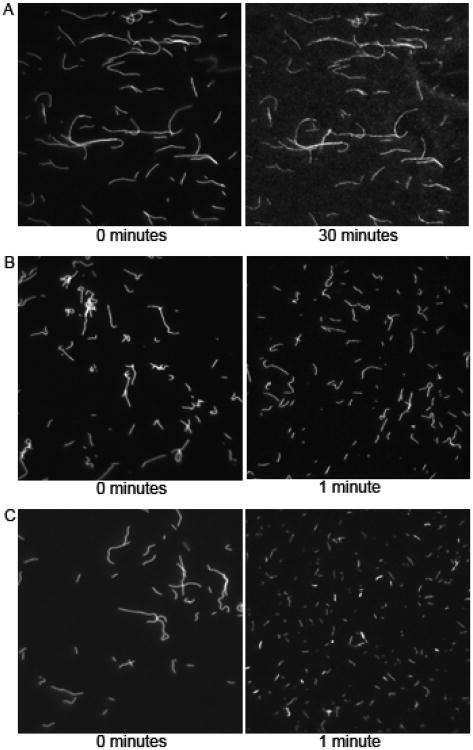
In the absence of myosin, actin filaments suspended over a nitrocellulose-coated coverslip in motility buffer (1 mM ATP) did not noticeably break over a period of 30 minutes (Fig. 2A), whereas during a myosin-based actin motility assay (1mM ATP) we observed significant actin filament fragmentation in less than one minute (Fig. 2B) showing that breaking is in fact myosin based. Actin filaments broke even more over this time period when [ATP] was decreased to 30 μM (Fig. 2C). We observed little or no [ATP]-dependence of actin filament fragmentation in the absence of myosin (data not shown). These data indicate that actin filament breaking observed in a motility assay is caused by forces generated between myosin heads.

Figure 2.

Actin breaking is myosin dependent. (A) Images of fluorescently labeled actin filaments in a flow cell with no myosin and 30 μM ATP obtained at 0 (left) and 30 minutes (right) after addition of actin. (B) Images of actin filaments during a myosin-based in vitro motility assay performed at 1 mM ATP obtained at 0 (left) and 1 minute (right) after addition of motility buffer. (C) Images of actin filaments during a myosin-based in vitro motility assay performed at 0.03 mM ATP obtained at 0 (left) and 1 (right) minute following addition of motility buffer.

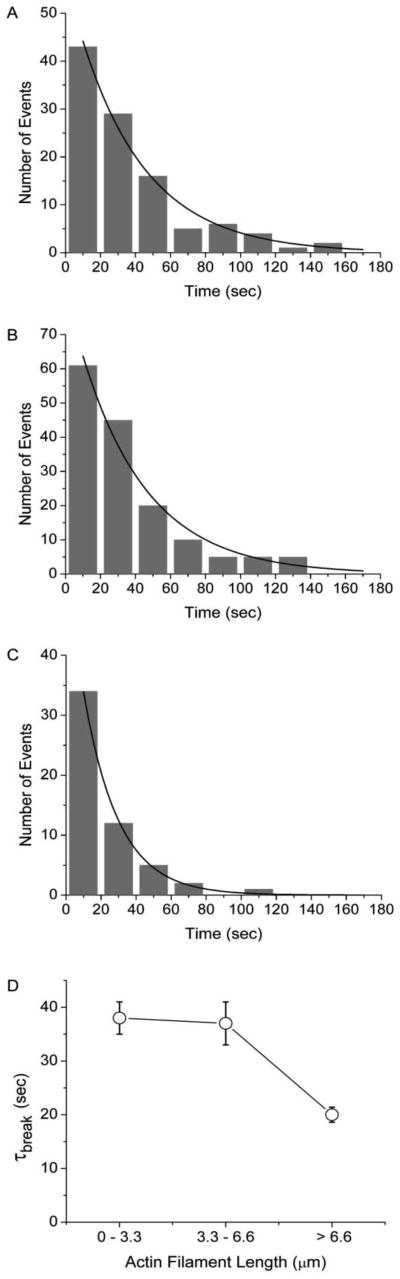
To determine the rate at which actin filaments break, we timed breaking events for individual actin filaments through a frame-by-frame analysis of actin filaments moving in a motility assay. For each actin filament we counted the number of frames elapsed before that filament broke, obtaining a time to break, τ_break, for that filament. We plotted these times in a histogram and fitted the data to a single exponential to obtain a mean actin filament lifetime (τ_break), or break rate (τ_break⁻¹). To test and control for potential actin-length dependences of τ_break, we grouped individual break times (τ_break) by actin filament length. Figure 3 shows histograms of τ_break values obtained at 30 μM ATP for actin filaments with lengths < 3.3 μm (Fig. 3A), 3.3 – 6.6 μm (Fig. 3B), and > 6.6 μm (Fig. 3C). The average time to break (τ_break) for each range of actin filament length was obtained by fitting each histogram to a single exponential and was plotted in Fig. 3D. These data show a small actin length-dependence of τ_break for filaments between 0 and 6.6 μm, but a significant decrease in τ_break values for filaments > 6.6 μm, demonstrating that actin length is a variable that must be controlled when assessing P_i-dependent changes in τ_break.

Figure 3.

Length dependence of the rate of actin filament breaking. (A) Histogram of actin filament break times, τ_break, measured during an in motility assay performed at 30 μM ATP for actin filaments with lengths (A) between 0 and 3.3 μm (n = 106), (B) between 3.3 and 6.6 μm (n = 151), and (C) greater than 6.6 μm (n = 54). Each histogram is fitted to a single exponential (solid line) to obtain the actin filament lifetime (τ_break). (D) Actin lifetimes for 0 – 3.3 μm, 3.3 – 6.6 μm, and > 6.6 μm length actin filaments are plotted.

Relatively high interhead forces are generated in an in vitro motility assay at low [ATP]

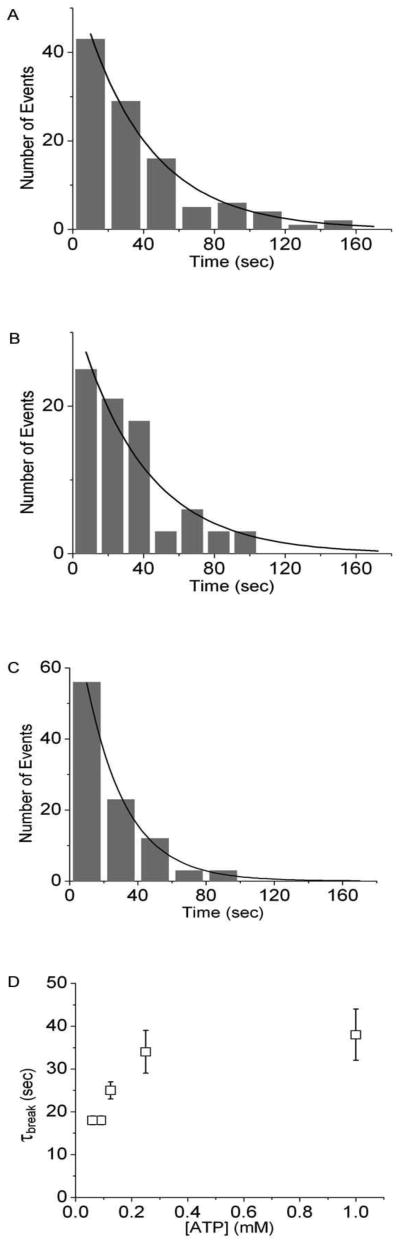
In an in vitro motility assay, actin sliding velocities measured at [ATP] > ∼100 μM exceed velocities predicted by a Michaelis-Menten analysis of velocities obtained at [ATP] < 100 μM (13,17,40). Interestingly, above this same critical ATP concentration, V becomes independent of P_i (Fig. 1A) (17). Both observations are consistent with a model in which at low [ATP], high forces are transmitted along actin filaments, whereas at high [ATP] less force is transmitted due to a smaller a, resulting either from a larger distance between heads at high [ATP] or from the mechanical acceleration of ADP release kinetics (15,17). To further test this hypothesis, we determined the [ATP]-dependence of the rate of actin filament breaking. Figures 4A – 4C show histograms of actin break times (τ_break) obtained at 1.0, 0.125, and 0.06 mM ATP. The ATP-dependence of the average actin filament lifetimes (τ_break) obtained from single exponential fits to the histograms shows a transition from slow break rates at high [ATP] (> 100 μM) to more rapid break rates at low [ATP] (< 100 μM), demonstrating that at high [ATP] force transmission, a, decreases. The data in Fig. 4 were acquired for actin filaments with lengths between 3.3 and 6.6 μm, and a similar [ATP]-dependence was observed for actin filament lengths > 6.6 μm (data not shown).

Figure 4.

ATP-dependence of the rate of actin filament breaking. Actin filament break times, τ_break, were measured at (A) 1.0 mM (n = 151), (B) 0.125 mM (n = 80), and (C) 0.06 mM (n = 76) ATP and plotted in histograms. Each histogram was fitted with a single exponential (solid line) to obtain actin filament lifetime (τ_break). (D) Actin filament lifetimes (τ_break) for 1.0, 0.250, 0.125, 0.06 and 0.03 mM ATP are plotted.

P_i and blebbistatin decrease force transmission along actin filaments

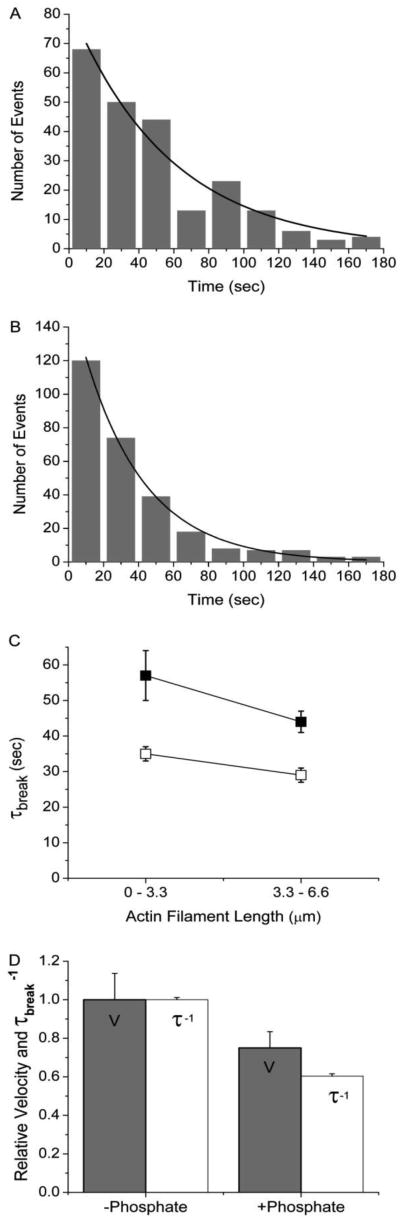
Hooft et al. argue that inhibition of V by P_i results from a decrease in the chemical forces that drive myosin-based actin motility (Fig. 1A). This model predicts that inhibition of V by P_i will be associated with a decrease in forces generated along actin filaments in an in vitro motility assay, resulting in a decrease in the rate at which actin filaments break. In contrast, a model in which P_i inhibits V by binding actin-bound myosin rigor heads predicts that the inhibition of V by P_i will increase forces exerted on actin (Fig. 1A), increasing the rate at which actin filaments break (20). To test these model predictions, we determined the effects of P_i on the rate of actin filament breaking (τ_break⁻¹) in a motility assay performed at 30 μM ATP. Figure 5 shows representative histograms of τ_break values obtained both in the presence (Fig. 5A) and absence (Fig. 5B) of 30 mM P_i for actin filaments < 3.3 μm. These and other histograms were fitted to single exponentials to obtain rates (τ_break⁻¹) of actin filament breaking (Fig. 5C). Figure 5D shows that the inhibition of V by P_i correlates with a decrease in the rate of actin filament breaking, indicating that P_i inhibits V by decreasing the driving forces of motility. These data support our hypothesis that driving forces associated with weak-to-strong binding kinetics influence actin sliding velocities.

Figure 5.

[P_i] dependence of actin sliding velocities and the rate of actin filament breaking. (A) Actin filament break times, τ_break, were measured in the presence of 30 mM P_i at 30 μM ATP for filaments < 3.3 μm and plotted in a histogram (n = 224). The data were fitted to a single exponential (solid line) to obtain the actin filament lifetime (τ_break). (B) Actin filament break times, τ_break, were measured in the presence 30 μM ATP with no added P_i for filaments < 3.3 μm and plotted in a histogram (n = 279). The data were fitted with a single exponential (solid line) to obtain the average time to break (τ_break). (C) Values for the actin filament lifetime (τ_break) obtained with (dark squares) and without (white squares) added P_i at 30 μM ATP are plotted both for actin filament lengths < 3.3 μm and for actin filament lengths between 3.3 and 6.6 μm. (D) For all actin filament lengths, mean actin sliding velocities (grey bars), normalized to 1.8 μm·sec⁻¹, and the rates of actin breaking (white bars), normalized to 0.029 sec⁻¹, obtained in the presence and absence of 30 mM P_i at 30 μM ATP are plotted, showing that the inhibition of V by P_i corresponds to a decrease in interhead forces.

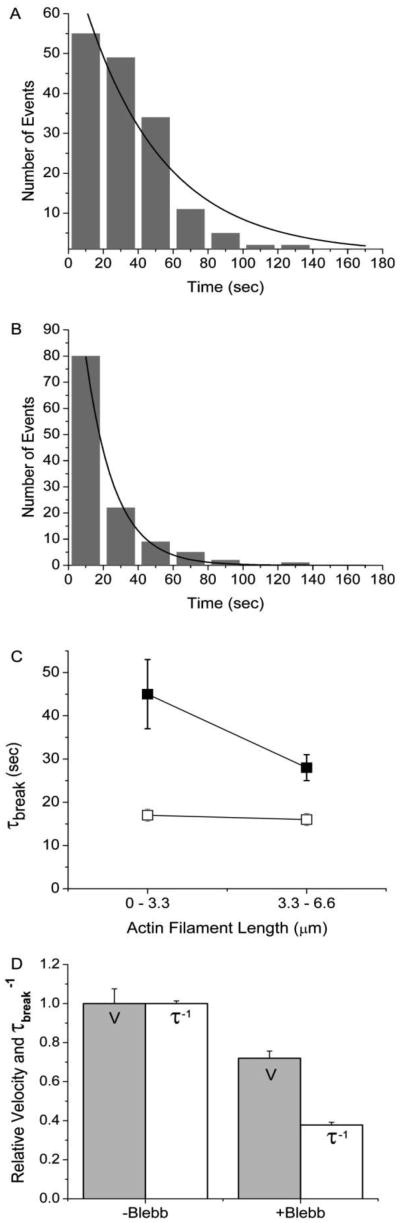
To further test this hypothesis, we studied the effects of blebbistatin on the rate of actin filament breaking. Blebbistatin is a small molecule inhibitor of actin-myosin ATPase activity, actin sliding velocities, and isometric muscle force (22,34). The kinetic basis for this effect is inhibition of myosin's force-generating, weak-to-strong binding transition (22). According to a model in which blebbistatin slows V by increasing resistive forces, inhibition of V by blebbistatin should increase the rate of actin filament breaking (Fig. 1A). In contrast, according to a model in which blebbistatin slows V by decreasing driving forces, inhibition of V by blebbistatin should decrease the rate of actin filament breaking (Fig. 1A). To test these models, we determined the effects of blebbistatin on both V and the rate (τ_break⁻¹) of actin filament breaking using a motility assay performed at 30 μM ATP. Figure 6 shows histograms of τ_break values obtained in the presence (Fig. 6A) and absence (Fig. 6B) of 50 μM blebbistatin. High concentrations (50 μM) of blebbistatin relative to those used in previous studies (45) were needed to inhibit V presumably because at the low [ATP] used in this study, ATPase activity becomes limited by ATP-induced actin-myosin detachment kinetics and thus inhibiting weak-to-strong binding is not rate limiting and thus its inhibition has less of an effect on V. Actin filament lifetimes (τ_break) were obtained from single exponential fits to each histogram and plotted in Fig. 6C. Figure 6D shows that blebbistatin decreased both V and τ_break⁻¹, implying that blebbistatin inhibits V by decreasing the driving force of the weak-to-strong binding transition.

Figure 6.

Blebbistatin dependence of actin sliding velocities and the rate of actin filament breaking. (A) Actin filament break times, τ_break, were measured in the presence (A, n = 158) and absence (B, n = 119) of 50 μm blebbistatin at 30 μM ATP for filaments < 3.3 μm and plotted in a histogram. These data were fitted to a single exponential (solid line) to obtain an actin filament lifetime, τ_break. (C) Actin filament lifetimes obtained at 30 μm ATP both with (dark squares) and without (white squares) 50 μM blebbistatin for actin filament lengths < 3.3 μm and between 3.3 and 6.6 μm. (D) For all actin filament lengths, mean actin sliding velocities (grey bars), normalized to 1.0 μm·sec⁻¹, and rates of actin filament breaking (white bars), normalized to 0.059 sec⁻¹, obtained in the presence and absence of 50 μM blebbistatin at 30 μM ATP are plotted, showing the inhibition of V by blebbistatin correlates with a decrease in interhead forces.

Inhibition of V with Blebbistatin cannot be recovered by increasing myosin density

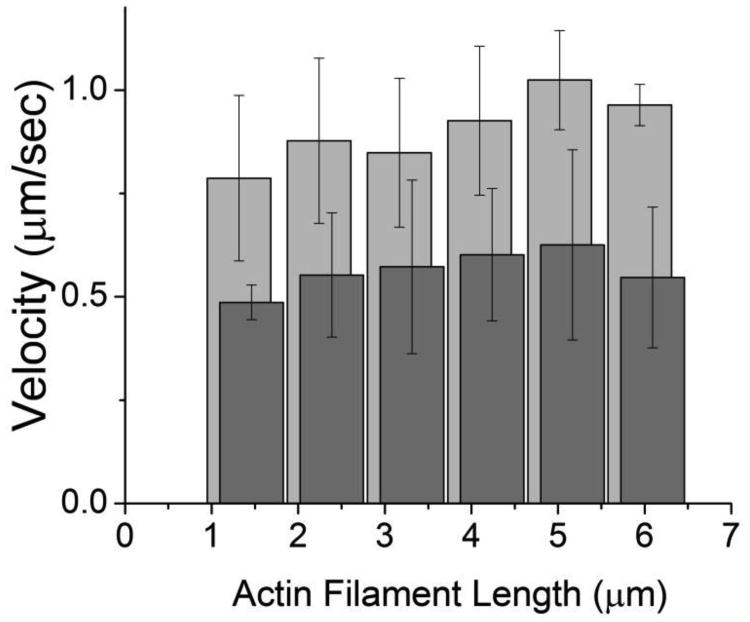
One alternative interpretation for the effects of blebbistatin on V and τ_break⁻¹ in Fig. 6 is that blebbistatin sequesters a non-cycling pool of myosin heads, leaving an insufficient number of myosin heads available for maximal velocity. To test this hypothesis, we determined whether inhibition of V by blebbistatin can be reversed by increasing the total number of myosin heads available to bind an actin filament. We measured the actin length dependence of V at 30 μM ATP both in the presence and absence of 50 μM blebbistatin and calculated the number of myosin heads available to bind an actin filament of a given length as previously described (16). Figure 7 shows that inhibition of V by blebbistatin is not reversed by increasing the number of myosin heads (number of myosin heads can be calculated based off of actin filament length) available to bind an actin filament, ruling out sequestering of non-cycling crossbridges as the primary mechanism by which blebbistatin inhibits V.

Figure 7.

The effects of increasing myosin density on blebbistatin-inhibited V. Actin filament velocities (V) are plotted as a function of actin filament length (n = 120), where longer actin filaments interact with a higher number of myosin heads (N). N can be calculated from actin filament length as previously described (16). Points are shown in the absence (light gray) and presence (dark gray) of 50 μM blebbistatin. These data show that the inhibition of V by blebbistatin cannot be reversed by increasing myosin density.

Discussion

During unloaded muscle shortening and in vitro myosin-based actin sliding, myosin heads generate force in the direction of actin movement (Fig. 1A) against a population of actin-bound myosin that resists actin movement (41). The conventional view of actin sliding (12,41) is that the driving force of a myosin head is well-defined by a molecular mechanical constant, d, and that the sole biochemical determinant of actin sliding velocities is the rate (τ_on⁻¹) at which resistive heads detach from actin (V = d·τ_on⁻¹).

Hooft et al. showed that, although τ_on influences actin sliding velocities, weak-to-strong binding kinetics also contribute to V(17). Specifically we showed that at low [ATP], actin sliding velocities decrease with added P_i, indicating a link between V, actin-myosin affinity, and the force generating capacity of myosin (13,18,42,43). This interpretation differs from the conventional view that P_i slows V by competing with ATP for myosin binding thereby increasing τ_on. Amrute-Nayak et al. (20) correctly argue that the two models can be tested by determining the effects of P_i on the forces exerted along actin by myosin heads in a motility assay, where changes in actin forces can be estimated from changes in the rate at which actin filaments break. In the present study, we further validate this assertion, showing in Fig. 2 that actin breaking in a motility assay is associated with the actin-myosin ATPase reaction.

Because the visible pool of actin filaments changes over time in a motility assay, it is important to measure filament breaking events rather than before-and-after snapshots of filaments when determining the rate of filament breaking. Moreover, because the starting length of actin filaments in a motility assay can be variable, the length-dependence of the rate of actin filament breaking demonstrated in Fig. 3 implies that actin filament lengths must be controlled when measuring the rate of filament breaking. We believe the above factors contribute to the discrepancies between our results and those reported by Amrute-Nayak et al.

Whereas Amrute-Nayak et al. inferred an increase in the rate of filament breaking upon addition of P_i, in Fig. 5 we show that τ_break⁻¹ decreases significantly upon addition of 30 mM P_i. This result implies that, as argued by Hooft et al., P_i slows V by decreasing the driving force of weak-to-strong binding, τ_off. These studies were performed at low [ATP] because the weak-to-strong binding transition is made reversible by P_i only under the relatively high forces (13,18,42) generated in a motility assay at low [ATP] (15,17).

To further test the hypothesis that V is influenced by τ_off, we studied the effects of blebbistatin on V and τ_break⁻¹. Blebbistatin is a small molecule inhibitor of actin-myosin ATPase activity, which inhibits isometric muscle force, muscle shortening velocities, and actin sliding velocities in vitro (22,36). The kinetic mechanism for its inhibitory effect is that blebbistatin slows the rate of weak-to-strong binding (21,22,44) with no significant effect on ADP release, ATP binding, or τ_on. These kinetic studies suggest that blebbistatin inhibits V through its effects on the weak-to-strong binding kinetics. Figure 6 shows that the decrease in actin sliding velocities induced by blebbistatin corresponds to a decrease in the rate of actin filament breaking, consistent with blebbistatin inhibiting V through a decrease in the forces transmitted along an actin filament with the weak-to-strong binding transition.

The data reported herein and in a previous paper (17) support a model in which actin sliding velocities depend not only on detachment kinetics but also on attachment kinetics and energetics. Interestingly, both blebbistatin and P_i inhibit actin-myosin affinity, isometric muscle force, actin sliding velocities, and driving forces generated during an in vitro motility assay. Our observations that P_i and blebbistatin similarly decrease both the forces transmitted along an actin filament and actin sliding velocities are consistent with a model in which P_i and blebbistatin decrease the force transmission term, a, in Eq. 1.

We describe a simple expression for a as follows. First, we assume that inefficient force transmission results when the mechanical step of a myosin head pulls out “slack” in a flexible actin filament rather than straining an adjacent myosin head, and we estimate this slack length by treating an actin filament as a worm-like chain. For simplicity, we assume that the worm-like chain stiffness of actin is negligible relative to that of actin-bound myosin heads. (Incorporating worm-like-chain stiffness into a model of muscle shortening results in attachment kinetics contributing directly to actin sliding velocities – an analysis developed elsewhere). According to a worm-like-chain model (47), the average slack, s, in the average length, L, of an actin filament spanning two myosin heads is

$$\text{s}=\sqrt{2\mathit{\text{PL}}\ast (\text{1}-\left(\frac{P}{L}\right)\ast (1-e^{-\frac{L}{P}}))}$$

where P is the persistence length of actin. The efficiency with which one myosin head can transmit forces a distance, L, along an actin filament is then a = (d – s)/d.

The effects of attachment kinetics on V can be accounted for by considering that the average distance, L, between two strongly bound heads on an actin filament is simply r/ρ, where ρ is the linear myosin head density along an actin filament and r = τ_on/(τ_on + τ_off) is the fraction of those myosin heads that are strongly bound to actin, or

$$a=(d-\sqrt{2\mathit{\text{Pr}}/\rho \ast (1-\frac{P\rho }{r}\ast (1-e^{-\frac{r}{P\rho }}))})/d$$ (Eq. 2)

Thus τ_off can influence V (Eq. 1) via the effects of duty ratio on force transmission, a. Equation 2 also provides a qualitative description of the internal forces generated during unloaded shortening. When the distance between myosin heads is large (i.e., ρ is small), the slack, s, exceeds myosin's step size, which means no force is transmitted, a = 0, and no internal forces are generated. When the distance between myosin heads is small (i.e., ρ is large), a approaches one and maximal internal forces are generated.

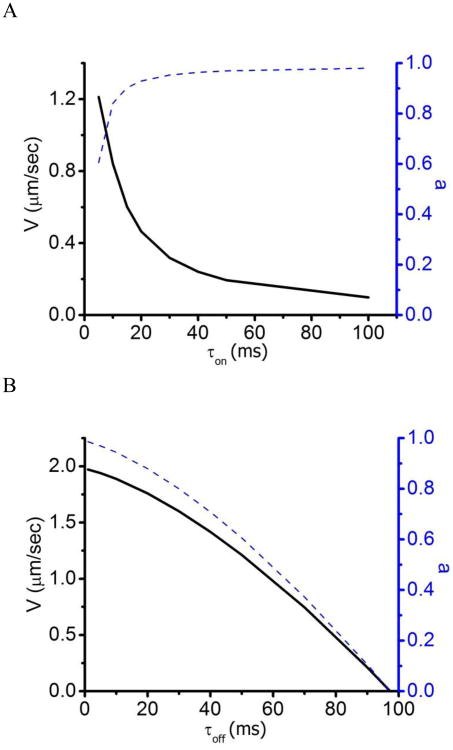
This model is consistent with the data reported herein. In Fig. 8, Eq. 1 (substituting a from Eq. 2) and Eq. 2 are plotted at different τ_on (Fig. 8A) and τ_off (Fig. 8B) values. Figure 8A shows that when V is inhibited through slowing actin-myosin detachment kinetics (i.e., increasing τ_on) a increases, resulting in an increase in the internal forces generated. This is consistent with the data in Fig. 4. In contrast, when V is inhibited through slowing actin-myosin attachment kinetics (i.e., increasing τ_off) a decreases, resulting in a decrease in internal forces generated. This is consistent with the data in Figs. 5 and 6. A more quantitative analysis will require developing a formal connection between force transmission, force generation, and the effects of force on the actin filament breaking rate, which is beyond the scope of this paper.

Figure 8.

The τ_off and τ_on dependence of Equations 1 and 2. (A) Plots of both V (Eq. 1, substituting a from Eq. 2, solid line) and a (Eq. 2, dashed line) at different τ_on values show that increasing τ_on inhibits V and increases internal forces, consistent with the data in Fig. 4 [τ_off = 50 ms; P = 2 mm; ρ = 1/(36 nm)]. (B) Plots of both V (Eq. 1, substituting a from Eq. 2, solid line) and a (Eq. 2, dashed line) at different τ_off values show that increasing τ_off inhibits V and decreases internal forces, consistent with the data in Figs. 5 and 6 [τ_on = 5 ms; P = 2 mm; ρ = 1/(36 nm)].

The above analysis suggests that, analogous to the effects of decreasing myosin density on V, blebbistatin and P_i inhibit V by decreasing the number of strongly bound myosin heads. It is also possible that P_i and blebbistatin inhibit V in the loaded (low [ATP]) motility assay by decreasing the average myosin step size, d, much like P_i inhibits the average force generated per myosin head in isometric muscle (46). Many other effectors of actin-myosin ATPase activity exhibit similar inhibition of both actin sliding velocities and isometric muscle force. The data presented above provide a potentially new perspective on the effects of many modulators of muscle contraction, including the small molecule inhibitors BDM and BTS (24-27), mutations associated with familial hypertrophic cardiomyopathy (28), and thin filament regulatory proteins troponin and tropomyosin (29).

Abbreviations and Textual Footnotes

P_i

Inorganic Phosphate