Abstract
People are sensitive to the summary statistics of the visual world (e.g., average orientation/speed/facial expression). We readily derive this information from complex scenes, often without explicit awareness. Given the fundamental and ubiquitous nature of summary statistical representation, we tested whether this kind of information is subject to the attentional constraints imposed by change blindness. We show that information regarding the summary statistics of a scene is available despite limited conscious access. In a novel experiment, we found that while observers can suffer from change blindness (i.e., not localize where change occurred between two views of the same scene), observers could nevertheless accurately report changes in the summary statistics (or “gist”) about the very same scene. In the experiment, observers saw two successively presented sets of 16 faces that varied in expression. Four of the faces in the first set changed from one emotional extreme (e.g., happy) to another (e.g., sad) in the second set. Observers performed poorly when asked to locate any of the faces that changed (change blindness). However, when asked about the ensemble (which set was happier, on average), observer performance remained high. Observers were sensitive to the average expression even when they failed to localize any specific object change. That is, even when observers could not locate the very faces driving the change in average expression between the two sets, they nonetheless derived a precise ensemble representation. Thus, the visual system may be optimized to process summary statistics in an efficient manner, allowing it to operate despite minimal conscious access to the information presented.
Keywords: Visual awareness, Change blindness, Face perception, Object recognition
The visual system is sensitive to summary statistical information about group or ensemble characteristics (e.g., average orientation/motion/expression) in the natural world (Alvarez & Oliva, 2009; Ariely, 2001; Chong & Treisman, 2003; Dakin & Watt, 1997; Torralba & Oliva, 2003; Watamaniuk & Duchon, 1992; Williams & Sekuler, 1984; for reviews, see Alvarez, 2011; Haberman & Whitney, in press). We derive summary statistics, or ensemble information, across a host of visual domains, ranging from the average orientation of Gabor patches to the average expression from crowds of faces (de Fockert & Wolfenstein, 2009; Haberman & Whitney, 2007, 2009; Parkes, Lund, Angelucci, Solomon, & Morgan, 2001). Ensemble coding operates over both space and time (Albrecht & Scholl, 2010; Haberman, Harp, & Whitney, 2009) and they can be represented implicitly (Haberman & Whitney, 2009). Recent evidence has converged, suggesting that ensembles are compressed codes, allowing for efficient representation of large-scale scene information (Alvarez & Oliva, 2008; Haberman & Whitney, 2010). Given the ubiquitous, and even fundamental, role that summary statistics seem to play in vision, we explore whether ensembles play a role in our phenomenal sense of visual completeness (Rensink, O’Regan, & Clark, 1997).
Change blindness, or the failure to notice differences in sequential scenes or images, is a well-established phenomenon, suggesting that we have a limited visual awareness from one moment to the next (Mitroff, Simons, & Franconeri, 2002; Rensink et al., 1997; Simons & Chabris, 1999; Simons & Levin, 1998). Although on the surface change blindness seems to suggest a sparse visual representation, an abundance of recent research has supported the notion that a failure to represent visual information is unlikely to drive this phenomenon. In fact, much of the incoming visual information is preserved in spite of change detection failures (Beck & Levin, 2003; Hollingworth, 2003; Hollingworth & Henderson, 2004; Mitroff, Simons, & Levin, 2004). For example, Beck and Levin (2003) showed that observers could identify an object change in the absence of a durable representation of that object. Mitroff et al. (2004) showed that this durable representation could even be used to aid in object identification. Furthermore, Hollingworth and Henderson (2004) found that visual scene information was preserved even when observers failed to detect a rotation in the scene.
The studies above suggest that despite the limited conscious access revealed by change detection experiments, the “gist” of a scene remains accessible (Oliva & Torralba, 2001; Potter, 1976; Thorpe, Fize, & Marlot, 1996). A gist broadly refers to abstract information that can be used to rapidly access memory representations of scene categories (Friedman, 1979; Henderson & Hollingworth, 1999; Potter, 1976). However, what exactly constitutes a gist is not well understood. Here, we explore the possibility that the nature of gist, at least in some capacity, corresponds to summary statistics. Given the efficiency with which ensembles are extracted, it is plausible that the limited conscious access that we have to scene information is nevertheless enough to generate a precise ensemble code.
Already there is some evidence that summary statistical information operates beyond the focus of attention (e.g., Alvarez & Oliva, 2008). However, this has only been demonstrated with low-level features (e.g., features thought to be analyzed at the earliest stages of cortical visual processing, such as orientation, contrast, and motion direction), which are expected to be processed in parallel (Watamaniuk & McKee, 1998). In the present experiment, we show that when viewing groups of faces, observers fail to localize a change, while still being sensitive to the summary statistical information in the group. The results show that ensemble coding may be the mechanism by which high-level scene information (i.e., gist) is extracted, even when conscious access to the details is limited. Our sensitivity to object-level ensemble or summary statistics may therefore contribute to the impression of a rich moment-to-moment visual world (Rensink et al., 1997).
In a modified version of the classical one-shot change blindness paradigm (Pashler, 1988; Phillips, 1974), observers viewed two successive sets of emotionally varying faces and performed two tasks: Mean discrimination and change localization. In the mean discrimination task (cf. Ariely, 2001; Chong & Treisman, 2003; Haberman & Whitney, 2007, 2009; Parkes et al., 2001; Watamaniuk & Duchon, 1992; Williams & Sekuler, 1984), observers indicated which of the two sets of images had on average the happier expression (vs. sad). In the change localization task, observers indicated where in the set of faces a change in emotional valence occurred.
Method
Participants
A group of 10 individuals (4 female, 6 male, mean age = 28.4 years) affiliated with the University of California, Davis, participated. Informed consent was obtained for all volunteers, who were compensated for their time and had normal or corrected-to-normal vision. Of the 10 participants, 8 were naïve as to the purposes of the experiment (there was no difference in performance between the nonnaïve and naïve participants).
Stimuli
We created a virtual circle of expressions by linearly interpolating (using Morph 2.5, 1998) between three images taken from the Ekman gallery (Ekman & Friesen, 1976). For this experiment, we generated 147 images ranging from happy, to neutral, to sad, and back to happy again. This circle effectively eliminated any emotional edges in our stimulus set. Morphed faces were nominally separated from one another by emotional units (e.g., Face 2 was one emotional unit sadder than Face 1). Face images were grayscaled (the average face had a 98% max Michelson contrast) and occupied 3.04° × 4.34° of visual angle. The background relative to the average face had a 29% max Michelson contrast.
The sets comprised four instances of each of four unique images, for a total of 16 faces per set (see Fig. 1a). The four unique images were separated from one another by at least 6 emotional units, a suprathreshold separation. The faces were randomly assigned positions on a fixed 4 × 4 grid. The sets contained faces ±3 and ±9 emotional units around a randomly selected set mean.
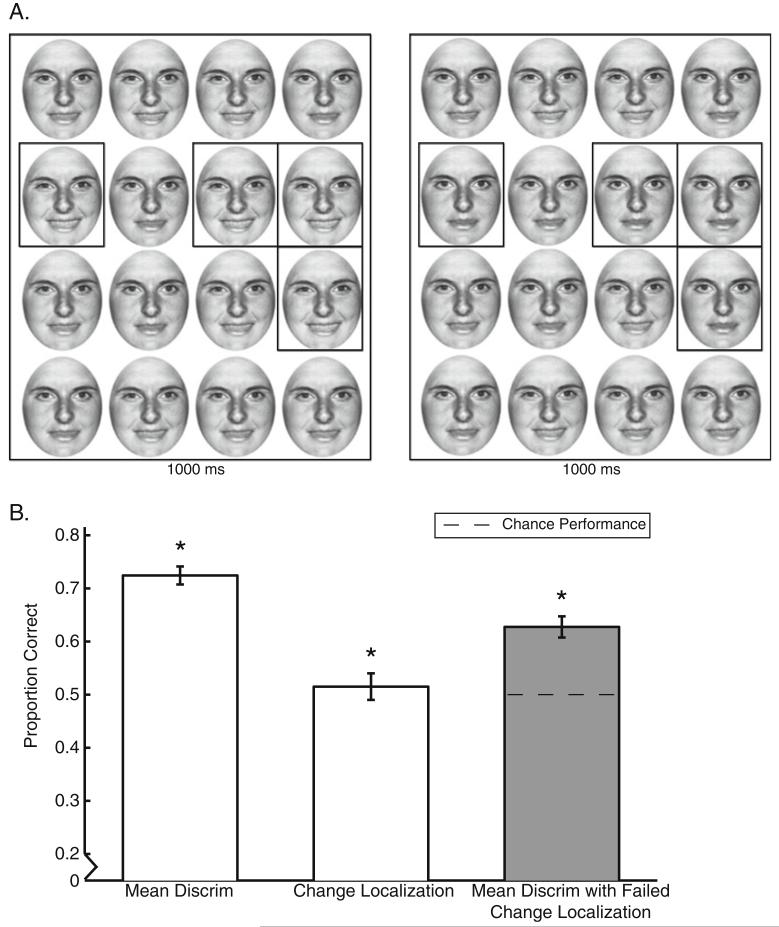
Fig. 1.
Change localization/mean discrimination dual-task experiment. a Example stimuli. Sets were displayed successively for 1,000 ms each, separated by a 500-ms interval. On each trial, observers had to indicate (1) which set had the happier average expression (two-interval forced choice, 50% guess rate) and (2) any one of the four items that changed between the two sets (indicated here by the black outlines, not seen by participants; 25% guess rate). b Results. Overall, mean discrimination performance (left bar) was well above chance. Performance on the change localization task indicated that observers could attend to approximately three faces in the time allotted (middle bar). However, even when observers did not correctly localize a change between the sets (change localization miss trials), they were still significantly above chance in the mean discrimination task (right, gray bar; p < .001). This indicates that observers were able to discriminate the average expression in the group of faces on the same trials in which they failed to localize any individual face that changed. The black dotted line indicates chance performance on mean discrimination when change localization fails. Error bars indicate 1 SEM. *Performance significantly above chance
Procedure
On each trial, observers viewed two successive sets for 1,000 ms each, separated by a 500-ms fixation interstimulus interval (Fig. 1a). Observers were free to scan the sets of faces. On the second set, 4 of the 16 most emotionally extreme faces (either the saddest or happiest 4, randomly determined) changed to the other emotional extreme. For example, in one trial the four saddest faces in the first set would become the four new happiest faces in the second set. These four faces were not duplicates of existing faces; the distribution of faces in the sets was always a boxcar, and the 4 faces that changed effectively shifted the boxcar along the morph continuum. This switch elicited a change in mean valence of 6 emotional units. Besides the 4-face switch, all other aspects of the two sets were identical.
Observers had to perform two tasks on every trial: In the first task, they had to identify which of the two sets was on average happier (mean discrimination) using a keypress indicating the first or second set. In the second task, observers had to identify any one (only one) of the four locations that changed between the two sets (change localization). They indicated their responses by pressing the letter displayed on the screen that corresponded to the location of a change. Observers performed two runs of 200 trials each.
Results and discussion
In the change localization task, the probability of guessing where a change in emotional valence occurred was 25% (4 of the 16 items changed on every trial). If observers attended to 2 or 3 of the items in the set, the probabilities of detecting at least one change rose to 45% and 61%, respectively. Figure 1b (middle bar) indicates that actual change localization performance was 51.5% correct across observers, suggesting that they were only able to derive sufficient information from between two and three faces on a given trial (this assumes that no correct localization response was a guess, which is conservative).
As indicated in the leftmost bar in Figure 1b, performance on mean discriminations was 72.4%, suggesting that observers had ensemble information about each set. However, since one can infer which set is happier on average simply by identifying one of the changes, this number by itself is not that informative [although it is significantly above a conservative calculation of chance, 67.7%1; t(9) = 2.73, p = .02].
The critical question is What happens to mean discrimination performance when we examine trials on which change localization actually failed? In this analysis, we excluded trials on which observers successfully localized a change and assessed performance on mean discrimination on the remaining trials—trials on which no change was localized. Surprisingly, Figure 1b (rightmost bar) indicates that mean discrimination performance remained significantly above chance, where chance is 50% [M = 62.8%; z(9) = 6.36, p < .001]. Thus, despite being unable to localize the changes driving the average valence shift between sets, observers nonetheless still had access to the summary statistical information.
This result is not an artifact of dual-task difficulty. In a control experiment, 5 observers from the first experiment performed the identical change localization task in isolation (identify one of the four expression shifts). There was no statistical difference between the dual-task and single-task change localization performance [M = 52.4%; t(4) = 0.27 p = .8], suggesting that change localization performance was not reduced because of the concurrent mean discrimination task.
Could observers make the mean discrimination judgment just by looking at one set and ignoring the other one altogether? That is, was there expression information present on one set that allowed observers to probabilistically determine the mean expression of the other set without ever looking at it? We ran a control experiment that conclusively ruled out this strategy. Three observers were asked to judge which set was on average happier, but were only allowed to view one of the two sets. Results showed that observer performance was not different from chance [M = 53.2%; t(2) = 2.00, p = .18].
There appears to be some cost to mean discrimination performance when change localization fails [if we compare mean discrimination across all trials with mean discrimination in the subset of change localization miss trials—i.e., the leftmost vs. the rightmost bar in Fig. 1b; t(9) = 7.0, p < .01]. This is not surprising, however, because localizing any change can give away the mean discrimination task; the mean discrimination performance is therefore a low estimate of how much summary statistical information observers had. It may be that there is some interaction between mechanisms supporting change localization and those driving summary statistical representation (e.g., explicit attention; cf. Simons & Ambinder, 2005). However, the critical point here is that mean discrimination performance, even when observers could not localize the change, did not drop to chance. This should have happened if the two judgments were equally dependent on explicit attention.
It should be noted that these results do not mean that summary statistics are always available when change detection fails, because change detection is thought to be distinct from change localization (Fernandez-Duque & Thornton, 2000; Mitroff et al., 2002; Watanabe, 2003). However, our results show some degree of independence between change localization and ensemble perception: One can perceive a change in the ensemble even when failing to localize the stimulus that drives the change in that ensemble percept.
Given the apparent cost when the change is missed, it is possible that change localization and mean discrimination partially share a common mechanism (akin to shared resources for local and global attention; Bulakowski, Bressler, & Whitney, 2007) but that mean discrimination operates more efficiently given limited access to scene information. In other words, the limited awareness revealed by change localization does not prevent summary representation processes. The information in a complex scene that seems to lie beyond conscious access may come in the form of summary statistics, suggesting that they play a role in creating our phenomenal sense of visual completeness. The evidence for this is that when observers fail to localize a change, they are still above chance at recognizing the ensemble information.
Acknowledgment
We are grateful to Cathleen Moore, Dan Simons, Jason Fischer, and two anonymous reviewers for helpful comments in an earlier draft of this manuscript.
Footnotes
This calculation was based on assuming that when observers localized the change correctly, they would get the mean discrimination right 100% of the time. Performance on change localization is defined as 51.5 = x + .25(100 − x) is the change localization performance when chance is included (Fig. 1b), x is change localization when guesses are filtered, and 0.25 is the guess rate on change detection. Solving for x yields 35.33%. If observers guess on the remaining mean discrimination trials [(100 − 35.33) * 0.5], overall chance performance is 67.7%. This is extremely conservative, because it assumes that observers resort to a nonaveraging strategy every time they correctly localize a change. That is why the bar on the far right of Fig. 1b is more informative, as it reflects performance on mean discrimination when change localization fails.
Contributor Information
Jason Haberman, The Center for Mind and Brain, University of California, Davis, CA, USA; Department of Psychology, Harvard University, 33 Kirkland Street, Cambridge, MA 02138, USA.
David Whitney, The Center for Mind and Brain, University of California, Davis, CA, USA; Department of Psychology, University of California, Berkeley, CA, USA.
References
- Albrecht AR, Scholl BJ. Perceptually averaging in a continuous visual world: Extracting statistical summary representations over time. Psychological Science. 2010;21:560–567. doi: 10.1177/0956797610363543. doi:10.1177/0956797610363543. [DOI] [PubMed] [Google Scholar]
- Alvarez GA. Representing multiple objects as an ensemble enhances visual cognition. Trends in Cognitive Sciences. 2011;15:122–131. doi: 10.1016/j.tics.2011.01.003. doi:10.1016/j.tics.2011.01.003. [DOI] [PubMed] [Google Scholar]
- Alvarez GA, Oliva A. The representation of simple ensemble visual features outside the focus of attention. Psychological Science. 2008;19:392–398. doi: 10.1111/j.1467-9280.2008.02098.x. doi:10.1111/j.1467-9280.2008.02098.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alvarez GA, Oliva A. Spatial ensemble statistics are efficient codes that can be represented with reduced attention. Proceedings of the National Academy of Sciences. 2009;106:7345–7350. doi: 10.1073/pnas.0808981106. doi:10.1073/pnas.0808981106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ariely D. Seeing sets: Representation by statistical properties. Psychological Science. 2001;12:157–162. doi: 10.1111/1467-9280.00327. [DOI] [PubMed] [Google Scholar]
- Beck MR, Levin DT. The role of representational volatility in recognizing pre- and postchange objects. Perception & Psychophysics. 2003;65:458–468. doi: 10.3758/bf03194575. [DOI] [PubMed] [Google Scholar]
- Bulakowski PF, Bressler DW, Whitney D. Shared attentional resources for global and local motion processing. Journal of Vision. 2007;7(10):10, 1–10. doi: 10.1167/7.10.10. doi:10.1167/7.10.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chong SC, Treisman A. Representation of statistical properties. Vision Research. 2003;43:393–404. doi: 10.1016/s0042-6989(02)00596-5. doi:10.1016/S0042-6989(02)00596-5. [DOI] [PubMed] [Google Scholar]
- Dakin SC, Watt RJ. The computation of orientation statistics from visual texture. Vision Research. 1997;37:3181–3192. doi: 10.1016/s0042-6989(97)00133-8. [DOI] [PubMed] [Google Scholar]
- de Fockert J, Wolfenstein C. Rapid extraction of mean identity from sets of faces. Quarterly Journal of Experimental Psychology. 2009;62:1716–1722. doi: 10.1080/17470210902811249. doi:10.1080/17470210902811249. [DOI] [PubMed] [Google Scholar]
- Ekman P, Friesen WV. Pictures of facial affect. Consulting Psychologists Press; Palo Alto: 1976. [Google Scholar]
- Fernandez-Duque D, Thornton IM. Change detection without awareness: Do explicit reports underestimate the representation of change in the visual system? Visual Cognition. 2000;7:323–344. [Google Scholar]
- Friedman A. Framing pictures: Role of knowledge in automatized encoding and memory for gist. Journal of Experimental Psychology: General. 1979;108:316–355. doi: 10.1037//0096-3445.108.3.316. [DOI] [PubMed] [Google Scholar]
- Haberman J, Harp T, Whitney D. Averaging facial expression over time. Journal of Vision. 2009;9(11):1, 1–13. doi: 10.1167/9.11.1. doi:10.1167/9.11.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haberman J, Whitney D. Rapid extraction of mean emotion and gender from sets of faces. Current Biology. 2007;17:R751–R753. doi: 10.1016/j.cub.2007.06.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haberman J, Whitney D. Seeing the mean: Ensemble coding for sets of faces. Journal of Experimental Psychology: Human Perception and Performance. 2009;35:718–734. doi: 10.1037/a0013899. doi:10.1037/a0013899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haberman J, Whitney D. The visual system discounts emotional deviants when extracting average expression. Attention, Perception, & Psychophysics. 2010;72:1825–1838. doi: 10.3758/APP.72.7.1825. doi:10.3758/APP.72.7.1825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haberman J, Whitney D. Ensemble perception: Summarizing the scene and broadening the limits of visual processing. In: Wolfe J, Robertson L, editors. Chapter to appear in an edited volume. A Festschrift in honor of Anne Treisman; 2011. in press. [Google Scholar]
- Henderson JM, Hollingworth A. High-level scene perception. Annual Review of Psychology. 1999;50:243–271. doi: 10.1146/annurev.psych.50.1.243. doi:10.1146/annurev.psych.50.1.243. [DOI] [PubMed] [Google Scholar]
- Hollingworth A. Failures of retrieval and comparison constrain change detection in natural scenes. Journal of Experimental Psychology: Human Perception and Performance. 2003;29:388–403. doi: 10.1037/0096-1523.29.2.388. [DOI] [PubMed] [Google Scholar]
- Hollingworth A, Henderson JM. Sustained change blindness to incremental scene rotation: A dissociation between explicit change detection and visual memory. Perception & Psychophysics. 2004;66:800–807. doi: 10.3758/bf03194974. [DOI] [PubMed] [Google Scholar]
- Mitroff SR, Simons DJ, Franconeri SL. The siren song of implicit change detection. Journal of Experimental Psychology: Human Perception and Performance. 2002;28:798–815. doi:10.1037/0096-1523.28.4.798. [PubMed] [Google Scholar]
- Mitroff SR, Simons DJ, Levin DT. Nothing compares 2 views: Change blindness can occur despite preserved access to the changed information. Perception & Psychophysics. 2004;66:1268–1281. doi: 10.3758/bf03194997. doi:10.3758/BF03194997. [DOI] [PubMed] [Google Scholar]
- Oliva A, Torralba A. Modeling the shape of the scene: A holistic representation of the spatial envelope. International Journal of Computer Vision. 2001;42:145–175. [Google Scholar]
- Parkes L, Lund J, Angelucci A, Solomon JA, Morgan M. Compulsory averaging of crowded orientation signals in human vision. Nature Neuroscience. 2001;4:739–744. doi: 10.1038/89532. [DOI] [PubMed] [Google Scholar]
- Pashler H. Familiarity and visual change detection. Perception & Psychophysics. 1988;44:369–378. doi: 10.3758/bf03210419. [DOI] [PubMed] [Google Scholar]
- Phillips WA. On the distinction between sensory storage and short-term visual memory. Perception & Psychophysics. 1974;16:283–290. doi:10.3758/BF03203943. [Google Scholar]
- Potter MC. Short-term conceptual memory for pictures. Journal of Experimental Psychology: Human Learning and Memory. 1976;2:509–522. [PubMed] [Google Scholar]
- Rensink RA, O’Regan JK, Clark JJ. To see or not to see: The need for attention to perceive changes in scenes. Psychological Science. 1997;8:368–373. doi:10.1111/j.1467-9280.1997.tb00427.x. [Google Scholar]
- Simons DJ, Ambinder MS. Change blindness—Theory and consequences. Current Directions in Psychological Science. 2005;14:44–48. [Google Scholar]
- Simons DJ, Chabris CF. Gorillas in our midst: Sustained inattentional blindness for dynamic events. Perception. 1999;28:1059–1074. doi: 10.1068/p281059. doi:10.1068/p2952. [DOI] [PubMed] [Google Scholar]
- Simons DJ, Levin DT. Failure to detect changes to people during a real-world interaction. Psychonomic Bulletin & Review. 1998;5:644–649. [Google Scholar]
- Thorpe S, Fize D, Marlot C. Speed of processing in the human visual system. Nature. 1996;381:520–522. doi: 10.1038/381520a0. [DOI] [PubMed] [Google Scholar]
- Torralba A, Oliva A. Statistics of natural image categories. Network: Computation in Neural Systems. 2003;14:391–412. doi:10.1088/0954-898X_14_3_302. [PubMed] [Google Scholar]
- Watamaniuk SNJ, Duchon A. The human visual-system averages speed information. Vision Research. 1992;32:931–941. doi: 10.1016/0042-6989(92)90036-i. [DOI] [PubMed] [Google Scholar]
- Watamaniuk SNJ, McKee SP. Simultaneous encoding of direction at a local and global scale. Perception & Psychophysics. 1998;60:191–200. doi: 10.3758/bf03206028. [DOI] [PubMed] [Google Scholar]
- Watanabe K. Differential effect of distractor timing on localizing versus identifying visual changes. Cognition. 2003;88:243–257. doi: 10.1016/s0010-0277(03)00025-8. [DOI] [PubMed] [Google Scholar]
- Williams DW, Sekuler R. Coherent global motion percepts from stochastic local motions. Vision Research. 1984;24:55–62. doi: 10.1016/0042-6989(84)90144-5. doi:10.1016/0042-6989(84)90144-5. [DOI] [PubMed] [Google Scholar]