Decomposing Noise in Biochemical Signaling Systems Highlights the Role of Protein Degradation

Abstract

Stochasticity is an essential aspect of biochemical processes at the cellular level. We now know that living cells take advantage of stochasticity in some cases and counteract stochastic effects in others. Here we propose a method that allows us to calculate contributions of individual reactions to the total variability of a system’s output. We demonstrate that reactions differ significantly in their relative impact on the total noise and we illustrate the importance of protein degradation on the overall variability for a range of molecular processes and signaling systems. With our flexible and generally applicable noise decomposition method, we are able to shed new, to our knowledge, light on the sources and propagation of noise in biochemical reaction networks; in particular, we are able to show how regulated protein degradation can be employed to reduce the noise in biochemical systems.

Introduction

Living cells need to constantly adapt to their changing environment. They achieve this through finely honed decision-making and stress response machineries that regulate and orchestrate the physiological adaptation to new conditions. In all studied genomes, a large number of proteins have as their primary function the transfer and processing of information. Such proteins are linked through a host of different mechanisms into biochemical circuits that perform a variety of information processing tasks including storage, amplification, and integration of, and marshalling the response to, environmental and physiological signals (1). The functioning of these information-processing networks depends on thermal or probabilistic encounters between molecules, resulting in a distortion of transferred information that is best understood as noise. Each reaction in the information processing machinery leads to an inevitable loss of information (2). Therefore, cell functions do not only rely on the necessity to make good decisions, but also on appropriate ways to cope with the uncertainties arising from the noisy signal transmission. To deal with the latter type of difficulty, we believe, evolution equipped cells with reliable signal transduction systems by using less noisy reactions or reaction configurations where needed (3).

The question which molecular species or parts of a network contribute most of the variability of a system or are responsible for most of the information loss has therefore attracted much attention in recent years. Numerous studies have analyzed noise in signaling networks in detail (4,5) and decomposed the noise into contributions attributable to fluctuations in mRNA and protein levels (6–11). Although many of these studies afford detailed and nontrivial insights into the origins of stochasticity, in total they provide us with a patchwork of different theoretical analyses: to our knowledge, a robust and sufficiently general mathematical framework to study this problem has been lacking. The lack of a more general formalism, has for example, led to repeated analyses of the roles of transcriptional and translational processes, whereas comparatively little attention has been paid to, e.g., the roles of activation and degradation steps in the stochasticity of biological signaling dynamics.

Here we present a unified theoretical perspective that allows us to calculate contributions of individual reactions to the total variability of the outputs of biochemical systems. This enables us to identify the origins of cell-to-cell variability in dynamical biochemical systems that allow us to pinpoint—if warranted—individual reactions. We derive a modified fluctuation-dissipation theorem that enables us to determine how much of the total variance results from each of the system’s reactions. We then obtain some unexpected but general rules governing the noise characteristics of biochemical systems. In particular, we shall show that in an arbitrary system with a sufficiently large number of molecules, degradation of the output (e.g., a reporter protein or a transcription factor) makes a (and frequently the) major contribution to the total variance of the system: the variance contribution of this single reaction equals at least half of the output's mean (i.e., contribution to the Fano factor is ≥0.5). More specifically, for the important class of open conversion systems, exactly half of the variance derives from the degradation step of the output signal. These results demonstrate that some reactions may be responsible for higher information loss than others; but our results also reveal that cells have the option of optimizing biochemical network structures to avoid the noisiest reactions if necessary. Based on these results, we propose a mechanism of controlled protein degradation based on a positive feedback that, combined with negative feedback on protein production, allows for an arbitrary reduction in the noise resulting from protein degradation.

Below we first introduce the general framework for modeling chemical reactions and derive a new, to our knowledge, method to decompose the noise in a biochemical system into contributions from different individual reactions. Furthermore, two general properties governing noise are presented. Finally, we use biological examples of signal transduction systems to provide novel, to our knowledge, insights into the origins of variability. In particular, we decompose the variance of the outputs of linear transduction cascades and Michaelis-Menten enzyme kinetics.

Results

Mathematical decomposition of molecular noise

We consider a general system of n chemical species (12) inside a fixed volume with x = (x₁,…,x_n)^T denoting the number of molecules. The stoichiometric matrix

$$S={\left\{s_{ij}\right\}}_{i=1,2,\dots ,n;j=1,2,\dots ,r}$$

describes changes in the population size due to r different reaction channels, where each s_ij describes the change in the number of molecules of type i from x_i to x_i + s_ij caused by the jth. The probability that the jth reaction occurs during the time interval [t,t + dt) equals f_j(x,t)dt, where the f_j(x,t) values are called the transition rates. This specification leads to a Poisson birth-and-death process described by the stochastic equation (13),

$$x\left(t\right)=x\left(0\right)+\sum _{j=1}^r{S}_{·j}{N}_j\left(\underset{0}{\overset{t}{\int }}{f}_j\left(x\left(s\right),s\right)ds\right),$$ (1)

where N_j are independent Poisson processes with rate 1.

Unfortunately, it is in general technically difficult to develop an analytical framework using the Poisson birth-and-death process’s formalism of Eq. 1, and the linear noise approximation (LNA) (12,14) offers a reliable alternative. Here, we show that the LNA allows us to calculate the contributions of individual reactions to the total variability of a biomolecular system, and illustrate how we can express the existing methodologies of noise decomposition (6–11) in a unified and more generally applicable framework.

The LNA allows us to model stochastic systems using stochastic differential equation which depend on Wiener processes, (W_j(s)), instead of Poisson processes, (N_j(s)) (12,14–16). It is valid for systems with a sufficiently large number of interacting molecules (14) and therefore imposes a limitation on the applicability of our method. Validity of the approximation is discussed in the further section. In the LNA the system’s state, x(t), is decomposed into a deterministic part φ(t) and a stochastic part ξ(t),

$$x\left(t\right)=\phi \left(t\right)+\xi \left(t\right).$$ (2)

Here φ(t) and ξ(t) are described by the deterministic and stochastic differential equations, respectively. The contributions from the noise are all subsumed in ξ(t), and we can solve for this (see the Experimental Methodology). Once we have this solution we can calculate the variance in the output, denoted here by Σ(t), and in the Experimental Methodology we show that this can be written as

$$\text{Σ}\left(t\right)={\text{Σ}}^{\left(1\right)}\left(t\right)+\dots +{\text{Σ}}^{\left(r\right)}\left(t\right),$$ (3)

where Σ⁽ⁱ⁾(t), for i = 1,…,r, is the contribution to the overall system noise (see Fig. 1 A) that results from the ith reaction. This is a perhaps surprisingly simple relationship which holds generally and which allows us to identify those reactions that contribute most to the overall noise in biochemical systems.

Figure 1.

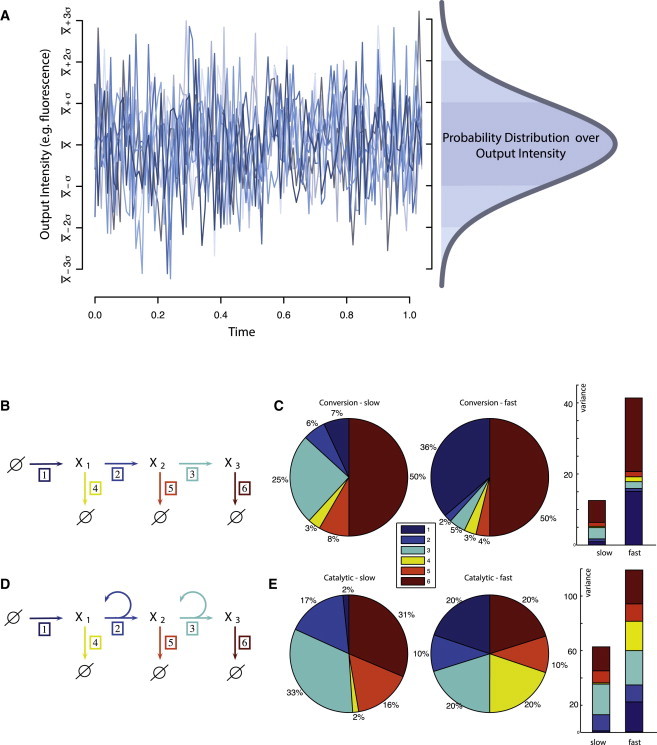
(A) Ten illustrative output trajectories representing stochastic dynamics of a hypothetical system. The observed intensity (e.g., experimentally measured fluorescence) exhibits stochastic dynamics, which results from each of the reactions present in the system. Equation 3 allows us to dissect the total variability. Decomposition describes how much of the observed variability is generated by each of the involved reactions. On the right-hand side is the probability distribution of system outputs, the variance of which is considered in our decomposition. (B) Three-step open conversion system with rates f_j for reactions j = 1,…, 6 have the form f₁ = k⁺₁, f₂ = k⁺₂x₁, f₃ = k⁺₃x₂, f₄ = k⁻₄x₁, f₅ = k⁻₅x₅, and f₆ = k⁻₆x₆. (C) Variance contributions of the different reactions in the three-step linear conversion system with parameters k⁺₁ = 50, k⁺₂ = 1, k⁺₃ = 1, k⁻₄ = 1, k⁻₅ = 1, and k⁻₆ = 1 or the slow conversion example, and k⁺₁ = 50, k⁺₂ = 10, k⁺₃ = 10, k⁻₄ = 1, k⁻₅ = 1, and k⁻₆ = 1 for the fast conversion case; all rates are per hour. (D) Three-step open conversion system with rates f_j as in panel B. (E) Variance contributions of the different reactions in the three-step linear catalytic cascade with parameters k⁺₁ = 50, k⁺₂ = 0.1, k⁺₃ = 0.1, k⁻₄ = 1, k⁻₅ = 0.1, and k⁻₆ = 0.1, for slow catalysis, and k⁺₁ = 50, k⁺₂ = 10, k⁺₃ = 10, k⁻₄ = 1, k⁻₅ = 10, and k⁻₆ = 10 for fast reactions.

Simple signaling cascades and exact results

With the decomposition equation (Eq. 3), it is, in principle, possible to attribute the contribution each reaction makes to the output variability of a biochemical reaction system. To illustrate what can be gained from such insights, we first consider conversion and catalytic linear cascades before moving on to more general reaction schemes. By catalytic cascades we mean cascades where each chemical entity catalyses creation of a downstream species. We start with cascades of length 3 and decompose variances numerically to study the contributions of individual intermediate reactions. For conversion cascades (Fig. 1 B), where molecules x₁ are generated at a certain rate k₁⁺ and information is transmitted to molecules x₃ using (possibly reversible) conversion reactions, we use two parameter sets corresponding to fast and slow conversions to demonstrate that increasing the rates of intermediate steps decreases their contribution as might intuitively be predicted (Fig. 1 C). For catalytic cascades (Fig. 1 D), increasing the rates of reactions at steps 2 and 3 (going from slow to fast) increases the contribution of reactions at the bottom of the cascades (Fig. 1 E). For slow dynamics during Steps 2 and 3, the relatively fast fluctuations at the start are filtered out (low-pass filtering). If the dynamics of all species occur at similar timescales then these fluctuation can efficiently propagate downstream.

Regardless of parameter values, Fig. 1, C and E, suggests a special role of the output degradation reactions, which appear to make dominant contributions to the overall noise. As we will demonstrate below, this observation holds also for very generic signaling systems; we can even prove two general propositions that assign surprisingly substantial contributions to the overall output noise to the reaction that describes the degradation of the output signal and these results can be made mathematically precise and hold for the Chemical Master Equation without the LNA (see the Experimental Methodology for proofs and details). Under suitably general conditions (such as the single stable equilibrium state of the corresponding deterministic system) we have the following two results:

Proposition 1

If x_n is an output of a general system being produced at rate not dependent on itself and degraded in the rth reaction at rate k_n⁻x_n, then the contribution of the output’s degradation to the total variance of the output is equal to the half of its mean; more specifically,

$${\left[{\text{Σ}}^{\left(r\right)}\right]}_{nn}=\frac{1}{2}\langle x_n\rangle .$$ (4)

Proposition 2

Now consider again a general system, but make the further assumption that it is an open conversion system where reaction rates are of mass action form and that only three types of reactions are allowed:

$$\text{Production}\text{from}\text{source:}\text{∅}\stackrel{k_i^{+}}{\to }{x}_i,$$

$$\text{Degradation:}{x}_i\stackrel{k_i^{-}}{\to }\text{∅},$$

$$\text{Conversion:}{x}_i\stackrel{k_{ij}{x}_i}{\to }{x}_j.$$

In this special case of a conversion pathway, regardless of parameter values, length of the pathway, and degradation of intermediates, the degradation of the output x_n, rather unexpectedly, contributes exactly half of the total variance of the system’s output,

$${\left[{\text{Σ}}^{\left(r\right)}\right]}_{nn}=\frac{1}{2}{\left[\text{Σ}\right]}_{nn},$$ (5)

where r is again the index of the output’s degradation reaction.

These propositions can be understood as balancing the contributions made to the overall noise by the production and degradation reactions. As exemplified in the next section, at equilibrium the fluctuations from birth and death processes must be equal. If the variance of the output is greater than the mean, this statement translates into Proposition 1, in case of the variance equal to the mean into the statement that half of the noise is attributable to the degradation. By hindsight the relative contributions of production and degradation steps to the overall variability in the output noise may seem obvious. However, to our knowledge, this question had previously not been asked, and instead the literature is replete with discussions of the impact of, e.g., transcription and translation on biomolecular noise.

The variance is, of course, only one measure of variability. The Fano factor, F = σ²/μ (where μ is the population average of the random variable under consideration), is a closely related measure and our analysis in Propositions 1 and 2 yields a unified, parameter-free statement, which holds generally for the Chemical Master Equation without the LNA assumption,

$$F_n^{\left(r\right)}=\frac{1}{2},$$ (6)

for any general reaction systems with linear rate of output production (i.e., Propositions 1 and 2).

The decomposition can be directly inserted into the equation for the Fano factor. Hence Propositions 1 and 2 can be expressed in a unified way in terms of the Fano factor as for open conversion systems: ${\left[{\text{Σ}}^{\left(r\right)}\right]}_{nn}=\langle x_n\rangle$. Thus, the Fano factor associated with the system output will be approximately equal to 1/2 for many signaling systems.

For the coefficient of variation, c_v = σ/μ, a further popular measure of divergence, our decomposition can also be applied but only yields numerical values for the standard deviation,

$$\sigma =\sqrt{\text{Σ}}=\sqrt{{\text{Σ}}^{\left(1\right)}\left(t\right)+\dots +{\text{Σ}}^{\left(r\right)}\left(t\right)}.$$

Our observation is particularly interesting as open conversion systems often offer good approximations to important biochemical reactions such as Michaelis-Menten enzymatic conversions or linear signal transduction pathways, to which we return below; more intriguingly, perhaps, our results also suggest that controlled degradation is an effective mechanism to decrease the overall contribution to variation in protein levels.

Michaelis-Menten enzyme kinetics

Michaelis-Menten kinetics are used to model enzymatic types of biochemical reactions: enzyme molecules (E) bind reversibly to substrate molecules (S) with the forward rate constant k₀ and the backward rate constant k₁ to form a complex (C), which then falls apart into the enzyme and a product (P) at rate k₂:

$$E+S\underset{k_1}{\overset{k_0}{\rightleftharpoons }}C\stackrel{k_2}{\to }E+P.$$

To ensure existence of the steady state, we assume that substrate molecules arrive at rate k_b and product molecules are degraded at rate k_d. At the unique steady state, the system is well approximated by a linear conversion cascade. Our theory therefore predicts that half of the noise in Michaelis-Menten kinetics operating in its linear range (abundant enzyme) is generated by degradation of the product molecules. In Fig. 2 we have calculated the contributions of each of the four reactions to the variance of all four species for the full model (without the monomolecular approximation). The contribution of the output degradation is as predicted by the monomolecular approximation. Note that for each molecular species there is a balance between the contributions to their respective variances resulting from the incoming and outgoing reactions. This simply reflects that we can treat each molecular species as a potential output, whence our statements from above apply.

Figure 2.

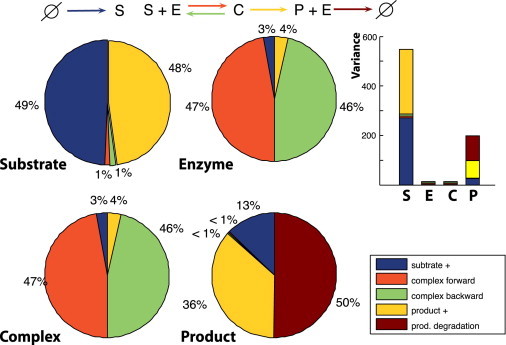
Variance decomposition for the four species of the Michaelis-Menten kinetics model. The following parameters were used: k₀ = 0.1, k₁ = 50, k₂ = 1, k_b = 20, and k_d = 0.1. Number of enzyme molecules was set to 50. All rates are per hour.

Protein expression

The canonical example of a linear catalytic pathway, which has been widely explored in the context of noise decomposition (2,6,7,9–11), is gene expression. It can simply be viewed as the production of RNA (x₁) from source (DNA) at rate k₁⁺, and production of protein (x₂) in a catalytic reaction at rate k₂x₁, together with first-order degradation of both species at rates k₁⁻x₁ and k₂⁻x₂. Here we use this model to demonstrate the applicability of our framework by revisiting earlier studies of Paszek (9), Paulsson (10), and Rausenberger and Kollman (11), which reported noise contributions arising at each level of expression (promoter state fluctuations, transcription, translation). Proposition 1 states that the part of the variance resulting from the protein degradation equals half of the mean protein level, and Eq. 3 allows us to derive the complete decomposition of the protein, x₂, variance

$${\text{Σ}}_{x_2}=\underset{\text{prot}.\text{degradation}}{\underbrace{\frac{1}{2}\langle x_2\rangle }}+\underset{\text{translation}}{\underbrace{\frac{1}{2}\langle x_2\rangle }}+\underset{\text{mRNA degradation}}{\underbrace{\frac{1}{2}\frac{k_p\langle x_2\rangle }{{\gamma }_r+{\gamma }_p}}}+\underset{\text{transcription}}{\underbrace{\frac{1}{2}\frac{k_p\langle x_2\rangle }{{\gamma }_r+{\gamma }_p}}}.$$ (7)

In Fig. 3 A, we consider a slightly more general model, where we also consider activation of the protein through phosphorylation and corresponding deactivation through dephosphorylation; both kinase and phosphatase are assumed to be abundant and their respective activities assumed to be constant. Fig. 3, B–D, exemplifies how the noise in the output (active protein) changes as dephosphorylation gains in importance. Increasing the rate of dephosphorylation slightly decreases the relative contribution made to the output signal that results from transcription (R1), translation (R3), and mRNA and (inactive) protein degradation (R2 and R4, respectively); these decreases are compensated for by a marked increase to the system output noise resulting from the phosphorylation. This, too, is in line with intuition suggesting that increasing later rates must decrease the contribution resulting from earlier reactions.

Figure 3.

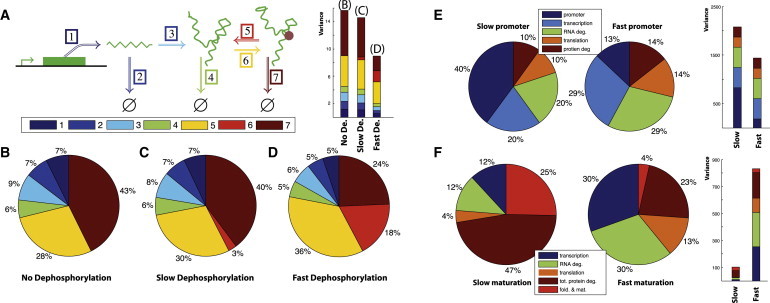
(A) Illustration of a protein expression and activation system with seven reactions; mRNA, protein, and activated protein are described in terms of their production, degradation, and potentially reversible (de-)activation through (de-)phosphorylation through kinases and phosphatases. (B) Variance decomposition of the noise in the output (active protein) when activation is not reversible. (C) Output variance decomposition for slow dephosphorylation. (D) Output variance for decomposition for fast dephosphorylation. For panels A–C, we use the following parameters: k⁺₁ = 40, k⁻₁ = 2, k⁺₂ = 2, and k⁻₂ = 1; for (A) k_phos = 0.5 and k_dephos = 0; for (B) k_phos = 0.5 and k_dephos = 0.1; for (C) k_phos = 0.5 and k_dephos = 1. (E) Contributions to the variance of the reactions involved in gene expression with fluctuating promoter states; here the transcription rate is modeled as $k_1^{+}=\left(Vy/H\right)/\left(1+y/H\right)$, and y denotes the stationary solution of $dy=\left(b-\gamma y\right)dt+\sqrt{2\gamma }dW$. The following parameters were used: V = 100, H = 50, k⁺₂ = 2k⁻₁ = 0.44, and k⁻₂ = 0.55. For fast promoter fluctuations we used b = 50 and γ = 1, and for slow promoter fluctuations we used b = 0.5 and γ = 0.01. (F) Variance contributions of the reactions involved in fluorescent protein maturation model for slowly (left) and quickly (right) maturing proteins (slow and fast proteins). The following parameters were used: k⁺₁ = 50, k⁻₁ = 0.44, k⁺₂ = 2, and k⁻₂ = 0.55. For slow maturation (average maturation time ≈ 5 h) we assumed folding and maturation rates to be k_f = 0.2 and k_m = 1.3, respectively. For fast maturation (average maturation time ≈ 0.5 h) we set k_f = 2.48 and k_m = 13.6. All rates are per hour.

To illustrate applicability of this framework further, we also investigate two extensions of the conventional protein expression model:

First, we assume that the promoter can fluctuate between on- and off-states (similarly to Paszek (9) and Rausenberger and Kollman (11)) and calculate contributions for different timescales of these fluctuations, but focusing on protein levels per se (rather than just active protein).

Second, we assume that the protein is a fluorophore that undergoes a two-step maturation process before it becomes visible (folding and joint cyclization with oxidation). Fig. 3 E presents contributions for fast and slow promoter kinetics, showing that fast fluctuations are effectively filtered out (contributing 10%) but remain a substantial contributor when they are slow (contributing 40%).

Variability in gene expression is often measured by means of fluorescent proteins that undergo maturation before becoming visible for detection techniques; but the process of maturation (17) itself is subject to stochastic effects, and can thus contribute significantly to the observed variability. We used typical parameters (17,18) for fast and slow maturing fluorescent proteins and found that maturation contributed 4 and 25%, respectively (Fig. 3 F) to the overall variability; here our method allows for the rigorous quantification of the effect’s single reactions, compared to previous analyses of steady-state statistics which were only able to consider the total noise levels (19,20).

Reducing the Contribution of Degradation Noise

Our mathematical results and examination of the examples above demonstrate that the noise resulting from the degradation of the output of a biochemical reaction system accounts for a substantial fraction of the output variability. An effective mechanism of noise suppression, therefore, should take this observation into account. One possibility to control noise attributable to the degradation reaction is to control its rate using a positive feedback loop. The consequences of a controlled degradation had previously only been discussed in the context of biochemical noise and compared with the negative feedback loop on production (21).

Here we propose the simple extension of a positive feedback loop on the degradation reaction, taking into account that our propositions arise on the grounds of the equilibrium noise balance between production and degradation. In any system at equilibrium the rates of the production and degradation reactions have to equal. The noise resulting from each of these reactions, as directly related to the rate, can be attenuated only if both equilibrium rates are simultaneously reduced. Therefore, combination of the positive feedback loop (21) on degradation with the negative feedback on production is more efficient than either of these loops separately. This is not only because the control is tighter but, importantly, also because intensity of these reactions at equilibrium is reduced.

For illustration and simplicity we consider a simple birth-and-death process, but the same mechanism is valid for general systems considered in Proposition 1. Here molecules x arrive at rate k⁺ and degrade at rate k⁻x. In the LNA this process can be expressed by the following stochastic differential equation:

$$dx=\left(k^{+}-k^{-}x\left(t\right)\right)dt+\underset{\text{birth noise}}{\underbrace{\sqrt{k^{+}}d{W}_1}}+\underset{\text{death noise}}{\underbrace{\sqrt{k^{-}\langle x\left(t\right)\rangle }d{W}_2}}.$$ (8)

The stationary distribution of this system is Poisson with the mean $\langle x\rangle =k^{+}/k^{-}.$ Therefore, in the stationary state, death events occur at rate k⁻〈x〉, which must be equal to the birth rate k⁺. The noise terms in the above equation are equal at stationarity, indicating that contributions of birth-and-death reactions are equal. It is straightforward to verify that the decomposition

$$\text{Σ}=\underset{\text{birth noise}}{\underbrace{\frac{1}{2}\langle x\rangle }}+\underset{\text{death noise}}{\underbrace{\frac{1}{2}\langle x\rangle }}$$ (9)

holds indeed.

Now suppose that the births and deaths rates are denoted by f(x) and g(x), respectively, and the system is described by

$$dx=\left(f\left(x\right)-g\left(x\right)\right)dt+\underset{\text{birth noise}}{\underbrace{\sqrt{f\left(\langle x\rangle \right)}d{W}_1}}+\underset{\text{death noise}}{\underbrace{\sqrt{g\left(\langle x\rangle \right)}d{W}_2}}.$$ (10)

At equilibrium, we have f(〈x〉) = g(〈x〉), and we can calculate that contribution of degradation as

$${\text{Σ}}^{\left(\text{death}\right)}=\frac{\frac{1}{2}g\left(\langle x\rangle \right)}{-\frac{\partial f\left(\langle x\rangle \right)}{\partial x}+\frac{\partial g\left(\langle x\rangle \right)}{\partial x}}.$$ (11)

For f(x) = k, g(x) = γx, this reduces, of course, to the previously discussed case ${\text{Σ}}^{\left(\text{death}\right)}=1/2\langle x\rangle$. Nevertheless, if functions f and g are of Hill and Michaelis-Menten types, respectively, then the contribution is related to the mean through functions f and g, and can be reduced to an arbitrary low level according to the above equation. Unlike in the single feedback loop mechanism (21) any decrease in the contribution compared to the mean results here from two sources: the reduced flux through both reactions, represented by the numerator in Eq. 11); and the autoregulatory control, represented by the derivatives in the denominator. The effects of the combined production and degradation control loops are depicted in Fig. 4.

Figure 4.

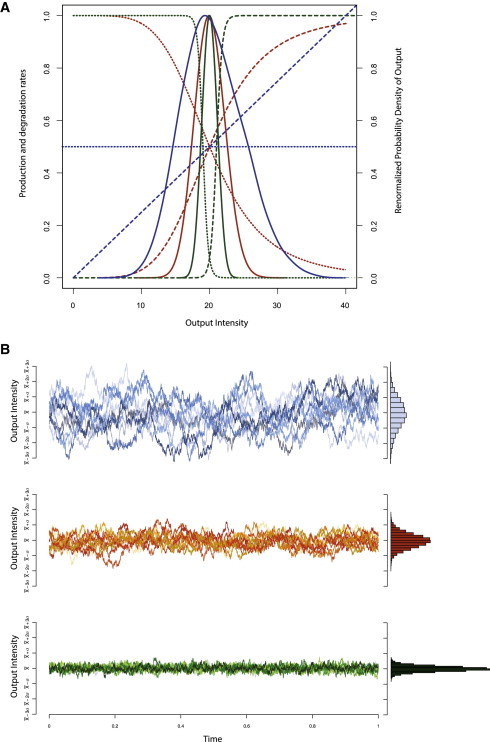
(A) The effect of noise reduction resulting from regulated degradation. The line styles describe production rate f(x) (dotted line), degradation rate (dashed line) and density of stationary distribution of x (solid line). (Blue) f(x) = 1/2 and g(x) = 0.025x. (Black) f(x) = 1/(1 +(x/20)⁵) and g(x) = (x/20)⁵/(1 + (x/20)⁵). (Green) f(x) = 1/(1 +(x/19)⁵⁰) and g(x) = (x/21)⁵⁰/(1 + (x/22)⁵⁰). Plotted densities are kernel density estimates based on 10,000 independent stationary samples generated using Gillespie’s algorithm (27). (B) Ten trajectories sampled for unregulated degradation (top, corresponding to blue curve in panel A), regulated (middle, corresponding to black in panel A), and tightly regulated (bottom, corresponding to green in panel A); on the right-hand side of the trajectories are the probability distributions over system outputs.

Recent experimental work on mRNA and protein degradation provides the evidence that degradation indeed exhibits Michaelis-Menten type kinetics (22,23), instead of the linear first-order kinetics that are usually used to model degradation. Although the above mechanism provides theoretical prescription for noise reduction, the biophysical implementation of functions f and g may need additional auxiliary reaction steps and reactants, and these additional reactions will contribute new sources of stochasticity. These sources, however, can be driven arbitrarily low by assuming that the auxiliary molecular species are present in very high numbers (2). Therefore identification of noisy reactions is important for our understanding of how (and if) resources might have been invested to achieve low noise levels in molecular systems.

Validity of the Obtained Results

Conclusions of Propositions 1 and 2 followed by the unified, parameter-free statement Eq. 6 hold in the setting of Markov processes modeled by the Chemical Master Equation. These statements are therefore limited only by the linear form of the degradation rate.

The developed noise decomposition method is based on the LNA and its applicability is strictly related to its range of validity. LNA is appropriate to model systems with large number of reacting molecules and is an analogy of the central limit theorem for Markov jump processes defined by The Master Equation. The main condition that ensures validity of the LNA is large size of studied systems. In small systems the approximation will begin to break down, because the count noise will result in the covariance of variables greater than that predicted by the LNA. Moreover in the nonlinear systems, the deterministic variable in the LNA is not exactly the mean value of the stochastic process it approximates. In bistable systems for instance the LNA will arrive at one stable point, but the mean will be affected by time spent at the other stable point. Although the LNA was originally designed to analyze systems at a steady state, it can also be applied out-of-steady-state given that the Jacobian of the deterministic equation has negative eigenvalues. A recent study (24) provides a new insight on LNA’s range of validity and supports its applicability to systems studied in the article.

Discussion

The noise decomposition method introduced here allows us to investigate in detail where and how noise enters biochemical processes, is propagated through reaction systems, and affects cellular decision-making processes. We have shown analytically that in a wide class of systems the signal degradation reaction contributes half of the noise in a system’s output regardless of parameter values. Our approach is, of course, much more widely applicable and does allow us to disentangle the different contributions to system output resulting from the different reactions in a system. Here we have shown (especially easy to see in Michaelis-Menten kinetics and the protein expression examples shown in Figs. 2 and 3, respectively) that changing the rates of individual reactions affects also the overall contributions stemming from the remaining reactions.

Set against these system-level properties of noise the wide applicability of Propositions 1 and 2 is really rather remarkable; to the best of our knowledge this has not been noted before. From the illustrative examples discussed above it is clear that even if the premises of Propositions 1 and 2 do not hold exactly, they still provide a rule of thumb (i.e., that the Fano factor of degradation is typically 1/2) as to how the noise in a system output—be it protein expression levels, protein activity (in particular transcription-factor activity), or metabolite concentrations—is affected qualitatively by the respective contributions resulting from production and degradation steps. In particular, the exalted role played by degradation has thus far not attracted the interest that it probably deserves.

This has indeed been the central biological result that we found and report here: the crucial role of degradation of the signal on the overall noise levels. The relevance of degradation has been observed before in the context of stochastic biochemical dynamics (7,21) but their exact contribution, to our knowledge, had not previously been quantified. In general, it is difficult to think of an experiment that would allow us to measure a contribution of any individual reaction to the overall variability. However, for the degradation reaction one possibility is to construct a nondegradable fluorescent protein and remove the fluorescent signal by photobleaching. In such a system only arrival events are registered. The comparison of the wild type noise with a nondegradable fluorescent protein mutant has the potential to reveal the contribution of the degradation reaction to the overall noise.

From our analysis emerge also means of controlling the overall noise in protein expression levels, which will, among other things, give rise to cell-to-cell variability among genetically identical cells. Targeting proteins for proteasomal degradation via polyubiquitination is an inherently cooperative process and increasing cooperativity will change, as shown in Fig. 4, the level of variability. In particular an increase—concomitant with an increase in the Hill coefficient—will lead to a decrease of the noise in protein expression; depending on the nature of the protein such diminishing variability should also affect levels of heterogeneity among a population of cells. In comparison, however, to phosphorylation dynamics that have been elucidated in increasingly exquisite detail and at the level of individual cells, the dynamics of polyubiquitination, to our knowledge, have thus far not been characterized at single cell levels.

Our method allow for a more complete understanding of previous findings on fluctuations in biochemical networks. For instance the independent fluctuations in nodes of a large class of metabolic networks (25) can be attributed in half to the arrival and departure events. In the context of noise suppression mechanism constituted by two feedback loops, proposed here, it is interesting to ask if the noise limits derived for feedback the loop on production (2) can be improved. Our results reveal that the experimental findings of nonlinear degradation rates (23) may have consequences for noisiness of biochemical networks and point out that a complete picture of stochasticity in biochemical networks must include experimental verification of stochasticity in proteolytic processes.

The surprisingly high contribution is particularly important as it may indicate potentially new therapeutic targets: in humans and other sequenced organisms, certainly, the repertoire of proteins involved in protein degradation, in particular ubiquitin-ligases, is as rich and diverse as the repertoire of proteins regulating their activation—the kinases (and phosphatases). Thus targeting the degradation of proteins appears as important to biological systems as protein activation and offers an attractive and broad range of new potential therapeutic targets. Quite generally, the ability to dissect noise propagation through biological systems does enable researchers better to understand the role of noise in function (and evolution), and will also enable synthetic biologists to either harness or dampen the effects of noise in molecular signaling and response networks.

Experimental Methodology

Mathematical derivation of noise decomposition

To define the contribution of the jth reaction (j = 1,…,r) to the variability of x(t) we first define 〈x(t)〉_(−j) as the expectation of x(t) conditioned on the processes N₁(t),…, N_j−1(t), N_j+1(t),…, N_r(t), so that 〈x(t)〉_(−j) is a random variable where timings of reaction j have been averaged over all possible times, keeping all other reactions fixed. Therefore x(t) − 〈x(t)〉_|−j is a random variable representing the difference between the native process x(t) and a process with averaged timings of jth reaction. Now the contribution of the jth reaction to the total variability of x(t) is

$${\text{Σ}}^{\left(j\right)}\left(t\right)\equiv \langle \left(x\left(t\right)-{\langle x\left(t\right)\rangle }_{|-j}\right){\left(x\left(t\right)-{\langle x\left(t\right)\rangle }_{|-j}\right)}^T\rangle ,$$ (12)

where 〈…〉 denotes the average over timings of all r reactions. This definition is similar to the one proposed in Eq. 11 to quantify the contributions of promoter states and mRNA fluctuations, respectively, to the protein level variability.

Unfortunately, in general, it is difficult (Eq. 11) to calculate or study properties of Eq. 12 using a Poisson birth-and-death process framework in Eq. 1. We note, however, that by using the LNA for the contributions from Eq. 12, it can be very easily calculated.

In the LNA the system’s state, x(t), is decomposed into a deterministic part φ(t) and a stochastic part ξ(t) described by the deterministic and stochastic differential equations

$$\phi \left(t\right)=\phi \left(0\right)+\underset{0}{\overset{t}{\int }}SF\left(\phi \left(s\right),s\right)ds,$$ (13)

$$\xi \left(t\right)=\xi \left(0\right)+\underset{0}{\overset{t}{\int }}A\left(\phi \left(s\right),s\right)\xi \left(s\right)ds+\sum _{j=1}^{r}S·j{W}_j\left(\underset{0}{\overset{t}{\int }}\sqrt{f_j\left(\phi \left(s\right),s\right)}ds\right),$$ (14)

respectively, and their coefficients are given by

$$F\left(\phi ,t\right)={\left(f_1\left(\phi ,t\right),\dots ,f_r\left(\phi ,t\right)\right)}^T$$ (15)

and

$${\left\{A\left(\phi ,t\right)\right\}}_{ik}=\sum _{j=1}^r{s}_{ij}\frac{\partial f_j\left(\phi ,t\right)}{\partial {\phi }_k}.$$ (16)

The above framework presents a simple way to compute contributions Σ_(j)t, and here we demonstrate how the total variance can be decomposed into the sum of individual contributions. To simplify notation, from now on we will write A(t) and E(t) instead of A(φ,t) and E(φ,t), respectively.

We write the explicit solution for the process ξ as

$$\xi \left(t\right)=\text{Φ}\left(0,t\right)\xi \left(0\right)+\underset{0}{\overset{t}{\int }}\text{Φ}\left(s,t\right)E\left(\phi ,s\right)dW\left(s\right),$$ (17)

and $E\left(\phi ,t\right)=S\text{diag}\left(\sqrt{f_1\left(\phi ,t\right))},\dots ,\sqrt{(f_r\left(\phi ,t\right)}\right),$ where Φ(s,t) is the fundamental matrix of the nonautonomous system of ordinary differential equations

$$\frac{d\text{Φ}\left(s,t\right)}{dt}=A\left(t\right)\text{Φ}\left(s,t\right),\text{Φ}\left(s,s\right)=I.$$ (18)

Now it is straightforward to verify that

$${\langle \xi \left(t\right)\rangle }_{|-j}=\text{Φ}\left(0,t\right)\xi \left(0\right)+\underset{0}{\overset{t}{\int }}\text{Φ}\left(s,t\right)E^{\left(-j\right)}\left(s\right)dW\left(s\right),$$ (19)

where $E^{\left(-j\right)}\left(t\right)=S^{\left(-j\right)}E\left(t\right),$ $E^{\left(j\right)}\left(t\right)=S^{\left(j\right)}E\left(t\right),$ $S^{\left(-j\right)}={\left\{s_{lk}^{\left(-j\right)}\right\}}_{l=1,\mathrm{..},n,k=1,\dots ,r},$ $S^{\left(j\right)}={\left\{s_{lk}^{\left(j\right)}\right\}}_{l=1,\dots ,n,k=1,\dots ,r},$ and

$$s_{lk}^{\left(-j\right)}=\{\begin{array}{cc}0& \text{for}k=j\\ s_{lk}& \text{for}k\ne j\end{array}{s}_{lk}^{\left(j\right)}=\{\begin{array}{cc}{s}_{lk}& \text{for}k=j\\ 0& \text{for}k\ne j.\end{array}$$

From Eqs. 17 and 19, we have

$$\xi \left(t\right)-{\langle \xi \left(t\right)\rangle }_{|-j}=\underset{0}{\overset{t}{\int }}\text{Φ}\left(s,t\right)E^{\left(j\right)}\left(s\right)dW\left(s\right).$$ (20)

With $x\left(t\right)-{\langle x\left(t\right)\rangle }_{|-j}=\xi \left(t\right)-{\langle \xi \left(t\right)\rangle }_{|-j}$ and the time derivative of $\langle \left(\xi \left(t\right)-{\langle \xi \left(t\right)\rangle }_{|-j}\right){\left(\xi \left(t\right)-{\langle \xi \left(t\right)\rangle }_{|-j}\right)}^T\rangle$, we obtain for Σ^(j)(t)

$$\frac{d{\text{Σ}}^{\left(j\right)}}{dt}=A\left(t\right){\text{Σ}}^{\left(j\right)}+{\text{Σ}}^{\left(j\right)}A{\left(t\right)}^T+D^{\left(j\right)}\left(t\right),$$ (21)

with

$$D^{\left(j\right)}\left(t\right)=E^{\left(j\right)}\left(t\right){\left(E^{\left(j\right)}\left(t\right)\right)}^T.$$ (22)

This is, of course, analogous to the fluctuation dissipation theorem, with the exception that the diffusion matrix contains zeros at all entries not corresponding to the jth reaction. Now the fact that the total variance

$$\text{Σ}\left(t\right)=\langle \left(x\left(t\right)-\langle x\left(t\right)\rangle \right){\left(x\left(t\right)-\langle x\left(t\right)\rangle \right)}^T\rangle$$

can be represented as the sum of individual contributions, Eq. 3,

$$\text{Σ}\left(t\right)={\text{Σ}}^{\left(1\right)}\left(t\right)+\dots +{\text{Σ}}^{\left(r\right)}\left(t\right),$$ (23)

results directly from the decomposition of the diffusion matrix $D\left(t\right)={\sum }_{j=1}^r{D}^{\left(j\right)}\left(t\right)$ and the linearity of the equation for Σ(t), given by the standard fluctuation dissipation theorem

$$\frac{d\text{Σ}}{dt}=A\left(t\right)\text{Σ}+\text{Σ}A{\left(t\right)}^T+D\left(t\right).$$ (24)

Proof of Proposition 1

• 1.
  Interactions of x_n with other species imply that a_ij = 0 for i = 1,…, n − 1, and j = n. Thus matrix A can be written as

  $$A=\left(\begin{array}{cc}\overline{A}& 0\\ a^T& -k_N^{-}\end{array}\right).$$
• 2.
  Equation 23 implies that all elements of matrix D^(r) are equal to 0 except $D_{nn}^{\left(r\right)}=k_n^{(-)}\langle x_n\rangle$, therefore D^(r) has the form

  $$D^{\left(r\right)}=\left(\begin{array}{cc}0& 0\\ 0& k_n^{-}\langle x_n\rangle \end{array}\right).$$
• 3.
  It is straightforward to verify that the n × n matrix

  $${\text{Σ}}^{\left(r\right)}=\left(\begin{array}{cc}0& 0\\ 0& \frac{1}{2}\langle x_n\rangle \end{array}\right)$$ (25)

  satisfies the equation

  $$A{\text{Σ}}^{\left(r\right)}+{\text{Σ}}^{\left(r\right)}{A}^T+D^{\left(r\right)}=0.$$ (26)

Proof of Proposition 2

In an open conversion system Σ_nn = 〈x_n〉 (see, e.g., Gadgil et al. (26)), therefore, from Proposition 1, we have ${\text{Σ}}_{nn}=2{\text{Σ}}_{nn}^{\left(r\right)}.$

Proof of Proposition 1 without the linear noise approximation

Here we present the proof of Proposition 1 in the general setting of Markov jump processes described by the Chemical Master Equation. Denote by z(t) the birth process of the final product of our system of reactions, that is, molecules of the nth type (i.e., the process counting the number of births of n-molecules until time t). We assume that z(t) together with the degradation of n-molecules (the final r-type reaction that follows the Poisson process with the intensity γ) generates a stationary mean value. Assume Δz = z(s + Δs) −z(s) is the random variable counting the number of n-molecules born in the time interval [s,s + Δs). If no birth events take place outside [s,s + Δs) the number of n-molecules at the time t is given by the binomial random variable x_n(t) with the probability of success exp(−γ(t – s)); and the following expressions for the conditional mean and the variance of x_n(t) hold:

$${\langle x_n\left(t\right)\rangle }_{|-r}=\text{exp}\left(-\gamma \left(t-s\right)\right)\text{Δ}z,$$

$${\langle {\left(x_n\left(t\right)-{\langle x_n\left(t\right)\rangle }_{|-r}\right)}^2\rangle }_{|-r}=\text{exp}\left(-\gamma \left(t-s\right)\right)\left(1-\text{exp}\left(-\gamma \left(t-s\right)\right)\right)\text{Δ}z.$$

Summing over all intervals in the limit of infinitely small [s,s + Δs), we get

$${\langle x_n\left(t\right)\rangle }_{|-r}=\underset{0}{\overset{t}{\int }}\text{exp}\left(-\gamma \left(t-s\right)\right)dz\left(s\right),$$

$${\langle {\left(x_n\left(t\right)-{\langle x_n\left(t\right)\rangle }_{|-r}\right)}^2\rangle }_{|-r}=\underset{0}{\overset{t}{\int }}\text{exp}\left(-\gamma \left(t-s\right)\right)\left(1-\text{exp}\left(-\gamma \left(t-s\right)\right)\right)dz\left(s\right).$$

Now we average over reactions 1,…,r − 1 hidden in z(t) and get

$$\begin{array}{l}\langle {\langle {\left(x_n\left(t\right)-{\langle x_n\left(t\right)\rangle }_{|-r}\right)}^2\rangle }_{|-r}\rangle =\langle \underset{0}{\overset{t}{\int }}\text{exp}\left(-\gamma \left(t-s\right)\right)\left(1-\text{exp}\left(-\gamma \left(t-s\right)\right)\right)dz\left(s\right)\rangle \\ =\langle \underset{0}{\overset{t}{\int }}\text{exp}\left(-\gamma \left(t-s\right)\right)dz\left(s\right)\rangle -\langle \underset{0}{\overset{t}{\int }}\text{exp}\left(-2\gamma \left(t-s\right)\right)dz\left(s\right)\rangle .\end{array}$$

By definition, the first is the mean of a process x_n(t) with degradation rate γ and the second is the mean of a version of the process x_n(t) with degradation rate 2γ. We have the Fano factor

$$F_n^{\left(r\right)}\left(t\right)=1-\frac{\langle \underset{0}{\overset{t}{\int }}\text{exp}\left(-2\gamma \left(t-s\right)\right)dz\left(s\right)\rangle }{\langle \underset{0}{\overset{t}{\int }}\text{exp}(-\gamma (t-s)\rangle }.$$

In the stationary state, the mean of the process x_n(t) with degradation rate γ is exactly twice of the mean of a version of the process x_n(t) with degradation rate 2γ, therefore

$$F_n^{\left(r\right)}=\frac{1}{2}\text{in}\text{the}\text{limit}t\to \mathrm{\infty }.$$