Anomalous Diffusion of Single Particles in Cytoplasm

Abstract

The crowded intracellular environment poses a formidable challenge to experimental and theoretical analyses of intracellular transport mechanisms. Our measurements of single-particle trajectories in cytoplasm and their random-walk interpretations elucidate two of these mechanisms: molecular diffusion in crowded environments and cytoskeletal transport along microtubules. We employed acousto-optic deflector microscopy to map out the three-dimensional trajectories of microspheres migrating in the cytosolic fraction of a cellular extract. Classical Brownian motion (BM), continuous time random walk, and fractional BM were alternatively used to represent these trajectories. The comparison of the experimental and numerical data demonstrates that cytoskeletal transport along microtubules and diffusion in the cytosolic fraction exhibit anomalous (nonFickian) behavior and posses statistically distinct signatures. Among the three random-walk models used, continuous time random walk provides the best representation of diffusion, whereas microtubular transport is accurately modeled with fractional BM.

Introduction

Diffusion plays a fundamental role in every biochemical process in living cells. Just as essential for intracellular transport is cytoskeletal migration, which includes all motor protein-mediated transport. Characterizing and distinguishing these and other transport mechanisms within a cell is critical to understanding cellular function. Topologic complexity of crowded intracellular space renders mathematical representations of processes as basic as molecular diffusion problematic. Whereas some studies (1,2) relied on Brownian motion to represent intracellular diffusion, others (3,4) found evidence of anomalous (nonFickian) diffusive behavior that requires the use of more evolved random walk models (e.g., fractional Brownian motion and continuous time random walk, described below).

Modeling cytoskeletal transport is even more challenging, because it involves a complex interplay of various mechanisms. These include the variety of molecular motors that traverse the cytoskeleton (5,6), cytoskeleton self-assembly kinetics (7,8), and the interaction between microtubule and actin filament transport (9,10). Many of these processes are fundamentally different from Fickian diffusion, and initial work has successfully modeled cytoskeletal transport as anomalous diffusion (11,12). A major goal of our analysis is to extend this knowledge by elucidating the underlying processes from single-particle measurements and to identify useful modeling tools for future efforts.

An immediate impetus for studying intracellular transport comes from electron microscopy studies, which revealed how large macromolecular complexes, organelles, and cytoskeletal components combine to produce a dense environment that interacting biomolecules must navigate, either through diffusion or cytoskeletal transport (13). However, the fixation required for electron microscopy arrests diffusive motion, making light microscopy critical for characterizing these processes. Recent advances in light microscopy gave rise to a number of experiments looking at intracellular transport (11,14–18). The three-dimensional (3D) single-particle tracking experiments reported below will add to the growing understanding of diffusion and other transport mechanisms in biological systems.

Experiment Description

We consider three distinct, biologically relevant conditions to acquire particle trajectories. Specifically, single fluorescent microspheres are tracked in a buffer solution, a cellular extract with microtubules intact, and an extract with depolymerized microtubules. The use of an extract prepared from Xenopus eggs (rather than from intact live cells) greatly simplifies the experiments, while maintaining an environment statistically similar to the in vivo intracellular space. The protein concentration in the cytosolic fraction was ∼100 mg/mL, similar to protein concentrations seen in live cells.

Single-particle tracking is a powerful technique that has become common in analyzing diffusion in biological systems (19). However, particle-tracking methods are typically limited to two dimensions due to the physical constraints on the speed of moving the sample or the microscope objective in the third dimension. We developed a light microscopy technique that employs acousto-optic deflectors (AODs) to realize 3D imaging of volumes with high temporal resolution and no macroscopically moving parts (20,21). Several recent AOD microscopes employed a 4-AOD setup to produce 3D random access, two-photon imaging in tissue; these devices use point scanning to increase temporal resolution (22–24). Point scanning is inappropriate for tracking single molecules, because the stochastic nature of their movements requires rapid scanning of the entire volume within which the particle is moving. Our microscope employs a simpler 2-AOD setup to perform rapid raster scans of small volumes, which enabled us to record single-particle trajectories.

Fickian and Non-Fickian Diffusion

Single-particle tracking microscopy enables one to track how the position X_i(t) of the i^th fluorescent microsphere changes with time t. These trajectories can be used to compute the mean-square displacement (MSD) over N microspheres,

$$\langle {\delta }^2\left(t\right)\rangle =\frac{1}{N}\sum _{i=1}^N{⋮{\mathbf{X}}_i\left(t\right)-{\mathbf{X}}_i\left(0\right)⋮}^2,$$ (1)

where 〈⋅〉 denotes the ensemble average. The MSD characteristic of Fickian diffusion grows linearly with time,

$$\langle {\delta }^2\rangle =6D_{\alpha }t,$$ (2)

where D_α is a diffusion coefficient. For diffusion in free space (solvent fluid), D_α can be calculated from the Stokes-Einstein relation

$$D_{\alpha }=\frac{k_{\text{B}}T}{6\pi \mu r},$$ (3)

where k_B is the Boltzmann constant, T is temperature, μ is the viscosity of the solvent fluid, and r is the radius of the diffusing molecule. If Fickian diffusion takes place in a crowded environment whose pores are filled with a solvent fluid, the value of D_α is reduced to account for the medium’s porosity and tortuosity. Such a reduction in effective diffusion coefficient D_α has been observed in a variety of biological phenomena (14,25,26).

Diffusion processes in which the MSD grows nonlinearly with time,

$$\langle {\delta }^2\rangle =6D_{\alpha }{t}^{\alpha },$$ (4)

are referred to as anomalous or nonFickian. A process is called subdiffusion if 0 < α < 1, and superdiffusion if 1 < α < 2. Here α = 1 corresponds to Fickian (classical) diffusion, and α = 2 is known as the ballistic limit (27). Anomalous diffusion has been observed at a variety of scales in a plethora of applications, including solute transport in geologic formations (28,29), transport of polynucleotides through pores (30,31), and diffusion of fluid through tissue (32,33). Anomalous diffusion has also been observed in cytoskeletal transport (11,12); a major goal of this report is to identify transport mechanisms that could give rise to this behavior.

A time-averaged MSD provides a useful alternative to the ensemble-averaged MSD, especially in biological systems in which it is common to have only a few trajectories with a relatively short observation time. The time-averaged MSD of the ith microsphere is defined by

$$\overline{{\delta }_i^2}\left(\text{Δ},t\right)=\frac{1}{t-\text{Δ}}\underset{0}{\overset{t-\text{Δ}}{\int }}{\left[\mathbf{X}\left(t^{\prime }+\text{Δ}\right)-\mathbf{X}\left(t^{\prime }\right)\right]}^2\text{d}{t}^{\prime },$$ (5)

where Δ is a lag time (34). The ensemble average of the time-averaged MSDs for all N experimental trajectories, $\langle \overline{{\delta }^2}\rangle =\left(1/N\right){\sum }_{i=1}^N\overline{{\delta }_i^2}$, is then fit with an equation

$$\langle \overline{{\delta }^2}\rangle =6D_{\alpha }{\text{Δ}}^{\alpha }+C.$$ (6)

The fitting parameter C accounts for noise in the measurements of trajectories, such that a noiseless MSD would be fit with C = 0. In the following analysis, the experimental MSD is shifted by subtracting this constant, which can be thought of as removing noise. Analysis without this shift gave qualitatively similar but quantitatively inferior results. Despite a long history of using the ensemble-averaged MSD for analyzing random walks (19), recent work has shown that it can produce misleading results (35,36). Furthermore, many single-particle tracking experiments in biology have shown that comparing the time-average MSD for different particles does not necessarily match the ensemble-averaged MSD (37).

Stochastic processes whose time-averaged behavior differs from their ensemble average (over multiple realizations) are called “nonergodic” (38). Ergodicity or lack thereof is an intrinsic property of a process. Experimental verification of a process’s ergodicity requires observation times that are sufficiently long for the process to self-average. The practical limits on observation time imposed by our microscope do not provide sufficient time for a given trajectory to self-average, making ergodicity analysis inappropriate. Instead, we analyze a pre-ergodic regime in which robust nonergodic measures can be observed (19). We define the dimensionless random variable ${\xi }_i=\overline{{\delta }_i^2}/\langle {\delta }^2\rangle$, and obtain a distribution ${\varphi }_{{\xi }_i}\left(\text{Ξ}\right)$ of time-averaged MSDs. This distribution can be used to characterize the ergodic properties of the process, such that the distribution ${\varphi }_{{\xi }_i}\left(\text{Ξ}\right)=\delta \left(\text{Ξ}-1\right)$, where δ is the Dirac delta function, denotes an ergodic process, and divergence from this distribution reveals ergodicity breaking.

Random Walk Models of Anomalous Diffusion

In classical random walk models, the final position X_N of a particle after N equal time steps is a sum of N random spatial increments Δx_n (n = 1,…,N),

$${\mathbf{X}}_N=\sum _{n=1}^N\text{Δ}{\mathbf{x}}_n.$$ (7)

The choice of a probability density function (PDF) for these increments, ψ_Δx(⋅), uniquely specifies a model of this class. For example, a Gaussian PDF ψ_Δx(⋅) corresponds to Brownian motion (BM).

The continuous time random walk (CTRW) generalizes this classical framework by allowing for time increments, Δt_n (n = 1,…,N), of variable (and random) duration. Thus, CTRW is characterized by two PDFs: one for random spatial increments, ψ_Δx(⋅); and the other for random time increments, ψ_Δt(⋅). After N steps of the CTRW, it takes a particle the time

$$T_N=\sum _{n=1}^N\text{Δ}{t}_n$$ (8)

to reach its position X_N given by Eq. 7. The choice of the PDFs ψ_Δx(⋅) and ψ_Δt(⋅) defines a manifold in the space of CTRW models. For example, selecting ψ_Δx(⋅) to be a power law and requiring ψ_Δt(⋅) to have a finite mean value yields a family of Lévy flight models. The latter were used to describe a wide range of seemingly random phenomena, such as search patterns of flying albatrosses (39), human travel (40), and financial markets (41). Another combination of these two PDFs, a Gaussian ψ_Δx(⋅) and a power-law ψ_Δt(⋅), results in a particle’s MSD that exhibits subdiffusive scaling with time (42,43) and was used to model subdiffusive transport in biological systems (37,44). In this regime, a particle’s MSD exhibits weak ergodicity breaking and the mean value of random time increments, Δt_n, does not exist (45). This renders the calculation of a time-averaged MSD problematic and necessitates the reliance on an analytically derived distribution of time-averaged MSDs (45):

$$\underset{t\to \mathrm{\infty }}{\text{lim}}{\varphi }_{{\xi }_i}\left(\text{Ξ}\right)=\frac{{\text{Γ}}^{1/\alpha }\left(1+\alpha \right)}{\alpha {\text{Ξ}}^{1+1/\alpha }}{l}_{\alpha }\left[\frac{{\text{Γ}}^{1/\alpha }\left(1+\alpha \right)}{{\text{Ξ}}^{1/\alpha }}\right].$$ (9)

Here α comes from the underlying temporal distribution used in the derivation ψ_Δt(⋅) ∼ Δt^−(1+α); Γ(x) is the gamma function; and l_α(x) is the one-sided Lévy stable distribution. Using this analytical distribution, the pre-ergodic analysis performed on the experimental data can be directly compared to a CTRW model.

Fractional Brownian motion (fBM) is another generalization of the classical random walk, which postulates that taking a step in one direction changes (i.e., increases or decreases, depending on the correlation) the probability that the next step will be in the same direction (46). This non-Markovian process is characterized by a two-point correlation function

$$\langle X_i\left(t_1\right)X_j\left(t_2\right)\rangle =K_H{\delta }_{ij}\left(t_1^{2H}+t_2^{2H}-{\left|t_1-t_2\right|}^{2H}\right),$$ (10)

where K_H is a fractional diffusion constant; δ_ij is the Krönecker delta; and H = α/2 is the Hurst exponent. In this case, X_i and X_j are uncorrelated when i ≠ j and the correlation function 〈X_iX_i〉 is isotropic. The fBM framework was used to model intracellular diffusion (47). It has been shown recently that fBM is ergodic in the limit of large observation times, although for short observation times this is not the case (19).

We use measurements of single-particle trajectories in cytoplasm to discriminate among these three alternative random-walk interpretations, i.e., to select a model that captures best both molecular diffusion in crowded environments and cytoskeletal transport along microtubules. To achieve a robust model selection, we rely on the fact that BM, CTRW, and fBM have distinct ergodic behaviors, particularly when observation time is short (19). This makes pre-ergodic analyses uniquely suited for single-particle tracking in biological systems (which are often characterized by strict limits on observation time). We show that a pre-ergodic analysis can be leveraged to differentiate each experimental condition and to identify a corresponding random walk model.

Methods

Xenopus egg extract preparation

Xenopus egg extract is prepared using the protocol described by Hetzer et al. (48). Only the cytosolic fraction described is used in this study.

Microsphere preparation and imaging

Streptavidin-coated fluorescent microspheres from Polysciences (Warrington, PA) are prepared as specified by manufacturer instructions, resuspended in PBS/BSA binding buffer (0.02 M phosphate-buffered saline, 8 mg/mL NaCL, and 10 mg/mL bovine serum albumin) at a concentration of 1.25% and stored at 4°C. The microspheres have a diameter of 1.019 μm (±0.018 μm), excitation frequency peak at 441 nm, and emission peak at 486 nm. These are introduced into extract at a concentration determined by experiment where a concentration is chosen based on sparse but plentiful microsphere coverage when viewed by microscope, allowing easy acquisition of long trajectories without capturing trajectories where some frames have overlapping microspheres. This resulting solution is deposited onto uncoated glass slides, covered with a coverslip, and sealed using nail polish to minimize evaporation. The sample thickness is estimated to be roughly 10 μm. This is determined by focusing on microspheres stuck to the slide, and measuring the distance traveled by the stage to put the microspheres stuck to the coverslip in focus. As the extract contains microtubules, there is also a question as to how they are ordered. Although this is difficult to determine with our setup, it is expected that the microtubules will be randomly distributed and unordered, although it may be there is some bias toward the plane of the slide, as the sample volume is comparatively narrow in the orthogonal direction. For the case of the buffer solution, the microspheres are diluted in PBS to again obtain a sparse coverage. To remove cytoskeletal transport along microtubules and investigate free diffusion in the cytosolic fraction, nocodazole is applied, which is known to interfere with microtubule polymerization. The extract is incubated at 37°C for 1 h with 10 μM nocodazole, similar to previous protocols (11). The resulting solution is again deposited onto coverslips with sparse coverage.

Acousto-optic deflector microscopy

In this study, we use a microscope that uses acousto-optic deflectors (AODs) to guide a laser beam instead of mirrors (20). A block diagram of this microscope can be found in Fig. 1 A. An AOD is a device that introduces sound waves into a transparent crystal to form a transient diffraction grating. The angle of optical diffraction is related to the frequency of sound so that the available range of beam deflection is given by the equation

$$\text{Δ}\theta \approx \frac{\lambda \text{Δ}f}{v},$$ (11)

where Δθ is the total sweep angle; λ is the optical wavelength; Δf is the acousto-optic bandwidth; and υ is the speed of sound in the acoustic medium. It is apparent from this equation that sweeping the acoustic frequency through a given range will direct the focus along a line. The use of two orthogonal AODs, therefore, produces raster scanning in the (x,y) plane (21). A cylindrical lensing effect is created by the finite propagation time of the sound wave, so that the effective focal length (F.L.) of an AOD sweeping through a range of acoustic frequencies is given by

$$F.L.=\frac{v^2}{\lambda }{\left(\frac{\text{d}f}{\text{d}t}\right)}^{-1},$$ (12)

where df/dt is the rate of change of the sound frequency. By prescribing a precise range of frequencies and several rates of sweeping, one for every desired focal plane, a full 3D volume can be imaged at a rate of ∼100 Hz (21).

Figure 1.

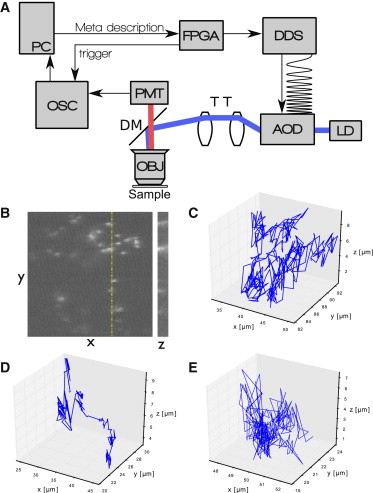
Summary of data collection and methods. (A) Block diagram of the microscope used in this work. Custom PC software controls all microscope functions and finalizes data acquisition. After scan parameters are entered, the scan program is sent to a field-programmable gate array (FPGA) as a metalanguage string of hexadecimal characters and saved into onboard memory. A Start command is sent with the number of repeats to begin a scan by driving a direct digital synthesis (DDS) board, producing a series of frequencies and chirp rates directing the acquisition of the volume, while a concurrent trigger signal is sent to the data acquisition oscilloscope. A laser diode (LD) is directed by the acousto-optic deflectors (AOD), through a telescope tube (TT), and reflected by a dichroic mirror (DM) onto the back-aperture of an objective (OBJ). The light emitted by the sample is collected on a photomultiplier tube (PMT) and converted into an image on the PC. (B) Example image from the microscope. Note that high and low concentrations, as seen here, are common, and that all trajectories are taken from single molecules that never overlap. (Dashed line) The z cut shown to the right. (C–E) Example trajectories of a bead in a (C) buffer solution; (D) extract; and (E) extract treated with nocodazole.

Our setup uses an integrated two-dimensional (2D) acousto-optic deflector, model No. 2DS-100-45-100 (Brimrose, Sparks, Maryland), which consists of two orthogonally mounted TeO2 AODs. This device is placed in line with a collimated 405-nm single mode laser diode. A 1:1 telescope directs the beam onto the back-aperture of a 40× oil immersion objective with 1.35 NA. The refractive index of the oil used for all slides imaged is 1.518. Emitted light is collected by a model No. H7422-40 photomultiplier tube (Hamamatsu, Bridgewater, NJ) and acquired by a WaveRunner 64Xi oscilloscope (LeCroy, Chestnut Ridge, NY). The AODs are driven by a model No. AD9959 direct digital synthesizer (DDS) (Analog Devices, Norwood, MA), which is controlled by custom firmware on a Cyclone 2 field-programmable gate array (FPGA) (Altera, San Jose, CA). The FPGA circuit is designed and implemented in-house and provides tight control over the timing of the scan. Further details can be found in Appendix A. All acquired images are saved in the NetCDF scientific data format (49), which preserves the intensity of each pixel and allows labeling with metadata for parameters such as voxel size in physical units. Conversion to common graphical formats for postprocessing and analysis is provided by an in-house plug-in employing the software ImageJ (National Institutes of Health, Bethesda, MD) (50). This setup results in a maximum field of view of ∼102 × 102 μm², and a varying focal length up to 20 μm from the fixed nominal focal plane of the objective.

In previous work using AODs, it was noted that a 2-AOD scanner necessarily produces astigmatic 3D scans (24). This is incorrect. A simple solution for the astigmatism is to scan at an angle to the 2-AOD system’s acoustic propagation axes. If both AOD channels are sweeping the sound frequencies at the same rate, this results in a raster scan oriented at 45° to the AOD devices’ orientations with the effective focal lengths of both AODs being equal, i.e., without astigmatism. If the two AODs are simply mounted behind one another without a 1:1 telescope between them as in our simple system, the effective focal planes will not be parfocal; in such a setup, the astigmatism is fully corrected by tilting the scan direction at an angle slightly different from 45° so the effective focal planes line up in space. The appropriate correction depends on the details of the entire optical system and must be calculated for every focal plane. In this work, proximity of the two AOD devices and small excursions from nominal focal plane make the astigmatism negligible relative to other sources of measurement error, so every plane is scanned at 45° to simplify volume reconstruction.

Imaging protocol

The protocol for imaging is the same for all acquisitions. The scan parameters used are 100 × 100 pixels, with a focal area of 102 × 102 μm². Each volume contained 10 focal planes, or slices, captured with a distance between them of 1 μm. An example of a single slice and z projection is shown in Fig. 1 B. The data acquisition rate is set at 1 MHz, so that with the time to fill the AOD the total acquisition time per volume is 86 ms. At these rates some slight smearing of the point spread function is apparent due to movement of the particle during the acquisition; this does not significantly affect the results of our analysis. Due to memory constraints on the oscilloscope used, 100 frames are collected before pausing to offload the memory, and then repeated 10 times for a total of 1000 frames. Each 100 frame acquisition takes 8.6 s, followed by ∼6 s spent clearing the oscilloscope memory. Therefore, for a full 10-repeat acquisition, the final observation occurs at 140 s. Throughout all experiments there are sufficient microspheres on a slide to image a single microsphere for one full scan, followed by focusing on a different particle. This minimized photobleaching, and assured a broad coverage of the available space for diffusion. Images are gathered for a maximum of 4 h per slide, at which time diffusive motion is no longer evident. This is due to the microspheres sticking to the slide and coverslip, as can be seen by moving the focal plain to show immobile populations in each plane. Whereas microspheres become stuck continually through the experiment, these are not tracked during the image analysis stage. No temperature control is used during the experiments. For all experiments room temperature is ∼22°C. Any small variation in temperature should have a small effect on the resulting behavior. Referring to Eq. 3, a difference of 1 K changes the diffusion constant by ∼0.3%, which is well within experimental error.

Data analysis

The resulting volumes are analyzed using the Imaris software suite (Bitplane, South Windsor, CT). A first pass of particle positions is automated by the software, using the internal particle tracking algorithm. This is followed by hand-picked filtering to eliminate extraneous points, and finally each frame is examined by eye to ensure proper positioning of particles. This step is very time-consuming and is the limiting factor in obtaining the 3D particle trajectories used in this study. The resulting output consists of the x, y, and z coordinates of each particle X_i over time t. Example trajectories for each experimental condition is shown in Fig. 1, C–E. These trajectories are analyzed as described in the Introduction.

Random walk model simulation

Brownian motion and fractional Brownian motion processes are simulated to compare with the experimental results. A BM process is simulated as a solution to a Langevin equation

$$\mathbf{X}\left(t+\text{d}t\right)=\mathbf{X}\left(t\right)+\mathbf{B}\left[\mathbf{X}\left(t\right)\right]\eta \sqrt{\text{d}t},$$ (13)

where η is Gaussian white noise with zero mean and unit variance, and B is a diffusion tensor, which in this case is diagonal and isotropic. fBM is characterized by zero mean, variance that scales algebraically, and a two-point correlation given in Eq. 10. The fBM trajectories are generated using the Hosking method (46).

The diffusion constants chosen are informed from the experimental results reported below. In the case of BM, the diffusion constant used is B = 0.92I where I is the identity matrix. In the case of fBM, K_H = 0.02. To calculate the correct value for B it is important to remember that the D_α reported in the experimental results is a 3D diffusion constant, where 〈δ²〉= 6D_αt. This is in contrast to simulations of random walks in each coordinate direction, which has the relation 〈X(t)²〉 = 2D_αt. Therefore, to find B, we take the experimental value and multiply it by 2. This is not the case for fBM, where we directly use the value found in experiments. The fBM simulations are calculated with H = 0.75, again chosen based on the experimental results. For both BM and fBM, 30 trajectories are simulated for 500 time steps, similar to the data available from the experimental results. Simulations of CTRW are not performed because with time steps of varying length, calculating a time-averaged MSD is unfeasible. All resulting trajectories are analyzed using the same methods as the experimental trajectories.

Results

Experimental results

As described above, images are acquired under three distinct conditions: for microspheres in buffer, in a cellular extract with intact microtubules, and in a cellular extract treated with nocodazole where the microtubules are depolymerized. There are 28, 40, and 31 trajectories acquired for each case, respectively. The time-averaged MSD is calculated for each trajectory according to Eq. 5. These trajectories are ensemble-averaged, and the resulting averaged trajectory is fit using Eq. 6. These average trajectories and the resulting fit parameters are shown in Fig. 2, A and B, for short and long times. An important note is that the variance grows with lag time, as there are fewer segments to average over as lag time increases. This accounts for the poor fitting seen at large lag times, and is the reason the full trajectory of 140 seconds is not shown.

Figure 2.

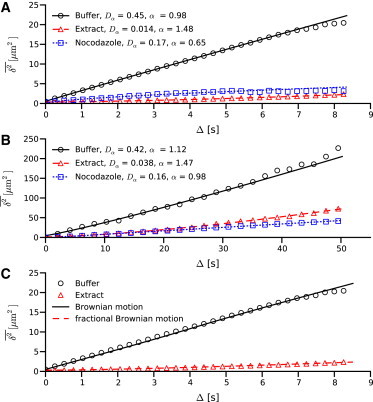
Time courses of mean-square displacement. (A and B) Comparison of averaged trajectories for diffusion in cellular extract, buffer solution, and cellular extract treated with nocodazole. (Symbols) Experimental data. (Solid lines) Fit using Eq. 6. (A) Short lag-time analysis. (B) Long lag-time analysis. (C) Comparison of random walk models to experimental results. Note that a time-averaged MSD of CTRW trajectories is inappropriate, therefore there is no comparison to the experimental condition of extract with nocodazole.

Looking at the buffer condition first, Eq. 6 is applied to both short and long lag-time data to obtain α = 0.98 and 1.12, respectively. This suggests normal Brownian motion, as expected for this case. Calculating the diffusion constant using Eq. 3 gives a diffusion constant of D_α = 0.24 μm²/s, which matches well with the experimental values of D_α = 0.42 and 0.45 μm²/s. The error most likely comes from uncertainty in position measurement during the image analysis phase.

For the extract condition, which captures cytoskeletal transport along microtubules, we find α = 1.48 and 1.47 for the short and long lag-time analysis. These values are consistent with the α = 1.47 (±0.07) reported in Caspi et al. (11) (our α is equivalent to their γ). Furthermore, the fact that α does not appear to be a function of time suggests the observed superdiffusive behavior arises from long-term correlations. Comparing the fit diffusion constant is inappropriate in this case due to the assumptions inherent to Eq. 3, namely that the observed particle is in a dilute suspension.

In the case of nocodazole-treated extract, α = 0.65 in the short lag-time analysis, but α = 0.98 is observed in the long-time lag case. This transition from anomalous to classic Fickian diffusion has been observed previously, and typically results from processes with a finite correlation length (51). Because α is not a function of time in the extract case, this suggests these two processes are fundamentally different. There have been a number of recent studies of intracellular anomalous diffusion in which this transition has been noted (11,15–18). These results also show that the diffusion constant D_α is smaller and similar in both extract cases compared to buffer, as would be expected for hindered diffusion. Again, comparison to Eq. 3 would be inappropriate.

Pre-ergodic analysis

As suggested above, analyzing experimentally obtained particle trajectories in terms of their ergodicity could potentially distinguish what type of underlying processes govern diffusion in each of our experimental conditions. Several groups have investigated the ergodicity of random walk processes and shown differences in the distribution of time-averaged MSDs ${\varphi }_{{\xi }_i}\left(\text{Ξ}\right)$, which act as a representation of the underlying ergodicity of the process (35,44,45). We calculate the parameter ${\xi }_i=\overline{{\delta }_i^2}/\langle {\delta }^2\rangle$ for each experimental condition and plot histograms of the distributions at four lag times in Fig. 3. These snapshots at discrete lag times give a good idea of the shape of these distributions, and suggest that they each evolve differently with respect to lag time Δ. To get a complete picture of the distribution with respect to lag time, the distribution for many values of Δ are plotted in Fig. 4. To help compare these figures, note that the y axis for all plots in Fig. 3 corresponds to the heat values in Fig. 4, whereas the y axis in Fig. 4, Δ, is a fine discretization of the four lag times spanned in Fig. 3 from the top to bottom row. With this in mind, it is immediately clear that each condition shows markedly different statistics.

Figure 3.

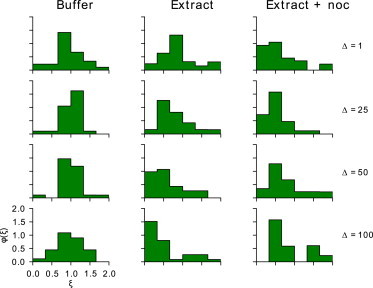
Time-averaged mean-square displacement distributions for all experiments. Snapshots of the distribution ${\varphi }_{{\xi }_i}\left(\text{Ξ}\right)$ for the three experimental conditions at four different lag times Δ. In the case of buffer, 28 trajectories are analyzed, in the untreated extract case, 40 are analyzed, and in the case of extract treated with nocodazole, 31 are analyzed. All figure axes mirror those in the bottom left, but are removed for clarity. The trend, in the cases of Buffer and Extract + noc (nocodazole), is independent of lag time whereas the case of Extract shows a shifting peak with increasing lag time. To see this trend more clearly, compare this figure with Fig. 4, which plots the distribution for many values of Δ.

Figure 4.

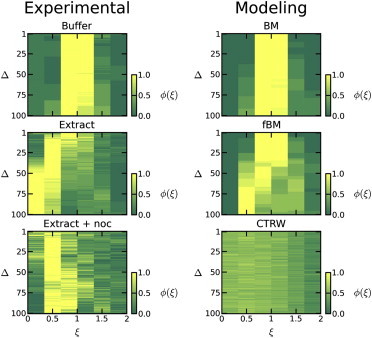
Temporal evolution of time-averaged MSD distributions. Comparison of distribution ${\varphi }_{{\xi }_i}\left(\text{Ξ}\right)$ for the three experimental and the three modeling conditions. BM denotes Brownian motion, CTRW denotes continuous time random walk, and fBM denotes fractional Brownian motion. In the case of the experimental data, although there is noise due to the limited number of trajectories, the trends in each case are distinctive. Furthermore, the three modeling conditions shown are quite similar to the paired experimental conditions, suggesting these processes are good representations of the biological process.

To categorize these distributions, the same statistics for random walk processes shown to result in anomalous diffusion are examined. Based on a comparison of the plots in Fig. 4 with previous work (19), we use CTRW with a power-law ψ_Δt(⋅) to model the free diffusion condition (extract + nocozadole) and fBM to describe the cytoskeletal transport condition (extract). Both BM and fBM random walks are simulated, and the MSD is calculated for each resulting trajectory. The ensemble-averaged MSD from these simulations is compared to the experimental results in Fig. 2 C, which shows excellent agreement between a BM process and the buffer case, and fBM and the extract case.

In addition, a distribution of time-averaged MSDs is calculated from the simulated trajectories. For the case of CTRW, an analytically derived distribution of time-averaged MSDs, Eq. 9, is used. Note that the distribution does not depend on lag time Δ. Although this distribution assumes an infinite observation time, is has been shown that this result matches simulated data with a much shorter observation time, on the order of 100 time steps (19). To aid visual comparison, Gaussian white noise (μ = 0, σ = 0.05) is added on top of the distribution to simulate the noisy appearance. Using this analytic distribution and the simulated data, the distribution ${\varphi }_{{\xi }_i}\left(\text{Ξ}\right)$ is plotted as a function of lag time in Fig. 4. In the simulations of fractional Brownian motion α = 1.5, as seen in the experimental data. For the CTRW distribution, a best fit is obtained with α = 0.6. This value is motivated from the short lag-time result, as it appears normal Fickian diffusion is recovered at long lag times, and we are interested in the anomalous behavior.

Examining the distributions of time-averaged MSDs and recalling that these distributions are analogous to ergodicity, the differences between these processes become clear. As seen in Fig. 4, for a BM process the distribution remains Gaussian and centered around ξ = 1 for all lag times, as expected. fBM is ergodic at short lag times with a peak centered at ξ = 1, and slowly shifting toward ξ = 0 with increasing lag time. This evolution of the distribution of time-averaged MSDs with lag time is similar to previously reported results looking at fBM with short observation times (19). CTRW is a nonergodic process which is characterized by a peak independent of lag time and shifted toward ξ = 0, and again was reported previously in He et al. (45).

Discussion

Comparing the experimental and model plots in Fig. 4, similarities are immediately apparent. For free diffusion in a buffer, the distribution has the same characteristics as a BM process. For the case of free diffusion in the extract after treatment with nocodazole, a shifted distribution that is independent of lag times is observed, similar to a CTRW process. An interesting facet of this result is that although we saw a transition from anomalous to Fickian diffusion in the MSD analysis, in the ergodicity analysis it appears there is no dependence on lag time. However, as we are analyzing these results in a pre-ergodic regime, this may simply reflect the lack of self-averaging achieved over the time period analyzed. Future investigation of this relationship may provide insight into the relationship between ergodicity and this transition. Finally, in the case of cytoskeletal transport along microtubules (extract), a distribution starting centered and slowly shifting toward zero with increasing lag time is seen. In the untreated extract case, one would expect free diffusion and cytoskeletal transport along microtubules to occur in concert, but the statistics suggest that cytoskeletal transport dominates in this experimental condition. The similarities to the simulated data are striking and illuminating. A word of caution: it is very important to recognize that there are a variety of random walk processes and the field remains one that is rapidly evolving. We are not claiming that the intracellular processes are exactly represented by the described random walk processes, but simply that the statistics seen here appear to be well modeled by such processes.

The lack of consensus in the published literature suggests that intracellular transport is very complicated. Here, we have shown that cytoskeletal transport along a microtubule is statistically distinct from free diffusion within the examined cytosolic fraction. This result shows cytoskeletal transport is not simply diffusion with a higher diffusion constant, but a distinct process, providing a unique method for transport. This supports the idea that cytoskeletal transport is essential, as traditional diffusion would be unable to mimic this behavior. Furthermore, we have shown these processes are well modeled by fBM and CTRW, respectively. Despite this success, there is still contrary evidence regarding the intracellular diffusion process. As already mentioned, both fBM (47) and CTRW (44) have successfully modeled experimental data from free diffusion in the cytosol. Our data and analysis suggests that CTRW is a more accurate model for intracellular free diffusion, although the difference between our experiments on a slide and results from living cells may explain this discrepancy. Although they are instructive, the measures of diffusion used here, the scaling over time (α) and a measure of ergodicity (ξ), provide an incomplete description of these processes. Organization and structure within cells likely has a major impact on transport, and improvements in tracking smaller particles in living cells, for extended observation times, will allow a more complete characterization of intracellular transport. However, the models proposed here present a powerful tool for beginning to understand these processes.

There are a few previous results that relate to what we have shown here. In this work, the boundary effects present with cell membranes are not accounted for, yet previous work has shown that boundaries can have a nonnegligible effect on random walk processes (52,53). Therefore, an important next step is to perform these experiments in vivo to properly account for these effects in experiments. Another recent study focused on the diffusion of membrane-bound proteins in migrating cerebellar granule cells; the authors observed a net forward transport toward the leading front (54). This biased diffusion was modeled using Brownian motion with a drift component, despite the presence of bursts of biased motion in which the observed protein moved in the same direction for several consecutive steps. The similarity with our observations in the extract case suggests that an fBM process with positive correlation may provide an accurate model for the described behavior. An important distinction is their finding that the process is dependent on the motor protein myosin II, which interacts with actin filaments. In our case, the transport appears to be microtubule-mediated, but cytoskeletal transport on either actin or microtubules have similar mechanics, suggesting the models proposed here may be appropriate. Another intriguing result involves assuming the cytoskeletal transport is modeled by a fractional Brownian process, as suggested above. The Hurst exponent can be calculated for the cytoskeletal transport data to be H = 0.75 from the definition α = 2H. The Hurst exponent is a measure of long-term correlations in a time series (55). Deng and Barkai (56) found that the ergodic behavior of fBM is dependent on the Hurst exponent, and that a nonsmooth transition occurs as H → 0.75. Although it is not clear exactly how this detail affects the physical process, it is intriguing. Future experiments and theory may shed light on whether this is important or merely a coincidence.

Understanding intracellular transport is essential to understanding complicated cellular processes. Although there remain many questions, we have shown strong evidence that CTRW with power-law distributed temporal increments is a good model for intracellular free diffusion, and similarly fBM is a good model for cytoskeletal transport along microtubules. The fact that these are statistically distinct processes, as opposed to parametrically different examples of a single process, is an interesting and powerful result. Future studies exploring this result in vivo combined with extensive modeling will continue to improve the characterization of a variety of intracellular processes. These results also offer an interesting perspective on cellular processes that take place in the cytosol. Cells could be organized in a way that CTRW-like processes directly impact reaction processes, where the locally anomalous diffusion increases reaction rates by increasing the encounter rate. This increase in encounter rate emerges from the long waiting times that can occur in a CTRW process, keeping a molecule in a given local space longer than would be expected for a BM process. Opposing this is an fBM-like process that can act as a regulatory mechanism to transport proteins away from local traps and separate reaction partners as necessary. This idea is supported by the correlated stepping seen in fBM that could lead to a rapid removal of a molecule from a local space. The interplay of these processes would allow fine control over cellular processes without relying on organelles or membranes for segregation. Proving this interaction will require clever experiments to tease out the details, but the work presented here suggests the appropriate mechanisms exist.

Appendix A: Microscope Control Details

Initial designs of our microscope used a software solution to communicate with the DDS using the common USB protocol. This allowed simple scanning, but was limiting due to USB packet timing constraints and the inherent asynchrony in USB. To reach the physical limits of our scanner, for this study a custom FPGA firmware is developed to drive the DDS. An FPGA provides an affordable and powerful method to implement a hardware solution, which is excellent for time-sensitive tasks where hardware will greatly outperform software. The main problem this avoids is the intrinsic USB interpacket delays, therefore guaranteeing excellent timing control. Furthermore, limits on USB packets require repeated volume scans to be broken into smaller chunks, which creates obvious problems due to interpacket delays, but also creates synchronization issues due to limits on the number of sync signals that an oscilloscope will recognize in a single acquisition. By ensuring that timing is fully controlled by the FPGA with the only control coming from a single external start signal, we greatly improve our scan capabilities, given the limitations of the hardware.

Standard operation proceeds as follows. A description of the volume to acquire is sent over USB using a metalanguage in hexadecimal characters, and saved into memory. At that point, either a Start signal can be included in the original signal, or the FPGA will stand ready waiting for a new signal, in both cases containing the number of repeats and instructions to begin scanning. At the start of a scan, the metalanguage is converted into a series of commands that are delivered to the DDS, which will perform the required series of frequency sweeps to produce the desired scan pattern. The Start signal will also pulse a synchronization to the oscilloscope, triggering the acquisition of the incoming photomultiplier output. Finally, the acquired data is computationally reconstructed into a final stack of images for each time point.