Predictive encoding of moving target trajectory by neurons in the parabigeminal nucleus

Abstract

Intercepting momentarily invisible moving objects requires internally generated estimations of target trajectory. We demonstrate here that the parabigeminal nucleus (PBN) encodes such estimations, combining sensory representations of target location, extrapolated positions of briefly obscured targets, and eye position information. Cui and Malpeli (Cui H, Malpeli JG. J Neurophysiol 89: 3128–3142, 2003) reported that PBN activity for continuously visible tracked targets is determined by retinotopic target position. Here we show that when cats tracked moving, blinking targets the relationship between activity and target position was similar for ON and OFF phases (400 ms for each phase). The dynamic range of activity evoked by virtual targets was 94% of that of real targets for the first 200 ms after target offset and 64% for the next 200 ms. Activity peaked at about the same best target position for both real and virtual targets. PBN encoding of target position takes into account changes in eye position resulting from saccades, even without visual feedback. Since PBN response fields are retinotopically organized, our results suggest that activity foci associated with real and virtual targets at a given target position lie in the same physical location in the PBN, i.e., a retinotopic as well as a rate encoding of virtual-target position. We also confirm that PBN activity is specific to the intended target of a saccade and is predictive of which target will be chosen if two are offered. A Bayesian predictor-corrector model is presented that conceptually explains the differences in the dynamic ranges of PBN neuronal activity evoked during tracking of real and virtual targets.

movements in reaction to extrapersonal objects generally require more than a sensory replica of the external world. The internal representation of object location must take into account object motion, self-generated movements, and periods of time when the object may be momentarily inaccessible to the relevant sensory systems. Here, in the context of the oculomotor system, we examine the extent to which these requirements are met in the encoding of object location in the parabigeminal nucleus (PBN), a small satellite nucleus of the superior colliculus (SC).

We focus on the PBN because its activity appears entirely devoted to a representation of the location of targets that are the object of visual tracking behavior. Cui and Malpeli (2003) trained cats to fixate laser spots, which, when moved at constant velocity, were tracked primarily with catch-up saccades. They found that PBN activity was determined by the angular distance and direction between current fixation and target¹ and was largely, if not entirely, unaffected by the orbital position of the eyes or the relative velocity between fixation and target. In particular, PBN activity usually rose monotonically as target distance increased along some best direction, peaked at a characteristic distance, and dropped with further increases in distance. They referred to target position along this best direction as retinal position error (RPE) and to the relationship between activity and RPE as the cell's response function—conventions that are also adopted in this report.

The PBN receives most of its known inputs from the ipsilateral SC and returns projections to both ipsilateral and contralateral SC that constitute the major cholinergic input to the tectum (Baizer et al. 1991; Graybiel 1978; Mufson et al. 1986; Sherk 1979b). It is present in all mammals and its homolog, the nucleus isthmi, in all other vertebrates. The PBN and SC are so tightly interconnected that the PBN might be considered a physically displaced node in an internal SC circuit. However, PBN cells are far more homogeneous in their properties than SC cells, in that none displays premotor bursts of activity in relation to saccades or saccade-linked activity for eye movements in the dark (Cui and Malpeli 2003). Thus the PBN serves as a purer platform for examining the issues at hand, and because of its intimate relationship to the SC it may provide unique insights into specific SC functions.

To lay down a foundation for these experiments, we needed to first test in the awake animal the assumption that PBN response fields cover the entire oculomotor range. Sherk (1978, 1979b) previously demonstrated that the PBN of the anesthetized cat is retinotopically organized in a map that covers most, if not all, of the visual field. Cui and Malpeli (2003) reported that PBN response fields in the awake cat are retinotopically organized in a manner consistent with Sherk's (1979a) PBN map. However, their sample covered a narrow range of eccentricities, within a few degrees of the area centralis. Given that PBN activity appears specific to attended targets, and that Sherk's map was derived in the anesthetized cat, it is not clear whether the receptive fields that she observed extending to peripheral visual space are descriptive of the response fields in the awake animal. This leaves open the possibility that the PBN is concerned only with targets near the point of fixation and is engaged primarily for what Cui and Malpeli (2003) referred to as “close-order tracking.” Therefore the first goal of the present study was to obtain a larger sample of PBN cells in order to see whether response fields defined in the awake animal span at least the entire oculomotor range.

Cats trained to pursue moving targets will continue to do so when the targets are briefly extinguished, whether with smooth pursuit (Missal et al. 1995) or with a combination of smooth pursuit and saccades (de Brouwer et al. 2001), indicating that the future positions of momentarily unseen targets are extrapolated to guide tracking behavior. The primary goal of the present study was to determine whether the PBN encodes the estimated positions of such invisible targets. For this, we utilized a paradigm in which cats tracked blinking laser spots moving at constant velocity while eye movements and action potentials from individual PBN cells were recorded. We refer to the visible targets of ON phases as real targets and the invisible targets of OFF phases as virtual targets. Our hypothesis was that internal estimates of virtual-target position would be reflected in PBN activity—specifically, that the relationship between activity and target location relative to fixation would be similar for real and virtual targets. As will be shown, PBN cells respond to virtual targets, but with a more limited range of activity than for real targets. Furthermore, the response field is broader for virtual than for real targets, although its peak is in the same location for both. Consequently, the virtual response is smaller than the real response near the peak but can be larger than the real response away from the peak. To understand the computational mechanisms that could give rise to these findings, we propose a Bayesian predictor-corrector model for PBN activity that estimates target position during the ON and OFF phases of a blinking target and examine some of its fundamental properties.

Tracking moving objects must take into account changes in the retinal position of targets caused by eye movements, in addition to target motion per se. Thus, if neural activity encodes estimates of extrapolated target distance, it should rapidly reset to appropriate levels when saccades are made to virtual targets without the benefit of visual feedback. This was tested directly by examining perisaccadic activity during target OFF phases.

The rationale of this study is based on the assumption that PBN activity is determined by the current subject of visual tracking behavior and not by unattended stimuli. However, the paradigms mentioned above (or used by Cui and Malpeli 2003) employ only a single target, so they do not directly test this proposition. If it is correct, then when the animal is presented with multiple targets PBN activity should predict which will be chosen before an eye movement toward the selected target is initiated. Using a paradigm in which two moving targets are presented simultaneously (dual-target task), we provide evidence that PBN activity is indeed determined by the intended target, and not by other targets of equal visual prominence.

METHODS

General procedures.

All animal use followed protocols approved by the University of Illinois Animal Care and Use Committee and met the standards of the U.S. Public Health Service Policy and National Institutes of Health guidelines. The data presented here were obtained from six PBN in four cats. All were adult spayed females who worked for food rewards. Details of animal preparation, animal care, training, head immobilization, electrophysiological recording, eye movement monitoring, and stimulus generation were identical to those used previously (Cui and Malpeli 2003; Lee and Malpeli 1998).

A fixture surgically implanted on the skull allowed the head to be rigidly fixed during behavioral sessions (Malpeli et al. 1992). A gold-plated copper ring was implanted under the conjunctiva of each eye to monitor eye position with the double magnetic-induction method (Bour et al. 1984) as implemented by Malpeli (1998). The apparatus for recording eye movements was calibrated with behavioral criteria as described by Kang and Malpeli (2003). For all experiments the display was binocularly viewed; for both recording sessions and data analysis we used the position signals from the eye for which position monitoring was considered more accurate.

Miniature bases permanently affixed to the skull supported removable microdrives used to advance microelectrodes into the brain (Malpeli et al. 1992). Microelectrodes consisted of short segments of quartz-coated platinum-tungsten wire (Thomas Recording, Giessen, Germany) pulled to a fine taper, ground to a sharp point, and mounted in large-bore micropipettes. For the experiments to examine the ranges of RPE represented in the PBN, spikes were detected and time-stamped for future analysis. For the virtual-target task, neural and behavioral data were acquired and analyzed off-line with the Plexon data acquisition system (Plexon, Dallas, TX).

The stimulus display consisted of a rear-projection screen subtending 60° horizontally by 50° vertically, onto which small laser spots (targets; ∼0.1° diameter) were directed and moved via computer-controlled scanning galvanometers. Background illumination, when desired, was provided by an LCD projector.

It usually took an extensive, systematic exploration to locate the PBN. This was aided by the results of Sherk (1979a, 1979b) and an unpublished PBN/SC map supplied by her. Vague visual and/or eye movement-related activity was often encountered dorsal and medial to the PBN, similar to that described for the brachium of the inferior colliculus by Doubell et al. (2003). Upon entry into the PBN, both activity of resolved cells and background activity were strongly modulated in a ramplike fashion associated with the cat's saccadic tracking, so it was obvious when the PBN was located.

Deriving response functions during saccadic tracking of continuously visible targets.

Cats were trained to track targets moving at constant speed (10°/s) along straight trajectories passing though the display center. Usually eight target directions, separated by 45°, were pseudorandomly presented, although for a few cells only six directions were employed. The targets appeared 500 ms after a warning tone, 15–20° from the center of the display, and traveled through the center to a point equidistant on the opposite side. If the cat maintained fixation within a tolerance window throughout the trial, a food reward was delivered at trial end; if not, the trial was terminated without reward.

Naive head-fixed cats make only low-gain, low-velocity smooth pursuit eye movements, although they can engage in relatively good smooth pursuit after being specifically trained to do so (Missal et al. 1995). The logic of our experiments required that cats attend the target continuously but not fixate it tightly. Had they tracked closely, the data would be of little value in defining response functions, since most response functions peaked at RPE considerably larger than tracking errors associated with good smooth pursuit behavior. So as not to encourage continuous close fixation of the moving targets, large tolerance windows (±10° to ±15°) were centered on the targets for most of their trajectories. Consequently, although the cats continually tracked the targets, they did so with catch-up saccades, as did the naive cats of Missal and those of Cui and Malpeli (2003).

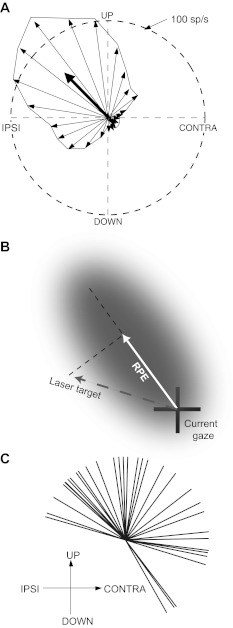
The best RPE direction was determined as illustrated in Fig. 1A. The direction of each thin vector corresponds to one of twenty-four 15° bins of instantaneous angle of the target relative to the area centralis; each vector's length is proportional to the average activity evoked when the target fell in the corresponding sector. Because the saccades used to track moving targets did not always fall on the path traced by the target, a range of RPE direction was explored for any given target direction. Consequently, the precision of determining the best direction of RPE was not limited by the number of target directions employed. In contrast, the magnitude of sampled RPE was typically restricted, because for most of each trial the targets were fairly closely followed with catch-up saccades. Therefore data density for RPE magnitude was usually quite uneven for larger target distances, so for determining best RPE direction, only data for target distances ≤10° were used. The 24 vectors were averaged, and the preferred direction of RPE taken as the angle of the resultant vector (heavy arrow in Fig. 1A), is mathematically equivalent to the gradient along which activity changed with steepest slope. This method is described in detail by Mardia (1972), Zar (1974), and Batschelet (1981) and has been employed in studies of orientation and directional selectivity (Leventhal et al. 1995; Levick and Thibos 1982; Worgotter and Eysel 1987).

Fig. 1.

Procedure for deriving parabigeminal nucleus (PBN) response functions. A: illustration of how best direction of retinal position error (RPE) was determined, using data from 1 cell (cell 20 in Fig. 2). The orientation of each thin vector corresponds to 1 of 24 15° bins of angle between the area centralis and target; the length of each vector is proportional to the average activity evoked by targets in the corresponding bin. The best direction of RPE is determined by averaging the individual vectors, as shown by the heavy arrow. B: illustration of how the scalar value of target distance was calculated. The shaded area represents a hypothetical response field, and the dashed line passing through the center of the response field represents the best direction of RPE, as determined in A. Typically, the vector connecting gaze and target positions denotes RPE, but for purposes of deriving response functions here we define RPE as a scalar value, namely, as the projection of the target vector (dashed line) onto the best direction of RPE, i.e., the solid white vector. The sign of RPE is positive for the direction indicated and negative for the opposite direction. C: distribution of best directions of RPE of 36 PBN cells.

Once the best RPE direction was determined, the response function (i.e., the relationship between response magnitude and magnitude of RPE) was derived. The response function is determined without reference to target motion but refers only to the instantaneous positional relationships of the eye and target, as illustrated in Fig. 1B. The dashed line passing thorough the center of the hypothetical response field in Fig. 1B represents best RPE direction, and the RPE associated with any given target location was taken as the projection of the target vector onto this line. The response function was then calculated by averaging activity at each RPE, using all data, as opposed to the ≤10° criterion for determining best RPE direction. Typically 80–90% of spikes contributing to the response function were associated with targets positioned in a constant-width, 4°-wide band centered on the best RPE direction. Although the relationships illustrated in Fig. 1A are defined by vectors, here we treat RPE as a scalar quantity in the response function. Basically, the response function as described below represents a slice though the center of a response field; the overall shape and full extent of response fields were not determined.

In these experiments we frequently changed the electrode trajectory slightly between recording sessions to maximize the area of PBN sampled. However, because the PBN is so small (presenting a target no more than 1 mm long in the anterior-posterior dimension and a maximum of 0.3–0.4 mm across in the medial-lateral dimension), so deeply located, and so close to the surface of the lateral edge of the midbrain, it was difficult to predict which part (if any) of the PBN would be sampled after changes in the nominal trajectory of the electrode. Also, whenever a microelectrode was exchanged for a new one, the resulting perturbations in the electrode trajectory were comparable to the dimensions of the PBN, often resulting in the PBN being missed entirely. Thus the sampling of PBN cells should be considered random rather than systematic.

Blinking-target task.

If the PBN responds to virtual targets, then similar response functions should be found for real and virtual targets. The procedure used to derive response functions for the blinking-target task was a simplified version of that employed in the previous section. Once a neuron was isolated, its preferred direction of RPE was estimated by online monitoring of activity while the animal tracked continuously visible moving targets. Because we did not intend to sample the PBN broadly for this experiment, we recorded as many cells as possible along each electrode pass. As expected for a retinotopically organized structure, the best RPE directions were similar for nearby cells, so we could quickly estimate the best direction by preliminary presentation of continuously visible targets with trajectories bracketing the expected best direction. Only two directions of target motion were employed for the blinking target: with and opposite to the preferred direction of RPE. We excluded any data for which eye position deviated out of a 4°-wide band centered on the target trajectory; within this band, the RPE magnitude associated with any given position was determined as in Fig. 1B.

For assessing responses to virtual targets, spots moving at constant velocity (6°/s) were blinked on (400 ms) and off (400 ms). This duty cycle was chosen because it is long enough so that all retinal persistence of the target would have faded by the middle of the OFF phase. Also, as shown below, it is long enough for transient bursts of activity associated with target onset or offset to be fully contained within a 200-ms quarter-cycle, allowing periods with and without these transients to be analyzed separately. On the other hand, it is short enough to allow several cycles to be presented during one trial. Typically, at least 60 trials were taken for each neuron (30 in each direction).

The cats required no additional training to follow blinking targets but tracked them well from their first appearance. As with tracking of continuous targets in the previous section, we wished to encourage attentiveness while at the same time using a fixation-tolerance window wide enough to obtain sufficient ranges of RPE for defining response fields. Consequently, we often began trials with a fairly wide window (as wide as ±15°) but narrowed the window near trial end to ±5°. Occasional training sessions with relatively narrow fixation-tolerance windows were interspersed with recording sessions to keep performance from becoming too lax.

The laser was turned on and off with a fast solid-state relay, and the times taken to reach full intensity or to darken completely were negligible (<2 ms). There were no sources of light in the testing chamber other than the laser and LCD projector, so when the projector was turned off nothing was visible but the laser targets. Conducting the experiments with no background provided more definitive evidence that visual stimuli are not required to evoke responses in the absence of a target but had the disadvantage that cats were less attentive, tracked targets more poorly, and tended to make fewer, less crisp saccades.

Dual-target task.

The purpose of this task was to directly test the hypothesis that the activity of a PBN neuron is modulated by stimuli falling within its response field only when it is being attended as a possible saccade target. Only PBN sites with response fields near the horizontal meridian, centered between 8° and 12° eccentricity, were used. Each trial began with a warning tone, followed 500 ms later by the appearance of a central fixation point. After 1,000 ms the fixation point was extinguished, and two targets appeared simultaneously, one in the response field and one symmetrically on the opposite side of the central fixation point, moving toward the fixation point at 2°/s. The cat's task was to fixate one of these within 2,000 ms. Response fields are large at this eccentricity, so the low target speed kept one target within the response field until the choice was made. Both targets were extinguished 500 ms after one was acquired, and the animal was rewarded for acquiring either target. Trials in which the cat's behavioral response latency was <100 ms were excluded from analysis because the animal's choice was assumed to have been made before the targets actually appeared. Trials with response latencies above 1,000 ms were excluded because for these the animals perseverated between the targets and usually made no choice.

To ensure that the retinal trajectories of the moving targets were identical up to the point of saccade initiation, the trajectories of both targets were dynamically stabilized on the retina until the start of a saccade to one target (i.e., until the eye left a tolerance window centered on the stationary fixation point), at which point stabilization was turned off. The two targets were produced with a single laser beam, slewed back and forth rapidly from one target location to another. The beams were extinguished (with a rapid solid-state relay) before slewing to eliminate any comet tail streaking between the two locations. When the targets were of equal brightness, the dwell time on each target was 8 ms, and 6 ms was consumed by slewing to the next target. Thus the total duty cycle was 28 ms, so the targets were refreshed at 35.7 Hz. The relative brightness of the targets could be controlled by unequally dividing the total dwell time of the laser between the two locations.

The rationale of this experiment requires that the animal divide its choices reasonably equally between right and left targets. However, the cat would typically be highly biased toward the first target selected in a session (although not necessarily to the same side each day), which required inducing it to switch targets by temporarily rewarding only one choice and/or by making the desired target relatively brighter.

Data analysis and modeling.

All analyses of physiological data and simulations for the modeling were performed with MATLAB (version 7.1). For most analyses P values were derived with two-sample Kolmogorov-Smirnov (K-S) tests, a nonparametric, distribution-free method (for a description, see Mood et al. 1991). This test compares cumulative distributions of a given parameter under two conditions and reports the K-S statistic, which is the maximum difference between the distributions, and the P value of the comparison. The only exception to the use of the K-S statistic was for linear regressions. For these (see Fig. 4C and Fig. 6, C and D) the data obviously violate homoscedasticity (i.e., variance increases along the fitted line), so one cannot legitimately estimate confidence intervals for slopes or intercepts with the normal methods of linear regression. Instead, we used permutation tests: We randomly interchanged the two values for each item in the regression (with 50/50 probability), calculated the difference between the resulting slope (intercept) from unity (zero), repeated the processes for 100,000 iterations, and plotted the distributions of differences to determine whether the slopes (intercepts) of the real data differ significantly from unity (zero).

Fig. 4.

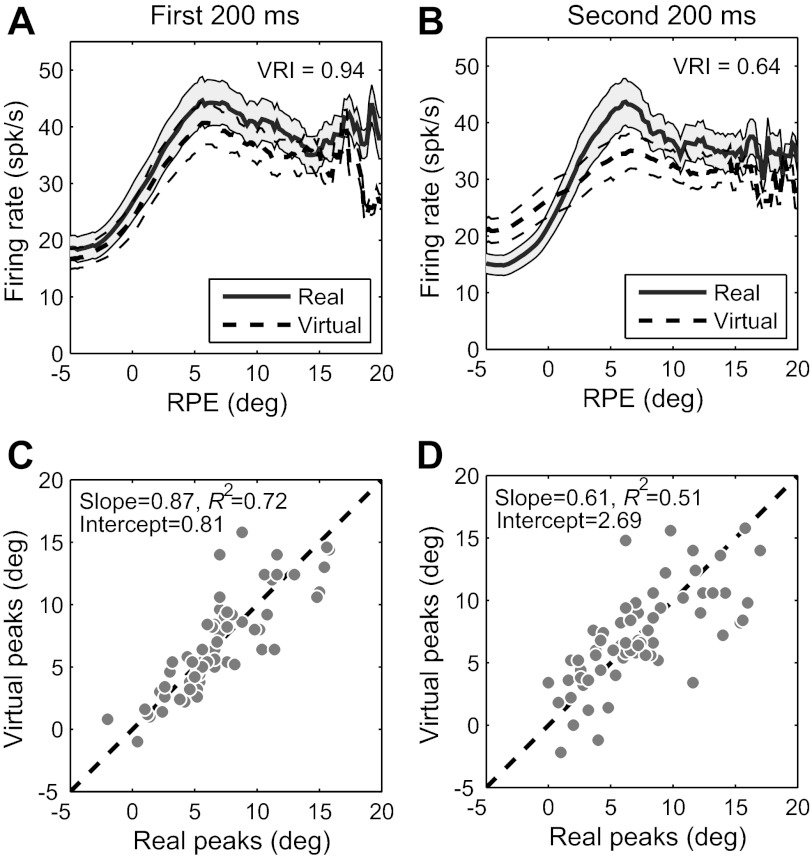
Results of blinking-target task. A: definition of virtual response index (VRI), illustrated with response functions for real and virtual targets of the same cell in Fig. 3. P_on and V_on mark peaks and valleys of the response function for the real target (i.e., the ON phase of the target), while P_off and V_off mark the peaks and valley for the virtual target (i.e., the OFF phase of the target). The VRI is the ratio of the dynamic ranges of the two response functions: VRI = (P_off − V_off)/(P_on − V_on). B: frequency histograms of VRI for 63 PBN cells, including and excluding saccades. The mean VRI was identical (0.73) for both. The results of all analyses of the virtual response were also essentially identical with and without the inclusion of saccades, and for subsequent figures we arbitrarily chose to include saccades. C: locations of peaks of response functions compared for real and virtual targets. The dashed line indicates unity slope and zero intercept. For each cell, the eccentricity of the peak RPE for the virtual target is plotted against that of the real target. The distributions of peak eccentricities for real and virtual targets do not differ significantly (P = 0.93); the slope and intercept are not significantly different from unity and zero, respectively (P = 0.27 for slope, 0.61 for intercept). D: grand average RPE response functions for real and virtual targets, calculated for the full 400-ms ON and OFF phases: VRI is 0.68. Firing rates are averaged across the entire sample of PBN cells (n = 63). SE is shown for real and virtual targets by shading and dashed lines, respectively.

Fig. 6.

Summary of virtual response of all 63 PBN cells for the first and second 200 ms of each ON and OFF target phase. Analysis is for full spike trains, including saccades. A: responses to real and virtual targets in the first 200 ms, averaged across the entire sample. B: responses to real and virtual targets in the second 200 ms, averaged across the entire sample. SE is shown for real and virtual targets by shading and dashed lines, respectively, in A and B. C: peak RPE for virtual targets plotted against peak RPE for real targets in the first 200 ms. The distributions of peak eccentricities for real and virtual targets do not differ significantly (P = 0.81); the slope and intercept are not significantly different from unity and zero, respectively (P = 0.64 for slope, 0.77 for intercept). D: peak RPE for virtual targets plotted against peak RPE for real targets in the second 200 ms. The distributions of peak eccentricities for real and virtual targets do not differ significantly (P = 0.81); the slope and intercept are not significantly different from unity and zero, respectively (P = 0.043 for slope, 0.063 for intercept).

A Gaussian filter with fixed standard deviation of 12 ms was used to smooth spike trains for displaying activity as a function of time (i.e., in Figs. 3, 8, and 9); such filtering does not apply to the derivation of response functions, which estimate activity as a function of RPE.

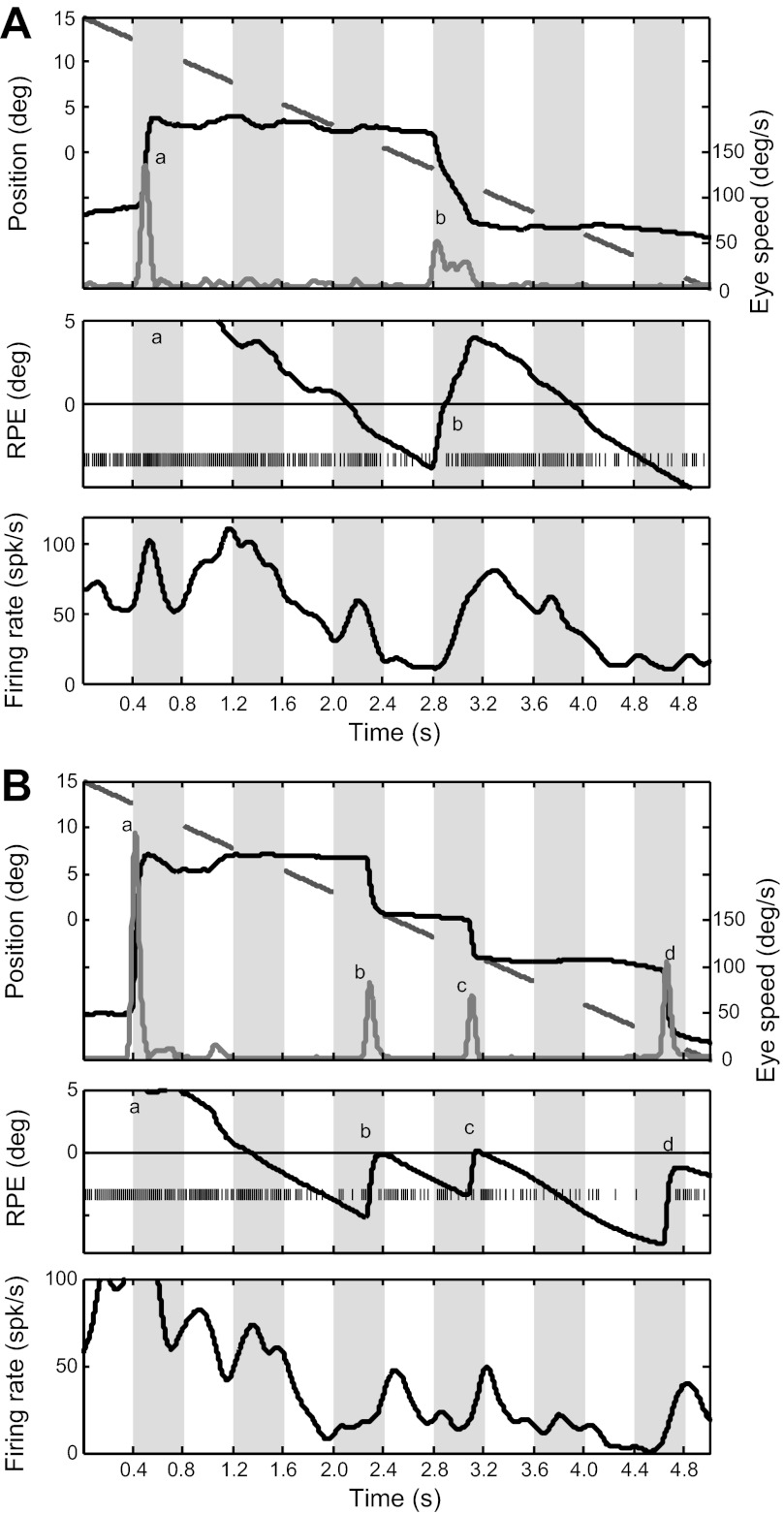
Fig. 3.

Behavioral and electrophysiological data for 2 trials (1st trial, A; 2nd trial, B) for 1 PBN cell during the blinking-target task. ON and OFF phases are indicated by white and gray stripes, respectively. Top: for each trial, the broken line segments indicate the blinking laser target position in the ON phases, the steplike trace shows eye position, and the gray trace at bottom shows eye velocity. Saccades are recognized by velocity peaks, labeled a and b for the 1st trial (A) and a–d for the 2nd trial (B). Middle: RPE and the spike raster. Bottom: firing rate smoothed with a Gaussian filter (SD = 12 ms). For this and other figures illustrating single cells, there was no background illumination, so OFF cycles were in complete darkness.

Fig. 8.

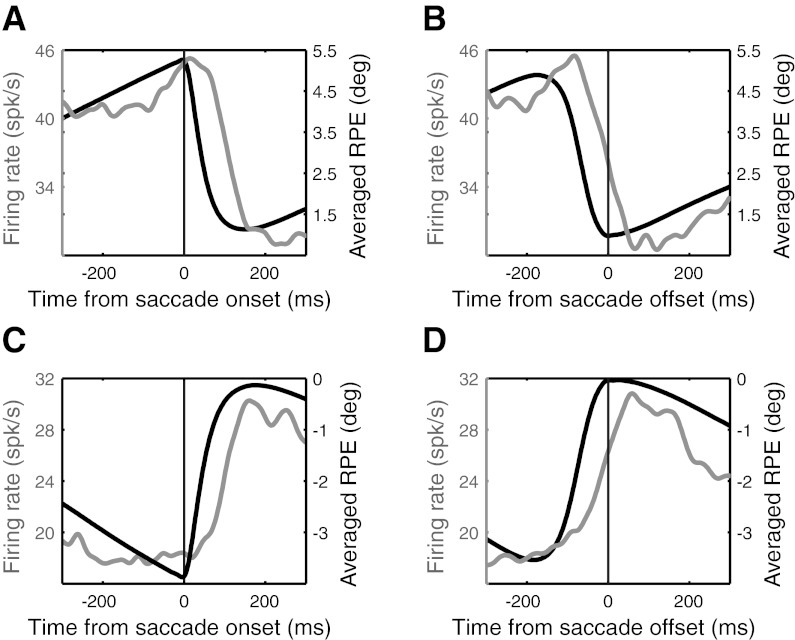
Perisaccadic RPE (black curve) and PBN (gray curve) activity without any visual feedback. RPE is averaged across all saccades for all cells (n = 63); activity is averaged across all cells for all saccades, smoothed with a Gaussian filter (SD = 12 ms). A and B: data for saccades that decreased RPE. C and D: data for saccades that increased RPE.

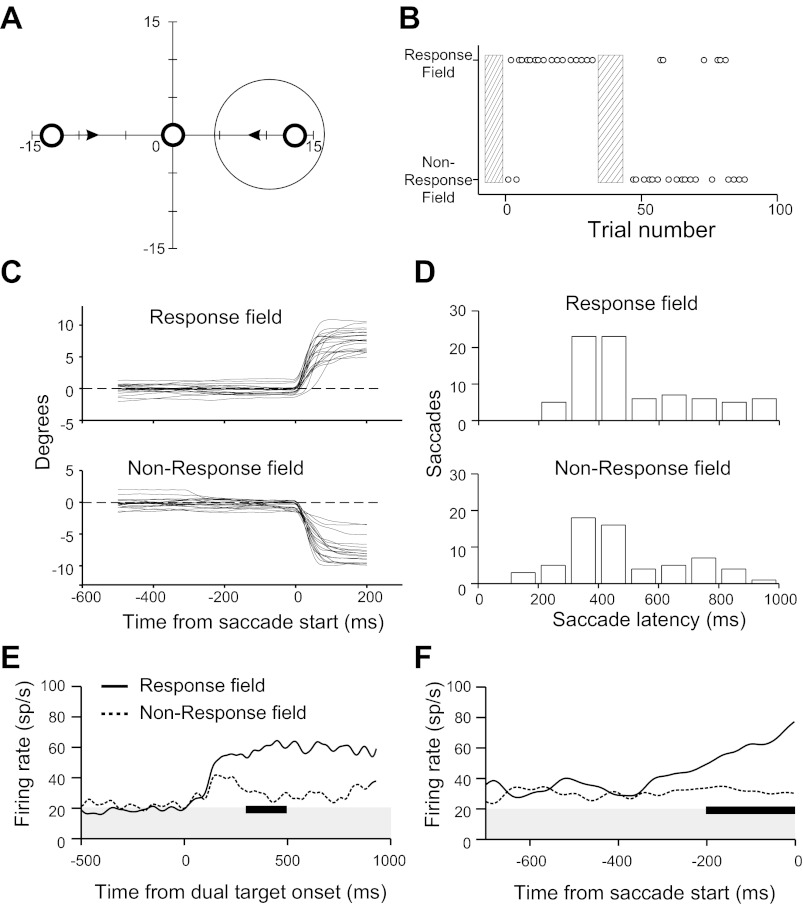
Fig. 9.

PBN activity during dual-target task. A: schematic of task. Large circle represents PBN response field. At trial start cats fixated a laser spot centered on the display. One second later, that spot went off and 2 targets (laser spots) appeared at locations indicated by small open circles, moving centrally at 2°/s, as indicated by arrows. A saccade to either target terminated the trial. B: cat's choices of target (indicated by small circles) in 1 of the 4 recording sessions that contributed to the data. Hatched bars encompass trials in which the animal was encouraged to choose one target over the other (see text), which in this case shifted its predominant choice from the target appearing in the response field to the target appearing opposite to the response field. The trials used to bias behavior did not contribute to the analyzed data; for all other trials the animal was rewarded for a successful saccade to ether target. C: horizontal eye positions for saccades toward and away from the response field for the session illustrated in B. D: distributions of latencies (from target onset) of saccades made toward and away from the response field. All data from the 4 multiunit recording sessions that contributed to the results are included in these panels and in E and F. E and F: summed activity synchronized on target onset (E) and saccade start (F) for saccades toward (solid line) and away from (dotted line) the response field, smoothed with a Gaussian filter (SD = 12 ms). Activity baselines, marked by the gray area in E and F, are the average firing rates in the 500-ms interval before target onset. The difference in activity between the 2 saccade directions in the intervals marked by the dark bars are significant (2-sample Kolmogorov-Smirnov test) for both E (P < 0.0001 for the 200-ms interval from 300 to 500 ms after target onset) and F (P < 0.0001 for the 200-ms interval before saccade onset). The interval for statistical analysis in E was chosen because the data density was highest for this interval (see D).

To derive response functions, RPE was divided into 0.2° bins and the spike count for each divided by the time spent in that bin. Response functions were smoothed with adaptive Gaussian filters, i.e., Gaussian kernels whose standard deviations are inversely proportional to the square root of the data density (Silverman 1986). Here, however, data density refers not to spike count but to the time spent at any particular RPE. Details of this procedure, along with comparisons of smoothed and raw data, have been previously published by Cui and Malpeli (2003). In the present study, broader filtering was employed to smooth the response functions: The Gaussian filters, as scaled to the data density, were four times as broad as those used by Cui and Malpeli (2003). The additional smoothing reduced noise to locate peaks of response functions with less ambiguity but did not result in significant distortion of the response functions or the response magnitude at peaks or valleys.

For comparing responses evoked by real and virtual targets, it was necessary to estimate activity at the peaks and troughs of the real and virtual response functions. For this we first applied the following rules: Peaks were taken as the largest local maxima in the range of RPE from −16° to +16°; troughs were the smallest local minima in this same range of RPE. For a few cells, the peak or trough was assigned by visual inspection of the response function.

In deriving response functions we did not adjust the data to take into account sensory transmission delays. It should not be assumed that such adjustments are appropriate, because given the highly predictable motion of the targets it is possible that PBN activity is already compensated for transmission delays. In any event, the target displacement associated with the expected delays would result in a change in activity (as estimated from the response functions) far too small to be detected for the vast bulk of the sampled cells.

RESULTS

Range of response functions exceeds the cat's oculomotor range.

Response fields were examined for 29 cells. In addition, for this analysis we include 7 cells from Cui and Malpeli (2003) for which sufficient data were available to determine the best direction of RPE, for a total sample of 36 cells.

The distribution of best RPE directions is uneven, biased strongly toward upper directions and somewhat toward contralateral directions (Fig. 1C). This should not be interpreted as poor representation of lower visual fields in the PBN but as a result of our sampling strategy, which favored the dorsal and lateral parts of the nucleus (dorsal to avoid excessive damage by deep penetrations, lateral to avoid excessive damage to the midbrain). The overrepresentation of upward directions is consistent with Sherk's (1979a) retinotopic map, in which the upper field is represented laterally and dorsally. The slight underrepresentation of the ipsilateral quadrant is to be expected, because in Sherk's (1979b) map it comprises a small fraction of the nucleus. Thus it is highly likely that all visual directions are represented in the PBN.

Most PBN cells had large response fields, often extending well beyond the cat's oculomotor range. The relationships between activity and RPE along the best directions were similar to those described by Cui and Malpeli (2003), with an asymmetric profile about the peaks of response functions (Fig. 2). Even cells whose response functions peaked at low RPE within the area centralis often had large response fields, with activity slowly declining with increasing RPE after the peak response. Consequently, Gaussians usually provided poor fits to the data. The following exponentially decaying sigmoidal function was empirically determined to provide a better fit to the typical PBN response field than Gaussians:

$$F\left(r\right)=A·\frac{\exp \left(-\frac{r}{K}\right)}{1+\exp \left(-\frac{r-a}{b}\right)}+c$$ (1)

where r is RPE amplitude along the best direction, A is a scaling factor determining amplitude, C is baseline firing rate, and a, b, and K are arbitrary constants. Constants a and b are primarily associated with the monotonically rising phase of RPE-activity curves, whereas K is primarily associated with the declining phase and the peripheral extent of the response field.

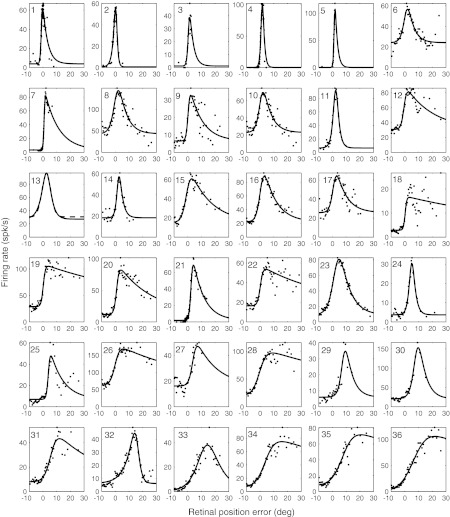
Fig. 2.

Activity as a function of RPE along the best direction of RPE (i.e., the direction illustrated by the white arrow in Fig. 1B) for 36 PBN cells, arranged according to increasing eccentricity of peak. The response functions of 7 cells (1–5, 7, and 21) are obtained from the data of Cui and Malpeli (2003). Cells 1 and 2 were not included in Fig. 1C because they were localized to the area centralis and did not show significant directional tuning. Dots indicate mean firing rates of each PBN cell at each RPE; solid and dashed lines show activity-RPE curves obtained by fitting an exponentially decaying sigmoidal function to the spike data (see text). The cats' behavior determined how much time was spent in each RPE bin; if this time was below a criterion value, that bin contributed nothing to the data. Consequently, not all bins are represented and the density of dots is often variable across the horizontal axis.

Figure 2 gives the empirical response functions and fitted curves for all 36 cells (parameters of the fitting function are given for each cell in Supplemental Table S1).² Response functions generally rise monotonically over some range of RPE, then peak and decline. The ascending limbs are usually roughly linear over most of their range. For some cells (e.g., cells 1–5, 11, 13, 14, 24, 32, and 33), the decline is almost as rapid as the rise. These tend to have response fields peaking in the area centralis, but this is not inevitable (e.g., cells 24, 32, and 33). However, for most cells the falling phase of the response function is prolonged, including some that peak fairly centrally (e.g., cells 9, 15, 16, 19, and 20). It is apparent that all cells respond for small RPE—few had response fields that exclude the area centralis.

These data provide a clear answer to one of the questions motivating this study: Coverage of PBN retinotopy, at the very least, exceeds the oculomotor range of the head-fixed cat, which, in our experience, is 15–20°.

PBN activity encodes an internal estimate of virtual target location.

An underlying assumption of this study is that cats would consider the target to have a continuous existence, spanning both ON and OFF phases, and would attempt to track virtual as well as real targets. During the blinking-target task, RPE averaged across all cells, all trials, and both stimulus phases was 0.71° (i.e., on average the eye lagged the target by this amount). The accuracy of tracking was somewhat better for virtual targets, with the frequency of saccades 25% higher than for real targets (P < 0.001). Consistent with this observation, the saccade frequency was slightly higher during OFF cycles (0.59 saccades/s for ON cycles vs. 0.73 saccades/s for OFF cycles; P = 0.0082). These data show that the cats attended and tracked the virtual targets at least as attentively as they did real targets.

As noted above, the cats seldom made robust smooth pursuit movements. We calculated the gains of smooth pursuit in the intersaccade periods for all trials in the blinking-target task, excluding the first 500 ms of each trial, to allow time for the cats to notice the target. The average gains of smooth pursuit were 0.25 and 0.33 for ON and OFF phases of the target, respectively. Thus the cats relied primarily on saccades to track the targets, which is also evident from the eye movement records shown below, as well as those published by Cui and Malpeli (2003).

Data were obtained from 63 cells for the blinking-target task. In contrast to the previous section, we did not attempt to sample the PBN broadly but aimed for its center, both to maximize yield and to locate cells whose response functions peaked from ∼4° to 8°, which, given the cat's typical tracking behavior, is a good range for defining the response function. All cells were recorded in the part of the PBN mapping the contralateral hemifield (i.e., the posterior two-thirds).

For visible targets, PBN activity is determined by RPE, and this is so whether RPE changes as the result of target motion or eye movements (Cui and Malpeli 2003). Responses of individual cells were usually consistent with the idea that this relationship also holds for virtual targets. This could often be observed for single trials, as illustrated in Fig. 3. This cell's response function peaked ∼7° to the right of the area centralis, and since RPE was usually below 7° in the illustrated trials, activity increased with increasing RPE for these examples. In Fig. 3A, the initial saccade (a) fell far short of the target, and the cat subsequently tracked it poorly, making only a single catch-up saccade (b) that overshot. Although saccade b was initiated and completed in darkness (for this session, there was no background illumination), activity increased with increasing RPE during the saccade. Activity continued to reflect RPE across several ON-OFF cycles, particularly after saccade b. The higher saccade frequency in Fig. 3B is more typical. At trial start, the animal was looking at the corner of the screen opposite to the target, and, as often happened, activity was quite high before the cat attended the target. After the target was acquired with the first saccade (a), activity tended to follow RPE, decreasing while the eyes were stationary and increasing with saccades that increased RPE (b, c, and d).

Since it was often difficult to determine by simple inspection whether activity tracked virtual RPE continuously, we pooled data for each cell separately for ON and OFF phases to derive response functions for real and virtual targets, one of which is shown in Fig. 4A for the same cell illustrated in Fig. 3. The response functions determined separately for ON and OFF phases were similar in shape to those typically generated with continuously visible targets, rising monotonically with RPE to a peak and then dropping with further increases in RPE. Although the virtual response function for this cell had a reduced dynamic range, with higher baseline and lower peak activity, it peaked at about the same RPE as the response function for the real target. Thus activity not only persisted during OFF phases but also reflected an internal estimate of the continually changing retinal distance of the virtual target.

To quantify the magnitude of response to the virtual target relative to the real target, we define a virtual response index (VRI) as the ratio of peak-to-valley differences between virtual and real response functions, as illustrated in Fig. 4A. One consideration was whether to include activity occurring during saccades. Spikes during saccades accounted for a small fraction of activity (6.9% overall, ranging from 1.8% to 13.0% for individual cells, using a 10°/s criterion for saccade onset and offset), so they would not be expected to have a major impact on response functions. Furthermore, as we document below, PBN activity rapidly adjusts for changes in RPE resulting from saccades. Nevertheless, it seemed conceivable that subtle differences in saccades during ON and OFF phases of the target could distort the VRI. Therefore we derived response functions both for the full spike trains and for spike trains with saccadic epochs removed: The distributions of VRI calculated with and without saccades did not differ significantly (Fig. 4B; P = 0.95; response functions of all cells, calculated separately with and without saccades, are available in Section A of the document found at the URL given in the endnote). We performed all analyses related to VRI both ways, and the results for the two were always virtually identical. We arbitrarily chose to show the data for the full spike trains, including saccades, for all subsequent figures involving VRI. Encoding of virtual target position was also independent of background illumination: mean VRI = 0.71 (20 cells) with background and 0.74 (43 cells) without background (P > 0.5). Consequently, data with and without background illumination are pooled for all analyses.

If PBN activity encodes estimates of virtual target position, the peaks of the response functions for real and virtual targets should occur at the same RPE. The distributions of peak RPE for real and virtual targets did not differ significantly (P = 0.93). Furthermore, the positions of peaks for real and virtual targets were well correlated, falling close to the 45° diagonal of a scatterplot (Fig. 4C); the slope of the regression, 0.75, did not differ significantly from unity (P = 0.27). Since the PBN is retinotopically organized, to the extent that these data cluster along the 45° diagonal the physical loci of maximum activity in the PBN will be the same for real and virtual targets at the same (retinocentric) point in visual space.

We further examined the population response by averaging all individual response functions to derive a grand-average VRI of 0.68 (Fig. 4D),³ which is in reasonable agreement with the single-cell analysis. This analysis has the advantage of smoothing out the considerable noise that was present in most single-cell response functions. Although this procedure lumps together cells whose response functions peak over a range of RPE, it works reasonably well because the distribution of these peaks was well clustered for the blinking-target data (around 5°).

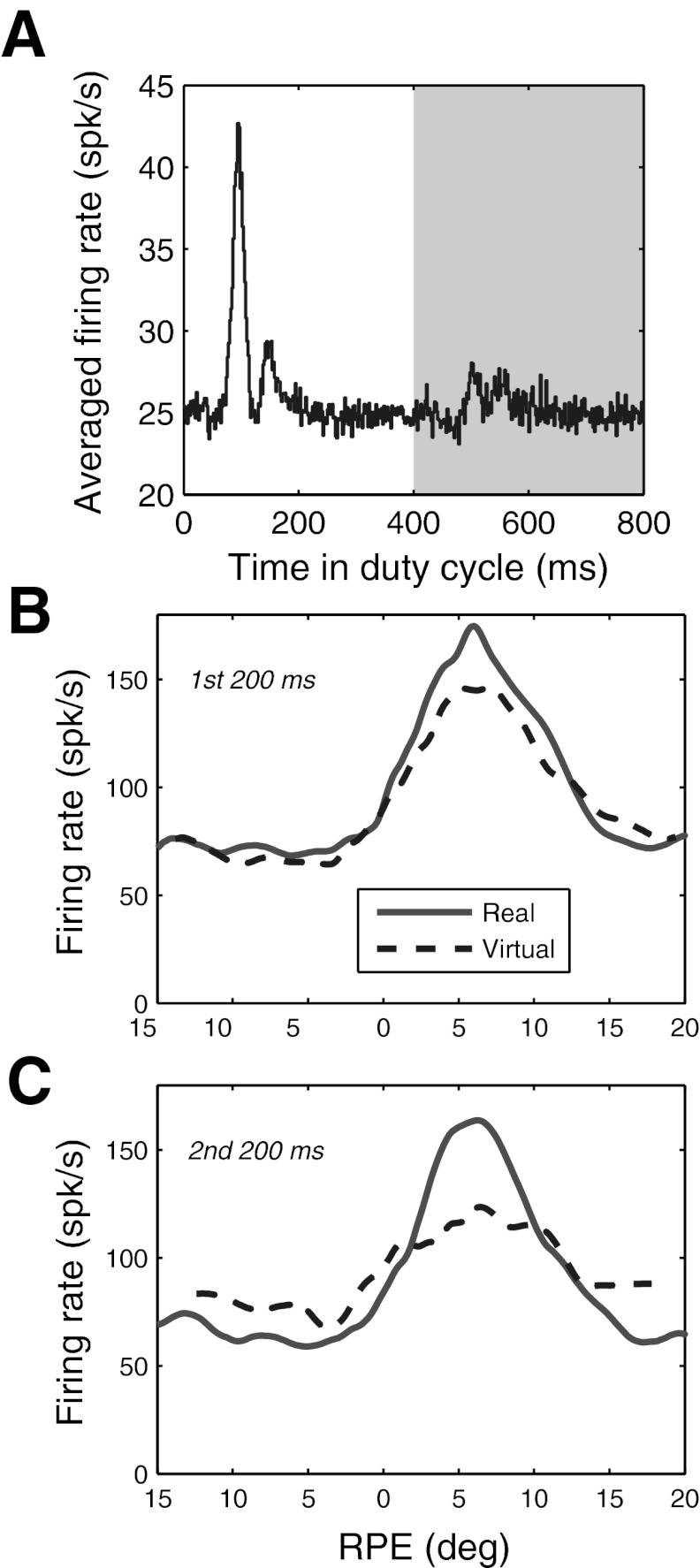
In addition to comparing activity between the two 400-ms half-cycles of the blinking targets, we also compared the VRI calculated separately for the first and last 200 ms of each 400-ms half-cycle. One motive for doing so was to determine how rapidly responses to virtual targets decay. Another was to avoid falsely attributing activity resulting from the slow decay of afferent signals to true predictive responses. For example, retinal ganglion cell activity may take as long as 180 ms to decay after the abrupt offset of an excitatory stimulus (Enroth-Cugell and Shapley 1973). Such coasting of afferent signals could be misinterpreted as a predictive response encoding the presence of the virtual target (although it is difficult to see how it could signal the continually changing RPE of a virtual target). Finally, target onsets and offsets were often accompanied by a transient response (Fig. 5A), and it is unclear how these might affect the analysis. All of these considerations apply to the first 200 ms of each half of the duty cycle (i.e., 0–200 ms and 400–600 ms of each full cycle) but not to the second 200 ms (i.e., 200–400 ms and 600–800 ms of each full cycle).

Fig. 5.

Comparison of responses to real and virtual targets for the same cell as in Fig 3, calculated separately for first and second halves of each ON and OFF target phase. A: average firing rate of PBN cells as a function of temporal position in ON-OFF duty, illustrating transient responses evoked by target onset and offset. B: response functions calculated for the first 200 ms of each ON and OFF target phase, which include onset and offset transients. C: response functions calculated for the second 200 ms of each ON and OFF target phase, which excluded transients. Analysis is for full spike trains, including saccades.

Figure 5, B and C, illustrate the results of separately evaluating the first and second halves of each ON and OFF phase of the target for the same cell as in Fig. 4A. For the first 200 ms, the response was about the same for the real and virtual targets. For the last 200 ms, activity was lower near the peak of the response function but higher for RPE more central and more peripheral to the peak, compressing the dynamic range of activity and reducing the VRI. These features were quite typical overall. The mean response magnitude for the first 200 ms of virtual targets closely matched that of real targets, whether one considers population averages (Fig. 6A; VRI = 0.94) or the distribution of VRI for single cells (mean VRI = 0.89). Although the VRI was lower during the second 200-ms interval, it was still respectable for both the population averages (Fig. 6B; mean VRI = 0.64) and individual cells (mean VRI = 0.56). As with the example of the single cell in Fig. 4A, relative to that of the real targets, responses to virtual targets in the second 200 ms were larger for RPE distant from the best RPE and lower near the best RPE (Fig. 6B). These response characteristics clearly indicate an extraretinal contribution to PBN activity. They can be accounted for by using a Bayesian predictor-corrector model, as demonstrated below.

RPE peaks had highly similar distributions for real and virtual targets during both the first 200 ms and the second 200 ms (P = 0.81 for both epochs). RPE peaks were still well matched for real and virtual targets during the second 200 ms of the OFF periods, although the strength of the correlation dropped substantially compared with the first 200 ms (Fig. 6, C and D). The slopes of the regression lines were 0.87 for the first 200-ms epoch (not significantly different from unity; P = 0.64) and 0.61 for the second (marginally different from unity; P = 0.043). Therefore, retinotopic encoding appears to provide an excellent estimate of retinal target position early in the target's OFF phase, but one that degrades with time. The trend toward lower slopes with time suggests that as the OFF phase is extended, target distance would be increasingly underestimated for larger RPE were it based solely on PBN response magnitude.

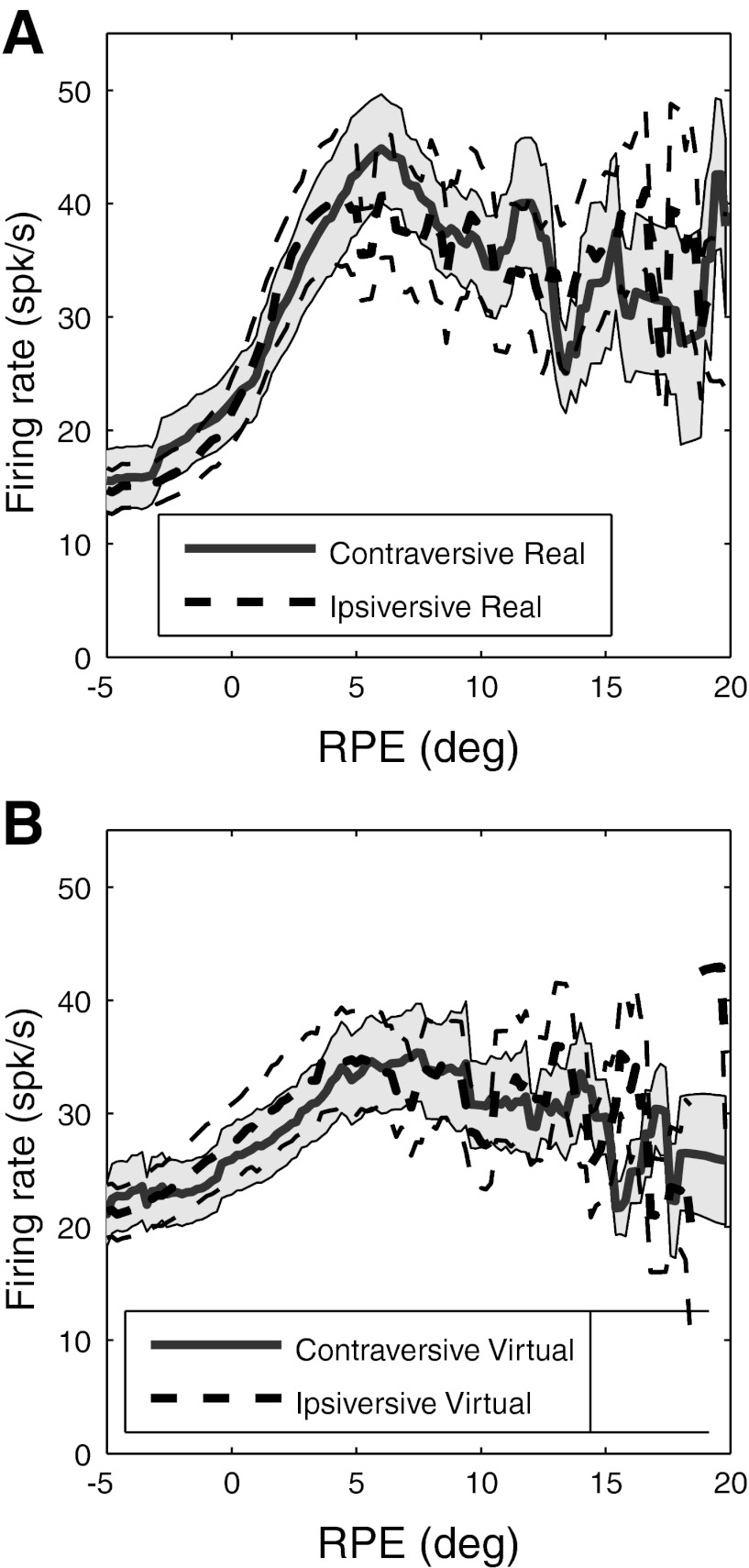
An implicit assumption in our derivations of response functions is that one can sum together data for targets moving in opposite directions. This is equivalent to assuming that the primary determinant of PBN activity is target position on the retina (i.e., RPE) and that retinal slip velocity per se does not play an important role, because the sign of slip velocity is reversed for opposite directions of motion. We have evaluated this assumption by examining response functions separately for ipsiversive and contraversive tracking and find no evidence that slip velocity per se contributes in any substantive way to PBN activity, either for real or for virtual targets, whether evaluated by the population response (Fig. 7) or the individual response functions (all individual response functions are available in Section B of the document found at the URL given in the endnote).

Fig. 7.

Grand average response functions for real (A) and virtual (B) targets calculated separately for contraversive (bold solid curves) and ipsiversive (bold dashed curves) tracking. Shading and dashed lines indicate SE. Analysis is for full spike trains, including saccades.

In the absence of visual feedback, PBN activity resets to encode target location after saccades.

Here we examine the resetting of activity after saccades in the absence of visual feedback. The analysis is restricted to saccades beginning and ending in OFF cycles of the targets. It was generally not possible to define such changes for individual saccades, because the spike density was normally too low to make accurate estimates of activity changes. Averaging the spike data across all saccades for a single cell was also usually problematic because, except for a handful of cells, the number of saccades toward virtual targets was too small to yield conclusive results. It was only by averaging over all saccades for all cells that we could get a precise estimate of the latency of activity changes related to the saccade. The grand-average latencies for activity changes after saccade onset or offset were 56 and 68 ms, respectively, as measured by the temporal difference between the midpoints of the step changes in activity and RPE trajectories (Fig. 8). Saccade resetting was symmetric in that activity reset appropriately whether saccades decreased (Fig. 8, A and B) or increased (Fig. 8, C and D) RPE. Examination of individual trials (e.g., Fig. 3) never produced any clear evidence for sudden changes in activity prior to saccade start (i.e., premotor burst or pauses).

PBN activity predicts which of two available targets will be chosen.

The dual-target task, in which two centripetally moving targets appear simultaneously on either side of a central fixation point, one in the response field and the other in the opposite hemifield, is illustrated in Fig. 9A. The requirements that response fields peak in a rather limited region of visual space and that the choice of targets be reasonably balanced in a given recording session, along with the substantial time required to obtain adequate data for this paradigm, frustrated our attempts to obtain single-unit data, so here we rely on multiple-unit recordings from four sites obtained in four separate recording sessions. However, the results were consistent across these sessions and quite robust.

In each session, the cat shifted its choice of target sufficiently through the session to provide balanced data for saccades toward and away from the PBN response fields, as illustrated for one session in Fig. 9B. The hatched bars in Fig. 9B indicate trials in the session that were used to direct the cat's attention to one side by temporarily making the desired target brighter and by rewarding the cat only for rewards to the desired target. Trials used for biasing the choice of target were not included in the analysis. All other trials were included, regardless of which target was chosen by the cat, and for these the two targets were identical and the animal was rewarded for acquiring either.

There was no significant difference in eye position prior to saccades for the two targets (Fig. 9C). The dynamic stabilization of the trajectories of laser targets on the retina prior to saccade start further guaranteed that the two targets were always on the same retinal locations before the saccade, moving at the same retinal velocity, regardless of the animal's choice and presaccadic variations in eye position.

The distributions of saccade latencies were similar for the two targets (Fig. 9D). The cats were not pushed to make rapid choices of targets, so saccade latencies were fairly long. Baseline PBN activity, taken as activity prior to target onset (shown by shading in Fig. 9, E and F), did not differ significantly with choice of target. On trials for which the target in the response field was chosen, activity rose after target onset with a latency of roughly 100 ms and stayed fairly constant thereafter (Fig. 9E, solid line). On trials for which the cats chose the other, mirror image target, target onset evoked a much smaller response that quickly died away (Fig. 9E, dotted line). Trials with saccade latency >1,000 ms were excluded from analysis, so activity data for saccades to either target, as well as the saccade latency distributions in Fig. 9E, are truncated at 1,000 ms. Because no data are included in the analysis after saccade start, the number of trials contributing to this activity is progressively reduced with time from target onset. Thus the data become noisier with time from target onset.

Activity synchronized on saccade start initially increased modestly for both choices (Fig. 9F, solid and dotted lines prior to −400 ms). When the animal choose the target in the response field, activity began to increase ∼300–350 ms before the saccade and rose monotonically until saccade start, quadrupling relative to spontaneous activity by saccade onset (Fig. 9F, solid line). In contrast, when the animal chose the other target, activity remained flat and ∼50% higher than baseline (Fig. 9F, dotted line). Since the physical stimuli were identical prior to saccade onset, we conclude that PBN activity is primarily determined not by the simple presence of a visual stimulus in the response field but by the behavioral relevance of the target.

An optimal inference model predicts differences between real and virtual response functions.

Bayesian inference is a general (and optimal) approach for estimation under conditions of uncertainty. Here we present a Bayesian predictor-corrector model that is based on the assumption that the PBN makes an optimal estimate of current target position using both an uncertain sensory input from the real target and an uncertain internal model of target motion. The model conceptually explains the salient features of PBN neuron responses to blinking targets. Specifically, it explains why the virtual response would be lower than the real response at the peak of the response function but higher than the real response at lower and higher RPE. An introduction to this PBN modeling approach is made in Anastasio (2010). The outcome of the simulation is shown in Fig. 10.

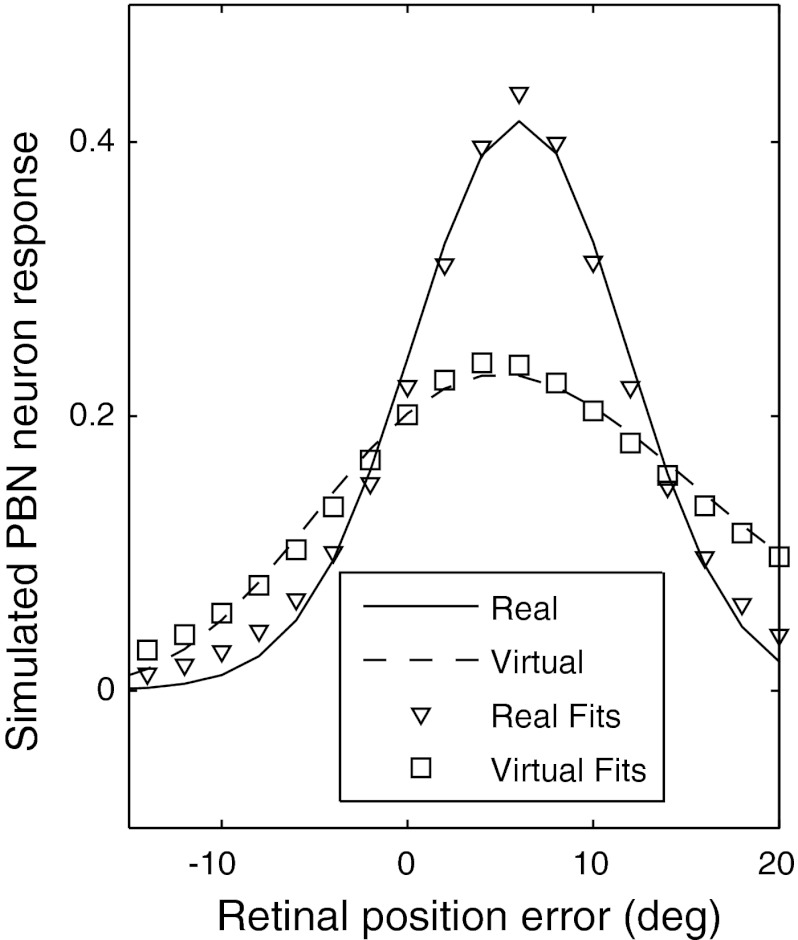
Fig. 10.

PBN response for real (solid curve) and virtual (dashed curve) targets simulated with the optimal interference model. The symbols are decaying sigmoid functions fit to the simulated data (see also Fig. 2). Details of the shapes of the simulated curves and the magnitude of overshoot and undershoot of the response to the virtual target can be manipulated by the choice of parameters, but the presence of the overshoot and undershoot per se are fundamental to the model and independent of its parameters.

Model PBN neurons estimate the probability that the target is located within a preferred RPE range. RPE is equivalent to target position relative to the fovea in retinal coordinates, so we will use the terms “RPE” and “target position” interchangeably. The current target position (i.e., RPE) probability estimate is derived from a prediction based on the previous RPE (i.e., target position) probability estimate. When visual input is available it sharpens this estimate, so that target probability can be much higher within the preferred range of a PBN neuron than outside of it. When visual input is not available the target probability estimate flattens out, and this reduces target probability within the preferred range of a PBN neuron but increases it outside that range. Thus the model PBN neuron response (proportional to firing rate) is lower for virtual targets within its preferred RPE range but higher outside that range, and this recapitulates the main features of the data.

The predictor-corrector model of the PBN is designed to be as simple as possible in order to illustrate its essential features with a minimum of detail. For simplicity, we consider a one-dimensional environment and a one-dimensional visual input that would be provided by a hypothetical one-dimensional retinotopic SC representation. The model is updated for every 2° of simulated target motion. This spacing is small enough to provide a clear view of the simulated PBN response function (Fig. 10) but large enough so that model target position and probability estimates can be illustrated on every update. The following equations describe the predictor-corrector algorithm:

$$P\left(T\left(t\right)\right)={\displaystyle \sum _{T\left(t-1\right)}P\left(T\left(t\right)|T\left(t-1\right),S\left(t-1\right)\right)P\left(T\left(t-1\right)|V\left(t-1\right)\right)}$$ (2)

$$P\left(T\left(t\right)|V\left(t\right)\right)=\frac{P\left(V\left(t\right)|T\left(t\right)\right)}{P\left(V\left(t\right)\right)}P\left(T\left(t\right)\right)$$ (3)

$$P\left(V\left(t\right)\right)={\displaystyle \sum _{T}P\left(V\left(t\right)|T\left(t\right)\right)}P\left(T\left(t\right)\right)$$ (4)

In Eqs. 2–4, random variable T represents target position (real or virtual), S represents a (probably proprioceptive) saccade signal, and V represents target position as encoded by sensory activity at the appropriate site in the SC retinotopic map and transmitted to the PBN. At time t, the posterior probability P(T(t)|V(t)) of target position given visual input is computed from the likelihood P(V(t)|T(t)), evidence P(V(t)), and prior target probability P(T(t)) according to Bayes' rule (Eq. 3). The model is predictor-corrector in the sense that the prior P(T(t)) serves as a prediction of target position that is corrected by the observation P(V(t)|T(t))/P(V(t)). The evidence P(V(t)) is computed according to the principle of total probability (Eq. 4). Prior probability (prediction) P(T(t)) at time t is a function of the posterior probability P(T(t − 1)|V(t − 1)) at the previous time step and the conditional probability P(T(t)|T(t − 1), S(t − 1)). P(T(t)|T(t − 1), S(t−1) = S*) accounts for the resetting of the PBN response due to saccades and describes the effect of a saccade of size S* on target position probability. In contrast, P(T(t)|T(t − 1), S(t − 1) = 0) describes the movement of the target between saccades and can be thought of as an internal probabilistic model of target movement (Eq. 2). P(T(t)|T(t − 1), S(t − 1) = 0) embodies the Markovian assumption that current target position depends only on its previous position. In principle, a conditional probability P(T(t)|T(t − 1), T(t − 2),…,T(t − n), S(t − 1) = 0) could be specified instead, which would take target positions at n previous time points into account, but since the end result in any case is the determination of P(T(t)), the Markovian assumption here entails no loss of generality.

For any specific target position T*, the conditional probabilities P(T(t) = T*|T(t − 1), S(t − 1)) have a Gaussian distribution. For any specific visual input V*, the likelihood P(V(t) = V*|T(t)) is described by a Gaussian distribution for real targets and a uniform distribution for virtual targets. Thus target position is relatively uncertain according to the internal model of target motion or according to sensory input from the real target (Gaussian distributions, variances 1° and 8°, respectively), but it is completely uncertain according to sensory input from the virtual target (uniform distribution, variance 2,133°). Note that the variance of the uniform distribution is much higher than those of the Gaussian distributions. We assume that the initial prediction P(T(t = 0)) is also a uniform distribution, so that the target could start off from anywhere. Sensory input from a real target at its start position begins the process of estimation.

The model updates the posterior probability of a target at all positions on each time step and chooses as its estimate of target position that position at any time t that has the highest posterior target probability P(T(t)|V(t)). The target position estimated by the model is the same for real and virtual targets, and this is consistent with the data showing that PBN neurons have similar peak response RPEs for real and virtual targets. However, the posterior target probability distribution on which the model estimate is based has a larger variance for virtual than for real targets, because the variance of the uncertain sensory input [i.e., likelihood P(V(t) = V*|T(t))] is much larger for virtual than for real targets (see preceding paragraph). The simulated PBN response is computed from the target posterior probability distribution (see Eq. 5). Because the posterior probability distribution for the virtual target has a larger variance, the simulated PBN response is more spread out for the virtual than for the real target, and this accounts for the ability of the model to capture the salient features of the data.

The model assumes that the firing rate of a PBN neuron is proportional to the probability that a target is within a particular RPE range. Given preferred RPE ranges that vary retinotopically, the set of PBN neurons together would provide a retinotopic encoding of estimated target position. Response b(t) of a simulated PBN neuron is computed from the posterior probability distribution at any time t according to

$$b\left(t\right)=P\left(T\left(t\right)=T{*}_b|V\left(t\right)\right)+P\left(T\left(t\right)=T{*}_b+1|V\left(t\right)\right)+\dots +P\left(T\left(t\right)=T{*}_b+g|V\left(t\right)\right)$$ (5)

where T_b* is the beginning target position and g is the target position range. Smaller or larger values of g produce simulated PBN responses that fall sharply or more gradually and can simulate the various empirical response function shapes (i.e., Fig. 2). Like the empirical results for the PBN response (i.e., Fig. 5C), the simulated PBN response for the virtual target is lower than that for the real target at the peak RPE but higher at low and high RPE (Fig. 10). The simulated real and virtual PBN response functions are also fit well by the decaying sigmoid that was used to fit real data in Fig. 2 (see Supplemental Table S1, last two rows, for the best-fit parameters and correlation coefficients). Thus the simulated PBN responses capture the essential features of the empirical RPE response functions for real and virtual targets. The ability of the model to do so results from the flattening of the virtual target posterior probability distribution, which is due in turn to the uniformity of the virtual target likelihood distribution, which is a fundamental, parameter-free property of the model. Agreement between the model and the data suggests that the estimation of virtual target position as encoded in the PBN may be derived from a predictor-corrector mechanism. (Additional information illustrating the model is available in Section C of the document found at the URL given in the endnote).

DISCUSSION

Encoding of real and virtual target position in the PBN.

Here we extend Cui and Malpeli's (2003) results by showing that the PBN encodes the retinotopic position of saccade goals over a span of RPE that readily exceeds the oculomotor range of the cat. Given that the retinotopic map in the anesthetized cat covers the full visual field (Sherk 1978, 1979b), in all likelihood such encoding is available for all gaze saccades in the head-free animal. Our results also add strong support to Cui and Malpeli's (2003) conclusion that the PBN encodes RPE per se, and not slip velocity, since reversing the sign of retinal slip velocity did not systematically change the relationship between activity and RPE.

The blinking-target experiment demonstrates that the encoding of saccade goals is not limited to visible targets: When the trajectory of target motion is predicable, PBN activity encodes an internal estimate of target trajectory in time and space during brief periods when the target is not visible. This is in part accomplished by a rate code in which the relationship between firing rate and target distance for visible targets is largely preserved for virtual targets. However, our results also are consistent with virtual-target position being represented by a place code. A key observation of the present study is that response functions for both real and virtual targets peak at about the same best RPE (Fig. 4C, Fig. 6, C and D). This implies that the hot spots of activity for a real and a virtual target at the same RPE are located in approximately the same physical site within the PBN. Furthermore, when the target moves on the retina, the path traced by the evoked moving hot spot (the peak of a spatial “hill” of activity) will be similar for the real and virtual targets, but the hill will be wider and flatter for virtual than for real targets and will get progressively flatter as the time without visual input increases, a phenomenon predicted by the hypothesis that the PBN computes an optimal estimate of target position.

Our analysis indicates that the accuracy of encoding virtual target location decays with time from target offset for both rate and place codes. For the first 200 ms after target disappearance both codes in the PBN are excellent, but both decay somewhat in the next 200 ms. The rate code, as quantified by the VRI, decays from 94% of the response to real targets to 64% within 200–400 ms after target disappearance. The place code, judged by the correlation of peaks of response functions for real and virtual targets, also decays between these two intervals: R² decays from 0.72 to 0.51; the slope decays from 0.87 (P = 0.64) to 0.61 (P = 0.04). Although there are no obvious grounds for ranking the importance of one code above the other, the addition of population encoding eliminates the ambiguity that would be associated with a rate code based on a single-neuron response function.

The saccadic interception of moving targets is fairly robust in the face of involuntary saccades induced by SC electrical stimulation, even in the absence of visual stimuli (Fleuriet and Goffart 2012). The rapid resetting of PBN activity after saccades in the dark clearly demonstrates a nonvisual contribution that can provide such compensation, and the timing of the resetting suggests that proprioceptive signals may be involved. One candidate for the resetting signal, the nucleus prepositus hypoglossi (NPH), projects to the PBN (Baleydier and Magnin 1979) and is believed to supply an internal model of eye position during saccades via the integration of velocity signals (Cannon and Robinson 1987). The NPH also receives proprioceptive signals from orbital tissue, which could provide eye position information to the PBN (Ashton et al. 1988). Another potential source of proprioceptive signals has been discovered in primary somatosensory cortex of awake, behaving monkeys (Wang et al. 2007), and this might have access to the PBN via cortical inputs to the SC. If the saccade-related resetting of PBN activity is due to neural integration in the NPH, it should begin before or slightly after saccade onset (Escudero et al. 1992). If, on the other hand, it reflects proprioceptive inputs, changes in PBN activity should significantly lag saccades. The latency relative to saccade onset was 56 ms, which is consistent with proprioceptive inputs and inconsistent with efference copy.

Comparison of PBN and SC responses to virtual targets.

Given the high degree of interconnectivity between the SC and the PBN, one may wonder to what extent the properties of cells in the latter reflect those of the former. Although substantial differences in behavioral paradigms between previous experiments on the SC and the present study of the PBN make quantitative comparisons impossible, the literature on the cat SC points to several similarities. SC activity appears to retinotopically encode the tracked midpoint of two visible targets (Hafed and Krauzlis 2008). Also, SC activity rates encode target distance during intersaccade periods, including positions of unseen targets (Bergeron et al. 2003; Munoz and Guitton 1991). The close correspondence of the shapes and peaks of response functions for real and virtual targets suggests that whatever pattern of activity is evoked in the PBN by a moving visible target is repeated for a virtual target with the same trajectory. This is similar to the “quasi-visual” cells of the primate SC described by Mays and Sparks (1980): Both encode the retinal position error of visible and invisible targets, both take into account changes in eye position via a nonvisual signal, and neither exhibits a motor component of activity.

As opposed to the SC, there is no hint of any motor component in PBN activity. In particular, saccade-related changes in activity clearly lag all phases of saccades (start, peak velocity, and termination), whether saccades are to visible moving or stationary targets, are evoked by virtual moving targets, or are spontaneously made in the dark (Cui and Malpeli 2003). McPeek and Keller (2002) examined SC activity in monkeys making saccades to targets hidden among distractors. Although not directly comparable to our dual-target task (which is based on choice rather than search), it is interesting to note that they observed target discriminatory activity only in cells whose activity displayed a motor component and not in those with pure sensory responses. The fact that PBN responses are target specific, although they show no motor component, suggests that the PBN-SC circuit may be involved in the development of target-specific responses in movement-related SC cells.

Specificity of PBN activity.

The interpretation of all of the single-target tasks hinges on the assumption that PBN activity is specific to the attended target. The results of the dual-target task provide a direct verification of this assumption. Although these data are limited to multiple-unit activity obtained from a few recording sites, the differences in activity evoked by the target to which the animal will subsequently launch a saccade and that evoked by the alternative target were profound. This activity was predictive of target choice well before any motor act was initiated. Thus the PBN appears to be engaged not by visual stimuli in general but specifically by the current subjective choice of a potential saccade target. These results support Cui and Malpeli's (2003) suggestion that PBN activity encodes target position without regard to physical features of the target. The fact that the PBN encodes the extrapolated positions of virtual targets in both time and space is also consistent with this idea, because a virtual target has no physical features. It may be that PBN neurons encode not real or virtual target position per se but the expected utility of targets. In simplest form, the expected utility would be the probability of a target at a specific location weighted by target utility, which would be higher for a target that a cat is currently pursuing than for one it has chosen to ignore.

The increase in PBN activity associated with saccades toward the response field in the dual-target task began ∼350 ms before saccade start and monotonically increased up to the point of saccade onset (Fig. 9F). The gradual buildup of activity may have resulted from attention becoming progressively more focused in each individual trial up to the point of saccade onset. Alternatively, it is possible that when attention was biased toward one target it resulted in a stepwise increase of activity that was maintained until saccade onset but that the time between the shift of attention and the launching of the saccade varied from trial to trial. At present we cannot disentangle these possibilities, in large part because our data are from multiple units.

Outcome of optimal inference model.

Our optimal inference model of virtual target tracking produced results that are quite similar to the empirical data. In particular, the model explains why PBN activity overestimates virtual target position for low (and negative) and high RPE but underestimates it for RPE at and near the peak of the response function, and why response functions broaden with time as the animal tracks virtual targets. The decaying sigmoid function that was fitted to the response functions of each cell (i.e., Fig. 2, solid curves) fits the simulated real and virtual PBN response functions equally well (Fig. 10). Still, our goal in modeling PBN activity from an optimal-inference viewpoint was not to match any specific piece of empirical data exactly but to capture the essential features of PBN responses in general. These outcomes are fundamental to the algorithm and are independent of parameter values—they are a natural outcome of the increased uncertainty of virtual target position with time. Of particular relevance here is the study of Hafed and Krauzlis (2008), in which monkeys were required to track the midpoint between two visible targets. They report that the tracked virtual goal activates the appropriate location in the SC and that this activated area is broadened relative to the tracking of a real target—a broadening that they attribute to the uncertainty of the location of the virtual target.

Overall, these results are consistent with the idea that the estimation of virtual-target position as encoded in the PBN may be derived from a predictor-corrector mechanism. The predictive component could, in principle, be implemented via positive feedback occurring within the PBN or between the PBN and SC. The lack of data on the synaptic organization of the PBN precludes further speculation concerning how a predictive computation may actually be implemented.

Function of the PBN in visuomotor behavior.

It is well established that the oculomotor system utilizes predictions about target trajectories to guide saccades to moving targets, including those that are briefly blinked off (Barborica and Ferrera 2004; de Brouwer et al. 2001). Visual tracking of moving targets involves a coordinated interplay between the saccade and smooth pursuit systems, and although these systems are dominated by position and motion signals, respectively, stimulus motion affects the programming of saccades and stimulus position affects pursuit velocity (see Orban de Xivry and Lefèvre 2007 for a comprehensive review). Consistent with this interplay, activity in the SC, whose output directs saccades to specific spatial locations, is also influenced by moving targets that are fixation goals (see Krauzlis 2004 for a review), and this activity is maintained during blinks of targets as they are tracked via smooth pursuit (Krauzlis 2001). It appears that the PBN displays such encoding in a highly purified form without the complication of motor-related responses, providing dynamic moment-to-moment estimations of the retinotopic position of unseen, moving targets based on their last observed trajectories. These estimates are quickly updated after eye movements, using information consistent in timing with orbital proprioceptive signals. Acting as a satellite of the SC, the PBN could receive sensory and eye movement input from the SC (and elsewhere) and use that to maintain an estimate of current target position based in part on an estimation of future target position that could be generated by the PBN itself. The PBN could send its target position estimate back to the SC to activate or facilitate the activation of SC neurons that would command saccades to the positions specified by the PBN.

Our experiments do not directly address the questions of how and where the signals that underlie the PBN response are generated or how the PBN response is used to guide visuomotor behavior. We do not know which characteristics of PBN activity are generated internally, which are generated in the SC and transmitted to the PBN, which depend on interactions between the two structures, and which are generated outside of the midbrain and transmitted through the SC to the PBN. We do not know whether these signals are used for immediate guidance of saccades to targets, involved in longer-term calibrations of the saccade system, or, perhaps, relayed to cortex via the SC and pulvinar to aid in target localization at levels well above saccade initiation circuits. We can only speculate that in addition to continuously encoding the positions of visible saccade targets, the PBN through its interactions with the SC may play a formative role in extrapolating the trajectory of unseen moving targets.

GRANTS

This research was supported by National Eye Institute Grant EY-14558 and by the National Science Foundation (Grant 0080789).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

ENDNOTE

At the request of the authors, readers are herein alerted to the fact that additional materials related to this manuscript may be found at the institutional website of one of the authors, which at the time of publication they indicate is http://malpeli.psychology.illinois.edu/papers/Ma_et_al_PBN_2013_supplementary.pdf. These materials are not a part of this manuscript, and have not undergone peer review by the American Physiological Society (APS). APS and the journal editors take no responsibility for these materials, for the website address, or for any links to or from it.

AUTHOR CONTRIBUTIONS

Author contributions: R.M., H.C., S.-H.L., T.J.A., and J.G.M. conception and design of research; R.M., H.C., S.-H.L., T.J.A., and J.G.M. performed experiments; R.M., H.C., S.-H.L., T.J.A., and J.G.M. analyzed data; R.M., H.C., S.-H.L., T.J.A., and J.G.M. interpreted results of experiments; R.M., H.C., S.-H.L., T.J.A., and J.G.M. prepared figures; R.M., H.C., S.-H.L., T.J.A., and J.G.M. drafted manuscript; R.M., H.C., S.-H.L., T.J.A., and J.G.M. edited and revised manuscript; R.M., H.C., S.-H.L., T.J.A., and J.G.M. approved final version of manuscript.