A computational model for optimal muscle activity considering muscle viscoelasticity in wrist movements

Abstract

To understand the mechanism of neural motor control, it is important to clarify how the central nervous system organizes the coordination of redundant muscles. Previous studies suggested that muscle activity for step-tracking wrist movements are optimized so as to reduce total effort or end-point variance under neural noise. However, since the muscle dynamics were assumed as a simple linear system, some characteristic patterns of experimental EMG were not seen in the simulated muscle activity of the previous studies. The biological muscle is known to have dynamic properties in which its elasticity and viscosity depend on activation level. The motor control system is supposed to consider the viscoelasticity of the muscles when generating motor command signals. In this study, we present a computational motor control model that can control a musculoskeletal system with nonlinear dynamics. We applied the model to step-tracking wrist movements actuated by five muscles with dynamic viscoelastic properties. To solve the motor redundancy, we designed the control model to generate motor commands that maximize end-point accuracy under signal-dependent noise, while minimizing the squared sum of them. Here, we demonstrate that the muscle activity simulated by our model exhibits spatiotemporal features of experimentally observed muscle activity of human and nonhuman primates. In addition, we show that the movement trajectories resulting from the simulated muscle activity resemble experimentally observed trajectories. These results suggest that, by utilizing inherent viscoelastic properties of the muscles, the neural system may optimize muscle activity to improve motor performance.

an ongoing goal in motor neuroscience is to understand how the central nervous system (CNS) organizes body coordination. The dynamics of the musculoskeletal system permit redundancy in the performance of motor tasks. Body coordination involves finding an optimal solution from the redundant set of possible candidates. With regard to a hand-reaching task, for example, there are infinite possible patterns of joint motion to reach a single target. In addition, since the total number of muscles exceeds that of the joints, infinite muscle activation patterns can result in the same joint motion. However, despite these biomechanical redundancies, stereotypical motor patterns have been observed in a variety of voluntary movements. It is well known that the tangential velocity profile of a reaching movement is bell-shaped (Morasso 1981; Atkeson and Hollerback 1985; Uno et al. 1989). In reaching tasks of the upper limb (Flanders et al. 1996) and step-tracking wrist rotation tasks (Hoffman and Strick 1999), muscle activities are modulated in a smooth cosine-like fashion as a function of target direction.

In computational motor neuroscience, optimal control theory has been utilized to explain the neural mechanism in which particular motor patterns are favored among infinite possible alternatives. Many optimal control models for reaching tasks have succeeded in predicting stereotypical kinematic patterns of movement trajectories (Flash and Hogan 1985; Uno et al. 1989; Harris and Wolpert 1998; Nakano et al. 1999; Sakaguchi and Ikeda 2007; Ben-Itzhak and Karniel 2008). Most of those models were designed to optimize movement trajectory or joint torque. Since the relationship between joint torque and muscle recruitment is one-to-many, it is an ill-posed problem to derive a set of activation levels across multiple muscles from a given joint torque. On the contrary, a unique joint torque is determined from a given set of muscle activation levels. Therefore, an optimal movement trajectory can be automatically derived from optimal muscle activity. Several optimal control models have been proposed to predict movement trajectory of upper limb movements by directly optimizing muscle activation levels (Lan 1997; Gonzalez et al. 1999; Kashima et al. 2000; Ohta et al. 2004). Although Gonzalez et al. (1999) succeeded in predicting a triphasic temporal muscle burst pattern in reaching movements, it was not reported if their models can predict spatiotemporal characteristics of muscle activation, e.g., cosine-like spatial modulation. Haruno and Wolpert (2005) applied the minimum variance model (Harris and Wolpert 1998) to a linear wrist musculoskeletal system and succeeded in predicting some of the spatiotemporal characteristics of muscle activity observed in the experiment of Hoffman and Strick (1999). However, they mentioned the necessity of a more realistic muscle model to predict experimentally observed muscle activation patterns that were not predicted in their simulation.

In Hoffman and Strick (1999), human and monkey subjects performed point-to-point wrist rotations, hereafter referred to as step-tracking wrist movements, while grasping the handle of a two-axis manipulandum. The manipulandum was designed to measure the angles of the wrist in the planes of flexion-extension and radial-ulnar deviation. The two angles were mapped onto the horizontal and vertical axes of a screen, and a cursor moved on the screen in proportion to wrist rotations. Subjects were required to make step-tracking movements from a starting point, corresponding to the neutral position of the wrist, to different target points arranged in a circle around the starting point. Electromyographic (EMG) recordings of four wrist muscles demonstrated several characteristic spatiotemporal patterns in the muscle activity: 1) an amplitude-graded pattern in which only the amplitude of muscle burst varies over movement direction, 2) a temporally shifted pattern in which the timing of muscle burst systematically changes over movement direction, 3) an early suppression in which the activation level is suppressed before movement onset, 4) a cosine tuning of both agonist and antagonist integrated muscle activities with movement direction, 5) a mismatch between the directions of maximum agonist activity (agonist preferred direction) of each muscle and their pulling directions, and 6) an asymmetric relationship of agonist and antagonist preferred directions for each muscle. In addition to these muscle activation patterns, some spatiotemporal features can be found in the movement trajectories. Cursor paths were almost straight for the four targets on the axes of flexion-extension and radial-ulnar deviation. However, when the movements included some degree of radial/ulnar deviation, the paths were convex upward/downward. Also, peak tangential velocities during radial and ulnar deviation movements were larger than those during flexion and extension movements. As a result, movement durations were shorter for radial and ulnar deviation than flexion and extension.

Recently, we proposed a motor control model for reaching tasks and showed that it can predict experimentally observed trajectories of upper limb point-to-point reaching movements (Kambara et al. 2009). One of the main features of our model is that it can generate a command signal at the muscle level. Therefore, it can be utilized to simulate muscle activities during movement. In addition, it can be applied to nonlinear dynamical systems. In this study, we applied our motor control model to step-tracking wrist movements actuated by mathematical muscles that change their viscoelastic properties according to activation level. We chose to consider wrist movement because the associated spatiotemporal patterns have been well studied by Hoffman and Strick (1999). Another feature of our model is that it possesses two controllers, an inverse statics model and a feedback controller. The inverse statics model is the feedforward controller that can control equilibrium of the musculoskeletal system. The two controllers are optimized, in a trial-and-error manner, by the combination of the actor-critic method (Doya 2000) and feedback-error-learning scheme (Kawato et al. 1987). Utilization of the two controllers in motor control offers goal-directed point-to-point movements in which a desired trajectory is no longer needed. Furthermore, the duration of movement becomes a result of motor control optimization instead of a constraint for the optimization. Here, we demonstrate that the optimization of wrist movement actuated by viscoelastic muscle models yields a better prediction of the spatiotemporal muscle activation patterns observed in Hoffman and Strick (1999). Further, we show that our motor control model can predict the dependency of movement curvature and duration on movement direction.

METHODS

Motor Control Model

Figure 1 shows a schematic block diagram of the motor control model applied to step-tracking wrist movements. At the beginning of each trial, a target position of the wrist is given to the model. The position of the wrist is defined by the set of joint angles in flexion-extension and radial-ulnar deviation. Motor command signals are determined at every time step during the movement given a sensory feedback signal of the wrist musculoskeletal system. Therefore, it can be said that the entire motor control system works as a feedback controller. The model consists of three components, an inverse statics model (ISM), a forward dynamics model (FDM), and a feedback controller (FBC). The role of each component is as follows. First, the ISM generates a set of static feedforward motor commands that remain constant throughout the movement. It receives the target position as an input and generates the motor commands shifting the wrist's equilibrium position to the target. Second, the FDM predicts a subset of the wrist's state. It takes the efference copy of the current motor command and sensory feedback of the current wrist state as input. Then, the FDM predicts the position that the wrist will reach after a few hundred milliseconds. Let us call it a predicted future position for the simplicity. The FDM also predicts a time derivative of the predicted future position. Finally, the FBC generates a feedback motor command. It receives the error between the target and predicted future position of the wrist and its time derivative. The total sum of the outputs of the ISM and FBC becomes the motor command for the muscles.

Fig. 1.

Schematic block diagram of the motor control model for step-tracking wrist movement. At the beginning of each movement, a target position θ^d is given to the model. Here, the position of the wrist is defined by the vector θ = [θ₁, θ₂]^T, where θ₁ and θ₂ are joint angles of flexion-extension and radial-ulnar deviation, respectively. At every time step t, the model generates a motor command u(t) given a wrist state x(t). The model has 3 main components, the inverse statics model (ISM), feedback controller (FBC), and forward dynamics model (FDM). The ISM generates a time-invariant feedforward motor command u^ism that shifts the wrist's equilibrium to the target position θ^d. At every time step t, the FBC generates a feedback motor command u^fbc(t) that reduces a position error θ^e(t) [= θ^d − θ^p(t)] and its time derivative θ̇^e (t). Here, the vector θ^p(t) is a predicted position that the wrist will reach after T_f seconds from time step t. The predicted position θ^p(t) and its time derivative θ̇^p(t) are predicted by the FDM, given an efference copy of the motor command u(t) and the wrist state x(t). Finally, the sum of u^ism and u^fbc(t) becomes the motor command u(t) sent to the wrist muscles. Note that the state vector of the wrist is defined as x(t) = [θ(t)^T, θ̇(t)^T, a(t)^T, ȧ(t)^T ]^T, where θ̇(t), a(t), and ȧ(t) are a time derivative of the wrist position, muscle activation level, and its time derivative, respectively.

Note that the reaching movements can be generated without desired trajectory in our motor control model. The concept of goal-directed feedback control without a predetermined trajectory has produced successful results in predicting the features of several human movements (Todorov and Jordan 2002). In our model, the feedback controller is designed to work moderately well within the workspace, i.e., the feedback controller is not optimized for one particular target. It is optimized averagely for all targets. A drawback, however, is that this will worsen the end-point accuracy because the static force required to hold the wrist at a target depends on the target location. The ISM, the other controller in our model, can compensate for the position dependent static force at the target. Therefore, utilizing both the ISM and FBC will keep the FBC from being optimized for each target, while the end-point accuracy of the movement is assured.

Finally, the FDM is designed to predict the future state of the wrist joint, including the position and its time derivative. The muscle dynamics are known to have a second-order time delay between motor command and force generation (Mannard and Stein 1973). Because of this delay, the feedback command signal should be taken into account for stable control of not only wrist position and its time derivative but also muscle tension and its time derivative. However, the number of muscles is much larger than the number of joints. Therefore, the dimensions of the FBC input greatly increase, and optimization of the FBC becomes more difficult. To avoid the increase in dimensionality of the FBC input, we designed the FDM to predict future position of the wrist and the FBC to calculate the feedback command from the FDM prediction.

Musculoskeletal Model of the Wrist

In our simulation, the wrist is modeled as a dynamical system with two degrees of freedom moving in the planes of flexion-extension and radial-ulnar deviation. It is actuated by five wrist muscles; extensor carpi radialis longus (ECRL), extensor carpi radialis brevis (ECRB), extensor carpi ulnaris (ECU), flexor carpi radialis (FCR), and flexor carpi ulnaris (FCU). We assume that the forearm posture is in the middle of full pronation and full supination. The joint dynamics of the wrist in each of the flexion-extension and radial-ulnar directions is modeled as a linear mass-spring-damper system,

$${\tau }_i=M_i{\ddot{\theta }}_i+B_i{\dot{\theta }}_i+K_i{\theta }_i$$ (1)

where τ_i, θ_i, M_i, B_i, and K_i denote torque, angle, inertia, viscosity, and stiffness for the ith direction (i = 1, 2), respectively. The indexes i = 1 and 2 correspond to flexion-extension and radial-ulnar deviation, respectively. The θ₁ and θ₂ become positive when the wrist is moved toward extension and radial deviation, respectively.

We used a mathematical muscle model designed to have elastic and viscous elements in force generation. The elastic and viscous terms are approximated as linear functions of the activation level. In addition, the rest length of the muscle depends linearly on the activation level. This kind of muscle model is frequently used in computational simulations of upper limb movements (Katayama and Kawato 1993; Izawa et al. 2004; Kambara et al. 2009; Kim et al. 2009). Shin et al. (2009) incorporated this muscle model into a myokinetic arm model based on anatomical and physiological data. Their model succeeded in reproducing joint torque and stiffness from EMG signals. Here, the muscle tension T_j of the jth muscle is determined as

$$T_j\left(\theta ,\dot{\theta },a_j\right)=\left(k_j^0+k_j^1{a}_j\right)\left(l_j^0+l_j^1{a}_j-{\displaystyle \sum _{i=1}^2{d}_{ji}{\theta }_i}\right)-\left(b_j^0+b_j^1{a}_j\right)\left({\displaystyle \sum _{i=1}^2{d}_{ji}{\dot{\theta }}_i}\right)$$ (2)

where a_j is the activation level of the jth muscle (j = 1,…,5). The vectors θ = [θ₁, θ₂]^T and θ̇ = [θ̇₁, θ̇₂]^T represent the wrist's position and its time derivative, respectively. Meanwhile, k_j⁰ and b_j⁰ are the intrinsic elasticity and viscosity of the jth muscle, respectively. The k_j¹ and b_j¹ are the variation rates of elasticity and viscosity, respectively. The l_j⁰ and l_j¹ are the parameters with respect to the muscle's stretch length. Finally, d_ji is the moment arm of the jth muscle against ith rotation. The parenthetic terms in Eq. 2 represent, respectively, from left to right, the elastic coefficient, stretch length, viscosity coefficient, and contraction rate of the jth muscle. Here we assume that the displacement of the muscle length is approximated by the product of the joint angle displacement and moment arm. The moment arm of the jth muscle is determined by its pulling direction ϕ_j as follows.

$$\left[d_{j1},d_{j2}\right]=R\left[\sin {\phi }_j,\cos {\phi }_j\right].$$ (3)

Here, R represents combined magnitude of the moment arm. The pulling direction of each muscle is defined as the direction of wrist movement induced by an electrostimulation of that muscle in isolation (Hoffman and Strick 1999). We set the pulling directions ϕ_j in accordance with the values used in the simulation by Haruno and Wolpert (2005). The values are shown in Table 1. The joint torque is then determined as the sum of the products of muscle tensions and moment arms

$${\tau }_i={\displaystyle \sum _{j=1}^5{d}_{ji}{T}_j}$$ (4)

The relationship between muscle activation level a_j and motor command signal u_j is described as a second order linear system,

$$u_j={\kappa }_1{\kappa }_2{\ddot{a}}_j+\left({\kappa }_1+{\kappa }_2\right){\dot{a}}_j+a_j$$ (5)

where u_j is the motor command for the jth muscle. The parameters κ₁ and κ₂ are time constants representing excitation and activation, respectively. The range of u_j is constrained from 0 to 1. In addition, values of κ₁ and κ₂ used in the simulation (described in the next section) ensured a_j was constrained from 0 to 1.

Table 1.

Muscle's pulling direction

	ECRL	ECRB	ECU	FCU	FCR
Pulling direction	1.6°	18.4°	159.5°	198.3°	304.5°

Values of pulling directions are cited from Haruno and Wolpert (2005). ECRL, extensor carpi radialis longus; ECRB, extensor carpi radialis brevis; ECU, extensor carpi ulnaris; FCR, flexor carpi radialis; FCU, flexor carpi ulnaris. 0° = radial deviation; 90° = extension; 180° = ulnar deviation; 270° = flexion.

As a result, the state vector of the entire wrist musculoskeletal system becomes x(t) = [θ(t)^T, θ̇(t)^T, a(t)^T, ȧ(t)^T ]^T. The motor command vector of the system is u(t) = [u₁(t),…,u₅(t)]^T. Differential equations of the state transition can be drawn by Eqs. 1–5.

The musculoskeletal parameter values that we used for our simulation are listed in Table 2 with their biologically plausible ranges. The ranges were determined from past anatomical and biomechanical studies as follows. The combined magnitude of moment arm at the neutral posture ranges from 0.010 to 0.023 m among the five wrist muscles (Loren et al. 1996). Charles and Hogan (2012) calculated the range of moment of inertia for the hand by applying the inertial parameter equation (de Leva 1996). Their values ranged from 0.0010 to 0.0033 kg m² in flexion-extension and from 0.0011 to 0.0038 kg m² in radial-ulnar deviation. In addition, the inertia of the manipulandum used by Hoffman and Strick (1999) was 0.0025 kg m² in radial-ulnar deviation, while for flexion-extension, Charles and Hogan (2012) estimated a value of 0.0050 kg m². In accordance with these values, we determined the possible range of the combined inertia of the hand and the manipulandum to be 0.0036 kg m² (minimum value in radial-ulnar deviation) to 0.0083 kg m² (maximum value in flexion-extension). The passive viscosity of the wrist was estimated to be from 0.020 to 0.033 Nms/rad for the direction of flexion extension (Gielen and Houk 1984). The passive stiffness ranges from 0.33 (Gielen and Houk 1984) to 3 Nm/rad (De Serres and Milner 1991) in the direction of flexion-extension.

Table 2.

Musculoskeletal parameters

Parameter	Value in the Simulation	Biologically Plausible Range
R, m	0.015	0.01 to 0.023
Mi, kg m2	0.005	0.0036 to 0.0083
Bi, Nms/rad (i = 1, 2)	0.03	0.0197 to 0.0328
Ki, Nm/rad (i = 1, 2)	0.1	0.33 to 3
kj0, N/m (j = 1,…,5)	1,000	880 to 2,510
kj1, N/m (j = 1,…,5)	3,000	1,760 to 5,020
bj0, Ns/m (j = 1,…,5)	100	60 to 170
bj1, Ns/m (j = 1,…,5)	300	120 to 340
lj0, m (j = 1,…,5)	0.033	—
lj1, m (j = 1,…,5)	0.07	—
κ1, s	0.0926	—
κ2, s	0.0605	—

See text for definitions.

While joint stiffness and viscosity of the wrist were measured or estimated by past studies, the coefficients of wrist muscle elasticity (k⁰, k¹) and viscosity (b⁰, b¹) were not estimated directly. To determine the range of those parameters, we used joint stiffness of the wrist estimated by Kawase et al. (2012). In their experiment, wrist joint torque of flexion-extension was represented by a function of EMG signals and the joint angle. The parameters in the function were optimized so as to match measured and estimated torque. By differentiating the function with the joint angle, joint stiffness can be estimated from EMG signals alone. The estimated stiffness in the direction of flexion-extension ranged from 0.2 to 0.57 Nm/rad for the relaxed wrist among seven subjects (personal communication). The stiffness estimated from EMG signals reflects the muscle elasticity (Shin et al. 2009), and the value for the relaxed wrist is considered to originate from intrinsic muscle elasticity, namely k⁰. The relationship between k₀ and the joint stiffness can be derived by differentiating Eq. 4 by θ and substituting u = 0 (see also Eq. 2). Therefore, we determined the range of k⁰ so as to match the range of the estimated stiffness of Kawase et al. (2012). The range of k¹ was set to the twice of the range of k⁰. This was because the range of estimated stiffness at 50% maximum voluntary contraction in Kawase et al. (2012) was nearly twice the range for a relaxed wrist (personal communication). In addition, we determined the ranges of b⁰ and b¹ using ratios with k⁰. In Katayama and Kawato (1993), b⁰ equaled 0.067 k⁰ and b¹ was twice of b⁰. We applied these ratios to the range of k⁰ and calculated the ranges of b⁰ and b¹.

For the computer simulation, we set the values of the parameters as follows. In accordance with the simulation of Haruno and Wolpert (2005), the inertia, viscosity, and stiffness of the wrist were set to M_i = 0.005 kg m², B_i = 0.03 Nms/rad, and K_i = 0.1 Nm/rad for both i (= 1, 2). Next, the combined magnitude of moment arm was set to R = 0.015 m. Muscle parameters were set to k_j⁰ = 1,000 N/m, k_j¹ = 3,000 N/m, b_j⁰ = 100 Ns/m, b_j¹ = 300 Ns/m, l_j⁰ = 0.033 m, and l_j¹ = 0.07 m. With the exception of l_j⁰, these values were set so that the average duration of simulated step-tracking movements were nearly the same as the experimental data of Hoffman and Strick (1999). The value of l_j⁰ is determined as the minimum value that keeps the intrinsic stretch length (l_j⁰ −∑_j=1² d_jiθ_i) of all muscles positive within the range of −90° ≤ θ₁, θ₂ ≤ 90°. Note that all four parameters k⁰, k¹, b⁰, and b¹ are within the possible range listed in Table 2. Since the possible range of l⁰ and l¹ could not be derived from past studies, we cannot confirm if the values used in our simulation are in biological range. However, the maximum joint torque calculated by Eqs. 2 and 4 with the parameters listed above lays within reasonable range. The range of maximum wrist toque in flexionextension and radial-ulnar deviations is 3.4 to 18.7 Nm (Delp et al. 1996). Their range in our musculoskeletal model was 3.7 to 14.6 Nm. Finally, time constants in Eq. 5 were set to κ₁ = 92.6 ms and κ₂ = 60.5 ms. The values of the two time constants were used for reconstructing muscle tension from surface EMG in humans (Koike and Kawato 1995).

Computer Simulation of Step-Tracking Wrist Movements

Implementation of the motor control model.

In the following, we describe how the motor control model shown in Fig. 1 is implemented in the computer simulation. First, the FDM in the model is implemented by using the equations of the wrist's dynamics (Eqs. 1–5). Given the current state of the wrist x(t) and the efference copy of the motor command u(t), the FDM predicts future position θ^p(t), the position that the wrist will reach within T_f [s] from time t, and its time derivative θ̇^p(t). Note that the superior “p” of θ^p(t) and θ̇^p(t) is adopted from the term “prediction.” The predicted future position and its time derivative are calculated by iteratively integrating the differential equations of the wrist dynamics. A fourth-order Runge-Kutta method is used for numerical integration with step time Δt[s]. Then numerical integrations are iterated T_f/Δt times while fixing the motor command at u(t). In the simulation, we set T_f as 120 ms.

Next, the ISM and FBC are each implemented with normalized Gaussian radial basis function networks (Bugmann 1998). The input and output dimensions of the ISM network are two and five, respectively. The input vector is the target position θ^d = [θ₁^d, θ₁^d]^T, in which the superior “d” is adopted from the term “desired.” The output vector is the feedforward motor command u^ism = [u₁^ism,…,u₅^ism]^T. The ISM network has 17 × 17 Gaussian basis functions located on a grid with an even interval in each dimension of the input space −80° ≤ θ₁^d, θ₂^d ≤ 80°. The logistic sigmoid function is applied to the output of the network so as to keep the feedforward motor command in the range 0 ≤ u_j^ism ≤ 1.

The dimensions of input and output vectors of the FBC network are four and five, respectively. The input vector at time t is described as [θ^e(t)^T, θ̇^e(t)^T ]^T, where θ̇^e(t) is the error between target θ^d and predicted future position θ^p(t), such that θ^e(t) = θ^d − θ^p(t). θ̇^e(t) is the time derivative, where θ̇^e(t) = −θ̇^p(t). Here the superior “e” is adopted from the term “error.” The output vector is the feedback motor command u^fbc(t) = [u₁^fbc(t),…,u₅^fbc(t)]^T. The FBC network has 11 × 11 × 9 × 9 Gaussian basis functions located on a grid with an even interval in each dimension of the input space −120° ≤ θ₁^e, θ₂^e ≤ 120° and −720°/s ≤ θ̇₁^e, θ̇₂^e ≤ 720°/s. The range of the feedback motor command is constrained to −0.5 ≤ u_j^fbc(t) ≤ 0.5 by subtracting 0.5 from each element of the network's output after applying the logistic sigmoid function.

Finally, the total motor command u_j(t) is determined by the following equation, so as to take a value within the range from 0 to 1.

$$u_j\left(t\right)=\{\begin{array}{l}0\text{f}\text{or}{u}_j^{ism}\left(t\right)+u_j^{fbc}\left(t\right)<0\hfill \\ 1\text{f}\text{or}{u}_j^{ism}\left(t\right)+u_j^{fbc}\left(t\right)>1\hfill \\ u_j^{ism}\left(t\right)+u_j^{fbc}\left(t\right)\text{otherwise}\hfill \end{array}$$ (6)

Network training.

For the motor control model to work appropriately, the networks of the ISM and FBC have to be trained. We used a learning algorithm (Kambara et al. 2009) that can simultaneously train both of the networks during training trials of step-tracking movements. The learning algorithm is a combination of the feedback-error-learning scheme (Kawato et al. 1987) and the actor-critic method (Doya 2000), which is one of the major frameworks of reinforcement learning. The FBC network is trained by the actor-critic method in which the instantaneous reward evaluating movement performance is defined as

$$r\left(t\right)=\exp \left(-\frac{{\Vert {\theta }^d-\theta \left(t\right)\Vert }^2}{{\sigma }^2}\right)-k^u{\Vert \text{u}\left(t\right)\Vert }^2$$ (7)

where σ and k^u are parameters that affect movement accuracy and command signal magnitude, respectively. A small σ requires more accuracy, and a large k^u requires less motor command magnitude. In our study, we set those values to σ = 5° and k^u = 0.075. The weight parameters in the FBC network are trained so as to maximize cumulative reward signal. The ISM network, on the other hand, is trained with a feedback-error-learning scheme in which the output of the FBC network is used as the error signal. In other words, it is trained so as to make the output of the FBC 0 when the wrist is in the target position. Detailed equations for the update rules of weight parameters can be found in Kambara et al. (2009).

In the training trials, we also added biological noise w_j(t) to the motor command u_j(t),

$$u_j\left(t\right)\leftarrow u_j\left(t\right)+w_j\left(t\right)$$

The noise w_j(t) is modeled as a Gaussian noise with zero mean and variance of k^sdnu_j²(t). In the training trials, we set the coefficient of the noise to k^sdn = 0.01. The reason we introduce this kind of signal-dependent noise (SDN) is that it is an inherent property of the musculoskeletal system (Harris and Wolpert 1998). In addition, it seems to affect the result of the network training. The effect of the signal-dependent noise on network training is explained further in the discussion.

The whole network training consisted of 50,000 training trials of step-tracking wrist movement. At the beginning of each trial, the initial position of the wrist was determined randomly within the range of −70° ≤ θ₁, θ₂ ≤ 70°. The target was also determined randomly within the same range. The state of the wrist x(t) was updated in every 0.01 s by integrating the differential equations of the wrist with the fourth-order Runge-Kutta method. The motor command u(t) and weight parameters in the network were also updated every 0.01 s. Each trial lasted 2 s.

After the 50,000 training trials, we tested whether the motor control model had been implemented properly to generate accurate step-tracking movements toward arbitrary targets. Step-tracking movements were simulated using the trained networks on 900 different targets equally spaced within the range of −70° ≤ θ₁, θ₂ ≤ 70°. For each of the 900 targets, 10 step-tracking movements were simulated starting from randomly chosen initial positions. Accuracy was measured as the distance between the target and wrist position at the last moment of each movement. We confirmed that all movements ended within 1° of the targets. Mean and standard deviation of movement accuracy were 0.26 and 0.14°, respectively. From this result, we can infer that the networks of the ISM and FBC in the motor control model were trained properly. Note that the same weight parameter sets of the ISM and FBC networks were used to simulate all step-tracking movements. That is, the weight parameters in the two networks were not optimized for one particular target. Instead, they were tuned to optimize average performance of the step-tracking movements against all targets within the range.

Simulation of step-tracking wrist movement.

Center-out step-tracking wrist movements were simulated using the motor control model with weight parameter sets trained after 50,000 trials. Sixteen targets were positioned radially around the neutral position of the wrist (Fig. 2A). Each target was identified according to its clock time position. For example, the target in the middle of target 12:00 (radial deviation) and 3:00 (extension) is denoted as 1:30. Each movement started from the central neutral position. The distance from the neutral position to the targets was 20°. In each trial, the θ^d given to the model was set to the neutral position for 1 s. We refer this time period as the holding period. After the holding period, the θ^d was switched to 1 of the 16 targets. The wrist state and motor command were updated every 0.001 s.

Fig. 2.

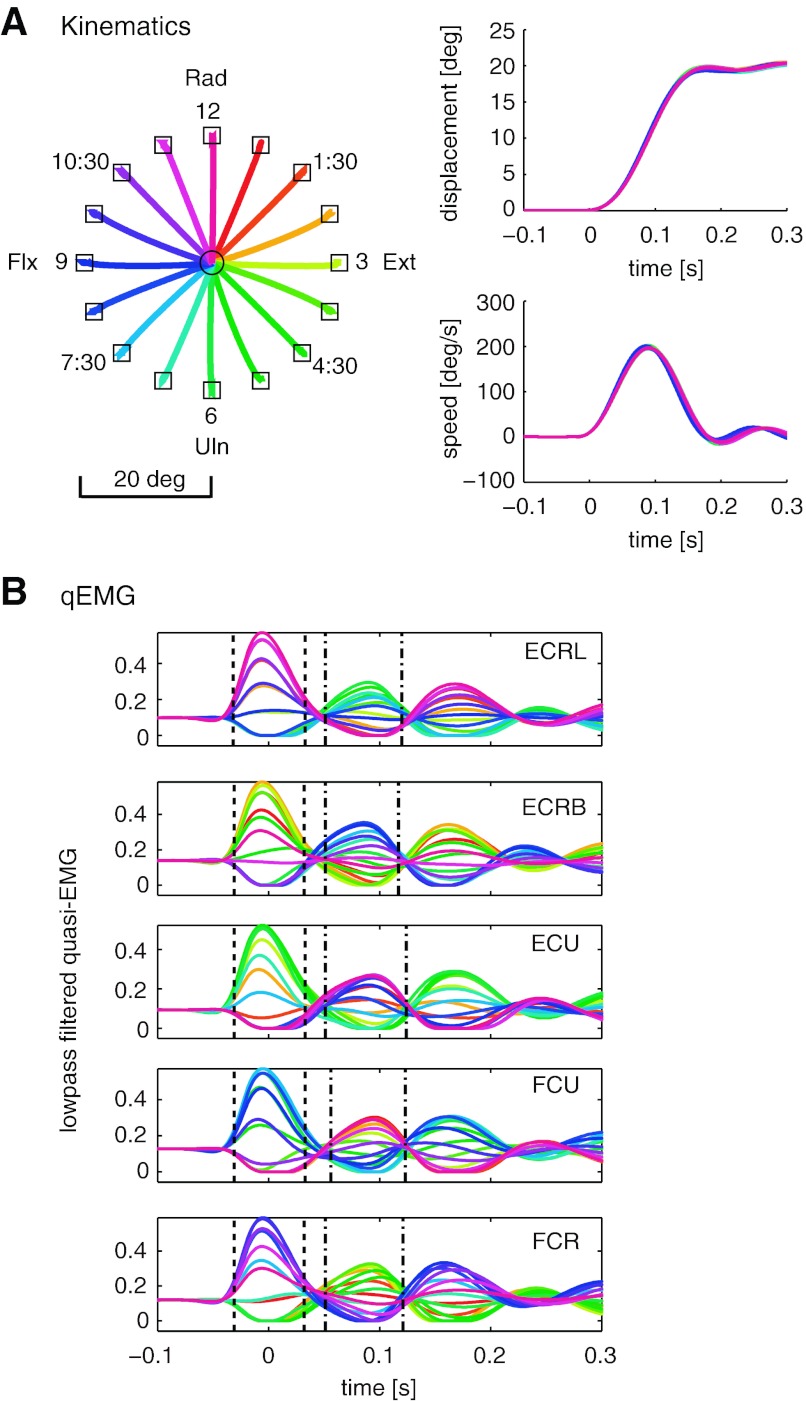
Kinematics of step-tracking wrist movements. A: paths of wrist motion. Step-tracking movements started from the neutral position (a black circle) toward 16 radially located targets (black squares). Targets are identified by their clock time positions. Flx, flexion; Ext, extension; Rad, radial deviation; Uln, ulnar deviation. B: time series of wrist displacement from initial position. C: time series of wrist speed (1st time derivative of wrist displacement). D: time series of wrist speed during movements toward four cardinal targets, 3, 6, 9, and 12, extracted from C. Line colors represent the target direction shown in A; 0 s corresponds to the timing of movement onset.

Data processing.

Motor command u, the output of the motor control model, is considered a quasi-EMG signal (qEMG) and compared with EMG signals measured by Hoffman and Strick (1999). We compare u with EMG signals because it precedes muscle force by the same amount of time as EMG activity measured by Koike and Kawato (1995).

Before processing qEMG, the onset timings of each of the 16 movements were determined from time series of wrist displacement. Here, the wrist displacement is defined as the distance between wrist position and the neutral position. We refer to its first and second time derivatives as movement speed and acceleration, respectively. The movement onset is then defined as the time that the movement speed first exceeded 5% of its maximum within each movement.

For the muscle activity analysis, a series of data processes were applied to the qEMG of each of the five muscles similarly to how Hoffman and Strick (1999) processed their EMG signals. First, qEMG signals were smoothed with a zero-phase forward and inverse low-pass filter (4th-order Butterworth) with a 20-Hz cutoff frequency. The average of qEMG during the holding period was denoted as baseline level and subtracted from each qEMG signal. We then normalized qEMG such that the maximum level within the 16 movements was 1 and the baseline level was 0.

Second, the best agonist and antagonist directions were determined for each muscle. The best agonist/antagonist direction corresponds to the target direction with the largest agonist/antagonist burst. Note that a qEMG signal is considered an agonist burst when its first positive peak lies between the movement onset and the first positive peak of movement acceleration, and an antagonist burst when between the first positive and negative peaks of movement acceleration. We also defined the agonist/antagonist burst interval as the time when the normalized qEMG for the best agonist/antagonist direction remained >25% of its peak amplitude. Note that each of the five muscles has their own best agonist and antagonist directions. Hence, the agonist and antagonist burst intervals differ among the five muscles.

Finally, the normalized qEMG signals were integrated over the agonist and antagonist burst intervals. The agonist and antagonist integrated qEMG can be considered as quantitative measures of the strength of the agonistic and antagonistic activities. They are used to analyze how each muscle changes its activity as agonist or antagonist according to the direction of movement.

RESULTS

Movement Kinematics

The trajectories of simulated step-tracking wrist movements are shown in Fig. 2. As seen in Fig. 2A, the paths of wrist position were almost straight lines from neutral position to the four cardinal targets, 12:00 (radial deviation), 3:00 (extension), 6:00 (ulnar deviation), and 9:00 (flexion). Other movements showed gently curved paths. When the movement included some degree of radial deviation, its path was convex upward. With some degree of ulnar deviation, its path was convex downward. This kind of systematic spatiality in the movement paths is supported by the monkey subject data in Hoffman and Strick (1999).

Time series of wrist displacement from initial position (Fig. 2B) show that the amount of wrist displacement in all 16 movements came close to 20° within 0.20 s from movement onset. To analyze duration of step-tracking movements, we calculated the time needed for the wrist to reach the area within 1.75° of the target. The value 1.75° corresponds to the target radius of the monkey experiment in Hoffman and Strick (1999). Mean duration and standard deviation were 0.159 and 0.014 s, respectively. This result is also consistent with the monkey subject data of Hoffman and Strick (1999), where the average duration was <0.2 s. Therefore, it is confirmed that the parameters in the muscle model (Eq. 2) were set appropriately to generate roughly the same movement duration as the experiment data.

Time series of wrist speed (Fig. 2C) show that the temporal waveforms of the wrist speed were smooth bell-shaped. From Fig. 2C, we can also see that peak values of wrist speed varied with target direction. Hoffman and Strick (1999) reported that the average of peak tangential velocities was higher in the movements toward radial and ulnar deviation than in those toward flexion and extension. This difference in movement speed arises in the simulated movements as well (Fig. 2D). The speed profiles of radial and ulnar deviation were steeper and higher in magnitude compared with those of extension and flexion. The peak speeds were 211 and 216°/s for radial and ulnar deviation, and 167 and 173°/s for extension and flexion, respectively. Note that the speed profiles do not have large negative peaks during the later half of the movements. This indicates that there were no substantial overshoots like those seen in the experiment data of human subjects (see Fig. 2D of Hoffman and Strick 1999). However, the simulated movements showed the same dependency of movement speed on target direction as in human and monkey movements.

Spatiotemporal Patterns in Muscle Activity

Amplitude-graded pattern.

Simulated muscle activities of 5 muscles during 16 step-tracking movements are shown in Fig. 3. In Fig. 3, low-pass filtered qEMG signals of each muscle are plotted in each of the five graphs. In addition, the agonist and antagonist burst intervals of each muscle are shown by vertical black dashed and dash-dotted lines, respectively. It can be said that each muscle worked as an agonist or antagonist when qEMG peaked during agonist or antagonist burst intervals, respectively. From the Fig. 3, we can see that each muscle worked as an agonist in a different set of target directions, meaning that each muscle has its own agonist directions. The qEMG amplitude of each muscle decreased as the target rotated from its best agonist direction. Timing of peak agonist bursts, on the other hand, hardly changed as the target direction varied. The same tendency can be seen for the antagonist bursts of each muscle. This spatiotemporal pattern of muscle activity is referred to as an amplitude-graded pattern and has been observed in step-tracking movements of humans and monkeys (Hoffman and Strick 1999).

Fig. 3.

Simulated muscle activities. Time series of quantitative (q)EMG signals, motor command signals sent to the 5 muscles, are smoothed by a fourth-order 20-Hz low-pass Butterworth filter and plotted with respect to each of the 5 muscles [from the top, extensor carpi radialis longus (ECRL), extensor carpi radialis brevis (ECRB), extensor carpi ulnaris (ECU), flexor carpi radialis (FCR), and flexor carpi ulnaris (FCU)]. qEMG signals of all 16 step-tracking movements are aligned at movement onset (time = 0 s). Colors of the temporal waveforms represent the target directions shown in Fig. 2A. The time intervals between pairs of vertical dashed lines and vertical dash-dotted lines are, respectively, agonist and antagonist burst intervals of each muscle.

To highlight the amplitude-graded patterns of agonist and antagonist bursts, we extracted several qEMG signals from Fig. 3 and plotted each pattern separately in Fig. 4. The agonist bursts of all five muscles show clear amplitude-graded patterns. In the case of FCU, for example, the best agonist direction was 6:45. The amplitude of agonist bursts decreased as the target rotated clockwise, while the timing of their peaks changed only slightly. The best antagonist direction for FCU was 0:45. The antagonist burst amplitude decreased as the target rotated counter-clockwise, while the peak timings did not change in time.

Fig. 4.

Characteristic qEMG patterns. Top row: graphs show amplitude-graded patterns of the agonist bursts of the 5 muscles. Middle row: graphs show the amplitude patterns of the antagonist bursts. Bottom row: graphs show the muscle activation patterns other than the amplitude-graded pattern. Note that temporally shifted patterns can be seen in the activities of FCR in the target directions 6:00, 6:45, and 7:30. The double-burst pattern can be seen in ECU during the movement towards target 7:30. In addition, the shortened early suppression of antagonist burst can be seen in ECRB for target 9:45.

In Fig. 4, the amplitude-graded patterns can be observed more prominently in qEMG signals of agonist bursts than those of antagonist bursts. In ECU, for example, the antagonist burst amplitude did not change for different targets. In FCR, the timing of antagonist burst changed for different targets. In addition, it can be seen in most of the muscles that qEMG signals of antagonist bursts decreased before movement onset. This suppressive activity of antagonist muscles, called early suppression, was also observed in the experiment with monkeys (see Fig. 11 of Hoffman and Strick 1999).

Complex patterns.

In Hoffman and Strick (1999), characteristic muscle activation patterns other than the amplitude-graded pattern could also be seen in the EMG data. A so-called temporally shifted pattern was observed in which the timing of EMG burst in some movements was systematically shifted from the typical timing of agonist burst to that of antagonist burst. In another, called a double-burst pattern, EMG peaked during both agonist and antagonist burst intervals. Furthermore, a shortened and reduced early suppression pattern was also observed in antagonist muscles of the monkeys. All of these muscle activation patterns were observed during the movements almost orthogonal to the best agonist and antagonist burst directions.

Simulated muscle activities also exhibited the three complex patterns mentioned above, temporally shifted, double-burst, and shortened early suppression (Fig. 4, bottom row). A temporally shifted pattern can be seen in FCR. Peak qEMG timing for target 6:45 was in the period between the agonist and antagonist burst intervals. When the target rotated toward the best agonist direction (9:45), the burst timing occurred earlier. Conversely, as the target rotated toward the best antagonist direction (3:45), burst timing occurred later. ECU exhibited a double burst pattern for target 7:30, which corresponds to the intermediate direction between the best agonist (4:30) and antagonist (10:30) directions. Finally, a qEMG signal for ECRB showed a shortened and reduced early suppression for target 9:45. Although early suppression can be seen in the qEMG signals of normal antagonist bursts (Fig. 4, middle row), the duration of the early suppression was shorter than that of the best antagonist burst. Furthermore, the level of qEMG, in contrast to normal antagonist bursts, returned to baseline level during the agonist burst interval.

Directional Tuning Pattern

In Fig. 5, integrated qEMGs during agonist and antagonist burst intervals are plotted against target direction. To clarify the spatial modulation of agonist and antagonist activities, we fitted cosine curves to the integrated qEMG. In all five muscles, both agonist and antagonist integrated qEMG are well represented by cosine functions of target direction. R² values for cosine fitting exceeded 0.9 in most of the muscles. The mean R² for cosine fittings of agonist and antagonist were 0.94 and 0.96, respectively. Agonist and antagonist preferred directions, i.e., the target directions for which cosine curves peaked, are listed in Table 3.

Fig. 5.

Cosine-like tuning of the integrated qEMG. Integrated qEMG during agonist burst intervals (bottom) and antagonist burst intervals (top) are plotted, with colored circles, against target direction. Colors of the circles correspond to the target directions shown in Fig. 2. Note that maximum values of each of the agonist and antagonist integrated qEMG are scaled to 100 for each muscle. Cosine fitting curves on the integrated qEMG are superimposed with black solid lines. Goodness of the cosine fitting, measured by R², is also superimposed.

Table 3.

Preferred directions

	ECRL	ECRB	ECU	FCU	FCR
Agonist PD	9.5°	44.8°	139.2°	211.6°	288.8°
Antagonist PD	168.0°	239.4°	291.5°	59.2°	101.1°

PD, preferred direction. 0° = radial deviation; 90° = extension; 180° = ulnar deviation; 270° = flexion.

In Fig. 6, agonist integrated qEMG is plotted in polar coordinates, with the agonist and antagonist preferred direction and muscle's pulling direction. Filled and unfilled dots indicate positive and negative values of the integrated qEMG, respectively. From Fig. 6, we find several features common between simulated muscle activities and the experimental data of Hoffman and Strick (1999). First, coactivation of at least two muscles can be seen for all of the 16 target directions. For example, ECRL and ECRB coactivated as agonists in the target directions from 11:15 to 3:00. Even though the wrist could be moved toward the target direction 12:00 by ECRL alone, ECRB and FCR also pulled the wrist. Second, all five muscles exhibited a difference between the pulling direction and agonist preferred direction. The amount of difference was larger for ECRB and ECU than that of ECRL, FCU, and FCR. This tendency is also consistent with monkey subject data in Hoffman and Strick (1999). Third, agonist integrated qEMG was negative in some target directions approximately opposite to the agonist preferred direction (small unfilled circles in Fig. 6). A negative qEMG integral means that there was a suppression of muscle activity during the agonist burst interval. These negative integrals were also observed in some muscles of the monkeys in Hoffman and Strick (1999). Finally, agonist and antagonist preferred directions were not 180° opposite each other. Although antagonist preferred directions of monkeys are not shown in Hoffman and Strick (1999), they reported that agonist and antagonist preferred directions of some muscles in human subjects were not 180° opposite each other. In the simulation, the angular deviation between agonist and antagonist preferred directions was <170° in ECRL, ECRB, ECU, and FCU.

Fig. 6.

Directional tuning of agonist integrated qEMG in 5 wrist muscles. Integrals of qEMG during agonist bursts interval are plotted as small black circles in polar coordinates. Sign of the integrals is indicated by the type of the circles (filled = positive; unfilled = negative). Bold arrows point toward the agonist preferred directions. Thin arrows indicate the antagonist preferred directions. Gray short bars represent the muscles' pulling directions. Outer circles correspond to the maximum agonist integrated qEMG for 16 step-tracking movements.

Simulation with Isotropic Muscle Pulling Directions

As listed in Table 1, we used the pulling directions unevenly arranged in the space of flexion-extension and radial-ulnar deviation. To reveal the effect of muscle pulling directions on movement features, the pulling directions were rearranged isotropically. We set the pulling direction of ECRL to 0° and set the others in equally spaced intervals (ECRB: 72°, ECU: 144°, FCU: 216°, and FCR: 288°). The other musculoskeletal parameters were unchanged and the weight parameters of the ISM and FBC networks were optimized for the new set of pulling directions.

The results of the simulation with isotropic pulling directions are shown in Fig. 7. In contrast to the original condition (see also Fig. 2), the paths of wrist position were nearly straight for all targets and speed profiles were almost identical for all targets. Simulated muscle activities also showed differences from the original condition (see also Fig. 3). Although the amplitude-graded pattern was preserved, other complex muscle activity seemed to disappear.

Fig. 7.

Simulated movements with isotropic pulling directions. A: movement kinematics. Paths of wrist position, time series of wrist displacement, and time series of wrist speed. B: simulated muscle activities.

To analyze the difference in movement features for the isotropic and anisotropic pulling directions, we quantified the features of kinematics and muscle activities. The amount of movement curvature is defined by the maximum distance of the wrist position perpendicular to the straight line between initial and target positions. Its sign is set to be positive when the path rotates in the clockwise direction. Furthermore, we counted the number of muscle activities showing the three complex patterns, temporally shifted, double-burst, and shortened early suppression of antagonist. The counting rules were as follows. First, the temporally shifted pattern was counted when the positive peak timing of a qEMG signal lay within an interval determined by the maximum agonist and antagonist burst timings of the corresponding muscle. The center of the temporally shifted interval was set at the middle of the maximum agonist and antagonist burst timings, and its duration was set to 30% of the interval of the two maximum burst timings. Next, a qEMG signal having a positive peak during both of the agonist and antagonist burst intervals was counted as a double-burst pattern. Finally, a qEMG signal showing an early suppression with a duration <75% that of the early suppression of the maximum antagonist qEMG was counted as a shortened early suppression. Note that qEMG signals with positive peaks <25% of the maximum antagonist burst were eliminated from the analysis. In addition, a qEMG signal was considered to be an early suppression when its normalized value fell below −0.2 during the agonist burst interval of the corresponding muscle. The parameters mentioned above were set such that the three patterns shown in Fig. 4 would be counted.

Figure 8 shows how the movement features changed as the set of muscle pulling directions changed from anisotropic to isotropic. Note that for each of the anisotropic and isotropic conditions, we used six sets of weight parameters for the ISM and FBC networks optimized from different initial values. While the path curvature shows systematic dependency on the target direction in the original condition, it was almost 0 for all targets in the isotropic condition. The same was seen for peak speed as well. The dependency of peak speed on target direction disappeared in the isotropic condition. Complex muscle activity patterns also decreased in the isotropic condition. We also analyzed the gap between muscle pulling direction and agonist preferred direction, and the angle deviation of the antagonist preferred direction from 180° opposite of the agonist preferred direction. While agonist preferred direction deviated from muscle pulling direction by a substantial amount in the anisotropic condition, it was closer to 0 in the isotropic condition. In addition, agonist and antagonist preferred directions were closer to 180° opposite each other in the isotropic condition.

Fig. 8.

Features of movements with isotropic and anisotropic muscle pulling directions. A: path curvature against target direction. Path curvature is defined as the maximum deviation from a straight line. B: peak speed against target direction. C: number of muscle activities with temporally shifted, double-burst, shortened early suppression, and their total. D: gap between agonist preferred direction (agoPD) and muscle pulling direction (musclePD) and deviation of antagonist preferred direction (antPD) from direct opposite of agonist preferred direction (agoPD). Both values are the averages among the 5 muscles.

DISCUSSION

In this study, we applied our motor control model to step-tracking wrist movements actuated by muscles with dynamic viscoelastic properties. Simulated muscle activities resulted in several characteristic spatiotemporal features in common with the experimental data observed in Hoffman and Strick (1999). Those features are summarized as follows: 1) amplitude-graded pattern, 2) cosine-like modulation of integrated EMG, 3) deviation of agonist preferred direction and pulling direction, 4) early suppression of antagonist burst, 5) complex temporal patterns (temporally shifted, double-burst, and shortened early suppression), 6) agonist and antagonist preferred directions that are not 180° opposite each other, 7) movement path curvature dependency on target direction, and 8) movement speed dependency on target direction.

Features Independent of Muscle Viscoelasticity

Some of the features mentioned above were also well predicted by Fagg et al. (2002) and Haruno and Wolpert (2005), who applied optimal control models to step-tracking wrist movements. Spatial features such as features 2 and 3 were seen in both studies. Spatiotemporal feature 1 was also seen in Haruno and Wolpert (2005). In their studies, simple linear muscle models without viscoelasticity were used to simplify the optimization of the movements. Therefore, features 1, 2, and 3 are considered to be independent of the viscoelastic dynamics of the muscle. The origins of cosine tuning in EMG are suggested to be the redundant muscles and optimization of those activities against various cost functions, i.e., squared muscle force (Buchanan and Shreeve 1996), squared muscle activation (Fagg et al. 2002), and end-point variance disturbed by signal-dependent noise (Todorov 2002; Haruno and Wolpert 2005). In our simulation, the controllers ISM and FBC were trained to maximize cumulative reward (Eq. 7) under the existence of signal-dependent noise. The reward signal includes a positional error term and square of muscle activation. Therefore, the optimization criterion in our simulation is considered as the combination of two criterion used by the simulations of Fagg et al. (2002) and Haruno and Wolpert (2005). By optimizing redundant muscle activity against the reward signal, cosine-like modulation of EMG was reproduced just as in the previous control models. To study the origin of the amplitude-graded pattern, a motor control model predicting time-varying muscle activity is required. Just like the model of Haruno and Wolpert (2005), our model can predict time-varying command signals and successfully reproduces amplitude-graded patterns. The deviation of the agonist preferred direction and pulling direction seems to be derived from the anisotropic allocation of five pulling directions (Fagg et al. 2002; Haruno and Wolpert 2005). This could be supported by the result of the simulation using isotropic pulling directions (see Fig. 8).

Features Dependent on Muscle Viscoelasticity

In this study, we also succeeded in predicting muscle activation patterns that were not reproduced by the two previous models (Fagg et al. 2002; Haruno and Wolpert 2005). Those patterns are as follows: early suppression of antagonist burst, complex temporal muscle activation patterns, agonist and antagonist preferred directions not 180° opposite each other, and dependency of movement path and speed on target direction. Note that all of these patterns, except for early suppression, disappeared when the set of muscle pulling directions was changed to isotropic (see Fig. 8). However, this does not mean that the anisotropic pulling direction is the sole condition to reproduce those patterns. Although Fagg et al. (2002) and Haruno and Wolpert (2005) used the same set of anisotropic pulling directions that we applied, those patterns could not be seen in their simulation. Therefore, those patterns seem to be derived from the combination of the anisotropic muscle pulling direction, viscoelastic muscle properties, and the motor control model proposed in this study.

Movement path curvature.

In our simulation, the paths of wrist position were nearly straight lines for the four cardinal targets on the axes of flexion-extension and radial-ulnar deviation (Fig. 2). The paths for the diagonal targets, those between the four cardinal targets, were systematically curved toward either the radial or ulnar axes. The paths were convex upward for movements with some degree of radial deviation and convex downward for movements with some degree of ulnar deviation. The path curvature for monkeys exhibited the same dependency on target direction (Hoffman and Strick 1999). A similar pattern was also found in human subject movements observed by Charles and Hogan (2010). In their successive work, Charles and Hogan (2012) suggested that the anisotropic passive stiffness of the wrist can explain this characteristic of path curvature. They simulated a second order linear dynamical system of the wrist and applied step torque input to shift the equilibrium to the desired target. The simulated movement showed the observed path curvature when the wrist stiffness was modeled demonstrably realistically, i.e., higher stiffness in radial-ulnar deviation than in flexion-extension. We believe the path curvature found in our simulation was basically due to reasons similar to those of Charles and Hogan (2012). We also believe that movement depends not only on the characteristics of the musculoskeletal system but also on how the CNS controls the musculoskeletal system. Here we discuss how the two controllers in our model contribute to path curvature.

In our model, the ISM generates, from the beginning to the end of movement, static motor command signals u^ism that can hold the wrist at target position θ^d. In other word, u^ism shift the equilibrium to the target. When the wrist is at the neutral position, u^ism does not create net joint torque parallel to θ^d because of the elastic property of the muscle and anisotropic muscle pulling direction. The ISM net torque τ^ism at neutral position can be derived as

$${\tau }^{ism}=\left[K+D^{T}S\left({\text{u}}^{ism}\right)D\right]{\theta }^d$$ (8)

where K = diag([K₁, K₂]) and S(u^ism) = diag([k₁⁰ + k₁¹u₁^ism,…,k₅⁰ + k₅¹u₅^ism]) represent stiffness matrices of the wrist joint and the muscle elasticity, respectively. D is a 5 × 2 matrix consisting of the moment arm of the five muscles (see Eq. 3). Note that D^TS(u^ism)D represents the effect of muscle elasticity S(u^ism) on the joint dynamics. We call this D^TS(u^ism)D the muscle-originated stiffness matrix. Equation 8 tells us that the τ^ism becomes the sum of the linear transformations of target vector θ^d by the wrist joint stiffness matrix and muscle-originated stiffness matrix. To understand how the direction of τ^ism is rotated from θ^d, we plotted stiffness ellipses defined by the eigenvectors and eigenvalues of the muscle-originated stiffness matrix (Fig. 9A). The major and minor axes of the ellipses correspond to eigenvectors of the muscle-originated stiffness matrix with larger and smaller eigenvalues, respectively. When θ^d parallels either the major or minor axis, the direction of τ^ism does not rotate from θ^d. On the other hand, when θ^d lies in between the two axes, the direction of τ^ism does rotate toward the major axis. The magnitude of the rotation is maximum when θ^d is in the middle of the major and minor axes. Since u^ism differs by target position θ^d, we plotted muscle originated stiffness ellipses for eight targets centered on each target position. In the Fig. 9A, the ISM net torques τ^ism are also plotted by solid arrows. Looking at the shapes of the ellipses, they hardly changed despite being for different targets. This means that the shape of the ellipse depends mainly on the moment arm matrix D and the anisotropy of D keeps the ellipse from being a circle. In addition, we can see that the major axis of each ellipse corresponds to the radial-ulnar deviation directions. As a result, τ^ism points almost straight for the four cardinal target positions and rotates toward radial-ulnar deviation for the diagonal targets. Note that the muscle-originated stiffness ellipses are circular for the isotropic muscle pulling directions. As a consequence, the direction of τ^ism parallels each of the eight targets.

Fig. 9.

Effect of the ISM and FBC on initial movement direction. A: muscle originated stiffness ellipses (solid lines) and initial torque vectors with respect to the ISM command signal (arrows). The size of the stiffness ellipses and torque vectors are rescaled with the same value for all targets. Straight dashed lines connect the neutral position to each of the 8 targets. For clarity, data for only 8 targets are displayed. B: position feedback gain ellipse.

In addition to the ISM, the FBC also seems to contribute to the directionally dependent curvature. The effect of the FBC on path curvature is illustrated by a positional feedback gain ellipse in Fig. 9B. The feedback gain ellipse is based on the matrix derived by a partial differential of net joint torque τ^fbc with respect to position error θ^e against θ^e = θ̇^e = 0. Note that τ^fbc is defined as the net joint torque for a set of muscle tensions calculated by substituting u^fbc into Eq. 2. The major and minor axes of the feedback gain ellipses correspond to eigenvectors of that matrix with larger and smaller eigenvalues, respectively. The feedback gain ellipse illustrates how τ^fbc changes according to target direction. As we can see from Fig. 9, the shape of the feedback gain ellipse is similar to that of the muscle-originated stiffness ellipse. As a result, τ^fbc is rotated by a small amount for θ^e close to the radial-ulnar and flexion-extension directions. In contrast, τ^fbc is rotated toward the radial-ulnar directions when θ^e points between cardinal directions. Although the FBC affects the direction of movement curvature in the same way as the ISM, it is difficult to validate the feedback gain analytically because of the nonlinearity of the musculoskeletal system caused by the viscoelastic properties of the muscle dynamics. In other words, we cannot derive an optimal feedback gain analytically for a nonlinear system. On the other hand, there is no doubt that the anisotropy of the muscle pulling directions affects the curvature of the movements. This is because the feedback gain ellipse is circular in the case of isotropic muscle pulling directions (Fig. 9B).

Complex muscle activation patterns and asymmetry of agonist and antagonist preferred directions.

The temporally shifted muscle activation pattern, where the timing of muscle burst differs depending on target direction, has been observed not only in wrist movement (Hoffman and Strick 1999) but also in upper limb movements (Flanders 1991; Flanders et al. 1996). However, its origin remains to be clarified. It is proposed that the CNS is modulating not only the amplitude but also the timing of muscle activity with respect to target direction (Flanders et al. 1994, 1996; d'Avella et al. 2006). On the other hand, Hoffman and Strick (1999) argued that the temporally shifted pattern is functioning to reduce the amount of movement curvature. Charles (2008) also proposed that the temporally shifted pattern is important to reduce the amount of path curvature caused by anisotropic stiffness of the wrist, when the corresponding muscle can apply force perpendicular to the target direction. Our simulation supports the hypotheses of Hoffman and Strick (1999) and Charles (2008) that the temporally shifted pattern is related to path curvature. Moreover, two other complex patterns, double-burst and shortened early suppression, also seemed to be caused by curved paths. In our simulation, the ISM generates time-invariant command signals. Therefore, the source of time-varying muscle activations is the FBC. To clarify, let us approximate that the feedback command signal of jth muscle u_j^fbc is determined by position error gain G_j^p and velocity error gain G_j^v such that

$$u_j^{fbc}=G_j^p\left({\theta }^d-\theta \right)-G_j^v\dot{\theta }$$ (9)

Here, the directions of the two gain vectors G_j^p and G_j^v are considered to be close to the pulling direction of the corresponding muscle. The magnitudes of position error θ^d − θ and velocity error θ̇ are maximum at the beginning and midterm of the movement, respectively. Therefore, at the beginning of the movement, u_j^fbc is mainly related to position error. At the midterm of the movement, however, it is mainly affected by velocity error. When the target direction is close to G_j^p and G_j^v, u_j^fbc bursts at the beginning and is suppressed at the midterm of the movement. This temporal pattern corresponds to the typical agonist burst pattern. It can be said that when the muscle acts as an agonist, two components of the feedback command, G_j^p(θ^d − θ^e) and G_j^v θ̇^e, remain positive throughout the movement. On the other hand, when the wrist moves toward the target opposite to G_j^p and G_j^v, u_j^fbc is suppressed at the beginning and bursts at the midterm of the movement. This pattern corresponds to the typical antagonist burst with early suppression. It can be said that when the muscle acts as an antagonist, the two components of the feedback command always take negative values. Additionally, when a movement goes straight toward the target, the signs of the two components of the feedback command signal do not change during the movement. In that case, the muscle is considered to act as either an agonist or antagonist throughout the movement. However, when the target direction is near perpendicular to the gain vectors G_j^p and G_j^v, there is a possibility that the signs of the two components can change if the movement path curves. This may cause a transition of the role of the muscle as an agonist to antagonist or vice versa during the movement. The complex muscle activation patterns in our simulation are generated in this type of situation. The temporally shifted pattern and shortened early suppression of antagonist tended to occur when a muscle was a weak antagonist at the beginning of the movement. If the movement path curved and the position error rotated toward the feedback gain vector, the role of the muscle transposed to a weak agonist. Then, the feedback command with respect to position error would burst just after a normal agonist burst but earlier than a normal antagonist burst. In contrast, double burst patterns seemed to occur when a muscle was first a weak agonist and turned into an antagonist as the movement path curved. The first burst of the double-burst is related to position error and the second is related to viscosity error. Taken together, we can say that the direct cause of the three complex muscle activation patterns is the transposition of the role of the feedback controller elicited by curved movements. Since curved movements are derived from the combination of anisotropic pulling direction, viscoelastic properties of muscle, and the motor control system, we can say that the origin of the complex activation pattern in our simulation is the combination of these factors.

Finally, the reason agonist and antagonist preferred directions were not 180° opposite each other seems to be due to the deviation of the directions of positional gain G_j^p and velocity gain G_j^v. Since those gains cannot be derived analytically, we cannot determine the origin of the asymmetric agonist and antagonist preferred directions. However, anisotropy of muscle pulling direction is not sufficient as the condition for this asymmetry. Other conditions seem to be responsible. This is because the agonist and antagonist preferred directions were almost 180° opposite in the simulation of Haruno and Wolpert (2005) even though the set of pulling directions was the same as that used in our simulation.

Early suppression of antagonist bursts.

Early suppression was the one and only feature that did not disappear when the set of muscle pulling directions was changed to isotropic (see Fig. 7). Therefore, the feature seems to be independent of anisotropy of the muscle pulling directions. Instead, it is derived from the viscoelastic properties of muscles and motor control system, which can optimize coactivation level of antagonistic muscles.

The early suppression represents a reduction in the activation level of the antagonist muscle from the baseline level during the agonist burst interval. Here, the baseline level corresponds to the activation level during the holding period before movement onset. Note that the early suppression occurs only if the baseline level is higher by some amount than the minimum activation level. If the baseline level is 0, then there is no room for suppression. On the contrary, when the baseline level of some muscle is higher than 0, the suppression of that muscle's activity supports the acceleration of the wrist moving toward the target opposite to its pulling direction. As a consequence, the amplitude of agonist burst in other muscles is reduced, and energy consumption becomes smaller. Therefore, the early suppression in antagonist bursts seems to be an optimal solution if the baseline level is higher than 0. In the experiment by Hoffman and Strick (1999), the early suppression was observed in the ECRL and ECRB of a monkey. In addition, they reported that it was also observed in some muscles of human subjects, although smaller than that of the monkey. On the other hand, the early suppression could not be seen in the simulated muscle activity of Haruno and Wolpert (2005). This is because the baseline level of all muscles had been fixed to 0 in their simulation. Moreover, even if the baseline level had been optimized to minimize positional variance during the holding period, it would remain small as long as a simple linear muscle model was used. In general, the higher activation level will increase the noise level due to the signal-dependent noise inherent in the musculoskeletal system. Thus coactivation of pairs of antagonistic muscles should be avoided for the sake of noise reduction. This raises the question why the nonzero baseline level was chosen as the optimal solution by our model. The answer seems to come from the properties of the muscle model that we used. The elasticity and viscosity of each muscle increase as the activation level increases (see Eq. 2). Therefore, a higher coactivation level of antagonistic muscles leads to higher impedance of the wrist joint. As a result, the position control of the wrist becomes more robust against noise. However, it also induces larger muscle energy consumption. It is thought that the coactivation level of multiple muscles is determined under the balance of movement accuracy and energy consumption (Osu et al. 2009). In several experiments of reaching movements, it was observed that coactivation level of antagonistic muscles was modulated against required end-point accuracy (Gribble et al. 2003; Nonaka et al. 2003; Osu et al. 2004). In this study, the motor control model was optimized according to the reward signal including a tradeoff between accuracy and energy consumption. Therefore, the nonzero baseline level of the five muscles seems to have been selected to hold the wrist at the neutral posture as accurately as possible under the existence of the signal-dependent noise, while keeping the energy consumption relatively small. Since the output of the FBC in our model is 0 when the wrist is at the neutral position, coactivation of the antagonistic muscles is realized by the ISM. Therefore, it can be said that the nonzero baseline level of the antagonistic muscles generated by the ISM was suppressed by the FBC during agonist burst intervals.

Movement Speed Dependence on Target Direction

In addition to the curvature of the movement path, duration of the simulated step-tracking movements was modulated by the target direction. Mean duration of the two movements for targets 6:00 and 12:00 was shorter than that for targets 3:00 and 9:00. This indicates that radial and ulnar deviation movements were faster than flexion and extension movements. In fact, peak speeds during the radial and ulnar deviation movements were ∼44°/s larger than those during the flexion and extension movements. This kind of directional modulation of movement speed was also observed in the experiments of Hoffman and Strick (1999). On the other hand, the duration of simulated movements in Haruno and Wolpert (2005) was not modulated by the direction of the targets. This is because the minimum-variance model (Harris and Wolpert 1998) used in Haruno and Wolpert (2005) treats the duration as a constraint for the movement optimization and prefixes it to the same value for all targets. In addition to the minimum-variance model, almost all existent motor control models assume predetermined movement duration to optimize point-to-point movements. In our daily lives, however, often the speed of reaching motion changes depending on the objective and conditions of the task. From the experiment of Fitts (1954), it is well known that there is a tradeoff, called Fitts' law, between speed and accuracy of movement. Therefore, the duration is not a constraint determined independently from other movement parameters. Instead, it can be considered a consequence of movement optimization. With regard to our motor control model, the duration is derived from the movement generated by the motor command being optimized to gain higher reward. The reward signal of Eq. 7 includes two terms associated with movement accuracy and energy consumption. To make the movement faster, a larger motor command is required to generate larger joint torque. However, that raises energy consumption and lowers the reward signal. In addition, a larger motor command induces larger signal-dependent noise and movement accuracy deteriorates. Although coactivation of antagonistic muscles can improve movement accuracy, it consumes more energy and consequently lowers the reward signal. Therefore, there are tradeoffs between movement speed and both movement accuracy and energy consumption. The motor control model is trained under the balance of these tradeoffs. Consequently, the movement duration will only be known after the motor control model generates motion.

The nonuniform duration of the simulated movements is considered to arise from the anisotropy of the muscle pulling directions for the five wrist muscles. This is confirmed by the fact that the peak speed of the simulated movements was almost uniform for all targets when the isotropic set of pulling directions was used (see Fig. 8B). In the set of anisotropic pulling directions we used, the ECRL and ECRB were close to the direction of radial deviation (Table 1). Those of ECU and FCU were close to the ulnar deviation direction. Only one muscle, FCR, had the pulling direction close to the flexion direction. Note that the projection of a muscle torque on a target direction would be larger when the pulling direction of that muscle is closer to the target direction. Therefore, it is reasonable that the movements toward the target directions of radial and ulnar deviation were faster than those of flexion and extension.

We should emphasize that the reason we succeeded in predicting experimentally observed modulations of movement duration is that the two controllers in our model do not treat the duration as a constraint for movement optimization. Recently, Tanaka et al. (2006) proposed a motor control model that can predict movement duration of point-to-point movements as a result of movement optimization. Their model minimizes movement duration with the satisfaction of an end-point accuracy requirement in the presence of signal-dependent noise. They showed that the dependency of movement duration on movement magnitude and required accuracy could be well predicted by their model. Their model was applied to movements of a dynamical system controlled by joint torque motor commands. In this study, however, we applied our model to the wrist dynamical system controlled by motor commands of muscles. We demonstrated that uneven arrangement of the muscles caused the modulation of movement duration with movement direction.

Sensitivity of Movement Features on Muscle Parameters

We suggest that the viscoelastic properties of the muscles are important to reproduce experimentally observed movement features. To test the effects of the muscle's viscoelastic parameters (k⁰, k¹, b⁰, b¹) on the movement features, we altered each parameter individually within the biologically plausible range listed in Table 2. After doing so, we did not observe a notable change in the movement features summarized at the beginning of the discussion. However, we found some relationship between the parameter value and the movement feature. First, when either elastic coefficient k⁰ or k¹ was increased, amount of movement curvature also increased. In addition, the difference between peak speeds for radial-ulnar deviation and flexion-extension became higher. Since the muscle-originated stiffness and the feedback gain ellipse shown in Fig. 9 grew larger and steeper as the elastic coefficient of the muscles grew larger, the tendency that movements curved more as muscle elasticity increased is consistent with our argument about the origin of movement path curvature. In contrast to its response to the elastic coefficients, the amount of movement curvature decreased as the intrinsic viscosity b⁰ increased. We did not observe notable effects of b¹ on path curvature. On the other hand, the number of complex muscle activities did not show clear change against parameter value. Although we argued that the curvature of the movement trajectory seems to elicit complex muscle activation patterns, the relationship between the amount of movement curvature and occurrence frequency of the complex muscle activity is still not clear.

In addition to the viscoelastic parameters, we also altered the other muscle parameters (l⁰, l₁, κ₁, and κ₂) that we could not determined the biologically plausible range from past studies. Muscle's stretch length parameters (l⁰ and l¹) were changed within the ranges from 0 to twice the values used in the main simulation. Time constants representing muscle excitation and activation (κ₁ and κ₂) were changed within the ranges from half to twice the values used in the main simulation. As a result, we did not observe notable correlation between those parameters and occurrence frequency of the complex muscle activities except for shortened early suppression. The occurrence frequency of the shortened early suppression became smaller as l⁰ and l¹ got larger. The reduction in the number of shortened early suppression seems to originate from the reduction of baseline activation level, i.e., muscle activation level at neutral position. Since unintended torque due to signal dependent noise becomes larger as the l⁰ and l¹ become larger, it is better to reduce the motor control level to lessen the level of signal dependent noise. This made the baseline activation level to become smaller. As the result, the number of shortened early suppression became smaller.

Biological Plausibility of the Motor Control Model

We adopted a nonlinear muscle model that includes elastic and viscous properties of biological muscle to reproduce a variety of key features of muscle activation. The biological musculoskeletal system is a dynamical system with strong nonlinearity. This makes it difficult to apply optimal control theories to biological motion. Recently, Todorov and his colleagues proposed efficient algorithms for finding the optimal control law of nonlinear systems (Li and Todorov 2007; Todorov 2009). However, the neural mechanism underlying the optimization of motor control still remains to be solved. The motor control model utilized in this study was composed of a FBC, FDM, and ISM. The two controllers, the FBC and ISM, were optimized with the combination of the actor-critic method (Doya 2000) and the feedback-error-learning scheme (Kawato et al. 1987). The networks in the two controllers were trained, in a trial-and-error manner, to maximize the performance of step-tracking movements defined by a reward signal. The actor-critic method, one of the major frameworks of reinforcement learning, has been proposed as a model of learning in the basal ganglia (Barto 1995; Doya 1999). In addition, feedback-error-learning is the learning scheme originally proposed as a computational coherent model of cerebellar motor learning (Kawato et al. 1987). Its validity as a learning model in the cerebellum is also supported from several physiological data (Kawato and Gomi 1992; Schweighofer et al. 1998; Kawato 1999). The existence of FDM, internal predictors of the body state, in the CNS is supported by psychophysical experiments (Wolpert et al. 1995; Bard et al. 1999; Flanagan et al. 2003). In this study, the FDM of the wrist was implemented by the equation of wrist dynamics. Note that we are not assuming that a complete predictor of the wrist dynamics exists innately in the CNS. It should be acquired through the motor learning process just like the acquisition of the two controllers, the FBC and the ISM. In addition, it should be adjusted in accordance with the change in the dynamics of the musculoskeletal system. The training of the FDM, however, seems to not be as difficult as the training of the two controllers. Since a teaching signal can be obtained from sensory feedback, it can be trained in a supervised learning manner. In our previous study (Kambara et al. 2009), we implemented a FDM of the upper limb with a 3-layered forward neural network and showed that it could be trained through the gradient descent method. In addition, a learning curve of the FDM preceded those of the two controllers. Therefore, in this study, we assumed that there would be no significant effect from using a prefixed complete FDM on the training of the two controllers and implemented the FDM through the dynamics equation.

Limitations of This Study

Although various patterns of muscle activity observed in the experiment of Hoffman and Strick (1999) were reproduced in our simulation, there were some differences between the simulation and experiment results. First, the temporally shifted pattern was observed in different muscles. It was observed in ECRL and ECU in the experiment but FCR in our simulation. It is possible that the difference in the balance of the five muscles' parameters caused the difference in muscle activity. The force each muscle can generate is considered to be different muscle to muscle. However, we used the same parameter values for all muscles. In addition, we used a set of muscle pulling directions determined from experiment data with monkeys (Hoffman and Strick 1999; Fagg et al. 2002). It is possible that the difference in pulling directions also resulted in different muscles exhibiting the temporally shifted pattern.

In Hoffman and Strick (1999), the temporally shifted pattern was only seen in human subjects. Also, shortened early suppression of antagonist bursts were exclusive to monkeys. In our simulation, both patterns were observed. As previously discussed, both patterns are caused by the role switching of a muscle from antagonist to agonist when the movement curves. The deciding factor for the occurrence of either pattern seems to be the baseline level of the corresponding muscle activity. Shortened early suppression occurs when muscle activation level is >0 by some amount at neutral position (see ECRB in Fig. 4). The temporally shifted pattern, in contrast, seems to occur when the baseline level is close to 0 (see FCR in Fig. 4). This tendency does not contradict the observation of Hoffman and Strick (1999) that human subjects with little coactivation of antagonistic muscles prefer temporally shifted patterns.

In addition to muscle activity, there were some differences in kinematics of movement between the simulation and experiment. First, the movement paths of human subjects were relatively straight for all targets (Hoffman and Strick 1999), while those of the simulation showed a certain level of curvature for diagonal targets. At the same time, subject movements against the diagonal targets included directional misalignments between the target and initial movement directions. Interestingly, the directions of the misalignments correspond to those reproduced by our model in the simulation. That is to say, the initial movement directions rotated toward radial or ulnar deviation in the movements requiring some degree of radial or ulnar deviation, respectively. As a result, correctional movements for target overshoot showed convexities similar to the simulated trajectories. However, the amount of overshoot in the movements of human subjects was substantial compared with that of simulated movements. Haruno and Wolpert (2005) demonstrated that overshooting is the optimal control strategy against a highly stiffened wrist. We confirmed the existence of substantial overshoot when we applied our motor control model to the musculoskeletal system with high joint stiffness. In common with Haruno and Wolpert (2005), the antagonist burst did not disappear in the high joint stiffness condition. On the other hand, Charles and Hogan (2010) suggested that small but nonnegligible inertia of the manipulandum might have caused the wrist to overshoot the targets in Hoffman and Strick (1999). Charles and Hogan (2010) reported that overshoots were not observed in their experiment in which human subjects made step-tracking wrist movements while grasping a lightweight motion sensor. They also showed that the overshoots can be reproduced by simulating the wrist dynamics with a combination of estimated hand and the manipulandum inertia values (Charles and Hogan 2012). In common with Charles and Hogan (2012), we confirmed the existence of overshoot by applying our motor control model to the wrist with a higher inertia value.

Finally, our motor control model succeeded in predicting many features of step-tracking wrist movements observed by Hoffman and Strick (1999). However, there are some fine differences between the results of the simulation and experiment. Our future work will be to fit the parameters of the wrist musculoskeletal system subject by subject and test whether individual differences in movement features can be predicted by applying our motor control model to custom fitted musculoskeletal models. In addition, it is interesting to test whether our model can predict difference in movement features caused by the difference in forearm posture. Step-tracking wrist movements in pronated, supinated, and their midway postures were well measured by Kakei et al. (1999). They found that the amount of rotation in muscle's preferred direction becomes much smaller than the amount of rotation in forearm posture. In addition, the wrist movement curved in a different direction as the forearm posture was rotated. It is also our future work to see whether our model can reproduce the features of step-tracking wrist movements in three different forearm postures.

GRANTS

This research was partially supported by the Japan Science and Technology Agency, CREST (JST JY210174) and the Ministry of Education, Culture, Sports, Science and Technology in Japan, Strategic Research Program for Brain Sciences (GJY23RR32).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).