Discretization of continuous features in clinical datasets

Abstract

Background

The increasing availability of clinical data from electronic medical records (EMRs) has created opportunities for secondary uses of health information. When used in machine learning classification, many data features must first be transformed by discretization.

Objective

To evaluate six discretization strategies, both supervised and unsupervised, using EMR data.

Materials and methods

We classified laboratory data (arterial blood gas (ABG) measurements) and physiologic data (cardiac output (CO) measurements) derived from adult patients in the intensive care unit using decision trees and naïve Bayes classifiers. Continuous features were partitioned using two supervised, and four unsupervised discretization strategies. The resulting classification accuracy was compared with that obtained with the original, continuous data.

Results

Supervised methods were more accurate and consistent than unsupervised, but tended to produce larger decision trees. Among the unsupervised methods, equal frequency and k-means performed well overall, while equal width was significantly less accurate.

Discussion

This is, we believe, the first dedicated evaluation of discretization strategies using EMR data. It is unlikely that any one discretization method applies universally to EMR data. Performance was influenced by the choice of class labels and, in the case of unsupervised methods, the number of intervals. In selecting the number of intervals there is generally a trade-off between greater accuracy and greater consistency.

Conclusions

In general, supervised methods yield higher accuracy, but are constrained to a single specific application. Unsupervised methods do not require class labels and can produce discretized data that can be used for multiple purposes.

Background and significance

With the adoption of electronic medical records (EMRs), the quantity and scope of clinical data available for research, quality improvement, and other secondary uses of health information will increase markedly.¹ Concurrently, there has been an increasing need to develop new and effective ways of processing, visualizing, analyzing, and interpreting these data. Algorithms from the fields of data mining and machine learning show promise in this regard.^2–4

Such methods have been successfully used with clinical data, including data from EMRs, to predict the development of retinopathy in type I diabetes,⁵ the quality of glycemic control in type II diabetes,⁶ and the diagnosis of pancreatic cancer.⁷ Similar methods have also been used in the development of classification models that aim to identify cohorts within which patients fulfill certain diagnostic criteria, experience similar outcomes, or are considered alike in other ways. For example, EMR data have been used to identify cohorts of patients with peripheral arterial disease, providing valuable phenotype data for genome-wide associations studies.⁸ In pulmonary and critical care, machine learning with clinical data has been used to identify subtypes of heterogeneous disease syndromes such as sepsis⁹ and chronic obstructive pulmonary disease.^{10 11}

Current issues in machine learning with clinical data include model selection, feature selection and ranking, parameter estimation, performance estimation, semantic interpretability, and algorithm optimization.⁴ By contrast, there has been less focus on data preprocessing measures such as the transformation of continuous variables into a range of discrete intervals, which might also affect the performance of predictors and classifiers.

There are a few ways in which discretization can be a useful preprocessing step in machine learning and data mining tasks. First, many popular learning methods—including association rules, induction rules, and Bayesian networks—require categorical rather than continuous features.^{12 13} With naïve Bayes classifiers, continuous features can be used, but this demands a strong supposition about the distribution of its values. Discretization eliminates the need for this assumption by providing a direct evaluation of the conditional probability of categorical values based on counts within the dataset.

Second, widely used tree-based classifiers—including classification and regression trees (CART) and random forests—can be made more efficient through discretization, by obviating the need to sort continuous feature values during tree induction. Discretization can derive more interpretable intervals in the data that can improve the clarity of classification models that use rule sets.¹² It can also help reveal non-linear relationships in a dataset, including associations occurring at discontinuous regions of a frequency distribution.¹⁴ Discretization can homogenize the attributes of a dataset in which some features are continuous and others are categorical. Finally, by creating categorical variables, discretization enables the derivation of count data, which would otherwise not be possible with continuous data.

Methods for discretization can be classified as either supervised, in which information from class labels is used to optimize the discretization, or unsupervised, in which such information is not available, or not used.^{13 15} While the former methods tend to produce more predictive categories, the latter are more versatile in their scope of applications.^{13 16} The method by which continuous features are partitioned into discrete intervals can have a significant impact on the performance and accuracy of classification algorithms.^{15 17} Ideally, discretization should result in partitions that reflect the original distribution of the continuous attribute, maintain any patterns in the attribute without adding spurious ones, and are interpretable and meaningful to domain experts.¹⁸

Though many different discretization algorithms have been devised and evaluated, few studies have examined the discretization of clinical data specifically. Dougherty's foundational paper on discretization¹³ used a number of datasets from the University of California Irvine (UCI) Machine Learning Repository, some of which included medical data.¹⁹ For the most part, however, these contained only a limited number of clinical attributes, many of which were already categorical in nature. Another study using the UCI datasets looked specifically at the performance of a new supervised method.¹⁵ Studies have been aimed specifically at testing methods of discretizing high throughput genomic data,^{12 20} but such evaluations need only consider a small number of data types, and do not include clinical data.

In clinical medicine, one study that we know of has considered the role of discretization as part of a broader evaluation of classifiers for a trauma surgery dataset.²¹ This study looked at decision trees and naïve Bayes classifiers, and evaluated their performance with both equal frequency discretization (quartiles), and an entropy-based supervised method that included oversight by a domain expert. The supervised method showed marginal but statistically significant improvement over the use of quartiles. Clarke and Barton developed a discretization algorithm using clinical data from the National Heart, Lung, and Blood Institute (NHLBI) National Growth and Health study,²² which also used an entropy-based method for deriving partitions of certain clinical attributes, including blood pressure and body mass index. In each of these cases, class labels were known for each observation, and these were used to minimize the loss of information caused by discretization.

Continuous features from clinical datasets include vital signs and other physiologic measurements, laboratory data, drug delivery data (such as dose or rate of infusion), and output from organ support systems such as ventilators and dialysis machines. While not categorically different from machine learning repository data such data types often have unique properties, suggesting the need for a tailored approach to their discretization.⁴

First, artifacts may be more prevalent in some types of features than others. Laboratory data are subject to very stringent quality control and verification, and are therefore somewhat insulated against measurement artifacts.²³ By contrast, physiologic measurements such as those obtained from central venous pressure monitoring, involve multiple complex steps, are seldom automated, are susceptible to perturbation, and therefore generate data that are inherently noisy. Determining which values are artifacts can range from the trivial (a value for fraction of inspired oxygen greater than 100% or less than 21% is clearly an artifact), to the more nuanced (a heart rate measurement of 250 may be an artifact, or representative of a patient in extremis). Second, the ranges and distributions of clinical features may vary significantly. Determining what values are statistical outliers and distinguishing artifacts from outliers can therefore be challenging, and can have a significant impact on the success of discretization. Equal width discretization, for example, is particularly susceptible to the influence of outliers.^{14 24}

In this study, we undertake an examination of discretization methods to determine how well they work with clinical data features. We use both laboratory and physiologic data, and test six different discretization methods: two supervised methods (minimum descriptive length-based and ChiMerge), three unsupervised methods (equal width, equal frequency, and k-means), and one method specific to clinical data with both supervised and unsupervised components (reference range based). We evaluate each of these methods using a widely used approach in which the relative success of discretization is assessed by the classification accuracy of the discretized features as compared with the continuous features, in both decision tree and naïve Bayes classification tasks.^{12 13 15 24–26}

Materials and methods

The analyses described were carried out using the R software environment for statistical computing and graphics (http://www.r-project.org/), with functions taken from the rpart, e1071, discretization, and infotheo libraries. The project was determined by our institutional review board to be non-human subjects research, and approval was granted to extract the deidentified data that was used.

Clinical datasets

All clinical data were extracted from the Stanford Translational Research Integrated Database Environment (STRIDE), a research and development project at Stanford University that includes a comprehensive clinical data warehouse.²⁷ Data were derived from patients in the adult intensive care units of Stanford University Medical Center and were fully de-identified. For the analysis of laboratory data, we used a set of 7872 arterial blood gas (ABG) measurements in which each observation included values for 17 common laboratory measurements, including basic electrolytes, co-oximetry, pH, and others (table 1). For physiologic data, we used a set of 5748 cardiac output measurements (CO) derived from pulmonary artery catheters, pulse oximetry monitoring, and cardiac telemetry (table 1), each with 14 features. All measures within a given set were taken within 30 min of each other aside from urine output, which was taken from over the nearest hour.

Table 1.

Features of the arterial blood gas (ABG) and cardiac output (CO) datasets

ABG dataset features	CO dataset features
Ionized calcium	Heart rate
Chloride	Systolic arterial blood pressure
Sodium	Diastolic arterial blood pressure
Potassium	Mean arterial blood pressure
Glucose	Respiratory rate
HCO3	Pulse oximetry
pH	Temperature
pCO2	Corrected QT interval
pO2	Urine output
Total CO2	Cardiac index
Oxyhemoglobin	Pulmonary artery systolic pressure
Carboxyhemoglobin	Pulmonary artery diastolic pressure
Methemoglobin	Systemic vascular resistance
Oxygen content	Central venous pressure
Hemoglobin
Hematocrit
Base excess

For the derivation and testing of the classification algorithms, the datasets were divided into training and test sets, with the former taken as the first two-thirds of the observations, and the latter as the remaining one-third.

Data preprocessing

Only observations with complete data were used in the analyses. For the ABG dataset, we eliminated the features ‘carboxyhemoglobin’, ‘methemoglobin’, and ‘oxyhemoglobin’ because they lacked reference ranges for normal values. For the CO dataset, we eliminated the features ‘corrected QT interval’ (74% missing values) and ‘temperature’ (42% missing values), as well as the ‘pulse oximetry’ feature, owing to the absence of a reference range for normal values. We then used a series of rules to identify and remove observations that contained logical inconsistencies, such as those in which the diastolic blood pressure was greater than the systolic (table 2). We generated individual boxplots for each attribute (web appendices 3 and 4), and removed extreme outliers identified by visual inspection.

Table 2.

Logic rules used to identify artifacts and other observations not suitable for use

Logic rule	Violations (N)
Missing value	732 (CO dataset)
Negative value	84 (CO dataset)
Blood pressure violation*	32 (CO dataset)
Respiratory rate=0	20 (CO dataset)
CVP>50	19 (CO dataset)
Violation of Henderson-Hasselbach†	0 (ABG dataset)
Total violations	887

*Diastolic>systolic, diastolic>mean, or systolic<mean.

†Reported HCO₃ differs from calculated value by >0.09 mEq/l.

ABG, arterial blood gas; CO, cardiac output; CVP, central venous pressure.

Class label assignment

In order to determine the accuracy of the classification algorithms using each of the discretization methods, we assigned class labels to each observation in each of the datasets. Two different class labeling schemas were used—one based on clustering, and one based on clinically recognizable disease states. For the ABG dataset, clinical labels were assigned using a previously published algorithm²⁸ that classifies ABG measurements into 1 of 13 categories (web appendix 1). For the physiologic dataset, clinical labels were derived to reflect four different categories of circulatory shock (web appendix 2). The algorithm was developed by one of us (DMM) with experience in critical care medicine, to reflect a classification heuristic commonly used in clinical practice. Shock is initially characterized by low mean arterial pressure, a parameter frequently used to identify patients at substantial risk of inadequate end-organ perfusion. In this setting, a cardiac index (cardiac output divided by body surface area) below the lower limit of normal was used to classify patients with either hypovolemic shock (eg, shock arising from hemorrhage or other causes of low effective circulating volume) or cardiogenic shock (ie, pump failure). These two were distinguished on the basis of elevated central venous pressures in the latter. Patients with low mean arterial pressure but normal or increased cardiac index were classified as having distributive shock. At each branch point, splits were chosen to identify distinct shock phenotypes as clearly as possible, while still maintaining a classification scheme that was both mutually exclusive and mutually exhaustive.

For the cluster-derived labels, observations were partitioned into k different clusters based on a partitioning around medoids algorithm, a variant of k-means clustering that computes medoids instead of centroids as cluster centers.²⁹ Only the features that were used to assign the clinical labels were used in the cluster-based labeling. The optimal number of clusters was chosen based on the highest average silhouette value, a measure of comparative cluster tightness and separation.³⁰

Discretization methods

We evaluated three unsupervised discretization methods (equal width interval binning (EW), equal frequency interval binning (EF), and k-means clustering (KM)), two supervised discretization methods (minimal descriptive length based (MDL), and ChiMerge (CM)), and one method based on the reference range (RR) for the clinical feature being discretized. To determine the maximum number of bins (k) for EW, EF, and KM, we used a heuristic from Dougherty, in which k=max{1, 2×log(l)}, where l is the number of distinct observed values for the attribute being partitioned.¹³ This value ranged from 7 to 14 for the attributes in the ABG dataset, and from 7 to 15 in the CO dataset. We therefore used values of k ranging from 2 to 15. For RR binning, we used k=3 (‘low’, ‘normal’, ‘high’), as well as k=6, k=9, k=12, and k=15.

For EW, the range of values was divided into k bins of equal width. For EF, the range was divided into k bins such that there were equal numbers of observations in each bin. For KM, the observations were partitioned into k non-overlapping bins using an algorithm that aims to minimize the distance within bins, and owing to the probabilistic nature of this clustering algorithm, we used a 10-fold cross validation and took the median value obtained as representative for that number of bins. The RR method was similar to the unsupervised EW method, but initiated with ‘high’, ‘normal’, and ‘low’ partitions derived from labels extrinsic to the distributions themselves. Reference ranges were determined from a variety of online sources.^31–33

MDL discretization was based on the algorithm of Fayyad and Irani,³⁴ which uses an entropy minimization principle based on the class labels assigned to each observation. The algorithm partitions the continuous range of values recursively, until a stopping criterion, based on the minimal description length principle, is met. The ChiMerge algorithm is a merging, rather than splitting, technique.³⁵ The continuous range is first sorted, and each distinct value considered a separate interval. The χ² test is applied to all pairs of adjacent intervals, and these are then merged if the corresponding class labels in those intervals are sufficiently similar. We used a significance level of 0.05 as a stopping criterion for the merging of similar intervals.

Performance evaluation

We examined the impact of discretization on three key values—accuracy, consistency, and simplicity.²⁵ For determination of accuracy, we partitioned the features using each of the methods described above, across the range of k values, and then trained two different classification models—a decision tree model (DT) based on the CART model of Breiman et al,³⁶ and a naïve Bayes model (NB). We used training data for model learning, and test data to determine the classification error. The classification error using the raw, continuous data was used as a comparator. Pairwise comparisons between each of the unsupervised discretization methods were made using two-sided unpaired t tests.

To evaluate the methods for consistency, we derived an inconsistency count for each discretization experiment. In a discretization process, two instances are considered inconsistent if they are discretized to the same interval, but have different class labels. For each pattern of inconsistency, we measured the inconsistency count by taking the total number of instances of that inconsistency pattern, and subtracting the number of cases belonging to the majority class represented.²⁵

As a measure of simplicity, we counted the number of nodes in each of the decision trees generated by each of the discretization methods. Simpler models were considered to be those with fewer nodes overall.

Results

A total of 887 observations were eliminated based on the logic rules used to identify artifacts (table 2). An additional two observations were identified as artifacts and eliminated, based on inspection of the distributions. Following these preprocessing steps, the ABG dataset consisted of 7867 observations with 14 attributes each, and the CO dataset consisted of 4839 observations with 11 attributes each.

Based on the average silhouette widths, the number of clusters for the cluster-based class labeling was set at two for both the ABG dataset and the CO dataset (web appendix 5). Baseline classification error rates based on the raw continuous data are shown in table 3. Decision trees produced consistently low classification error rates. The error rates for the various discretization methods are shown in figures 1 and 2. Supervised discretization methods produced error rates close to those achieved with the raw data itself. In general, discretization improved the performance of naïve Bayes, but not decision tree classifiers. Accuracy improved as the number of bins increased, but in general these gains became less pronounced beyond a k value of 9. Results of t-tests comparing the performance of the unsupervised discretization methods with each classification model are shown in table 4.

Table 3.

Baseline classification error rates based on continuous features

	ABG dataset		CO dataset
	Clinical label	Cluster label	Clinical label	Cluster label
DT	0.011	0.030	0.050	0.001
NB	0.136	0.169	0.111	0.066

ABG, arterial blood gas; CO, cardiac output; DT, decision tree; NB, naïve Bayes.

Figure 1.

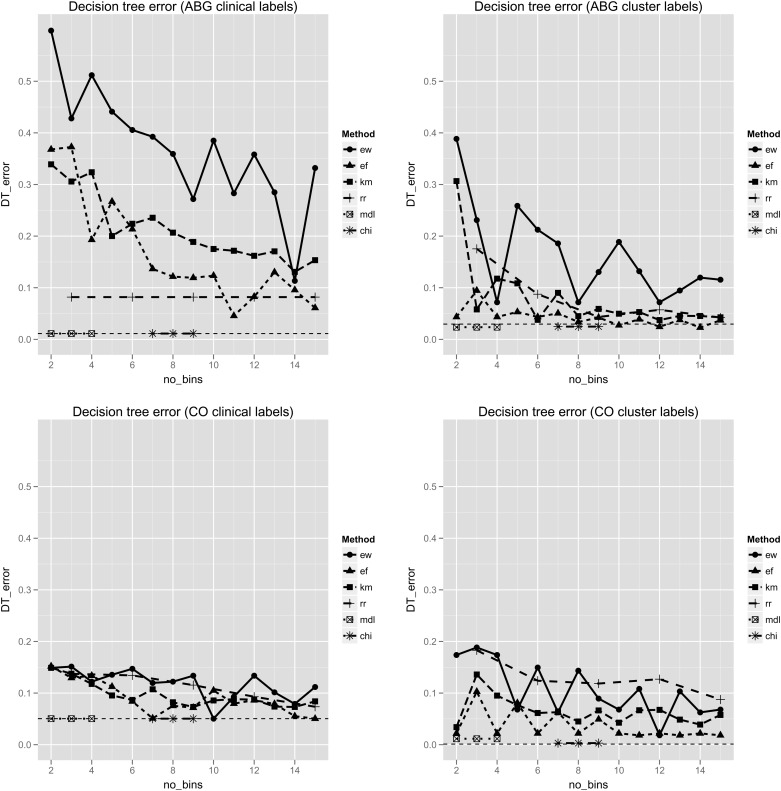
Error rates from the decision tree classifiers. Error rates (y axis) are shown for the ABG (top) and CO (bottom) datasets, with features partitioned into 2–15 discrete bins (x axis). Results for clinically labeled (left) and cluster labeled (right) observations are shown. In each plot the horizontal dashed line represents the error rate using the raw, continuous data. The minimal descriptive length (MDL) and ChiMerge (CHI) methods have fixed numbers of bins, and are therefore plotted as short line segments, unrelated to the x axis. ABG, arterial blood gas; CO, cardiac output; DT, decision tree; EF, equal frequency; EW, equal width; KM, k-means clustering; RR, reference range. This figure is only reproduced in colour in the online version.

Figure 2.

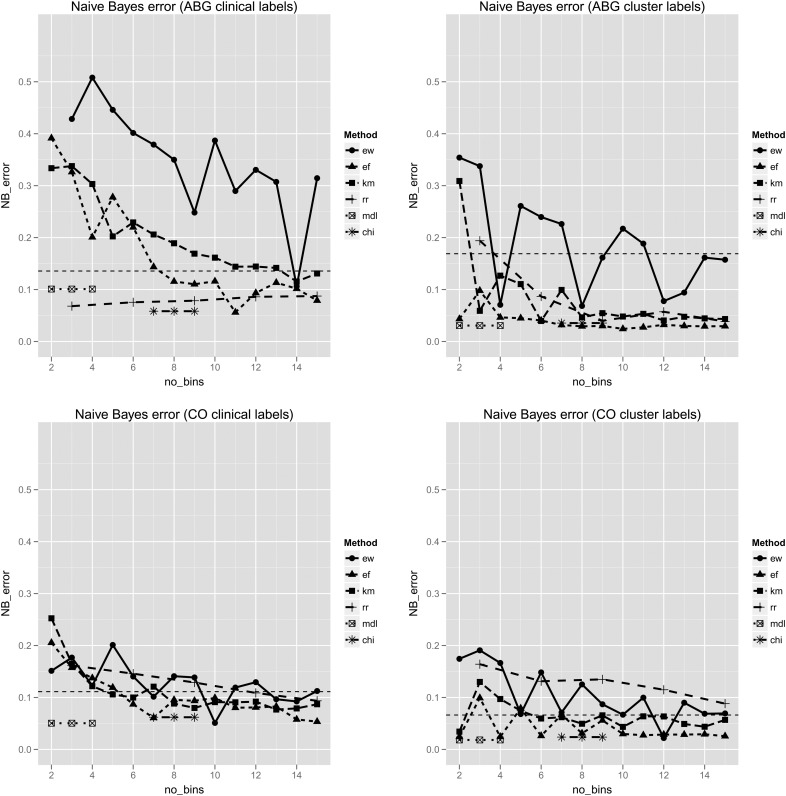
Error rates from the naïve Bayes classifiers. Error rates (y axis) are shown for the ABG (top) and CO (bottom) datasets, with features partitioned into 2–15 discrete bins (x axis). Results for clinically labeled (left) and cluster labeled (right) observations are shown. In each plot the horizontal dashed line represents the error rate using the raw, continuous data. The minimal descriptive length (MDL) and ChiMerge (CHI) methods have fixed numbers of bins, and are therefore plotted as short line segments, unrelated to the x axis. ABG, arterial blood gas; CO, cardiac output; DT, decision tree; EF, equal frequency; EW, equal width; KM, k-means clustering; RR, reference range. This figure is only reproduced in colour in the online version.

Table 4.

Pairwise comparisons of discretization methods using Student's t-test for statistical significance

	Clinical labels		Cluster labels
Comparison	DT	NB	DT	NB
ABG dataset
EF vs EW	5.00E-05	9.00E-05	0.00022	4.00E-05
KM vs EW	0.00028	0.00029	0.01074	0.00227
RR vs EW	4.33E-07	7.35E-07	0.03713	0.0213
EF vs KM	0.16886	0.33541	0.08473	0.05179
RR vs EF	0.00979	0.00628	0.19585	0.19711
RR vs KM	4.57E-06	4.00E-05	0.92912	0.93024
CO dataset
EF vs EW	0.02408	0.09419	0.00027	0.00049
KM vs EW	0.03639	0.32672	0.01595	0.01504
RR vs EW	0.63575	0.95124	0.30333	0.22484
EF vs KM	0.61336	0.55719	0.00951	0.02076
RR vs EF	0.20774	0.13185	0.00177	0.00075
RR vs KM	0.31817	0.3508	0.0102	0.0037

DT, decision tree; EF, equal frequency; EW, equal width; KM, k-means clustering; NB, naïve Bayes; RR, reference range.

ABG dataset

With class labeling derived from the clinical algorithm, neither of the supervised methods showed a decrease in classification accuracy compared with the original continuous data. RR discretization performed best amongst the unsupervised methods, and showed a consistent improvement over the continuous data in the performance of naïve Bayes classification. This effect was seen even when the features were simply partitioned into ‘low’, ‘normal’, and ‘high’ values. EW discretization was significantly less accurate than any of the other methods. There was no difference between EF and KM discretization under any of the conditions evaluated. EW discretization produced a similar pattern of error rates across both classification algorithms. With clinical labels, the minimum error occurred with 14 bins, while with cluster labels, local minima were seen with 4, 8, and 12 bins.

CO dataset

Overall, differences between discretization methods were less pronounced with the CO dataset, and error rates remained similar to those achieved with the continuous features. Discretization did result in modest improvements in classification error for naïve Bayes classifiers. EW discretization was significantly less accurate than EF discretization. With cluster labels, RR discretization was significantly less accurate than both EF and KM discretization.

Consistency and simplicity

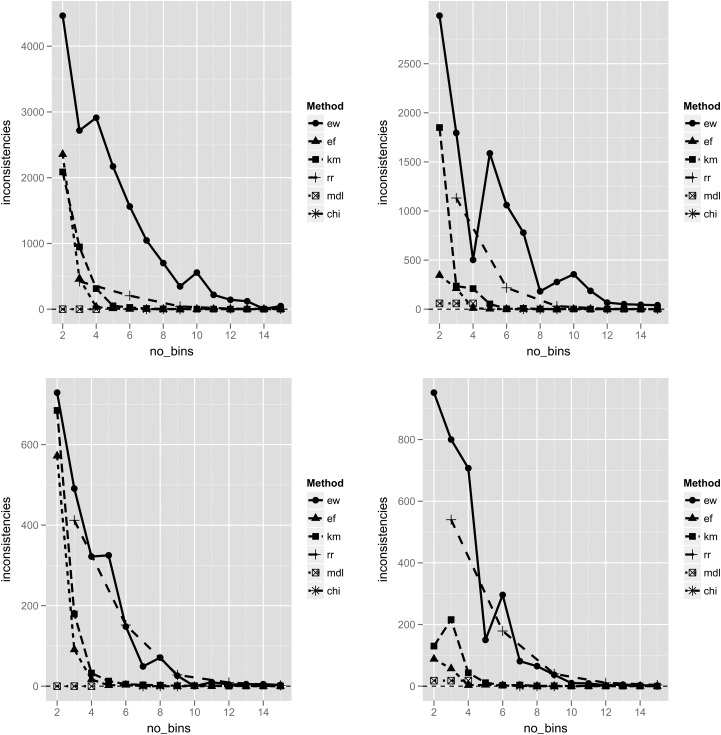
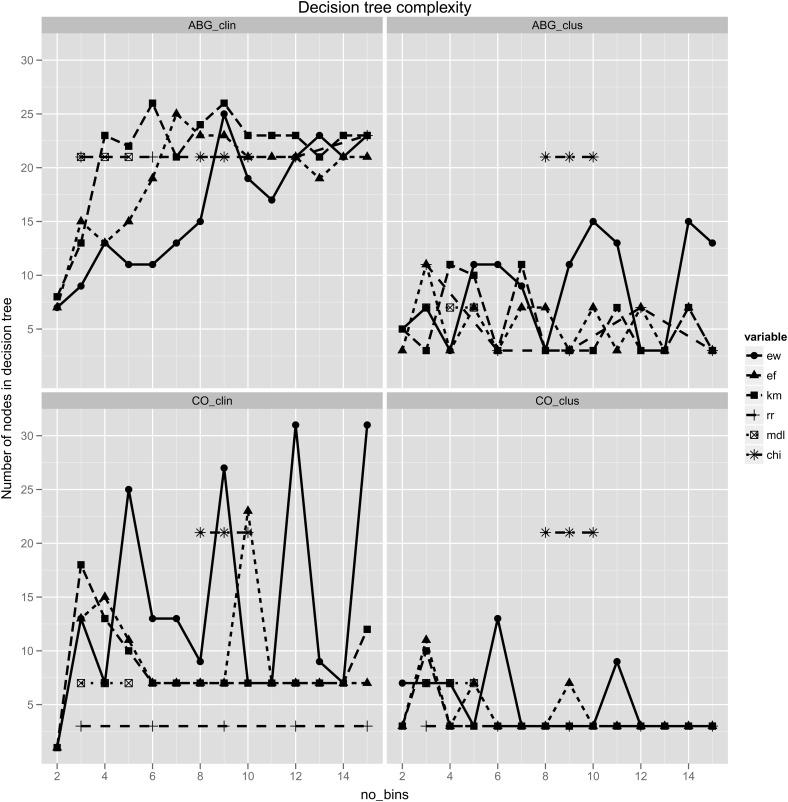
The supervised methods produced either very few inconsistencies, or none at all. For the unsupervised methods, the inconsistency rate seemed to reach an asymptote in each case, but did so sooner with EF and KM discretization, at a k value of approximately 4 (figure 3). In terms of simplicity, the supervised methods—and in particular the ChiMerge method—tended to produce a larger number of bins. With cluster labeling of the ABG dataset, ChiMerge in fact generated 274 bins for 14 features (nearly 20 bins per feature, on average). This translated into more complex decision tree models as well, with greater than 20 nodes in each of the experimental conditions tested (figure 4). The simplest decision tree models were those derived for the CO dataset using the RR discretization method. For the ABG dataset with clinical labels, the unsupervised methods showed an increasing level of complexity as the number of bins increased. Local minima were again seen with EW discretization.

Figure 3.

Inconsistency counts for each of the discretization methods. Inconsistency is measured by taking the total number of instances of each inconsistency pattern, and subtracting the number of cases belonging to the majority class represented. Top left—ABG dataset with clinical labels. Top right—ABG dataset with cluster labels. Bottom left—CO dataset with clinical labels. Bottom right—CO dataset with cluster labels. The minimal descriptive length (MDL) and ChiMerge (CHI) methods have fixed numbers of bins, and are therefore plotted as short line segments, unrelated to the x axis. ABG, arterial blood gas; CO, cardiac output; DT, decision tree; EF, equal frequency; EW, equal width; KM, k-means clustering; RR, reference range. This figure is only reproduced in colour in the online version.

Figure 4.

Number of nodes in the decision trees resulting from each of the discretization methods. Top left—ABG dataset with clinical labels. Top right—ABG dataset with cluster labels. Bottom left—CO dataset with clinical labels. Bottom right—CO dataset with cluster labels. The minimal descriptive length (MDL) and ChiMerge (CHI) methods have fixed numbers of bins, and are therefore plotted as short line segments, unrelated to the x axis. ABG, arterial blood gas; CO, cardiac output; DT, decision tree; EF, equal frequency; EW, equal width; KM, k-means clustering; RR, reference range. This figure is only reproduced in colour in the online version.

Discussion

The increasing volume of electronic clinical data being produced in healthcare necessitates the development and validation of reliable informatics methods designed to enable data-driven clinical research and analysis. An important first step in this process is an examination of how data preprocessing and modeling methods applied in other domains perform with clinical data. Discretization of continuous data, a necessary initial step in a variety of widely used machine learning and data mining applications, is one important element in the preprocessing and modeling of clinical data.

This is, we believe, the first evaluative study of supervised and unsupervised discretization methods using EMR data in the biomedical informatics literature. Though data derived from the EMR are not de facto fundamentally different from the data contained in machine learning repositories, some of which contain biomedical data, it is possible that EMR data may present challenges, in terms of distributions, presence of outliers and missing values, and other factors, that could influence discretization.

Our results confirm the findings of previous studies, which show that discretization in general improves the accuracy of naïve Bayes classifiers.^{13 17 37} This is thought to be due to the ability of discretization to approximate the distribution of the continuous attribute, which otherwise would be assumed to be Gaussian.^{13 17} We might therefore expect the greatest gains to occur for datasets in which the attributes are not normally distributed. In such cases, the assumption of normality within the continuous data would lead to a lower accuracy overall, which should be somewhat overcome by the discretization process. An examination of the histograms and Q–Q plots³⁸ for the datasets examined (web appendices 6–9) suggests that there are fewer features in the ABG dataset than the CO dataset for which the Gaussian assumption is justified. This is in keeping with our findings of greater gains in accuracy following discretization for the ABG dataset.

Our results also confirm the finding that supervised discretization tends to produce more accurate classifiers than unsupervised.^{13 25 35} This reflects the fact that unsupervised methods assign split points without accounting for known class differences between observations. Consider, for example, a dataset of white blood cell counts ranging from 1/cm³ to 100 000/cm³, being used to classify patients according to whether or not they have an infection, typically indicated by a raised white blood cell count. If the attribute is divided into three bins of equal width, the first interval will contain counts that are low, normal, and high, whereas all the values in the second and third intervals will be high. Such a discretization may not be useful for classifying patients according to whether or not they have an infection, as patients with raised counts will appear in all three intervals. Supervised methods account for the class labels assigned to each observation, and are therefore more suited to supervised classification tasks.¹⁴

The accuracy of the various discretization methods evaluated varied considerably depending on how class labels were assigned. In the ABG dataset, RR binning was very effective with the clinical labels, but less so with the cluster labels. This was also seen with the CO dataset, in which RR binning was similar to EF and KM binning with the clinical labels, but significantly worse than these with the cluster labels. This effect may reflect the use of reference ranges in the derivation of the clinical labels themselves. Results also varied with the number of distinct class labels used, as well as the method used to assign them (data not shown).

Overall, these findings suggest that the optimal choice of discretization method is influenced by the choice of class labels, a factor that in certain applications may not be known a priori. In such situations, only unsupervised methods can be used. Among these, EW binning was less accurate, and both EF and KM binning most consistent, in our experimental results.

Based on the results of this and previous studies, discretization is an important consideration when preprocessing clinical datasets for use in machine learning classification tasks. The relative importance of discretization depends on the classification algorithm used. Methods such as support vector machines, which are designed to handle continuous variables in multidimensional space, may not benefit at all from discretization. Classifiers from the decision tree family perform discretization of continuous features implicitly when determining optimal split points,² but may use different discretization approaches depending on the type of decision tree induction algorithm used. These methods may benefit from extrinsic discretization as a preprocessing step in order to enhance computational efficiency.³⁹ Accuracy can also be improved in cases in which the extrinsic discretization used before induction is better suited than the method intrinsic to the decision tree induction itself.^{13 40} In our study, the finding that none of the discretization methods improved upon the classification accuracy of decision trees trained on the continuous data reflects the fact that the MDL-based discretization strategy internal to the decision tree algorithm in this case selects split points in order to maximize accuracy. Naïve Bayes classifiers, which make assumptions about the distributions of continuous attributes unless otherwise specified, benefit the most from discretization.

Beyond improving classification accuracy, there may be other important reasons to discretize clinical data for use in machine learning. Discretization is likely to improve model comprehensibility, especially in rule and decision tree models. When deployed with Bayesian networks, discretization might also disclose important relationships between features in a dataset. Discretization can also significantly increase the efficiency of decision tree induction in that the sorting step required by continuous data at each branch point can be reduced to a single sort for each attribute at the time of discretization.³⁹

Identifying a universal discretization strategy for all classification tasks is problematic.¹⁷ Nonetheless, some general observations can be made to help optimize the choice of discretization method. Where reliable class labels are available, previous work suggests that supervised discretization method will produce greater accuracy than unsupervised methods, and our results confirm this finding.^{12 13 16 20} This reliance on class labels, however, limits the use of supervised methods to specific applications, since a dataset discretized using a given class label assignment might not be optimally discretized for a different class labeling schema. Unsupervised methods, in contrast, resulted in lower classification accuracy, but can be applied to datasets even in the absence of class labels.

Of the unsupervised methods, EF and KM discretization provided the most consistent performance in terms of classification accuracy, while remaining relatively insensitive to the choice of classification algorithm, class label assignment, and number of bins. KM has the conceptual advantage of avoiding boundary cases, in which two observations of the same value fall on different sides of an equal frequency boundary, necessitating an arbitrary decision about which interval should contain the observations. KM also has the potential to uncover potentially meaningful patterns.

These methods also require that a value for k be specified a priori, without a clear indicator of the optimal choice. Determining the optimal number of bins into which a continuous distribution should be split has long been an area of investigation by statisticians, with many possible heuristic and algorithmic approaches proposed.⁴¹ Our results help to inform this decision, but may not be applicable to other datasets with different distributions and properties. Reasonable accuracy was achieved with k=4, a value at which consistency was also nearly maximized. In general, greater accuracy was seen with an increasing number of bins.

The strengths of this study include the large number of observations in the clinical datasets, which allowed for adequately sized, disjoint training and test datasets. The data were extracted from a working EMR, rather than a machine learning repository, and therefore better approximate real life conditions. We included preprocessing steps aimed at identifying and eliminating artifacts and inconsistent values that could impact the discretization process. We also evaluated six separate discretization methods using two different classification algorithms, and two class labeling schemes—one based on clinically meaningful distinctions and one based on a robust clustering process.

Although we focused on static discretization techniques, which treat each feature in isolation and do not account for possible dependencies between them, it is possible that certain dynamic methods that account for such dependencies produce different results. It is also possible that methods which use a mixture of different discretization methods within a single dataset could lead to improved classification accuracy. We also limited our evaluation to supervised classification algorithms that have been used in similar studies of domain non-specific discretization.

Conclusion

Discretization of continuous data is an important step in a number of classification tasks that use clinical data. Overall, discretization has the greatest impact on the performance of naïve Bayes classifiers, especially where the features in question do not fit a normal distribution. The relative success of any discretization strategy may depend on the method by which class labels are assigned to the observations, the number of class labels assigned, and the number of discrete bins generated. While it is unlikely that any one strategy will have universal applicability, our results can be used to inform the choice of discretization method in the context of specific applications. For single use cases in which class labels are known, the supervised methods MDL and CM showed a high degree of accuracy. When class labels are not available, only the unsupervised methods can be used. In such cases, EF and KM discretization produce more consistent and favorable results than the other unsupervised methods. RR discretization can under some conditions lead to very accurate classification, often with as few as three bins, but this effect may be seen only when the class labels are also derived from reference range values. Furthermore, RR discretization is at least equally likely to result in poor classifier performance, and can be used only where reference ranges are known. In selecting the number of bins for the unsupervised methods, we found that consistency improved very little beyond k=4, and that accuracy improved only sporadically and unpredictably beyond k=9. In general, the choice of discretization method and choice of k must be guided by the objectives of the discretization task.