Structural models used in real-time biosurveillance outbreak detection and outbreak curve isolation from noisy background morbidity levels

Abstract

Objective

We discuss the use of structural models for the analysis of biosurveillance related data.

Methods and results

Using a combination of real and simulated data, we have constructed a data set that represents a plausible time series resulting from surveillance of a large scale bioterrorist anthrax attack in Miami. We discuss the performance of anomaly detection with structural models for these data using receiver operating characteristic (ROC) and activity monitoring operating characteristic (AMOC) analysis. In addition, we show that these techniques provide a method for predicting the level of the outbreak valid for approximately 2 weeks, post-alarm.

Conclusions

Structural models provide an effective tool for the analysis of biosurveillance data, in particular for time series with noisy, non-stationary background and missing data.

Introduction

With the advent of health information exchanges, automated biosurveillance platforms, and interest in the detection of bioterrorist events, the quantity of biosurveillance data is increasing rapidly, making the need for automated processing methods essential. One of the main objectives of this processing is early event detection (EED), see Fricker.¹ Another aspect of the processing of biosurveillance data is the need for background modeling or background subtraction. Biosurveillance data in the form of time series of count data (which may or may not be spatially resolved) are frequently complex, with weekly and seasonal cycles superimposed on non-stationary trends. Subsequent processing generally requires a way to separate this background cleanly from the counts due to the outbreak of interest. As an example, such a separation is required to fit the time series of outbreak counts to a parameterized outbreak curve for purposes of outbreak forecasting. This procedure requires a model of the background, the ‘normal background model’ (NBM), which is accurate for a length of time relevant to the analysis of interest. Of course, background modeling and EED are related; as discussed below, EED involves projecting the NBM forward by 1 day and looking for a statistically significant discrepancy with incoming data.

Current methods for EED in biosurveillance applications generally fall into three categories: (1) Serfling-type methods (regression models with linear trends and fixed cyclic terms typically corresponding to seasonal disease dynamics) for background modeling; (2) autoregressive integrated moving average (ARIMA) models, using fit diagnostics to determine event status; and (3) variants of local smoothing algorithms, for example, exponentially weighted moving average (EWMA). A review of these methods is given in Yan et al² and Buckeridge et al;³ Xing et al⁴ have recently produced a study of comparative performance using surveillance data. These methods have significant shortcomings. Serfling type methods require large ‘training’ datasets to determine the cyclic components; these models may also not be appropriate for diseases that do not show clear seasonal trends. ARIMA models generally use differencing techniques to reduce the data to a stationary time series. This differencing tends to multiply the effect of missing data. In addition, cyclic terms are not easily incorporated in the ARIMA formalism, and the development of the likelihood function for the ARIMA model uses approximations that break down for short time series.⁵ Finally, EWMA models do not provide a statistical framework for determining detection thresholds, and require preprocessing for handling non-stationary data. A detailed discussion of ARIMA models, EWMA models and their relationship to structural modeling can be found in Harvey.⁵ For a discussion of problems of moving average filters applied to EED, see Bloom et al.⁶ Here we demonstrate a method for EED in biosurveillance data, which overcomes all of these limitations, while maintaining excellent early detection characteristics. This method is also easily modified to address the problem of formulating a NBM and separating background count data from the epidemic signal. Change point analysis methods have recently been proposed as an effective complement to traditional detection systems,⁷ and these can easily be adapted to the methods described here.

Methods

The method discussed in this paper is known in the economics literature as ‘structural modeling’. This technique was developed for econometric time series applications, and has recently found application in other areas such as environmental monitoring⁸ and analysis of medical data.⁹ The technique requires the specification of a stochastic model that reflects the dynamics underlying the observed time series, and provides a method for determining the parameters of the model, based on a recursive algorithm. The model is completely specified by these parameters governing the stochastic nature of the model. The simplest model of this type is a random walk with additive Gaussian noise. We discuss this model here because it forms the basis for the model we are using, below, and provides an instructive example of the method. The model is specified by:

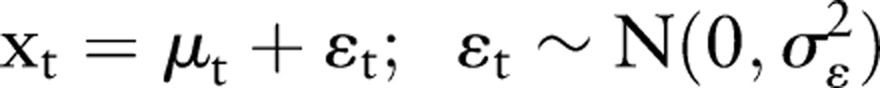1.1

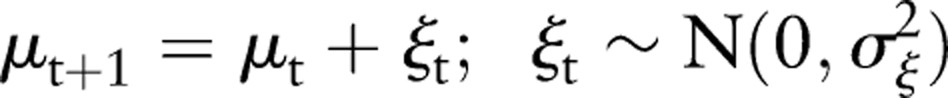1.2

Here μ_t is the time series level at time t, uncorrupted by noise, which is being estimated, and x_t is the observation of this level. The terms ε_t and ξ_t are zero mean, Gaussian random noise terms with SD σ_ε and σ_ξ, respectively, the former representing additive Gaussian noise and the latter the step size of the random walk. The model is then specified by the parameters (σ_ε, σ_ξ).

The problem to be solved is therefore: given a set of data, and the functional form of the data generation process given above, what values of the parameters best represent the data? It is possible to approach this problem using the methods of classical multivariate statistics. The probability density of a given time series x_t derived from the above generation process is a multivariate Gaussian distribution, N(0, Σ), where the form of the covariance matrix Σ is specified by the generation process (equations 1.1 and 1.2) to be:⁸

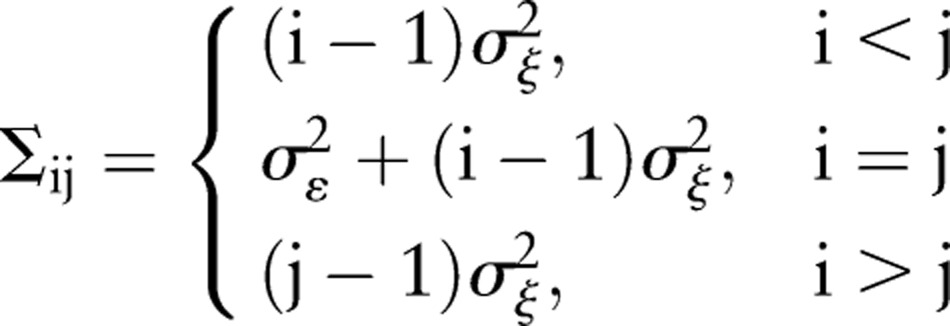2

Here i, j=1, …, n where n is the number of data points. We are assuming, for the purposes of this example, that the initial value x₁ is known to be 0. For this case, the mean of x_t, unconditioned on the data, is equal to 0 for all t (this can be seen by taking the expectation of both sides of equation 1.2). From the form of the distribution function, the log likelihood function can be constructed as:

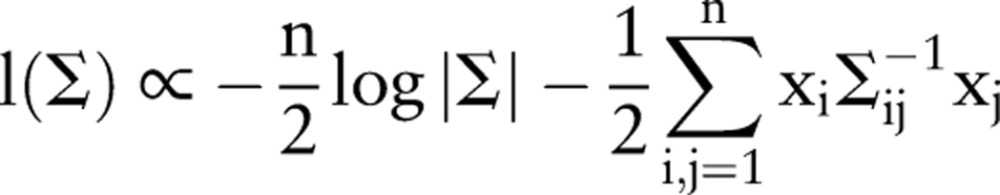3

where |Σ| is the determinant of Σ, and Σ⁻¹ is its inverse. In principle, values of σ_ε and σ_ξ can be derived, which maximize this quantity. Conditional on the data, the covariance matrix then determines the values of the (conditional) means μ_t. For large values of n, however, this approach becomes cumbersome, because it requires the inversion of a n×n matrix. Therefore, in practice, the computations are carried out using a recursive technique based on the Kalman filter,¹⁰ which only requires the inversion of small matrices at each recursion step. This formalism also has a number of advantages compared to other time series analysis methods, including providing a statistical framework for EED inference (as opposed to methods such as moving averages), and the ability to handle data gaps in a straightforward manner.¹⁰

As discussed above, biosurveillance data typically show pronounced short-term variations, trends, and weekly cycles. The model we have chosen reflects all of these characteristics and is given by the following equations:

4.1

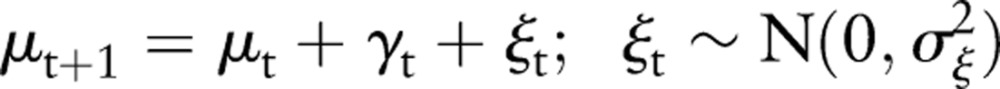4.2

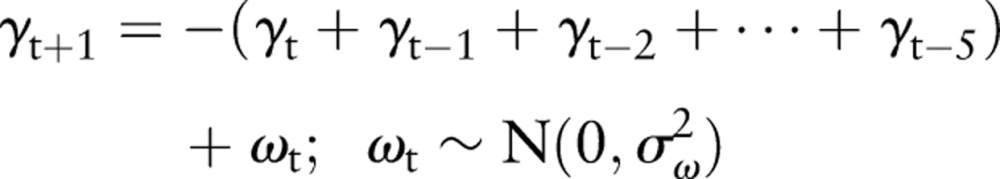4.3

This model is a random walk in local level μ_t with a zero mean 1-week cyclic component (equation 4.3), which also contains a stochastic term. The observed count rate x_t is the sum of the local level plus an additive, zero mean Gaussian noise term with SD σ_ε (equation 4.1). The terms σ_ξ, σ_ω represent the SD of the step size of the random walk in the local level and weekly cycle, respectively.

The model is thus specified by three parameters: σ_ε, σ_ξ, σ_ω. As discussed above, given this model, a likelihood function can be specified, analogous to equation 3 above, but containing terms corresponding to the weekly cycle as described in equations 4.2 and 4.3. For a particular set of data, x₁, x₂, …, x_n, this likelihood can be computed recursively on the data (using the Kalman filter) as a function of the parameters. The selection of best-fit parameters is then found using a numerical optimization routine to maximize the likelihood that incorporates the constraint that σ_ε, σ_ξ, σ_ω must all be larger than zero.¹¹ The details of implementation for similar models can be found in Harvey⁵ and Durbin and Koopman.¹⁰

Once the model parameters have been fit, the above model can be used within the Kalman filter formalism to do forward prediction of the local level for an arbitrary future time, as well as to provide an estimate of the uncertainty in the prediction at these times. For EED, we use one-step-ahead prediction at time t−1 to form a standardized residual at time t. The standardized residual is then used to infer the existence of an anomaly at time t. If μ(t|t−1) is the forecast data for the time series at time t given the data up to time t−1, and σ(t|t−1) is the uncertainty in this quantity, the standardized residual is given by:

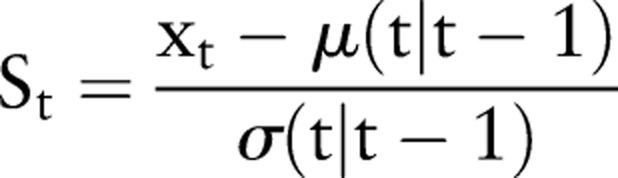5

A threshold on the value S_t is used to determine whether or not an alarm condition is present at time t. The value of the threshold chosen is based on the desired false alarm rate. Generally, values between 2 and 3 have been used, corresponding to false alarm rates of approximately 8/year and 0.5/year, respectively, following the assumption that the residuals are Gaussian. The detection results using this method will be discussed below.

For the multiday forward prediction used in background modeling, the structural model discussed above can be used, but it does not account for a local trend in the background. While the existence of long-term trends in random walks is expected when considering the data globally, when modeling the background over a period of several days or weeks these features appear as a local trend. We have included a local trend term in the structural model, but find it does not give consistent results, indicating that the data are already well fit by the random walk plus the weekly cycle. Therefore, to de-trend the data when performing multiday modeling of the background, a local slope must be determined at the start of the period to be modeled. To determine this slope at time t, we fit a quadratic polynomial to the series μ_t−n, μ_t−n+1, …, μ_t−1, μ_t (where μ_t is the best estimate of the level of the time series at time t, without the weekly cycle or additive noise) for n=30, and calculated the local slope from this curve fit. The results were not sensitive to the number of previous days fit, and fewer days were used when the full 30 days were not available. The local slope was combined with the cyclic term derived from the structural model in the following manner:

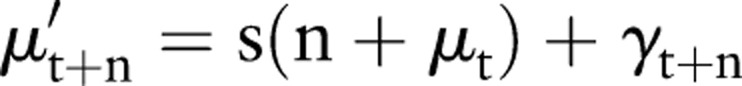6

where 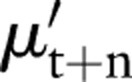is the prediction of the level at time t+n, s is the slope as calculated above, and γ_t+n is the forward projection of the cyclic term derived from equation 4.3. The results for forward prediction in the context of background subtraction are discussed below. For the data considered here, this procedure accurately models the background for approximately 2 weeks.

Tests

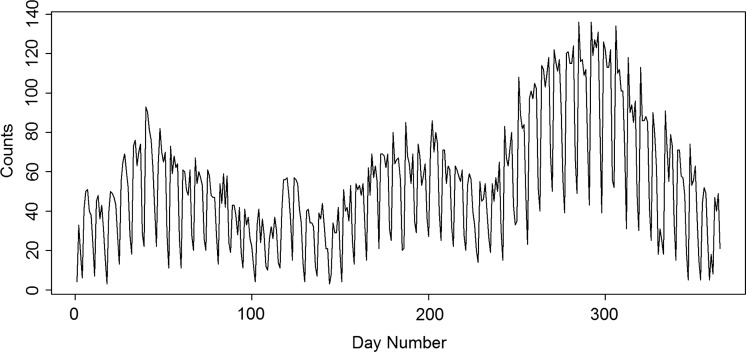
To test the methods described above, we constructed a dataset representing an anthrax bioterror attack in a major US metropolitan area. This dataset consists of background counts representing the normal daily visits to care providers, plus superimposed counts calculated from a realistic model of anthrax exposure. The type of outbreak that is possible to detect with syndromic surveillance systems must be large enough to be able to be distinguished from the background of routine patient counts, while at the same time presenting symptoms that make diagnosis difficult, unexpected, or easily confused with other diseases. This represents a typical scenario in which statistically based biosurveillance methodologies are useful, as described by Fricker.¹ We thus anticipate an attack with some hundreds or thousands of individuals exposed simultaneously (by plume dispersal, for example) and eventually presenting symptoms. Similar scenarios have been investigated in Buckeridge et al.¹² The data we have used to represent the background counts are a time series of daily International Classification of Disease, release 9 (ICD-9) codes obtained from hospitals in the greater Miami, Florida, area. These data were provided by IMS Health, LLC, of Plymouth Meeting, Pennsylvania, and consist of daily counts of approximately 500 inpatient ICD-9 discharge codes, date stamped and identified by patient zip code. Because the symptoms of anthrax in its early stages are similar to influenza, a plausible set of ICD-9 codes for biosurveillance of anthrax would be symptom codes associated with influenza. However, because it is not possible to identify unambiguously a patient associated with a set of influenze-like illness (ILI)-specific ICD-9 codes in the data, we have used clinical diagnostic codes for influenza (487.0, 487.1, and 487.8) as a proxy for the total number of influenza cases that would be determined using syndrome data. While the timeliness of ICD-9 discharge codes generally limits their use in EED biosurveillance applications, here we are using them only to model the background, and this is not a concern. The diagnostic data are shown in figure 1 for 1 year, starting from 1 January 2009. While the data include the 2009 H1N1 outbreak, unlike some other cities, its temporal signature in the ICD-9 time series is consistent with that of seasonal tropical influenza.¹³ We have used these data for our study because they show a complicated non-seasonal peak structure, as well as effects that are characteristic of biosurveillance data streams, including a pronounced weekly cycle (with lower counts on Saturday and Sunday), intraweekly structure, long-term trends, and short-term count rate spikes. This type of structure is also characteristic of other data used in biosurveillance, such as over-the-counter drug sales.

Figure 1.

One year of data for Miami, Florida, counts of International Classification of Disease, release 9 codes related to influenza. Day number 0 corresponds to 1 January 2009. The data show weekly cycles and non-stationary structure typical of biosurveillance data. Note that the data do not have a pronounced winter peak.

To simulate an anthrax attack, we used the methods described in Ray et al.¹⁴ Briefly, this is a plume model in which individuals are allocated a dose-dependent incubation period per Wilkening's A2 model.¹⁵ A visit delay based on the log normal distribution¹⁶ is added to the incubation period. These together determine the time series of the patient visits for the anthrax exposure. The original calculation was done for a total number of cases equal to 12 485, with a median count of approximately 5000 spores. Because the course of an anthrax outbreak does not involve secondary infections, the results can be scaled to provide a time series for any number of cases. Figure 2, left, shows an outbreak size of 1125 superimposed on a segment of the Miami ICD-9 counts as an example, and figure 2, right, shows the residuals for this case, with a detection (standardized residual equal to 3) at day 135, 5 days after the start of the anthrax attack on day 130. Holiday periods have been flagged in data, as these typically show anomalously low count rates, and the Kalman filter treats them as days with missing data.

Figure 2.

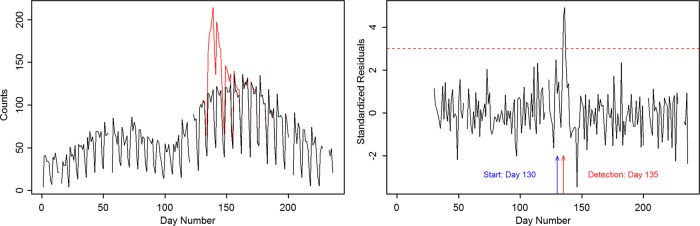
Left: The red line shows an example injected outbreak of anthrax in the Miami population, with an outbreak size of 1125 superimposed on a segment of the data in figure 1. In this particular example, the time series is shifted and day 0 corresponds to day 133 in figure 1. The anthrax outbreak size is calculated from the Wilkening A2 model and includes a visit delay. Right: The standardized residuals for the figure on the left, with a detection at day 135 for a threshold set at 3 (5 days after the start of the anthrax attack on day 130). The incubation period for anthrax is approximately 3–4 days.

Early event detection

To analyze the sensitivity and timeliness of this technique for EED, we have calculated the receiver operating characteristic (ROC) curves, as well as the activity monitoring operating characteristic curves, discussed below.

ROC curve analysis is a well-known technique for evaluating and comparing classification algorithms. For threshold-based classifiers, the ROC analysis maps the classifier response into a two-dimensional space where each point represents the true positive rate versus the false alarm rate.

Detailed discussions on the theory and practice of ROC curves have been presented elsewhere.¹⁷ Here we will present only a brief overview of the problem from the point of view of anomaly detection in time series data, and some discussion of the details of calculation of the ROC curves particular to this problem.

As discussed above, the anomaly detector uses a 1-day-ahead prediction capability provided by the Kalman filter to produce a standardized residual for data received on a particular day. This value is thresholded to provide classification: a particular day is classified as anomalous if the standardized residual exceeds the selected threshold for that day. Conversely, a day in which the standardized residual is below the selected threshold is classified as normal. This classification capability, used with a test dataset with simulated outbreak, can be used to calculate the ROC curve response of the anomaly detector.

Our ROC curve calculation has one subtlety that should be noted. A classification of ‘outbreak present’ or ‘true positive’ is valid for standardized residuals exceeding the threshold anywhere in the range of days in which an outbreak is known to occur. In contrast, any single day outside of the time at which an outbreak is known to occur represents a potential false alarm (‘false positive’). Thus defined, the tests for ‘true positive’ and ‘false positive’ required for calculation of ROC curves are not compatible. To work around this difficulty, we used a windowing technique to calculate both true positive and false positive rates. This technique calculates the true positive and false positive rates within 10-day windows at different starting points within the data. In every window, the data are tested for a false alarm within that window (anthrax data not included), as well as for true positive (anthrax data included starting on day 1 of the window). The detailed procedure for calculating the ROC curves is given below:

• 1. Divide the Miami background dataset into 10-day, non-overlapping windows, from days 40 to 300 of the Miami dataset (1 year of data). (The windows size was chosen to be a compromise between being long enough to capture all of the detections within the 60-day outbreak period, and short enough to provide a relatively large number of non-overlapping windows used for calculating detection and false alarm rates, see below).

• 2. For each window, use the anomaly detector to determine whether detection occurred at a particular threshold for the background data, and also for the background data with the outbreak data inserted, when this insertion is done in such a way that the outbreak starts on the first day of the window. If detection occurs anywhere in the 10-day window with outbreak present, increment the ‘true positive’ counter N_TP. If detection occurs anywhere in the window in the data without the outbreak included, increment the ‘false positive’ counter N_FP.

• 3. Repeat the above procedure for different threshold values. We used the detection thresholds (SD) from 0 to 5 in steps of 0.05.

• 4. For each threshold value plot the value of N_TP/N versus N_FP/N, where N is the number of windows used in the calculation. This resultant curve is the ROC curve.

The above procedure was repeated for different sized anthrax outbreaks. In addition, we varied the start time and length of the windows and found the effects to be negligible. Figure 3, left, shows the ROC curves for four outbreaks of different sizes, ranging from 124 to 873, out of a total Miami population size of 2.5 million, obtained by scaling the original anthrax outbreak (12 485 infected) by 0.01, 0.03, 0.05, and 0.07. Figure 3, right, shows an example of two of the anthrax attacks considered superimposed on the background of ILI counts. For comparison, counts in excess of background at day 5 and at the peak (day 10) for the attack sizes considered are listed in table 1.

Figure 3.

Left: Receiver operating characteristic curves for anthrax outbreaks of different numbers of total infected (out of a population size of 2.4 million). Near-perfect detection performance is obtained when for outbreaks with total size greater than 873 (0.038% of the population). Right: Simulated anthrax attack superimposed on background influenza data for two of the outbreak sizes shown on the left.

Table 1.

Counts for the anthrax epidemic curve at day 5 and day 10 for the attack sizes used to calculate the ROC curve

Attack size	Peak counts (day 10)	Counts (day 5)
124	11	6
374	33	17
624	54	28
873	76	40

ROC, receiver operating characteristic.

The ROC curves show marginal detection efficiency for the smallest anthrax attack sizes, while for an attack size greater than approximately 900 the detection efficiency is essentially perfect; that is, a threshold can be found such that the detection efficiency is 100% and the false alarm rate is 0. However, even for attack sizes as small as 400 (0.016% of the population infected), a threshold value can be found that gives perfect detection efficiency, while still maintaining a false alarm rate of one per 25 days. This shows that the detector can operate well at low signal levels, although with higher false alarm rates. This false alarm rate could be reduced further by requiring detection coincidence between similar sets of ICD-9 diagnostic codes if it is desirable to make detections close to the noise level. While ROC curve analysis is useful for describing detector performance, it is not required for setting detector thresholds. One of the strengths of the method is that the threshold relates to a desired false alarm rate via the (Gaussian) statistical framework implicit in the method (see the discussion of equation 5, above, a threshold set to 3 SD corresponds to approximately one false alarm per year). This eliminates the need to perform detailed analysis of background and outbreak models for setting thresholds via, as would be required for, for example, moving average techniques.

Figure 4 shows a detail of the detection for an anthrax attack with 873 infected starting at day 175. The red circles represent the 1-day-ahead prediction from the Kalman filter, and associated uncertainty prediction. The black line is the data, which are the sum of the Miami ILI data and the scaled anthrax attack starting at day 175. The 3 SD detection (standardized residual 3) in this case occurs on day 180, or 5 days after the start of the attack. The incubation period for anthrax is 3–4 days, so detection would not occur before this time with any detector.

Figure 4.

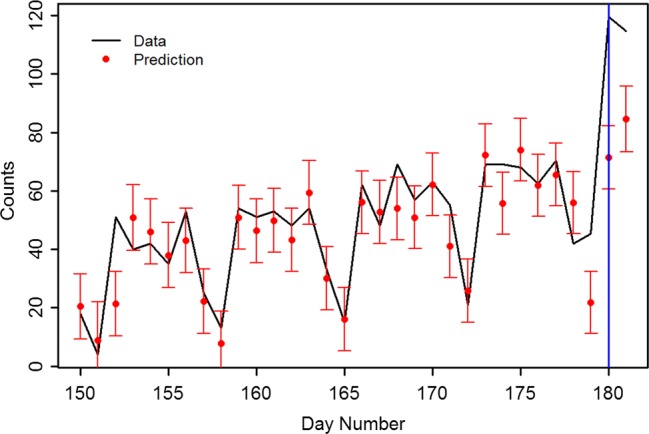
Detail of an anthrax attack, starting on day 175, with a 3 SD detection occurring on day 180 (blue line). Red points are one-step-ahead prediction and prediction uncertainties derived from the structural model.

The timeliness of the detection can be investigated using activity monitoring operating characteristic curves, a plot of time required for detection against the false positive rate. This is shown in figure 5, where the false positive rate is calculated per year. This is compared to results calculated by fitting an EWMA model to the data, where differencing (at lags 7 days and 1 day) has been used to reduce the non-stationary character of the data. The structural models generally show better timeliness at low background rates than the EWMA model, by approximately 1 day. It should be noted that for the EWMA model, unlike the structural model, missing data or holidays cannot be handled within the framework of the model, and must be treated in an ad-hoc manner (for these data, holiday count data were replaced by local averages), which is likely to increase the noise level for these time periods.

Figure 5.

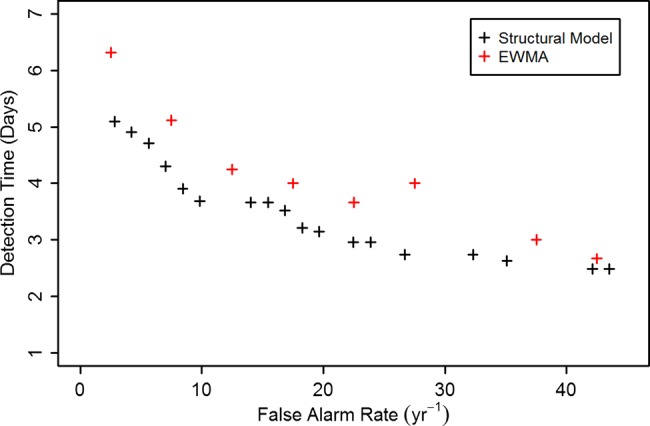
Activity monitoring operating characteristic curves, calculated for structural model and exponentially weighted moving average (EWMA) model for anthrax attack size equal to 873.

Background subtraction

Using the methods discussed above, we tested the multiday forward prediction of our structural models by testing the separation background counts from an outbreak. This requires determining the local slope at a point within the data, and projecting the structural model forward and including the slope (equation 6). An example of this procedure is shown in supplementary figure S1, available online only. In this figure, forward prediction started on day 130, with a quadratic fit to μ_t for 30 days before used to determine the local slope at the start of the prediction. This shows good forward prediction for 20 days from day 130. These results are not strongly affected by the length of the data used in the quadratic fit, and shorter fits can be used if 30 days of previous data are not available.

Figure 6 shows background subtraction results for anthrax progressions with 680, 1120, and 2250 index cases. In all cases this technique shows good background subtraction capabilities out to approximately 2 weeks post-attack. Calculating the root mean square difference in the observed and predicted value for the data shown, as a fraction of the total number infected for the outbreaks, we obtain values of 1.9%, 1.1%, and 0.05%, respectively. While it is difficult to determine an intuitive performance metric for the background subtraction, we have used these capabilities in a system to fit epidemic curves to noisy data during the early stages of the epidemic, and tested this methodology using data similar to those described in this paper. These results will be reported elsewhere.

Figure 6.

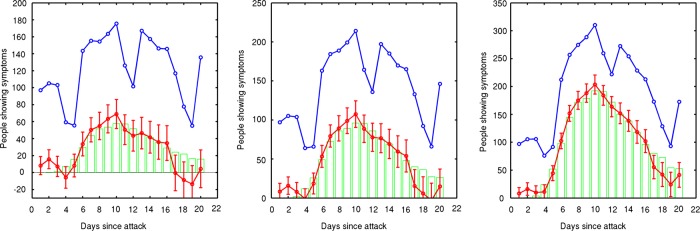
Simulated outbreak is correctly isolated from ‘normal’ background signal for greater than 2 weeks into the future. The blue line is the raw data (real data plus simulated anthrax attack. The red line is the background subtracted data using the structural model. The green bars show the original injected simulated anthrax attack. These three plots correspond to 680, 1120, and 2250 index cases out of a Miami population size of 2.4 million.

Conclusions

We have studied the use of structural time series modeling in biosurveillance using a realistic set of data derived from hospital ICD-9 codes superimposed on a calculated anthrax outbreak. Our technique is uniquely applicable for performing EED in situations in which the background count rates have noisy, non-stationary structure, and weekly and long-term cycles, such as are observed in syndromic ICD-9 data and over-the-counter drug sales data. Structural time series models have several advantages over other techniques currently in use. Unlike moving average-based methods, alarm thresholds can be mapped directly to confidence levels or to the acceptable false positive rate. In addition, structural models can easily handle gaps in the data, which are problematic for other methods. Finally, the method does not require a large dataset to ‘train’ model parameters. We have successfully used these techniques both for EED and for background modeling to obtain outbreak count rates from noisy data. While techniques for signal extraction from background have been reported before, these have only been for retrospective studies.¹⁸ We have implemented these techniques in a prototype system for early stage detection, characterization, and forecasting of partly observed outbreaks or epidemics.¹⁹