A social network of hospital acquired infection built from electronic medical record data

Abstract

Objective

Social networks have been used in the study of outbreaks of infectious diseases, including in small group settings such as individual hospitals. Collecting the data needed to create such networks, however, can be time consuming, costly, and error prone. We sought to create a social network of hospital inpatients using electronic medical record (EMR) data already collected for other purposes, for use in simulating outbreaks of nosocomial infections.

Materials and methods

We used the EMR data warehouse of a tertiary academic hospital to model contact among inpatients. Patient-to-patient contact due to shared rooms was inferred from admission-discharge-transfer data, and contact with healthcare workers was inferred from clinical documents. Contacts were used to generate a social network, which was then used to conduct probabilistic simulations of nosocomial outbreaks of methicillin-resistant Staphylococcus aureus and influenza.

Results

Simulations of infection transmission across the network reflected the staffing and patient flow practices of the hospital. Simulations modeling patient isolation, increased hand hygiene, and staff vaccination showed a decrease in the spread of infection.

Discussion

We developed a method of generating a social network of hospital inpatients from EMR data. This method allows the derivation of networks that reflect the local hospital environment, obviate the need for simulated or manually collected data, and can be updated in near real time.

Conclusions

Inpatient social networks represent a novel secondary use of EMR data, and can be used to simulate nosocomial infections. Future work should focus on prospective validation of the simulations, and adapting such networks to other tasks.

Background and significance

Hospital acquired infections (HAIs) are infections contracted during the course of hospital-based treatment of an unrelated condition. HAIs include surgical site infections, catheter-related urinary tract infections, ventilator-associated pneumonia, and Clostridium difficile associated diarrhea, among others.¹ HAIs can occur sporadically or in the setting of outbreaks, in which infection spreads rapidly through contact between patients and their environments, or patients and their healthcare workers (HCWs). For example, numerous hospital outbreaks of methicillin-resistant Staphylococcus aureus (MRSA) have been described,² and respiratory viruses such as influenza can spread rapidly through a hospital environment, infecting both patients and HCWs alike.³

HAIs are generally considered to be preventable adverse events, and thus constitute an important target in the efforts to improve the quality and safety of healthcare delivery worldwide. HAIs lead to prolonged hospital stays, disability, antimicrobial resistance, high costs, and excess mortality. In developed countries, 3.5% to 12% of hospitalized patients acquire at least one HAI, with about 4 million cases occurring annually in Europe, and a further 1.7 million cases in the USA.⁴ Such infections are not only highly prevalent, but deadly, with a mortality rate of nearly 6%.⁵ In the USA, the direct costs associated with HAIs have been estimated at greater than $30 billion annually.⁶

Previous work has resulted in a variety of approaches to the mathematical modeling of the spread of infectious diseases. Traditionally, epidemiologists have used differential equations to model the dynamics of disease spread in community settings.^7–9 Such deterministic systems, however, may be less accurate in approximating the behavior of smaller, confined environments such as hospitals, in which the point prevalence of a given infectious pathogen can vary substantially, and stochastic effects become significant.^10–17 Moreover, differences in the types of locations and the roles of individuals must also be accounted for. A nurse in the intensive care unit (ICU), for example, may have sustained contact with a small number of patients, all within the same physical space, whereas a consulting physician may visit many patients, both in and outside of the ICU, and thus have a very different role in the propagation of an infectious outbreak.

More recently, social networks have been investigated as a tool to model infection transmission.^{8 18–20} In general, such models represent individuals as nodes, and the epidemiologic links between them as edges. These methods have been used to model community-based health problems such as smallpox,^{10 21–23} H5N1 influenza,²⁴ obesity,²⁴ and sexually transmitted infections.²⁵ Infection in the hospital setting has been modeled to a lesser extent.^{21 26 27} Stochastic simulations using such contact networks have been used to derive insights into the dynamics of how HAIs are propagated.^{10 12–15 17 21–23}

One specific challenge faced by social network modeling is to collect the data that describe the nodes and edges. In some simulation-based studies, edges are generated by a series of random permutations, in order to evaluate the effects of different connections.^{20 28} In community-based outbreaks, such as outbreaks of sexually transmitted infections, contact between individuals can be determined by interviewing affected individuals,²⁹ or by direct observation of patients and their surroundings.²⁵ Newer approaches include the use of web-based surveys to characterize temporal patterns of social contact among larger groups.³⁰ In hospital settings, contacts among patients and HCWs can also be determined based on direct observations by researchers.²⁷

Each of these methods has important limitations that may impede the successful implementation of social network analysis techniques.³¹ Simulated connectivity data may be inaccurate or unrealistic. Data from direct observation may be costly to collect, and result in networks that lack generalizability. While survey data may be easier to collect, these may lack sufficient detail and completeness to yield realistic models. The increasing abundance of electronic medical record (EMR) data presents an opportunity to provide highly granular and accurate information regarding the epidemiologic links that connect hospital inpatients and staff.

In this study, we created a social network of hospital inpatients using EMR data, in which patients are connected according to shared rooms and shared contact with HCWs. We used a modular design structure to allow the incorporation of additional epidemiological data where available. We then used the network as a platform to simulate nosocomial outbreaks of both MRSA and influenza, and identify potentially mitigating interventions.

Materials and methods

The study was conducted using EMR data collected at Stanford University Medical Center, a 611-bed academic hospital. All clinical data were extracted from the Stanford Translational Research Integrated Database Environment (STRIDE), a research and development project at Stanford University that includes a comprehensive clinical data warehouse.³² Data were fully de-identified and date-shifted in order to maintain compliance with Health Insurance Portability and Accountability Act (HIPAA) guidelines. The University's Institutional Review Board deemed the project to be non-human subjects research, and granted approval for the extraction and analysis of de-identified data.

Data extraction

We extracted data covering a 70-day period of hospital admissions, all of which were used to derive summary statistics. In order to eliminate boundary cases, only data from days 35–45 were used in the simulations. All patients were included, resulting in 4891 unique patient-days. Data were retrieved by means of structured SQL queries designed to run against the STRIDE database schema. We extracted data from the hospital's admission-discharge-transfer (ADT) system, which provides room and bed location, as well as dates and times for both admission and discharge to and from each bed. In order to represent connections based on shared contact with HCWs, we extracted metadata from clinical documents, which include the document type, a unique anonymized author identifier, and the author's HCW role type (eg, ‘occupational therapist,’ ‘registered nurse,’ ‘anesthesiologist,’ etc).

Data aggregation and graph formation

We developed a Python library that uses data files derived from the SQL queries in order to generate pairwise connections between individual patients based on sharing of rooms, shared contact with HCWs, or both. For each calendar day, we calculated the amount of time in seconds during which two patients were in the same room at the same time. For shared contacts with HCWs, we used a directional approach in which one patient was considered to be connected to another if a HCW had written a clinical note on the first patient within the 2 h preceding their writing a note on the second. One of us (DMM) provided domain knowledge of the care of hospital inpatients, in order to determine which HCWs were likely to have direct physical contact with patients, and which clinical document types were likely to reflect a direct physical encounter with a patient. These likelihoods were compared with empiric data generated in a separate study by Polgreen et al,²⁷ in order to verify their validity. Based on these evaluations, a binary value was assigned to each HCW role and note type (see online supplementary table 1). These were then used to infer shared contact with a HCW between each pair of patients on each day. Weights corresponding to the transmission probabilities were then generated for the graph's edges, based on a function of the room-sharing time, and shared HCW contact.

We combined the networks for successive calendar days into a directed acyclic graph (DAG) of epidemiologic links that change with time. This DAG was used as the framework for the probabilistic simulations of infectious outbreaks. We also evaluated a number of network and hospital characteristics, including the number of visits per ward, and the ward-specific distributions of length of stay.

Probabilistic model of infection spread

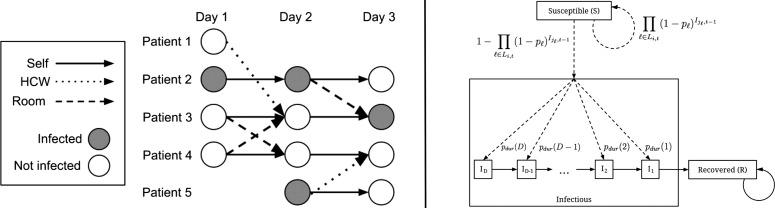
We used the social network described above to develop a probabilistic model of the spread of infection through the hospital (figure 1). The model consists of a group of N hospital inpatients that persists over T days. There are therefore NT state variables q_i,t for i∈{1...N} and t∈{1...T}, where q_i,t is the infection state of patient i on day t. Once a patient is infected, the duration of the infection in days (d) is drawn from a discrete distribution, d∼P_dur, where P_dur∈{1 … D}, and D is the maximum duration allowable. Each state variable q_i,t has domain {S, I₁, … , I_D, R}, where S indicates the patient is not infected but susceptible, R indicates the patient is recovered from infection, and I_d indicates that the patient is currently infectious and will remain so for d−1 more days. I₁ indicates the patient will enter the recovered state on the next day.

Figure 1.

Probabilistic model for the spread of influenza within a social network, using a ‘S-I-R’ (susceptible-infected-recovered) schema. (i) Each day is considered as a collection of nodes that represent the patients in the hospital on that day. Individual patients are either infected, or not infected (one of ‘Susceptible’ or ‘Recovered’), and transition between states based on their state at the previous time step, as well as the state of their incoming nodes, connected by either room-sharing or healthcare workers-sharing links. (ii) The infected state is divided into sub-states (I₁ through I_D) that reflect the number of days remaining during which the patient is infectious. Patient transitions between the various states are governed by the probabilities shown. L_i,t is the set of incoming links for patient i on day t. j_ℓ is the source patient of link ℓ. I_i,t is a binary variable indicative of infection, where I_i,t=1 (infected) if q_i,t∈{I₁, … ,I_D}, and 0 (not infected) if q_i,t∈{S,R}. q_∗,t denotes the set of states for all patients on day t. Solid arrows represent deterministic transitions, while dashed arrows represent probabilistic transitions (see text for details). HCW, healthcare worker.

A patient can transition from the susceptible state (S) to an infectious state (I_d for some d) by acquiring the infection from another patient (figure 1A). An infection passed from an infected patient i on day t−1, to a second patient, j, on day t, must travel along a link, k, which is a potential route of infection associated with a probability p_k. This probability reflects the strength of association between i and j as determined by either the room-sharing or HCW-sharing parameters, depending on the type of link. For room-sharing links, p_k depends on the duration of shared-room contact:

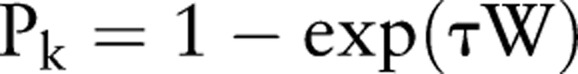where τ is a constant specified by the user based on how contagious the disease is, and W is the duration of room-sharing in seconds. For HCW-sharing links, the probabilities (p_k) are all set to the same value, after clinical documents deemed not to reflect physical contact have been excluded, as described above.

Let K_i,t be the set of incoming links for patient i on day t, and let j_k be the source patient of link k. Let I_i,t be a binary variable indicative of infection, where I_i,t=1 (infected) if q_i,t∈{I₁, … , I_D}, and 0 (not infected) if q_i,t∈{S,R}. Let q_*,t denote the set of states for all patients on day t. The probabilities of each possible transition q_i,t−1→q_i,t are then as defined by the following set of equations:

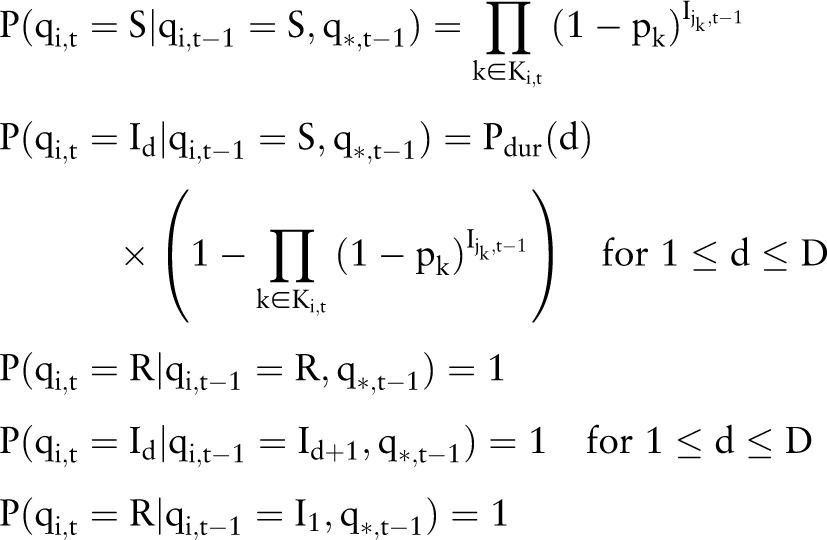Simulation analysis framework

Using the probabilistic model described above, we simulated nosocomial outbreaks of both MRSA and influenza. We used parameters based on empirically derived estimates from the medical literature, and tested the effects of various infection control measures. Simulations were initiated by artificially infecting an individual patient or small group of patients, running the simulation forward in time, and counting the number of infections within a target set of patients at a pre-specified endpoint. The source set and target set were defined by filtering on certain boolean attributes of patient nodes, such as ‘the patient was in the operating room on this day.’ Using this simple kernel, a variety of complex analyses can then be composed, such as ‘estimate the probability that a patient who is on the orthopedic unit will become infected by an outbreak started in the emergency department (ED) three days earlier.’

We conducted a number of simulations originating in the ED, a medical step-down unit, and a psychiatry unit, using the parameters shown in table 1. For each of the various hospital departments, we estimated the probability that any given patient would become infected after 15 days (for MRSA) or 6 days (for influenza).

Table 1.

Parameters for outbreak simulations

Parameter	MRSA	Influenza	Source
Mean duration of colonization (MRSA) or infection (influenza)	75 days	3 days	Kajita et al,13 van den Dool et al17
Baseline room-sharing probability of infection (day−1)	0.12	0.26*	Nerby et al,33 van den Dool et al17
Baseline HCW-sharing probability of infection (contact−1)	0.0169†	0.13*	McBryde et al,15 van den Dool et al17
Vaccine efficacy	NA	86%	Thomas et al34

*Based on estimating HCW contact as ‘casual’ contact, and room-sharing as ‘close’ contact.

†Based on single contact risk squared.

HCW, healthcare workers; MRSA, methicillin-resistant Staphylococcus aureus.

Results

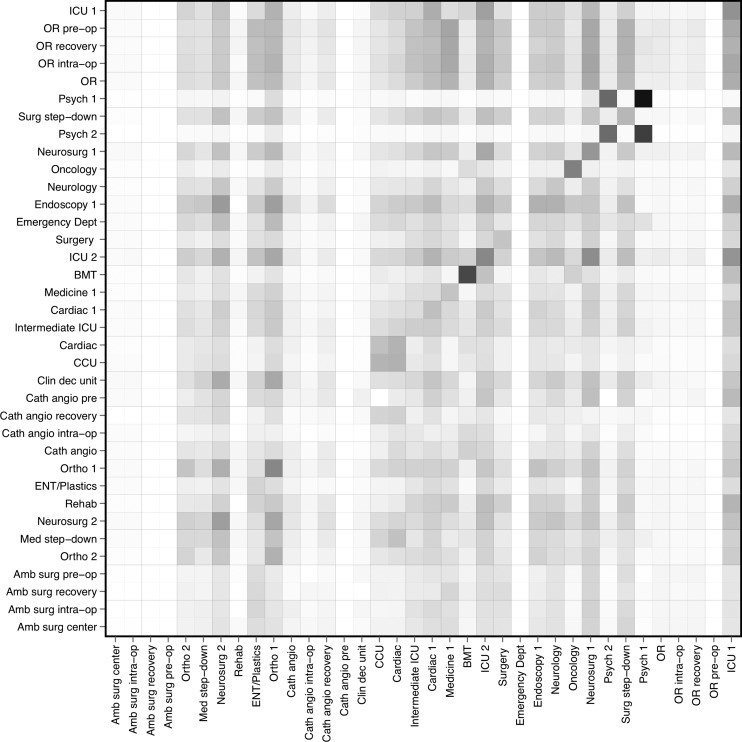
A visual representation of the social network is shown in figure 2. Most connections between patients were based on shared HCWs, with fewer based on room-sharing. The greatest number of patient encounters occurred in the ED, followed distantly by the main operating room (see online supplementary figure 1). These departments had relatively short lengths of stay, whereas departments such as the ICUs and psychiatry units had longer stays, with greater variance (see online supplementary figure 2). The probabilities for the spread of influenza between individual departments are shown in figure 3. The risk of spread between wards was greatest between the two psychiatry units, and between the cardiac unit and coronary care unit. Simulated outbreaks initiated in the bone marrow transplant unit tended to propagate locally. Both the ED and the operating areas (main operating room, ambulatory surgery center, and catheterization angiography laboratory) tended to have low levels of incoming infection. Results were similar for MRSA, but with lower probabilities overall (see online supplementary figure 3).

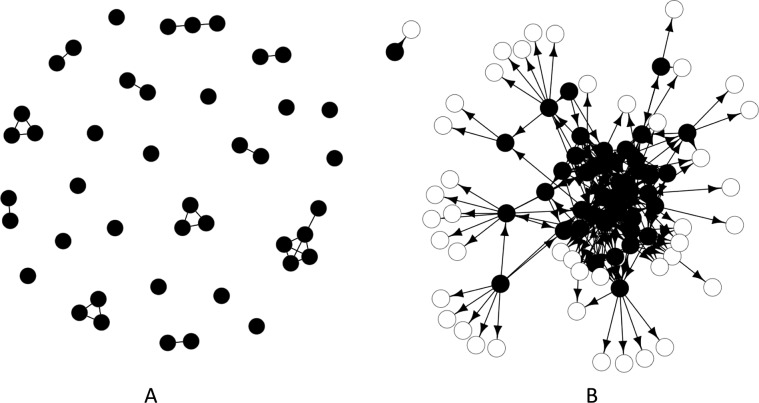
Figure 2.

Social networks of hospital inpatients derived from electronic medical record data in which patients are represented by nodes, and the epidemiologic links between them are represented by edges. Images shown depict patients on an single medical ward, on a single day. (A) Network showing links based on room-sharing only. (B) Network showing links based on healthcare workers-sharing. Closed circles represent patients on the medical ward itself, while open circles represent patients in other units.

Figure 3.

Matrix showing the probabilities for spread of influenza between wards. The rows are the source departments and the columns are the target departments. The shading in each cell indicates the probability of disease transmission from the ward indicated by the row, to the ward indicated by the column, with darker cells reflecting higher probabilities. BMT, bone marrow transplant; CCU, coronary care unit; ICU, intensive care unit; OR, operating room.

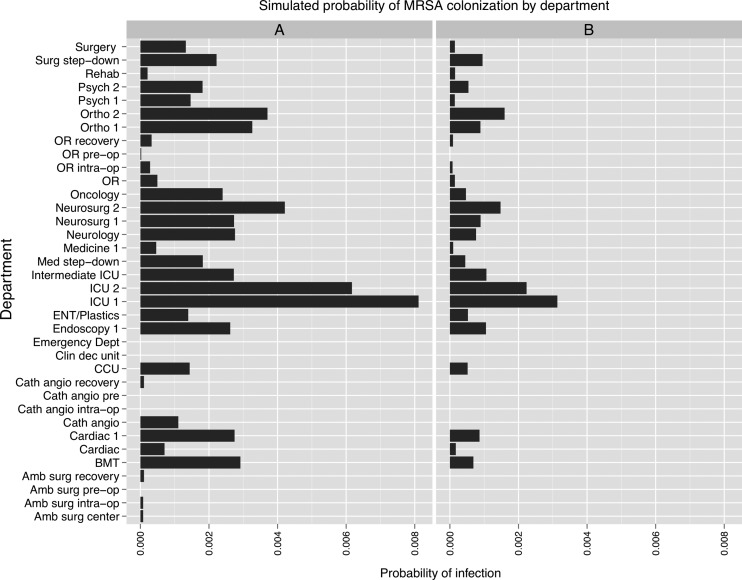
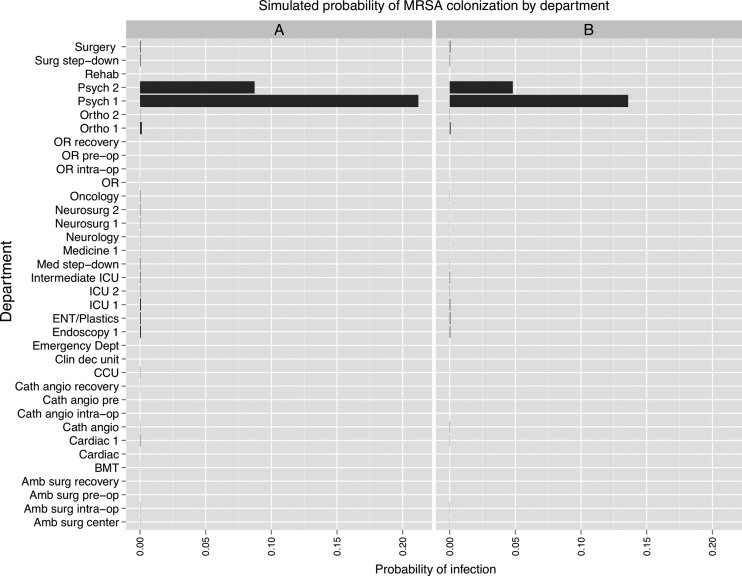
The MRSA simulations predicted that an infection originating in the medical step-down unit propagated to the ICUs, and to a lesser extent, the neurosurgical, orthopedic, and cardiac units (figure 4). Areas such as the ED and operating rooms were relatively spared. A 50% increase in hand hygiene compliance substantially mitigated the risk of transmission, while preserving the overall pattern of spread. In the case of the simulations initiated in the psychiatric unit, the infection spread almost exclusively within the originating unit and the second psychiatric unit, with little effect on the other departments (figure 5). Modeling the exclusive use of private rooms on the psychiatry units predicted a decrement of one-third to one-half in the probability of infection.

Figure 4.

Results of methicillin-resistant Staphylococcus aureus (MRSA) simulations conducted using a social network of hospital inpatients. The x-axis shows the per-patient probability of colonization at the end of 15 days. (A) Simulation initiated with one infected patient in a medical step-down unit (‘Intermediate ICU’). (B) Effect of a 50% increase in hand hygiene among healthcare workers.

Figure 5.

Results of methicillin-resistant Staphylococcus aureus (MRSA) simulations conducted using a social network of hospital inpatients. The x-axis shows the per-patient probability of colonization at the end of 15 days. (A) Simulation initiated with one infected patient in ‘Psych 1’ unit. (B) Effect of assigning all patients to private rooms.

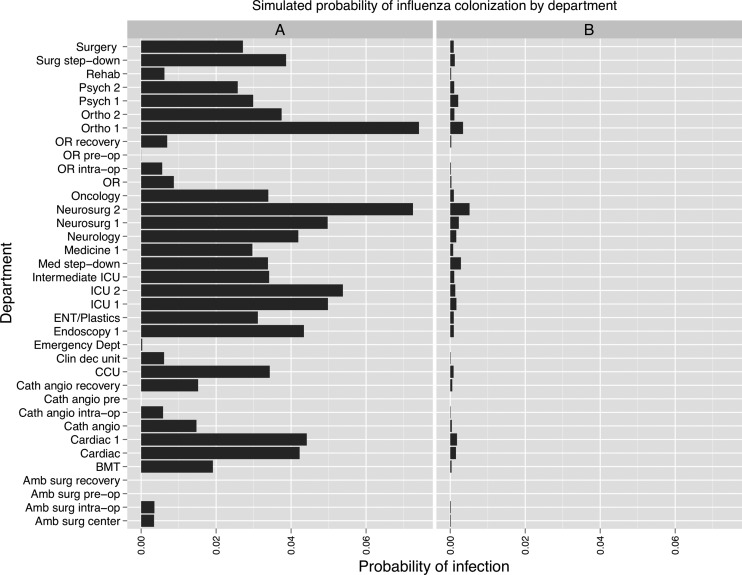
The influenza simulation predicted that an infection originating in the ED spread diffusely throughout the hospital, without propagating in the ED itself (figure 6). Staff vaccination was predicted to decrease the spread of infection markedly.

Figure 6.

Results of influenza simulations conducted using a social network of hospital inpatients. The x-axis shows the per-patient probability of colonization at the end of 6 days. (A) Simulation initiated with one infected patient in the Emergency Department. (B) Effect of healthcare worker vaccination with 100% compliance and 86% vaccine efficacy.

Discussion

While social networks have proven to be useful tools in modeling and investigating large scale outbreaks and pandemics, their use in smaller settings such has hospitals has been less extensive. The data required to build such networks are often collected manually, and as such can be incomplete, inaccurate, and costly to gather. An alternative to this approach is to rely on simulated data, which may make numerous assumptions and be overly simplistic. A potential solution is enabled by the increasing prevalence of EMRs, which represent an important and valuable source of health information available for secondary uses.

Our study is the first social network of hospital inpatients generated using EMR data. Our approach has three important benefits. First, rather than collecting data de novo, we used existing data collected in the course of clinical care, which was then retrieved from an EMR data repository. Second, the data derived from a particular hospital's EMR reflect the local staffing and patient flow patterns unique to that institution, and are therefore ideally suited to characterize the nodes and edges of the network. Third, our approach allows for near real-time updating of social networks, as the EMR data itself is updated. This feature ensures that changes in staffing and patient flow practices are reflected in updated versions of the network, in contrast to empirically derived networks that may become outdated.

Our results demonstrate the utility of social networks in deriving insight into the spread of HAIs. In the case of an influenza outbreak that starts in the ED, our model predicts that the infection spreads throughout the hospital, predominantly to the medical wards and intensive care areas that are common destinations for patients admitted from the ED. Despite the high number of patients co-localized in the ED, the probability of infection in the ED itself remains low, which likely reflects the transient nature of admissions to that unit. By contrast, the model MRSA outbreak originating in one of the psychiatry units spreads extensively through this unit, as well as to the only other psychiatric unit in the hospital. This pattern reflects the staffing model of these units, which relies on specialized practitioners who are likely to travel between these two units, but not elsewhere in the hospital.

Our results also illustrate the utility of social networks in modeling the effects of infection control interventions such as patient isolation, hand hygiene, and staff vaccination. In the simulations of MRSA, spread is mitigated by eliminating the room-sharing connections, suggesting that patient isolation could be efficacious in limiting the scope and extent of an outbreak. In the case of influenza, decreasing the weight of HCW-sharing in the model results in a substantial reduction in the probability of transmission, suggesting that staff vaccination may be an effective infection control measure. With the model framework established, simulation parameters can be adjusted to reflect the infection dynamics of different types of nosocomial diseases.

There are numerous use cases for EMR-derived social networks, most notably in the area of infection control. Hospital-based infection control practitioners (ICPs) could use such networks to determine staffing and patient flow practices that might increase the risk of propagating HAI outbreaks, and to model the impact of specific changes in said practices. When combined with additional EMR data, such as vital sign, laboratory, and microbiologic data, social networks could be used to track numerous different HAIs within the inpatient environment, and provide real-time analytics to ICPs. Future work in this area should focus on applying machine learning methodologies to social networks in order to generate predictive models of the spread of HAIs based on clinical features. EMR-derived social networks could also be developed to model the effects of social structures on practice patterns within the hospital, and to optimize patient flow pathways.

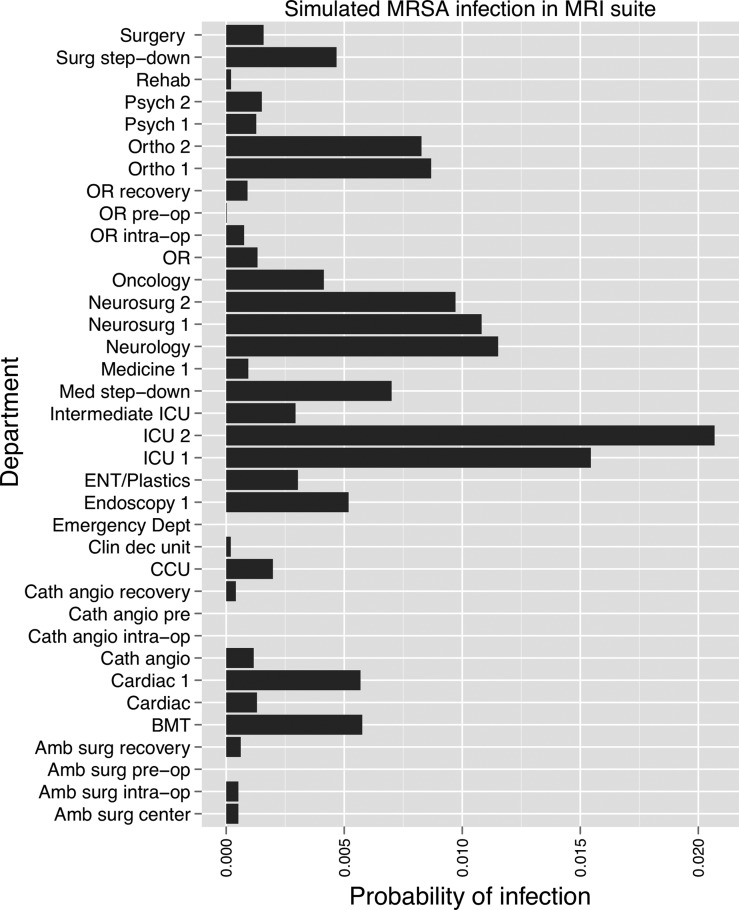
We used a modular design in constructing the social network, such that additional data describing physical interactions between patients, hospital staff, and the hospital environment could be easily incorporated. For example, we extracted EMR data related to diagnostic imaging procedures that were used to infer additional epidemiologic links between patients based on visits to the same radiology department on the same day. We simulated a case of MRSA in the MRI department, which carried a 1% risk of transmission to any other patient visiting the department on that day, an estimated parameter representing the probability of transmission from either contaminated equipment or colonized departmental staff members. After 3 days, the risk of infection was greatest for patients in the ICUs, and on the neurology and neurosurgical wards (figure 7). Other sources of data might include EMR login data,³⁵ as well as hospital real-time location systems that use radiofrequency identification, wi-fi, or wireless local area networks to track hospital equipment, personnel, and patients.³⁶

Figure 7.

Results of methicillin-resistant Staphylococcus aureus (MRSA) simulation conducted using a social network of hospital inpatients, starting with one infection in the magnetic resonance imaging (MRI) department. The x-axis shows the probability of infection in each department at the end of 3 days, and is based on room-sharing and healthcare worker-sharing links, as well as patient visits to the MRI suite.

Our study has a few limitations that must be considered. First, the quality of the social network derived depends on the accuracy and coverage of the EMR data on which it is based. In the case of the present study, the ADT data that were used to derive the room-sharing intervals were collected at a highly granular level, such that transfers between rooms on the same unit are registered, and length of stay in each room was recorded to the second. We used authorship of clinical documents as a surrogate for contact between HCWs and patients. This attribution assumes that the authors of the given notes had some form of physical interaction with the patient on the day the note was written, and that HCWs documented their patient contacts in the same order that the encounters themselves occurred.

Second, our model does not capture contacts outside of those documented in the EMR. The influence of hospital personnel who do not generate clinical documentation, including food service workers and porters, is therefore not accounted for, nor are brief or secondary visits that are not associated with a specific clinical note. Also not encompassed are the effects of visitors to the hospital, which in the case of seasonal respiratory viruses such as influenza, might be considerable.

Third, the results of our simulations are determined by the parameters chosen to represent the infection dynamics of the pathogen under consideration. Although we used parameter estimates derived from previous empirical and simulation studies reported in the literature, the accuracy of these in the setting of our hospital environment is not known. Further work should focus on refining the parameters used in the simulations, and ultimately verifying the accuracy of predictions against a previously documented outbreak.

As with any study of HAI at a particular hospital, our results cannot be generalized to other centers. However, unlike previous studies, our methods for generating social networks and simulating outbreaks can be applied to any hospital with an EMR implementation that supports ADT tracking, clinical documentation, and data warehousing. A less robust version could also be built upon ADT data alone, although this would fail to capture the important epidemiologic links between patients and hospital staff.

Conclusion

We developed a method of generating social networks from EMR data already collected for other purposes. Such networks have the advantage of directly reflecting the staffing and patient flow patterns of the hospital from which the data were taken, and of being easily updated in near real time. As a proof of concept, we applied this method to the problem of HAI, by conducting probabilistic simulations of MRSA and influenza infection across the network generated. We tested the effects of implementing various infection control measures on transmission patterns.

Our methods can be applied most readily to the modeling and understanding of HAIs, but might also be used to refine staffing and patient flow practices within a hospital, or to examine the influence of social structures on clinical practice patterns. Future work should focus on refining the parameters used to describe the infection dynamics of various HAIs, prospective validation of the simulation experiments carried out, and the integration of machine learning methodologies in order to generate more robust predictive models, based on more types of clinical data.