SUMMARY
Many fundamental aspects of DNA replication, such as the exact locations where DNA synthesis is initiated and terminated, how frequently origins are used, and how fork progression is influenced by transcription, are poorly understood. Via the deep-sequencing of Okazaki fragments, we comprehensively document replication fork directionality throughout the S. cerevisiae genome; this permits the systematic analysis of initiation, origin efficiency, fork progression and termination. We show that leading-strand initiation preferentially occurs within a nucleosome-free region at replication origins. Using a strain in which late origins can be induced to fire early, we show that replication termination is a largely passive phenomenon that does not rely on cis-acting sequences or replication fork pausing. The replication profile is predominantly determined by the kinetics of origin firing, allowing us to reconstruct chromosome-wide timing profiles from an asynchronous culture.
INTRODUCTION
Chromosomal replication origins in S. cerevisiae, have been mapped at high-resolution using a variety of techniques and, unusually among eukaryotes, consensus sequences sufficient for origin activity have been identified (Kearsey, 1984; Marahrens and Stillman, 1992; Rao et al., 1994). Most recent approaches to origin mapping and replication profiling rely on pulse-chase experiments in which cultures are synchronously released into S-phase, harvested along a time course, and assayed for incorporation of detectable nucleotides (Fachinetti et al., 2010; Raghuraman et al., 2001) increased copy number (Yabuki et al., 2002), single-stranded DNA (Feng et al., 2006), or occupancy of replication fork proteins (Sekedat et al., 2010); these approaches provide a wealth of data describing average replication behavior across a population of cells, informing mathematical models of genome replication (de Moura et al., 2010; Yang et al., 2010). Pioneering work (Raghuraman et al., 2001) provided evidence that distinct subsets of replication origins fire with predictable timing and efficiencies at defined intervals during S-phase. However, in contrast to the somewhat deterministic view of genome-wide replication obtained from such studies, detailed single-molecule analysis of S. cerevisiae chromosome VI via DNA combing (Czajkowsky et al., 2008) provided evidence that no two cells have identical patterns of origin use, implying a globally stochastic pattern of independent origin firing.
Current replication profiling techniques are limited by the lack of a direct readout of replication fork directionality in regions more than a few kilobases from efficient origins. The extent of variation within a population has therefore proved difficult to assay directly: assignment of signal to a given origin becomes difficult once signals arising due to convergent forks have merged. Because one cannot clearly distinguish between incoming replication forks from either direction or the firing of inefficient origins that are predominantly passively replicated, quantitative analysis of origin efficiencies has only been carried out in a low-throughput fashion, e.g. (Friedman et al., 1997; Yamashita et al., 1997).
Relative to replication initiation, comparatively little is known about how and where convergent replication forks terminate. In some regions of eukaryotic genomes, the sites of fork convergence are precisely determined by cis-acting barriers analogous to the Tus-Ter system in E. coli (Hill and Marians, 1990). For example, a polar barrier within the S. cerevisiae rDNA repeat, comprising the Fob1 protein in complex with the replication fork blocking sequence RFB, impedes the passage of replication forks moving in one direction (Brewer and Fangman, 1988; Kobayashi and Horiuchi, 1996) and thus ensures unidirectional replication of the repeat region. However, termination at RFBs likely accounts for a tiny fraction of all regions of termination. Genomic regions with high occupancy of non-nucleosomal proteins, such as centromeres and highly transcribed genes, are known to be problematic for replication fork progression and can elicit stable replisome pausing (Deshpande and Newlon, 1996; Greenfeder and Newlon, 1992; Ivessa et al., 2003). Passage of the replication fork through potential pausing elements is promoted by the action of the Rrm3 helicase (Ivessa et al., 2003), but recent work has postulated the existence of specific termination zones (TERs) in which chromosomal features that mediate fork pausing can slow replication fork progression to the extent that converging forks will likely meet in their vicinity, restricting termination to a defined region (Fachinetti et al., 2010).
Here, we analyze Okazaki fragments by deep sequencing to generate a high-resolution view of the S. cerevisiae replication program. We provide detailed measurements of the efficiencies of all replication origins and regions of termination and demonstrate a preference for leading-strand initiation within the nucleosome-free region generally found at origins. In addition, we present evidence that S-phase follows a temporal program dominated by replication origins firing with high probability within distinct time intervals. Contrary to expectation, we find that centromeres and highly transcribed regions are not strong determinants of replication termination; rather, termination generally occurs midway between two adjacent replication origins at positions dictated by their relative firing times. Sites of termination are therefore indicative of origin firing time, allowing us to reconstruct the temporal dynamics of the replication program using data from an asynchronous culture.
RESULTS
Deep sequencing Okazaki fragments for replication profiling
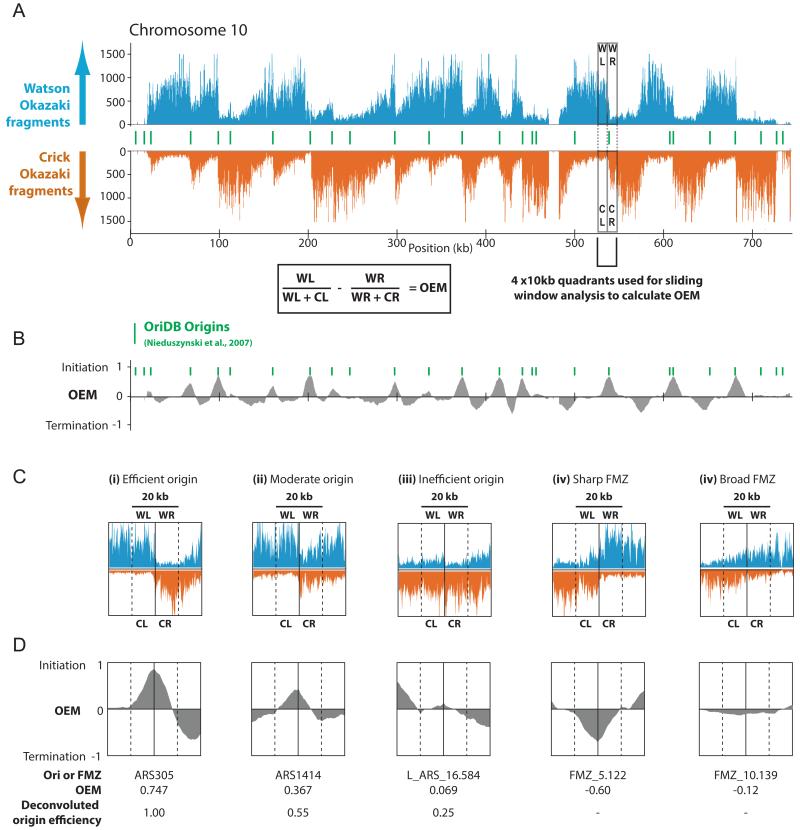
We have developed methods for the purification and deep sequencing of Okazaki fragments from S. cerevisiae (Smith and Whitehouse, 2012): DNA ligase I is degron-tagged and placed under the control of a doxycycline-repressible promoter. After ligase repression, short single-stranded DNA fragments are purified and sequenced using Illumina Hi-seq or Ion Torrent platforms. An important aspect of our strategy is the preservation of strand identity, which allows us to unambiguously distinguish Okazaki fragments replicated as the Watson or Crick strand (arising, respectively, from leftward- or rightward-moving replication forks). Replication origins are readily detected as sharp transitions from leftward- to rightward-moving replication forks: origin efficiency – a measure of the likelihood that a replication origin is used during S-phase – is proportional to the magnitude of the transition at the origin. A unique advantage of our methodology is that regions of termination, arising from the convergence of two oppositely oriented replication forks, can also be detected as transitions with the opposite strand bias to origins (Fig. 1).
Figure 1. Quantitative identification of replication origins and fork merger zones (FMZs) from Okazaki fragment maps.
(A) Sequenced Okazaki fragments mapping to the Watson (blue) or Crick (orange) strand on S. cerevisiae chromosome 10. Watson- or Crick strand fragments indicate leftward- or rightward-moving replication forks, respectively. Both replication origins and fork merger zones (FMZs) can be readily identified using a sliding window to generate an origin efficiency metric (OEM). (B) Across a 20kb window, the proportion of Watson strand hits in the right half is subtracted from that in the left, generating peaks at origins whose height is proportional to firing efficiency, and analogous troughs at FMZs. Positions of replication origins listed as ‘confirmed’ in the OriDB yeast origin database (Nieduszynski et al., 2007) are indicated in green. Other chromosomes are shown in Fig. S6.
(C&D) Okazaki fragment density and OEM across a 40kb window for representative origins of (i) high, (ii) moderate, and (iii) low efficiency, and for representative sharp (iv) and broad (v) FMZs. Raw OEM score and calculated origin efficiency differ due to the deconvolution process described in the methods section and Figs. S1-3.
We reasoned that transiently repressing DNA ligase I in an asynchronous culture would provide a “snapshot” of Okazaki fragments produced throughout S-phase, and were able to obtain coverage of the entire genome from a single library after 2.5 hours of repression. We developed a computational framework to systematically identify replication origins and sites of termination from our data: our method compares the density of Okazaki fragments on the Watson and Crick strands within a four-part sliding window composed of equally sized, strand-specific 10kb quadrants around each base pair of each chromosome (see methods). The upper two quadrants (WL and WR) measure Okazaki fragment density in the left and right quadrants on the Watson strand; whereas the lower two (CL and CR) measure density in the left and right quadrants on the Crick strand (Fig. 1 A&C). All quadrant scores are normalized with respect to total Okazaki fragment density within the left or right side of the sliding window, as appropriate, such that WLn=WLraw/(WLraw+CLraw). At an idealized origin that fires in each cell in the population, left quadrants would entirely indicate leftward fork motion (WLn=1, CLn=0) and right quadrants would entirely indicate rightward fork motion (WRn =0, CRn =1). We use quadrant values to calculate an origin efficiency metric (OEM: defined as OEM = WLn – WRn) ranging from −1 to 1 for each base in the genome. Localized maxima in the OEM score represent replication origins, with OEM (from 0 to 1) proportional to origin firing efficiency (Fig. 1B&D). Regions of termination are captured on our OEM plot as localized minima: the degree of termination at each position can be measured from 0 to −1 (where −1 theoretically represents a point terminator between two origins that invariably fire) Fig. 1D. Since sites of termination often span several KB, we term them “fork merger zones” (FMZs).
Global analysis of replication origin location and efficiency
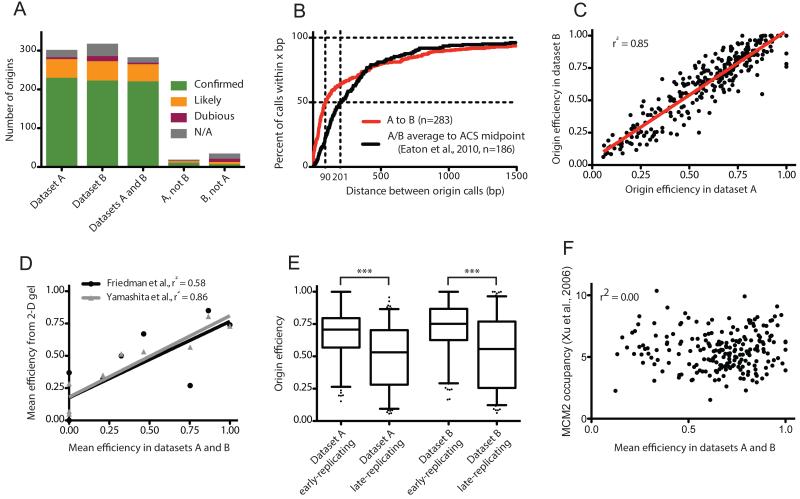
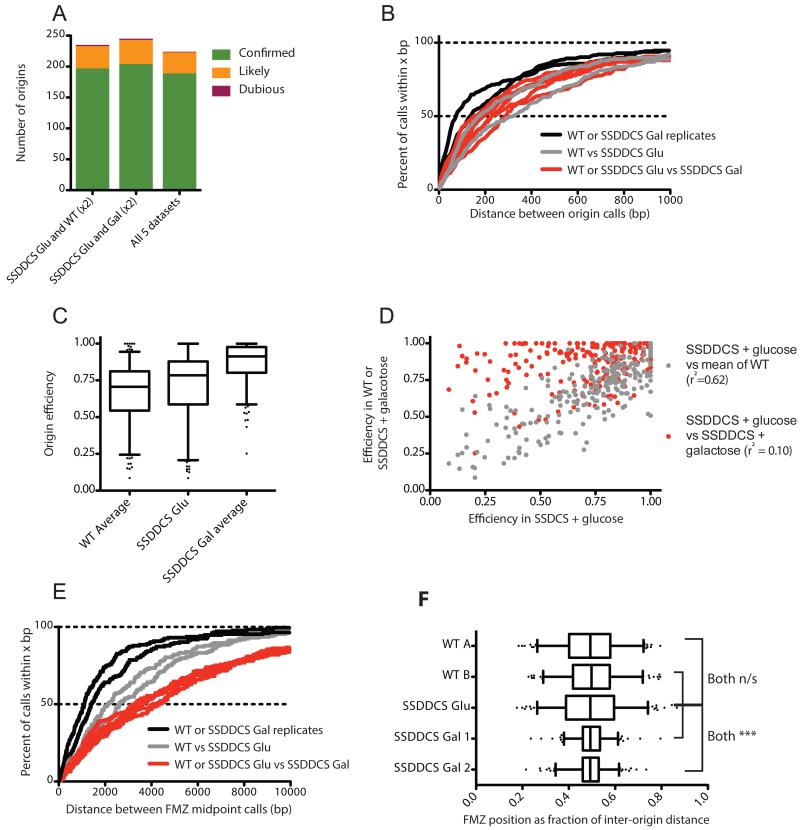
To assay the robustness of our origin location and efficiency calls, we applied our algorithm to replicate datasets of a lig4Δ, rad9Δ strain (hereafter referred to as wild-type) used previously (Smith and Whitehouse, 2012). Of 302 and 318 origins meeting the minimum criteria in replicate datasets A and B, respectively, 283 were shared between the two sets. An essentially complete list of sequences capable of acting as replication origins in S. cerevisiae is available in the OriDB (Nieduszynski et al., 2007), with each origin classified as ‘confirmed’, ‘likely’ or ‘dubious’ depending on the number and type of experimental approaches validating its use. For origins predicted in both datasets, 221 (213 unambiguously) corresponded to (defined as lying within 2.5 kb) a confirmed origin, 44 (42 unambiguously) to likely and 4 (all unambiguously) to dubious OriDB origins; a further 14 could not be assigned to any OriDB origin (Fig 2A). Ambiguous calls result from OriDB origins that are closer together than can be distinguished by our matching protocol.
Figure 2. Validation of replication origins identified from Okazaki fragment sequencing, and global evaluation of origin efficiency across replicate datasets.
(A) Identified origins correspond well with previous reports. Column graphs indicate the number of origins identified in replicate datasets lying within ±2.5kb of OriDB (Nieduszynski et al., 2007) origins listed as ‘confirmed’, ‘likely’, or dubious: N/A indicates an origin that is not within 2.5 kb of any OriDB entry. Origins within 5kb of one another in replicate datasets were deemed to be the same.
(B) Origins are accurately identified in replicate datasets. The percentage of the 284 matched origin pairs called less than x bp apart in replicate datasets is plotted in red on the Y axis: median distance between matched origins is 90 bp. 186 origins lie within ±2.5kb of an ACS sequence corresponding to an active origin (Eaton et al., 2010); the black line represents the percentage of these origins within x bp of the ACS midpoint, and has a median of 201 bp.
(C) Origin efficiencies are consistent in replicate datasets. The red line corresponds to a linear regression.
(D) Origin efficiencies agree well with values determined by 2-D gel electrophoresis. Mean efficiencies calculated biochemically for origins across chromosome 6 (Friedman et al., 1997; Yamashita et al., 1997) are compared to mean efficiencies for the corresponding origins across our two datasets. Origins not detected in our analysis are assigned an efficiency of zero. Lines correspond to linear regressions.
(E) Origins in early-replicating regions of the genome are significantly more efficient than those in late-replicating regions: origins were ranked by trep (Raghuraman et al., 2001) and divided into bins above and below the median value; p<0.0001 for each dataset. Box represents lower quartile, median and upper quartile; whiskers denote the 5th and 95th percentiles.
(F) Origin efficiency does not correlate with Mcm2 ChIP. Mean origin efficiency for origins identified in replicate wild-type datasets and within 2.5kb of Mcm2 ChIP peaks (Xu et al., 2006), is plotted against Mcm2 occupancy.
See also Fig. S4.
The correspondence between our predictions and pre-existing origin identifications in S. cerevisiae indicates that our methodology represents an effective way to locate replication origins: those identified in only one dataset were significantly less likely to match with confirmed origins (Fig. 2A). Poor correspondence with OriDB and low efficiency scores (Fig. S4a) suggest either that these calls represent extremely inefficient origins that fall below the detection limit across a variety of datasets, or false positives resulting from noise in our experimental data. Furthermore, our data provide high spatial resolution: the median distance between replicate origin midpoint calls was 90 bp, with over 90% of midpoints falling within a ±1.5kb range (Fig. 2B). Of 253 origin ARS consensus sequence (ACS) sites mapped by Eaton et al., 186 lie within 2.5kb of an active origin in both datasets, with a median distance of ~200 bp to the ACS midpoint (Fig. 2B).
The efficiency of equivalent origins in replicate datasets was highly correlated (Fig. 2C, r2 = 0.85); across chromosome 6 (Fig. 2D) our measured origin efficiencies agree well with those previously obtained via 2-D gels (Friedman et al., 1997; Yamashita et al., 1997). Additionally, we find that origins that replicate within the first half of S-phase are significantly more efficient than those generally replicated in the second half (Fig. 2E), although we note that many examples of inefficient early origins and efficient late origins do exist. Interestingly, we find no correlation between origin efficiency and ORC or MCM levels as determined by ChIP (Xu et al., 2006) (Fig. 2F & S4b), suggesting that the presence of multiple pre-RCs does not significantly contribute to origin efficiency as previously proposed (Yang et al., 2010).
Leading-strand synthesis is preferentially initiated within the nucleosome-free region at origins
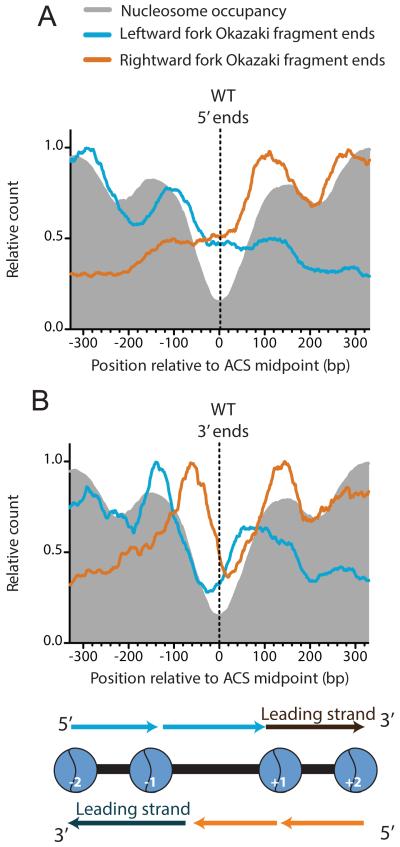
As well as providing a global view of replication origin use, our high-resolution sequence data allow us to investigate whether initiation occurs at locations specified by the ACS that is asymmetrically located within a nucleosome-free region (NFR) at most active replication origins in S. cerevisiae (Eaton et al., 2010). At each origin, the 5′ end of the leading strand will be juxtaposed with the 3′ end of the first Okazaki fragment synthesized by the oppositely oriented replication fork. Although our spatial resolution is limited by degradation of the RNA primer and a variable amount of DNA from the 5′ end of the leading strand by RNase H, Pol δ and associated exonucleases (Stith et al., 2008) we can infer leading strand initiation sites by mapping Okazaki fragment 3′ ends at replication origins. We aligned Okazaki fragment termini around the 186 ACS sequences predicted to be used as origins in both of our datasets. Replication forks moving away from the ACS in either direction generate an overlapping pair of Okazaki fragments whose 5′ and 3′ ends cluster, respectively, around the −1 and +1 nucleosomes flanking the NFR (Fig 3 A&B); Okazaki fragment end density falls rapidly to background levels in regions that are replicated on the leading strand. Thus, much like the rest of the genome, the ends of the Okazaki fragments we map at replication origins are generally positioned by nucleosome-inhibited strand-displacement synthesis by the lagging-strand polymerase, Pol δ (Smith and Whitehouse, 2012). We note that this analysis indicates a preference for initiation within the NFR, but does not rule out initiation outside this region at some origins.
Figure 3. Leading strand initiation preferentially occurs within the nucleosome-free region (NFR) at replication origins.
Distribution of 5′ (A) and 3′ (B) ends observed for Okazaki fragments arising from leftward-(blue) or rightward-moving (orange) forks. Data are oriented such that the T-rich strand of the ACS runs from left to right, and are aligned to the ACS midpoint (Eaton et al., 2010). As expected if leading strand initiation occurs within the NFR and Pol δ is removed during strand displacement by nascent nucleosomes (Smith and Whitehouse, 2012), a pair of overlapping Okazaki fragments spans the NFR with their termini clustering over the flanking +1 and −1 nucleosomes.
Global analysis of mergers between convergent replication forks
Recently, replication terminators (TERs) have been proposed to play a role in the replication of the yeast genome. TERs were operationally defined as genomic regions un-replicated late in S-phase when replication is slow (hydroxyurea or 16°C) (Fachinetti et al., 2010). TERs were shown to be correlated with genomic features such as centromeres and sites of high Pol II or Pol III transcription, which can induce replication fork pausing. Our data, which report population-wide replication fork directionality, make possible a systematic genome-wide analysis of replication fork convergence.
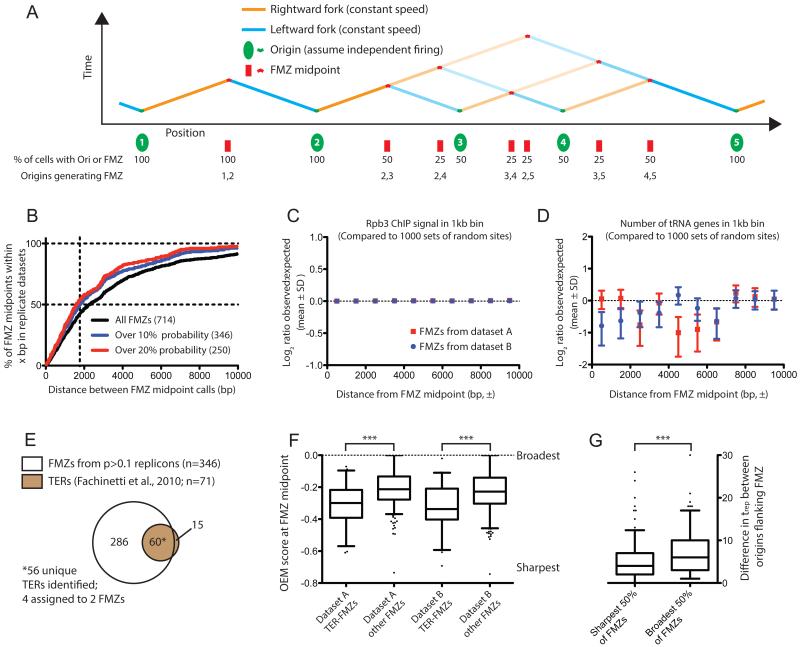
We divided the yeast genome into segments, each comprising two replication origins and their corresponding fork merger zone (FMZ). FMZ midpoint was calculated using a folded cumulative probability distribution (Monti, 1995) (see methods); a probability was calculated for the FMZ in each segment as the product of the efficiency of each flanking origin and the probability of skipping each intervening origin between the two (Fig. 4A and see methods). Of the 714 FMZs shared between our replicate wild-type datasets, most were predicted to be rarely used: applying a probability cutoff of 0.1 in each dataset produced 346 shared FMZs and reduced the median distance between calculated FMZ midpoints to ~1800 bp (Fig. 4B). FMZs with probability greater than 0.1 were used for all subsequent analyses, as applying a more stringent cutoff of 0.2 did not substantially improve the correspondence between replicate midpoints (Fig. 4B). Contrary to the previously reported association between termination regions and high transcription, we observed no enrichment of either RNA Pol II occupancy (Fig. 4C) or tRNA genes (Fig. 4D) around FMZ midpoints as compared to equal numbers of random genomic locations. Although our technique is not sufficiently sensitive to detect pausing at a specific site by a small percentage of forks, the lack of enrichment of highly transcriptionally active loci about FMZs is inconsistent with a widespread role for such loci in termination.
Figure 4. Global analysis of replication fork mergers.
(A) Schematic depiction of FMZ midpoint location and probability for a hypothetical chromosomal region containing origins with various efficiencies.
(B) The midpoints of moderate and high-probability FMZs can be reproducibly identified. For FMZs identified in replicate datasets (within 5kb). The percentage of replicate FMZ midpoints less than x bp apart is plotted on the Y axis. Probability cutoffs of 0 (black line), 10% (blue) or 20% (red) are shown. The 346 FMZs with efficiency over 10% in each replicate dataset (i.e. present in >10% of cells in the population) were used for subsequent analyses.
(C) Sites of high transcription are not enriched around FMZs. For FMZs in either dataset A or dataset B calculated to have probability >10% (n=511 for dataset A, 536 for dataset B), the total Rbp3 ChIP signal from (Fachinetti et al., 2010) was calculated in 1kb bins up- and downstream of the FMZ midpoint; an identical analysis was carried out for an equal number of (i.e. 511 or 536) of random genomic sites, and the ratio of signal around FMZs to signal around random sites (i.e. observed:randomly expected) calculated in each bin for each sample; this process was iterated 1000 times. The Log2-transformed ratio of observed:expected is plotted (mean ± SD) for the 1000 iterations of random sites. FMZs from dataset A are plotted in red; those from dataset B are in blue. Error bars are too small to be visualized in this plot. Significant deviation above zero, which would indicate enrichment of RNA PolII around FMZs, is not observed.
(D) tRNA genes are not enriched around FMZs. Analysis is identical to that in (C), but follows the presence of tRNA genes around FMZs or random genomic sites. As in (C), significant deviation above zero is not observed.
(E) FMZs identified by our analysis encompass the majority of TER regions previously identified (Fachinetti et al., 2010). 56 of 71 TERs were located within ±5kb of at least one calculated FMZ midpoint: 4 TERs were assigned to two FMZs, as they could not be unambiguously assigned to a single one.
(F) FMZs previously identified as TERs are generally sharper than bulk FMZs. The OEM score at the FMZ midpoint is plotted (p<0.0001 for each dataset). OEM negatively correlates with FMZ sharpness: a theoretical point terminator between origins that invariably fire will give rise to an OEM of −1, while 0 indicates no termination or origin activity (cf. Fig 1 C&D).
(G) Origins flanking sharp FMZs fire at approximately the same time. FMZs were binned by mean OEM score across two datasets. The difference between trep values for each origin in the replicon is plotted (p<0.0001 by t-test). Note that for origins with efficiency >0.5, half-maximal replication time (i.e. trep) is equivalent to average firing time.
See also Fig. S5.
60 of our FMZ midpoints were located within ±5 kb of a region identified as a TER (Fachinetti et al., 2010), with 56 of 71 TERs matched: 4 TERs were located within 5 kb of more than one FMZ: in these ambiguous situations, both FMZs were assigned TER status (Fig. 4E). FMZs corresponding to TER regions are hereafter referred to as TER-FMZs. We noticed several significant differences between TER- and non-TER FMZs: the former have disproportionately high probabilities (Fig. S5a) and replicate early in S-phase (S5b). Additionally, we found TERs to be ‘sharper’ – i.e. to represent abrupt transitions from Crick strand to Watson strand Okazaki fragments, which is indicative of termination occurring over a narrow genomic range (Fig. 4F: cf. Fig. 1C&D). Because our OEM score reports directly on merger sharpness, with more negative OEM indicating sharper mergers, we can assess the range over which convergent forks merge. TER-FMZs showed significantly more negative OEM scores than other FMZs (Fig. 4F, p<0.0001 in each dataset). Sharp transitions from rightward- to leftward-moving forks could arise due to replication fork stalling at cis elements but, in light of the observation that TERs are generally flanked by early-firing efficient origins whose firing times presumably overlap, we speculated that sharp terminators could simply arise from the near-synchronous firing of adjacent origins. Consistent with our hypothesis, termination tends to occur at the midpoint between two origins (see below); and, assuming that trep – the time of half-maximal replication (Raghuraman et al., 2001) – can be used to approximate firing time for efficient origins, the origins flanking a sharp FMZ are more likely to fire at similar times to one another than those flanking a broad FMZ (Fig. 4G, p<0.0001) (Raghuraman et al., 2001).
Altering the replication program and FMZs
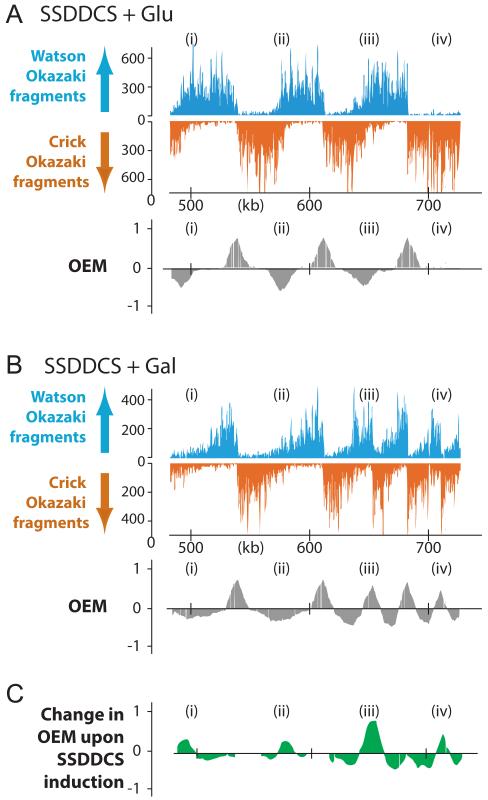
To extend our analysis of the replication program and test the hypothesis that the locations of FMZs are passively determined by origin firing kinetics, we wished to sequence Okazaki fragments from a strain in which the normal replication profile can be altered. We used a strain recently described by the Zegerman laboratory, in which additional copies of Sld2, Sld3, Dbf4, Dpb11, Cdc45 and Sld7 (SSDDCS) – six factors limiting for origin activation – can be overexpressed by induction with galactose and thereby cause the premature firing of many normally late-firing origins (Mantiero et al., 2011). We obtained single-end sequencing reads of nucleosome-sized Okazaki fragments (Smith and Whitehouse, 2012) from cultures grown in YEP with either glucose (one dataset) or galactose (two replicate datasets) prior to- and during ligase shutoff. Consistent with expectations, many origins become highly efficient when cells are grown in inducing conditions (Fig. 5 A-C: see Fig. S6 for all chromosomes). Our algorithm identified 245 common origins in the three SSDDCS datasets, of which 224 were shared among all five datasets analyzed in this work (Fig. 6A; details of origins and FMZs identified in each dataset are provided as supplemental files). Importantly, the spatial precision with which origins were identified by our algorithm was almost entirely unaffected by strain background and SSDDCS overexpression (Fig. 6B).
Figure 5. Alteration of the global replication profile by the overexpression of limiting factors.
(A & B) Sequenced Okazaki fragments mapping to the Watson or Crick strands in a 250kb region of chromosome 10 in the SSDDCS strain, in which additional copies of Sld2, Sld3, Dbf4, Dpb11, Cdc45 and Sld7 are expressed from galactose-inducible promoters (Mantiero et al., 2011). Cells were grown in YEP + glucose or galactose for 4h prior to ligase inactivation for 2 hours. OEM is shown for each growth condition, together with a difference map in (C) which was calculated by subtracting the OEM signal in 5A from the OEM signal in 5B. Several differences are highlighted: (i) FMZ moves and becomes broader, (ii), FMZ becomes broader, (iii) a latent origin is activated, resulting in FMZ movement, (iv), a latent origin is activated, generating new FMZs. See Table S1 for genotypes of strains used in this work.
Figure 6. The location of FMZs is predominantly determined by origin firing.
(A) As in Fig. 2A, column graphs indicate the number of origins lying within ±2.5kb of OriDB entries in datasets from wild-type or SSDDCS strains.
(B) The position of origin calls does not change substantially in different strain backgrounds or growth conditions: the distance between origin calls was calculated for all pairwise combinations of wild-type (two replicates) and SSDDCS (two replicates grown in galactose and one grown in glucose). The percentage of origin pairs called within x bp of one another in paired datasets is plotted on the Y axis. Comparisons between replicate datasets are shown as black lines; those between wild-type and glucose-grown SSDDCS in grey, and those between galactose-grown SSDDCS and any other sample in red.
(C) Overexpressing SSDDCS substantially increases global origin efficiency.
(D) Origin efficiency in the SSDDCS strain correlates well with that in wild-type strains only in the absence of limiting factor overexpression. Efficiencies in wild-type and SSDDCS + galactose (mean value from two replicates in each case) are plotted in grey and red, respectively.
(E) Globally, FMZ midpoints move substantially upon origin hyper-activation. As in (B), the distance between FMZ calls was calculated for all pairwise combinations. Comparisons between replicate datasets are shown as black lines; those between wild-type and glucose-grown SSDDCS in grey, and those between galactose-grown SSDDCS and any other sample in red. Analysis in panels E&F was conducted using the 173 FMZs with probability >0.1 in each of the five datasets.
(F) FMZ midpoints converge on inter-origin midpoints upon origin hyper-activation. FMZ midpoints are normally distributed about the midpoint of the inter-origin range: the variance of the distribution becomes significantly smaller upon SSDDCS overexpression (*** p<0.0001 for each SSDDCS galactose dataset vs the uninduced strain: t-test.).
As expected, global origin efficiency was substantially higher upon SSDDCS overexpression (Fig. 6C). Strikingly, the strong correlation between origin efficiencies in the wild-type strain and the SSDDCS strain was completely abolished upon galactose induction (Fig. 6D), indicating that the global efficiency increase is not simply due to a constant activation of each origin. Indeed, 31 of the 224 shared origins are more efficient in the wild-type strain than under conditions of origin hyper-activation – in large part due to increased passive replication from hyper-activated nearby origins. An obvious conclusion from these data is that origin efficiency is a composite of many factors, including, but not necessarily limited to, MCM loading and activation (Sheu and Stillman, 2006), SSDDCS activity, and the presence of nearby origins (which will tend to suppress firing by causing the origin to be passively replicated). With SSDDCS at saturating concentrations, other properties will, by definition, become limiting for firing efficiency, thus changing the global profile of origin use somewhat independently of normal origin efficiency.
We note that the origin efficiencies observed in the SSDDCS overexpression strain grown in glucose are generally slightly higher than those observed in the (lig4Δrad9Δwild-type strain (Fig. 6C). Checkpoint abrogation via RAD9 deletion (the SSDDCS overexpression strain contains a wild-type RAD9 gene) may lead to a small amount of fork stalling and the completion of replication via the use of inefficient cryptic origins (Doksani et al., 2009). Alternatively, low levels of leaky SSDDCS expression under glucose repression could produce a partial hyper-activation phenotype, as global firing efficiency is likely to be affected by even very small changes in SSDDCS protein levels. It is clear, however, that global differences are minimal (cf. chromosome-wide profiles for WT and SSDDCS + Glucose in Fig. S6) and that DNA replication can proceed robustly upon DNA ligase I depletion to allow replication profiling without using checkpoint mutants – further simplifying our approach.
If the effect of replication fork pause sites on the location of fork mergers is small relative to that of origin firing, then a change in the global distribution of origin firing times should alter the location of FMZs genome-wide. Origin usage changes dramatically upon SSDDCS overexpression (Fig. 5C & 6C), providing a means to test our hypothesis directly. Upon origin hyper-activation, we observed a pronounced and highly reproducible global alteration in the location of FMZ midpoints when compared to either the wild-type or the uninduced SSDDCS strain (meta-analysis is shown in Fig. 6E: anecdotal examples are highlighted in Fig. 5). Assuming roughly constant fork speed throughout the genome (Sekedat et al., 2010), temporally coordinated origin firing should give rise to FMZs that lie halfway between origins. Indeed, FMZ midpoints for both TER- and non-TER FMZs are normally distributed about the inter-origin midpoint (Fig. 6F and data not shown). Consistent with the global early activation of normally late-firing origins, FMZ midpoints move substantially and are tightly clustered about the midpoint of the inter-origin range after galactose induction (Fig. 6F, p<0.0001 for SSDDCS glucose vs either galactose replicate), confirming that origin firing time is the dominant determinant of FMZ location. Interestingly, FMZs generally appear less sharp when SSDDCS are overexpressed (Fig. 5, cf. A&B & see Fig. S6); a plausible explanation for this observation is that, upon SSDDCS induction, adjacent origins fire at similar times to one another but with much less precision than in normal conditions, suggesting that origin hyper-activation may disrupt or reduce the effect of origin clustering and lead to a reduction in temporal coupling (see discussion). An alternative – although not mutually exclusive – explanation for FMZ broadening is increased variability in replication fork speed as a result of the dNTP depletion observed when SSDDCS are overexpressed (Mantiero et al., 2011).
Reconstructing a replication map of the yeast genome
If the position of a given FMZ is indicative of the relative times at which two adjacent origins fire, we reasoned that we could use FMZ positions to determine whether one origin typically fires in advance of another; for example, if forks from adjacent origins travel the same distance, we assume their origins were activated at the same time; however, forks traveling different distances (i.e. the FMZ midpoint lies asymmetrically between two origins) will indicate that the origins fired at different times, with the degree of asymmetry being indicative of the difference in time. Thus, if the replication program is governed by origin firing, we should be able to reconstruct a replication profile from our asynchronous dataset.
We divided each chromosome into segments consisting of pairs of all possible firing origins. Initially, we considered only origin pairs in which each origin has a high firing probability (OEM >0.5); each replication origin was then assigned to its most probable neighbors (one each side). After establishing a baseline set of high probability segments, the relative times of origin firing were determined. To do this, the distance between flanking origins and their associated median merger position was divided by a 2.9 kb/min linear rate of replication (Raghuraman et al., 2001). Baseline segments were then adjusted relative to one another as units, ensuring that the same replication origin in adjacent segments was assigned the same time. Next, the lower probability segments were added to this baseline map.
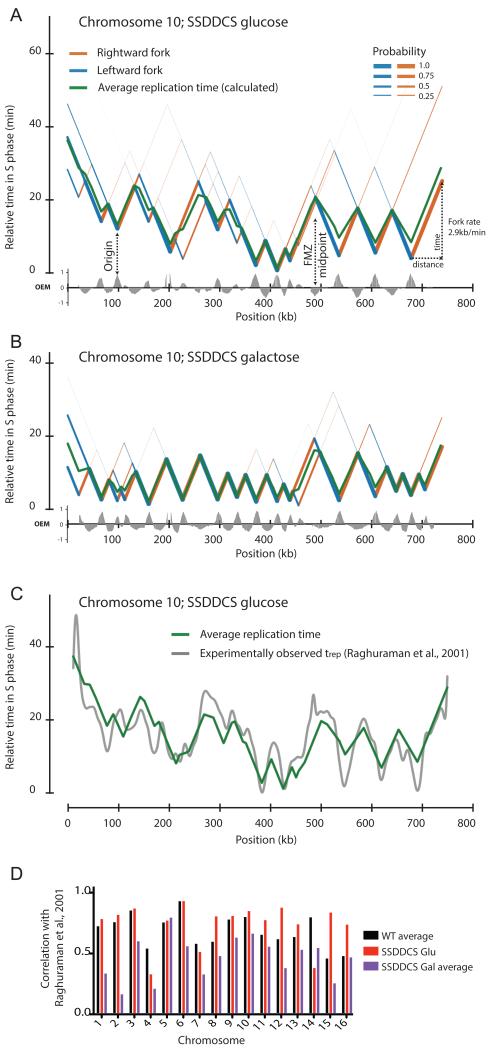
The replication map for a representative chromosome (Chr 10) from the uninduced SSDDCS strain is shown in Fig. 7A, together with the calculated average replication time at each position. As expected, the same chromosome from galactose-grown cells shows a substantially ‘flatter’ profile with earlier average replication times (Fig. 7B), consistent with a global shift towards early origin activation upon overexpression of limiting factors. The profiles generated from wild-type cells, and from the SSDDCS strain when grown in glucose (Fig. 7A and data not shown), contain distinct regions of early and late replication and reveal that chromosome replication is dominated by the activity of efficient origins firing within distinct time windows.
Figure 7. Reconstruction of chromosome-wide replication profiles from Okazaki fragment sequencing data obtained from asynchronous cultures.
(A&B) Using the algorithm described in the methods section, and assuming a constant fork speed of 2.9kb/min (Raghuraman et al., 2001), the replication dynamics of each chromosome can be modeled. Data is shown for chromosome 10 in the SSDDCS strain without (A) or with (B) galactose induction: leftward- and rightward-moving forks are colored blue and orange, respectively, with thickness proportional to probability. Replication forks diverge from origins (valleys) and progress at a constant rate until they converge at FMZs (peaks). The average replication time of each base pair is indicated by a green line. The earliest origin is set to t=0 in each case. Other chromosomes are shown in Fig. S7.
(C) Chromosome-wide comparison of our calculated average replication time and previously determined trep values (Raghuraman et al., 2001) for chromosome 10 in the uninduced SSDDCS strain.
(D) Column graph indicating the Pearson correlation between calculated timing profiles and previously determined trep values (Raghuraman et al., 2001) for wild-type (average of two datasets), and uninduced/induced (average of two datasets) SSDDCS strains. Reported correlation (RMSD) is for the entire chromosome calculated at 2.5kb intervals.
To confirm the validity of our contention that the replication program is governed by origin firing and executed by replication forks that proceed at a uniform rate, we compared our calculated timing profiles with the time of half-maximal replication (trep) determined directly from density-transfer time course experiments (Raghuraman et al., 2001). Timing profiles from wild-type and uninduced SSDDCS cells closely resemble the experimental trep data (Fig. 7C) and show correspondingly strong correlations (as judged by Pearson correlation coefficient - Fig. 7D); as anticipated, SSDDCS induction generally reduces the strength of this correlation.
DISCUSSION
Our genome-wide analysis of both replication origin efficiency and fork termination allows us to analyze both replication origins and termination regions, and thus to reconstruct the global replication profile of an asynchronous population of cells.
We observe that leading-strand initiation is biased towards the nucleosome-free region present at most S. cerevisiae replication origins. However, even highly efficient origins, or those whose locations we predict with high precision relative to the ACS, do not have a single sharp transition from the leading to the lagging strand. The heterogeneity of initiation sites may represent variability in the precise site of leading-strand initiation; differences in the amount of leading strand displaced by Pol δ during synthesis of the first Okazaki fragment, or both. Nevertheless, the clustering of initiation sites within the NFR indicates that the initial DNA unwinding event and subsequent primer synthesis is most likely to occur within this region. The structure of the NFR has been shown to be important for origin function and mutations that either restrict or expand NFR width diminish origin activity (Lipford and Bell, 2001; Simpson, 1990). DNA bound MCM2-7 double hexamers are known to slide along DNA (Remus et al., 2009); thus, the positioned nucleosomes either side of the ~125bp origin NFR may function to position a single MCM2-7 double hexamer (which occupies ~70bp) at the initiation site.
Highly transcribed regions appear to have little overall impact on fork progression and termination; however, we note these findings do not contradict the large body of data that show an apparent conflict between RNA transcription and DNA replication. Replication fork pauses appear simply to be infrequent and/or are of sufficiently short duration that they have little effect on the population as a whole. In keeping with this, the orientation of transcription across the yeast genome is not biased with respect to replication fork direction, suggesting that under normal circumstances there is little selective pressure to avoid collisions between the transcription and replication machineries; moreover, our genome-wide data reveal that a large fraction of the genome can be replicated in either orientation (Fig. S6). Uni- or bidirectional blocks affecting a substantial proportional of replication forks for an appreciable amount of time would be expected to generate discrete FMZs whose location and sharpness are insensitive to SSDDCS overexpression; our data are inconsistent with the existence of a significant number of such blocks. The stable pausing of a small proportion of replisomes, as observed by 2-D gel (Ivessa et al., 2003) or genome-wide ChIP (Sekedat et al., 2010) would not significantly affect the median behavior of the population, and thus cannot be detected by our method. For the special case of the rDNA repeat, we can infer the existence of the well-characterized RFB that specifically impedes rightward-moving forks from the strong strand bias of Okazaki fragments observed in this region, with 85-95% of hits arising from leftward-moving forks (see rDNA panel of Fig. S6). However, due to variation in sequence coverage, the repeat nature of this region and the unknown efficiency of rDNA origins, our data do not allow de novo determination of RFB location.
Our data argue against a strictly deterministic replication program; indeed, due to its implicit inflexibility, absolute determinism seems unlikely to give rise to behavior sufficiently robust as to be evolutionarily successful. The use of invariant patterns of origins and/or strong replication terminators genome-wide would almost certainly lead to an increase in incomplete replication and thus be subject to strong negative selective pressure. Instead, budding yeast appears to have adopted a somewhat flexible program in which active mechanisms exist to ensure that certain replication origins generally fire efficiently within distinct periods of time, while origins outside early-firing clusters remain competent to fire if they are not passively replicated before they have recruited all the factors necessary for firing. Ultimately, therefore, while the overall pattern of origin activation shows somewhat deterministic behavior, the only point at which active regulation is required is the initiation of the earliest firing origins.
Pre RCs are assembled at essentially all replication origins in G1-phase, yet a subset will ultimately be used during the following S-phase. It has been suggested that origin usage and time of activation throughout S-phase is governed by an origin’s sensitivity to initiation factors whose concentration increases during S-phase. Thus, an early firing origin will be more sensitive and fire in a narrow time period than a later firing origin, which will fire over a much larger time window. The fact that most origins fire early and efficiently when Sld2, Sld3, Dbf4, Dpb11, Cdc45 and Sld7 are over-expressed is in apparent agreement with this model. However, multiple initiator models require that later firing origins fire stochastically and inefficiently (Yang et al., 2010). While we do find overall origin efficiency decreases later in S-phase (Fig 2E) the trend is relatively weak and there are numerous examples of late origins that are very efficient and appear to fire within a discrete time period.
Our data are consistent with a model in which most replication origins are competent to fire if bound by factors required for initiation; but the temporal order of origin firing is at least partially conferred by the spatial distribution of replication origins and limiting factors within the 3-dimensional architecture of the nucleus. The replication program may be initiated by the physical association of select replication origins into replication factories with high local concentration of factors necessary for replication initiation (Cook, 1999; Meister et al., 2006). Origin participation within an early cluster may be promoted by proximity to centromeres (Pohl et al., 2012) or association with Forkhead (Knott et al., 2012), but inhibited by “repressive” chromatin structure or proximity to telomeres. Indeed, early origins and centromeres are known to cluster (Duan et al., 2010) and recent reports show that FKH-activated origins may be in close proximity to one another (Knott et al., 2012). Origin firing would be initially limited to these clusters – ensuring that although most origins within the cell are competent to fire, only a select few do so in the earliest stages of S-phase. Inspection of replication profiles reveals that origin activation time tends to progressively increase as a function of one-dimensional distance from an early firing origin (higher-order ‘V’ shapes can be observed in timing profiles in Fig 7A and timing profiles in Fig. S7); suggesting that positioning of an origin along chromosomes is an important determinant of origin timing. Indeed, initiation time has been shown to depend upon chromosomal context and is not an inherent property of replication origins (Ferguson and Fangman, 1992). Thus, an early firing origin could stimulate the firing of nearby origins, reminiscent of cascade effects observed in Human cells (Guilbaud et al., 2011); such a pattern of activation may be governed by sub-diffusive motion of factors limiting for activation that are recycled from recently fired replication origins (or moving replication forks) to proximal origins (Sporbert et al., 2002), and/or by the motion of proximal origins to active replication clusters (Gauthier and Bechhoefer, 2009). Overexpression of SSDDCS could override the normal replication program in two ways: first, a greater number of origins could participate in early clusters; second, activation of origins outside these clusters would be less reliant on the recycling of initiation factors and thus no longer spatially restricted to the vicinity of recently fired origins.
The high competence of S. cerevisiae origins and the general absence of specific, cis-acting termination sequences indicate that the replication program is dominated by origin firing. However, few origins are 100% efficient, implying that almost all will occasionally fail to fire prior to being replicated by an incoming fork. The temporal firing window for the majority of origins appears to be relatively broad – an assertion supported both by the widespread passive replication of origins and the observation that fork mergers occur over a large proportion of the inter-origin distance for most origin pairs. Instances (e.g. many centromeres, and the right arm of chromosome 10 shown in Fig 1) where sharp mergers exist halfway between a pair of origins are indicative of tight temporal coupling between the pair, and not necessarily of a narrowing of either origin’s firing window relative to the population as a whole. Although they are not the norm, we observe numerous such isolated sharp merger regions. Coupled origins are generally the earliest to fire within each chromosome and are sensitive to Fkh1/2 depletion (Knott et al., 2012) (data not shown), consistent with physical juxtaposition. Our approach can detect apparent coordination between adjacent origins but not putative longer-range and/or inter-chromosomal coupling, almost certainly leading to an underestimate of the extent of this phenomenon. The biological significance of such tight coupling remains unclear: it may reflect a mechanism to ensure that certain regions are replicated early, or a passive means to ensure that termination occurs in a distinct location. However, coordinated firing also imposes predictable asymmetry in replication patterns, giving rise to daughters with distinct chromosomal regions replicated exclusively on the leading or lagging strand. If chromatin is assembled differentially on the two strands, then such replication patterns could facilitate the asymmetric propagation of epigenetic information.
METHODS
Experimental methods
Okazaki fragments were purified and sequenced as described (Smith and Whitehouse, 2012) except that Ion Torrent 318 sequencing was used for the SSDDCS strain. Genotypes of all strains used in this study are listed in Table S1.
Computational methods
Quadrants and Origin Efficiency Metric (OEM)
For each position in the genome, we summed the cumulative fragment count within 10kb to the left and right; this was performed on each strand. We define four quadrants: Watson-strand Left (WL), Watson-strand Right (WR), Crick-strand Left (CL), and Crick-strand Right (CR) at each base pair on each chromosome (see figure 1). To account for differences in read depth due to base composition etc., and because the total amount of replication on both strands should be constant across the genome, we normalize to the total signal on either side of the sliding window – i.e. (WL+CL) or (WR+CR).
To find origins and FMZs, we convert quadrant data into an Origin Efficiency Metric (OEM) defined by equation 1 and dependent on equations 2 and 3:
| (1) |
| (2) |
| (3) |
WLn and WRn range from 1 to 0. In the case of an ideal 100% efficient point origin, from which two forks invariably diverge, WLn = 1 and WRn = 0: therefore, from equation (1) OEM = 1. In the analogous case of an ideal point merger between 100% efficient origins, at which two forks invariably converge, WLn = 0 and WRn = 1 to give OEM = −1.
OEM provides an averaged readout of heterogeneous behavior within a population. For an origin that fires in 50% of cells but is passively replicated by an incoming fork in the remaining 50%, the observed OEM will comprise a triangular signal from the 50% of cells in which the origin fires and a flat signal from the 50% in which it does not, generating a weighted average of 0.5. Theoretical model origins of varying efficiencies are shown schematically in Fig. S1, and real origins in Fig. 1C&D.
Origin positions and efficiencies
Origin positions were calculated using a three-point method whose algorithm identifies localized maxima in OEM within 10Kb ranges.
Deconvolution
The presence of FMZs in a sub-population of cells near origins fired in another sub-population convolutes OEM signal for both origins and FMZs, as the observed OEM is a composite of the subpopulations (Fig. S2). Because origins in S. cerevisiae are small and discrete while FMZ are large and diffuse, we can generally deconvolute our signal by assuming origins to be point entities and modeling ideal origin behavior about this point. Signal arising due to origins is deconvoluted first, and subsequently used to correct OEM at FMZs as described below. Deconvolution of theoretical model data is shown in Fig. S2; examples of the process using real data in Fig. S3.
Because OEM is calculated from a sliding window, at origins it will be triangular in shape and span 20kb. If an origin’s OEM signal is convoluted by underlying FMZ signal then its OEM is systematically reduced and some or the entire signal will lie below 0, causing the measured height of the OEM peak to provide an under-estimate of true origin efficiency.
To correct for under-estimated origin efficiencies, we measured the gradient of OEM at positions 5kb and 10kb either side of the origin and used the numerical mean of the larger two of these four values to fit an idealized triangle to each origin OEM. Fitted triangles are then used to calculate a deconvoluted origin OEMorigin, which forces the OEM signal to be above 0 throughout the 20Kb range spanned by the triangle. All origin efficiencies reported in this work represent OEMorigin, and only origins in which OEM was originally >0.05 were considered in our analysis.
Finally, to remove origin signal from OEM at FMZs, we subtract the OEMorigin calculated above from the original OEM to give OEMFMZ for each FMZ; analogously to origins, reported values of OEM at FMZs represent OEMFMZ. Due to space constraints further experimental detail can be found in supplementary methods.
Supplementary Material
HIGHLIGHTS.
Deep-sequencing Okazaki fragments provides a genome-wide record of DNA replication
Origin firing efficiency and fork convergence sites can be quantitatively determined
Genome-wide replication dynamics can be reconstructed from Okazaki fragment profiles
In S. cerevisiae, the replication profile is dominated by origin firing kinetics
ACKNOWLEDGEMENTS
We thank Philip Zegerman (Gurdon Institute) for the SSDDCS strain; Ken Marians, Dirk Remus, Toshi Tsukiyama (FHCRC), and members of the Molecular Biology Program and Whitehouse lab for discussions and comments on the manuscript. This work was supported by National Institute of Health Grant R01 GM102253 and an Alfred Bressler Scholars Endowment Award to I.W; D.J.S is a HHMI fellow of the Damon Runyon Cancer Research Foundation (DRG-#2046-10).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
ACCESSION NUMBERS
Sequencing data and timing analyses are available at the Gene Expression Omnibus (http://www.ncbi.nlm.nih.gov/geo) under accession numbers 33786 and 40696.
REFERENCES
- Brewer BJ, Fangman WL. A replication fork barrier at the 3′ end of yeast ribosomal RNA genes. Cell. 1988;55:637–643. doi: 10.1016/0092-8674(88)90222-x. [DOI] [PubMed] [Google Scholar]
- Cook PR. The organization of replication and transcription. Science. 1999;284:1790–1795. doi: 10.1126/science.284.5421.1790. [DOI] [PubMed] [Google Scholar]
- Czajkowsky DM, Liu J, Hamlin JL, Shao Z. DNA combing reveals intrinsic temporal disorder in the replication of yeast chromosome VI. J Mol Biol. 2008;375:12–19. doi: 10.1016/j.jmb.2007.10.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Moura AP, Retkute R, Hawkins M, Nieduszynski CA. Mathematical modelling of whole chromosome replication. Nucleic Acids Res. 2010;38:5623–5633. doi: 10.1093/nar/gkq343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deshpande AM, Newlon CS. DNA replication fork pause sites dependent on transcription. Science. 1996;272:1030–1033. doi: 10.1126/science.272.5264.1030. [DOI] [PubMed] [Google Scholar]
- Doksani Y, Bermejo R, Fiorani S, Haber JE, Foiani M. Replicon dynamics, dormant origin firing, and terminal fork integrity after double-strand break formation. Cell. 2009;137:247–258. doi: 10.1016/j.cell.2009.02.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duan Z, Andronescu M, Schutz K, McIlwain S, Kim YJ, Lee C, Shendure J, Fields S, Blau CA, Noble WS. A three-dimensional model of the yeast genome. Nature. 2010 doi: 10.1038/nature08973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eaton ML, Galani K, Kang S, Bell SP, MacAlpine DM. Conserved nucleosome positioning defines replication origins. Genes Dev. 2010;24:748–753. doi: 10.1101/gad.1913210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fachinetti D, Bermejo R, Cocito A, Minardi S, Katou Y, Kanoh Y, Shirahige K, Azvolinsky A, Zakian VA, Foiani M. Replication termination at eukaryotic chromosomes is mediated by Top2 and occurs at genomic loci containing pausing elements. Mol Cell. 2010;39:595–605. doi: 10.1016/j.molcel.2010.07.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng W, Collingwood D, Boeck ME, Fox LA, Alvino GM, Fangman WL, Raghuraman MK, Brewer BJ. Genomic mapping of single-stranded DNA in hydroxyurea-challenged yeasts identifies origins of replication. Nat Cell Biol. 2006;8:148–155. doi: 10.1038/ncb1358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferguson BM, Fangman WL. A position effect on the time of replication origin activation in yeast. Cell. 1992;68:333–339. doi: 10.1016/0092-8674(92)90474-q. [DOI] [PubMed] [Google Scholar]
- Friedman KL, Brewer BJ, Fangman WL. Replication profile of Saccharomyces cerevisiae chromosome VI. Genes Cells. 1997;2:667–678. doi: 10.1046/j.1365-2443.1997.1520350.x. [DOI] [PubMed] [Google Scholar]
- Gauthier M, Bechhoefer J. Control of DNA Replication by Anomalous Reaction-Diffusion Kinetics. Phys. Rev. Lett. 2009;102 doi: 10.1103/PhysRevLett.102.158104. [DOI] [PubMed] [Google Scholar]
- Greenfeder SA, Newlon CS. Replication forks pause at yeast centromeres. Mol Cell Biol. 1992;12:4056–4066. doi: 10.1128/mcb.12.9.4056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guilbaud G, Rappailles A, Baker A, Chen CL, Arneodo A, Goldar A, d’Aubenton-Carafa Y, Thermes C, Audit B, Hyrien O. Evidence for sequential and increasing activation of replication origins along replication timing gradients in the human genome. PLoS Comput Biol. 2011;7:e1002322. doi: 10.1371/journal.pcbi.1002322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill TM, Marians KJ. Escherichia coli Tus protein acts to arrest the progression of DNA replication forks in vitro. Proc Natl Acad Sci U S A. 1990;87:2481–2485. doi: 10.1073/pnas.87.7.2481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivessa AS, Lenzmeier BA, Bessler JB, Goudsouzian LK, Schnakenberg SL, Zakian VA. The Saccharomyces cerevisiae helicase Rrm3p facilitates replication past nonhistone protein-DNA complexes. Mol Cell. 2003;12:1525–1536. doi: 10.1016/s1097-2765(03)00456-8. [DOI] [PubMed] [Google Scholar]
- Kearsey S. Structural requirements for the function of a yeast chromosomal replicator. Cell. 1984;37:299–307. doi: 10.1016/0092-8674(84)90326-x. [DOI] [PubMed] [Google Scholar]
- Knott SR, Peace JM, Ostrow AZ, Gan Y, Rex AE, Viggiani CJ, Tavare S, Aparicio OM. Forkhead Transcription Factors Establish Origin Timing and Long-Range Clustering in S. cerevisiae. Cell. 2012;148:99–111. doi: 10.1016/j.cell.2011.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobayashi T, Horiuchi T. A yeast gene product, Fob1 protein, required for both replication fork blocking and recombinational hotspot activities. Genes Cells. 1996;1:465–474. doi: 10.1046/j.1365-2443.1996.d01-256.x. [DOI] [PubMed] [Google Scholar]
- Lipford JR, Bell SP. Nucleosomes positioned by ORC facilitate the initiation of DNA replication. Mol Cell. 2001;7:21–30. doi: 10.1016/s1097-2765(01)00151-4. [DOI] [PubMed] [Google Scholar]
- Mantiero D, Mackenzie A, Donaldson A, Zegerman P. Limiting replication initiation factors execute the temporal programme of origin firing in budding yeast. EMBO J. 2011;30:4805–4814. doi: 10.1038/emboj.2011.404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marahrens Y, Stillman B. A yeast chromosomal origin of DNA replication defined by multiple functional elements. Science. 1992;255:817–823. doi: 10.1126/science.1536007. [DOI] [PubMed] [Google Scholar]
- Meister P, Taddei A, Gasser SM. In and out of the replication factory. Cell. 2006;125:1233–1235. doi: 10.1016/j.cell.2006.06.014. [DOI] [PubMed] [Google Scholar]
- Monti KL. Folded Empirical Distribution Function Curves-Mountain Plots. The American Statistician. 1995;49:342–245. [Google Scholar]
- Nieduszynski CA, Hiraga S, Ak P, Benham CJ, Donaldson AD. OriDB: a DNA replication origin database. Nucleic Acids Res. 2007;35:D40–6. doi: 10.1093/nar/gkl758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pohl TJ, Brewer BJ, Raghuraman MK. Functional Centromeres Determine the Activation Time of Pericentric Origins of DNA Replication in Saccharomyces cerevisiae. PLoS Genet. 2012;8:e1002677. doi: 10.1371/journal.pgen.1002677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raghuraman MK, Winzeler EA, Collingwood D, Hunt S, Wodicka L, Conway A, Lockhart DJ, Davis RW, Brewer BJ, Fangman WL. Replication dynamics of the yeast genome. Science. 2001;294:115–121. doi: 10.1126/science.294.5540.115. [DOI] [PubMed] [Google Scholar]
- Rao H, Marahrens Y, Stillman B. Functional conservation of multiple elements in yeast chromosomal replicators. Mol Cell Biol. 1994;14:7643–7651. doi: 10.1128/mcb.14.11.7643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remus D, Beuron F, Tolun G, Griffith JD, Morris EP, Diffley JF. Concerted loading of Mcm2-7 double hexamers around DNA during DNA replication origin licensing. Cell. 2009;139:719–730. doi: 10.1016/j.cell.2009.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sekedat MD, Fenyo D, Rogers RS, Tackett AJ, Aitchison JD, Chait BT. GINS motion reveals replication fork progression is remarkably uniform throughout the yeast genome. Mol Syst Biol. 2010;6:353. doi: 10.1038/msb.2010.8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheu YJ, Stillman B. Cdc7-Dbf4 phosphorylates MCM proteins via a docking site-mediated mechanism to promote S phase progression. Mol Cell. 2006;24:101–113. doi: 10.1016/j.molcel.2006.07.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpson RT. Nucleosome positioning can affect the function of a cis-acting DNA element in vivo. Nature. 1990;343:387–389. doi: 10.1038/343387a0. [DOI] [PubMed] [Google Scholar]
- Smith DJ, Whitehouse I. Intrinsic coupling of lagging-strand synthesis to chromatin assembly. Nature. 2012;483:434–438. doi: 10.1038/nature10895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporbert A, Gahl A, Ankerhold R, Leonhardt H, Cardoso MC. DNA polymerase clamp shows little turnover at established replication sites but sequential de novo assembly at adjacent origin clusters. Mol Cell. 2002;10:1355–1365. doi: 10.1016/s1097-2765(02)00729-3. [DOI] [PubMed] [Google Scholar]
- Stith CM, Sterling J, Resnick MA, Gordenin DA, Burgers PM. Flexibility of eukaryotic Okazaki fragment maturation through regulated strand displacement synthesis. J Biol Chem. 2008;283:34129–34140. doi: 10.1074/jbc.M806668200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu W, Aparicio JG, Aparicio OM, Tavare S. Genome-wide mapping of ORC and Mcm2p binding sites on tiling arrays and identification of essential ARS consensus sequences in S. cerevisiae. BMC Genomics. 2006;7:276. doi: 10.1186/1471-2164-7-276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yabuki N, Terashima H, Kitada K. Mapping of early firing origins on a replication profile of budding yeast. Genes Cells. 2002;7:781–789. doi: 10.1046/j.1365-2443.2002.00559.x. [DOI] [PubMed] [Google Scholar]
- Yamashita M, Hori Y, Shinomiya T, Obuse C, Tsurimoto T, Yoshikawa H, Shirahige K. The efficiency and timing of initiation of replication of multiple replicons of Saccharomyces cerevisiae chromosome VI. Genes Cells. 1997;2:655–665. doi: 10.1046/j.1365-2443.1997.1530351.x. [DOI] [PubMed] [Google Scholar]
- Yang SC, Rhind N, Bechhoefer J. Modeling genome-wide replication kinetics reveals a mechanism for regulation of replication timing. Mol Syst Biol. 2010;6:404. doi: 10.1038/msb.2010.61. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.