HETEROGENEITY OF BONE MINERAL DENSITY AND FATIGUE FAILURE OF HUMAN VERTEBRAE

Abstract

There is increasing interest in using the heterogeneity of tissue properties in a bone for predicting its fracture risk. Heterogeneity of volum etric bone mineral density (BMD) as measured from quantitative computed tomography (QCT) is of particular interest as these measurements are clinically feasible. Previous examinations of the relationship between the BMD heterogeneity and the mechanical behavior of human vertebrae considered quasistatic strength only and were with limited number of samples. McCubbrey et al. studied the value of regional BMDs for predicting vertebral fatigue life, determined from short-cycle tests at force levels scaled with the estimated strength of the vertebra, but the focus of that work was in best predictor subsets without a specific focus on the heterogeneity of BMD or the positive vs negative direction of the relationships. The previous analysis also did not take into account the censored nature of the fatigue life data. As such, whether BMD heterogeneity is positively or negatively associated with fatigue life and whether this is independent from the average or minimum BMD are not clear. In the present work, we revisite d the McCubbrey data for a preliminary examination of the relationship between BMD heterogeneity and fatigue life using survival analysis. The analysis suggests that BMD heterogeneity measured as the intra-vertebral standard deviation of BMDs in a vertebra is negatively associated with short cycle (high-amplitude) fatigue life independent from the average BMD. The results motivate further studies on the role of BMD heterogeneity in fatigue failure and clinical fracture risk of human vertebrae.

INTRODUCTION

Bone qualities that are measurable via clinically available modalities and that can explain fracture risk beyond what is explainable by measures of average bone mineral density (BMD) (such as the areal or volumetric BMD from DEXA or QCT) are of significant interest. Evidence from literature suggests that the heterogeneity of volumetric BMD within a vertebra, in addition to the average volumetric BMD, may be an important determinant of the mechanical properties of a vertebra (Cody et al., 1991; McCubbrey et al., 1995; Yerramshetty et al., 2009) and risk of a clinical vertebral fracture (Dougherty, 1996; Briggs et al., 2012). Much of the experimental evidence comes from tests, in which vertebrae are monotonically loaded and relates BMD heterogeneity to the quasi-static properties of a vertebra (Cody et al., 1991; Yerramshetty et al., 2009). The appearance of clinical vertebral fractures is in the form of progressive deformities indicating that fatigue processes are involved. However, the relationships between BMD heterogeneity and fatigue properties of a vertebra are not well-understood.

McCubbrey and coworkers (McCubbrey et al., 1995) studied a large number of cadaveric human vertebrae, established that regional variations of volumetric BMD are important in determining the fatigue life of a vertebra and identified best combination of anatomic regions to be used for predicting vertebral fatigue. However, several issues remain unclear: 1) Although regional values of density within a vertebra are useful in improving prediction accuracy for vertebral mechanical properties, the variation of bone density between regions of a vertebra and the ability of the regions to predict vertebral strength may be different from study to study (Cody et al., 1991; McCubbrey et al., 1995; Hulme et al., 2007; Kim et al., 2007). This motivated us to consider statistical measures of density heterogeneity that are not necessarily functions of anatomic site. 2) Fracture was not observed for all specimens by the end of the fatigue tests 3 conducted by McCubbrey et al., i.e., the fatigue life data were right-censored. 3) It was not clear whether increasing BMD heterogeneity is associated with increased or decreased fatigue life and the extent to which this effect is independent from average BMD.

Fatigue experiments on large number of samples are costly and time-consuming. Therefore, as a first step, the objectives of the current study were to address the abovementioned issues by reanalyzing the volumetric BMD and fatigue results of McCubbrey et al. Specifically, a focus on the statistical rather than the spatial distribution of BMDs, accounting for censored fatigue life data using a survival analysis and, emphasis on the presence and the direction of the BMD heterogeneity effects separate from the average BMD were new additions to the historical analysis.

METHODS

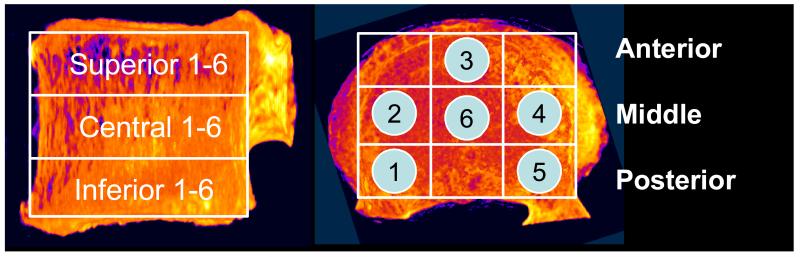
Under institutional approval, the data from the McCubbrey experiment were recovered from research archives. The experimental details were previously reported (McCubbrey et al., 1995). Briefly, T7 through L4 vertebra levels from 20 female cadaveric spines were utilized. The quantitative computed tomography (QCT) scans were obtained with the specimens in a device simulating human torso and using a Technicare system (Model HPS 1440, Technicare, Cleveland, OH). An analysis volume with 0.8 mm isotropic voxel size was generated from the original scans that used 1 mm slice thickness. After being scanned, the specimens were fatigue loaded under load control at 0.5 Hz, using load levels estimated from the strength values of vertebrae that were adjacent to those reserved for fatigue. Fatigue loading ended when the vertebra fractured or 1000 cycles were reached without fracture. Because not all specimens fractured by the end of the 1000 cycles, i.e., the fatigue life data were right-censored, we used survival analysis techniques in the current work in lieu of conventional regression analysis techniques. The main advantage of survival models over ordinary regression models is that a likelihood function can be calculated accurately due to the distinction survival models make between observed and unobserved (censored) events. Semi-parametric Cox regression models were used with a sandwich estimator of covariance to account for the clustering within donor (PROC PHREG, SAS v 9.2, SAS Institute Inc., Cary, NC). Proportional hazard assumptions were checked for BMD measures by including an interaction with time in each univariable model. The log-transformed fatigue life (number of cycles at the end of the test), as typically done in analysis of fatigue (Suresh, 1998), was the outcome variable with average BMD (BMD.Av), the within-specimen standard deviation of BMD (BMD.SD) and fatigue load as the predictor variables. Figures were constructed by Kaplan-Meier estimation of survival with the predictors dichotomized as the median to form a high and low group. BMD.Av and BMD.SD for each vertebra were calculated using 18 BMD values comprising the defined regions (Figure 1). (In the context of the current study, references to BMD should be interpreted as volumetric BMD.) To reflect the experimental design, all models include the loading parameter as a predictor. Alternatively, the model was reconstructed with log-transformed fatigue life normalized with fatigue load as the outcome variable, in which case the outcome variable was largely a function of fatigue resistance (Figure 2a). Additional tests using minimum and maximum BMD within the vertebra (BMD.Min and BMD.Max, respectively) were performed in the same analysis framework to gain insight into the nature of the information that is represented by BMD heterogeneity.

Figure 1.

Location and nomenclature of the 18 density regions measured in the original study (McCubbrey et al., 1995).

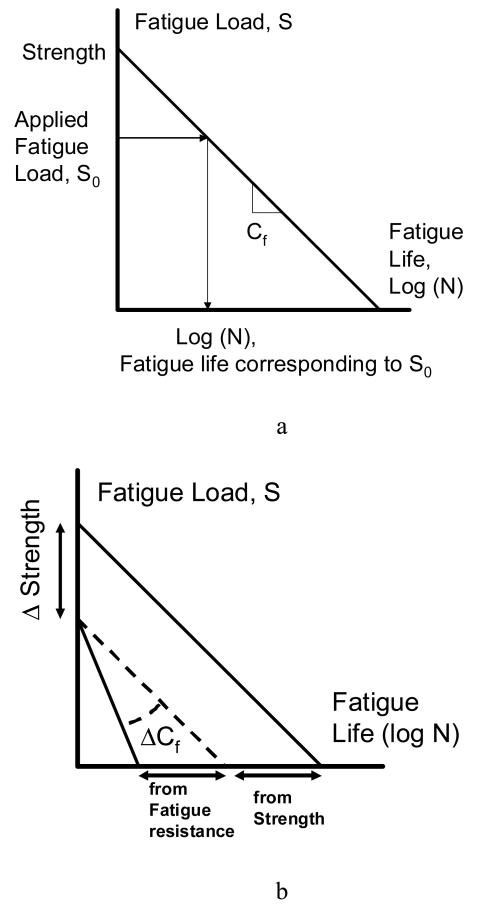
Figure 2.

a) Hypothetical S-N curve showing fatigue life in relationship with the applied loads. Note that the intercept represents the monotonic strength and the slope represents the fatigue compliance (or reciprocally, fatigue resistance) of the material (the smaller the absolute magnitude of the slope the less fatigue resistant the material is). In this experiment, fatigue life is scaled with the estimated strength of the vertebrae making the predicted fatigue life largely a function of fatigue resistance. b) Two hypothetical S-N curves (solid lines) showing strength (intercept) and fatigue resistance (slope) contributions to fatigue life. We hypothesize that density (BMD.Av) contributes to fatigue life by largely affecting strength whereas fatigue 2 resistance contribution to fatigue life is determined by tissue heterogeneity (BMD.SD).

Pearson’s correlation coefficients were used to determine associations between predictors. Donor-level clustering is not considered in these descriptive parameters. In order to 3 determine if specific vertebral regions are more influential on BMD.Av and BMD.SD, the correlations of BMD.Av and BMD.SD with regional BMD were examined using Fisher’s r to z transformation (Dowdy and Wearden, 1983).

RESULTS

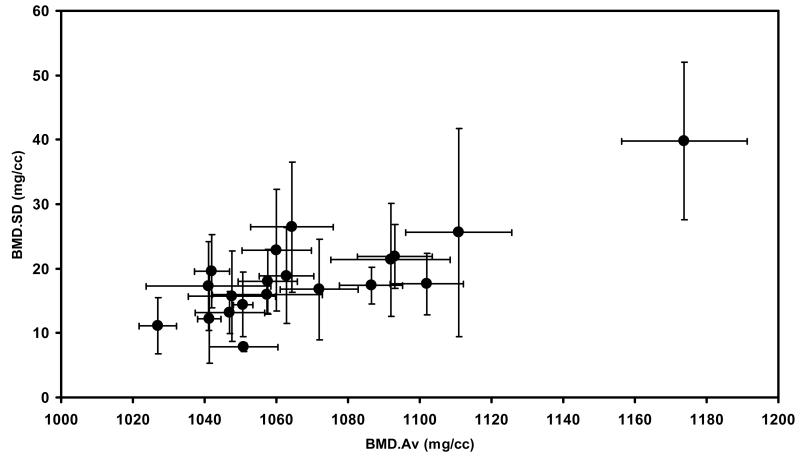
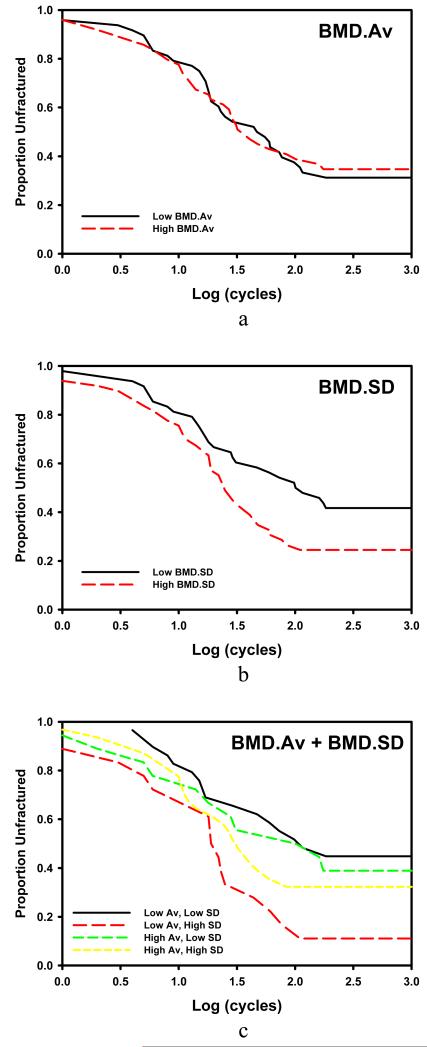
The intra-subject variability of BMD.SD, as measured by the coefficient of variation of BMD.SD among the vertebrae of a given subject, was significantly greater than that of BMD.Av (34.5% vs 1.0%, respectively; p<0.0001, paired t-test) (Figure 3). As determined from the semi-parametric Cox regression models described in methods, neither BMD.Av (p=0.1346) nor BMD.SD (p=0.2162) alone was a significant predictor of fatigue survival. Both were significant, when introduced into the model together, increasing the prediction ability for fatigue survival of the vertebrae (Figure 4). Increasing BMD.Av (p=0.0241) and decreasing BMD.SD (p=0.0161) were 2 associated with increasing likelihood of fatigue survival; see Figure 4. Increasing fatigue load levels were, marginally associated with decreasing likelihood of fatigue survival (p=0.0831) but were found to be a confounding effect when added to models of BMD.Av and BMD.SD. Specifically, BMD.Av becomes significant when the load level is accounted for (p=0.0015) whereas the effect of BMD.SD is mitigated (p=0.6754). In a joint model, BMD.Av (p=0.0026) and fatigue load (p=0.0008) were significant predictors with BMD.SD marginally so (p=0.1191). In the joint model with fatigue resistance as the outcome variable, BMD.Av was nonsignificant (p=0.6389) but BMD.SD was (p=0.0011).

Figure 3.

Donor-averaged BMD.SD vs donor-averaged BMD.Av ± 1 standard deviation showing the distribution of the BMD data.

Figure 4.

Kaplan-Meier survival curves depicting the proportion of vertebra unfractured (y-axis) by the number of cycles (x-axis, log10). For the purpose of visualization, the bones are stratified as having high or low BMD.Av and BMD.SD in this study set relative to the median of those measures. Panel c shows that the bones with higher BMD.SD perform worse (red, large dash) though the effect is less in those with high BMD.Av (yellow small dash).

Interestingly, the effect of BMD.Min, when replaced BMD.SD in the abovementioned models, was a significant predictor alone when adjusted for loading (p=0.0019) and increasing BMD.Min provided a protective effect. However, in a joint model with BMD.Av, neither predictor retained significance (BMD.Min p=0.267, BMD.Av p=0.779). Similarly, increasing BMD.Max had a significant protective effect in a model accounting for the loading (p=0.0376). In a joint model, the effect of BMD.Max was changed to be slightly detrimental when BMD.Av was included (p=0.0649, 0.0052, respectively). BMD.Min increased with increasing BMD.Max (r=0.78, p<0.0001) whereas BMD.Min and BMD.SD were not as strongly correlated (r=0.38, p<0.0001) indicating that increasing BMD.SD does not necessarily mean decreasing BMD.Min.

The strange effect of BMD.Av in models with BMD.Min or BMD.Max is likely due to multicollinearity since BMD.Av is strongly correlated with both BMD.Max (r=0.92, p<0.0001) and BMD.Min (r=0.92, p<0.001). In contrast, the correlation between BMD.Av and BMD.SD is less (r=0.63, p<0.0001) making it the optimal pair for joint models.

Examinations of correlations of BMDs from individual regions with BMD.Av and 1 BMD.SD suggested the inferior row of the middle column (i2, i4, i6) and the middle superior regions (s6) as stronger determinants of BMD.Av (r≥0.92 and p<0.057 to p<0.576 between correlations), while the two inferior posterior regions (i1, i5) were the stronger determinants of BMD.SD (r≥0.73 and p<0.133 between correlations) than other regions examined (Figure 5).

Figure 5.

All regional BMDs significantly (p<0.0001) correlate with BMD.Av (0.81<R<0.94) and BMD.SD (0.31<R<0.79). The correlations of BMDs from the colored regions are significantly greater than those that are not colored. The regions that provided highest correlates of BMD.Av and those provided highest correlates of BMD.SD are different.

DISCUSSION

The current data indicate that BMD heterogeneity may have a significant role in the fatigue life of a vertebra and could be important in improving accuracy for prediction of vertebral fracture risk. The BMD.SD term was not significant when fatigue load was present in the model. However, it is often difficult to know the physiological loads experienced by an individual. The significant relationship of BMD.SD with fatigue survival in absence of the fatigue load in the model is important in that fatigue life may be predictable from a set of internal parameters. It must be noted that in this experiment the fatigue load parameter is a composite of two competing factors on fatigue life due to the scaling of fatigue load with estimated strength of the vertebra. The relationship between fatigue load and fatigue life (S-N curve) expressed in a semi-log or a log-log scale is often represented with a linear model. A log-log representation would suggest that fatigue life is fully strength-adjusted in this experiment, thus the predicted component of fatigue life is largely related to fatigue resistance without the fatigue load. A semi-log representation would suggest an increasing fatigue life with increasing fatigue loads due to the association of high fatigue loads with high strength (but the effects do not cancel). In this case fatigue resistance would be proportional to the (log) fatigue life to fatigue load ratio. Detailed information on the S-N behavior of human vertebrae is not available. Nonetheless, when the model was constructed with this ratio as the outcome variable, BMD.Av became nonsignificant but BMD.SD remained significant, indicating that BMD.SD is associated with fatigue resistance in both considerations of the fatigue load-life curve.

While BMD alone is usually moderately correlated with strength, it is not a good predictor of vertebral fatigue (Hansson, 1987; Lindsey et al., 2005). Our data suggest that BMD.Av and BMD.SD could explain different aspects of fatigue life, perhaps one related to vertebral strength, the other to fatigue resistance and therefore be complementary to each other (Figure 2b).

The findings that BMD.Min is associated with increasing BMD.SD and BMD.Max and that it did not account for the effect of BMD.SD in fatigue survival suggest that the concept underlying heterogeneity is different from a “weakest link” effect which would be strongly associated with a negative effect of BMD.Min on fatigue life.

It seems that the highest density regions are associated with the inferior sections of the posterior column followed by other sections of the posterior column in this set of vertebrae. The significant and negative contribution of BMD.Max (for a given average) to fatigue survival suggests that stress-shielding effect of a small amount of high density regions in the bone, especially localized to form a column, may be detrimental to the vertebra.

This study was inherently limited by the limitations of the original study (McCubbrey et al., 1995). As a general limitation, BMD heterogeneity provides information on the macroscopic distribution of bone mass in the vertebra; however, QCT is inherently limited in its ability to provide information on the microscopic organization of bone mass and thus on the trabecular architecture. Vertebrae were fatigue loaded without removing intervertebral discs in this experiment. While this would provide more physiologically realistic load distributions on the vertebrae, it would inevitably affect displacement and stiffness measurements for the vertebral body alone. Therefore, the current analysis is limited to loads and fatigue life, and damage progression through displacement or stiffness changes has not been considered.

Perhaps the most important limitation of the study is that it was a low-cycle/high-magnitude fatigue study. In this case, much of the relationships observed may be largely related to fatigue load and slow processes that would determine fatigue resistance of the vertebrae may have been suppressed. The extent to which BMD heterogeneity contributes to fatigue life under high-cycle/low-amplitude fatigue that is conducted to failure remains to be determined. 8