Platelet Motion near a Vessel Wall or Thrombus Surface in Two-Dimensional Whole Blood Simulations

Abstract

Computational simulations using a two-dimensional lattice-Boltzmann immersed boundary method were conducted to investigate the motion of platelets near a vessel wall and close to an intravascular thrombus. Physiological volume fractions of deformable red blood cells and rigid platelet-size elliptic particles were studied under arteriolar flow conditions. Tumbling of platelets in the red-blood-cell depleted zone near the vessel walls was strongly influenced by nearby red blood cells. The thickness of the red-blood-cell depleted zone was greatly reduced near a thrombus, and platelets in this zone were pushed close to the surface of the thrombus to distances that would facilitate their cohesion to it. The distance, nature, and duration of close platelet-thrombus encounters were influenced by the porosity of the thrombus. The strong influence on platelet-thrombus encounters of red-blood-cell motion and thrombus porosity must be taken into account to understand the dynamics of platelet attachment to a growing thrombus.

Introduction

Understanding how platelets aggregate to form a thrombus requires understanding the interplay among many coupled chemical, mechanical, and hydrodynamic processes (1–4). For a platelet to adhere to an injury site or existing thrombus, it must be sufficiently close to the surface of interest and it must remain close for a time sufficient for platelet-subendothelium or platelet-platelet bonds to form. The number density of platelets near a vessel wall or thrombus as well as the motion of platelets near these surfaces likely strongly influence the initiation and growth of a thrombus in response to vascular injury. Platelet distribution and motion are, in turn, strongly affected by the motion of the red blood cells (RBCs) which make up a large fraction of the blood’s volume.

It has long been known that, in flowing whole blood, platelets have an enhanced concentration in a several-micron-wide fluid layer adjacent to the vessel walls. This platelet near-wall excess (NWE) has been observed both in vitro and in vivo (5–8). In contrast, there is very limited experimental information about the motion of individual platelets near the vascular surface (9) and how it influences the frequency and duration of platelet encounters with the surface. There is also a dearth of information about how the motion and distribution of red blood cells is changed in the presence of a thrombus protruding into the vessel lumen, and how these changes affect platelet interactions with the thrombus.

Recent three-dimensional computational studies have looked at the near-wall motion of single platelets in Stokes flow with particular attention to the influence of the resting platelet’s ellipsoidal shape on its near-wall motion (10,11). Among the important observations made in this work is that a platelet undergoes a periodic tumbling motion that brings it closest to the wall when it is oriented perpendicular to the surface, and that the rate of a platelet’s tumbling is affected by its distance from the vessel wall. These studies were done in the absence of RBCs, and so it is natural to wonder to what extent these results persist in the presence of RBCs and their strong impact on the blood’s motion.

Other recent computational studies have looked at flowing whole blood and the development of the platelet NWE. Crowl and Fogelson (12,13) used a two-dimensional lattice-Boltzmann immersed boundary (IB) method to solve the Navier-Stokes equations coupled with fluid-structure interactions between highly deformable RBCs and circular platelet-sized particles. Starting from a random distribution of RBCs and a uniform distribution of platelets, their simulations showed that RBCs move toward the vessel axis in the first 100–200 ms giving rise to a several-μm-wide RBC-depleted zone (RBC-DZ) along the vessel walls and that platelets subsequently accumulate in this zone during the next 400–500 ms of flow time. These studies suggested that RBC motions induce velocity fluctuations that give the platelets an effective diffusivity much larger than their Brownian diffusivity, and that this, in conjunction with volume-exclusion effects, explains the development of the NWE. In addition, the RBCs forming the edge of the RBC-DZ were observed to induce a localized biased motion of platelets into the RBC-DZ. More recently, Zhao and co-workers (14,15) reported on three-dimensional computations using the boundary integral method to examine red blood cell and platelet motions in Stokes flow between parallel plate walls. These studies support the qualitative explanations for the margination of platelets given in Crowl and Fogelson (12,13) (both the enhanced diffusivity and the barrier function of the RBCs at the edge of the RBC-DZ), but suggest that Crowl and Fogelson’s two-dimensional simulations overpredict the magnitude of the effective diffusity.

In this article, we use the methods developed in Crowl and Fogelson (12,13) to look at the motion of elliptic platelets near a vessel or thrombus surface in flowing whole blood. Our purpose is to begin to probe the influence of RBCs on platelet motion near the vessel wall, to look at how a thrombus disturbs the motion of the RBCs, and to characterize platelet interactions with a thrombus in the face of the disturbed RBC motion.

To this end, we first determined the spatial distribution of elliptic platelets across the vessel, in particular in the RBC-DZ, through margination simulations. Using this information, we examined platelet kinematics in the near-wall region and found that platelet tumbling near the vessel wall is strongly influenced by the motion of close-by red blood cells, so that the tumbling is erratic and a platelet’s tumbling period is not a simple function of its distance from the wall. We then examined how RBC and platelet motion is changed as blood moves over a preformed thrombus of specified porosity. We investigated the effect of several different porosities because recent studies suggest porosity may regulate thrombus formation (16,17). We observed that, to a degree that depended on the porosity, the RBC-DZ narrowed over the thrombus and platelets were squeezed close to the thrombus, increasing their opportunity for contact with it. The distribution of times that a platelet spent in close proximity to the thrombus was long-tailed. This implies that numerous platelets spend significantly longer periods near the thrombus than would be expected from simpler calculations, and we believe this has important implications for our understanding of the constraints on platelet activation kinetics and on the kinetics of platelet-thrombus cohesive bond formation.

Methods/Theory

Interactions among the RBCs, platelets, and plasma were simulated using the version of the IB method described in Crowl and Fogelson (12,13). In this method, the fluid velocity $\overrightarrow{\mathbf{u}}\left(\overrightarrow{\mathbf{x}},t\right)$ is approximated on a fixed Cartesian grid (mesh spacing h) using a lattice Boltzmann method. Each RBC and platelet is represented by a set of discrete Lagrangian points (IB points) which move through the Cartesian grid and whose locations, $\overrightarrow{\mathbf{X}}\left(q,t\right)$, are tracked as functions of time. From the instantaneous configurations of the IB points making up each cell, IB forces, $\overrightarrow{\mathbf{F}}$, are calculated at each IB point and distributed to the nearby Cartesian grid points according to a discrete version of the relation

$$\overrightarrow{\mathbf{f}}\left(\overrightarrow{\mathbf{x}},t\right)=\underset{\text{Γ}}{\int }\overrightarrow{\mathbf{F}}\left(q,t\right)\delta \left(\overrightarrow{\mathbf{x}}-\overrightarrow{\mathbf{X}}\left(q,t\right)\right)dq.$$ (1)

Here, $\overrightarrow{\mathbf{f}}$ is the force density acting on the fluid, q labels an IB point, $\overrightarrow{\mathbf{F}}\left(q,t\right)$ is the IB force at the location $\overrightarrow{\mathbf{X}}\left(q,t\right)$, δ is the Dirac delta function, and Γ denotes the set of q values labeling all of the IB points. Along with an applied pressure gradient, $\overrightarrow{\mathbf{f}}$ determines the fluid motion. The locations of the IB points change according to a discrete version of the no-slip relation,

$$\frac{d\overrightarrow{\mathbf{X}}}{dt}\left(q,t\right)=\underset{\text{Ω}}{\int }\overrightarrow{\mathbf{u}}\left(\overrightarrow{\mathbf{x}},t\right)\delta \left(\overrightarrow{\mathbf{x}}-\overrightarrow{\mathbf{X}}\left(q,t\right)\right)d\overrightarrow{\mathbf{x}},$$ (2)

in which Ω is the spatial domain. In calculations, the integrals in Eqs. 1 and 2 are approximated by discrete sums and the Dirac delta function is approximated by a discrete version, ${\delta }_h\left(\overrightarrow{\mathbf{x}}-\overrightarrow{\mathbf{X}}\right)$, which is nonzero only for grid points within a 4h × 4h box surrounding each IB point (18).

The forces generated by RBC deformations were calculated using a two-dimensional version of Skalak’s tension law along with a membrane bending law (19). This version of Skalak’s law is shear-hardening and severely penalizes changes in RBC membrane length (20). For a platelet, a Hookean tension law was combined with a bending resistance law so that the platelet was approximately rigid. These force functions are

$${\mathbf{F}}_{\text{RBC}}\left(X\right)=\frac{d}{ds}\left(G_{\text{RBC}}\left({\lambda }^2-1\right)\left(1+\frac{K_{\text{RBC}}}{G_{\text{RBC}}}{\lambda }^2\left({\lambda }^2+1\right)\right)\hat{\mathbf{t}}+E_{\text{RBC}}^b\left(\kappa -{\kappa }_0\right)\hat{\mathbf{n}}\right)$$ (3)

and

$${\mathbf{F}}_p\left(X\right)=\frac{d}{ds}\left(G_p\left({\lambda }^2-1\right)\hat{\mathbf{t}}+E_p^b\left(\kappa -{\kappa }_0\right)\hat{\mathbf{n}}\right)$$ (4)

for the RBC and platelet points, respectively. Here, λ is the local strain at a point $\overrightarrow{\mathbf{X}}$ on a cell membrane; κ and κ₀ are the actual local curvature and prescribed rest curvature of the cell membrane, respectively; s measures arclength along the membrane; G, K, and E_b are the shear, area expansion, and bending moduli, respectively; and $\hat{t}$ and $\hat{n}$ denote unit vectors tangent and normal to the membrane surfaces, respectively. Parameter values can be found in the Supporting Material. More information on the methodology and validation of the numerical methods is given in Crowl and Fogelson (12,13).

In the IB method, the effective distance between two immersed objects is shorter than the nominal distance between the two surfaces. This is because each IB force is applied to the fluid (and velocity is interpolated from the fluid) over a region of width the order of a computational meshwidth (h). Distances reported in this article include this effect; reported distances between two immersed objects are 2h less than their nominal distance, and distances to the vessel wall (a computational boundary) are h less than the nominal distance.

Results

Development of the platelet near-wall excess

To investigate the motion of platelets near the vessel wall or near a developed thrombus, we first determined how platelets are spatially distributed across the vessel lumen, in particular within the RBC-DZ. We considered a two-dimensional blood vessel 100-μm long and 50-μm wide under arteriolar flow conditions driven by a pressure gradient that resulted in a mean wall shear rate 1100 s⁻¹. We performed six separate simulations in each of which 12 elliptic platelets were placed uniformly in the y (transverse) direction across the vessel. The ellipses we used had a major axis diameter of 2.68 μm, and a minor axis diameter of 0.88 μm. The initial fluid velocity field and RBC configuration were taken from prior simulations with the appropriate hematocrit (Hct) measurements that were run to a pseudo steady state in which the time-averaged RBC concentration profile across the channel was no longer changing. In this initial RBC configuration, RBCs had migrated toward the center of the vessel and thus created a RBC-depleted zone (RBC-DZ) near the vessel wall. Platelets then migrated to the vessel wall to create the near-wall excess (NWE). The zone’s width was ≈7 μm and ≈3 μm for 20% and 40% Hct, respectively. This compares to widths of ≈4.8 μm and ≈7.0 μm for hematocrits of 20% and 10% in the three-dimensional simulations of Zhao et al. (15) which took place at nearly twice the shear. A snapshot of a simulation is shown in Fig. 1. See Table 1 for simulation parameters.

Figure 1.

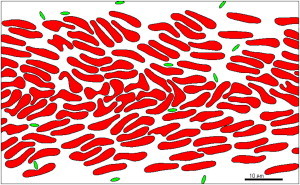
Simulation of whole blood flow at 40% Hct and 1100 s⁻¹ wall shear rate. After 600 ms of flow, the platelets are distributed preferentially near the wall.

Table 1.

Simulation parameters

Parameter	Description	Value
GRBC	RBC shear modulus	6 × 10−3 dynes/cm
KRBC	RBC area expansion modulus	5 × 102 dynes/cm
EbRBC	RBC bending modulus	2 × 10−12 dynes cm
GP	Platelet shear modulus	1 × 10−1 dynes/cm
Ebp	Platelet bending modulus	2 × 10−11 dynes cm
Δt	Time step	5 × 10−8 s
Δx	Mesh width	0.143 μm
NRBC	No. of IB points per RBC	600
NP	No. of IB points per platelet	100

After 600 ms of simulated time, the histograms of platelet distribution across the vessel for elliptic platelets closely match those of simulations with circular platelets for the same Hct (13). A quantity of 44.4% of the platelets migrated into the RBC-DZ in the 20% Hct case and 33.3% did so in the 40% Hct case. As shown in Fig. 2, the platelet distribution across the RBC-DZ is not uniform. It is skewed so that more platelets are located near the inner edge of the RBC-DZ (away from the vessel wall). Using the 40% Hct data for platelets in this zone, we fit a β-distribution for the probability that a platelet in the RBC-DZ is found a certain distance from the wall as

$$f\left(y\right)=\frac{{\left(y-y_{\text{lower}}\right)}^{\alpha -1}{\left(y_{\text{upper}}-y\right)}^{\beta -1}}{{\left(y_{\text{upper}}-y_{\text{lower}}\right)}^{\alpha +\beta -1}B\left(\alpha ,\beta \right)}.$$ (5)

Here, y_lower = 0.5 μm and y_upper = 3 μm are the lower and upper bounds of the RBC-DZ, α = 4.320 and β = 4.974 are parameters of the distribution, and B is the β-function (21). Then the probability that a platelet is found a distance between y and y + dy away from the wall is ∼f(y)dy. This distribution was used to initialize platelet positions in the experiments involving flow past a thrombus that are described below.

Figure 2.

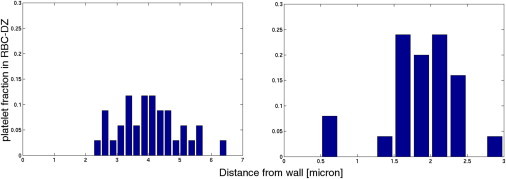
Platelet distribution histograms inside the RBC-DZ after 600 ms. Distance is measured from the wall to the platelet’s center of mass. Bin width is 250 nm.

Platelet near-wall behavior

Fig. 3 shows the time- and x-averaged fluid velocity in the vessel. Because of the observed velocity gradients in the RBC-DZ, it is expected that a platelet with an approximately rigid elliptic body will tumble (11,22), and, indeed, this is what we saw. For the 40% Hct case, out of 24 platelets in the RBC-DZ, 22 tumbled and the remaining two slid along the wall. For the 20% Hct case, all 32 platelets in the RBC-DZ tumbled. Understanding the tumbling behavior of a platelet is important because it influences whether any part of the platelet’s surface becomes close enough to the vessel wall to detect an injury and to adhere to it. Fig. 4 shows several examples of how the distance between a platelet’s surface and the vessel wall varied over an observation of 20 ms. Initial platelet adhesion is primarily accomplished by formation of bonds between platelet GPIb receptors and vascular-wall-bound von Willebrand Factor (vWF). vWF is a large, dynamic multimer with a mean length in its extended state of 350 nm (23). However, this length may vary due to self-association/disassociation, conformational changes due to shear, and enzymatic processes (24–26). Therefore, it is unclear what distance best characterizes a platelet-wall interaction. Neglecting the two sliding platelets (which are very close to the wall), if we characterized the interaction distance as 250 nm, six platelets approached the wall closer than this distance and the mean duration of their interactions was 3.5 ms. Likewise, if the distance was set to 350 nm, we saw 12 platelets interact with the wall for a mean duration of 2.7 ms. Other data include (distance (nm) (platelets) mean duration (ms)):

$$450\left(15\right)3.1;550\left(15\right)3.1;650\left(29\right)2.9;750\left(34\right)3.3.$$

Note that even though we report mean duration times, interaction times were not normally distributed (see Fig. 4) and a significant fraction of the interacting platelets were within the specified distance from the wall for much longer than the mean times reported.

Figure 3.

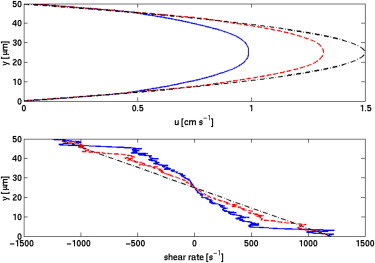
Fluid velocity and shear rate across the channel for 20% (red, dash), 40% (blue, solid), and 0% (black, dot-dash) Hct cases. Shear rate ∂u/∂y is approximated with a finite-difference. Values of shear rate and fluid velocity are then averaged over the length of the domain and over 10 ms of time.

Figure 4.

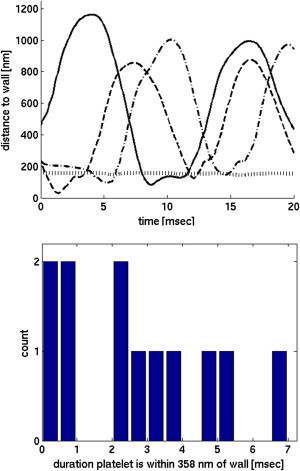
(Top) Distances from the wall for four different platelet trajectories. In three trajectories (solid, dashed, and dash-dot) the platelets are tumbling, and in one (dotted) the platelet is sliding. (Bottom) Histogram of time intervals that tumbling platelets spend within 350 nm of the wall.

We found that for platelets in the RBC-DZ, the platelet tumbling periods (mean ± standard deviation) were 16.4 ± 2.7 ms for $20\text{\%}$ Hct and 19.0 ± 2.6 ms for 40% Hct. Analyses of a single three-dimensional platelet’s tumbling near a wall but without RBCs show a trend of slower tumbling as the distance to the wall decreases (10,11). In Fig. 5, the solid circles show tumbling periods for single two-dimensional platelets (without RBCs) in a simulation with a background linear shear flow (shear rate 1100 s⁻¹.) We see a clear slowing of the tumbling rate as the wall is approached. The figure also shows tumbling periods in simulations with RBCs, and again we see a trend toward slower tumbling with decreased distance from the wall. We note that for each specified distance from the wall, there is significant scatter in the platelet tumbling periods, and that platelet tumbling with RBCs is slower than without them.

Figure 5.

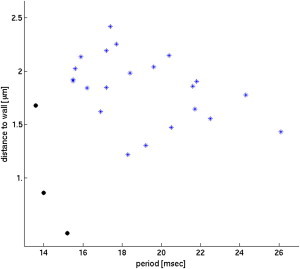
Tumbling period versus distance from the wall for shear rate 1100 s⁻¹. (Asterisks) Data from whole blood simulations at Hct 40%; (circles) shear flow simulations without RBCs.

During 20 ms of observation, a platelet was, on average, closest to ∼10 different RBCs with a mean duration 1.9 ms of being closest to each particular RBC at Hct 40% (or ∼11 RBCs with a mean duration of 1.7 ms at Hct 20%). This rapid switching of which RBC is nearest to the platelet may account, in part, for the scatter in the observed tumbling periods. The timescale of these individual RBC interactions was an order of magnitude less than the tumbling period, implying that the platelets did not tumble in a regular fashion. In fact, the timescale is shorter than the mean duration of a platelet’s close encounter with the wall, indicating that each such encounter may be perturbed by multiple RBCs.

Motion of elliptic platelets around a thrombus

Platelets do not just sample the vessel wall to respond to injury. They also must traverse an existing thrombus and adhere to it in order for the thrombus to grow. Thus, it is critical to understand the motion of platelets past existing thrombi to determine if the kinematics change compared with those near the vessel wall and how these changes affect possible platelet adhesion.

Significant growth of even a moderate-sized thrombus occurs on a timescale long compared to that of an individual platelet’s motion past the thrombus. We therefore constructed a preformed idealized thrombus on one vessel wall and kept this thrombus fixed in size as we observed the motion of platelets near it. The thrombus occupied a trapezoidal region with height 11.5 μm, top length 24.0 μm, and bottom length 44.0 μm. It was composed of 75 circular sets of IB points that were held in place using stiff springs to tether them to prescribed spatial locations (see Fig. 6 A). Using this approach to model a thrombus allows us the ability to change its porosity by modifying the centers and radii of the constitutive IB circles. The effect of varying the thrombus’ porosity is discussed in later sections.

Figure 6.

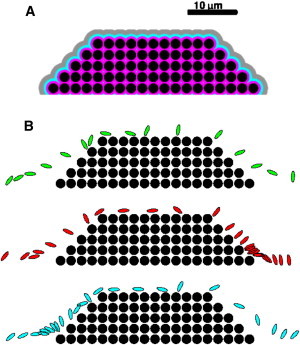
(A) Region 1 (magenta) contains locations within 250 nm of the thrombus. Region 2 (blue) and Region 3 (gray) contain locations between 250 and 750 nm, and 750 and 1750 nm, from the thrombus, respectively. (B) Superimposed snapshots (3 ms apart) of platelets moving past a thrombus.

For each thrombus, we solved the fluid dynamic and RBC equations of motion with wall shear rate 1100 s⁻¹ and Hct $40\text{\%}$ until a pseudo-steady state was achieved and we saved time snapshots of the RBC distributions and velocity fields produced by this process. These were used to initialize the velocity field and RBC distribution in the studies of platelet motion around the thrombus. For each platelet simulation, we placed a platelet at a prescribed location in the RBC-DZ upstream of the thrombus (more details are presented below). We then tracked the platelet’s motion as it moved past the thrombus. We measured the amount of time each platelet spent in each of three regions close to the thrombus. A platelet was counted as being in Region 1, Region 2, or Region 3, respectively, if the distance of its closest point to the thrombus was <250 nm, between 250 and 750 nm, or between 750 and 1750 nm (Fig. 6 A). These regions can be interpreted as regions where adhesion is mediated by vWF from the plasma bound to the thrombus, ultralarge vWF released from the α-granules of activated platelets in the thrombus, and platelet pseudopodia, respectively (27,28).

The pseudo-steady state RBC distribution shows that the RBC-DZ shrank as the flow moved past the thrombus (see Fig. 10 later in text). The width of this region was 3 μm away from the thrombus, consistent with the previous simulations. Over the top of the thrombus, it shrank to only 1.12 μm, because the RBCs were squeezed through a narrower channel. This forced platelets in the RBC-DZ closer to the thrombus.

Figure 10.

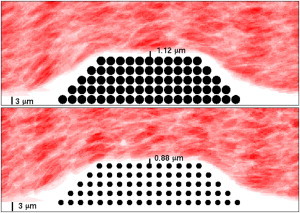
Widths of the RBC-DZs over a thrombus with porosity 0.21 (top) and 0.67 (bottom). (Shading) Time-averaged hematocrit.

Effect of platelet initial position

We investigated how a platelet’s trajectory, and, more specifically, the length of time that a platelet spent in each of Regions 1–3 varied with respect to changes in its initial position and orientation. The center of mass of each platelet was placed at an x location 20-μm upstream of the thrombus. The initial y coordinate of the platelet’s center of mass was chosen using the β-distribution equation, Eq. 5. Its initial orientation was chosen from a uniform distribution for the angle that its major axis makes with the positive x direction. We sampled n = 30 realizations from this joint distribution and examined the statistics of the time spent by the platelets near the thrombus. For these simulations, the initial RBC configuration and fluid velocity field were fixed.

Fig. 6 B shows three sample platelet trajectories. We observe platelets sliding along and tumbling over the thrombus surface. (See Movies in the Supporting Material.) Table 2 shows statistics for the time platelets spent in each of Regions 1–3. Note in Fig. 6 B that platelets can move past the thrombus somewhat uniformly (top panel) or spend disproportionate times at the upstream (bottom panel) or downstream (middle panel) edges of the thrombus. There is a large difference between the 10th and 90th percentiles; this suggests that small changes in the platelet’s initial condition and orientation can produce very different trajectories around the thrombus. (Simulations with a fixed initial platelet configuration and different RBC/fluid distributions produced results with a smaller difference between the 10th and 90th percentiles, indicating that the platelet’s initial position plays a larger role than any specific initial RBC distribution in affecting platelet behavior near the thrombus.) A histogram showing the times spent within 250 nm of the thrombus is shown in Fig. 7. We observe that this is a long-tailed distribution, which allows for values much larger than the mean to occur with significant probability. Fig. 8 shows that platelets are more likely to be within 250 nm (in Region 1) of the thrombus near its upstream corner and along the top of the thrombus. Platelets within 250 nm of the thrombus are also more likely to be oriented nearly perpendicular or nearly parallel to it than in any other orientation (Fig. 9). We observed that the platelet tumbling rate increased approximately twofold for platelets located above the thrombus. This is not surprising as this is the region near the thrombus with the largest shear rate.

Table 2.

Statistics (median and [10th, 90th] percentile) for the residence time (ms) distributions for Regions 1–3 for platelets moving past thrombi of differing porosities

Porosity	Flux	Region 1	Region 2	Region 3
0.21	0.023	9.0 [0.5, 38.7]	11.9 [4.4, 57.0]	10.8 [6.4, 62.3]
0.46	0.043	15.2 [2.6, 65.6]	13.3 [3.8, 21.0]	10.2 [5.1, 77.6]
0.67	0.085	14.1 [6.1, 72.4]	10.7 [6.0, 57.5]	12.6 [7.1, 82.8]
0.82	0.118	N/A	N/A	N/A
0.93	0.340	N/A	N/A	N/A

n = 30 for all cases. Relative fluid flux (percent) through the thrombus compared to the total flux through the vessel.

Figure 7.

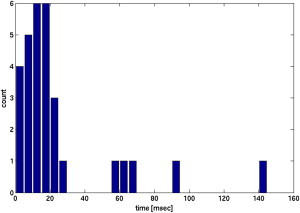
Histogram of the residence times of platelets within 250 nm of a thrombus of porosity 0.46.

Figure 8.

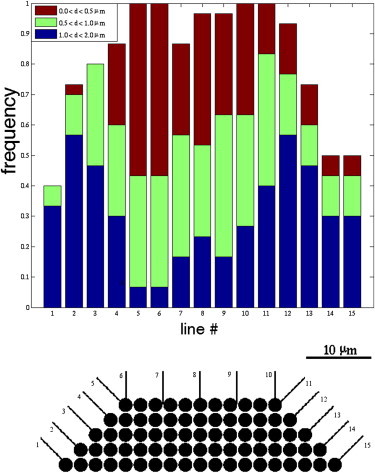
Histograms showing platelet distance from the thrombus as they cross the specified lines around the leading edge and top of the thrombus. Observe that platelets are most often closest to the thrombus near its upstream corner.

Figure 9.

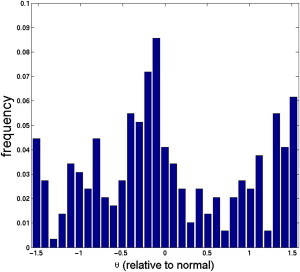
Orientation of the platelets within 250 nm of the thrombus. The value θ is the angle the platelet makes with respect to the direction normal to the thrombus’s surface.

Effect of thrombus porosity

Thrombi can have different porosities because of variations in the number of platelets, their states of adhesion and activation, and the structural permeability of the fibrin mesh (16,29–31). We examined how variation in porosity affects the motion of platelets traveling near our idealized thrombus. We defined a thrombus’ porosity to be the fraction of the thrombus not enclosed by the circular IB objects. Using a radius of h larger than the nominal radius (due to force spreading in the IB method) in calculating the area enclosed by each IB object gives a porosity of 0.21 for the thrombus shown in Fig. 6 A.

We generated thrombi of different porosities by varying the radii of the circular IB objects that make up the thrombus. The locations of the centers of these circular IB objects were transformed linearly so that the edges of the outermost IB objects coincided with the edges of the trapezoidal region used to define the thrombus. These IB objects were held in place by stiff tethers as before. We investigated five thrombi with porosity values ranging between 0.21 and 0.93. These correspond to setting the radii of the circular IB objects to values between 1.0 and 0.2 times, as used in previous sections.

For each thrombus, we first ran simulations of the flow with RBCs (and no platelets) to a pseudo-steady state and calculated the flux through the thrombus. Values of the flux through the thrombus as a percentage of the total flux through the channel are reported in Table 2. We see that as the porosity increased the flux through the thrombus also increased, although the magnitude of the flux stayed small. We also see that as the porosity increased, the width of the RBC-DZ above the thrombus decreased. As shown in Fig. 10, this region was ∼1.12-μm wide for flow past a thrombus with porosity 0.21 and 0.88 μm for porosity 0.67. This forced platelets moving past more porous thrombi closer to the thrombus than platelets moving past less porous thrombi. (See Movies in the Supporting Material.) Table 2 gives statistics for the time spent by platelets at various distances from the thrombus as the porosity was changed. The most striking observation is that the 90th percentile of the residence time a platelet spent within 250 nm of the thrombus increased substantially as the thrombus porosity changed from 0.21 to 0.46, but changed little more with a further increase in porosity to 0.67. Also noteworthy is that for thrombi with porosity >0.82, platelets very seldom moved over the thrombus. Instead, the platelet penetrated into the interstices of the thrombus. Most of these platelets became immobilized (without any adhesion processes); two platelets actually passed entirely through the thrombus and exited through the thrombus’ downstream edge. We again observe that platelet tumbling increased when the platelets were located above the thrombus. This effect is enhanced in the cases with more porous thrombi, which we attribute to the RBCs having been closer to the platelets—thus able to exert more influence on their motion—because the width of the RBC-DZ shrank as the porosity increased.

Discussion

In this article, we describe a two-dimensional computational study of the motion and distribution of elliptic platelets in flowing whole blood. We performed margination computations to determine the spatial distribution of platelets in the red blood cell depleted zone (RBC-DZ) near the vessel walls. With these data, we set up and conducted simulations to examine the motion and tumbling behaviors of platelets in this region. The latter are important in determining the ability of platelets to sample the wall to detect and make an initial response to a vascular injury or to contact and adhere to a growing thrombus.

This study shows that the RBCs can have a strong effect on the motion of platelets near the vessel wall. Because of the RBCs, platelets near the wall tumble more slowly than platelets in a flow without RBCs. Simulation results (not shown) suggest that several mechanisms may play a factor in slowing down the tumbling motion of platelets. These include the disturbances to the local flow field and velocity gradients by RBCs; RBC-induced lateral motion of the platelets, particularly near the edge of the RBC-DZ; and the relative positioning of the platelets with respect to individual RBCs. For example, the standard deviations (over x and t) of the velocity gradient (∂u/∂y) at each y location in the RBC-DZ are comparable in magnitude to the means shown in Fig. 3. More investigation is needed to identify which mechanisms are dominant in affecting platelet tumbling. Platelet-RBC interactions and the rapid timescale of these interactions suggest that the near-wall motion of the platelet is not adequately captured by explorations in a simple shear flow (10,11).

In our simulations, the presence of a thrombus protruding into the vessel lumen diverted the flow and the RBCs away from the vessel wall so that almost all of the flux through the channel passed over the thrombus. The thrombus did not otherwise dramatically perturb the motion of the RBCs. Because the channel over the thrombus was narrower than the vessel, the RBC-DZ was thinner above the thrombus. For the base thrombus (porosity 0.21) and 40% Hct, the width above the midpoint of the thrombus was 1.12 μm compared to 3 μm both upstream and downstream of the thrombus. The layer was, in fact, even thinner than this along the upstream and downstream portions of the thrombus top. For a more porous thrombus (porosity 0.67), the RBC-DZ was only 0.88-μm wide above the thrombus’ midpoint and was again thinner near the thrombus’ upstream and downstream top corners.

Because of the thinning of the RBC-DZ over the thrombus, platelets in it were forced close to the thrombus, thereby increasing their opportunity for interaction with it. As platelets in the RBC-DZ moved over the thrombus, they both slid and tumbled over its surface. We saw that a platelet whose closest point to the thrombus surface was within 250 nm was likely to be oriented approximately perpendicularly to that surface, thus indicating the importance of platelet tumbling in promoting interactions with the thrombus.

For a developing thrombus, its porosity varies (16) as the number density of platelets in the thrombus changes and also as the shape of the platelets and the closeness with which they appose one another change. Consequently, the ease with which fluid permeates the thrombus varies as well. We sought to obtain insight into the effect this would have on platelet interactions with the thrombus by constructing a number of different thrombi with different porosities. As noted earlier, for thrombi with greater porosity the RBC-DZ over the thrombus was thinner. Further, the rate of tumbling of platelets in this region was greater for the more porous thrombi. This is because for these thrombi, the RBCs were nearer to the platelets in the RBC-DZ, exerted a greater influence on their motion, and thereby increased the platelets’ tumbling rate and frequency of sampling of the thrombus surface. The median time that platelets spent in close proximity to the thrombus also was higher for more porous thrombi. Possibly even more important was the substantial increase in the upper 10–20% of times spent near the thrombi; it increased by close to a factor of 2 from ∼37 ms to ∼72 ms. These numbers are for the platelets that passed over the thrombus. For thrombi with pores sufficiently large to contain a platelet, platelets did not pass over the thrombus, but instead penetrated into the thrombus where they became trapped. Based on all of these observations, thinking of the sequence of thrombi in order of decreasing porosity as representative of different stages of a thrombus’s development, we speculate that platelets spend relatively longer periods of time near a thrombus early in its development when it is most porous, and less later when it is more consolidated. This may help to promote early growth and curtail late growth of the thrombus.

In this study we observed that in the presence of a thrombus, there is a long-tailed distribution of the time platelets spent in close proximity to the thrombus. Whereas most platelets spent <20 ms close to the 44-μm-long model thrombus used in this study, a substantial fraction (1 in 6) spent over three times as long near the thrombus. These platelets would have a significantly increased time to respond to activation signals and firmly adhere to the thrombus via integrin-mediated bonds (4,32,33) even if no transient GPIb-vWF bonds formed to further slow their passage over the thrombus.

Although it is clear that two-dimensional simulations cannot always provide quantitatively accurate predictions of three-dimensional behavior, they can still yield illuminating qualitative results that can guide new three-dimensional computations and stimulate new experimental directions. In particular, detailed three-dimensional computations will be required to elucidate which RBC-platelet interaction mechanism is predominantly responsible for slowing platelet tumbling in the presence of RBCs. Three-dimensional simulations and experiments should also be used to explore more quantitatively the thinning of the RBC-DZ near a thrombus, how this impacts the proximity of platelets to the thrombus and their extended residence time there, and how these are further affected by the porosity of the thrombus.