Abstract
Fibroblast growth factors (FGFs) utilize cell surface heparan sulfate as a coreceptor in the assembly of signaling complexes with FGF-receptors on the plasma membrane. Here we undertake a complete thermodynamic characterization of the assembly of the FGF signaling complex using isothermal titration calorimetry. Heparin fragments of defined length are used as chemical analogs of the sulfated domains of heparan sulfate and examined for their ability to oligomerize FGF1. Binding is modeled using the McGhee-von Hippel formalism for the cooperative binding of ligands to a monodimensional lattice. Oligomerization of FGFs on heparin is shown to be mediated by positive cooperativity (α = 6). Heparin octasaccharide is the shortest length capable of dimerizing FGF1 and on longer heparin chains FGF1 binds with a minimal footprint of 4.2 saccharide units. The thermodynamics and stoichiometry of the ternary complex suggest that in solution FGF1 binds to heparin in a trans-dimeric manner before FGFR recruitment.
Introduction
Mammalian fibroblast growth factors (FGFs) are a family of 22 highly conserved polypeptides. They are involved in a plethora of biological processes, including cell proliferation, differentiation, cell migration, and angiogenesis (1,2). FGFs signal through four FGF receptors (FGFR1–4), which are high affinity cell surface receptor tyrosine kinases (3). FGFRs have three extracellular immunoglobulin-like domains (D1, D2, and D3), of which only D2 and D3 are required for FGF binding (4). Receptors 1–3 undergo alternative mRNA splicing to generate b- and c-isoforms with altered ligand specificities and affinities (5). FGF1 is capable of binding all receptor isoforms, and is sometimes regarded as the universal ligand (6,7).
Heparan sulfate (HS), a glycosaminoglycan present in the extracellular matrix and uniformly distributed around virtually all mammalian cells, is essential for FGF signaling (8). HS contains linear regions of 50–150 repeating disaccharides of N-acetyl- or N-sulfoglucosamine and uronic acid joined by (1→4) linkages (9) with typical concentrations of HS on the cell surface in the range of 105–106 molecules cell−1 (10). The length of an extended HS chain with average molecular mass of 30 kDa would be ∼50 nm (11). It is variably polysulfated with highly sulfated residues existing predominantly in contiguous regions (6–14 units), or S-domains (12). Although heparin is used as a functional and structural analog of these regions, it is more heavily sulfated than the majority of S-domain sequences (13). Heparin is sufficient to promote the mitogenic action of FGFs on cells deficient in HS (14) and also protects FGFs from proteolysis and thermal denaturation (15,16). FGFs vary in their specificities for different HS sulfation patterns, with heparin being a particularly good analog for FGF1, which requires N, 2-O, and 6-O sulfate groups for both high affinity binding and activation (17).
FGF1 adopts a β-trefoil fold with pseudo-threefold symmetry (18). The crystal structures of FGF2 bound to heparin tetra- and hexasaccharide (PDB: 1BFB and PDB: 1BFC) (19) and the NMR structure of FGF1 complexed to a hexasaccharide (PDB: 2ERM) (20) reveal that the heparin-binding region consists of three surface loops (Fig. 1 a). FGF interaction with heparin is achieved through sulfate groups and does not induce any significant conformational change in FGF upon binding, although a distortion of the heparin helix is a common observation (21). Heparin decasaccharide was shown to dimerize FGF1 in a trans configuration with two FGF1 polypeptides related by a quasi 21 symmetry axis that runs perpendicular to the helical axis of the intercalated heparin molecule (Fig. 1 b) (22). The complex is characterized by a complete absence of FGF-FGF interactions as all contacts are mediated through the heparin molecule.
Figure 1.
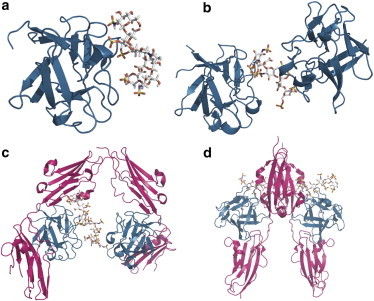
The interaction between FGF1, FGFR, and heparin is structurally well characterized with structures of (a) FGF1 bound to heparin hexasaccharide (PDB: 2ERM); (b) FGF1 dimerized on heparin decasaccharide (PDB: 1AXM); (c) the asymmetric FGF1:FGFR2c:heparin complex with 2:2:1 stoichiometry (PDB: 1E0O); and (d) a symmetric 2:2:2 FGF2:FGFR1c:heparin complex (PDB: 1FQ9). In images a–c, one FGF1 molecule and the heparin are in the same orientation. FGF is shown in cartoon representation and heparin in stick representation.
Formation of a ternary complex in which the FGF receptors are both dimerized and activated is necessary for signaling to occur. Two crystal structures of a ternary complex between FGF, FGFR (extracellular domains D2 and D3), and heparin have been determined, each of which contains a common substructure with 1:1:1 stoichiometry (23,24). In this 1:1:1 substructure, FGF interacts extensively with D2 and D3 as well as the highly conserved linker between the two domains, and heparin interacts with a cationic patch formed by both FGF and D2. However, two different possible modes of dimerization are suggested by the crystal data. The structure of the complex defined by Schlessinger et al. (23) (PDB: 1FQ9) contains two 1:1:1 complexes related by a crystallographic twofold axis and dimerized through direct FGFR-FGFR contacts, as well as secondary FGF-FGFR and heparin-FGFR interactions (Fig. 1 d). The two heparin molecules lie in an antiparallel orientation with their nonreducing ends facing one another within a cationic canyon formed by dimerization of the FGF-FGFR. This arrangement raises the question as to whether both molecules are simultaneously occupying the canyon in the crystal structure—or whether these two sites are partially occupied in a way that would be generated by disorder of two 2:2:1 complexes around the crystallographic twofold axis. The structure of the complex defined by Pellegrini et al. (24) (PDB: 1E0O) contains a similar structure with a canyon reminiscent of that observed in the 2:2:2 model but with only one heparin molecule, so leading to a 2:2:1 complex. In addition, an interaction around a heparin molecule generated by the crystal symmetry gives rise in the lattice to a different 2:2:1 complex with minimal receptor-receptor contacts (Fig. 1 c). The heparin is bound primarily by two FGF molecules in a manner similar to that observed in the FGF1-octasaccharide crystal structure (22).
It is not clear which architecture is observed in solution or whether both architectures can form under different circumstances. In principle, the 2:2:1 complex can form internally upon a HS chain, whereas steric hindrance dictates that the 2:2:2 complex can only form on the nonreducing ends of two separate but proximal HS chains.
In previous articles using size exclusion chromatography (SEC) to study FGF-FGFR-heparin interactions we suggested that formation of the ternary complex may be driven by cooperative binding of FGFs (FGF1 and FGF2) to heparin saccharides of sufficient length and sulfation to dimerize the growth factors (25,26). It has been reported that the interaction between FGF2 and heparin octasaccharide displays pronounced cooperativity (27). Nondissociative mass spectrometry, SEC and ultracentrifugation demonstrated that multiple complexes can form on saccharide chains of physiological length (26,28) with lengths as short as 16 saccharide units capable of supporting a higher order complex resembling a 4:4:1 FGF:FGFR:heparin assembly.
It is clear that more information is needed on the molecular interactions, affinities, and stoichiometries of the complexes that form during the assembly of the FGF signaling system in solution. Here we dissect the thermodynamics of complex formation by investigating the role of heparin length on FGF1 oligomerization and subsequent recruitment of the FGFR to form a signaling complex.
Methods
Preparation of components
Recombinant human FGF1 and FGFR2c ectodomain (residues 148–366, encompassing immunoglobulin-like domains D2 and D3) were prepared as described in Pellegrini et al. (24). After purification, the proteins were dialyzed to 10 mM HEPES pH 7.2, 150 mM NaCl. Size-defined oligosaccharides were prepared from partial heparinase digests of heparin samples by SEC (17).
Isothermal titration calorimetry of FGF-heparin interactions
Isothermal titration calorimetry (ITC) experiments were performed using a MicroCal VP-ITC machine (GE Healthcare, Little Chalfont, United Kingdom). Titrations involved the addition of 10 μL aliquots of ligand via a rotating stirrer-syringe to the calorimetric cell containing 1.407 mL of the receptor at 4-min intervals. A constant temperature of 25°C and stirring speed of 300 rpm was maintained throughout. A total of 25 injections per experiment were conducted. Heats of dilution/dissociation determined in the absence of receptors were subtracted from the titration data before curve fitting. Additionally, an initial 4 μL injection was discarded from each dataset to remove the effect of titrant diffusion across the syringe tip during the equilibration process.
Analysis of ITC binding data
Experimental data for the binding of FGF to heparin were fitted to a theoretical model based on the McGhee-von Hippel formalism for the binding of nonspecific ligands to overlapping binding sites on a monodimensional lattice (29) modified for the analysis of isotherms (30,31). For the binding of FGF1 to heparin hexasaccharide, the data were fitted to a noncooperative model, but for saccharide chains capable of binding more than one FGF1 molecule a cooperative McGhee-von Hippel formalism was employed. In the noncooperative model, the heat effect associated with each injection (qi) is given by Eq. 1,
| (1) |
where V0 is the total cell volume (1.407 mL), [Mt] is the total macromolecule concentration, v is the injection volume, and ν is the number of ligand molecules bound per macromolecule, given by Eq. 2,
| (2) |
where KD is the dissociation constant, N is the potential number of binding sites distributed along the molecule, and l is the minimal number of repeat units necessary to support binding and [X] is the ligand concentration.
The cooperative model considers three different binding modes that a ligand can adopt on a monodimensional lattice—isolated binding (νiso); binding adjacent to a prebound ligand in a singly contiguous mode (νsc); and binding with ligands either side in a doubly contiguous mode (νdc) (reviewed by Brown (31)). The heat associated with each injection is the summation of each of these modes given by Eq. 3,
| (3) |
where each of the different modes is evaluated as
| (4) |
| (5) |
| (6) |
| (7) |
where Δh is the enthalpy associated with cooperativity and α is the cooperativity factor.
Isothermal titration calorimetry of FGF-FGFR interactions
Data for the binding of FGF to FGFR were fitted to a one-site model by nonlinear least-squares fitting (32) and a full set of thermodynamic parameters derived using the relationships shown in Eq. 8,
| (8) |
where ΔG, ΔH, and ΔS are the Gibbs free energy, enthalpy, and entropy of binding, respectively. T is the absolute temperature and R = 1.98 cal mol−1 K−1 is the ideal gas law constant.
Size-exclusion chromatography
Size-exclusion chromatography (SEC) was performed using a Superdex 200 10/300 HR column (GE Healthcare) equilibrated with 10 mM HEPES pH 7.2, 150 mM NaCl. All experiments were run on the AKTA Explorer chromatography system (GE Healthcare) at a flow rate of 0.5 mL min−1 and the absorbance at 280 nm was recorded.
Results
For complete characterization of the FGF-heparin interaction it is necessary to determine the binding affinity, the binding site size (l), whether ligand binding is cooperative, and the thermodynamic parameters of both the intrinsic and cooperative interaction (if present). Using ITC, it is possible to extract this information using a modified version of the McGhee-von Hippel formalism (29,30). This model is appropriate for both cooperative and noncooperative processes. It has previously been implemented in determining thermodynamic parameters from ITC data for proteins binding to chitosan, a linear polysaccharide similar to heparan sulfate (33). By using defined-length heparin oligosaccharides similar to those used in structural studies, it is possible to link the thermodynamics of the FGF-heparin interaction to the known x-ray and NMR structures.
Monovalent FGF-heparin interactions
Homogenously purified FGF1 titrated into a solution of heparin hexasaccharide gave a sigmoidal profile (Fig. 2 a) where saturation of heparin binding sites is achieved at higher FGF1 concentrations. From the NMR structure of FGF1 bound to heparin hexasaccharide it is known that only one FGF molecule can bind hexasaccharide concomitantly (20). Therefore, the isotherm was analyzed using the noncooperative McGhee-von Hippel model for nonspecific binding to a monodimensional lattice (Eq. 1), as 1:1 interactions are devoid of cooperative processes. In this, and all subsequent analyses, the value of N was fixed. N reflects the number of repeating units per macromolecule, which in the case of FGF binding to carbohydrates is the number of saccharide moieties. Therefore, in the analysis of monovalent interactions N was set at 6.0, reflecting the six saccharide moieties present.
Figure 2.
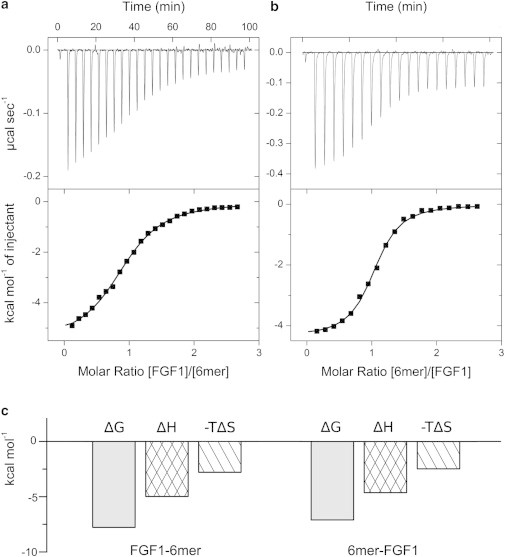
Analysis of FGF1-heparin hexasaccharide interaction by direct (a) and reverse (b) titrations. In the direct titration, 100 μM FGF1 was titrated into 7 μM hexasaccharide and in the reverse titration, 100 μM heparin was titrated into 12.5 μM FGF1. (Upper panel) Calorimetric titration trace with the integrated isotherms (shown in lower panel). (Solid lines) Best fit to the noncooperative McGhee-von Hippel model. (c) Thermodynamic dissection of the interaction between FGF1 and heparin hexasaccharide. (Shading) Free energy of binding (ΔG); (crosshatch) enthalpy of binding (ΔH); (diagonal shading) entropy of binding (−TΔS).
The binding site length was determined as 4.7 saccharide units, the affinity as low micromolar (1.9 μM) with an enthalpy of −5.0 kcal mol−1. From these values, ΔG and ΔS were obtained (Table 1).
Table 1.
ITC-derived thermodynamic parameters for the binding of heparin saccharides of defined length to FGF1
| Titration | KD (μM) | ΔG (kcal mol−1) | ΔH (kcal mol−1) | −TΔS (kcal mol−1) | l (moieties) | α | Δh(kcal mol−1) |
|---|---|---|---|---|---|---|---|
| FGF1–6-mer | 1.9 ± 0.2 | −7.8 | −5.0 ± 0.1 | −2.80 | 4.7 ± 0.1 | n.a. | n.a. |
| 6-mer-FGF1 | 1.1 ± 0.2 | −8.1 | −4.5 ± 0.0 | −3.6 | 5.0 ± 0.2 | n.a. | n.a. |
| FGF1–8-mer | 1.1 ± 0.1 | −8.1 | −5.7 ± 0.0 | −2.4 | 3.7 ± 0.1 | 7.0 ± 0.3 | 3.0 ± 0.2 |
| 8-mer-FGF1 | 3.0 ± 0.2 | −7.5 | −6.8 ± 0.0 | −0.7 | 4.7 ± 0.2 | 4.5 ± 0.1 | 2.6 ± 0.2 |
| FGF1–16-mer | 1.2 ± 0.1 | −8.1 | −8.8 ± 0.0 | 0.7 | 3.8 ± 0.1 | 6.1 ± 0.0 | 1.8 ± 0.3 |
| 16-mer-FGF1 | 1.5 ± 0.2 | −7.9 | −9.0 + 0.1 | 1.1 | 3.1 ± 0.3 | 5.2 ± 0.0 | 1.7 ± 0.3 |
In all cases, the number of repeat units, N, was fixed as the number of saccharide moieties present in the heparin molecules. The binding of heparin hexasaccharide (6-mer) to FGF1 was analyzed using the noncooperative McGhee-von Hippel formalism, for which cooperativity (α) and enthalpy of cooperativity (Δh) are not applicable (n.a.). The binding of FGF1 to heparin 8-mer and 16-mer were analyzed with the cooperative model.
By performing reverse titrations, where the titrant and titrand orientations are reversed, the stoichiometry and the suitability of the binding model can be checked. For monovalent biomolecular reactions it is expected that the measured thermodynamic parameters are invariant when changing the orientation of the experiment. However, this is often not the case as one species may display greater aggregation when concentrated. If the stoichiometry is not 1:1 and the binding sites are not equivalent or demonstrate cooperativity, comparison of both experiments reveals substantial differences in the titration profile.
Analysis of the reverse titration of heparin hexasaccharide to FGF1 (Fig. 2 b) reveals FGF1 binds with an affinity of 1.1 μM to a minimal footprint of 5.0 saccharide units. The value is greater than observed for the forward titration (4.7) with variations in this parameter reflecting the fact that l is a composite of not only the real stoichiometry, but also differences in the active concentration of FGF1 from the measured total concentration. These discrepancies may be accentuated as concentration and heterogeneity effects due to heparin also contribute to the value of l as N was fixed during the fitting procedure.
FGF-heparin thermodynamics
ITC accurately determines the thermodynamic contributions of enthalpy (ΔH) and entropy (−TΔS) changes to free energies of binding (ΔG). Physical phenomena that contribute to the enthalpy term include van der Waals, hydrogen bonding, and electrostatic complementarity. Changes in conformational and configuration space (roto-translational entropy) and solvation upon complex formation contribute to the entropy term (34). Interpretation of thermodynamics alongside published crystal structures allows insight into the processes of complex formation. The thermodynamic profiles for both the normal and reverse titration of heparin hexasaccharide with FGF1 are shown in Fig. 2 c.
The binding of FGF1 to heparin hexasaccharide is driven by both enthalpy (ΔH = −5.0 kcal mol−1) and entropy (−TΔS = −2.8 kcal mol−1). A similar favorable entropic contribution of −22 kcal mol−1 was estimated from the NMR order parameters of the FGF1-hexasaccharide interaction (35). The enthalpy term reflects the strong, ionic interactions that form between the side chains of basic residues in the three surface loops of the heparin binding site and the sulfate and carboxylate groups of heparin. As well as ionic interactions, the FGF1-heparin interaction is also stabilized by hydrogen bonds and van der Waals interactions.
Divalent FGF-heparin interactions
To investigate the reported formation of a heterotrimer of two FGF1 molecules on a single heparin fragment when oligosaccharides greater than six moieties in length are available (22), homogeneously purified FGF1 was titrated to a solution of octasaccharide. The titration profile is biphasic (Fig. 3 a). The apparent maximal number of ligand molecules bound per macromolecule can be inferred from the localization of the inflection point of the titration plot. The inflection point of the octasaccharide to FGF1 titration is ∼2.0, suggesting that heparin octasaccharide is capable of binding two FGF1 molecules concomitantly. Therefore, the data were analyzed according to the McGhee-von Hippel model for cooperative data, with N fixed at 8.0, reflecting the eight saccharide moieties present in the heparin octasaccharide.
Figure 3.
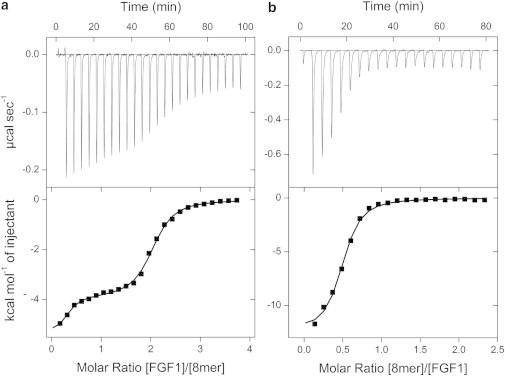
Analysis of FGF1-heparin octasaccharide interaction by direct (a) and reverse (b) titrations. In the direct titration, 100 μM FGF1 was titrated into 7 μM octasaccharide and in the reverse titration, 100 μM octasaccharide was titrated into 12.5 μM FGF1. (Upper panel) Calorimetric titration trace with the integrated isotherms (shown in lower panel). (Solid lines) Best fit to the cooperative McGhee-von Hippel model.
The minimal footprint required to support FGF1 binding, determined from the titration of FGF1 to heparin hexasaccharide, is approximately five saccharide moieties. However, previous studies have suggested that four saccharide units are the minimal footprint. In either case, a heparin octasaccharide is theoretically incapable of binding more than two FGF1 molecules concomitantly. The McGhee-von Hippel model for cooperative binding assumes that a ligand is capable of binding to a lattice in three modes: isolated (iso), singly contiguous (sc), and doubly contiguous (dc). However, in the binding of FGF1 to octasaccharide, it is not possible to have doubly contiguous FGF1, as it would require three FGF1 molecules bound to a single octasaccharide. Therefore, only isolated and singly contiguous binding modes (Eqs. 4 and 5) were used to evaluate the normalized heat effect upon binding.
The McGhee-von Hippel model was proposed for a linear array of binding sites, in which neighboring molecules sit adjacent to one another. However, heparin is a helical molecule that presents linear arrays of binding sites on opposing sides of the molecule (36). Therefore, assuming FGF1 binds heparin in the trans configuration observed in the crystal structures (22), the Δh term is not the enthalpy associated with the direct interaction between neighboring bound ligands, but rather the enthalpy change associated with interactions mediated through heparin.
After fitting, the affinity of the interaction was determined to be 1.1 μM, which is slightly higher than the affinity of FGF1 for heparin hexasaccharide (1.9 μM). This may be due to the presence of additional saccharide moieties that form supplementary interactions to those observed in the FGF1-6-mer interaction. The enthalpy of binding is slightly greater, again reflecting the presence of additional contacts (−5.7 kcal mol−1, compared with −5.0 kcal mol−1). There is a compensatory decrease in the entropic term (−2.4 compared to −2.8 kcal mol−1), however, it is still favorable, suggesting that interface desolvation is still a considerable factor despite the formation of a higher molecular weight species (2:1) that might be expected to have a negative effect on the entropic contribution.
The McGhee-von Hippel model allows cooperative parameters to be measured. The binding of FGF1 to heparin octasaccharide displays positive cooperativity (α = 7.0). Interestingly, the positive cooperativity is not driven by enthalpy but rather by entropy with Δh determined as ∼3 kcal mol−1. Entropy-driven positive cooperativity is consistent with binding of one FGF1 molecule restricting the number of conformations heparin can adopt, favoring a conformation suitable for FGF binding. The affinity of the second FGF1 molecule is given by αKD = 157 nM (ΔG = −9.3 kcal mol−1). Thus, formation of a heparin-linked FGF1 dimer is strongly favored over the formation of 1:1 complexes.
To characterize further the interaction, the experiment was performed in reverse, in which FGF1 was titrated to heparin octasaccharide (Fig. 3 b). The concentrations of FGF1 and heparin were consistent with those used for the reverse titration of hexasaccharide to FGF1. Therefore, direct comparison of Figs. 2 b and 3 b clearly demonstrates that saturation is achieved much earlier due to the ability of octasaccharide to dimerize FGF1 (the inflection point is ∼0.5, consistent with a 2:1 stoichiometry).
After fitting, the binding affinity was determined to be 3.0 μM, which is lower than observed in the direct titration. Alongside the lower intrinsic affinity, the cooperativity parameter (α) was determined as 4.5. Therefore, the affinity of the second FGF1 molecule is 667 nM (ΔG = −8.4 kcal mol−1). The cooperative interaction has a Δh of 2.6 kcal mol−1, which is again lower than that obtained from the direct titration.
Having determined that the binding of FGF1 to heparin hexa- and octasaccharide is 1:1 and 2:1, respectively, the data were reanalyzed using one-site and two-site binding models to see whether the data could be equally well explained with simpler models. The results of the data fitting are shown in Fig. S1 and Table S1 in the Supporting Material. While the 1:1 interaction can be modeled using a simplistic model, the biphasic FGF1-8-mer data cannot. This demonstrates there is a need to fit this with a model that takes into consideration cooperativity and overlapping binding sites, for which the McGhee-von Hippel model is the most appropriate.
Oligomeric FGF-heparin interactions
The binding of FGF1 to heparin octasaccharide was modeled according to the McGhee-von Hippel model with the restriction that a maximum of two FGF1 molecules can bind the heparin fragment simultaneously. This model was validated by calculation of the maximal number of ligand molecules bound per macromolecule as N/l = 8/3.74 = 2.13. In the restricted model, FGF1 molecules were only permitted to exist in either isolated or singly contiguous bound states. To investigate the influence of the ability of FGF1 to bind in a doubly contiguous state, the binding of FGF1 to heparin 16-mer was investigated. Based on the assumption that l is ∼4, a 16-mer is theoretically capable of binding four FGF1 molecules.
FGF1 was titrated to heparin 16-mer in the calorimetric cell. To permit saturation while avoiding significant dilution effects due to high concentrations, 100 μM FGF1 was titrated into just 2.5 μM heparin. Despite the low concentration of macromolecule, the heat event was still sufficiently exothermic to permit a good signal/noise ratio. The isotherm displayed complex multiphasic behavior, therefore to allow full characterization of the isotherm, the number of injections was increased to 40, with a compensatory decrease in injection volume to 6 μL. The resulting isotherm is shown in Fig. 4.
Figure 4.
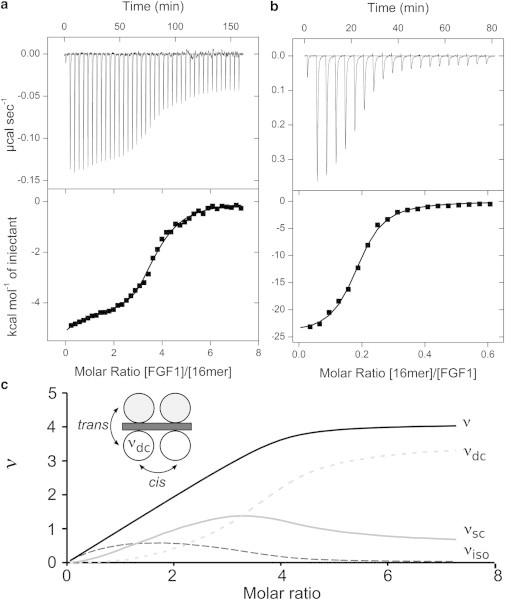
ITC analysis of FGF1-heparin 16-mer by direct (a) and reverse (b) titrations. A trace of calorimetric titration (upper panel) and integrated isotherms (lower panel). Solid lines represent the best fit to the cooperative McGhee-von Hippel model. (c) The evolution of the number of ligand molecules bound, ν, are shown as the summation of those bound in an isolated state (νiso); those bound in a singly contiguous state (νsc) and those in a doubly-contiguous state (νdc) are plotted as a function of the molar ratio for the direct titration of FGF1 to heparin 16-mer. (Inset) A theoretical model of four FGF molecules bound to heparin 16-mer showing two linear arrays in which doubly-contiguous molecules are in cis and trans conformations.
The intrinsic affinity of FGF1 for heparin was determined as 1.2 μM, in agreement with previously determined values. The minimal length of heparin saccharide units capable of supporting FGF1 binding (l) is 3.8, validating the assumption that approximately four FGF1 molecules can bind heparin 16-mer simultaneously. Therefore, FGF1 molecules can bind in all three possible states.
The progression of saturation is shown in Fig. 4 c. Initially isolated bound FGF1 species dominate, due to the large excess of macromolecule to FGF1. However, as the titration proceeds, the presence of positive cooperativity ensures that the population of singly and doubly contiguous species increase rapidly. At the titration midpoint, virtually no 1:1 complexes persist, with the population of doubly contiguous bound species dominating. At saturation, the majority of species are doubly contiguous (>80%). These doubly contiguous species can be in both cis and trans orientations.
The interaction is again characterized by nonenthalpy-driven positive cooperativity. The best fit to the data was obtained with a cooperativity parameter of 6.1 (a value of 7.0 was obtained for the FGF1–8-mer direct titration) and a Δh of 1.80 kcal mol−1. The enthalpy due to cooperativity is less positive than that observed in the 8-mer-FGF1 titration. This may result from FGF1 being able to bind in both trans and cis orientations on the longer chain of heparin—modes of binding that may have different thermodynamics. In the ITC experiment it is only possible to determine the macroscopic cooperativity enthalpy, i.e., the overall enthalpy; it is not possible to separate the individual binding events.
The reverse titration is shown in Fig. 4 b. The intrinsic affinities and thermodynamics are similar to that observed in the direct titration. Similarly, the cooperativity parameters (α = 5.2 and Δh = 1.7 kcal mol−1) are in very close agreement with those obtained in the direct titration (6.1 and 1.8 kcal mol−1, respectively).
Thermodynamic assembly of FGF1:FGFR2c: heparin ternary complex
FGF1 titrated into FGFR2c ectodomain (Fig. 5 a) produces a hyperbolic rather than sigmoidal curve, which does not allow precise determination of stoichiometry. For curve fitting, n was fixed at 1.0, reflecting the 1:1 stoichiometry observed in the crystal structure (37) with the resulting values given in Table 2. The interaction has a KD of 4.3 μM, which is weaker than previously reported (0.5 μM (38)), and is enthalpy-driven (ΔH = −14.7 kcal mol−1), as ∼2400 Å2 of accessible surface is buried upon formation of the binary complex (37).
Figure 5.
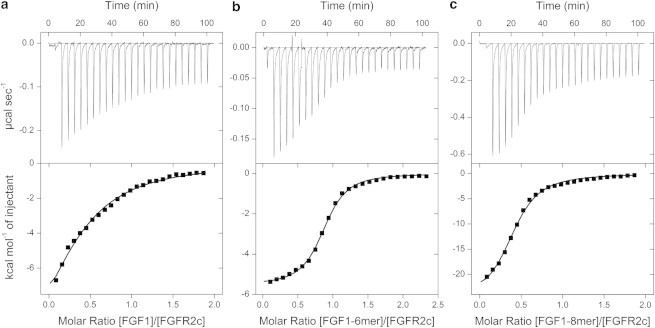
ITC analysis of FGF1 binding to FGFR2c in the absence (a) and presence of heparin hexa- (b) and octasaccharide (c). To determine the interaction between FGF1 and FGFR2c, 100 μM FGF1 was titrated into 10 μM FGFR2c. For panel b, 125 μM complex of FGF1–6-mer preincubated in a 1:1 ratio was titrated into 10 μM FGFR2c and for panel c, 100 μM FGF1–8-mer complex was titrated into 10 μM receptor. Trace of calorimetric titration (upper panel) and integrated isotherms (lower panel). (Solid lines) Best fit to a one-site model. For analysis of the FGF1-FGFR2c titration, n was fixed as 1.0.
Table 2.
ITC-derived thermodynamic parameters for the binding of FGF1 to FGFR2c in the absence and presence of heparin hexa- and octasaccharide
| Titration | KDa (nM) | ΔG (kcal mol−1) | ΔHb (kcal mol−1) | −TΔS (kcal mol−1) | nc |
|---|---|---|---|---|---|
| FGF1-FGFR2c | 4310 | −7.2 | −6.9 | −0.3 | 1.0 |
| [FGF1:6-mer]-FGFR2c | 325 | −9.9 | −5.6 | −3.3 | 0.9 |
| [FGF1:8-mer]-FGFR2c | 826 | −8.0 | −26.2 | 18.2 | 2.4 |
Errors in KD are <14.0%.
Errors in ΔH are <4.5%.
Errors in experimentally derived values of n are <3.5%.
FGF1 was then preincubated with hexasaccharide in a 1:1 stoichiometry. The titration of this complex into FGFR2c ectodomain (Fig. 5 b, Table 2) shows a binding stoichiometry of 1:1 (n = 0.9). The measured affinity is 325 nM, which is an order of magnitude greater than for the formation of the binary complex in the absence of heparin. The interaction has both favorable enthalpy and entropy terms (ΔH = −5.6 kcal mol−1, −TΔS = −3.3 kcal mol−1). The favorable entropy term is presumably a result of expulsion of structured waters to bulk. In comparison, the binary interaction shows a greater enthalpic contribution, while being less reliant on the entropic term. The simple heat evolution does not provide evidence for a secondary heat event caused by the dimerization of the two 1:1:1 complexes, as might be expected from the model proposed by Schlessinger et al. (23), but does not explicitly rule out the possible formation of a 2:2:2 complex.
The titration of FGF1 dimerized on heparin octasaccharide to FGFR2c (Fig. 5 c, Table 2) shows a binding stoichiometry of 1:2. This concurs with the 2:2:1 model (24), where the central FGF1-dimer dimerizes FGFR2c. The interaction between FGF1-8-mer and FGFR2c displays a high enthalpic term (ΔH = −26.2 kcal mol−1), but with a large positive entropic contribution (−TΔS = 18.2 kcal mol−1). It should be noted that within the calorimetric cell, several additional association and dissociation events might be occurring simultaneously alongside the FGF-heparin to FGFR association (FGF-heparin dissociation and association; FGF binding to FGFR and FGFR-heparin association).
To confirm the stoichiometry of the complexes formed during the titration experiments, the products were analyzed by SEC (Fig. 6). We have previously shown that analysis by SEC is sufficient to determine FGF-FGFR-heparin stoichiometries consistent with those from nondissociative mass spectrometry and analytical ultracentrifugation (26). Molecular weights of the complexes were estimated from the peak elution volumes after column calibration. The resulting product of the titration of preformed FGF1-6-mer complex to a suspension of FGFR2c shows two peaks corresponding to a 1:1:1 FGF1:FGFR2c:6-mer heparin complex and, as the titrant is added to excess, the 1:1 complex of FGF1-6-mer. The resulting product of the titration of preformed 2:1 FGF1-8-mer heparin complex with FGFR2c is consistent with a 2:2:1 complex and excess titrant. No higher order species were observed.
Figure 6.
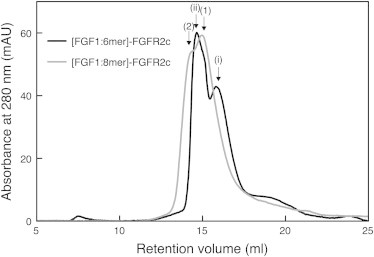
The products of the ITC experiments were applied to a Superdex 200 10/300 column equilibrated with 20 mM Tris pH 8.0, 150 mM NaCl. Absorbance of the eluate was monitored at 280 nm. Peak labeling: (i) 1:1 FGF1:heparin hexasaccharide; (ii) 1:1:1 FGF1:FGFR2c:heparin hexasaccharide; 1), 2:1 FGF1:heparin octasaccharide; and 2), 2:2:1 FGF1:FGFR2c:heparin octasaccharide.
Discussion
FGF signaling requires the formation of a ternary complex consisting of FGF, FGFR, and HS. However, the stoichiometry and architecture of this complex in solution remains unclear, with crystal structures suggesting alternative modes of interaction are possible. The role of HS cannot be defined with biophysical and structural studies utilizing mostly small heparin fragments of unphysiological length. Longer HS chains, such as those that occur in vivo, are capable of oligomerizing FGFs with a 16-kDa chain capable of binding 11–15 molecules of FGF1 (38,39). Several studies have also attempted to establish the minimal length of HS/heparin required for FGF binding and oligomerization. While a tetrasaccharide is capable of binding FGF1, saccharides shorter than an octasaccharide cannot facilitate dimerization and support a strong mitogenic signal (22,25,40–42). However, different FGFs may have different length requirements.
Previous attempts to determine the binding of FGFs to heparan sulfate analogs by ITC have typically not taken into consideration the repetitive nature of heparin (38,43,44). Guzmán-Casado et al. (45) have previously suggested that FGF1 interacts with heparin noncooperatively. This study used a heterogeneous commercial preparation of heparin with an average molecular mass of 3000 g mol−1, which was suggested as comprising heparin molecules between 8 and 10 saccharide units in length. In their analysis using a binding polynomial equation it was assumed that these molecules would present two FGF-binding sites that are identical and independent. However, such a model does not take into consideration overlapping binding sites and assumes the length of the binding footprint. The FGF1-octasaccahride crystal structure clearly shows two FGF1 protomers making different contacts with heparin, therefore the FGF1 binding sites cannot be considered identical.
Here, we have used McGhee-von Hippel formalism to dissect the thermodynamic profile and stoichiometry of FGF1 binding to heparin fragments of defined length. FGF1 has a binding footprint of 4.2 saccharide units (the mean of all values of l determined from both forward and reverse titrations of FGF1 with different heparin fragments). Consistent with this, the data suggest that a heparin octasaccharide is the shortest fragment capable of forming a 2:1 heterotrimer, whereas hexasaccharide is only able to bind in a 1:1 stoichiometry. The average intrinsic affinity of FGF1 for heparin was determined as 1.6 μM, which is lower than previously reported by Spivak-Kroizman et al. (38), as prior measurements have not taken into consideration the statistical effect of increasing the number of overlapping binding sites available. However, the intrinsic affinity of FGF1 for heparin is greater than that of Heparin Cofactor II, a coagulation factor, that binds with an affinity of 640 mM as determined by applying the McGhee-von Hippel model to fluorescence data (46).
The data presented here demonstrate that FGF1 binding to heparin is facilitated by positive cooperativity. This agrees with the observation that FGF1 preferentially forms oligomers rather than 1:1 complexes in the presence of long-chain heparins (25). Previous studies have also shown that the binding of FGF2 to heparin octasaccharide is cooperative (27,42), suggesting cooperative binding to heparin is not limited to FGF1. Saxena et al. (27) used NMR 1H T2 measurements to record binding curves for the stepwise titration of heparin octasaccharide to FGF2. Using a two-step model, they determined that the first molecule of FGF2 bound with an affinity of 100 nM and the second with an affinity of 5.8 nM. However, this, and their corresponding ITC data, did not take into consideration the fact that heparin acts as a monodimensional lattice in which the binding sites are not necessarily distinct. Upon taking this into consideration, we show that the second FGF1 molecule binds with an approximate sixfold higher affinity than the first. Similar positive cooperativity determined by application of the McGhee-von Hippel model to ITC data has been observed for the binding of proteins to chitosan, another monodimensional lattice (33). This suggests the possibility of a consistent mechanism whereby carbohydrate chains promote oligomerization through positively cooperative mechanisms.
The FGF-heparin positive cooperativity is mediated through more favorable entropy. Mechanisms of cooperativity generally involve electrostatic coupling, lowering of the entropic penalty, and/or conformational changes. Given that there is no significant conformational change in FGF1 tertiary structure upon binding heparin (19), any positive cooperativity due to conformational changes must be mediated through the heparin molecule. In solution, heparin forms a relatively rigid helical conformation with dyad symmetry (36). Detailed conformational analysis of all FGF-heparin cocrystals revealed that FGF induces a localized kink in heparin (21). This change in backbone torsion angles occurs at the trisaccharide level and is enhanced by the ability of the iduronic acid to adopt multiple ring formations, with the kink augmented by the 1C4 conformation. In FGF1-heparin structures the kink is closer to the reducing end and spans three monosaccharide units where the iduronate is flanked by two glucosamines. The kink permits optimal ionic and van der Waals contact with the FGF, while maintaining the overall 21 helical symmetry.
The cooperative trans-dimerization of FGF1 on HS octasaccharides and oligomerization on large HS chains is probably key to subsequent receptor dimerization and potentiation of receptor signaling. However, this assumption is only true if FGF1 binds heparin before interacting with FGFR. Previously reported Kon rates from surface plasmon resonance favors the formation of an initial FGF-heparin complex (47). For FGF2, the Kon rate for heparin was 1.1 × 107 M−1 s−1, compared to 9.6 × 104 M−1 s−1 for the interaction with the receptor (FGFR1) in the absence of heparin. This suggests that, after secretion, FGF is concentrated upon cell surface HS. This concentration effect is physiologically important, as exceptionally low concentrations of FGF are capable of signaling (48).
What effect does trans-dimerization have on FGFR recruitment? In comparison with the formation of the binary complex (4.3 μM), the octasaccharide-dimerized FGF1 binds FGFR2c with a higher affinity (826 nM) and permits FGFR dimerization as shown both in the midpoint of the titration curve and also by SEC. The architecture presumably adopts that of the 2:2:1 complex with a central heparin-mediated FGF1 dimer sequestering two FGFR2c molecules. Dimerization of the binary complex cannot occur in the absence of heparin (28,38), and in solution, we do not observe formation of a 2:2:2 complex even with heparin hexasaccharide present. Each FGF1:6-mer complex only recruits a single FGFR to form a 1:1:1 complex. The absence of evidence of a 1:1:1 dimerization mediated by FGF and FGFR interactions suggests that FGF1, when already assembled on heparin hexasaccharide, cannot stimulate FGFR dimerization, as might be expected from the 2:2:2 complex. However, it is possible that formation of this complex may occur by a separate pathway in which FGF1 is not already bound to heparin, or may only form on HS that features sulfation patterns at the nonreducing ends that do not permit FGF1 dimerization.
In conclusion, the observations described here favor a preassembly model in solution where FGF1 is first bound to heparin in a trans-dimeric manner before the recruitment of two FGF receptors and the activation of the signaling response. The absence of evidence of a 2:2:2 dimerization mediated by FGFR and FGF interactions in solution does not preclude its existence at the membrane, as it can coexist with the 2:2:1 complex assembled on heparin. In this case, a two-dimensional cluster of FGFR, FGF, and heparin will assemble, which may mediate the activation of signaling pathways and/or receptor-mediated endocytosis.
Acknowledgments
T.L.B. thanks the Wellcome Trust for support through Program grant No. RG44650 (The Structural Biology of Cell Signaling and Regulation: Multiprotein Systems and the Achievement of High Signal-To-Noise Ratios). A.B. thanks the Biotechnology and Biological Sciences Research Council (UK) for a PhD studentship.
Footnotes
This is an Open Access article distributed under the terms of the Creative Commons-Attribution Noncommercial License (http://creativecommons.org/licenses/by-nc/2.0/), which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Supporting Material
References
- 1.Ornitz D.M. FGFs, heparan sulfate and FGFRs: complex interactions essential for development. Bioessays. 2000;22:108–112. doi: 10.1002/(SICI)1521-1878(200002)22:2<108::AID-BIES2>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
- 2.Presta M., Dell’Era P., Rusnati M. Fibroblast growth factor/fibroblast growth factor receptor system in angiogenesis. Cytokine Growth Factor Rev. 2005;16:159–178. doi: 10.1016/j.cytogfr.2005.01.004. [DOI] [PubMed] [Google Scholar]
- 3.Powers C.J., McLeskey S.W., Wellstein A. Fibroblast growth factors, their receptors and signaling. Endocr. Relat. Cancer. 2000;7:165–197. doi: 10.1677/erc.0.0070165. [DOI] [PubMed] [Google Scholar]
- 4.Johnson D.E., Williams L.T. Structural and functional diversity in the FGF receptor multigene family. Adv. Cancer Res. 1993;60:1–41. doi: 10.1016/s0065-230x(08)60821-0. [DOI] [PubMed] [Google Scholar]
- 5.Werner S., Duan D.S., Williams L.T. Differential splicing in the extracellular region of fibroblast growth factor receptor 1 generates receptor variants with different ligand-binding specificities. Mol. Cell. Biol. 1992;12:82–88. doi: 10.1128/mcb.12.1.82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ornitz D.M., Xu J., Goldfarb M. Receptor specificity of the fibroblast growth factor family. J. Biol. Chem. 1996;271:15292–15297. doi: 10.1074/jbc.271.25.15292. [DOI] [PubMed] [Google Scholar]
- 7.Beenken A., Eliseenkova A.V., Mohammadi M. Plasticity in the interactions of the N-terminus of fibroblast growth factor (FGF)-1 with FGF receptors underlies FGF1's promiscuity. J. Biol. Chem. 2011;287:3067–3078. doi: 10.1074/jbc.M111.275891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Burgess W.H., Maciag T. The heparin-binding (fibroblast) growth factor family of proteins. Annu. Rev. Biochem. 1989;58:575–606. doi: 10.1146/annurev.bi.58.070189.003043. [DOI] [PubMed] [Google Scholar]
- 9.Sugahara K., Kitagawa H. Heparin and heparan sulfate biosynthesis. IUBMB Life. 2002;54:163–175. doi: 10.1080/15216540214928. [DOI] [PubMed] [Google Scholar]
- 10.Hook M., Kjellén L., Johansson S. Cell-surface glycosaminoglycans. Annu. Rev. Biochem. 1984;53:847–869. doi: 10.1146/annurev.bi.53.070184.004215. [DOI] [PubMed] [Google Scholar]
- 11.Yanagishita M., Hascall V.C. Cell surface heparan sulfate proteoglycans. J. Biol. Chem. 1992;267:9451–9454. [PubMed] [Google Scholar]
- 12.Gallagher J.T., Turnbull J.E., Lyon M. Patterns of sulphation in heparan sulphate: polymorphism based on a common structural theme. Int. J. Biochem. 1992;24:553–560. doi: 10.1016/0020-711x(92)90326-v. [DOI] [PubMed] [Google Scholar]
- 13.Merry C.L.R., Lyon M., Gallagher J.T. Highly sensitive sequencing of the sulfated domains of heparan sulfate. J. Biol. Chem. 1999;274:18455–18462. doi: 10.1074/jbc.274.26.18455. [DOI] [PubMed] [Google Scholar]
- 14.Rapraeger A.C., Krufka A., Olwin B.B. Requirement of heparan sulfate for bFGF-mediated fibroblast growth and myoblast differentiation. Science. 1991;252:1705–1708. doi: 10.1126/science.1646484. [DOI] [PubMed] [Google Scholar]
- 15.Gospodarowicz D., Cheng J. Heparin protects basic and acidic FGF from inactivation. J. Cell. Physiol. 1986;128:475–484. doi: 10.1002/jcp.1041280317. [DOI] [PubMed] [Google Scholar]
- 16.Sommer A., Rifkin D.B. Interaction of heparin with human basic fibroblast growth factor: protection of the angiogenic protein from proteolytic degradation by a glycosaminoglycan. J. Cell. Physiol. 1989;138:215–220. doi: 10.1002/jcp.1041380129. [DOI] [PubMed] [Google Scholar]
- 17.Ostrovsky O., Berman B., Ron D. Differential effects of heparin saccharides on the formation of specific fibroblast growth factor (FGF) and FGF receptor complexes. J. Biol. Chem. 2002;277:2444–2453. doi: 10.1074/jbc.M108540200. [DOI] [PubMed] [Google Scholar]
- 18.Zhu X., Komiya H., Rees D.C. Three-dimensional structures of acidic and basic fibroblast growth factors. Science. 1991;251:90–93. doi: 10.1126/science.1702556. [DOI] [PubMed] [Google Scholar]
- 19.Faham S., Hileman R.E., Rees D.C. Heparin structure and interactions with basic fibroblast growth factor. Science. 1996;271:1116–1120. doi: 10.1126/science.271.5252.1116. [DOI] [PubMed] [Google Scholar]
- 20.Canales A., Lozano R., Jiménez-Barbero J. Solution NMR structure of a human FGF-1 monomer, activated by a hexasaccharide heparin-analogue. FEBS J. 2006;273:4716–4727. doi: 10.1111/j.1742-4658.2006.05474.x. [DOI] [PubMed] [Google Scholar]
- 21.Raman R., Venkataraman G., Sasisekharan R. Structural specificity of heparin binding in the fibroblast growth factor family of proteins. Proc. Natl. Acad. Sci. USA. 2003;100:2357–2362. doi: 10.1073/pnas.0437842100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.DiGabriele A.D., Lax I., Hendrickson W.A. Structure of a heparin-linked biologically active dimer of fibroblast growth factor. Nature. 1998;393:812–817. doi: 10.1038/31741. [DOI] [PubMed] [Google Scholar]
- 23.Schlessinger J., Plotnikov A.N., Mohammadi M. Crystal structure of a ternary FGF-FGFR-heparin complex reveals a dual role for heparin in FGFR binding and dimerization. Mol. Cell. 2000;6:743–750. doi: 10.1016/s1097-2765(00)00073-3. [DOI] [PubMed] [Google Scholar]
- 24.Pellegrini L., Burke D.F., Blundell T.L. Crystal structure of fibroblast growth factor receptor ectodomain bound to ligand and heparin. Nature. 2000;407:1029–1034. doi: 10.1038/35039551. [DOI] [PubMed] [Google Scholar]
- 25.Robinson C.J., Harmer N.J., Gallagher J.T. Cooperative dimerization of fibroblast growth factor 1 (FGF1) upon a single heparin saccharide may drive the formation of 2:2:1 FGF1.FGFR2c.heparin ternary complexes. J. Biol. Chem. 2005;280:42274–42282. doi: 10.1074/jbc.M505720200. [DOI] [PubMed] [Google Scholar]
- 26.Harmer N.J., Robinson C.J., Blundell T.L. Multimers of the fibroblast growth factor (FGF)-FGF receptor-saccharide complex are formed on long oligomers of heparin. Biochem. J. 2006;393:741–748. doi: 10.1042/BJ20050985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Saxena K., Schieborr U., Schwalbe H. Influence of heparin mimetics on assembly of the FGF·FGFR4 signaling complex. J. Biol. Chem. 2010;285:26628–26640. doi: 10.1074/jbc.M109.095109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Harmer N.J., Ilag L.L., Blundell T.L. Towards a resolution of the stoichiometry of the fibroblast growth factor (FGF)-FGF receptor-heparin complex. J. Mol. Biol. 2004;339:821–834. doi: 10.1016/j.jmb.2004.04.031. [DOI] [PubMed] [Google Scholar]
- 29.McGhee J.D., von Hippel P.H. Theoretical aspects of DNA-protein interactions: co-operative and non-co-operative binding of large ligands to a one-dimensional homogeneous lattice. J. Mol. Biol. 1974;86:469–489. doi: 10.1016/0022-2836(74)90031-x. [DOI] [PubMed] [Google Scholar]
- 30.Velázquez-Campoy A. Ligand binding to one-dimensional lattice-like macromolecules: analysis of the McGhee-von Hippel theory implemented in isothermal titration calorimetry. Anal. Biochem. 2006;348:94–104. doi: 10.1016/j.ab.2005.10.013. [DOI] [PubMed] [Google Scholar]
- 31.Brown A. Analysis of cooperativity by isothermal titration calorimetry. Int. J. Mol. Sci. 2009;10:3457–3477. doi: 10.3390/ijms10083457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wiseman T., Williston S., Lin L.N. Rapid measurement of binding constants and heats of binding using a new titration calorimeter. Anal. Biochem. 1989;179:131–137. doi: 10.1016/0003-2697(89)90213-3. [DOI] [PubMed] [Google Scholar]
- 33.Kasimova M.R., Velázquez-Campoy A., Nielsen H.M. On the temperature dependence of complex formation between chitosan and proteins. Biomacromolecules. 2011;12:2534–2543. doi: 10.1021/bm200344d. [DOI] [PubMed] [Google Scholar]
- 34.Gohlke H., Klebe G. Approaches to the description and prediction of the binding affinity of small-molecule ligands to macromolecular receptors. Angew. Chem. Int. Ed. Engl. 2002;41:2644–2676. doi: 10.1002/1521-3773(20020802)41:15<2644::AID-ANIE2644>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
- 35.Canales-Mayordomo A., Fayos R., Jiménez-Barbero J. Backbone dynamics of a biologically active human FGF-1 monomer, complexed to a hexasaccharide heparin-analogue, by 15N NMR relaxation methods. J. Biomol. NMR. 2006;35:225–239. doi: 10.1007/s10858-006-9024-y. [DOI] [PubMed] [Google Scholar]
- 36.Mulloy B., Forster M.J., Davies D.B. N.M.R. and molecular-modeling studies of the solution conformation of heparin. Biochem. J. 1993;293:849–858. doi: 10.1042/bj2930849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Stauber D.J., DiGabriele A.D., Hendrickson W.A. Structural interactions of fibroblast growth factor receptor with its ligands. Proc. Natl. Acad. Sci. USA. 2000;97:49–54. doi: 10.1073/pnas.97.1.49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Spivak-Kroizman T., Lemmon M.A., Lax I. Heparin-induced oligomerization of FGF molecules is responsible for FGF receptor dimerization, activation, and cell proliferation. Cell. 1994;79:1015–1024. doi: 10.1016/0092-8674(94)90032-9. [DOI] [PubMed] [Google Scholar]
- 39.Mach H., Volkin D.B., Mattsson L. Nature of the interaction of heparin with acidic fibroblast growth factor. Biochemistry. 1993;32:5480–5489. doi: 10.1021/bi00071a026. [DOI] [PubMed] [Google Scholar]
- 40.Ornitz D.M., Yayon A., Leder P. Heparin is required for cell-free binding of basic fibroblast growth factor to a soluble receptor and for mitogenesis in whole cells. Mol. Cell. Biol. 1992;12:240–247. doi: 10.1128/mcb.12.1.240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Fromm J.R., Hileman R.E., Linhardt R.J. Interaction of fibroblast growth factor-1 and related peptides with heparan sulfate and its oligosaccharides. Arch. Biochem. Biophys. 1997;346:252–262. doi: 10.1006/abbi.1997.0299. [DOI] [PubMed] [Google Scholar]
- 42.Goodger S.J., Robinson C.J., Gallagher J.T. Evidence that heparin saccharides promote FGF2 mitogenesis through two distinct mechanisms. J. Biol. Chem. 2008;283:13001–13008. doi: 10.1074/jbc.M704531200. [DOI] [PubMed] [Google Scholar]
- 43.Thompson L.D., Pantoliano M.W., Springer B.A. Energetic characterization of the basic fibroblast growth factor-heparin interaction: identification of the heparin binding domain. Biochemistry. 1994;33:3831–3840. doi: 10.1021/bi00179a006. [DOI] [PubMed] [Google Scholar]
- 44.Guzmán-Casado M., Sánchez-Ruiz J.M., Parody-Morreale A. Energetics of myo-inositol hexasulfate binding to human acidic fibroblast growth factor effect of ionic strength and temperature. Eur. J. Biochem. 2000;267:3477–3486. doi: 10.1046/j.1432-1327.2000.01371.x. [DOI] [PubMed] [Google Scholar]
- 45.Guzmán-Casado M., García-Mira M.M., Parody-Morreale A. Energetics of heparin binding to human acidic fibroblast growth factor. Int. J. Biol. Macromol. 2002;31:45–54. doi: 10.1016/s0141-8130(02)00065-x. [DOI] [PubMed] [Google Scholar]
- 46.O’Keeffe D., Olson S.T., Huntington J.A. The heparin binding properties of heparin cofactor II suggest an antithrombin-like activation mechanism. J. Biol. Chem. 2004;279:50267–50273. doi: 10.1074/jbc.M408774200. [DOI] [PubMed] [Google Scholar]
- 47.Ibrahimi O.A., Zhang F., Linhardt R.J. Kinetic model for FGF, FGFR, and proteoglycan signal transduction complex assembly. Biochemistry. 2004;43:4724–4730. doi: 10.1021/bi0352320. [DOI] [PubMed] [Google Scholar]
- 48.Lander A.D. Proteoglycans: master regulators of molecular encounter? Matrix Biol. 1998;17:465–472. doi: 10.1016/s0945-053x(98)90093-2. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


